1 Introduction

The successful operation of the large hadron collider (LHC) has allowed one to accumulate a wealth of collision data in the search of new physics in the ATLAS and CMS experiments, at centre-of-mass (CM) energies of 7, 8 and 13 TeV. With the ever-increasing statistics, measurements beyond simple event counts are possible, which provide further insight into the standard model (SM) processes and possible new physics. Of particular interest are polarisation measurements, possible for particles with a short lifetime, through analyses of the angular distributions of their decay products.

For spin-1 / 2 fermions there are three independent spin observables, which can be conveniently taken as the expectation values of the spin operators in three orthogonal directions. At the LEP experiments, this program was exploited for \(\tau \) leptons [1] and, for general \(e^+ e^-\) colliders, proposed for heavy quarks [2,3,4,5]. But for spin-1 vector bosons the number of independent spin observables is eight, requiring a more elaborate discussion. There have been various studies of spin observables or decay angular distributions for vector bosons, often focusing on specific processes [6, 7]. In previous work [8] some of us have provided a full model-independent analysis of the W boson spin observables. For the Z boson the framework is quite similar, the main difference being that while for the W boson the couplings to leptons violate parity maximally, for the Z boson they do not. This difference can be taken into account by the introduction of an additional coupling factor relating the observed angular distributions to the Z boson spin observables, a factor which we may call the polarisation analyser. This study has been applied to an \(e^+e^-\) collider [9].

The purpose of this paper is to demonstrate that the information content in the eight multipole parameters of the Z boson, polarisations and alignments, is able to clearly discriminate among different production mechanisms, acting as messengers of the physics involved in the process. This is particularly important at the LHC, taking into account the hadronic environment. In Sect. 2 we write down the relation between Z boson spin observables and the parameters of the decay angular distributions. Beyond the application to Drell–Yan Z plus jets events at LHC, considered in Sect. 3, we move to the study of the production of a Z boson plus missing transverse energy (\(\text {MET}\)) in Sect. 4, where the discrimination between the SM production mechanism and that for extended models is apparent. In Sect. 5 we discuss in detail the predictions for the eight spin observables of Z (or W) bosons produced from the two-body decay of a heavy resonance of spin 0, 1 / 2 or 1. Our conclusions are presented in Sect. 6.

2 Formalism

The spin state of Z bosons is described, as for any other spin-1 massive particle, by a \(3 \times 3\) density matrix \(\rho \), Hermitian with unit trace and positive semidefinite. We follow closely the analysis and notation introduced [8] for the analysis of the W boson spin.Footnote 1 If we fix a coordinate system \((x',y',z')\) in the Z boson rest frame, we can write the spin density matrix as

$$\begin{aligned} \rho = \frac{1}{3} {\mathbbm {1}} + \frac{1}{2} \displaystyle \sum _{M=-1}^1 \langle S_M \rangle ^* S_M + \displaystyle \sum _{M=-2}^2 \langle T_{M} \rangle ^* T_{M} , \end{aligned}$$
(1)

with \(S_{\pm 1} = \mp \textstyle \frac{1}{\sqrt{2}}(S_1 \pm i S_2)\), \(S_0 = S_3\) the spin operators in the spherical basis and \(T_M\) five rank 2 irreducible tensors,

$$\begin{aligned}&T_{\pm 2} = S_{\pm 1}^2 , \nonumber \\&T_{\pm 1} = \frac{1}{\sqrt{2}} \left[ S_{\pm 1} S_0 + S_0 S_{\pm 1} \right] , \nonumber \\&T_{0} = \frac{1}{\sqrt{6}} \left[ S_{+1} S_{-1} + S_{-1} S_{+1} + 2 S_0^2 \right] . \end{aligned}$$
(2)

Their expectation values \(\langle S_M \rangle \) and \(\langle T_M \rangle \) are the multipole parameters corresponding to the three polarisation and five alignment components. The second term in Eq. (1) can be rewritten using the spin operators in the Cartesian basis, and the third one defining the Hermitian operators

$$\begin{aligned} A_1 = \frac{1}{2} (T_1-T_{-1}) , \quad A_2 = {\frac{1}{2 i}} (T_1 + T_{-1}) , \nonumber \\ B_1 = \frac{1}{2} (T_2+T_{-2}) , \quad B_2 = {\frac{1}{2 i}} (T_2 - T_{-2}) . \end{aligned}$$
(3)

Therefore, the Z boson density matrix elements, parameterised in terms of expectation values of observables, read

$$\begin{aligned} \begin{aligned}&\rho _{\pm 1 \pm 1} = \frac{1}{3} \pm \frac{1}{2} \langle S_3 \rangle + \frac{1}{\sqrt{6}} \langle T_0 \rangle , \\&\rho _{\pm 10} = \frac{1}{2\sqrt{2}} \left[ \langle S_1 \rangle \mp i \langle S_2 \rangle \right] \mp \frac{1}{\sqrt{2}} \left[ \langle A_1 \rangle \mp i \langle A_2 \rangle \right] , \\&\rho _{00} = \frac{1}{3} - \frac{2}{\sqrt{6}} \langle T_0 \rangle , \\&\rho _{1\, -1} = \langle B_1 \rangle - i \langle B_2 \rangle , \end{aligned} \end{aligned}$$
(4)

and \(\rho _{m'm}=\rho _{mm'}^*\). The angular distribution of the Z boson decay products in its rest frame is determined by \(\rho \). Let us restrict ourselves to leptonic decays \(Z \rightarrow \ell ^+ \ell ^-\), with \(\ell = e\) or \(\ell = \mu \). Using the helicity formalism of Jacob and Wick [10], the amplitude for the decay of a Z boson with third spin component m giving \(\ell ^-\) with helicity \(\lambda _1\) and \(\ell ^+\) with helicity \(\lambda _2\) is written as

$$\begin{aligned} \mathcal {M}_{m \lambda _1 \lambda _2} = b_{\lambda _1 \lambda _2} D_{m \lambda }^{1*} (\phi ^*,\theta ^*,0) , \end{aligned}$$
(5)

with \((\theta ^*,\phi ^*)\) the polar and azimuthal angles of the \(\ell ^-\) momentum in the Z boson rest frame, \(\lambda = \lambda _1 - \lambda _2\) and

$$\begin{aligned} D_{m'm}^j (\alpha ,\beta ,\gamma ) = e^{-i \alpha m'} e^{-i \gamma m} d_{m'm}^j (\beta ) \end{aligned}$$
(6)

the so-called Wigner D functions [11]; \(b_{\lambda _1 \lambda _2}\) are constants, and all the dependence of the amplitude on the angular variables of the final state products is given by the D functions. Here, at variance with W boson decays,Footnote 2 we have two possible helicity combinations \((\lambda _1,\lambda _2) = (\pm 1/2, \mp 1/2)\). The differential decay width reads

$$\begin{aligned}&\frac{\mathrm{d}\Gamma }{\mathrm{d}\cos \theta ^* \mathrm{d}\phi ^*} \nonumber \\&\quad = C \sum _{m, m' ,\lambda _1 \lambda _2}\rho _{mm'} | b_{\lambda _1 \lambda _2} |^2 e^{i (m-m')\phi ^*} \mathrm{d}_{m\lambda }^{1} (\theta ^*) \mathrm{d}_{m'\lambda }^{1}(\theta ^*),\quad \end{aligned}$$
(7)

with \(\lambda =\lambda _1-\lambda _2 = \pm 1\). The constants \(b_{1/2 \, -1/2}\) and \(b_{-1/2 \, 1/2}\) are, respectively, proportional to the right- and left-handed couplings of the Z boson to the charged leptons \(g_R^\ell \), \(g_L^\ell \),

$$\begin{aligned} b_{1/2 \, -1/2} \;:\; b_{-1/2 \, 1/2}= & {} g_R^\ell \;:\; g_L^\ell . \end{aligned}$$
(8)

The angular distribution of the Z boson decay products can easily be obtained from the distribution for \(W^\pm \) decays [8] by noting that the only terms that change sign when replacing \(\lambda \) by \(-\lambda \) are those proportional to \(\langle S_k \rangle \), \(k=1,2,3\). By introducing the polarisation analyser,

$$\begin{aligned} \eta _\ell = \frac{(g_L^\ell )^2 - (g_R^\ell )^2}{(g_L^\ell )^2 + (g_R^\ell )^2} = \frac{1-4 s_W^2}{1-4 s_W^2 + 8 s_W^4} , \end{aligned}$$
(9)

with \(s_W\) the sine of the weak mixing angle, we get

$$\begin{aligned} \frac{1}{\Gamma } \frac{\mathrm{d}\Gamma }{\mathrm{d}\cos \theta ^* \mathrm{d}\phi ^*}= & {} \frac{3}{8\pi } \nonumber \\&\times \left\{ \frac{1}{2} (1+\cos ^2 \theta ^*) -\eta _\ell \langle S_3 \rangle \cos \theta ^* \right. \nonumber \\&+ \left[ \frac{1}{6} - \frac{1}{\sqrt{6}} \langle T_0 \rangle \right] \left( 1-3\cos ^2 \theta ^* \right) \nonumber \\&-\eta _\ell \langle S_1 \rangle \cos \phi ^* \sin \theta ^* {-}\eta _\ell \langle S_2 \rangle \sin \phi ^* \sin \theta ^* \nonumber \\&- \langle A_1 \rangle \cos \phi ^* \sin 2\theta ^* {-} \langle A_2 \rangle \sin \phi ^* \sin 2\theta ^* \nonumber \\&+ \langle B_1 \rangle \cos 2 \phi ^* \sin ^2 \theta ^*\nonumber \\&\left. + \langle B_2 \rangle \sin 2 \phi ^* \sin ^2 \theta ^* \right\} . \end{aligned}$$
(10)

The angular asymmetries introduced in Ref. [8] for the measurement of W boson spin observables can be straightforwardly used for the Z boson as well, with the appropriate replacements. We have

$$\begin{aligned} A_\text {FB}^{x'}= & {} \frac{1}{\Gamma } \left[ \Gamma (\cos \phi ^*> 0) - \Gamma (\cos \phi ^*< 0) \right] = - \frac{3}{4} \eta _\ell \langle S_1 \rangle , \nonumber \\ A_\text {FB}^{y'}= & {} \frac{1}{\Gamma } \left[ \Gamma (\sin \phi ^*> 0) - \Gamma (\sin \phi ^*< 0) \right] = - \frac{3}{4} \eta _\ell \langle S_2 \rangle , \nonumber \\ A_\text {FB}^{z'}= & {} \frac{1}{\Gamma } \left[ \Gamma (\cos \theta ^*> 0) - \Gamma (\cos \theta ^*< 0) \right] = - \frac{3}{4}\eta _\ell \langle S_3 \rangle , \nonumber \\ A_\text {EC}^{z'}= & {} \frac{1}{\Gamma } \left[ \Gamma \left( |\cos \theta ^*|> \frac{1}{2} \right) - \Gamma \left( |\cos \theta ^*|< \frac{1}{2} \right) \right] \nonumber \\= & {} \frac{3}{8} \sqrt{\frac{3}{2}} \langle T_0 \rangle , \nonumber \\ A_\text {FB}^{x',z'}= & {} \frac{1}{\Gamma } \left[ \Gamma (\cos \phi ^* \cos \theta ^*> 0) - \Gamma (\cos \phi ^* \cos \theta ^*< 0) \right] \nonumber \\= & {} - \frac{2}{\pi } \langle A_1 \rangle , \nonumber \\ A_\text {FB}^{y',z'}= & {} \frac{1}{\Gamma } \left[ \Gamma (\sin \phi ^* \cos \theta ^*> 0) - \Gamma (\sin \phi ^* \cos \theta ^*< 0) \right] \nonumber \\= & {} - \frac{2}{\pi } \langle A_2 \rangle , \nonumber \\ A_\phi ^1= & {} \frac{1}{\Gamma } \left[ \Gamma (\cos 2 \phi ^*> 0 ) - \Gamma (\cos 2\phi ^*< 0) \right] = \frac{ 2}{\pi } \langle B_1 \rangle , \nonumber \\ A_\phi ^2= & {} \frac{1}{\Gamma } \left[ \Gamma (\sin 2 \phi ^* > 0) - \Gamma (\sin 2\phi ^* < 0) \right] = \frac{2}{\pi } \langle B_2 \rangle .\nonumber \\ \end{aligned}$$
(11)

As seen, these asymmetries separate out the eight multipole parameters one by one.

3 Drell–Yan production

The angular distribution (10) has been investigated by the CDF [12], CMS [13] and ATLAS [14] Collaborations in Drell–Yan Z production in hadron collisions, using the Collins–Soper coordinate system [15]. The doubly differential angular distribution is parameterised using unknown coefficients labelled \(A_{0}\)–\(A_{7}\). The density matrix analysis of the Z boson decay provides an interpretation of the measured coefficients in terms of Z boson spin observables,

$$\begin{aligned} A_0&= \frac{2}{3} - 2 \sqrt{\frac{2}{3}} \langle T_0 \rangle , \quad A_1 = -2 \langle A_1 \rangle , \nonumber \\ A_2&= 4 \langle B_1 \rangle , \quad A_3 = -2 \eta _\ell \langle S_1 \rangle , \\ A_4&= -2 \eta _\ell \langle S_3 \rangle , \quad A_5 = 2 \langle B_2 \rangle , \nonumber \\ A_6&= -2 \langle A_2 \rangle , \quad A_7 = -2 \eta _\ell \langle S_2 \rangle .\nonumber \end{aligned}$$
(12)

Experiments have measured these coefficients differentially, as a function of the transverse momentum and rapidity of the Z boson. An interpretation in terms of Z spin observables, apart from providing more insight into the nature of the physical observables measured, provides a rationale for the smallness of \(A_3\), \(A_4\) and \(A_7\), since they are proportional to the small polarisation analyser \(\eta _\ell \simeq 0.14\). The most recent measurement by the ATLAS Collaboration [14] exhibits a noticeable deviation in \(A_2\) with respect to next-to-leading order [16] and next-to-next-to-leading order [17] SM predictions. Nevertheless, the CMS Collaboration finds agreement with the multi-leg SM prediction from MadGraph5_aMC@NLO [18]. This coefficient corresponds to the rank-two alignment \(\langle B_1 \rangle \).

We also point out that – besides the method commonly used to extract the angular coefficients \(A_{0-7}\) based on integration with suitable weight functions [7] – the asymmetries in (11) provide an alternative way for their determination. Whether this simpler method also gives more precise results depends on the systematic uncertainties in each case, and a detailed analysis is compulsory to draw any conclusion.

4 Z boson plus \(\text {MET}\) production

The production at the LHC of final states containing a same-flavour opposite-sign lepton (electron or muon) pair with invariant mass around the Z boson mass, possibly jets, and large \(\text {MET}\) is very relevant in the search by ATLAS [19] and CMS [20] of Supersymmetry (SUSY) signals and collider production of Dark Matter [21]. Besides the simple event counting, the use of spin observables in these \(Z+\text {MET}\) searches provides an additional handle to test the SM predictions and uncover possible effects of new physics.

Fig. 1
figure 1

SM predictions for \(\langle S_3 \rangle \) and \(\langle T_0 \rangle \) for \(Z+\text {MET}\) final states, as a function of the lower cut on \(\text {MET}\). Above them, the same result from the BSM model described in the text

Full size image

Similarly to the previous section, the full angular distribution (10) can be measured differentially as a function of the \(\text {MET}\) in these final states. The leading SM processes yielding Z plus missing energy are (1) ZZ production, with \(ZZ \rightarrow \ell ^+ \ell ^- \nu \bar{\nu }\); (2) WZ production, with \(Z \rightarrow \ell ^+ \ell ^-\), \(W \rightarrow \ell ' \nu \), and the additional charged lepton \(\ell '\) undetected, because of having a small transverse momentum or large rapidity. We have used MadGraph5_aMC@NLO to simulate these processes at the tree level, followed by hadronisation by Pythia [22], in order to estimate the SM prediction for the \(Z+\text {MET}\) final state in pp collisions at a CM energy of 13 TeV. We restrict our analysis to events happening at the Z peak, with the two charged leptons in an invariant mass window of 88–94 GeV.

Fig. 2
figure 2

Neutralino (decaying to Z plus gravitino) production mechanisms considered in the SUSY dark matter model

Full size image

We set our reference system in the Z boson rest frame with the \(\hat{z}^\prime \) axis in its momentum direction, while the other two axes are left unspecified – so the non-diagonal elements of the density matrix vanish, leaving only \(\langle S_3 \rangle \) and \(\langle T_0 \rangle \) as observables. The calculated values of \(\langle S_3 \rangle \) and \(\langle T_0 \rangle \), as a function of the lower cut on \(\text {MET}\), are presented in Fig. 1. The bands represent the Monte Carlo statistical uncertainty of our results. Notice that our simulation only includes signal events, so the meaning of these MET cuts is dynamical, i.e. the inclusion of a MET threshold leads to a different production mechanism of the Z boson. For the SM predictions (blue and orange bands), the large dependence of these two observables on the \(\text {MET}\) cut makes their measurement very interesting to test the SM, as well as providing a reference for beyond the standard model (BSM) searches.

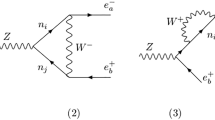
To illustrate the power of the declared strategy, we compare with the expected values of these observables in a SUSY dark matter model with the gravitino \(\tilde{G}\) as lightest supersymmetric particle (LSP) and the lightest neutralino \(\tilde{\chi }^0_1\) as next-to-LSP. We consider a massless gravitino and a lightest neutralino \(\chi _1^0\) whose mass is around 100 GeV. For simplicity, we assume the direct electroweak production of a pair \(\tilde{\chi }^0_1 \tilde{\chi }^0_1\) from quark–antiquark, as shown in Fig. 2. The simulation is performed within the MadGraph5_aMC@NLO framework utilising the gravitino implemented in FeynRules output in the Universal FeynRules Output (UFO) [23]. The BSM values of \(\langle T_0 \rangle \) and \(\langle S_3 \rangle \) do not depend on the MET threshold. The former is \(\langle T_0 \rangle = 1/\sqrt{6}\) due to angular momentum conservation, as discussed in the next section (with \(j=1/2\), \(j^\prime = 3/2\)). The latter is fixed for a particular process, but may change in the presence of an additional production channel. Since in both diagrams in Fig. 2 we have the same incoming and outgoing particles, \(q \bar{q} \rightarrow \chi _1^0 \chi _1^0 \rightarrow Z \tilde{G} Z \tilde{G}\), the kinematical distributions, including the missing transverse momentum, should be the same. Therefore, the change in the MET threshold should not affect the relative contribution of each diagram, and \(\langle S_3 \rangle \) should be independent of the MET cut.

The consideration of Z boson plus MET production in SUSY models with gravitinos is motivated by previous work [24], where it was shown that Gauge Mediation models could lead to a privileged new production mechanism of Z bosons. In this model, the production mechanism of Z bosons plus \(\text {MET}\) is \(\tilde{\chi }^0 \rightarrow Z\; \tilde{G}\), which produces Z bosons with the diagonal spin parameters shown in Fig. 1 (green and red bands).

5 Z bosons from heavy particle decays

Let us consider that a Z boson is produced in the two-body decay of some spin-j particle A, yielding also a spin-\(j'\) particle B as decay product,

$$\begin{aligned} A(j,m) \rightarrow Z(1,\lambda _1) B(j',\lambda _2) , \end{aligned}$$
(13)

where \(\lambda _1\), \(\lambda _2\) are the helicities of Z and B in the rest frame of the decaying particle A, and m its third spin component. Let us fix a \((\hat{x},\hat{y},\hat{z})\) coordinate system in the rest frame of A. The amplitude for the decay can be written as

$$\begin{aligned} \mathcal {M}_{m \lambda _1 \lambda _2} = a_{\lambda _1 \lambda _2} D_{m \lambda }^{j*} (\phi ,\theta ,0) , \end{aligned}$$
(14)

with \(\theta \) and \(\phi \) the polar and azimuthal angle of the Z boson momentum, in full analogy to the Z boson decay discussed in Sect. 2. Restricting ourselves to particles up to spin 3 / 2, we have six combinations for j and \(j'\), collected in Table 1. We assume that spin 3 / 2 particles are massless, so their only possible helicities are \(\pm 3/2\); furthermore, the decaying particle A cannot have spin 3 / 2 in this case. For each pair \(j,j'\), angular momentum conservation implies that only a subset of \(a_{\lambda _1 \lambda _2}\) are non-zero; these combinations are also given in Table 1.

Table 1 Non-zero amplitudes for \(A(j,m) \rightarrow Z(1,\lambda _1) B(j',\lambda _2)\) with arbitrary spins
Full size table

Angular momentum conservation restricts the form of the Z boson spin density matrix, whose elements also depend on the angles \(\theta \) and \(\phi \). Differential measurements of the Z spin observables as functions of \(\theta \) and \(\phi \) are possible with sufficient statistics, but for simplicity we consider here the integrated density matrix, using for the Z boson rest frame the \((\hat{x}',\hat{y}',\hat{z}')\) coordinate system implied by the standard boost from the rest frame of A, with the \(\hat{z}'\) axis in the Z helicity direction.Footnote 3 Experimentally, this would require the measurement of the momentum of the B particle too, in order to reconstruct the momentum of A and choose a coordinate system in its rest frame. (In the previous section we have not made such assumption.) With this setup, integrating over \(\theta \) and \(\phi \) does not generally give a diagonal \(\rho \), and a dependence on the values of \(\langle S_3 \rangle \) and \(\langle T_0 \rangle \) for the particle A, denoted here as \(\langle S_3^A \rangle \) and \(\langle T_0^A \rangle \), respectively, is retained. This subtle effect is due to the fact that, when performing the above specified standard boost from the rest frame of A, the \(\hat{y}'\) axis is always in the xy plane (see for example Ref. [25] for a detailed discussion) irrespectively of the values of \(\theta \) and \(\phi \), and the integration over these two angles is not equivalent to considering an isotropic distribution of the \(\hat{x}'\) and \(\hat{y}'\) axes.

The predictions for the different combinations of \(j,j'\) are as follows.

  • \(j=1/2\), \(j' = 3/2\). The density matrix has all entries vanishing except \(\rho _{11}\) and \(\rho _{-1 -1}\), implying \(\langle S_1 \rangle = \langle S_2 \rangle = 0\), \(\langle A_1 \rangle = \langle A_2 \rangle = 0\), \(\langle B_1 \rangle = \langle B_2 \rangle = 0\). The only non-trivial observables are

    $$\begin{aligned} \langle S_3 \rangle = \left[ |a_{1 \, 3/2}|^2 - |a_{-1 \, -3/2}|^2 \right] / \mathcal {N} ,\quad \langle T_0 \rangle = 1/\sqrt{6}.\nonumber \\ \end{aligned}$$
    (15)

    Here and below, \(\mathcal {N}\) is the sum of the moduli squared of all the non-zero amplitudes in Table 1 for the case under consideration. These results were referred to in Sect. 4 of this paper.

  • \(j=1/2\), \(j' = 1/2\). Here \(\rho _{1 -1} = 0\), therefore \(\langle B_1 \rangle = \langle B_2 \rangle = 0\). The remaining observables can be non-zero,

    $$\begin{aligned} \langle S_3 \rangle= & {} \left[ |a_{1 \, 1/2}|^2 - |a_{-1 \, -1/2}|^2 \right] / \mathcal {N} , \nonumber \\ \langle T_0 \rangle= & {} \frac{1}{\sqrt{6}} \left\{ 1 - 3 \left[ |a_{0 \, 1/2}|^2 + |a_{0 \, -1/2}|^2 \right] /\mathcal {N} \right\} , \nonumber \\ \langle S_1 \rangle= & {} -\frac{\pi }{\sqrt{2}} \langle S_3^A \rangle {\text {Re}}[ a_{-1 \,-1/2} \, a_{0 \,-1/2}^* + a_{1 \,1/2} \, a_{0 \,1/2}^* ] / \mathcal {N} , \nonumber \\ \langle S_2 \rangle= & {} -\frac{\pi }{\sqrt{2}} \langle S_3^A \rangle {\text {Im}}[ a_{-1 \,-1/2} \, a_{0 \,-1/2}^* - a_{1 \,1/2} \, a_{0 \,1/2}^* ] / \mathcal {N} , \nonumber \\ \langle A_1 \rangle= & {} -\frac{\pi }{2\sqrt{2}} \langle S_3^A \rangle {\text {Re}}[ a_{-1 \,-1/2} \, a_{0 \,-1/2}^* - a_{1 \,1/2} \, a_{0 \,1/2}^* ] / \mathcal {N} , \nonumber \\ \langle A_2 \rangle= & {} -\frac{\pi }{2\sqrt{2}} \langle S_3^A \rangle {\text {Im}}[ a_{-1 \,-1/2} \, a_{0 \,-1/2}^* + a_{1\, 1/2} \, a_{0 \, 1/2}^* ] / \mathcal {N} .\nonumber \\ \end{aligned}$$
    (16)

  • \(j=1\), \(j'=0,1\). In these two cases all the density matrix elements and Z boson spin observables are generally different from zero. We can write them as

    $$\begin{aligned} \langle S_3 \rangle= & {} \left[ C_{1} - C_{-1} \right] / \mathcal {N} , \nonumber \\ \langle T_0 \rangle= & {} \frac{1}{\sqrt{6}} \left[ 1 - 3 C_0 /\mathcal {N} \right] , \nonumber \\ \langle S_1 \rangle= & {} -\frac{3\pi }{8} \langle S_3^A \rangle {\text {Re}}[ C_{-10} + C_{10} ] / \mathcal {N} , \nonumber \\ \langle S_2 \rangle= & {} -\frac{3\pi }{8} \langle S_3^A \rangle {\text {Im}}[ C_{-10} - C_{10} ] / \mathcal {N} , \\ \langle A_1 \rangle= & {} -\frac{3\pi }{16} \langle S_3^A \rangle {\text {Re}}[ C_{-10} - C_{10} ] / \mathcal {N} , \nonumber \\ \langle A_2 \rangle= & {} -\frac{3\pi }{16} \langle S_3^A \rangle {\text {Im}}[ C_{-10} + C_{10} ] / \mathcal {N} , \nonumber \\ \langle B_1 \rangle= & {} \sqrt{\frac{3}{2}} \langle T_0^A \rangle {\text {Re}}C_2 , \nonumber \\ \langle B_2 \rangle= & {} \sqrt{\frac{3}{2}} \langle T_0^A \rangle {\text {Im}}C_2 ,\nonumber \end{aligned}$$
    (17)

    where we have abbreviated products of amplitudes \(a_{\lambda _1 \lambda _2}\) for \(j'= 0\) (\(j' = 1\)) as

    $$\begin{aligned} C_{1}= & {} |a_{1\,0}|^2 \;( \;+ \;|a_{1\,1}|^2 ) , \nonumber \\ C_{-1}= & {} |a_{-1\,0}|^2 \;( \;+ \;|a_{-1\,-1}|^2 ) , \nonumber \\ C_{0}= & {} |a_{0\,0}|^2 \;( \;+ \;|a_{0 \,1}|^2 + |a_{0 \,-1}|^2 ), \\ C_{10}= & {} a_{1\,0} a_{0\,0}^* \;( \;+ a_{1\,1} \, a_{0\,1}^* ) , \nonumber \\ C_{-10}= & {} a_{-1\,0} \, a_{0\,0}^* \;( \;+ a_{-1\,-1} \, a_{0\,-1}^* ) , \nonumber \\ C_2= & {} a_{-1 \, 0} \, a_{1 \, 0}^*.\nonumber \end{aligned}$$
    (18)

  • \(j=0\), \(j' = 1\). The Z spin density matrix is diagonal, implying \(\langle S_1 \rangle = \langle S_2 \rangle = 0\), \(\langle A_1 \rangle = \langle A_2 \rangle = 0\), \(\langle B_1 \rangle = \langle B_2 \rangle = 0\). The diagonal spin observables are

    $$\begin{aligned} \langle S_3 \rangle= & {} \left[ |a_{1 \, 1}|^2 - |a_{-1 \, -1}|^2 \right] / \mathcal {N} , \nonumber \\ \langle T_0 \rangle= & {} \frac{1}{\sqrt{6}} \left[ 1 - 3 |a_{0 \, 0}|^2 /\mathcal {N} \right] . \end{aligned}$$
    (19)

  • \(j=0\), \(j' = 0\). This case is particularly interesting, implying a full longitudinal Z (helicity \(\lambda =0\)) or, equivalently, a p-wave (orbital angular momentum \(l=1\)) state. The only non-zero density matrix element is \(\rho _{00} = 1\), therefore \(\langle S_1 \rangle = \langle S_2 \rangle = \langle S_3 \rangle = 0\), \(\langle A_1 \rangle = \langle A_2 \rangle = 0\), \(\langle B_1 \rangle = \langle B_2 \rangle = 0\) and

    $$\begin{aligned} \langle T_0 \rangle= & {} -\frac{2}{\sqrt{6}}. \end{aligned}$$
    (20)

    It would be the situation in the decay \(A(0^-)\rightarrow Z + h(0^+)\) in the Higgs sector of SUSY and left–right models.

This analysis can be applied to current and future heavy resonance searches. If a new resonance is discovered, the use of spin observables in the Z leptonic decay products might shed light into its nature. If any spin observable is measured to have a non-trivial value, or \(\langle T_0 \rangle \ne -2/\sqrt{6}\), the \(j=0\), \(j' = 0\) hypothesis is discarded. If, additionally, a non-zero value is found for any off-diagonal spin observable, the \(j=0\), \(j'=1\) hypothesis can be discarded too. Furthermore, a non-trivial value for \(\langle B_{1,2} \rangle>\) can only be explained by a \(j=1\) parent. However, discriminating the two \(j=1\) possibilities requires an analysis of the decay of the extra particle B.

To conclude this section we remark that, as anticipated, the classification and relation of spin observables with decay amplitudes obtained also apply for a W boson, namely to the decay

$$\begin{aligned} A (j,m) \rightarrow W(1,\lambda _1) B(j',\lambda _2) \end{aligned}$$
(21)

because we have not used any other property than the spin. In particular, one example of \(j=1/2\), \(j'=1/2\) decays is given by \(t \rightarrow W b\), studied in Ref. [8].

6 Conclusions

With the wealth of collision data being accumulated by LHC experiments, the measurement of the eight Z boson spin observables becomes feasible from the angular distribution of its leptonic decay. We have proved in this work the discriminating power of these polarisation and alignment observables for identifying the production mechanism of the Z boson, with apparent different values for known processes in the SM and for extended models. These observable quantities thus play the role of messengers from the hidden physics leading to the Z boson production.

Interesting physical processes include the Drell–Yan Z boson production, for which we have given the physical interpretation of the parameters of the lepton angular distribution measured by ATLAS and CMS, pointing out the alternative method of extracting the Z boson spin observables by means of selected asymmetries. When we move to processes able to generate large missing transverse energy, the SM reference values for the Z boson longitudinal polarisation \(\langle S_3 \rangle \) and alignment \(\langle T_0 \rangle \) present a characteristic rapid variation above 100 GeV of MET, contrary to the values and behaviour obtained from SUSY models with new sources of Z boson production like the decay of neutralinos to gravitinos. For two-body decays of a heavy particle involving a Z boson (or W boson) in its decay products, we have demonstrated that different spin assignments of the parent and daughter particles lead to specific zeros and values of the Z boson polarisations and alignments. The use of these observables will increasingly become an invaluable interesting handle to test the SM predictions and look for new physics.