1 Introduction

The generic function in f(R) gravity is a coupling-free function which helps to resolve many cosmological issues. Nojiri and Odintsov [1] proposed the concept of a non-minimal curvature–matter coupling, which led to fresh insight among researchers. This coupling successfully incorporates clusters of galaxies or dark matter in galaxies, yielding natural preheating conditions corresponding to inflationary models and thus one introduced the idea of traversable wormholes in the absence of any exotic matter [2,3,4,5]. Harko et al. [6] proposed a new version of modified theory whose generic function incorporates curvature as well as matter, known as f(R, T) gravity (T is the trace of the energy-momentum tensor). This function induces strong interactions of gravity and matter, which play a dynamical role in analyzing the current cosmic expansion [7]. Sharif and Zubair [8,9,10,11,12,13] investigated some cosmic issues like energy conditions, thermodynamics, anisotropic exact solutions, reconstruction of some dark energy models, and also they studied the stability issue in this theory of gravity.

The interest in exact solutions of higher order non-linear differential equations keeps researchers motivated as these are extensively used to investigate different cosmic aspects. Harko and Lake [14] discussed exact solutions of the cylindrical spacetime in the presence of non-minimal coupling between R and matter Lagrangian density (\(\mathcal {L}_\mathrm{m}\)). The higher order non-linear differential equations of f(R, T) gravity attract many researchers as they perform cosmological analysis via exact solutions of the field equations. Sharif and Zubair [15] considered exponential and power-law expansions to evaluate some exact solutions and kinematical quantities of the Bianchi type I (BI) model in this gravity. Shamir and Raza [16] formulated exact solutions corresponding to cosmic strings as well as a non-null electromagnetic field. Shamir [17] found exact solutions of a locally rotationally symmetric BI model and studied the physical behavior through cosmological parameters.

In mathematical physics and theoretical cosmology, continuous symmetry reduces the complexity of non-linear systems, which successfully yields exact solutions. In a dynamical system, Noether symmetry points to a correspondence between infinitesimal symmetry generator and conserved quantity. Capozziello et al. [18] used this approach to find exact solutions of spherically symmetric spacetime in f(R) gravity. Hussain et al. [19] investigated the existence of Noether symmetry of a power-law f(R) model and found the boundary term to vanish for the flat FRW universe model but Shamir et al. [20] obtained a non-zero boundary term of the same model. Momeni et al. [21] explored a Noether point symmetry of the isotropic universe in mimetic f(R) and f(R, T) gravity theories. Shamir and Ahmad [22] constructed exact solutions in \(f(\mathcal {G},T)\) gravity (\(\mathcal {G}\) denotes the Gauss–Bonnet term).

Sanyal [23] determined exact solutions of the Kantowski–Sachs (KS) universe model through the Noether symmetry technique in non-minimally coupled gravity with a scalar field. Camci and Kucukakca [24] extended this work by adding BI as well as BIII universe models and formulated explicit forms of the scalar field. Kucukakca et al. [25] discussed the presence of Noether symmetry to formulate exact solutions of a locally rotationally symmetric BI universe. Camci et al. [26] generalized this work for anisotropic universe models such as BI, BIII and KS. We have obtained exact solutions of a f(R) power-law model [27] as well as of a f(R, T) model admitting indirect non-minimal curvature–matter coupling [28].

In non-minimally coupled gravitational theory, the Noether symmetry approach is extensively used to study different cosmological models and the dynamical role of various scalar field models [29]. Vakili [30] identified the existence of Noether point symmetry along with a conserved quantity for the flat FRW universe and studied the behavior of effective equation of state (EoS) parameter for the quintessence model in f(R) gravity. Zhang et al. [31] explored a multiple scalar field scenario and formulated a relationship of the potential function with quintessence and phantom models. Jamil et al. [32] ensured the presence of Noether symmetry with conservation law for the f(R) tachyon model. Sharif and Shafique [33] obtained exact solutions of isotropic and anisotropic universe models in scalar–tensor theory non-minimally coupled with the torsion scalar.

In this paper, we discuss the existence of Noether symmetries of non-minimally coupled f(R, T) gravity interacting with generalized scalar field model. The format of the paper is as follows. Section 2 introduces some basic aspects of this gravity. In Sect. 3, we discuss all possible Noether symmetries with associated conserved quantities for two particular models of this theory. We also formulate exact solutions for dust as well as perfect fluid distribution and study their physical behavior through some cosmological parameters. In the last section, we present final remarks.

2 Some basics of f(R, T) gravity

We consider the action incorporating gravity, matter and scalar field:

$$\begin{aligned} \mathcal {I}=\int \mathrm{d}^4x\sqrt{-g}[\mathcal {L}_g+\mathcal {L}_\mathrm{m}+\mathcal {L}_{\phi }], \end{aligned}$$
(1)

where g denotes the determinant of the metric tensor, \(\mathcal {L}_g\) and \(\mathcal {L}_{\phi }\) represent gravity and scalar field Lagrangian densities. For non-minimal coupling, the gravitational Lagrangian is considered to be a generic function f(R, T) admitting minimal coupling only with \(\mathcal {L}_\mathrm{m}\) and \(\mathcal {L}_{\phi }\) [6]. In this case, the metric variation of \(\mathcal {L}_g\) and \(\mathcal {L}_\mathrm{m}\) yields

$$\begin{aligned}&f_R(R,T)R_{\mu \nu }-\frac{1}{2}f(R,T)g_{\mu \nu }\\&\quad +(g_{\mu \nu } \nabla _{\mu }\nabla ^{\mu }-\nabla _\mu \nabla _\nu )f_R(R,T)+f_T(R,T) T_{\mu \nu }\\&\quad +f_T(R,T)\left( g_{\mu \nu }\mathcal {L}_\mathrm{m} -2T_{\mu \nu }{-}2g^{\alpha \beta }\frac{\partial ^2\mathcal {L}_\mathrm{m}}{\partial g^{\alpha \beta }\partial g^{\mu \nu }}\right) = \kappa ^2T_{\mu \nu }, \end{aligned}$$

where the subscripts R and T describe corresponding partial derivatives of f, \(\nabla _{\mu }\) indicates the covariant derivative and \(T_{\mu \nu }\) represents the energy-momentum tensor. The divergence of the energy-momentum tensor leads to

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }= & {} \frac{f_T}{\kappa ^2-f_T}\Bigg [(T_{\mu \nu } +\Theta _{\mu \nu })\nabla ^{\mu }\ln f_T\\&+\nabla ^{\mu }\Theta _{\mu \nu }-\frac{g_{\mu \nu }\nabla ^{\mu }T}{2}\Bigg ]. \end{aligned}$$

In non-minimally coupled modified gravity, the energy-momentum tensor no more remains conserved. This non-zero divergence introduces an extra force in the equation of motion which is responsible for a deviation of massive test particles from the geodesic trajectories.

A generalization of some anisotropic and homogeneous universe models is given as [34]

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a^2(t)\mathrm{d}r^2+b^2(t)(\mathrm{d}\theta ^2+\zeta (\theta )\mathrm{d}\phi ^2), \end{aligned}$$
(2)

where a and b are scale factors and \(\zeta (\theta )={\theta ,~\sin h\theta ,~\sin \theta }\) identify BI, BIII and KS models with the following relationship:

$$\begin{aligned} \frac{1}{\zeta }\frac{\mathrm{d}^2\zeta }{\mathrm{d}\theta ^2}=-\xi . \end{aligned}$$

For \(\xi =0,-1,1\), the spacetime (2) corresponds to the BI, BIII and KS universe models, respectively. For a perfect fluid, the energy-momentum tensor is

$$\begin{aligned} T_{\mu \nu }=(\rho _\mathrm{m}+p_\mathrm{m})u_\mu u_\nu +p_mg_{\mu \nu }, \end{aligned}$$

where \(p_\mathrm{m}\) and \(\rho _\mathrm{m}\) define pressure and energy density, respectively whereas u represents the four-velocity of the fluid. For the action (1), the Lagrangian density of matter and scalar fields are defined as [35, 36]

$$\begin{aligned} \mathcal {L}_\mathrm{m}=p_\mathrm{m}(a,b),\quad \mathcal {L}_\phi =\frac{\epsilon }{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi -V(\phi ), \end{aligned}$$
(3)

where \(V(\phi )\) denotes the potential energy of the scalar field and \(\epsilon =1,-1\) indicate scalar field models, i.e., quintessence and phantom models.

Phantom model suffers with number of troubles like violation of dominant energy condition, the entropy of phantom-dominated universe is negative and consequently, black holes disappear. Such a universe ends up with a finite time future singularity dubbed a big-rip singularity [37]. Different ideas are proposed to cure the troubles of this singularity such as considering phantom acceleration as transient phenomenon with different scalar potentials or to modify the gravity, couple dark energy with dark matter or to use particular forms of EoS for dark energy taking into account some quantum effects (giving rise to the second quantum gravity era) which may delay/stop the singularity occurrence [38,39,40,41,42]. Inserting Eq. (3) into (1), we obtain

$$\begin{aligned} \mathcal {I}= & {} \int \mathrm{d}^4x\sqrt{-g}\bigg [\frac{f(R,T)}{2\kappa ^2}+p_\mathrm{m}(a,b)\nonumber \\&+\frac{\epsilon }{2} g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi -V(\phi )\bigg ], \end{aligned}$$
(4)

where

$$\begin{aligned} R= & {} \frac{2}{ab^2}(\ddot{a}b^2+2ab\ddot{b} +2b\dot{a}\dot{b}+a\dot{b^2}+a\xi ),\\&\quad T=3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b). \end{aligned}$$

To evaluate Lagrangian corresponding to the action (4) for configuration space \(\mathcal {Q}=\{a,b,R,T,\phi \}\), we use the Lagrange multiplier approach which yields

$$\begin{aligned} \mathcal {L}= & {} ab^2\bigg [f(R,T)-Rf_R(R,T)+f_T(R,T)(3p_\mathrm{m}(a,b)\nonumber \\&-\rho _\mathrm{m}(a,b)-T)-\frac{\epsilon \dot{\phi }^2}{2}+p_\mathrm{m}(a,b)-V(\phi )\bigg ]\nonumber \\&-(4b\dot{a}\dot{b}+2a\dot{b}^2-2a\xi )f_R(R,T)\nonumber \\&-(2b^2\dot{a}\dot{R}+4ab\dot{b}\dot{R})\nonumber \\&\times f_{RR}(R,T)-(2b^2\dot{a}\dot{T}+4ab\dot{b}\dot{T})f_{RT}(R,T). \end{aligned}$$
(5)

In a dynamical system, the Euler–Lagrange equation, the Hamiltonian (\(\mathcal {H}\)) and conjugate momenta (\(p_i\)) play a significant role to determine basic features of the system, defined as

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial q^i}-\frac{\mathrm{d}p_i}{\mathrm{d}t}=0,\quad \mathcal {H}=\sum _i\dot{q}^ip_i-\mathcal {L},\quad p_i=\frac{\partial \mathcal {L}}{\partial \dot{q}^i}, \end{aligned}$$

where \(q^i\) refers to n coordinates of the system. For the Lagrangian (5), the conjugate momenta take the following form:

$$\begin{aligned} p_a= & {} -4b\dot{b}f_R -2b^2(\dot{R}f_{RR}+\dot{T}f_{RT}),\quad p_{\phi }=-ab^2\epsilon \dot{\phi },\\ p_b= & {} -4f_R(a\dot{b}+b\dot{a}) -4ab(\dot{R}f_{RR}+\dot{T}f_{RT}),\\ p_R= & {} -(4ab\dot{b}+2b^2\dot{a})f_{RR},\quad p_T= -(4ab\dot{b}+2b^2\dot{a})f_{RT}. \end{aligned}$$

The dynamical equations of the system are

$$\begin{aligned}&2f_R(R,T)\left( \frac{\dot{b^2}}{b^2}+\frac{2\ddot{b}}{b}+\frac{2\xi }{b^2}\right) +f-Rf_R\nonumber \\&\quad +f_T (3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b)-T)\nonumber \\&\quad +p_\mathrm{m}(a,b)-\frac{\epsilon \dot{\phi }^2}{2} -V(\phi )\nonumber \\&\quad +a\{f_T(3p_\mathrm{m},_{_a}-\rho _\mathrm{m},_{_a})+p_\mathrm{m},_{_a}\} +4b^{-1}\dot{b}\dot{R}f_{RR} \nonumber \\&\quad +4b^{-1}\dot{b}\dot{T}f_{RT} +2\ddot{R}f_{RR}+2\dot{R}^2f_{RRR}+4\dot{R}\dot{T}f_{RRT}\nonumber \\&\quad +2\ddot{T}f_{RT} +2\dot{T}^2f_{RTT}=0, \end{aligned}$$
(6)
$$\begin{aligned}&2f_R\left( \frac{\ddot{a}}{a}+\frac{\dot{a}\dot{b}}{ab} +\frac{\ddot{b}}{b}\right) \nonumber \\&\quad +f-Rf_R +f_T(3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b)-T)\nonumber \\&\quad +p_\mathrm{m}(a,b)-\frac{\epsilon \dot{\phi }^2}{2} -V(\phi ) +\frac{b}{2}\{f_T(3p_\mathrm{m},_{_b}-\rho _\mathrm{m},_{_b}))\nonumber \\&\quad +p_\mathrm{m},_{_b}\}+2(a^{-1}\dot{a} \dot{R}+\ddot{R})f_{RR}+2\dot{R}^2\nonumber \\&\quad \times f_{RRR}+2(a^{-1}\dot{a} \dot{T}+\ddot{T})f_{RT}+2(b^{-1}\dot{b}\dot{R}\nonumber \\&\quad +2\dot{R}\dot{T}+\dot{T}^2)f_{RRT} +2b^{-1}\dot{b}\dot{T}f_{RTT}=0, \end{aligned}$$
(7)
$$\begin{aligned}&f_{RT}(3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b)-T)=0,\nonumber \\&f_{TT}(3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b)-T)=0,\nonumber \\&\epsilon \ddot{\phi }+2\epsilon b^{-1}\dot{b}\dot{\phi } +\epsilon a^{-1}\dot{a}\dot{\phi }-V'(\phi )=0. \end{aligned}$$
(8)

In order to evaluate the total energy of the dynamical system, we formulate the Hamiltonian as

$$\begin{aligned} \mathcal {H}= & {} 2f_R\left( \frac{\dot{b^2}}{b^2}+\frac{2\dot{a}\dot{b}}{ab}\right) +2\left( \frac{2\dot{b}}{b}+\frac{\dot{a}}{a}\right) \dot{R}f_{RR}\nonumber \\&+2\left( \frac{2\dot{b}}{b}+\frac{\dot{a}}{a}\right) \dot{T}f_{RT}+f-Rf_R\nonumber \\&+f_T(3p_\mathrm{m}(a,b)-\rho _\mathrm{m}(a,b)-T) +p_\mathrm{m}(a,b)\nonumber \\&+\frac{\epsilon \dot{\phi }^2}{2} -V(\phi )+\frac{2\xi f_R}{b^2}. \end{aligned}$$
(9)

The Hamiltonian constraint \(\mathcal {H}=0\) yields the total pressure of the dynamical system.

3 Noether symmetry and conserved quantities

The Noether symmetry approach helps to solve complicated non-linear system of partial differential equations yielding exact solutions at theoretical grounds of physics and cosmology. Noether theorem states that if Lagrangian of a dynamical system remains invariant under a continuous group then group generator leads to the associated conserved quantity. The conservation of energy and linear momentum appears for translational invariant Lagrangian in time and position, respectively whereas the angular momentum is conserved for rotationally symmetric Lagrangian [43]. In gravitational theories, the presence of conserved quantities also enhances physical interpretation of theory but if it does not appreciate the existence of any conserved quantity, then the theory will be abandoned due to its non-physical features.

To investigate the existence of Noether symmetry and associated conserved quantity in non-minimally coupled gravitational theory, we consider the first order prolongation \(K^{[1]}\) of continuous group defined as

$$\begin{aligned} K^{[1]}=K+(\varphi ^j,_t+\varphi ^j,_i\dot{q}^i-\vartheta ,_t\dot{q}^j -\vartheta ,_i\dot{q}^i\dot{q}^j)\frac{\partial }{\partial \dot{q}^j}, \end{aligned}$$
(10)

where the cosmic time t is considered to be an affine parameter and K represents the symmetry generator given by

$$\begin{aligned} K= & {} \vartheta (t,q^i)\frac{\partial }{\partial t}+\varphi ^j(t,q^i)\frac{\partial }{\partial q^j}. \end{aligned}$$
(11)

Here \(\vartheta \) and \(\varphi ^j\) are unknown coefficients of the generator. The existence of Noether symmetry is ensured when K follows the invariance condition,

$$\begin{aligned} K^{[1]}\mathcal {L}+(D\vartheta )\mathcal {L}=DB(t,q^i),\quad D=\frac{\partial }{\partial t}+\dot{q}^i\frac{\partial }{\partial q^i}, \end{aligned}$$
(12)

where D is the total derivative, while B represents a boundary term of K. When the symmetry generator becomes independent of the affine parameter then boundary term along with first order prolongation vanishes yielding

$$\begin{aligned} K=\varrho ^i(q^i)\frac{\partial }{\partial q^i}+\left[ \frac{\mathrm{d}}{\mathrm{d}t}(\varrho ^i(q^i))\right] \frac{\partial }{\partial \dot{q}^i}, \quad L_K\mathcal {L}=0, \end{aligned}$$
(13)

where L identifies Lie derivative. The symmetries coming from symmetry generators (9) and (13) lead to corresponding conservation law through the first integral defined as

$$\begin{aligned} \Sigma =B-\vartheta \mathcal {L}-(\varphi ^j-\dot{q}^j\vartheta ) \frac{\partial \mathcal {L}}{\partial \dot{q}^j},\quad \Sigma =-\eta ^j \frac{\partial \mathcal {L}}{\partial \dot{q}^j}. \end{aligned}$$
(14)

For \(Q=\{t,a,b,R,T,\phi \}\), the infinitesimal symmetry generator and corresponding first order prolongation take the form

$$\begin{aligned}&K=\tau \frac{\partial }{\partial t}+\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial b}+\gamma \frac{\partial }{\partial R}+\delta \frac{\partial }{\partial T}+\eta \frac{\partial }{\partial \phi },\nonumber \\&K^{[1]}=\tau \frac{\partial }{\partial t}+\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial b}\nonumber \\&\quad +\gamma \frac{\partial }{\partial R}+\delta \frac{\partial }{\partial T}+\dot{\alpha }\frac{\partial }{\partial \dot{a}}+\dot{\beta }\frac{\partial }{\partial \dot{b}}+\dot{\gamma }\frac{\partial }{\partial \dot{R}}+\dot{\delta }\frac{\partial }{\partial \dot{T}}+\dot{\eta }\frac{\partial }{\partial \dot{\phi }},\nonumber \\ \end{aligned}$$
(15)

where the time derivative of the unknown coefficients \(\tau ,~\alpha ,~\beta ,~\gamma ,~\delta \) and \(\eta \) are

$$\begin{aligned} \dot{\sigma }_{_l}= & {} D\sigma _{_l}-\dot{q}^iD\tau ,\quad l=1,\ldots , 5, \end{aligned}$$
(16)

Here \(\sigma _1,~\sigma _2,~\sigma _3,~\sigma _4\) and \(\sigma _5\) correspond to \(\alpha ,~\beta ,~\gamma ,~\delta \) and \(\eta \), respectively.

In order to discuss the presence of Noether symmetry generator and relative conserved quantity of the model (2), we insert the first order prolongation (10) along with (11) in (12), it obeys a system of equations given in Appendix A. From Eq. (A7), we have either \(f_R,~f_{RR},~f_{RT}=0\) with \(\tau ,_{_a},~\tau ,_{_b},~\tau ,_{_R},~\tau ,_{_T}\ne 0\) or vice versa. For non-trivial solution, we consider second possibility (\(\tau ,_{_a},~\tau ,_{_b},~\tau ,_{_R},~\tau ,_{_T}=0\)) as the first choice yields trivial solution. We investigate the existence of symmetry generators, relative conserved quantities for the following two models [6]:

  • \(f(R,T) = R+2g(T)\),

  • \(f(R,T) =F(R)+h(R)g(T)\).

We also formulate corresponding exact solutions to analyze cosmological picture of these two models.

3.1 \(f(R,T)=R+2g(T)\)

This model incorporates an indirect non-minimal curvature–matter coupling and also admits a correspondence with standard cosmological constant cold dark matter (\(\Lambda \)CDM) model if it comprises a trace dependent cosmological constant defined as

$$\begin{aligned} f(R,T)=R+2\Lambda (T)+g(T). \end{aligned}$$
(17)

To evaluate the coefficients of symmetry generator (9), we solve the system (A1)–(A22) via separation of variables method which gives

$$\begin{aligned} \alpha= & {} \alpha _1(t)\alpha _2(a)\alpha _3(b)\alpha _4(R)\alpha _5(T)\alpha _6(\phi ),\nonumber \\ \delta= & {} \delta _1(t)\delta _2(a)\delta _3(b)\delta _4(R)\delta _5(T)\delta _6(\phi ),\nonumber \\ \gamma= & {} \gamma _1(t)\gamma _2(a)\gamma _3(b)\gamma _4(R)\gamma _5(T)\gamma _6(\phi ),\nonumber \\ \eta= & {} \eta _1(t)\eta _2(a)\eta _3(b)\eta _4(R)\eta _5(T)\eta _6(\phi ),\nonumber \\ \beta= & {} \beta _1(t)\beta _2(a)\beta _3(b)\beta _4(R)\beta _5(T)\beta _6(\phi ),\nonumber \\ \tau= & {} \tau _1(t),\nonumber \\ B= & {} B_1(t)B_2(a)B_3(b)B_4(R)B_5(T)B_6(\phi ). \end{aligned}$$
(18)

For these coefficients, the system (A1)–(A22) yields

$$\begin{aligned} \alpha= & {} -2ac_{_1},\quad \beta =c_{_1}b,\quad \gamma =0,\quad \delta =0,\quad \eta =c_{_4},\\ B= & {} c_{_2}t+c_{_3},\quad \tau =c_{_5},\quad V(\phi )=c_{_6}\phi +c_{_7}, \end{aligned}$$
$$\begin{aligned} p_\mathrm{m}(a,b)= & {} -\frac{c_{_4}c_{_6}\ln a+2c_{_1}a^{\frac{1}{2}}b}{2c_{_1}} -\frac{2\xi }{b^2}-\frac{c_{_2}\ln a}{2c_{_1}ab^2},\end{aligned}$$
(19)
$$\begin{aligned} \rho _\mathrm{m}(a,b)= & {} -\frac{3c_{_4}c_{_6}\ln a+2c_{_1}a^{\frac{1}{2}}b}{2c_{_1}} -\frac{6\xi }{b^2}-\frac{3c_{_2}\ln a}{2c_{_1}ab^2}, \end{aligned}$$
(20)

where the \(c_i\) \((i=1,\ldots , 7)\) denotes arbitrary constants. For these coefficients, we split the symmetry generator and corresponding first integral into the following form:

$$\begin{aligned} K_1= & {} \frac{\partial }{\partial t},\quad \Sigma _1=-ab^2\{f-Rf_R+f_T(3p_\mathrm{m}-\rho _\mathrm{m}-T)\\&+p_\mathrm{m}-c_{_6}\phi -c_{_7}\}\\&+2a\xi f_R-4b\dot{a}\dot{b}f_R-2a\dot{b}^2f_R-\frac{\epsilon \dot{\phi }^2ab^2}{2},\\ K_2= & {} -2a\frac{\partial }{\partial a}+b\frac{\partial }{\partial b},\quad \Sigma _2=-4ab\dot{b}f_R+4b^2\dot{a}f_R,\\ K_3= & {} \frac{\partial }{\partial \phi },\quad \Sigma _3=\epsilon ab^2\dot{\phi }. \end{aligned}$$

For the model (17), the system (A1)–(A22) yields three symmetry generators and associated conserved quantities. In this case, the symmetry generator \(K_1\) leads to energy conservation while \(K_2\) represents the scaling symmetry corresponding to conservation of linear momentum.

Next, we explore the presence of Noether symmetry in the absence of affine parameter and boundary term of extended symmetry which leads to establish corresponding conservation law. In this case, the infinitesimal generator of continuous group for \(\mathcal {Q}=\{a,b,R,T,\phi \}\) turns out to be

$$\begin{aligned} K= & {} \alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial b}+\gamma \frac{\partial }{\partial R}+\delta \frac{\partial }{\partial T}+\eta \frac{\partial }{\partial \phi }+\dot{\alpha }\frac{\partial }{\partial \dot{a}}+\dot{\beta }\frac{\partial }{\partial \dot{b}}\nonumber \\&+\dot{\gamma }\frac{\partial }{\partial \dot{R}}+\dot{\delta }\frac{\partial }{\partial \dot{T}}+\dot{\eta } \frac{\partial }{\partial \dot{\phi }}, \end{aligned}$$
(21)

where \(\dot{\alpha }=\dot{q^i}\frac{\partial \alpha }{\partial q^i},~\dot{\beta }=\dot{q^i}\frac{\partial \beta }{\partial q^i},~\dot{\gamma }=\dot{q^i}\frac{\partial \gamma }{\partial q^i},~\dot{\delta }=\dot{q^i}\frac{\partial \delta }{\partial q^i}\) and \(\dot{\eta }=\dot{q^i}\frac{\partial \eta }{\partial q^i}\). Due to the absence of affine parameter, the separation of variables method yields

$$\begin{aligned} \alpha= & {} \alpha _1(a)\alpha _2(b)\alpha _3(R)\alpha _4(T)\alpha _5(\phi ),\\ \beta= & {} \beta _1(a)\beta _2(b)\beta _3(R)\beta _4(T)\beta _5(\phi ),\\ \gamma= & {} \gamma _1(a)\gamma _2(b)\gamma _3(R)\gamma _5(\phi ),\\ \delta= & {} \delta _1(a)\delta _2(b)\delta _3(R)\delta _4(T)\delta _5(\phi ),\\ \eta= & {} \eta _1(a)\eta _2(b)\eta _3(R)\eta _4(T)\eta _5(\phi ). \end{aligned}$$

In order to explore the consequences of indirect non-minimal curvature–matter coupling, we evaluate symmetry generators with corresponding conservation laws for non-existing boundary term. We also establish cosmological analysis through exact solutions for both dust and perfect fluid distributions.

3.1.1 Dust case

Dust fluid investigates matter contents of the universe when the existence of radiations is not so worthy and the formation of massive stars is possible only if dust particles interact with radiations. Here we consider \(T_{\mu \nu }=\rho _\mathrm{m} u_\mu u_\nu \) and solve the system for (21) via separation of variables which yields

$$\begin{aligned}&\alpha =-2ac'_{_1},\quad \beta =c'_{_1}b,\quad \gamma =0,\quad \delta =0,\quad \eta =0,\\&\rho _\mathrm{m}(a,b)= \frac{\xi }{b^2c'_{_2}}+a^{\frac{1}{2}}b,\quad \Lambda (T)=-\frac{g(T)}{2}+c'_{_2}T+c'_{_3}, \end{aligned}$$

where the \(c'_{_j}\) \((j=1,\ldots , 3)\) represent arbitrary constants. The corresponding symmetry generator and associated conserved quantity are

$$\begin{aligned} K=-2ac'_{_1}\frac{\partial }{\partial a}+c'_{_1}b\frac{\partial }{\partial b},\quad \Sigma =4c'_{_1}ab\dot{b}f_R-4c'_{_1}b^2\dot{a}f_R. \end{aligned}$$

For dust fluid, there exists only scaling symmetry in the absence of affine parameter as well as boundary term of extended symmetry and the model (17) reduces to

$$\begin{aligned} f(R,T)=R+2c'_{_2}T+2c'_{_3}. \end{aligned}$$
(22)

For exact solution of equations of motion, we insert density of dust fluid and model (22) in Eqs. (6) and (7) yielding

$$\begin{aligned} a(t)=\frac{(40c'_{_2}t+40c'_{_3})^{\frac{4}{5}}}{16}, \quad b(t)=\frac{c'_{_1}(40c'_{_2}t+40c'_{_3})^{\frac{2}{5}}}{4}. \end{aligned}$$

This leads to expansion of the universe whether it is accelerated or decelerated. The power-law scale factor \((a(t)=t^\lambda )\) identifies both expansions as for \(\lambda >1\), it measures accelerated expansion while it corresponds to decelerated expansion for \(\lambda <1\). When \(\lambda =\frac{1}{2}\) and \(\lambda =\frac{2}{3}\), we have radiation and matter dominated eras of the universe.

Fig. 1
figure 1

Plots of scale factors a(t) (left) and b(t) (right) versus cosmic time t for \(c'_{_1}=0.24\), \(c'_{_2}=0.45\) and \(c'_{_3}=5.5\)

Full size image
Fig. 2
figure 2

Plots of Hubble H(t) (left) and EoS parameters \(\omega _\mathrm{eff}\) (right) versus cosmic time t

Full size image

To analyze the behavior of power-law type exact solution, we construct cosmological analysis through some cosmological parameters such as Hubble, deceleration, r–s and EoS. These parameters are useful to study current expansion as well as different eras of the universe. The Hubble parameter (H) determines the rate of expansion, while the deceleration parameter (q) evaluates the nature of cosmic expansion, telling whether we have the decelerated (\(q>0\)), accelerated (\(q<0\)) or constant (\(q=0\)) case, respectively. In the case of anisotropic universe models, these parameters turn out to be

$$\begin{aligned} H=\frac{64c'_{_2}(40c'_{_2}t+40c'_{_3})^{-1}}{3},\quad q=\frac{7}{8}. \end{aligned}$$

The relevant pair of r–s parameters explores the characteristics of dark energy candidates by establishing a correspondence between constructed and standard cosmic models. When the pair lies in the (\(r,s)=(1,0)\) region, this corresponds to standard \(\Lambda \)CDM model while the trajectories with \(s>0\) and \(r<1\) correspond to quintessence and phantom phases of dark energy. In the present case, we obtain \(r=0\) with \(s=-\frac{8}{9}\) indicating that the constructed model does not correspond to any standard dark energy universe model. The EoS parameter \((\omega )\) investigates different cosmic eras such as it identifies radiation and matter dominated eras for \(\omega =\frac{1}{3}\) and \(\omega =0\), respectively. This parameter specifies dark energy era (\(\omega =-1\)) into quintessence and phantom phases when \(-1<\omega \le -1/3\) and \(\omega <-1\), respectively. The corresponding effective EoS parameter is

$$\begin{aligned} \omega _\mathrm{eff}=\frac{128c'_{_2}+(40c'_{_2}t+40c'_{_3})^{\frac{4}{5}} (5c'^2_{_2}c'_{_1}t^2+10c'_{_1}c'_{_2}c'_{_3}t+5c'_{_1}c'^2_{_3})}{128c'_{_2}} \end{aligned}$$

The potential and kinetic energies of the scalar field play a dynamical role to study cosmic expansion. For accelerated expansion, the field \(\phi \) evolves negatively and potential dominates over the kinetic energy (\(\frac{\dot{\phi }^2}{2}<V(\phi )\)) whereas negative potential follows the kinetic energy for decelerated expansion of the universe (\(\frac{\dot{\phi }^2}{2}>-V(\phi )\)). Using Eq. (8), we obtain

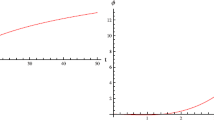
$$\begin{aligned}&\phi =\int \frac{1}{20\epsilon (c'_{_2}t+c'_{_3})}((-\epsilon c'_{_2}(25c'^2_{_2}(40c'_{_2}t+40c'_{_3})^{\frac{4}{5}}c'_{_1}t^2\\&\quad +50 (40c'_{_2}t+40c'_{_3})^{\frac{4}{5}}\\&\quad \times c'_{_2}c'_{_1}c'_{_3}t+25(40c'_{_2}t +40c'_{_3})^{\frac{4}{5}}c'_{_1}c'^2_{_3}+896c'_{_2}))^{\frac{1}{2}}),\\&V(\phi )=\frac{1}{800(c'^2_{_2}t^2 +2c'_{_2}c'_{_3}t+c'^2_{_3})}[25c'_{_1}(5c'^3_{_2}t^2\\&\quad +5c'_{_2}c'^2_{_3}+10c'^2_{_2}c'_{_3}t)(40c'_{_2}t \\&\quad +40c'_{_3})^{\frac{4}{5}}+8c'_{_2}c'_{_3}(-200c'_{_2} t^2+400c'_{_3}t)\\&\quad -8(48c'^2_{_2}+200c'^3_{_3})]. \end{aligned}$$

Figure 1 shows the graphical analysis of the scale factors for the dust case. The scale factor a(t) indicates large cosmic expansion in the x-direction but b(t) represents that the universe is expanding very slowly in the y- and z-directions. Figure 2 (left plot) indicates that the Hubble parameter is decreasing with the passage of time. In the right plot of Fig. 2, the effective EoS parameter identifies that, initially, the universe associates with a radiation dominated era and, after some time, it corresponds to a dark energy era by crossing the matter dominated phase.

Figures 3 and 4 analyze the behavior of scalar field and cosmic expansion via phantom and quintessence models. The left plot of Fig. 3 shows that the scalar field is positive initially yielding decelerated expansion but gradually, it starts increasing negatively which describes accelerated expansion. In case of quintessence model, the scalar field grows from negative to positive indicating decelerated expansion of the universe. The right plots of 3 and 4 satisfy \(\frac{\dot{\phi }^2}{2}<V(\phi )\) and \(\frac{\dot{\phi }^2}{2}>-V(\phi )\), implying that the phantom model yields accelerated expansion, while the quintessence model corresponds to decelerated expansion.

Fig. 3
figure 3

Plots of scalar field \(\phi (t)\) (left) versus cosmic time t and potential energy \(V(\phi )\) versus kinetic energy \(\frac{\dot{\phi }^2}{2}\) (right) for \(\epsilon =-1\)

Full size image
Fig. 4
figure 4

Plots of scalar field \(\phi (t)\) (left) versus cosmic time t and potential energy \(V(\phi )\) versus kinetic energy \(\frac{\dot{\phi }^2}{2}\) (right) for \(\epsilon =1\)

Full size image

To analyze a big-rip free model, the key point is that if the EoS parameter rapidly approaches \(-1\) and the Hubble rate tends to be constant (asymptotically de Sitter universe), then it is possible to have a model in which the time required for a singularity is infinite, i.e., the singularity effectively does not occur [44]. The occurrence of a maximum potential of a phantom scalar field is another evident issue as regards avoiding this singularity [45]. The graphical behavior of the EoS parameter represents that \(\omega _\mathrm{eff}\) rapidly approaches \(-1\) and the Hubble rate is decreasing but the potential is not maximum. We may avoid the big-rip singularity in the present case if we choose \(c_2'\) to be negatively large, which yields an asymptotic behavior of the Hubble rate.

3.1.2 Non-dust case

At large scales, the perfect fluid successfully illustrates a cosmic matter distribution in the presence of radiation. In the absence of a boundary term and an affine parameter, the coefficients of the symmetry generator (21) corresponding to \(a,b,R,T,\phi \) remain the same as in the presence of a boundary term of extended symmetry. Thus, the generator of the Noether symmetry and the associated first integrals reduce to

$$\begin{aligned} K= & {} -2ac_{_1}\frac{\partial }{\partial a}+c_{_1}b\frac{\partial }{\partial b}+c_{_2}\frac{\partial }{\partial \phi },\\ \Sigma= & {} -4c_{_1}ab\dot{b}f_R+4c_{_1}b^2\dot{a}f_R+\epsilon c_{_2}ab^2\dot{\phi }. \end{aligned}$$

In order to formulate an exact solution of the dynamical equations for a perfect fluid distribution, we insert Eqs. (19) and (20) into (6) and (7), yielding

$$\begin{aligned} a(t)= & {} \frac{\left( \frac{5}{c_{_9}}\right) ^{\frac{2}{5}}(c_{_2}\sin (c_{_{10}}t) +c_{_3}\cos (c_{_{10}}t))^{\frac{4}{5}}}{5^{\frac{4}{5}}},\\ b(t)= & {} \frac{c_{_4}\left( \frac{5}{c_{_9}}\right) ^{\frac{1}{5}}(c_{_2}\sin (c_{_{10}}t) +c_{_3}\cos (c_{_{10}}t))^{\frac{2}{5}}}{5^{\frac{2}{5}}}. \end{aligned}$$

This describes an oscillatory solution of the f(R, T) model admitting an indirect non-minimal curvature–matter coupling. To study the cosmological behavior of this solution, we consider the cosmological parameters as follows:

Fig. 5
figure 5

Plots of scale factor a(t) (left) and b(t) (right) versus cosmic time t for \(c_2=c_3=c_9=5.5\) and \(c_{10}=0.005\)

Full size image
Fig. 6
figure 6

Plots of H(t) (left) and q(t) (right) versus cosmic time t

Full size image
$$\begin{aligned}&H=\frac{8c_{_{10}}(c_{_2}\sin (c_{_{10}}t) +c_{_3}\cos (c_{_{10}}t))}{15(c_{_2}\sin (c_{_{10}}t) +c_{_3}\cos (c_{_{10}}t))}, \\&q=\frac{-8c^2_{_2}\cos ^2(c_{_{10}}t)+7c^3_{_3}+8c^2_{_3} \cos ^2(c_{_{10}}t){+}15c^2_{_2}{+}16c_{_2}c_{_3}\cos (c_{_{10}}t) \sin (c_{_{10}}t)}{8(c_{_2}\sin (c_{_{10}}t) {+}c_{_3}\cos (c_{_{10}}t))^2},\\&s=(-45((4c^4_{_2}-4c^4_{_3})\cos ^2(c_{_{10}}t) -c^4_{_3}-6c^2_{_2}c_{_3}-5c^4_{_2}-(8c^3_{_2}c_{_3}+8c_{_2} c^3_{_3})\\&\quad \times \cos (c_{_{10}}t)\sin (c_{_{10}}t))) /256((c^4_{_2}+c^4_{_3}-6c^2_{_2}c^2_{_3})\cos ^4(c_{_{10}}t) +(6c^2_{_2}c^2_{_3}-2c^4_{_3})\\&\quad \times \cos ^2(c_{_{10}}t) +(-4c^3_{_2}c_{_3}+4c_{_2}c^3_{_3})\sin (c_{_{10}}t) \cos ^3(c_{_{10}}t)-4c_{_2}c^3_{_3}\cos (c_{_{10}}t)\\&\quad \times \sin (c_{_{10}}t)+c^4_{_3}),\\&\omega _\mathrm{eff}=\frac{\chi (3p_\mathrm{m}-\rho _\mathrm{m})+p_\mathrm{m} -\frac{\epsilon \dot{\phi }^2}{2}-V(\phi )+\frac{2\xi }{b^2} +a(3p_\mathrm{m},_{_a}-\rho _\mathrm{m},_{_a})+p_\mathrm{m},_{_a}}{\chi (3p_\mathrm{m}-\rho _\mathrm{m})+p_\mathrm{m} +\frac{\epsilon \dot{\phi }^2}{2}-V(\phi )+\frac{2\xi }{b^2}}. \end{aligned}$$

The scalar field and the corresponding kinetic and potential energies identify the early as well as the current cosmic expansion and also characterize the decelerated expansion of the universe when the kinetic energy dominates the negative potential. In this case, Eq. (8) yields

$$\begin{aligned} \phi =\int \frac{\epsilon c_{_4}-\frac{5c_{_6}c^2_{_2}\cos (2c_{_{10}}t) \left( -2_{2}F_{1}\left[ \frac{3}{10},\frac{1}{2},\frac{13}{10},\sin \left[ \frac{\pi }{4}+c_{_{10}}t\right] ^2\right] +\sqrt{2-2\sin [2c_{_{10}}t]}\right) }{16 c_{_{10}}\sqrt{\cos \left[ \frac{\pi }{4}+c_{_{10}}t\right] ^2}(c_{_2} (\cos [c_{_{10}}t]+\sin [c_{_{10}}t]))^{2/5}}\mathrm{d}t}{\epsilon (c_{_2} \cos [c_{_{10}}t]+c_{_2}\sin [c_{_{10}}t])^{8/5}}, \end{aligned}$$

where \(_{2}F_{1}\) represents the hypergeometric function.

Fig. 7
figure 7

Plot of \(\omega _\mathrm{eff}\) and r–s parameters versus cosmic time t for \(c_2=c_3=5.5\) and \(c_{10}=0.005\)

Full size image
Fig. 8
figure 8

Plots of scalar field \(\phi (t)\) (left) versus cosmic time t and potential energy \(V(\phi )\) versus kinetic energy \(\frac{\dot{\phi }^2}{2}\) (right) for \(c_2=5.5\), \(c_4=-10^{3}\), \(c_6=0.5\) and \(c_{10}=0.005\)

Full size image

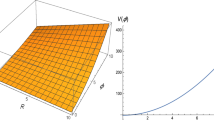
In Fig. 5, the right plot shows that the universe experiences an immense amount of expansion in the y- and z-directions, whereas the left plot shows a small amount of expansion in the x-direction. Figure 6 provides information as regards an increasing rate of expansion through the Hubble parameter, while the negatively increasing deceleration parameter ensures accelerated cosmic expansion. The left plot of Fig. 7 characterizes the quintessence phase of the dark energy era, while the right plot identifies the r–s parameter trajectories in the quintessence and phantom phases as \(s>0\) when \(r<1\). Both plots of Fig. 8 verify the current cosmic expansion for quintessence as well as phantom models as \(\phi \) is continuously increasing negatively, and the potential energy of the field is dominating over the kinetic energy. The graphical interpretation of the EoS parameter yields \(\omega _\mathrm{eff}<-1\), which is not a sufficient condition for the existence of a singularity as the potential turns out to be maximum with the passage of time. Thus, we may avoid a big-rip singularity if the Hubble rate decreases asymptotically in the presence of minimal coupling of f(R, T) gravity with scalar field.

3.2 \(f(R,T) =F(R)+h(R)g(T)\)

To analyze the effect of a direct non-minimal curvature–matter coupling, we consider this model and evaluate the symmetry generators as well as the associated conservation laws. Inserting the model in Eqs. (A2)–(A4), (A10), (A11) and (A15) and using separation of variables approach, we obtain

$$\begin{aligned}&\beta =-\frac{b\alpha }{2a}+\phi Y_1(t,a,b)+ Y_2(t,a,b),\\&F(R)=\frac{\epsilon }{4d_3}\left( -d_3Y_{12}(R)+d_2Y_9(R)\right) +d_5R+d_6,\\&h(R)=-\frac{\epsilon }{4d_3}\left( -d_3Y_{9}(R),_{_R}+d_1R\right) +d_4,\\&\quad g(T)=d_2+d_3Y_{10}(T), \\&\eta =\frac{1}{b}[Y_1(t,a,b)(Y_{10}(T)(d_1+Y_{9}(R),_{_R})\\&\quad -\phi ^2+Y_{12}(R),_{_R})+b\phi \tau ,_{_t}-2\phi \\&\quad \times Y_2(t,a,b)+b Y_{14}(t,a,b)], \end{aligned}$$

where the \(d_i\) (\(i=1,\ldots , 7\)) denote constants. We substitute these values in Eqs. (A1), (A8) and (A9) which yield

$$\begin{aligned}&\tau =\int -\frac{Y_{23}(t)}{\epsilon }\mathrm{d}t+d_8t+d_9,\\&\quad B=\frac{1}{6d_4}\left[ 6ab(Y_{19}(T)d_1 +d_4\epsilon \phi ^2\right. \\&\quad +Y_{19}(T) d_4e^{-R})Y_2(t,a,b),_{_t}\\&\quad +6ab\phi (\frac{1}{3}d_4\epsilon \phi ^2+Y_{19}(T)d_4e^{-R} +Y_{19}(T)\\&\quad \times d_1)Y_{16} (t,b),_{_t}+3d_4(2Y_{22}(t,a,b)\\&\left. +2\phi Y_{21}(t,a,b),_{_t}+ab^2\phi ^2Y_{23}(t),_{_t})\right] , \\&Y_1(t,a,b)=Y_{16}(t,b)+Y_{15}(a,b),\\&\quad Y_{10}(T)= -\frac{Y_{19}(T)d_3+\epsilon d_2d_4}{\epsilon d_3d_4},\\&Y_{12}(R)=-\frac{d_2d_4e^{-R}}{d_3}+d_6R+d_7,\\&\quad Y_{9}(R)= -e^{-R}d_4-2d_1R+d_2,\\&Y_{14}(t,a,b)=-\frac{Y_{21}(t, a, b)}{b^2a\epsilon }\\&\quad -\frac{bad_2\epsilon d_1Y_{16}(t, b)+d_6\epsilon bad_3Y_{16}(t, b)}{\epsilon b^2ad_3}+Y_{24}(b, a). \end{aligned}$$

To evaluate remaining unknown functions, we insert the above functions into \(\beta ,~\eta ,~F,~g,~h\) and solve Eqs. (A5)–(A7) with (A12)–(A14) and (A16)–(A21), leading to

$$\begin{aligned}&Y_{21}(t, a, b)=Y_{26}(a, b),\quad Y_{22}(t, a, b)=d_{10}t,\\&\quad Y_{16}(t, b)=-d_{12}b, \\&Y_{15}(a,b)=d_{12}b,\quad Y_{24}(b,a)=0,\quad Y_{2}(t,a,b)=d_9 b,\\&Y_{23}(t)=\epsilon (-2 d_9+e^{-R}d_4d_3d_{11}e^{R}+d_8),\quad \delta =0,\\&\quad \gamma = \frac{d_{11}e^{R}T}{d_13}\\&\quad \times (e^{-R}d_4Td_{13}d_3-d_1d_{13}d_3T\\&\quad +(2((-2d_5 +\frac{1}{2}\epsilon d_6)d_3+d_1d_2\epsilon ))d_4). \end{aligned}$$

Using these solutions in Eq. (A22) with \(d_{11}=0\) and \(d_6=\frac{d_2d_1}{d_3}\), it follows that

$$\begin{aligned}&\tau =3d_9,\quad \alpha =d_{10}a,\quad \beta =b(d_9-\frac{d_{10}}{2}),\\&\quad \delta =0,\quad \gamma =0,\\&B=d_{10}t,\quad \eta =-\frac{d_1}{\epsilon }+2d_{12}d_6,\\&\quad F(R)= d_6+d_5R-\frac{3d_6\epsilon R}{4}, \\&h(R)=d_4-\frac{\epsilon }{4d_3}(d_4e^{-R}+d_1R-2d_1),\\&\quad g(T)=d_2-\frac{d_2d_4\epsilon -d_3d_{13}T}{d_4\epsilon }. \end{aligned}$$

Inserting F,  h and g, the f(R, T) model becomes

$$\begin{aligned} f(R,T)= & {} -\frac{3\epsilon d_6R}{4}+d_5R+d_6\\&+(d_4-\frac{\epsilon }{4d_3}(d_4e^{-R}+d_1R-2d_1)) \left( \frac{d_3d_{13}T}{d_4\epsilon }\right) . \end{aligned}$$

Thus, the constructed model also experiences a direct coupling between curvature and matter parts. In this case, the symmetry generators and associated conserved quantities are

$$\begin{aligned} K_1= & {} 3\frac{\partial }{\partial t}+b\frac{\partial }{\partial b}, \quad \Sigma _1=\frac{1}{4d_3\epsilon }(-4ab^2\epsilon ^2d_3\dot{\phi }^2\\&+4d_{10}d_3\epsilon t+3\mathrm{tab}^2d_1RTd_3\epsilon \\&- 9\mathrm{tab}^2d_1Rp_\mathrm{m}d_3\epsilon +3\mathrm{tab}^2d_1R\rho _\mathrm{m} d_3\epsilon \\&-12td_1T\dot{a}\dot{b}bd_3\epsilon -4b^2d_4T\\&\times \dot{a}e^{-R}d_3\epsilon -4b^2a\dot{T} d_4e^{-R}d_3\epsilon \\&-9\mathrm{tab}^2d_4p_\mathrm{m}e^{-R}d_3\epsilon +3\mathrm{tab}^2d_4\rho _\mathrm{m}\\&\times e^{-R}d_3\epsilon + 6td_4Ta\dot{b}^2e^{-R}d_3\epsilon \\&+6td_4\mathrm{Taq}e^{-R}d_3\epsilon -4bd_4Ta\dot{b}e^{-R}d_3\epsilon \\&+4b^2a\dot{R}d_4Te^{-R} d_3\epsilon +4b^2a\dot{T}d_1d_3\epsilon \\&-12\mathrm{tab}^2 d_2d_1\epsilon -12\mathrm{tab}^2p_\mathrm{m}\\&\times d_3\epsilon +12\mathrm{tab}^2 V(\phi )d_3\epsilon \\&-24td_5a\dot{b}d_3\epsilon -24td_5aqd_3\epsilon +16bd_5a\dot{b} \\&\times d_3\epsilon +36\mathrm{tab}^2d_3^2d_4p_\mathrm{m}-12\mathrm{tab}^2d_3^2d_4\rho _\mathrm{m}\\&+18t\epsilon ^2d_2d_1a\dot{b}^2+18t\epsilon ^2 \\&\times d_2d_1aq -12b\epsilon ^2d_2d_1a\dot{b}+4b^2d_1T\dot{a}d_3\epsilon \\&-12b^2\epsilon ^2d_2d_1\dot{a}+16b^2d_5\\&\times \dot{a}d_3\epsilon -3\mathrm{tab}^2Rd_4Te^{-R}d_3\epsilon +12td_4T\dot{a}\dot{b}be^{-R} d_3\epsilon \\&+36t\epsilon ^2d_2d_1\dot{a}\dot{b}b\\&+ 4bd_1Ta\dot{b} d_3\epsilon +6\mathrm{tab}^2e\dot{\phi }^2d_3\epsilon \\&+18\mathrm{tab}^2d_1p_\mathrm{m}d_3\epsilon -6\mathrm{tab}^2d_1\rho _\mathrm{m}d_3\epsilon \\&-48td_5\dot{a}\dot{b}bd_3\epsilon -6td_1Ta\dot{b}^2 d_3\epsilon -6td_1\mathrm{Taq}d_3\epsilon ),\\ K_2= & {} a\frac{\partial }{\partial a}-\frac{b}{2}\frac{\partial }{\partial b},\quad \Sigma _2=-\frac{b}{2d_3}(-a\dot{b}d_1Td_3\\&\quad +3a\dot{b}\epsilon d_2d_1+a\dot{b}d_4Te^{-R}d_3\\&-4a\dot{b}d_5d_3+bd_1T\dot{a}d_3 +4bd_5\dot{a}d_3\\&-3b\epsilon d_2d_1\dot{a}-bd_4T\dot{a}e^{-R}d_3), \\ K_3= & {} -\frac{1}{\epsilon }\frac{\partial }{\partial \phi },\quad \Sigma _3=ab^2\dot{\phi },\quad K_4=2d_{12}\frac{\partial }{\partial \phi },\\&\quad \Sigma _4=2d_{12}ab^2\epsilon \dot{\phi }. \end{aligned}$$

We see that scaling symmetry appears through generator \(K_2\) with the first integral \(\Sigma _2\) leading to conserved linear momentum.

Now we investigate the existence of Noether symmetry in the absence of affine parameter and boundary term of the extended symmetry and also study the effect of direct curvature–matter coupling on conservation laws. For this purpose, we solve Eqs. (A5), (A6), (A9) and (A12)–(A21), which gives

$$\begin{aligned}&\delta = -\frac{a}{2Y_9(T),_{_T}}\bigg (\frac{1}{3}Y_4(a, b),_{ _a}\phi ^3\\&\quad +2Y_4(a, b),_{ _a}Y_9(T)\phi +2Y_4(a, b),_{ _a}Y_8(b)\phi \\&\quad +\phi ^2Y_5(a, b),_{ _a}+2Y_7(a, b),_{_a}\phi \bigg )\\&\quad +Y_{12}(a,R,T,b),\quad F(R)=k_4R+k_5,\\&\beta =-\frac{b}{2a}(Y_{10}(a, R,T,b)+aY_5(a, b)),\\&\quad g(T)=k_1+Y_9(T)k_2,\\&\eta = \frac{1}{2}(\phi ^2+2Y_9(T)+2Y_8(b))Y_4(a, b)\\&\quad +Y_5(a, b)\phi +Y_7(b, a),\\&h(R)=\frac{\epsilon R}{2(k_2+k_3)},\quad \gamma =Y_{11}(a,b,R,T),\\&\alpha =-Y_4(a, b)a\phi +Y_{10}(a,b,R,T), \end{aligned}$$

where the \(k_l\) (\(l=1,\ldots ,5\)) are arbitrary constants. Inserting these solutions into the remaining equations of the system, we obtain

$$\begin{aligned}&V(\phi )=k_{10}\phi +k_{11},\quad Y_{10}(a,R,T,b)=k_8a,\quad Y_4(a, b)= 0,\\&Y_{12}(a, R, T, b) = -\frac{k_8}{2k_2}((\epsilon (k_6T+k_7)+2k_4)k_2+\epsilon k_1),\\&Y_5(a, b)=-\frac{k_6k_8\epsilon }{2},\\&Y_7(b, a)= k_9,\quad Y_9(T) = k_6T+k_7, \\&p_\mathrm{m}=\frac{2k_9k_{10}}{\epsilon k_8k_6}-k_5+k_{11}+\frac{2k_2k_4k_3}{\epsilon }\nonumber \\&\quad +a^{-\frac{k_6\epsilon }{2}}\epsilon k_6ba^{\frac{1}{2}-\frac{\epsilon k_6}{4}}, \\&\rho _\mathrm{m}=\frac{k_7}{k_6}+\frac{6k_2k_4k_3}{\epsilon } -3k_5+3k_{11}+\frac{2k_4}{k_6\epsilon }+\frac{6k_9k_{10}}{k_8k_6\epsilon }+\frac{k_1}{k_2k_6}\\&\quad +a^{-\frac{k_6\epsilon }{2}}\epsilon k_6ba^{\frac{1}{2}-\frac{\epsilon k_6}{4}}. \end{aligned}$$

The corresponding Noether symmetry generator with the associated first integral take the form

$$\begin{aligned} K_1= & {} a\frac{\partial }{\partial a}-\frac{b}{2}\left( 1-\frac{k_6\epsilon }{2}\right) \frac{\partial }{\partial b}\\&+R\frac{\partial }{\partial R}-(k_1\epsilon +k_2(\epsilon (k_6T+k_7)+2k_4))\\\times & {} \frac{1}{2k_2}\frac{\partial }{\partial T}-\frac{k_6\epsilon \phi }{2}\frac{\partial }{\partial \phi },\quad \Sigma _1=ab\dot{b}\epsilon k_6T\\&-\frac{b^2\epsilon k_1\dot{a}}{k_2}-b^2\epsilon k_6T\dot{a}-ba\epsilon k_6k_4\dot{b}\\&-\frac{ba\epsilon ^2k_6^2T\dot{b}}{2} -\frac{ba\epsilon ^2k_6k_7\dot{b}}{2}+\frac{ab\dot{b}\epsilon k_1}{k_2}\\&+ab\dot{b}\epsilon k_7 -\frac{ba\epsilon ^2k_6k_1\dot{b}}{2k_2} -\frac{ab^2\epsilon ^2\dot{\phi }k_6\phi }{2}\\&+2ab\dot{b}k_4 -2b^2k_4\dot{a}-b^2\epsilon k_7\dot{a}+\frac{b^2a\epsilon ^2k_6^2\dot{T}}{2} ,\\ K_2= & {} \frac{\partial }{\partial \phi },\quad \Sigma _2=ab^2\epsilon \dot{\phi }k_9. \end{aligned}$$

Here the symmetry generator \(K_1\) yields the scaling symmetry.

4 Final remarks

In this paper, we have analyzed the existence of Noether symmetry in a non-minimally coupled f(R, T) gravity interacting with scalar field model for anisotropic homogeneous universe models like BI, BIII and KS models. Using Noether symmetry approach, we have found conserved quantities associated with symmetry generators and studied the contribution of direct as well as indirect curvature–matter coupling through two f(R, T) models. We have also formulated exact solutions for dust and perfect fluid distributions whose cosmological analysis is discussed through cosmological parameters.

For the f(R, T) model admitting indirect curvature–matter coupling, we have found three symmetry generators in the presence of an affine parameter and a boundary term. The first generator of translational symmetry in time yields the energy conservation law, whereas the second generator generates scaling symmetry. For the second model, we have formulated four conserved quantities associated with symmetry generators but only one generator provides the scaling symmetry leading to the conservation of linear momentum. In the absence of a boundary term of extended symmetry and an affine parameter, the symmetry generator of the first model ensures the existence of scaling symmetry for dust as well as perfect fluid, while we have found two symmetry generators for the second model.

For the first model, we have evaluated exact solutions without considering boundary term. For the dust distribution, we have found a power-law solution. The graphical analysis of scale factors and cosmological parameters leads to a decelerating phase of the universe. The positively increasing scalar field and the kinetic energy dominating over the potential energy ensure the decelerating behavior of the cosmos for the quintessence model. In the case of the phantom model, the scalar field rolls down positively and tends to increase negatively while the kinetic energy dominates over the potential energy for \(t\in [0.8,1.6]\). The graphical behavior of the effective EoS parameter reveals that the universe experiences a phase transition from a radiation dominated era to a dark energy era by crossing the matter dominated phase. For a perfect fluid, we have determined an oscillatory solution with increasing rate of the Hubble parameter, a negative deceleration parameter and \(\omega _\mathrm{eff}<-1\). The trajectories of the r–s parameters identify quintessence and phantom phases as \(s>0\) when \(r<1\). For the quintessence and phantom models, with the scalar field continuously increasing negatively, the potential energy of the field is dominating over the kinetic energy. This analysis indicates that an epoch of accelerated expansion is achieved for a non-dust distribution.

Shamir [17] investigated the exact solution of the BI model without using Noether symmetry approach in f(R, T) gravity. For indirect curvature–matter coupling, the exact solution is determined using a relationship between expansion and shear scalars. The study of corresponding cosmological parameters yields a positive deceleration parameter, \(\omega _\mathrm{eff}=1\), the volume and average scale factor turn out to be zero at \(t=0\). Thus, the analysis of this exact solution yields a decelerating epoch for the \(R+2f(T)\) model. For the \(f_1(R)+f_2(T)\) model, a power-law form of \(f_1(R)\) is considered that gives exponential and power-law solutions for different choices of \(f_2(T)\). For the exponential solution, the average Hubble parameter becomes zero, leading to the Einstein universe. Camci et al. [26] formulated exact solutions of these anisotropic models via the Noether symmetry approach in non-minimally scalar coupled gravity. The scale factors are found to be proportional to the inverse of the scalar field whose explicit form is not determined for any anisotropic model. Consequently, the cosmological analysis of these exact solutions is not established. In the present paper, we have found two exact solutions, power-law and oscillatory solutions, via the Noether symmetry approach, that correspond to decelerating as well as current accelerating universe for dust and non-dust distributions.

We conclude that the constructed f(R, T) models admit direct as well as indirect curvature–matter coupling. The existence of symmetry generators and associated conserved quantities is ensured for both f(R, T) models. It is worthwhile to mention here that we have found maximum symmetry generators along with conserved quantities for the second f(R, T) model in the presence of boundary term. This indicates that the model appreciating a direct curvature–matter coupling leads to more physical results relative to the first model, while the exact solutions describe cosmic evolution.