Is the color-octet mechanism consistent with the double $J/\psi$ production measurement at B-factories?

Abstract

Double $J/\psi$ production in $e^+e^-$ collisions involving color-octet channels are evaluated up to order $\alpha ^2\alpha _s^3$. Having implemented the variation of the parameters ($m_c$, $\mu _r$ and long-distance matrix elements), we found that the cross sections for producing double $J/\psi$ at B-factories range from $-0.016$ to 0.245 fb, which are even much smaller than that via the color-singlet mechanism. Accordingly, this result is consistent with the measurement by the Belle and BABAR Collaborations.

1 Introduction

The phenomenological study of the nonrelativistic QCD (NRQCD) effective theory [1] is making progress since the LHC started its running. Copious data not only provides evidence for the color-octet (CO) mechanism, but it also indicates challenges to the theory. In addition to the fact that the $J/\psi$ hadroproduction data can be well reproduced by the theoretical evaluations within the NRQCD framework [2,3,4], $\chi _c$ hadroproduction [5, 6] gives other strong support. In the low transverse momentum ($p_\mathrm{t}$) region, even though the factorization might not hold, the color-glass-condensate model [7,8,9] associated with NRQCD [10] did a good job in the description of the $J/\psi$ production in proton–proton and proton–nucleus collisions [11, 12]. Despite all the successes, we cannot overlook the challenges it is facing. The universality of the NRQCD long-distance matrix elements (LDMEs) has not yet been suggested in all the processes. As an example, the constraint [13] on the CO LDMEs indicated by the QCD next-to-leading order (NLO) study of the $J/\psi$ production at B-factories is apparently below the LDME values obtained through the fit of the $J/\psi$ production data at other colliders [3, 14,15,16]. The perspectives of the long-standing $J/\psi$ polarization puzzle still have not converged. Three groups [15, 17, 18] achieved the calculation of the $J/\psi$ polarization at hadron colliders at QCD NLO; however, with different LDMEs, their results are completely different from one another. Recently, the $\eta _c$ hadroproduction was measured by the LHCb Collaboration [19], which provides another laboratory for the study of NRQCD. Ref. [20] considers it as a challenge to NRQCD, while Refs. [21, 22] found this data to be consistent with the $J/\psi$ hadroproduction measurements. Further, with the constraint on the LDMEs obtained in Refs. [22, 23] discovered some interesting features of the $J/\psi$ polarization, and found a possibility of understanding the $J/\psi$ polarization within the NRQCD framework.

Fig. 1

Representative Feynman diagrams

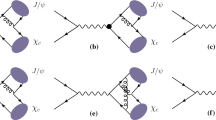
The $J/\psi$ pair production at B-factories is another challenge that NRQCD is facing. The Belle [24] and BABAR [25] Collaborations observed the process $e^+e^-\rightarrow J/\psi +$charmonium, and found no evidence for the $J/\psi$ pair events, while the QCD leading order (LO) calculation based on the color-singlet (CS) mechanism predicted a significant production rate [26,27,28,29]. This was understood by the QCD NLO corrections [30], which contribute a negative value and cancel the large LO cross sections. Reference [31] studied the resummation of the relativistic corrections to double $J/\psi$ production at B-factories, and one found that their results are also consistent with the measurements. Reference [30] only addressed the CS contributions. However, the Belle and BABAR measurements actually did not exclude the double $J/\psi$ plus light hadron events. Both of the experiments measured the $M_{\mathrm{res}}$ spectrum, where $M_{\mathrm{res}}$ denotes the invariant mass of all the final states except for the fully reconstructed $J/\psi$. These distributions exhibited no significant excess in the range of about 300 MeV above the $J/\psi$ mass, which suggested that the cross section for the $J/\psi$ pair plus light hadron (e.g. $\pi ^0$, $\pi ^+\pi ^-$) associated production is also too small to observe. To accord with NRQCD, the double $J/\psi$ production cross sections involving the CO channels must not be significant, which, however, is not manifest. Although suppressed by the CO LDMEs, the double $J/\psi$ yield due to the CO mechanism is enhanced by the powers of $\alpha _s/\alpha$, relative to via the CS channels. As is pointed out in Refs. [26, 30], at B-factories, double $c\bar{c}(^3S_1^{[1]})$ can be produced via two virtual photons generated through $e^+e^-$ annihilation, and the LO contribution is of order $\mathcal{O}(\alpha ^4\alpha _s^0)$. In contrast, as illustrated in Fig. 1a–c), the diagrams for the processes

$$\begin{aligned} e^+e^-\rightarrow c\bar{c}(m_1)+c\bar{c}(m_2), \end{aligned}$$

(1)

when $n_1$ and $n_2$ have the opposite charge conjugation, involve only a single virtual photon, and the LO contribution is of order $\mathcal{O}(\alpha ^2\alpha _s^2)$. For double $J/\psi$ production, $m_1$ and $m_2$ have only two possible configurations, which are $m_1=^3S_1^{[8]}$ and $m_2=^1S_0^{[8]}$, and $m_1=^3S_1^{[8]}$ and $m_2=^3P_J^{[8]}$. These two processes are suppressed by the CO LDMEs by a factor of $v^8\approx 0.002$, where v is the typical charm-quark velocity in the charmonium rest frame, however, enhanced by the coupling constants by a factor of $\alpha _s^2/\alpha ^2\approx 1000$, relative to via the CS channels. The double $J/\psi$ can also be produced through such a kind of process,

$$\begin{aligned} e^+e^-\rightarrow c\bar{c}(n_1)+c\bar{c}(n_2)+g, \end{aligned}$$

(2)

where g denotes a gluon. When $n_1=^3S_1^{[1]}$ and $n_2=^3S_1^{[8]}$ (or equivalently $n_1=^3S_1^{[8]}$ and $n_2=^3S_1^{[1]}$), this kind of processes is enhanced by the coupling constants by a factor of $\alpha _s^3/\alpha ^2\approx 200$ and reduced by the CO LDME by a factor of $v^4\approx 0.05$, relative to the processes involving only the CS channels. In sum, the processes involving CO states are enhanced by a synthetic factor of about 2–10, compared with the processes considered in Refs. [26, 30], the LO cross sections of which is large enough to be observed by Belle and BABAR experiments. Accordingly, we need to calculate the cross sections for the $J/\psi$ pair production involving the CO channels to see whether NRQCD can endure this paradox.

Table 1 Possible Feynman diagrams for each of the final-state-gluon-emission processes. The processes are abbreviated to the numbers of the equations, namely Eqs. (4), (5), (6), (7), (8), (9), in which the processes are presented

In this work, we will present a comprehensive study of the double $J/\psi$ production in $e^+e^-$ annihilation involving CO channels up to order $\mathcal {O}(\alpha ^2\alpha _s^3)$, and we check whether it is consistent with the measurements by Belle and BABAR Collaborations. The $J/\psi$ plus $\chi _c$ production at B-factories has already been studied in Refs. [32,33,34], and their results do not contradict the double $J/\psi$ measurements by Belle and BABAR Collaborations, regarding the branching ratios $\mathcal {B}(\chi _{c[0,1,2]}\rightarrow J/\psi )=[1.27$, 33.9, 19.2$\%]$ [35]. In this paper, we do not calculate the $c\bar{c}(^3S_1^{[1]})+c\bar{c}(^3P_J^{[1]})$ production. We also notice that the $J/\psi$ may come from the $\chi _{cJ}$ feed down, where the $\chi _{cJ}$ can be produced via the $^3S_1^{[8]}$ channel. By employing the LDMEs obtained in Refs. [6, 23], $\langle O^{\chi _{c0}}(^3S_1^{[8]})\rangle =2.01\times 10^{-3}\mathrm {~GeV}^3$ and $\langle O^{J/\psi }(^3S_1^{[8]})\rangle =1.08\times 10^{-2}\mathrm {~GeV}^3$ in association with the branching ratios listed above, we find that this contribution is much smaller than that from the $J/\psi$ directly produced through the $^3S_1^{[8]}$ channel. Similarly, the $J/\psi$ production cross sections via the $\psi (2s)$ feed down is also smaller than that for the directly produced ones. For this reason, we completely omit the discussions on the feed down contributions from both $\chi _c$ and $\psi (2s)$.

The rest of this paper is organized as follows. In Sect. 2, we outline the formalism of the calculation. Section 3 presents the numerical results and related discussions, followed by a concluding remark in Sect. 4.

2 Double $J/\psi$ production in NRQCD framework

Following the NRQCD factorization, the total cross sections for the $J/\psi$ pair production can be expressed as

$$\begin{aligned}&\sigma (e^+e^-\rightarrow J/\psi +J/\psi +X)\nonumber \\&\quad =\sum _{n_1,n_2}\hat{\sigma }(e^+e^-\rightarrow c\overline{c}(n_1)+c\overline{c}(n_2)+X)\nonumber \\&\quad \quad \times \langle O^{J/\psi }(n_1)\rangle \langle O^{J/\psi }(n_2)\rangle , \end{aligned}$$

(3)

where $n_1$, $n_2$ run over all the possible configurations of the $c\overline{c}$ intermediate states with certain color and angular momentum, $\hat{\sigma }$ is the short-distance coefficient (SDC), and $\langle O^{J/\psi }(n_1)\rangle$ and $\langle O^{J/\psi }(n_2)\rangle$ are the corresponding LDMEs. When at least one of $n_1$ and $n_2$ is a CO state, the LO contributions are of order $\mathcal {O}(\alpha _s^2\alpha ^2)$. At this order, all the processes have the form of Eq. (1), in which the only possible configurations of $m_1$ and $m_2$ are $m_1=^3S_1^{[8]}$, $m_2=^1S_0^{[8]}$ and $m_1=^3S_1^{[8]}$, $m_2=^3P_J^{[8]}$, and the representative Feynman diagrams are illustrated in Fig. 1a–c. At QCD NLO ($\mathcal {O}(\alpha _s^3\alpha ^2)$), in addition to the virtual corrections (the representative Feynman diagrams for which are shown in Fig. 1d–f) to the processes presented in Eq. (1), double $c\bar{c}$ states in association with a gluon production are also required for consideration, as illustrated in Eq. (2). The real-correction processes to the LO ones are

$$\begin{aligned} \begin{aligned}&e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^1S_0^{[8]})+g, \\&e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^3P_J^{[8]})+g, \end{aligned} \end{aligned}$$

(4)

in addition to which five processes are also at this order, as listed below, and they will be calculated in our paper. We have

$$\begin{aligned} e^+e^-\rightarrow c\overline{c}(^3S_1^{[1]})+ c\overline{c}(^3S_1^{[8]})+g, \end{aligned}$$

(5)

$$\begin{aligned} e^+e^-\rightarrow c\overline{c}(^1S_0^{[8]})+ c\overline{c}(^1S_0^{[8]})+g, \end{aligned}$$

(6)

$$\begin{aligned} e^+e^-\rightarrow c\overline{c}(^3S_1^{[8]})+ c\overline{c}(^3S_1^{[8]})+g, \end{aligned}$$

(7)

$$\begin{aligned} e^+e^-\rightarrow c\overline{c}(^1S_0^{[8]})+ c\overline{c}(^3P_J^{[8]})+g, \end{aligned}$$

(8)

$$\begin{aligned} e^+e^-\rightarrow c\overline{c}(^3P_J^{[8]})+ c\overline{c}(^3P_J^{[8]})+g. \end{aligned}$$

(9)

The representative Feynman diagrams for the final-state-gluon-emission processes are presented in Fig. 1g–i. However, not all the processes have the three types of diagrams. So, we summarize the possible diagrams for each of the processes in Table 1.

Before we present the numerical results, we first address the divergences rising from the processes listed above. First of all, the LO processes are divergence free, and we denote their total cross sections as $\sigma ^{LO}=\sigma ^{LO}_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^{LO}_{^3S_1^{[8]}+^3P_J^{[8]}}$. The virtual corrections to $\sigma ^{LO}$ contain both ultraviolet (UV) and infrared (IR) divergences. The UV divergences can be eliminated through the renormalization procedure, while the IR divergences will be canceled by those emerging in the real corrections, the processes for which are presented in Eq. (4). We denote the renormalized virtual-correction total cross sections as $\sigma ^V=\sigma ^V_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^V_{^3S_1^{[8]}+^3P_J^{[8]}}$, and the real corrections to $\sigma ^{LO}$ as $\sigma ^R=\sigma ^R_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^R_{^3S_1^{[8]}+^3P_J^{[8]}}$. The complete QCD NLO corrections to $\sigma ^{LO}$ can be expressed as

$$\begin{aligned} \sigma ^{NLO}\equiv \sigma ^V+\sigma ^R=\sigma ^{NLO}_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^{NLO}_{^3S_1^{[8]}+^3P_J^{[8]}}, \end{aligned}$$

(10)

where

$$\begin{aligned} \begin{aligned}&\sigma ^{NLO}_{^3S_1^{[8]}+^1S_0^{[8]}}=\sigma ^V_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^R_{^3S_1^{[8]}+^1S_0^{[8]}}, \\&\sigma ^{NLO}_{^3S_1^{[8]}+^3P_J^{[8]}}=\sigma ^V_{^3S_1^{[8]}+^3P_J^{[8]}}+\sigma ^R_{^3S_1^{[8]}+^3P_J^{[8]}}. \end{aligned} \end{aligned}$$

(11)

Both $\sigma ^{NLO}_{^3S_1^{[8]}+^1S_0^{[8]}}$ and $\sigma ^{NLO}_{^3S_1^{[8]}+^3P_J^{[8]}}$ are divergence free. The total cross sections for the $J/\psi$ pair production through $^3S_1^{[8]}+^1S_0^{[8]}$ and $^3S_1^{[8]}+^3P_J^{[8]}$ channels are the sum of their LO and NLO contributions.

$$\begin{aligned} \begin{aligned}&\sigma _{^3S_1^{[8]}+^1S_0^{[8]}}=\sigma ^{LO}_{^3S_1^{[8]}+^1S_0^{[8]}}+\sigma ^{NLO}_{^3S_1^{[8]}+^1S_0^{[8]}}, \\&\sigma _{^3S_1^{[8]}+^3P_J^{[8]}}=\sigma ^{LO}_{^3S_1^{[8]}+^3P_J^{[8]}}+\sigma ^{NLO}_{^3S_1^{[8]}+^3P_J^{[8]}}. \end{aligned} \end{aligned}$$

(12)

Note that we adopt the on-shell (OS) renormalization scheme for the renormalization of c-quark mass and the wave functions of the c-quark and gluon, and the modified-minimum-subtraction ($\overline{MS}$) scheme for that of the QCD coupling constant, which coincide with Ref. [36]. The corresponding renormalization constants, $Z_m^{OS}$ (for the c-quark mass), $Z_2^{OS}$ (for the c-quark wave function), $Z_3^{OS}$ (for the gluon wave function), and $Z_g^{\overline{MS}}$ (for the QCD coupling constant), are

$$\begin{aligned} \begin{aligned}&\delta Z^{OS}_{m}=-3C_{F}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{UV}}-\gamma _{E}+\ln \frac{4\pi \mu ^{2}_{r}}{m^{2}_{c}}+\frac{4}{3}\right] , \\&\delta Z^{OS}_{2}=-C_{F}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{UV}}+\frac{2}{\epsilon _{IR}}-3\gamma _{E}+3\ln \frac{4\pi \mu ^{2}_{r}}{m^{2}_{c}}+4\right] , \\&\delta Z^{OS}_{3}=\frac{\alpha _{s}}{4\pi }\left[ (\beta '_{0}-2C_{A})\left( \frac{1}{\epsilon _{UV}}-\frac{1}{\epsilon _{IR}}\right) \right. \\&\quad \quad \quad \quad \quad -\frac{4}{3}T_F\left( \frac{1}{\epsilon _{UV}}-\gamma _{E}\left. +\ln \frac{4\pi \mu ^{2}_{r}}{m^{2}_{c}}\right) \right] , \\&\delta Z^{\overline{MS}}_{g}=-\frac{\beta _{0}}{2}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{UV}}-\gamma _{E}+\ln (4\pi )\right] , \end{aligned} \end{aligned}$$

(13)

where $\mu _r$ is the renormalization scale, $\gamma _E$ is Euler’s constant, $\beta _0=\frac{11}{3}C_A-\frac{4}{3}T_Fn_f$ is the one-loop coefficient of the QCD beta function, $n_f$ is the number of active quark flavors. In SU(3)$_c$, color factors are given by $T_F=\frac{1}{2}$, $C_F=\frac{4}{3}$, $C_A=3$, and $\beta '_{0}\equiv \beta _{0}+(4/3)T_F=(11/3)C_A-(4/3)T_Fn_{lf}$, where $n_{lf}\equiv n_f-1 =3$ is the number of light quark flavors. Actually, in the NLO total amplitude level, the terms proportional to $\delta Z^{OS}_{3}$ cancel each other; thus the result is independent of the renormalization scheme of the gluon field.

The cross sections for the processes listed in Eqs. (8) and (9) also have divergences, which, however, can be eliminated through the renormalization of the SDCs for them. We take the process (8) as an example. The cancellation of its divergences requires the calculation of the NLO corrections to $\langle O^{J/\psi }(^3S_1^{[8]})\rangle$. The bare LDME can be expressed as

$$\begin{aligned} \langle O^{J/\psi }(^3S_1^{[8]})\rangle _{\mathrm{bare}}= & {} \langle O^{J/\psi }(^3S_1^{[8]})\rangle -\frac{\alpha _s}{\pi m_c^2}\frac{N_c^2-4}{N_c}\nonumber \\&\times \left( \frac{1}{\epsilon _{IR}}-\frac{1}{\epsilon _{UV}}\right) \langle O^{J/\psi }(^3P_0^{[8]})\rangle ,\nonumber \\ \end{aligned}$$

(14)

where $m_c$ is the c-quark mass, and $N_c=3$ for SU(3) gauge theory. Here we adopt the $\mu _\Lambda$-cutoff renormalization scheme [6] to subtract the UV divergence. By substituting the relation between the bare and renormalized LDMEs,

$$\begin{aligned}&\langle O^{J/\psi }(^3S_1^{[8]})\rangle _{\mathrm{bare}}\nonumber \\&\quad =\langle O^{J/\psi }(^3S_1^{[8]})\rangle _{\mathrm{renorm}}+\frac{\alpha _s}{\pi m_c^2}\frac{N_c^2-4}{N_c} \nonumber \\&\quad \quad \times \left( \frac{1}{\epsilon _{UV}}-\gamma _E+\frac{5}{3}+ln\left( \frac{\pi \mu ^2}{\mu _\Lambda ^2}\right) \right) \langle O^{J/\psi }(^3P_0^{[8]})\rangle , \nonumber \\ \end{aligned}$$

(15)

into Eq. (14), we obtain the renormalized LDME as

$$\begin{aligned}&\langle O^{J/\psi }(^3S_1^{[8]})\rangle _{renorm}\nonumber \\&\quad =\langle O^{J/\psi }(^3S_1^{[8]})\rangle -\frac{\alpha _s}{\pi m_c^2}\frac{N_c^2-4}{N_c} \nonumber \\&\quad \quad \times \left( \frac{1}{\epsilon _{IR}}-\gamma _E+\frac{5}{3}+ln\left( \frac{\pi \mu ^2}{\mu _\Lambda ^2}\right) \right) \langle O^{J/\psi }(^3P_0^{[8]})\rangle . \nonumber \\ \end{aligned}$$

(16)

Then process $e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^1S_0^{[8]})$ contributes an additional divergent term,

$$\begin{aligned}&\sigma _{div}(e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^1S_0^{[8]}))\nonumber \\&\quad =-\frac{\alpha _s}{\pi m_c^2}\frac{N_c^2-4}{N_c}\left( \frac{1}{\epsilon _{IR}}-\gamma _E+\frac{5}{3}+ln\left( \frac{\pi \mu ^2}{\mu _\Lambda ^2}\right) \right) \nonumber \\&\quad \quad \times \, \hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^1S_0^{[8]}))\langle O^{J/\psi }(^3P_0^{[8]})\rangle , \nonumber \\ \end{aligned}$$

(17)

which cancels the IR singularities arising from the process (8). In this sense, we can redefine the SDC for the process (8) as

$$\begin{aligned}&\hat{\sigma }_{\mathrm{renorm}}(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_J^{[8]})+g)\nonumber \\&\quad =\hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_J^{[8]})+g) \nonumber \\&\quad \quad -\frac{\alpha _s}{\pi m_c^2}\frac{N_c^2-4}{N_c}\left( \frac{1}{\epsilon _{IR}}-\gamma _E+\frac{5}{3}+ln\left( \frac{\pi \mu ^2}{\mu _\Lambda ^2}\right) \right) \nonumber \\&\quad \quad \times \, \hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^3S_1^{[8]})+c\bar{c}(^1S_0^{[8]})), \end{aligned}$$

(18)

where

$$\begin{aligned}&\hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_J^{[8]})+g)\nonumber \\&\quad =\hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_0^{[8]})+g) \nonumber \\&\quad \quad +\,3\hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_1^{[8]})+g)\nonumber \\&\quad \quad +\,5\hat{\sigma }(e^+e^-\rightarrow c\bar{c}(^1S_0^{[8]})+c\bar{c}(^3P_2^{[8]})+g) \end{aligned}$$

(19)

has been implicated in Eq. (18) (the same convention applies to the SDCs with the subscript “renorm”). $\hat{\sigma }_{\mathrm{renorm}}$ is a finite quantity, therefore, we can replace, in Eq. (3), the divergent one by it. The same operation can be done for the process (9) as well. Then we denote all the divergence-free total cross sections for the processes listed in Eqs. (5), (6), (7), (8), (9) as $\sigma _{n_1+n_2}$, where $n_1$ and $n_2$ are the corresponding $c\bar{c}$ states.

3 Numerical results

In our analytic calculation, we use our Mathematica package with the employment of FeynArts [37], FeynCalc [38], FIRE [39] and Apart [40]. As a cross check, we also compute the processes using the FDC package [41], except for the process (9). To subtract the IR divergences in the gluon-emission processes, we adopt the two-cutoff slicing strategy [42]. The independence of the cutoff has been checked.

We have the following global choices of the parameters in our calculation: $\alpha =1/137$, and the colliding energy of the electron and positron is $\sqrt{s}=10.6\mathrm {~GeV}$. The $J/\psi$ mass is fixed to $M_{J/\psi }=2m_c$ to keep the gauge invariance. The default values of $m_c$ and the renormalization scale ($\mu _r$) are $m_c=1.5\mathrm {~GeV}$ and $\mu _r=3.0\mathrm {~GeV}$, respectively. Since we investigate the $\mu _r$ dependence of the total cross sections, the two-loop running $\alpha _s$ is employed in our computation. The values of the SDCs for all the processes are listed in Table 2, where the SDCs for the $^3P_J^{[8]}$ channels are defined by multiplying a factor of $m_c^2$ to those defined in Ref. [1], in order to keep the homogeneity of the dimensions (for double $^3P_J^{[8]}$ production, this factor should be $m_c^4$). The LO SDCs for $^1S_0^{[8]}+^3S_1^{[8]}$ and $^3S_1^{[8]}+^3P_J^{[8]}$ productions are 60.07 and $290.9\mathrm {~fb}/\mathrm{GeV}^6$, respectively.

Table 2 The values of $\hat{\sigma }_{n_1+n_2}$ in ($\mathrm {~fb}/\mathrm{GeV}^6$) up to order $\mathcal {O}(\alpha ^2\alpha _s^3)$. The convention introduced in Eq. (19) is adopted labeltab

Table 3 The values of $\sigma _{n_1+n_2}$ in ($\mathrm {~fb}$) up to order $\mathcal {O}(\alpha ^2\alpha _s^3)$. The convention introduced in Eq. (19) is adopted. The LDMEs are taken from Refs. [22, 23]

Employing the LDMEs obtained in Refs. [22, 23], namely

$$\begin{aligned}&\langle O^{J/\psi }(^3S_1^{[1]})\rangle =0.65 \mathrm {~GeV}^3 \nonumber \\&\langle O^{J/\psi }(^1S_0^{[8]})\rangle =0.78\times 10^{-2} \mathrm {~GeV}^3 \nonumber \\&\langle O^{J/\psi }(^3S_1^{[8]})\rangle =1.08\times 10^{-2} \mathrm {~GeV}^3 \nonumber \\&\langle O^{J/\psi }(^3P_0^{[8]})\rangle /m_c^2 =2.01\times 10^{-2} \mathrm {~GeV}^3 \end{aligned}$$

(20)

we list the cross sections for each channel in Table 3.

Fig. 2

$\sigma$ as a function of $m_c$. The renormalization scale is fixed to $\mu _r=3.0\mathrm {~GeV}$

Fig. 3

$\sigma$ as a function of $\mu _r$. The c-quark mass is fixed to $m_c=1.5\mathrm {~GeV}$

Table 4 The total cross sections for the double $J/\psi$ inclusive production in $e^+e^-$ annihilation at B-factory energy employing different sets of the LDMEs. The values of the LDMEs are taken from Refs. [14,15,16, 18]. The first, second and third uncertainties are from the charm mass, the renormalization scale and the uncertainties of the LDMEs.

The total cross section for double $J/\psi$ production at B-factories up to order $\mathcal {O}(\alpha ^2\alpha _s^3)$ is the sum of those for different channels. Note that the two processes which are symmetric in the sense of switching $n_1$ and $n_2$ are only counted once to avoid the double counting. We obtain this value as $\sigma =0.118\mathrm {~fb}$. As a comparison, we list the results of the exclusive double $J/\psi$ production cross sections at B-factories given in Ref. [30]. Adopting different values of $m_c$ and $\mu _r$, the QCD NLO results range from $-3.350$ to $2.312\mathrm {~fb}$, comparing with which, our results on the double $J/\psi$ production in association with light hadrons are even smaller. The constraint on the double $J/\psi$ production cross section given in Ref. [24] is $\sigma (J/\psi +\hbox {res})\times \mathcal {B}_{>2}\!\!<\!\!9.1\mathrm {~fb}$, where $\mathcal {B}_{>2}$ denotes the branching fraction for final states with more than two charged tracks. Apparently, our results are consistent with the Belle measurement.

To investigate the uncertainties brought about by the two scales, we vary $m_c$ from 1.2 to 1.7$\mathrm {~GeV}$ and $\mu _r$ from $3.0\mathrm {~GeV}$ to $\sqrt{s}/2$ and calculate the corresponding total cross sections. When one of these scales varies its value, the other is fixed. Note that the LDMEs used in our calculation are obtained with the configuration $m_c\!=\!1.5\mathrm {~GeV}$. When investigating the $m_c$ dependence, we need to take the scaling rule, $\langle O^{J/\psi }(n)\rangle \propto m_c^3$, into account.

The total cross section as a function of the charm-quark mass $m_c$ is presented in Fig. 2. We can see that the $^3S_1^{[8]}+^3P_J^{[8]}$ and $^3P_J^{[8]}+^3P_J^{[8]}$ channels provide the largest contributions, while the others have smaller contributions with visible hierarchy. Especially, both the $^1S_0^{[8]}+^3P_J^{[8]}+g$ and the $^3P_J^{[8]}+^3P_J^{[8]}+g$ cross sections are negative. The total cross section increases from about 0.09$\mathrm {~fb}$ to about $0.15\mathrm {~fb}$ as $m_c$ increases from 1.2 to $1.7\mathrm {~GeV}$. The $\mu _r$ dependence of the total cross section is presented in Fig. 3, and the $\sigma$ decreases from 0.118$\mathrm {~fb}$ to 0.09$\mathrm {~fb}$ as $\mu _r$ increases from $3.0\mathrm {~GeV}$ to $\sqrt{s}/2$. The dependence on the two scales is not strong, which indicates good convergence of the perturbative expansion.

Since there are several parallel extractions of the LDMEs, we need to investigate the uncertainties brought about by the different values of them. In Table 4, we present the results for four sets of the LDMEs, associated with the uncertainties arising from the variation of $m_c$ and $\mu _r$. The first, second and third uncertainties are from $m_c$, $\mu _r$ and the uncertainties of the LDMEs. The values of the errors presented here are the largest deviation of the cross sections from the default value when one of the parameters vary from its minimum to maximum values, while the other two parameters are fixed. In our calculation, $m_c$ ranges from 1.2 to $1.7\mathrm {~GeV}$ and $\mu _r$ ranges from $3.0\mathrm {~GeV}$ to $\sqrt{s}/2=5.8\mathrm {~GeV}$. As is shown in Table 4, the total cross sections obtained by using the LDMEs in Ref. [16] are almost the double of ours; however, they are still too small to be observed by the experiment.

4 Summary and conclusion

We calculated the total cross sections for double $J/\psi$ production in $e^+e^-$ annihilation at the B-factory energy up to $\mathcal {O}(\alpha ^2\alpha _s^3)$ within the framework of NRQCD. We studied the $m_c$ and $\mu _r$ dependence of the total cross sections, and found that the results ranges from 0.09 to $0.15\mathrm {~fb}$. Also, we investigated the uncertainties by trying different sets of the LDMEs. Even for the largest results, the total cross section is too small for Belle to observe any significant access. This result is consistent with the Belle measurement.