$\gamma \gamma \rightarrow M^{+}M^{-}(M=\pi , K)$ processes with twist-3 corrections in QCD

Abstract

We study the $\gamma \gamma \rightarrow M^{+}M^{-}(M=\pi , K)$ processes with the contributions from the two-particle twist-2 and twist-3 distribution amplitudes of pion and kaon mesons on BHL prescription in the standard hard-scattering approach. The results show that the contributions from twist-3 parts are actually not power suppressed compared with the leading-twist contributions in the low energy region. The cross sections with twist-3 corrections agree well with the experimental data in the two-photon center-of-mass energy $W>2.8$ GeV and we also predict the cross section ratio $\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})$, which is compatible with the experimental data from TPC and Belle.

1 Introduction

The common method of calculating hard exclusive processes in Quantum Chromodynamics (QCD) was developed in Refs. [1,2,3,4,5]. Especially, the exclusive processes at large momentum transfer have aroused much attention [3, 4] in the last few years. In pioneering work, Brodsky and Lepage [4, 5] put forward a systematic analysis, involving angular dependence, helicity structure, normalization of elastic and inelastic form factors and large-angle exclusive scattering amplitudes for hadrons and photons.

It is well known that the exclusive processes at large momentum transfer can afford a definite theoretical test for perturbative QCD. The two-photon processes, such as $\gamma ^{*}\gamma \rightarrow$ hadrons and $\gamma \gamma \rightarrow$ hadron pairs at large momentum transfer, have attracted much attention in theoretical [5,6,7,8,9,10] and experimental [11,12,13,14,15,16] fields over the past few decades. Due to the pointlike structure of the photon, the initial states are simple and controllable, and the strong interactions are presented only in final states. Such a structure not only has an important role in understanding the nonperturbative construction of QCD, but it also brings about convenience in the analysis of these exclusive hard-scattering amplitudes and perturbative mechanisms.

Fig. 1

Feynman diagrams for hard QCD contributions to $\gamma \gamma \rightarrow M^{+}M^{-}$

In this work, we focus on the two-photon annihilation into pseudoscalar mesons $\gamma \gamma \rightarrow M^{+}M^{-}$. However, what is troubling theorists is that the cross sections predicted in theory are noticeably below the experimental data [14]. Brodsky et al. provided the predicted results [5] as a $\sin ^{-4}\theta$ dependence of the differential cross section and a $W^{-6}$ dependence of the total cross section. Similar theoretical predictions have been put forward in Chernyak’s series of works on the two-photon exclusive processes [9, 10]. In 1986, Nižić [17] was the first researcher to calculate the one-loop corrections for the two-photon exclusive channels at large momentum transfer; then Goran Duplan$\check{\mathrm{c}}$i$\acute{\mathrm{c}}$ [18] perfected the leading-twist next-to-leading-order (NLO) radiative corrections. Their calculations indicated that the NLO corrections slightly change the leading-order predictions.

The early experimental work [11] has been suggested to test a QCD calculation in the model proposed by Brodsky and Lepage. Increasing interests in this problem, more experimental groups, for instance TPC [11], ALEPH [12], Belle [13,14,15] and so on have been attracted to address and present results of the theoretical analysis. Especially, the Belle Collaboration systematically measured the two-photon collisions at the center-of-mass energy $2.4~\mathrm{GeV}<W<4.1~\mathrm{GeV}$ and the scattering-angle region $|\cos \theta |<0.6$ [14]. This reaction will be studied with high precision at Belle-II in the near future; further theoretical research is particularly important.

Besides the QCD radiation correction [17, 18], which is very minor in this process, the next-leading-order correction can also come from high Fock states or high twist distribution amplitudes of the hadron, and the latter is considered in our work. From the naive point of view, the contributions of high twist distribution amplitudes are suppressed by the factor $1/Q^{2}$ for exclusive processes with large momentum transfer Q, but that has not always been the case. For example, the contributions from twist-3 distribution amplitudes are comparable with or even larger than the one from the leading-twist distribution amplitude of light pseudoscalar meson in the $\chi _{cJ}\rightarrow \pi ^{+}\pi ^{-}, K^{+}K^{-}$ decay channels [19] and the pion/kaon electromagnetic form factor [20, 21]. More discussion of the high twist corrections of vector mesons is presented in Refs. [22,23,24]. In this work, the main experimental data of $\gamma \gamma \rightarrow M^{+}M^{-}$ processes comes from the center-of-mass energy W below $4.0~\mathrm{GeV}$ and the momentum transfer is not large enough. So it is necessary to investigate the contributions from the two-particle high twist distribution amplitudes for those channels. Performing the standard calculation of the matrix element in the hard-scattering approach [5], one can easily find that the contributions from the twist-3 version are double-logarithmically divergent with the usual pion distribution amplitudes (DAs) [25, 26], which can be obtained by using a conformal expansion. Similar to the calculation of the electromagnetic form factor of the pion [27], this divergence can be removed by retaining the transverse momentum (${{\mathbf {k}}}_{\bot }$) dependence of hard-scattering amplitude ($T^{ij}$) and the dangerous soft regions are suppressed by the Sudakov factor. However, the Fourier transform of the hard-scattering amplitude becomes difficult in this situation. For an estimate of the twist-3 effect, we use the Brodsky–Huang–Lepage (BHL) prescription for the harmonic-oscillator wave function (WF) [28,29,30,31] in this paper, since the BHL DAs have a better endpoint behavior in the soft regions. Our results also indicate that the twist-3 distribution amplitudes of the pion and kaon make significant contributions at the energy region $W\in (1,6)$ GeV.

The structure of this paper is as follows. In Sect. 2, we present our calculation of the hard-scattering amplitude at tree level. A brief model of the twist-2 and twist-3 distribution amplitudes with BHL scheme is presented in Sect. 3. Section 4 is the numerical analysis and the last section is the conclusion to this work. The hard-scattering amplitudes for $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}, K^{+}K^{-}$ are given in Appendix A.

2 Calculation of hard-scattering amplitudes

In this section, we want to recalculate the hard-scattering amplitudes for

$$\begin{aligned}&\gamma _{1}(p_{1},\varepsilon ^{\lambda _{1}}_{1})+\gamma _{2}(p_{2}, \varepsilon ^{\lambda _{2}}_{2}) \rightarrow M^{+}(p_{3})+M^{-}(p_{4}),\nonumber \\&\qquad (M=\pi ,K) \end{aligned}$$

(1)

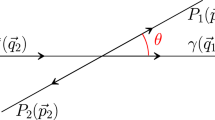
where the initial photons are real with the different polarization and the final states are flavor-nonsinglet helicity-zero mesons. $p_{1},p_{2}$ and $p_{3},p_{4}$ are four-momenta for the initial photons and the final pseudoscalar mesons, respectively. $\varepsilon ^{\lambda _{1}}_{1}(\varepsilon ^{\lambda _{2}}_{2})$ are the photons’ polarization and the $\lambda _{1}(\lambda _{2})=\pm 1$ represent two transversal photons. This process is described by the $\gamma \gamma \rightarrow (q\overline{q})+(q\overline{q})$ amplitude which is illustrated by two typical lowest order Feynman diagrams in Fig. 1. The other 18 diagrams, which can be obtained by exchanging the photons, gluons and quark lines, are not shown in the paper.

In the two-photon center-of-mass frame, we choose the direction of two-photon collision as the Z-axis with the total energy denoted by W and the scattering angle denoted by $\theta$. The four-momenta of incoming and outgoing particles are given as follows:

$$\begin{aligned}&p_{1}=\frac{W}{2}(1,0,0,1),\quad p_{2}=\frac{W}{2} (1,0,0,-1),\nonumber \\&\quad p_{3}=\frac{W}{2}(1,\sin \theta ,0,\cos \theta ),\nonumber \\&\quad p_{4}=\frac{W}{2}(1,-\sin \theta ,0,-\cos \theta ), \end{aligned}$$

(2)

where the masses of pion and kaon are vanish in the chiral limit. The polarization states of the photons are taken to be

$$\begin{aligned}&\varepsilon _{1}^{+}(p_{1})\!=\!\frac{1}{\sqrt{2}}(0,-1,-i,0),\quad \varepsilon _{1}^{-}(p_{1})\!=\!\frac{1}{\sqrt{2}}(0,1,-i,0),\nonumber \\&\varepsilon _{2}^{+}(p_{2})\!=\!\frac{1}{\sqrt{2}}(0,1,-i,0),\quad \varepsilon _{2}^{-}(p_{2})\!=\!\frac{1}{\sqrt{2}}(0,-1,-i,0).\nonumber \\ \end{aligned}$$

(3)

With the above choices, we work out the expression of cross section with the two-particle twist-3 distribution amplitudes of the final pion mesons in the hard-scattering approach [5] and it is written as

$$\begin{aligned}&\frac{\mathrm{d}\sigma (\gamma \gamma \rightarrow \pi ^{+}\pi ^{-})}{\mathrm{d} \cos \theta }=\frac{1}{32\pi W^{2}}\frac{1}{4}\sum _{\lambda _{1},\lambda _{2}=\pm 1} |A_{\lambda _{1}\lambda _{2}}|^{2},\end{aligned}$$

(4)

$$\begin{aligned}&A_{\lambda _{1}\lambda _{2}}(W,\theta )=\int _{0}^{1}\int _{0}^{1}\mathrm{d}x\mathrm{d}y \sum _{ij}\phi ^{i}_{\pi }(x,\mu _{F}^2)\nonumber \\&\quad \times T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )\phi ^{j}_{\pi }(y,\mu _{F}^2), \end{aligned}$$

(5)

where $A_{\lambda _{1}\lambda _{2}}$ is the transitional matrix element of the two-photon scattering process. $\phi ^{i}_{\pi }(x,\mu _{F}^{2})$ is the pion meson distribution amplitude with the longitudinal momentum fraction x and the factorization scale $\mu _{F}$. The notation $i=\pi$ represents the twist-2 distribution amplitude and the notation $i=p,\sigma$ represents the two twist-3 distribution amplitudes. The function $T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )$ is the hard-scattering amplitude from the different distribution amplitudes with the notation i and j.

To calculate the transitional matrix element, we take the vacuum saturation approximation and use the Fierz identity,

$$\begin{aligned} \overline{q}_{1\alpha }q_{2\beta }= & {} \frac{1}{4}I_{\beta \alpha } (\overline{q}_{1}q_{2})-\frac{1}{4}(i\gamma _{5})_{\beta \alpha } (\overline{q}_{1}i\gamma ^{5}q_{2})\nonumber \\&+\,\frac{1}{4}(\gamma _{\mu })_{\beta \alpha }(\overline{q}_{1} \gamma ^{\mu }q_{2})-\frac{1}{4}(\gamma _{\mu }\gamma _{5})_{\beta \alpha }(\overline{q}_{1} \gamma ^{\mu }\gamma ^{5}q_{2})\nonumber \\&+\,\frac{1}{8}(\sigma _{\mu \nu }\gamma _{5})_{\beta \alpha }(\overline{q}_{1} \sigma ^{\mu \nu }\gamma ^{5}q_{2}), \end{aligned}$$

(6)

where $q_{1}$ and $q_{2}$ are the quark fields. There are only three terms with the matrix $\gamma _5$ that have contributions for scattering amplitudes in the $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}$ process by the parity analysis. Finally, we find have the notation with nonvanishing terms $ij=\, \pi \pi , \, pp, \, p\sigma , \, \sigma p, \, \sigma \sigma$ for the hard-scattering amplitude $T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )$ of this reaction. The twist-2 and twist-3 distribution amplitudes of the pion are defined as the following relations:

$$\begin{aligned}&\langle \pi ^{+}(p)|\overline{u}(z_{1})\gamma ^{\mu }\gamma ^{5} \mathrm{d}(z_{2})|0\rangle \nonumber \\&\quad =-if_{\pi }p^{\mu }\int _{0}^{1}\mathrm{d}x\ e^{i(x\ p\cdot z_{1} +(1-x)\ p\cdot z_{2})} \phi _{\pi }^{\pi }(x),\end{aligned}$$

(7)

$$\begin{aligned}&\langle \pi ^{+}(p)|\overline{u}(z_{1})i\gamma ^{5}\mathrm{d}(z_{2})|0\rangle \nonumber \\&\quad =f_{\pi }\mu _{\pi }\int _{0}^{1}\mathrm{d}x\ e^{i(x\ p\cdot z_{1}+(1-x)\ p\cdot z_{2})} \phi _{\pi }^{p}(x),\end{aligned}$$

(8)

$$\begin{aligned}&\langle \pi ^{+}(p)|\overline{u}(z_{1})\sigma ^{\mu \nu }\gamma ^{5} \mathrm{d}(z_{2})|0\rangle \nonumber \\&\quad =\frac{i f_{\pi }\mu _{\pi }}{6}[p^{\mu }(z_{1}-z_{2})^{\nu }-p^{\nu } (z_{1}-z_{2})^{\mu }]\nonumber \\&\qquad \times \int _{0}^{1}\mathrm{d}x\ e^{i(x\ p\cdot z_{1}+(1-x) \ p\cdot z_{2})} \phi _{\pi }^{\sigma }(x), \end{aligned}$$

(9)

by the expanded form of hadronic matrix element [25, 32,33,34], where $f_{\pi }$ is the decay constant of pion, the parameter $\mu _{\pi }=\frac{m_{\pi }^{2}}{m_{u}+m_{\overline{d}}}$ is proportional to the chiral condensate and the variable x is the meson momentum fraction.

With the definitions of distribution amplitudes for final state mesons, the transitional matrix element of the $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}$ process is calculated and the hard-scattering amplitude $T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )$ is represented as

$$\begin{aligned} T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )=\frac{16}{3}\pi ^{2} \alpha \alpha _{s}(\mu _{R}^{2})C_{F}{\widehat{T}}^{ij}_{\lambda _{1} \lambda _{2}} \frac{1}{l_{1}^{2}l_{2}^{2}l_{3}^{2}}, \end{aligned}$$

(10)

where $C_{F}=\frac{4}{3}$ is the color factor and the masses of the light quarks are neglected. $\alpha$ is the electromagnetic coupling constant and $\alpha _{s}(\mu _{R}^{2})$ is the strong coupling constant with the renormalization scale $\mu _{R}$. The operator ${\widehat{T}}^{ij}_{\lambda _{1}\lambda _{2}}$ is related to the two-pion materialization of two photons with different twist distribution amplitudes and has diverse expressions from the various Feynman diagrams. For instance, it is given as

(11)

in the left diagram of Fig. 1, where $\varepsilon _{1}$ and $\varepsilon _{2}$ are abbreviations of the polarizations $\varepsilon _{1}^{\lambda _{1}}(p_{1})$ and $\varepsilon _{2}^{\lambda _{2}}(p_{2})$ of the initial photons, respectively. The partial $(\frac{\partial }{\partial l_{m\nu }}-\frac{\partial }{\partial l_{n\nu }})$ ($m,n=1,2,3$) comes from the $(z_{1}-z_{2})^{\nu }$ of Eq. (9). The momenta of the quark propagators are represented by $l_{1}$, $l_{2}$ and the gluon propagator is represented by $l_{3}$. In this diagram, they can be expressed in terms of the external momenta $l_{1}=-p_{1}+(1-x)p_{3}$, $l_{2}=p_{2}-y p_{4}$ and $l_{3}=-x p_{3}-(1-y)p_{4}$. Finally, we obtain the hard-scattering amplitudes $T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )$ with the notation $ij=\, \pi \pi , \, pp, \, p\sigma , \, \sigma p, \, \sigma \sigma$ by the sum of 20 Feynman diagrams and their detailed expressions are shown in Appendix A. One can find that the twist-2 part ($T^{\pi \pi }_{\lambda _{1}\lambda _{2}}$) is proportional to $\frac{1}{W^{2}}$, and the twist-3 part ($T^{pp}_{\lambda _{1}\lambda _{2}}, T^{p\sigma }_{\lambda _{1}\lambda _{2}}, T^{\sigma p}_{\lambda _{1}\lambda _{2}} ,T^{\sigma \sigma }_{\lambda _{1}\lambda _{2}}$) is proportional to $\frac{1}{W^{4}}$. Compared with the twist-2 part, the twist-3 part is obviously suppressed by a factor $\frac{1}{W^{2}}$.

3 The distribution amplitudes of pseudoscalar mesons

The twist-2 and twist-3 distribution amplitudes of pseudoscalar mesons are taken as the main nonperturbative input parameters in the above calculations of hard-scattering amplitude. In this section, we give a brief review for them in the BHL scheme [29,30,31]. One useful way of modeling the hadronic WF is to use the approximate bound-state solution of a hadron in terms of the quark model. We take the simplest possible model, viz., the harmonic-oscillator model. The BHL prescription of the WF is correctly obtained by connecting the equal time WF in the rest frame and the WF in the infinite momentum frame. This particular ${\mathbf {k}}_{\bot }$-dependence goes along with a factor $\exp [-\frac{1}{\beta ^{2}}(\frac{m_{q}^{2}}{x}+\frac{m_{{\bar{q}}}^{2}}{1-x})]$ in the harmonic-oscillator WF, i.e., the BHL WFs $\Psi (x,{\mathbf {k}}_{\bot })$ can be obtained by the replacement

$$\begin{aligned} \frac{{\mathbf {k}}_{\bot }^{2}}{x(1-x)}\rightarrow \frac{{\mathbf {k}}_{\bot }^{2}}{x(1-x)} +\frac{m_{q}^{2}}{x}+\frac{m_{{\bar{q}}}^{2}}{1-x}. \end{aligned}$$

(12)

Here, the quark masses $m_{q}$ and $m_{{\bar{q}}}$ are effective quark masses from the renormalization due to the reduction of higher Fock states as functionals of the valence state [35], not current quark masses, i.e., the quark masses appearing in the QCD Lagrangian. In Ref. [36], Brodsky showed the effective light quark masses $m_u=m_d=46$ MeV, $m_s=357$ MeV by fitting the quark masses to the observed masses of the $\pi$ and K. In Refs. [37, 38], the authors consider two cases, the values for the effective quark masses are fixed at a typical current one and a typical constituent one, respectively. As suggested above, the BHL WFs of the pseudoscalar meson can be written as

$$\begin{aligned} \Psi (x,{\mathbf {k}}_{\bot })\propto \exp \left[ -\frac{1}{8\beta ^{2}} \left( \frac{{\mathbf {k}}_{\bot }^{2}+m_{1}^{2}}{x}+\frac{{\mathbf {k}}_{\bot }^{2} +m_{2}^{2}}{1-x}\right) \right] \end{aligned}$$

(13)

from the harmonic-oscillator model at the rest frame. As the input parameters for the DAs, the effective quark masses $m_{i}(i=1,2)$ play an important role as model parameters. In our paper, they are scale independent and we hold them to be the typical constituent quark masses.

The $\beta$ refers to the harmonic parameter, which can be obtained from the definition of the average of the quark transverse momentum squared,

$$\begin{aligned} \langle {\mathbf {k}}_{\perp }^{2}\rangle _{M}=\frac{f_{M}^{2}}{24}\int \mathrm{d}x\frac{\mathrm{d}^{2}{\mathbf {k}}_{\perp }}{16\pi ^{3}}|{\mathbf {k}}_{\perp }^{2}|| \Psi _{M}(x,{\mathbf {k}}_{\perp })|^{2}/P^{M}_{q\overline{q}}, \end{aligned}$$

(14)

where $M=\pi$ for pion and $M=K$ for kaon mean the leading-twist wave functions $\Psi ^{\pi }_{\pi }$ and $\Psi ^{K}_{K}$. The decay constants are $f_{\pi }=0.132$ GeV for pion and $f_{K}=0.160$ GeV for kaon, respectively. In Refs. [29,30,31], $\langle {\mathbf {k}}_{\perp }^{2}\rangle _{\pi }$ and $\langle {\mathbf {k}}_{\perp }^{2}\rangle _{K}$ are all given as $(0.356~\mathrm{GeV})^{2}$ approximately. The probability of finding the $q\overline{q}$ leading-twist Fock state in the pseudoscalar meson is not larger than unity,

$$\begin{aligned} P_{q\overline{q}}^{M}=\frac{f_{M}^{2}}{24}\int \mathrm{d}x\frac{\mathrm{d}^{2}{\mathbf {k}}_{\perp }}{16\pi ^{3}}|\Psi _{M} (x,{\mathbf {k}}_{\perp })|^{2}\le 1. \end{aligned}$$

(15)

The classical forms of the twist-2 and twist-3 wave functions with BHL prescription are widely considered and have the immediate advantage to solve the endpoint singularity by the exponential suppression in the $x=0$ and $x=1$ points. In our work, we take the twist-2 wave functions of pion and kaon with the first three terms of the Gegenbauer polynomials and they are characterized as

$$\begin{aligned} \Psi _{\pi }^{\pi }(x,{\mathbf {k}}_{\perp })= & {} A_{\pi }^{\pi }\left[ 1 +B_{\pi }^{\pi }C_{2}^{\frac{3}{2}}(\xi )+C_{\pi }^{\pi }C_{4}^{\frac{3}{2}} (\xi )\right] \nonumber \\&\times \exp \left[ -\frac{{\mathbf {k}}_{\perp }^{2}+m_{q}^{2}}{8\beta _{\pi }^{2}x(1-x)}\right] ,\end{aligned}$$

(16)

$$\begin{aligned} \Psi _{K}^{K}(x,{\mathbf {k}}_{\perp })= & {} A_{K}^{K}\left[ 1+B_{K}^{K} C_{1}^{\frac{3}{2}}(\xi )+C_{K}^{K}C_{2}^{\frac{3}{2}}(\xi )\right] \nonumber \\&\times \exp \left[ -\frac{1}{8\beta _{K}^{2}}\left( \frac{{\mathbf {k}}_{\perp }^{2} +m_{q}^{2}}{x}+\frac{{\mathbf {k}}_{\perp }^{2}+m_{s}^{2}}{1-x}\right) \right] ,\nonumber \\ \end{aligned}$$

(17)

where $C_{n}^{\frac{3}{2}}(\xi )$ is associated with the Gegenbauer polynomials; we have the relationship $\xi =2 x-1$ and we take $n=2,4$ in the pion case for the SU(2) isotopic symmetry and $n=1,2$ in the kaon case for the SU(3)-flavor symmetry breaking. The constituent quark masses $m_{q}=0.30$ GeV $(q=u,d)$ and $m_{s}=0.45$ GeV [19] are given in the above formulas. To simplify the following numerical analysis, we write the twist-3 wave functions as

$$\begin{aligned}&\Psi _{\pi }^{p}(x,{\mathbf {k}}_{\perp })=\frac{A_{\pi }^{p}}{x(1-x)} \exp \left[ -\frac{{\mathbf {k}}_{\perp }^{2}+m_{q}^{2}}{8\beta _{\pi }^{2} x(1-x)}\right] ,\end{aligned}$$

(18)

$$\begin{aligned}&\Psi _{\pi }^{\sigma }(x,{\mathbf {k}}_{\perp })=A_{\pi }^{\sigma } \exp \left[ -\frac{{\mathbf {k}}_{\perp }^{2}+m_{q}^{2}}{8\beta _{\pi }^{2}x(1-x)}\right] , \end{aligned}$$

(19)

and

$$\begin{aligned}&\Psi _{K}^{p}(x,{\mathbf {k}}_{\perp })\nonumber \\&\quad =\frac{A_{K}^{p}}{x(1-x)} \exp \left[ -\frac{1}{8\beta _{K}^{2}}\left( \frac{{\mathbf {k}}_{\perp }^{2}+m_{q}^{2}}{x}+\frac{{\mathbf {k}}_{\perp }^{2} +m_{s}^{2}}{1-x}\right) \right] ,\end{aligned}$$

(20)

$$\begin{aligned}&\Psi _{K}^{\sigma }(x,{\mathbf {k}}_{\perp })\!=\!A_{K}^{\sigma } \exp \left[ -\frac{1}{8\beta _{K}^{2}}\left( \frac{{\mathbf {k}}_{\perp }^{2} \!+\!m_{q}^{2}}{x}\!+\!\frac{{\mathbf {k}}_{\perp }^{2}\!+\!m_{s}^{2}}{1-x}\right) \right] ,\nonumber \\ \end{aligned}$$

(21)

for the pion and kaon, respectively.

The above wave functions of twist-2 and twist-3 for pion and kaon follow the normalization condition,

$$\begin{aligned} \int \mathrm{d}x\frac{\mathrm{d}^{2}{\mathbf {k}}_{\perp }}{16\pi ^{3}}\Psi _{M}^{i} (x,{\mathbf {k}}_{\perp })=1, \end{aligned}$$

(22)

where the notation $i=\pi (K),p,\sigma$ refers to the different twist wave functions and the symbol $M=\pi (K)$ refers to the pion (kaon) meson. By integrating the transverse momentum of the wave function, the corresponding distribution amplitude is acquired from the relationship

$$\begin{aligned} \phi ^{i}_{M}(x,\mu _{F}^2)=\int _{|{\mathbf {k}}_{\perp }|<\mu _{F}} \frac{\mathrm{d}^{2}{\mathbf {k}}_{\perp }}{16\pi ^{3}}\Psi ^{i}_{M}(x,{\mathbf {k}}_{\perp }), \end{aligned}$$

(23)

where $\mu _{F}$ is the upper limit of integral which refers to the ultraviolet cutoff. In order to simplify the following calculation, one can safely take $\mu _{F}\rightarrow +\infty$ due to the smallness of the wave function in the region of $|{\mathbf {k}}_{\perp }|>\mu _{F}$. Substituting Eqs. (16)–(21) into Eq. (23), we obtain the meson distribution amplitudes

$$\begin{aligned}&\phi _{\pi }^{\pi }(x)=\frac{A_{\pi }^{\pi }\beta _{\pi }^{2}}{2\pi ^{2}}x(1-x) [1+B_{\pi }^{\pi }C_{2}^{\frac{3}{2}}(\xi )+C_{\pi }^{\pi } C_{4}^{\frac{3}{2}}(\xi )]\nonumber \\&\times \exp \left[ -\frac{m_{q}^{2}}{8\beta _{\pi }^{2}x(1-x)}\right] ,\end{aligned}$$

(24)

$$\begin{aligned}&\phi _{\pi }^{p}(x)=\frac{A_{\pi }^{p}\beta _{\pi }^{2}}{2\pi ^{2}} \exp \left[ -\frac{m_{q}^{2}}{8\beta _{\pi }^{2}x(1-x)}\right] ,\end{aligned}$$

(25)

$$\begin{aligned}&\phi _{\pi }^{\sigma }(x)=\frac{A_{\pi }^{\sigma }\beta _{\pi }^{2}}{2\pi ^{2}}x(1-x)\exp \left[ -\frac{m_{q}^{2}}{8\beta _{\pi }^{2} x(1-x)}\right] \end{aligned}$$

(26)

for the pion and

$$\begin{aligned} \phi _{K}^{K}(x)= & {} \frac{A_{K}^{K}\beta _{K}^{2}}{2\pi ^{2}} x(1-x) [1+B_{K}^{K}C_{1}^{\frac{3}{2}}(\xi )+C_{K}^{K} C_{2}^{\frac{3}{2}}(\xi )]\nonumber \\&\times \exp \left[ -\frac{(1-x)m_{q}^{2}+x m_{s}^{2}}{8\beta _{K}^{2}x(1-x)}\right] ,\end{aligned}$$

(27)

$$\begin{aligned} \phi _{K}^{p}(x)= & {} \frac{A_{K}^{p}\beta _{K}^{2}}{2\pi ^{2}}\exp \left[ -\frac{(1-x)m_{q}^{2}+x m_{s}^{2}}{8\beta _{K}^{2}x(1-x)}\right] ,\end{aligned}$$

(28)

$$\begin{aligned} \phi _{K}^{\sigma }(x)= & {} \frac{A_{K}^{\sigma }\beta _{K}^{2}}{2\pi ^{2}}x(1-x) \exp \left[ -\frac{(1-x)m_{q}^{2}+x m_{s}^{2}}{8\beta _{K}^{2}x(1-x)}\right] ,\nonumber \\ \end{aligned}$$

(29)

for the kaon, respectively. The above coefficients $A_{M}^{i},B_{M}^{i},C_{M}^{i},A_{M}^{p},A_{M}^{\sigma }$ and the harmonic parameters $\beta _{M}$ are worked out in the following discussion.

With the method of nonlocal operator product expansion and conformal symmetry, the distribution amplitudes of the pion [26] and kaon [39] have been studied and the general form of the leading-twist distribution amplitude with the expansion of Gegenbauer polynomials were described as

$$\begin{aligned} \phi _{M}^{i}(x,\mu ^{2}_{F})=6x(1-x)\left( 1+\sum _{n=1}^{\infty } a_{n}^{i}(\mu ^{2}_{F})C_{n}^{\frac{3}{2}}(2x-1)\right) .\nonumber \\ \end{aligned}$$

(30)

To leading logarithmic accuracy, the coefficients of nonperturbative Gegenbauer polynomials $a_{n}^{i}$ renormalize multiplicatively with

$$\begin{aligned} a_{n}^{i}(\mu ^{2}_{F})=L^{\frac{\gamma _{n}^{(0)}}{\beta _{0}}} a_{n}^{i}(\mu _{0}^{2}), \end{aligned}$$

(31)

where $L=\frac{\alpha _{s}(\mu ^{2}_{F})}{\alpha _{s}(\mu _{0}^{2})}$, $\beta _{0}=\frac{11 N_{c}-2 N_{f}}{3}$. The quantity n takes even values for the pion and positive integers for the kaon. The anomalous dimension $\gamma _{n}^{(0)}$ can be expressed as

$$\begin{aligned} \gamma _{n}^{(0)}=4C_{F}\left( \psi (n+2)+\gamma _{E}-\frac{3}{4} -\frac{1}{2(n+1)(n+2)}\right) .\nonumber \\ \end{aligned}$$

(32)

Those coefficients $a_{n}^{i}$ of the Gegenbauer polynomials were mainly calculated by QCD sum rules [26, 39,40,41]. Their values are

$$\begin{aligned}&a_{2}^{\pi }(1\ \mathrm{GeV})=0.25\pm 0.15,\quad a_{4}^{\pi } (1~\hbox {GeV})=0.04\pm 0.11,\nonumber \\&a_{1}^{K}(1\ \mathrm{GeV})=0.06\pm 0.03,\quad a_{2}^{K}(1~\hbox {GeV})=0.25\pm 0.15.\nonumber \\ \end{aligned}$$

(33)

Additionally, the recent values of the coefficient $a_{2}(\mu =2~\hbox {GeV})$ obtained from lattice QCD [42,43,44] are within the range that we adopted in our calculation.

Table 1 The parameters of twist-2,3 distribution amplitudes for the pion and kaon mesons in Eqs. (27)–(29) with the scale value $\mu _F=1$ GeV. The dimensions of the harmonic parameters $\beta _{\pi ,K}$ and normalization coefficients $A^i_M$ $(i=\pi ,K,p,\sigma ;M=\pi ,K)$ are GeV and (GeV)$^{-2}$, respectively. The others parameters are dimensionless

Fig. 2

The characteristic shapes of the distribution amplitudes for pion and kaon in BHL frame with the scale value $W\in (1,6)~\hbox {GeV}$. Left panel: Yellow band $\phi _{\pi }^{\pi }$; Blue band $\phi _{\pi }^{p}$; Green band $\phi _{\pi }^{\sigma }$. Dashed line the CZ distribution amplitude, $\phi _{\pi }^{CZ}(x)=30x_{d}x_{u}(x_{d}-x_{u})^{2}$, dotted line the asymptotic distribution amplitude, $\phi _{\pi }^{asy}(x)=6x(1-x)$. Right panel: Same for $\phi _{K}^{i}$; $\phi _{K}^{CZ}(x)=30x_{s}x_{u}[0.6(x_{s}-x_{u})^{2}+0.08+0.08(x_{s}-x_{u})]$

The moments of the leading-twist distribution amplitudes are defined by the following expression:

$$\begin{aligned} \langle \xi ^{n}\rangle ^{i}_{M}=\int _{0}^{1}(2x-1)^{n} \phi ^{i}_{M}(x)\mathrm{d}x. \end{aligned}$$

(34)

Here the scripts $n=0,2,4$ and $n=0,1,2$ are the first three moments for the pion and kaon meson, respectively. In this formula, the form of the distribution amplitude $\phi ^{i}_{M}(x)$ is taken as our BHL scheme Eqs. (24) and (27) and the general form Eq. (30). Equating the two sets of moments and taking the constraint $\langle {\mathbf {k}}_{\perp }^{2}\rangle _{\pi }\approx \langle {\mathbf {k}}_{\perp }^{2}\rangle _{K}\approx (0.356\ \mathrm{GeV})^{2}$, we figure out the harmonic parameters $\beta _{\pi ,K}$ and the twist-2 Gegenbauer coefficients $A_{M}^{i},B_{M}^{i},C_{M}^{i}(i=\pi ,K; M=\pi ,K)$. The coefficients $A_{\pi }^{p}$, $A_{\pi }^{\sigma }$ and $A_{K}^{p}$, $A_{K}^{\sigma }$ of the twist-3 distribution amplitudes can be directly worked out by the normalized condition Eq. (22). Substituting Eq. (33) into the previous discussion, the parameters of the distribution amplitudes and the probability of finding the $q{\bar{q}}$ leading-twist Fock state in the pion or kaon are listed in Table 1 with the scale value $\mu _F=1~$GeV. The deviation of those parameters comes from uncertainties of the twist-2 Gegenbauer coefficients in Eq. (33). We find that $P_{q{\bar{q}}}^{\pi }\le 0.27$ and $P_{q{\bar{q}}}^{K}\le 0.5$ are much smaller than unity. So higher twist and higher Fock states are also important components for the pion and kaon, which need to be taken into account in our work. In the above analysis, we only get the coefficients of the distribution amplitudes in the BHL scheme with the initial value $\mu _F=1$ GeV. Then we take the scale value $\mu _F^2=W^2$. According to the QCD evolution of the coefficients Eq. (31) and substituting Eq. (33) into Eq. (31), we can obtain the BHL distribution amplitudes with any scale value W using the previous method. The evolution method we adopt in our paper is equivalent to the famous evolution equation (2.17a) in Ref. [4]. A similar discussion as regards this evolution method can be found in Refs. [45, 46].

In Fig. 2, the twist-2 and twist-3 distribution amplitudes for the pion and kaon of the BHL scheme are illustrated with the variable scale $W\in (1,6)~\hbox {GeV}$. As can be seen from Fig. 2, the distribution amplitudes in the BHL prescription are obviously different from the common forms in the points $x=0$ and 1. The endpoint singularities coming from the hard-scattering amplitudes are suppressed by the effective endpoint behavior. The banded graphics of the distribution amplitudes mean the uncertainties of the parameters, which come from the strong coupling constant $\alpha _{s}$ with $\Lambda _{QCD}\in (0.15,0.3)~\hbox {GeV}$, the center-of-mass energy $W\in (1,6)~\hbox {GeV}$ and the Gegenbauer coefficients $a^{i}_{n}$ from Eq. (33). Especially, the area of the pion $\phi _{\pi }^{\pi }$ is more complicated than the one of the kaon $\phi _{K}^{K}$, since we take the Gegenbauer polynomials to the $C_{4}^{\frac{3}{2}}$ term with the coefficient $a_{4}^{\pi }$ changing from positive value to negative value for the pion, but the coefficient $a_{2}^{K}$ is always positive for the kaon. The graphics of the twist-3 distribution amplitudes without Gegenbauer polynomials are simple for the pion and kaon.

4 Numerical analysis

To analyze the scattering cross section of two-photon annihilation into pseudoscalar pairs numerically, we take the electromagnetic coupling constant $\alpha =\frac{1}{137}$ and the QCD running coupling constant calculated to two-loop accuracy given by

$$\begin{aligned} \alpha _{s}(\mu _{R}^{2})=\frac{4\pi }{\beta _{0}\mathrm{ln}\left( \frac{\mu _{R}^{2}}{\Lambda _{QCD}^{2}}\right) } \left\{ 1-\frac{\beta _{1}}{\beta _{0}^{2}}\frac{\mathrm{lnln} \left( \frac{\mu _{R}^{2}}{\Lambda _{QCD}^{2}}\right) }{\mathrm{ln}\left( \frac{\mu _{R}^{2}}{\Lambda _{QCD}^{2}}\right) }\right\} \end{aligned}$$

(35)

with $\beta _{0}=\frac{11 N_{c}-2 N_{f}}{3}$ and $\beta _{1}=\frac{34 N_{c}^{3}-13 N_{c}^{2} N_{f}+3 N_{f}}{3 N_{c}}$. The QCD scale is taken as $\Lambda _{QCD}\in (0.15,0.3)$ GeV and the interaction scale is chosen as $\mu _{R}^{2}=W^{2}$ in this work.

Fig. 3

Dependence of the prediction for $\gamma \gamma \rightarrow \overline{M}M$ transitional matrix element $A_{\lambda _{1}\lambda _{2}}$ on the energy W with $cos\theta =0$ in the pion and kaon case, respectively

Next, we focus on the chiral enhancing scale $\mu _{M}$, which is an important parameter with a significant influence to the contribution from twist-3 parts of the pseudoscalar meson in the $\gamma \gamma \rightarrow M^{+}M^{-}$ process. According to its definition,

$$\begin{aligned} \mu _{M}=\frac{m_{M}^{2}}{m_{q}+m_{\overline{q}}},\quad (M=\pi ,K; q,\overline{q}=u,d,s), \end{aligned}$$

(36)

and the one-loop expression for the running quark mass in the $\overline{\mathrm{MS}}$ scheme [47] is

$$\begin{aligned} m(\mu _{R}^{2})=m(\mu _{0}^{2})\left( \frac{\alpha _{s}(\mu _{R}^{2})}{\alpha _{s}(\mu _{0}^{2})}\right) ^{\frac{\gamma _{m}^{(0)}}{2\beta _{0}}} \end{aligned}$$

(37)

with the anomalous dimension of the quark mass $\gamma _{m}^{(0)}=6C_{F}$ and the $\beta$ function $\beta _{0}=\frac{11 N_{c}-2 N_{f}}{3}$ as defined above, we can get $\mu _{\pi }$ for the pion and $\mu _{K}$ for the kaon with the different energy scale $\mu _{R}^{2}=W^{2}$. The masses of the current quarks are $m_{\mu } (1~\hbox {GeV})=m_{d} (1~\hbox {GeV})=4$ MeV and $m_{s} (1~\hbox {GeV})=140$ MeV [39]. The masses of the pseudoscalar mesons $m_{\pi }=139.6$ MeV and $m_{K}=493.7$ MeV are quoted from PDG [48]. With the help of Eqs. (36) and (37), we work out $2.44~\hbox {GeV}\le \mu _{\pi }\le 3.66~\hbox {GeV}$ and $1.69~\hbox {GeV}\le \mu _{K}\le 2.55~\hbox {GeV}$ in the energy scale $W\in (1,6)$.

The transitional matrix elements $A_{\lambda _{1}\lambda _{2}}$ of the two-pion and two-kaon processes are shown in Fig. 3 with the two-photon energy W as a variable parameter. Here we choose $cos\theta =0$ and $a_{n}^{i}$ as the central value in Eq. (33) for the meson distribution amplitudes and $\Lambda _{QCD}=0.2~\hbox {GeV}$ for the strong coupling constant. Considering the polarization states of two photons, there are some relationships $A_{++}=A_{--}$ and $A_{+-}=A_{-+}$ in our calculation. In Fig. 3, the left two figures and the right two figures are the transitional matrix elements $A_{++}$ and $A_{+-}$ for the pion and kaon case, respectively. The green dashed curves are the contributions from twist-2 distribution amplitudes, the blue dot-dashed curves are contributions from twist-3 distribution amplitudes and the red solid curves are total contributions with twist-2 part and twist-3 part. Compared with the leading-twist contribution, we can see that the twist-3 contribution is suppressed in the transitional matrix element $A_{++}$ as the energy $W>3$ GeV (2 GeV) for the pion (kaon), while a similar condition occurred in the transitional matrix element $A_{+-}$ as the energy $W> 11$ GeV (8 GeV) for pion (kaon).

Fig. 4

Cross section for $\gamma \gamma \rightarrow \overline{M}M$ in the c.m. angular region $|cos\theta |<0.6$. The blue solid line is the result of a fit for the data among relevant ranges

Integrating over the scattering angular with $|\cos \theta |<0.6$, the cross sections $\sigma _{0}(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-})$ and $\sigma _{0}(\gamma \gamma \rightarrow K^{+}K^{-})$ are shown in Fig. 4. The banded structures come from the twist-3 correction. It is important to note that the phrase twist-3 correction in the text and the legend twist-3 in the figure all mean the contribution including the total twist-2 part and twist-3 part in the following paragraphs. The green band denotes twist-3(a) with the variable $a_{n}^{i}$ and $\alpha _{s}$ with $\Lambda _{QCD}\in (0.15,0.3)$ GeV. The yellow band is for twist-3(b) with the variable $a_{n}^{i}$ at $\Lambda _{QCD}=0.2~\hbox {GeV}$ for $\alpha _{s}$. Here we can see that the strong coupling constant $\alpha _{s}$ has little effect at the lower limit but it has an obvious effect to the upper limit from the areas of two bands. The choice of distribution amplitudes has a significant influence on the cross section from the yellow band. The magenta solid line named twist-2 stands for the contribution from twist-2 part with $\Lambda _{QCD}=0.2~\hbox {GeV}$ for $\alpha _{s}$ and $a_{n}^{i}$ chosen as the central value in Eq. (33). The experimental data from TPC [11], BELLE [14] and ALEPH [12] are also displayed simultaneously in Fig. 4 and we find that the twist-3 correction to the cross section is markedly improved, even more than an order of magnitude enhanced compared with the leading-twist contribution and the one-loop correction [18]. Especially, our results of the cross sections for the pion and kaon channels are in good agreement with the experimental data in the energy $W > 2.8$ GeV.

Our curves differ significantly from the predictions made before due to considering the contributions from twist-3 parts. We know the parametrization about the W dependence of the cross section, which has the form of $\sigma (\gamma \gamma \rightarrow M^{+}M^{-})\propto W^{-n_{M}}$. In Ref. [14], the BELLE Collaboration announce that they find $n_{\pi }=7.9\pm 0.4\pm 1.5$ and $n_{K}=7.3\pm 0.3\pm 1.5$ for $3.0~\hbox {GeV}<W<4.1~\hbox {GeV}$. In Ref. [18], the NLO results give the power $n_{\pi }=n_{K}=6.9(7.4)$ for $\mu ^{2}_{R}=W^{2}(W^{2}/15)$. On the other hand, we carry out a simple theoretic fitting for the experimental data, which are mentioned in Fig. 4 among $1.25~\hbox {GeV}<W<6(4.1)~\hbox {GeV}$ for pion (kaon), and we obtain $n_{\pi }=6.91$ and $n_{K}=6.02$ corresponding to the blue solid curves in Fig. 4. At the same time, we find that the powers are $n_{\pi }=6.76$ and $n_{K}=6.73$ from our twist-2 contributions and the powers are $n_{\pi }=9.63$ and $n_{K}=9.20$ from our twist-3 correction. The analysis of the powers shows that our predictions from twist-3 correction change faster than the experimental data but their values are of similar magnitude to the data from BELLE, ALEPH, TPC, and vice versa for twist-2 parts.

Fig. 5

Cross section ratio of $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}$ to $\gamma \gamma \rightarrow K^{+}K^{-}$. The experimental points are from TPC [11] and BELLE [14]

The ratio $K^{+}K^{-}$ to $\pi ^{+}\pi ^{-}$ is showed in Fig. 5. The experimental points are calculated from the data of TPC [11] with the energy $W\in (1.2, 2.0)$ GeV and BELLE [14] with the energy $W\in (2.4, 4.1)$ GeV. The red solid curve is the contribution of the twist-2 distribution amplitude from the first three terms Gegenbauer polynomials with the $\Lambda _{QCD}=0.2$ and $a_{n}^{i}$ taken as the center value of Eq. (33) and it is larger than the experimental data. The prediction in Ref. [6] approximately equals 1.06 and the one-loop prediction $f_{K}^{4}/f_{\pi }^{4}=2.23$ [18] coincides with the BL estimate [5] with the asymptotic leading-twist distribution amplitude, while the Belle measured value is $0.89\pm 0.04\pm 0.15$ in the energy $W\in (3.0, 4.1)$ GeV. The magenta band is from our twist-3 correction with the variable $a_{n}^{i}$ and $\alpha _{s}$ with $\Lambda _{QCD}\in (0.15,0.3)$ GeV and it is in agreement with the experimental data.

Fig. 6

Angular dependence of the cross section, $\sigma _{0}^{-1} \mathrm{d}\sigma / \mathrm{d}|\cos \theta |$ for $\pi ^{+}\pi ^{-},K^{+}K^{-}$. The experimental points are from the Belle Collaboration [14]

In Fig. 6, we display the angular dependence of cross section, $\sigma _{0}^{-1}\mathrm{d}\sigma /\mathrm{d}|\cos \theta |$ for the $\pi ^{+}\pi ^{-}$ and $K^{+}K^{-}$ processes, respectively. There is no obvious change to our prediction for the ratio by varying W from 2.4 to 4.1, where the Belle data [14] are covered. To simplify our analysis, we only discuss our prediction and the Belle data at the $W=3.2\sim 3.3$ GeV region. The discrete points come from the experimental data in the angular region $|\cos \theta |\le 0.6$. The dotted curves indicate the expectation from the $\sin ^{-4}\theta$ behavior predicted by Brodsky and Lepage [5]. The dot-dashed and solid curves correspond to the twist-2 contribution and twist-3 correction in the angular $|\cos \theta |\le 0.7$, respectively. One in particular is to expand the scattering angle to $|\cos \theta |\le 0.7$ in our drawing and it is aimed at reflecting the distinction between twist-2 contribution and twist-3 correction. It is no problem, because the deviation of $\sigma _{0}^{-1} \mathrm{d}\sigma / \mathrm{d}|\cos \theta |$ from the different cut-off $|\cos \theta |\le 0.6$ and $|\cos \theta |\le 0.7$ is less than $5\%$. In Fig. 6, we can see that our theoretical predictions are compatible with the experimental data. When we take $|\cos \theta |\le 0.6$, the curves from the twist-2 contribution and the twist-3 correction have similar changes with $\sin ^{-4}\theta$. But as we take $|\cos \theta |>0.6$, the curves from the twist-3 correction rapidly increase.

5 Conclusion

In this work, we recalculate the processes of two-photon annihilation into two pseudoscalar mesons with the corrections of the two-particle twist-3 distribution amplitudes of pseudoscalar mesons in the standard hard-scattering approach. In order to avoid the endpoint singularity from twist-3 distribution amplitudes, we take distribution amplitudes of the meson with the BHL prescription. The twist-3 corrections of cross sections for $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}, K^{+}K^{-}$ are markedly improved, even more than an order of magnitude enhanced compared with the twist-2 contributions. The results show that the contributions from twist-3 parts are actually not power suppressed compared with the leading-twist contributions, because momentum transfer is not large enough in those processes. The cross sections with twist-3 corrections have similar changes and are at the same order in magnitude with the data by varying the center-of-mass energy W from 1 to 6 GeV. We also discuss the cross section ratio $\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})$ and find it to be close to experimental results. Numerical analysis of the angular dependence of $\sigma _{0}^{-1} \mathrm{d}\sigma / \mathrm{d}|\cos \theta |$ shows that the ratios are independent of the distribution amplitudes and are in good agreement with the experimental data in the small-angle area, but the ratios with the twist-3 corrections increase faster than the ones from the twist-2 parts in the large-angle area.

Appendix A: The expression of hard-scattering amplitudes \(T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )\)

In this appendix, we present the detailed formulas of hard-scattering amplitudes $T^{ij}_{\lambda _{1}\lambda _{2}}(x,y,W,\theta )$ with the contributions from the two-particle twist-2 and twist-3 distribution amplitudes in the $\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}$ process and the relevant expressions for the $\gamma \gamma \rightarrow K^{+}K^{-}$ process can be obtained by making the replacements of $f_{\pi }\rightarrow f_{K}$, $\mu _{\pi }\rightarrow \mu _{K}$ and $e_{d}\rightarrow e_{s}$ in the following formulas.

The leading-twist hard-scattering amplitudes for the $\pi ^{+}\pi ^{-}$ channel are expressed as

$$\begin{aligned}&T^{\pi \pi }_{++}=T^{\pi \pi }_{--}\\&\quad =\frac{16\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}[-y+x(-1+2y)](e_{d}-e_{u})^{2}}{3(-1+t^{2})W^{2}(-1+x)x(-1+y)y},\\&T^{\pi \pi }_{+-}=T^{\pi \pi }_{-+}=\frac{4\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}}{3(-1+t^{2})W^{2}(-1+x)x(-1+y)y}\\&\qquad \times \left\{ 2[-1+x+y-4xy+t^{2}(-1+x+y)]e_{d}^{2}\phantom {\frac{1}{2}}\right. \\&\qquad +\,\frac{1}{[x(1+t-2y)+y-ty][-(1+t)y+x(-1+t+2y)]}\\&\qquad \times \{4\{-(-1+t^{2})(-1+y)y^{2}\\&\qquad +\,x^{3}(-1+2y)(-1+t^{2}+8y-8y^{2})\\&\qquad +\,x^{2}[-1+11y-32y^{2} +24y^{3}+t^{2}(1+5y-8y^{2})]\\&\qquad +\,xy[-2+11y-10y^{2}+t^{2}(-6+5y+2y^{2})] \}e_{d}e_{u}\}\\&\qquad \left. -\,[6-6y+2t^{2}(-1+x+y)+x(-6+8y)]e_{u}^{2} \phantom {\frac{1}{2}}\right\} , \end{aligned}$$

where $\alpha$ and $\alpha _{s}$ mean the electromagnetic coupling constant and the strong coupling constant, respectively. The variables x and y are the momentum fractions from the final pseudoscalar mesons. The quark charges are $e_{u}=\frac{2}{3}$ for the u quark and $e_{d(s)}=-\frac{1}{3}$ for the d(s) quark. The color factor is $C_{F}=\frac{N_{C}^{2}-1}{2N_{C}}$ with the color number $N_{C}=3$. If we make the replacement of $t\rightarrow \cos \theta$ in the above expression, we reduce them to new formulas that have the same forms as the theoretical prediction of Chernyak [9, 10], Brodsky [5] and Nižić [17] on the leading-twist order.

It is convenient to take $\cos \theta$ as t in the numerical analysis of the twist-3 parts and the twist-3 hard-scattering amplitudes are represented as follows:

$$\begin{aligned}&T^{pp}_{++}=T^{pp}_{--}=-\frac{8\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2}) C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{3(-1+t^{2})W^{4}(-1+x) x(-1+y)y}\\&\quad \times \left\{ -2\{2y+x[2+(-3+t^{2})y]\}e_{d}^{2}\phantom {\frac{1}{2}}\right. \\&\quad +\,\frac{1}{[x(1+t-2y)+y-ty][-(1+t)y+x(-1+t+2y)]}\\&\quad \times \,\{8 \{(-1+t^{2})(-1+y)y^{2}\\&\quad +\,x^{3}(-1+2y)[1-y+y^{2}+t^{2}(-1-y+y^{2})]\\&\quad +\,xy[2-4y+3y^{2} -t^{2}(-2+2y+y^{2})]\\&\quad -\,x^{2}[-1+4y-4y^{2}+3y^{3}+t^{2}(1+2y-8y^{2}+3y^{3})] \}e_{d}e_{u}\}\\&\quad \left. -\,2[1+x+t^{2}(-1+x)(-1+y)+y-3xy]e_{u}^{2}\phantom {\frac{1}{2}}\right\} ,\\&T^{pp}_{+-}=T^{pp}_{-+}=\frac{8\pi ^{2}\alpha \alpha _{s}(\mu _{R}^{2}) C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{3(1-t^{2})W^{4}}\\&\quad \times \left\{ \frac{2[-1+x(2-3y)+2y+t^{2}(-1+xy)]e_{d}^{2}}{(-1+x)^{2}(-1+y)^{2}}\phantom {\frac{1}{2}}\right. \\&\quad -\,\frac{8(1+t^{2})[-y+x(-1+2y)]e_{d}e_{u}}{[x(1+t-2y)+y-ty] [-(1+t)y+x(-1+t+2y)]}\\&\quad \left. +\,\frac{2\{x+[1+t^{2}(-1+y)-3y]+y-t^{2}y\}e_{u}^{2}}{x^{2}y^{2}} \phantom {\frac{1}{2}}\right\} ,\\&T^{p\sigma }_{++}=T^{p\sigma }_{--}=-\frac{16\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{9(-1+t^{2})^{2}W^{4} (-1+x)^{2}x^{2}}\\&\quad \times \left\{ -\frac{(-1+t^{2})(-1+x)(1+t^{2}x)e_{d}^{2}}{-1+y} \phantom {\frac{1}{2}}\right. \\&\quad +\,\frac{1}{(-1+y)y[-x(1+t-2y)+(-1+t)y](x-tx+y+ty-2xy)}\\&\quad \times \,\{2\{(-1+t^{2})(-1+y)y^{2}\\&\quad +\,xy[-1+y+2t^{2}y-2y^{2} +t^{4}(1-3y+2y^{2})]\\&\quad +\,x^{5}[1-4y+6y^{2}-4y^{3}+t^{4}(-1+2y)-6t^{2}y(1-3y+2y^{2})]\\&\quad +\,x^{2}y[-3+8y+2y^{2}+t^{4}(1+10y-12y^{2})+2t^{2}(1-13y+9y^{2})]\\&\quad +\,x^{3}[-1+6y-6y^{2}-8y^{3}+t^{2}(2-6y+42y^{2}-32y^{3})\\&\quad +\,t^{4} (-1-8y+4y^{2}+8y^{3})]\\&\quad +\,x^{4}[t^{4}(2+3y-8y^{2})+y(1-6y+10y^{2})\\&\quad +\,2t^{2}(-1+6y-21y^{2} +15y^{3})]\}e_{d}e_{u}\} \end{aligned}$$

$$\begin{aligned}&\quad \left. +\,\frac{(-1+t^{2})[-1+t^{2}(-1+x)]xe_{u}^{2}}{y} \phantom {\frac{1}{2}}\right\} ,\\&T^{p\sigma }_{+-}=T^{p\sigma }_{-+}=-\frac{8\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{9(-1+t^{2})^{2}W^{4} (-1+x)^{3}x^{3}}\\&\quad \times \left\{ \frac{(-1+t^{2})x^{2}[-1+2x+t^{2}(-1-2x+2x^{2})] e_{d}^{2}}{-1+y}\phantom {\frac{1}{2}}\right. \\&\quad +\,\frac{1}{(-1+y)y[x(1+t-2y)+y-ty][-(1+t)y+x(-1+t+2y)]}\\&\quad \times \{4(-1+x)^{2}x^{2}\{-(-1+t^{2})y^{2}[-1+2y+t^{2}(-3+4y)]\\&\quad +\,x^{3}[1-4y+6y^{2}-4y^{3}+t^{4}(-1+2y)-6t^{2}y(1-3y+2y^{2})]\\&\quad +\,xy[-1+4y-6y^{2}+t^{2}(2+8y-10y^{2})+t^{4}(-1-4y+8y^{2})]\\&\quad +\,x^{2}y[1+t^{4}(5-8y)-4y+6y^{2}+2t^{2}(1-10y+9y^{2})] \}e_{d}e_{u}\}\\&\quad \left. +\,\frac{(-1+t^{2})(-1+x)^{2}[1-2x+t^{2}(-1-2x+2x^{2})] e_{u}^{2}}{y} \phantom {\frac{1}{2}}\right\} ,\\&T^{\sigma p}_{++}=T^{\sigma p}_{--}=-\frac{16\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{9(-1+t^{2})^{2}W^{4} (-1+y)^{2}y^{2}}\\&\quad \times \left\{ -\frac{(-1+t^{2})(-1+y)(1+t^{2}y)e_{d}^{2}}{-1+x} \phantom {\frac{1}{2}}\right. \\&\quad +\,\frac{1}{(-1+x)x[x(1+t-2y)+y-ty][-(1+t)y+x(-1+t+2y)]}\\&\quad \times \{2\{-(-1+t^{2})(-1+y)y^{3}[1+t^{2}(-1+y)+y]\\&\quad +\,xy[-1-3y+6y^{2}+y^{3}-4y^{4}\\&\quad +\,2t^{2}y(1-3y+6y^{2}-3y^{3})+t^{4}(1+y-8y^{2}\\&\quad +\,3y^{3}+2y^{4})] -x^{3}(-1+2y)\\&\quad \times \,[1+2y^{2}-4y^{3}+2y^{4}+t^{4}(1+4y-4y^{2})\\&\quad +\,2t^{2}(-1-2y+5y^{2} -6y^{3}+3y^{4})]\\&\quad +\,x^{2}[-1+y+8y^{2}-6y^{3}-6y^{4}+6y^{5}\\&\quad +\,t^{4}(-1-3y +10y^{2}+4y^{3}-8y^{4})\\&\quad +\,2t^{2}(1+y-13y^{2}+21y^{3}-21y^{4}+9y^{5})]\}e_{d} e_{u}\}\\&\quad \left. +\,\frac{(-1+t^{2})[-1+t^{2}(-1+y)]ye_{u}^{2}}{x} \phantom {\frac{1}{2}}\right\} ,\\&T^{\sigma p}_{+-}=T^{\sigma p}_{-+}=-\frac{8\pi ^{2}\alpha \alpha _{s}(\mu _{R}^{2})C_{F}f_{\pi }^{2} \mu _{\pi }^{2}}{9(-1+t^{2})^{2}W^{4}(-1+y)^{3}y^{3}}\\&\quad \times \left\{ \frac{(-1+t^{2})y^{2}[-1+2y+t^{2}(-1-2y+2y^{2})] e_{d}^{2}}{-1+x}\phantom {\frac{1}{2}}\right. \\&\quad +\,\frac{1}{(-1+x)x[x(1+t-2y)+y-ty][-(1+t)y+x(-1+t+2y)]}\\&\quad \times \{4(-1+y)^{2}y^{2}\{-(-1+t^{4})y^{3}\\&\quad +\,xy[-1+y-4y^{2}+t^{2}(2+2y-6y^{2})\\&\quad +\,t^{4}(-1+5y+2y^{2})]+2x^{3}[1-3y+3y^{2}-2y^{3}\\&\quad +\,t^{4}(-2+4y) +t^{2}(1-5y+9y^{2}-6y^{3})]\\&\quad +\,x^{2}[-1+4y-4y^{2}+6y^{3}+t^{4}(3-4y-8y^{2})\\&\quad +\,2t^{2}(-1+4y-10y^{2} +9y^{3})]\}e_{d}e_{u}\}\\&\quad \left. +\,\frac{(-1+t^{2})(-1+y)^{2}[1-2y+t^{2}(-1-2y+2y^{2})]ye_{u}^{2}}{x} \phantom {\frac{1}{2}}\right\} ,\\&T^{\sigma \sigma }_{++}=T^{\sigma \sigma }_{--}=\frac{2\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{27(1-t^{2})^{2}W^{4}}\\&\quad \times \left\{ \frac{2(1+t^{2})[x(-1+y)-y]e_{d}^{2}}{(-1+x)^{2}x(-1+y)^{2}y} +(-1+t^{2})^{2}\right. \\&\quad \times \left\{ -\left\{ \frac{1}{(1+t)^{4}x^{2}(-1+y)^{2} [x(1+t-2y)+y-ty]^{2}}\right. \right. \end{aligned}$$

$$\begin{aligned}&\quad \times \,\{4\{-(-1+t)[-1+t(-1+y)-y](-1+y)y\\&\quad +\,x^{3}[-1+4y-6y^{2} +4y^{3}\\&\quad +\,t^{2}(-1+2y)+t(-2+6y-6y^{2})]\\&\quad +\,x[2-2y-2y^{2}+4y^{3}-t^{3} (-1+y^{2})\\&\quad +\,t(5-4y+3y^{2}-6y^{3})+2t^{2}(2-y-2y^{2}+y^{3})]\\&\quad +\,x^{2}[-1 +t^{3}(-1+y)\\&\quad \left. +\,4y^{2}-6y^{3}+t^{2}(-3+6y-4y^{2})+t(-3+5y-4y^{2}+6y^{3})]\} \}\phantom {\frac{1}{2}}\right\} \\&\quad +\,\frac{1}{(-1+t)^{4}x^{2}(-1+y)^{2}(x-tx+y+ty-2xy)^{2}}\\&\quad \times \,\{4\{(1+t)(-1+y)y[1+t(-1+y)+y]\\&\quad +\,x^{3}[1+t^{2}(1-2y)-4y+6y^{2}-4y^{3}\\&\quad +\,t(-2+6y-6y^{2})] +x[-t^{3}(-1+y^{2})\\&\quad +\,t(5-4y+3y^{2}-6y^{3})+2(-1+y+y^{2}-2y^{3})\\&\quad -\,2t^{2} (2-y-2y^{2}+y^{3})]\\&\quad +\,x^{2}[1+t^{3}(-1+y)-4y^{2}+6y^{3}+t^{2}(3-6y+4y^{2})\\&\quad +\,t(-3+5y-4y^{2}+6y^{3})]\}\}\\&\quad -\,\frac{1}{(-1+t)^{4}(-1+x)^{2}y^{2}[x(1+t-2y)+y-ty]^{2}}\\&\quad \times \,\{4\{(-1+t)^{2}(-2+t-y)(-1+y)y\\&\quad +\,x^{3}[-1+4y-6y^{2}+4y^{3}+t^{2}(-1+2y)+t(-2+6y-6y^{2})]\\&\quad -\,(-1+t)x[1-2y+t^{2}y^{2}+4y^{3}+t(1+2y-5y^{2}-2y^{3})]\\&\quad +\,x^{2}[t^{3}y+t^{2}(2-4y-4y^{2})-2y(1-2y+3y^{2})\\&\quad +\,t(2-3y+ 4y^{2}+6y^{3})]\}\}\\&\quad +\,\frac{1}{(1+t)^{4}(-1+x)^{2}y^{2}(x-tx+y+ty-2xy)^{2}}\\&\quad \times \,\{4\{(1+t)^{2}(-1+y)y(2+t+y)\\&\quad +\,x^{3}[1+t^{2}(1-2y)-4y+6y^{2}-4y^{3}+t(-2+6y-6y^{2})]\\&\quad -\,(1+t)x[1-2y+t^{2}y^{2}+4y^{3}+t(-1-2y+5y^{2}+2y^{3})]\\&\quad +\,x^{2}[t^{3}y+2y(1-2y+3y^{2})+t^{2}(-2+4y+4y^{2})\\&\quad \left. +\,t(2-3y+4y^{2} +6y^{3})]\}\}\phantom {\frac{1}{2}}\right\} e_{d}e_{u}\\&\quad \left. +\,\frac{2(1+t^{2})(-1+xy)e_{u}^{2}}{(-1+x)x^{2}(-1+y)y^{2}} \phantom {\frac{1}{2}}\right\} ,\\&T^{\sigma \sigma }_{+-}=T^{\sigma \sigma }_{-+}=\frac{4\pi ^{2}\alpha \alpha _{s} (\mu _{R}^{2})C_{F}f_{\pi }^{2}\mu _{\pi }^{2}}{27(-1+t^{2})W^{4}}\\&\quad \times \left\{ \frac{(1+t^{2})[2+x(-1+y)-y]e_{d}^{2}}{(-1+x)^{2}x(-1+y)^{2}y} -\frac{1}{(-1+t^{2})^{2}}\right. \\&\quad \times \,2\left\{ \frac{1}{x^{2}(-1+y)^{2}[x(-1+t-2y)+y-ty]^{2}}(-1+t)^{4}\right. \\&\quad \times \,\{1(-1+t) [-3+t(-1+y)-y]y^{2}\\&\quad +\,x^{3}[-1+4y-6y^{2}+4y^{3}+t^{2}(-1+2y)\\&\quad +\,t(-2+6y-6y^{2})]+x^{2} [-2+t^{3}(-1+y)\\&\quad +\,6y-4y^{2}-6y^{3}+t^{2}(-4+6y-4y^{2})\\&\quad +\,t(-5+11y-4y^{2}+6y^{3})] +x[1-4y\\&\quad +\,8y^{2}+4y^{3}-t^{3}(-1+y^{2})+t^{2}(3-4y^{2}+2y^{3})\\&\quad -\,t(-3+4y+3y^{2} +6y^{3})]\}\\&\quad -\,\frac{1}{x^{2}(-1+y)^{2}(x-tx+y+ty-2xy)^{2}}(1+t)^{4}\\&\quad \times \,\{(1+t)y^{2}[3+t(-1+y)+y]\\&\quad +\,x^{3}[1+t^{2}(1-2y)-4y+6y^{2}-4y^{3}\\&\quad +\,t(-2+6y-6y^{2})]+x^{2} [2+t^{3}(-1+y) \end{aligned}$$

$$\begin{aligned}&\quad -\,6y+4y^{2}+6y^{3}+t^{2}(4-6y+4y^{2})\\&\quad +\,t(-5+11y-4y^{2}+6y^{3})] -x[1-4y\\&\quad +\,8y^{2}+4y^{3}+t^{3}(-1+y^{2})+t^{2}(3-4y^{2}+2y^{3})\\&\quad +\,t(-3+4y+3y^{2}+6y^{3})]\}\\&\quad +\,\frac{1}{(-1+x)^{2}y^{2}[x(1+t-2y)+y-ty]^{2}}(1+t)^{4}\\&\quad \times \,\{(-1+t)^{2} y[1+t(-1+y)-2y-y^{2}]\\&\quad -\,(-1+t)xy[-4+(6-5t+t^{2})y-2(-2+t)y^{2}]\\&\quad +\,x^{3}[-1+4y-6y^{2}+4y^{3}+t^{2}(-1+2y)+t(-2+6y-6y^{2})]\\&\quad +\,x^{2}[-3+8y+t^{3}y-4y^{2}-6y^{3}+t^{2}(1-4y-4y^{2})\\&\quad +\,t(-2+3y+4y^{2}+6y^{3})]\}\\&\quad -\,\frac{1}{(-1+x)^{2}y^{2}(x-tx+y+ty-2xy)^{2}}(-1+t)^{4}\\&\quad \times \,\{(1+t)^{2} y[-1+t(-1+y)+2y+y^{2}]\\&\quad -\,(1+t)xy[-4+(6-5t+t^{2})y+2(2+t)y^{2}]\\&\quad +\,x^{3}[1+t^{2}(1-2y)-4y+6y^{2}-4y^{3}+t(-2+6y-6y^{2})]\\&\quad +\,x^{2}[3-8y+t^{3}y+4y^{2}+6y^{3}+t^{2}(-1+4y+4y^{2})\\&\quad \left. +\,t(-2+3y+4y^{2} +6y^{3})]\}\phantom {\frac{1}{2}}\right\} e_{d}e_{u}\\&\quad \left. +\,\frac{(1+t^{2})(1+xy)e_{u}^{2}}{(-1+x)x^{2}(-1+y)y^{2}}\right\} . \end{aligned}$$