Analysis of the mass and width of Y(4274) as axialvector molecule-like state

Abstract

In this article, we assign Y(4274) to the color octet–octet type axialvector molecule-like state with $J^{PC}=1^{++}$ tentatively, and construct the color octet–octet type axialvector current to study its mass and width with the QCD sum rules in details. The predicted mass favors assigning the Y(4274) to a color octet–octet type molecule-like state, but the predicted width strongly disfavors assigning the Y(4274) to the color octet–octet type molecule-like state. The Y(4274) may be the conventional charmonium state $\chi _{c1}(\mathrm 3P)$, and it is important to observe the decay $Y(4274)\rightarrow J/\psi \omega$ to diagnose the nature of Y(4274).

1 Introduction

In 2011, the CDF collaboration confirmed Y(4140) in the $B^\pm \rightarrow J/\psi \,\phi K^\pm$ decays with a statistical significance greater than $5\,\sigma$, and observed an evidence for a second structure (Y(4274)) with approximate significance of $3.1\,\sigma$. The measured mass and width are $\left( 4274.4^{+8.4}_{-6.7}\pm 1.9\right) \,\mathrm {MeV}$ and $\left( 32.3^{+21.9}_{-15.3}\pm 7.6\right) \,\mathrm {MeV}$, respectively [1]. The Y(4274) may be a S-wave $D_s\bar{D}_{s0}(2317)+h.c.$ molecular state [2,3,4], or not a S-wave $D_s\bar{D}_{s0}(2317)+h.c.$ molecular state [5]. In 2013, the CMS collaboration observed evidence for a second peaking structure besides Y(4140) with the mass $4313.8 \pm 5.3 \pm 7.3 \, \mathrm {MeV}$ and width $38^{+30}_{-15}\pm 16 \,\mathrm {MeV}$, respectively [6].

Recently, the LHCb collaboration performed the first full amplitude analysis of the decays $B^+\rightarrow J/\psi \phi K^+$ and confirmed the two old particles Y(4140) and Y(4274) in the $J/\psi \phi$ mass spectrum with statistical significances $8.4\sigma$ and $6.0\sigma$, respectively, and determined the quantum numbers to be $J^{PC} =1^{++}$ with statistical significances $5.7\sigma$ and $5.8\sigma$, respectively [7, 8]. The measured masses and widths are

$$\begin{aligned} \begin{aligned}&Y(4140) : M = 4146.5 \pm 4.5 ^{+4.6}_{-2.8} \text{ MeV }, \, \\&\quad \Gamma = 83 \pm 21 ^{+21}_{-14} \text{ MeV }, \\&Y(4274) : M = 4273.3 \pm 8.3 ^{+17.2}_{-3.6} \text{ MeV }, \, \\&\quad \Gamma = 56 \pm 11 ^{+8}_{-11} \text{ MeV }. \end{aligned} \end{aligned}$$

(1)

The LHCb collaboration determined the quantum numbers of the Y(4274) to be $J^{PC}=1^{++}$, which rules out the $0^{-+}$ molecule assignment, which is consistent with our previous work [5]. There have been several possible assignments, such as the color sextet–sextet type $cs\bar{c}\bar{s}$ tetraquark state [9, 10], the conventional orbitally excited state $\chi _{c1}(\mathrm 3P)$ [11, 12], the color triplet–triplet type $\frac{1}{\sqrt{6}}(u\bar{u}+d\bar{d}-2s\bar{s})c\bar{c}$ tetraquark state [13], etc.

In 2014, the Belle collaboration analyzed the $\bar{B}^0\rightarrow K^- \pi ^+ J/\psi$ decays and observed a resonance ($Z_c(4200)$) in the $J/\psi \pi ^+$ invariant mass distribution with a statistical significance of greater than $6.2\,\sigma$, the measured Breit–Wigner mass and width are $M_{Z_c(4200)} = 4196^{+31}_{-29}{}^{+17}_{-13} \,\mathrm {MeV}$ and $\Gamma _{Z_c(4200)} = 370^{+70}_{-70}{}^{+70}_{-132}\,\mathrm {MeV}$, respectively [14, 15]. The preferred spin–parity is $J^P = 1^+$.

In Ref. [16], we study the axialvector hidden charm and hidden bottom tetraquark states in details with the QCD sum rules and obtain the mass $M_{cu\bar{c}\bar{d},J^P=1^+}=(4.44 \pm 0.19)\,\mathrm {GeV}$ for the diquark–antidiquark type tetraquark state. In Ref. [17], Chen and Zhu study the vector and axialvector charmonium-like tetraquark states with the QCD sum rules in a systematic way and obtain the mass $M_{cu\bar{c}\bar{d},J^P=1^+}=(4.16 \pm 0.10)\,\mathrm {GeV}$ for the diquark–antidiquark type tetraquark state. In Ref. [16], we choose the input parameters $m_c(\mathrm 1\,GeV)$, $\langle \bar{q}q\rangle (\mathrm 1\,GeV)$, $\langle \bar{q}g_s \sigma Gq\rangle (\mathrm 1\,GeV)$, while in Ref. [17], Chen and Zhu choose the input parameters $m_c(m_c)$, $\langle \bar{q}q\rangle (\mathrm 1\,GeV)$, $\langle \bar{q}g_s \sigma Gq\rangle (\mathrm 1\,GeV)$. The different predictions for the $C\gamma _5\otimes \gamma _\mu C$ type axialvector tetraquark state in Ref. [16] and Ref. [17] originate from the different choice of the c-quark mass. If we take different choices of the heavy quark masses as a source of uncertainties, the predicted mass is about $M_{cu\bar{c}\bar{d},J^P=1^+}=(4.06$–$4.63)\,\mathrm {GeV}$.

In Ref. [18], we distinguish the charge conjugations of the interpolating currents, study the diquark–antidiquark type axialvector tetraquark states in a systematic way with the QCD sum rules by taking into account the energy scale dependence of the QCD spectral densities for the first time, and obtain the predictions $M_{X(3872)}=3.87^{+0.09}_{-0.09}\,\mathrm {GeV}$ and $M_{Z_c(3900)}{=}3.91^{+0.11}_{-0.09}\,\mathrm {GeV}$. In Ref. [19], Albuquerque et al. take into account the next-to-leading order and next-to-next-to-leading order factorizable radiative corrections to the perturbative terms, and obtain the predication $M_{cu\bar{c}\bar{d},J^P=1^+}=(3.888 \pm 0.130)\,\mathrm {GeV}$, which also depends on special choice of the energy scale $\mu$, in other words, the $\overline{MS}$ mass $m_c(\mu )$. The non-factorizable radiative corrections are still needed to make precise predictions. In leading order approximation, $M_{X(3872)}=3.87^{+0.09}_{-0.09}\,\mathrm {GeV}$ and $M_{Z_c(3900)}=3.91^{+0.11}_{-0.09}\,\mathrm {GeV}$ [18], after taking into account the next-to-leading order and next-to-next-to-leading order factorizable radiative corrections to the perturbative terms, $M_{cu\bar{c}\bar{d},J^P=1^+}=(3.888 \pm 0.130)\,\mathrm {GeV}$ [19], the predicted masses only change slightly. On the other hand, including the next-to-leading order and next-to-next-to-leading order factorizable radiative corrections to the perturbative terms leads to the value of the pole residue $\lambda _{cu\bar{c}\bar{d},J^P=1^+}$ undergoes the replacement $\lambda _{cu\bar{c}\bar{d},J^P=1^+}\rightarrow 1.09\,\lambda _{cu\bar{c}\bar{d},J^P=1^+}$. According to Refs. [18, 19], the masses of the ground state diquark–antidiquark type axialvector tetraquark states $cu\bar{c}\bar{d}$ are about $3.9\,\mathrm {GeV}$.

In Ref. [20], Chen et al. assign $Z_c(4200)$ to be the ground state axialvector tetraquark state $cu\bar{c}\bar{d}$, calculate its decay width with the QCD sum rules, and obtain the value $\Gamma _{Z_c(4200)}=435 \pm 180\,\mathrm { MeV}$. In Ref. [9], Chen et al. assign X(4140) to be the ground state axialvector tetraquark state $cs\bar{c}\bar{s}$. If $Z_c(4200)$ and X(4140) are the color triplet–triplet $C\gamma _5\otimes \gamma _\mu C$ type axialvector tetraquark states, it is more natural in the case that the X(4140) has larger mass than $Z_c(4200)$.

In Ref. [21], we assign $Z_c(4200)$ to the color octet–octet type axialvector molecule-like state $\bar{u}\lambda ^a c \bar{c}\lambda ^a d$, where the $\lambda ^a$ are the Gell-Mann matrices, and we construct the color octet–octet type axialvector current to study its mass (width) with the QCD sum rules by calculating the vacuum condensates up to dimension 10 (5) in the operator product expansion. The predictions $M_{Z_c(4200)}=4.19 \pm 0.08\,\mathrm {GeV}$ and $\Gamma _{Z_c(4200)}\approx 334\,\mathrm {MeV}$ are consistent with the experimental data $M_{Z_c(4200)} = 4196^{+31}_{-29}{}^{+17}_{-13} \,\mathrm {MeV}$ and $\Gamma _{Z_c(4200)} = 370^{+70}_{-70}{}^{+70}_{-132}\,\mathrm {MeV}$ from the Belle collaboration [14, 15], and favor assigning the $Z_c(4200)$ to be the color octet–octet type molecule-like state with $J^{PC}=1^{+-}$. Moreover, we study the energy scale dependence of the QCD spectral density of the molecule-like state in details and suggest an empirical energy scale formula to determine the ideal energy scale, in other words, to determine the ideal c-quark mass.

Also in Ref. [21], we discuss the possible assignments of $Z_c(3900)$, $Z_c(4200)$ and Z(4430) as the ground state color triplet–triplet diquark–antidiquark type tetraquark states with $J^{PC}=1^{+-}$ in details. The QCD sum rules support assigning $Z_c (3900)$ and Z(4430) to the ground state and the first radial excited state of the diquark–antidiquark type axialvector tetraquark states with $J^{PC}=1^{+-}$, respectively [18, 22]. If we assign $Z_c(4200)$ and Y(4274) to molecule-like states with $J^{PC}=1^{+-}$ and $1^{++}$, respectively, the mass difference $M_{Y(4274)}-M_{Z_c(4200)}\approx 77\,\mathrm {MeV}$. This is reasonable, as the SU(3) breaking effects are very small for the four-quark systems [16, 23, 24]. In this article, we assign Y(4274) to the color octet–octet type molecule-like state tentatively,

$$\begin{aligned} Y(4274)= & {} \frac{1}{\sqrt{2}}\left( {\mathcal {D}}^a_s\overline{\mathcal {D}}_s^{a*} - { \mathcal {D}}_s^{a*}\overline{\mathcal {D}}^a_s\right) \,\,\,(\mathrm{with}\,\,\,1^{++}), \end{aligned}$$

(2)

study its mass and decay width with the QCD sum rules in details, where the meson-like states ${\mathcal {D}}^a_s$ and ${\mathcal {D}}_s^{a*}$ have the same quark constituents as the mesons $D_s$ and $D_s^*$ respectively, but they are in the color octet representation, a corresponds to the Gell-Mann matrices.

The article is arranged as follows: we derive the QCD sum rules for the mass and width of the color octet–octet type axialvector molecule-like state Y(4274) in Sect. 2 and in Sect. 3, respectively; Sect. 4 is reserved for our conclusion.

2 The mass of the color octet–octet type axialvector molecule-like state

In the following, we write down the two-point correlation function $\Pi _{\mu \nu }(p)$ in the QCD sum rules,

$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} i\int \mathrm{{d}}^4x e^{ip \cdot x} \langle 0|T\left\{ J_\mu (x)J_\nu ^{\dagger }(0)\right\} |0\rangle , \end{aligned}$$

(3)

$$\begin{aligned} J_\mu (x)= & {} \frac{\bar{s}(x)i\gamma _5 \lambda ^a c(x)\bar{c}(x)\gamma _\mu \lambda ^a s(x)-\bar{s}(x)\gamma _\mu \lambda ^a c(x)\bar{c}(x)i\gamma _5 \lambda ^a s(x)}{\sqrt{2}},\nonumber \\ \end{aligned}$$

(4)

where the $\lambda ^a$ are the Gell-Mann matrices in the color space. We construct the color octet–octet type current $J_\mu (x)$ to study the molecule-like state Y(4274). One can consult Refs. [21, 25,26,27] for more literatures on the color octet–octet type currents. Under charge conjugation transform $\widehat{C}$, the current $J_\mu (x)$ has the property,

$$\begin{aligned} \widehat{C}J_{\mu }(x)\widehat{C}^{-1}= & {} + J_\mu (x). \end{aligned}$$

(5)

At the phenomenological side, we insert a complete set of intermediate hadronic states with the same quantum numbers as the current operator $J_\mu (x)$ into the correlation function $\Pi _{\mu \nu }(p)$ to obtain the hadronic representation [28,29,30], and isolate the ground state contribution,

$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} \frac{\lambda _{Y(4274)}^2}{M^2_{Y(4274)}-p^2}\left( -g_{\mu \nu } +\frac{p_\mu p_\nu }{p^2}\right) +\cdots , \end{aligned}$$

(6)

where the pole residue $\lambda _{Y(4274)}$ is defined by $\langle 0|J_\mu (0)|Y(4274)\rangle =\lambda _{Y(4274)}\, \varepsilon _\mu$, the $\varepsilon _\mu$ is the polarization vector of the axialvector meson Y(4274).

In the following, we briefly outline the operator product expansion for the correlation function $\Pi _{\mu \nu }(p)$. We contract the quark fields s and c in the correlation function $\Pi _{\mu \nu }(p)$ with the Wick theorem, and we obtain the result

$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} -\frac{i}{2} \lambda ^a_{jk}\lambda ^a_{mn}\lambda ^b_{k^{\prime }j^{\prime }}\lambda ^b_{n^{\prime }m^{\prime }} \int \mathrm{{d}}^4x e^{ip \cdot x} \nonumber \\&\times \left\{ \mathrm{Tr}\left[ \gamma _5 S_c^{kk^{\prime }}(x)\gamma _5 S^{j^{\prime }j}(-x)\right] \right. \nonumber \\&\times \mathrm{Tr}\left[ \gamma _\mu S^{nn^{\prime }}(x)\gamma _\nu S_c^{m^{\prime }m}(-x)\right] \nonumber \\&+\mathrm{Tr}\left[ \gamma _\mu S_c^{kk^{\prime }}(x)\gamma _\nu S^{j^{\prime }j}(-x)\right] \nonumber \\&\times \mathrm{Tr}\left[ \gamma _5 S^{nn^{\prime }}(x)\gamma _5 S_c^{m^{\prime }m}(-x)\right] \nonumber \\&-\; \mathrm{Tr}\left[ \gamma _\mu S_c^{kk^{\prime }}(x)\gamma _5 S^{j^{\prime }j}(-x)\right] \nonumber \\&\times \mathrm{Tr}\left[ \gamma _5 S^{nn^{\prime }}(x)\gamma _\nu S_c^{m^{\prime }m}(-x)\right] \nonumber \\&- \;\mathrm{Tr}\left[ \gamma _5 S_c^{kk^{\prime }}(x)\gamma _\nu S^{j^{\prime }j}(-x)\right] \nonumber \\&\left. \times \mathrm{Tr}\left[ \gamma _\mu S^{nn^{\prime }}(x)\gamma _5 S_c^{m^{\prime }m}(-x)\right] \right\} , \end{aligned}$$

(7)

where

$$\begin{aligned} S^{ij}(x)= & {} \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4} -\frac{\delta _{ij}m_s}{4\pi ^2x^2}-\frac{\delta _{ij}\langle \bar{s}s\rangle }{12} +\frac{i\delta _{ij}\!\not \!{x}m_s \langle \bar{s}s\rangle }{48}\nonumber \\&-\;\frac{\delta _{ij}x^2\langle \bar{s}g_s\sigma Gs\rangle }{192}+\frac{i\delta _{ij}x^2\!\not \!{x} m_s\langle \bar{s}g_s\sigma Gs\rangle }{1152}\nonumber \\&-\;\frac{ig_s G^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2} -\frac{i\delta _{ij}x^2\!\not \!{x}g_s^2\langle \bar{s} s\rangle ^2}{7776}\nonumber \\&-\;\frac{\delta _{ij}x^4\langle \bar{s}s \rangle \langle g_s^2 GG\rangle }{27648}-\frac{1}{8}\langle \bar{s}_j\sigma ^{\mu \nu }s_i \rangle \sigma _{\mu \nu } \nonumber \\&-\;\frac{1}{4}\langle \bar{s}_j\gamma ^{\mu }s_i\rangle \gamma _{\mu }+\cdots , \end{aligned}$$

(8)

$$\begin{aligned} S_c^{ij}(x)= & {} \frac{i}{(2\pi )^4}\int \mathrm{{d}}^4k e^{-ik \cdot x} \left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c}\right. \nonumber \\&\left. -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}\right. \nonumber \\&\left. +\frac{g_s D_\alpha G^n_{\beta \lambda }t^n_{ij}(f^{\lambda \beta \alpha }+f^{\lambda \alpha \beta }) }{3(k^2-m_c^2)^4}\right. \nonumber \\&\left. -\frac{g_s^2 (t^at^b)_{ij} G^a_{\alpha \beta }G^b_{\mu \nu }(f^{\alpha \beta \mu \nu }+f^{\alpha \mu \beta \nu }+f^{\alpha \mu \nu \beta }) }{4(k^2-m_c^2)^5}+\cdots \right\} , \nonumber \\ \end{aligned}$$

(9)

$$\begin{aligned} f^{\lambda \alpha \beta }= & {} (\!\not \!{k}+m_c)\gamma ^\lambda (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c),\nonumber \\ f^{\alpha \beta \mu \nu }= & {} (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c)\gamma ^\mu (\!\not \!{k}+m_c)\nonumber \\&\times \gamma ^\nu (\!\not \!{k}+m_c), \end{aligned}$$

(10)

and $t^n=\frac{\lambda ^n}{2}$, $D_\alpha =\partial _\alpha -ig_sG^n_\alpha t^n$ [30], then compute the integrals both in the coordinate space and in the momentum space, and we obtain the correlation function $\Pi _{\mu \nu }(p)$, therefore the QCD spectral density through dispersion relation. For technical details, one can consult Ref. [18].

Now we take the quark–hadron duality below the continuum threshold $s_0$ and perform Borel transform with respect to the variable $P^2=-p^2$ to obtain the QCD sum rule:

$$\begin{aligned} \lambda ^2_{Y}\, \exp \left( -\frac{M^2_{Y}}{T^2}\right) = \int _{4m_c^2}^{s_0} \mathrm{{d}}s\, \rho (s) \, \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(11)

where

$$\begin{aligned} \rho (s)= & {} \rho _{0}(s)+\rho _{3}(s) +\rho _{4}(s)+\rho _{5}(s)+\rho _{6}(s)\nonumber \\&+\;\rho _{7}(s) +\rho _{8}(s)+\rho _{10}(s). \end{aligned}$$

(12)

The explicit expressions of the QCD spectral densities $\rho _{0}(s)$, $\rho _{3}(s)$, $\rho _{4}(s)$, $\rho _{5}(s)$, $\rho _{6}(s)$, $\rho _{7}(s)$, $\rho _{8}(s)$ and $\rho _{10}(s)$ are given in the Appendix. Even in the leading order approximation, the strong coupling constant $g_s^2(\mu )=4\pi \alpha _s(\mu )$ appears according to the equation of motion $\left( D_\alpha G_{\beta \alpha }\right) ^a=g_s\sum \nolimits _{q=u,d,s}\bar{q}\gamma _\beta t^aq$, see the terms $g_s^2\langle \bar{s}s\rangle ^2$ in the spectral density $\rho _6(s)$. So we have to consider the energy scale dependence of the QCD sum rules, the preferred c-quark mass is the $\overline{MS}$ mass $m_c(\mu )$.

The on-shell quark propagator has no infrared divergences in perturbation theory, and this provides a perturbative definition of the quark mass [31, 32]. But the pole mass cannot be used to arbitrarily high accuracy because of nonperturbative infrared effects in QCD. The pole mass $\widehat{m}_c$ and the $\overline{MS}$ mass $m_c(m_c)$ have the relation,

$$\begin{aligned} \widehat{m}_c= & {} m_c(m_c)\left[ 1+\frac{4}{3}\frac{\alpha _s(m_c)}{\pi }+\cdots \right] . \end{aligned}$$

(13)

The value $m_c(m_c)=1.275 \pm 0.025\,\mathrm { GeV}$ from the Particle Data Group corresponds to $\widehat{m}_c=1.67 \pm 0.07\,\mathrm { GeV}$ [33]. If we take the pole mass, then $2\widehat{m}_c> M_{J/\psi }>M_{\eta _c}$, at the phenomenological side of the QCD sum rules for $J/\psi$ and $\eta _c$,

$$\begin{aligned} \begin{aligned}&\int _{4\widehat{m}_c^2}^{s_0} \mathrm{{d}}s\, f_{J/\psi }^2 M_{J/\psi }^2\, \delta \left( s-M_{J/\psi }^2 \right) \, \exp \left( -\frac{s}{T^2} \right) =0, \\&\int _{4\widehat{m}_c^2}^{s_0} \mathrm{{d}}s\, \frac{f_{\eta _c}^2 M_{\eta _c}^2}{4\widehat{m}_c^2}\, \delta \left( s-M_{\eta _c}^2 \right) \, \exp \left( -\frac{s}{T^2} \right) =0. \end{aligned} \end{aligned}$$

(14)

If we want to obtain nonzero values, we have to choose smaller pole mass, $2\widehat{m}_c< M_{\eta _c}<M_{J/\psi }$ [34, 35]. For an observable particle such as the electron, the physical mass appears as the pole mass, irrespective of the leading order, next-to-leading order, next-to-next-to-leading order, $\ldots$, radiative corrections are concerned. In the leading order approximation, $\widehat{m}_c=m_c(m_c)$, however, $m_c(m_c)$ originates from the radiative corrections and renormalization, which are beyond the leading order approximation. So in the leading order approximation, the definition of the pole mass $\widehat{m}_c$ is of arbitrary. Again, we can see that the preferred c-quark mass is the $\overline{MS}$ mass $m_c(\mu )$. Moreover, the full quark propagator has no pole because the quarks are confined. The pole mass corresponds to a non-confined particle, at the QCD side of the QCD sum rules for $J/\psi$ and $\eta _c$, the heavy quarks c and $\bar{c}$ are confined particles.

We derive Eq. (11) with respect to $\tau =\frac{1}{T^2}$, then eliminate the pole residue $\lambda _{Y(4274)}$ to obtain the QCD sum rule for the mass,

$$\begin{aligned} M_{Y}^2= & {} - \frac{\int _{4m_c^2}^{s_0} \mathrm{{d}}s \, \frac{\mathrm{{d}}}{\mathrm{{d}} \tau }\,\rho (s)e^{-\tau s}}{\int _{4m_c^2}^{s_0} \mathrm{{d}}s \rho (s)e^{-\tau s}}. \end{aligned}$$

(15)

Now we choose the input parameters at the QCD side of the QCD sum rules. We take the vacuum condensates to have the standard values $\langle \bar{q}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3$, $\langle \bar{s}s \rangle =(0.8\pm 0.1)\langle \bar{q}q \rangle$, $\langle \bar{s}g_s\sigma G s \rangle =m_0^2\langle \bar{s}s \rangle$, $m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33\,\mathrm {GeV})^4$ at the energy scale $\mu =1\, \mathrm {GeV}$ [28,29,30, 36], and take the $\overline{MS}$ masses $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ and $m_s(\mu =2\,\mathrm {GeV})=(0.095\pm 0.005)\,\mathrm {GeV}$ from the Particle Data Group [33]. Moreover, we take into account the energy-scale dependence of the quark condensate, mixed quark condensate and $\overline{MS}$ masses from the renormalization group equation [33, 37],

$$\begin{aligned} \begin{aligned} \langle \bar{s}s \rangle (\mu )&=\langle \bar{s}s \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{4}{9}}, \\ \langle \bar{s}g_s \sigma Gs \rangle (\mu )&=\langle \bar{s}g_s \sigma Gs \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}},\\ m_c(\mu )&=m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}},\\ m_s(\mu )&=m_s(\mathrm{2GeV} )\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(\mathrm{2GeV})}\right] ^{\frac{4}{9}}, \\ \alpha _s(\mu )&=\frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t}\right. \\&\left. +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] , \end{aligned} \end{aligned}$$

(16)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213\,\mathrm {MeV}$, $296\,\mathrm {MeV}$ and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, 4 and 3, respectively [33].

As the quark masses $m_c(\mu )$, $m_s(\mu )$, the quark condensate $\langle \bar{s}s \rangle (\mu )$, the mixed condensate $\langle \bar{s}g_s \sigma Gs \rangle (\mu )$ all depend on the energy scale $\mu$, the QCD spectral density $\rho (s)$ depends on the energy scale $\mu$, we have to determine the energy scales of the QCD sum rules for those molecule-like states in a consistent way.

The hidden charm (or bottom) four-quark systems $q\bar{q}^{\prime }Q\bar{Q}$ can be described by a double-well potential. In the four-quark system $q\bar{q}^{\prime }Q\bar{Q}$, the heavy quark Q serves as a static well potential and combines with the light quark q to form a heavy diquark $\mathcal {D}^i$ in color antitriplet, $q+Q \rightarrow \mathcal {D}^i$ [18, 22,23,24, 38,39,40,41,42], or combines with the light antiquark $\bar{q}^\prime$ to form a heavy meson in color singlet (meson-like state in color octet), $\bar{q}^\prime +Q \rightarrow \bar{q}^{\prime }Q\,\, (\bar{q}^{\prime }\lambda ^{a}Q)$ [21, 27, 43]; the heavy antiquark $\bar{Q}$ serves as another static well potential and combines with the light antiquark $\bar{q}^\prime$ to form a heavy antidiquark $\overline{\mathcal {D}}^i$ in color triplet, $\bar{q}^{\prime }+\bar{Q} \rightarrow \overline{ \mathcal {D}}^i$ [18, 22,23,24, 38,39,40,41,42], or combines with the light quark q to form a heavy meson in color singlet (meson-like state in color octet), $q+\bar{Q} \rightarrow \bar{Q}q\,\, (\bar{Q}\lambda ^{a}q)$ [21, 27, 43], where i is color index, the $\lambda ^a$ are the Gell-Mann matrices. Then

$$\begin{aligned} \begin{aligned} \mathcal {D}^i+\overline{\mathcal {D}}^i&\rightarrow \mathrm{compact \,\,\, tetraquark \,\,\, states}, \\ \bar{q}^{\prime }Q+\bar{Q}q&\rightarrow \mathrm{loose \,\,\, molecular \,\,\, states}, \\ \bar{q}^{\prime }\lambda ^aQ+\bar{Q}\lambda ^a q&\rightarrow \mathrm{molecule-like \,\,\, states}, \end{aligned} \end{aligned}$$

(17)

the two heavy quarks Q and $\bar{Q}$ stabilize the four-quark systems $q\bar{q}^{\prime }Q\bar{Q}$, just as in the case of the $(\mu ^-e^+)(\mu ^+ e^-)$ molecule in QED [44].

The four-quark systems $q\bar{q}^{\prime }Q\bar{Q}$ are characterized by the effective heavy quark mass ${\mathbb {M}}_Q$ and the virtuality $V=\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ [18, 21,22,23,24, 27, 38,39,40,41,42,43]. It is natural to take the energy scale $\mu =V$. The ${\mathbb {M}}_Q$ is just an empirical parameter to determine the optimal energy scales of the QCD spectral densities, and has no relation to the pole mass $\hat{m}_Q$ or the $\overline{MS}$ mass $m_Q(\mu )$.

In Refs. [18, 21,22,23,24, 27, 38,39,40,41,42,43], we observe that there exist three universal values for the effective heavy quark masses ${\mathbb {M}}_Q$, which correspond to the compact tetraquark states, molecular states, molecule-like states, respectively. The empirical energy scale formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ works well in assigning X(3872), $Z_c(3900)$, Y(3915), $Z_c(4020/4025)$, Y(4140), $Z_c(4200)$, Y(4260), Y(4360), $Z_c(4430)$, X(4500), Y(4630 / 4660), X(4700), $Z_b(10610)$, $Z_b(10650)$, etc.

Fig. 1

The mass and pole residue of $M_{Y(4274)}$ with variation of the Borel parameter $T^2$

We evolve all the input parameters in the QCD spectral density to the special energy scale determined by the empirical formula,

$$\begin{aligned} \mu= & {} \sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2} \, . \end{aligned}$$

(18)

In Ref. [21], we obtain the effective mass ${\mathbb {M}}_c=1.98\,\mathrm {GeV}$ for the molecule-like states. Then we re-checked the numerical calculations and corrected a small error concerning the mixed condensate, the updated value is ${\mathbb {M}}_c=2.01\,\mathrm {GeV}$. From the empirical energy scale formula, we can obtain the energy scale $\mu =1.45\,\mathrm {GeV}$. After taking into account the SU(3) symmetry breaking effect $m_s-m_{u/d}\approx 0.1\,\mathrm {GeV}$, we obtain the optimal energy scale $\mu =1.25\,\mathrm {GeV}$ for the QCD spectral density $\rho (s)$. If we neglect the SU(3) symmetry breaking effect, the effective c-quark mass ${\mathbb {M}}_c$ can be taken as ${\mathbb {M}}_c=2.04\,\mathrm {GeV}$.

Now we search for the Borel parameter $T^2$ and continuum threshold parameter $s_0$ to satisfy the following three criteria:

• 1. Pole dominance at the phenomenological side;

• 2. Convergence of the operator product expansion;

• 3. Appearance of the Borel platforms.

The resulting Borel parameter and continuum threshold parameter are $T^2=(3.1$–$3.5)\,\mathrm {GeV}^2$ and $\sqrt{s_0}=(4.8\pm 0.1)\,\mathrm {GeV}$, respectively. At the Borel window, the pole contribution is about $(41-62)\%$, the contributions of the vacuum condensates of dimension 8 and 10 are about $|D_8|=(5-7)\%$ and $D_{10}<1\%$, respectively, the first two criteria are satisfied.

We take into account all uncertainties of the input parameters, and we obtain the values of the mass and pole residue, which are shown explicitly in Fig. 1,

$$\begin{aligned} \begin{aligned} M_{Y(4274)}&=(4.27\pm 0.09) \, \mathrm {GeV},\\ \lambda _{Y(4274)}&=(4.67\pm 0.74)\times 10^{-2} \, \mathrm {GeV}^5. \end{aligned} \end{aligned}$$

(19)

In Fig. 1, we plot the mass and pole residue of the Y(4274) with variation of the Borel parameter $T^2$ at a larger interval than the Borel window. From the figure, we can see that there appear platforms, criterion $\mathbf {3}$ is also satisfied. Now the three criteria are all satisfied, it is reliable to extract the ground state mass. The predicted mass $M_{Y(4274)}=(4.27\pm 0.09) \, \mathrm {GeV}$ is consistent with the experimental value $4273.3 \pm 8.3 ^{+17.2}_{-3.6} \text{ MeV }$ from the LHCb collaboration [7, 8], which supports assigning Y(4274) to the color octet–octet type $\bar{s}\lambda ^a c\bar{c}\lambda ^a s$ molecule-like state.

In Ref. [19], Albuquerque et al. study the hidden-charm and hidden-bottom molecular states and tetraquark states by taking into account the next-to-leading order and next-to-next-to-leading order radiative corrections to the perturbative terms from the factorizable Feynman diagrams (without including the non-factorizable Feynman diagrams). The numerical results indicate that the predicted masses are slightly modified, while the decay constants (which relate to the pole residues) are modified significantly, the largest modification amounts to multiplying the decay constants by a factor 1.8. So we expect that the predication $M_{Y(4274)}=(4.27\pm 0.09) \, \mathrm {GeV}$ survives approximately even if the next-to-leading order radiative corrections to the perturbative terms are taken into account. Moreover, at the present time, even the next-to-leading order factorizable contributions are not available for the color octet–octet type molecule-like states, it is a challenging work to calculate both the next-to-leading order factorizable and non-factorizable Feynman diagrams.

3 The width of the color octet–octet type axialvector molecule-like state

We can study the strong decay $Y(4274)\rightarrow J/\psi \phi$ with the three-point correlation function $\Pi _{\alpha \mu \nu }(p,q)$,

$$\begin{aligned} \Pi _{\alpha \mu \nu }(p,q)= & {} i^2\int \mathrm{{d}}^4x\mathrm{{d}}^4y e^{ipx}e^{iqy}\langle 0|T\nonumber \\&\times \left\{ J_\alpha ^{J/\psi }(x)J_{\mu }^{\phi }(y)J_{\nu }(0)\right\} |0\rangle , \end{aligned}$$

(20)

where the currents

$$\begin{aligned} \begin{aligned} J_\alpha ^{J/\psi }(x)&=\bar{c}(x)\gamma _\alpha c(x), \\ J_\mu ^{\phi }(x)&=\bar{s}(y)\gamma _\mu s(y), \end{aligned} \end{aligned}$$

(21)

interpolate the mesons $J/\psi$ and $\phi (1020)$ according to the current–hadron couplings,

$$\begin{aligned} \begin{aligned} \langle 0|J_{\alpha }^{J/\psi }(0)|J/\psi (p)\rangle&=f_{J/\psi }M_{J/\psi }\xi _\alpha , \\ \langle 0|J_{\mu }^{\phi }(0)|\phi (q)\rangle&=f_{\phi }M_{\phi }\zeta _\mu , \end{aligned} \end{aligned}$$

(22)

$f_{J/\psi }$ and $f_{\phi }$ are the decay constants, the $\xi _\alpha$ and $\zeta _\mu$ are polarization vectors of the mesons $J/\psi$ and $\phi (1020)$, respectively.

At the phenomenological side, we insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_\alpha ^{J/\psi }(x)$, $J_\mu ^{\phi }(y)$, $J_{\nu }(0)$ into the three-point correlation function $\Pi _{\alpha \mu \nu }(p,q)$ and isolate the ground state contributions to obtain the result

$$\begin{aligned} \Pi _{\alpha \mu \nu }(p,q)= & {} \frac{f_{\phi }M_{\phi } f_{J/\psi }M_{J/\psi }\lambda _{Y}G_{YJ/\psi \phi } }{(M_{Y}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\phi }^2-q^2)} \,\varepsilon ^{\lambda \tau \rho \theta }p^{\prime }_\lambda \nonumber \\&\times \left( -g_{\nu \tau }+\frac{p_{\nu }^{\prime }p^{\prime }_{\tau }}{p^{\prime 2}} \right) \left( -g_{\alpha \rho }+\frac{p_{\alpha }p_{\rho }}{p^{ 2}} \right) \nonumber \\&\times \left( -g_{\mu \theta }+\frac{q_{\mu }q_{\theta }}{q^{ 2}} \right) +\cdots \nonumber \\= & {} \left\{ \frac{f_{\phi }M_{\phi } f_{J/\psi }M_{J/\psi }\lambda _{Y}G_{YJ/\psi \phi } }{(M_{Y}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\phi }^2-q^2)} \right. \nonumber \\&+\left. \frac{1}{(M_{Y}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)}\right. \nonumber \\&\left. \times \int _{s^0_\phi }^\infty \mathrm{{d}}t\frac{\rho _{Y\phi }(p^2,t,p^{\prime 2})}{t-q^2}\right. \nonumber \\&\left. + \frac{1}{(M_{Y}^2-p^{\prime 2})(M_{\phi }^2-q^2)}\right. \nonumber \\&\left. \times \int _{s^0_{J/\psi }}^\infty \mathrm{{d}}t\frac{\rho _{YJ/\psi }(t,q^2,p^{\prime 2})}{t-p^2}+\cdots \right\} \nonumber \\&\times \left( \varepsilon _{\alpha \mu \nu \lambda }p^\lambda +\cdots \right) +\cdots \nonumber \\= & {} \left\{ \frac{f_{\phi }M_{\phi } f_{J/\psi }M_{J/\psi }\lambda _{Y}G_{YJ/\psi \phi } }{(M_{Y}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\phi }^2-q^2)} \right. \nonumber \\&\left. + \frac{C_{Y\phi }}{(M_{Y}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)} \right. \nonumber \\&\left. + \frac{C_{YJ/\psi }}{(M_{Y}^2-p^{\prime 2})(M_{\phi }^2-q^2)} +\cdots \right\} \nonumber \\&\times \left( \varepsilon _{\alpha \mu \nu \lambda }p^\lambda +\cdots \right) +\cdots , \end{aligned}$$

(23)

where $p^\prime =p+q$, $G_{YJ/\psi \phi }$ is the hadronic coupling constant, which is defined by

$$\begin{aligned} \langle J/\psi (p,\xi )\phi (q,\zeta )|Y(p^{\prime },\varepsilon )\rangle= & {} i G_{YJ/\psi \phi } \, \varepsilon ^{\lambda \tau \rho \theta } p^\prime _\lambda \varepsilon _\tau \xi _\rho \zeta _\theta .\nonumber \\ \end{aligned}$$

(24)

In this article, we choose the tensor structure $\varepsilon _{\alpha \mu \nu \lambda }p^\lambda$ to study the coupling constant $G_{YJ/\psi \phi }$.

Fig. 2

The hadronic coupling constant $G_{YJ/\psi \phi }$ with variations of the Borel parameters $T^2_1$ and $T_2^2$, respectively

The two unknown functions $\rho _{Y\phi }(p^2,t,p^{\prime 2})$ and $\rho _{YJ/\psi }(t,q^2,p^{\prime 2})$ parameterize transitions between the ground states and the higher resonances or the continuum states, the net effects can be parameterized by $C_{Y\phi }$ and $C_{YJ/\psi }$,

$$\begin{aligned} \begin{aligned} C_{Y\phi }&=\int _{s^0_\phi }^\infty \mathrm{{d}}t\frac{ \rho _{Y\phi }(p^2,t,p^{\prime 2})}{t-q^2}, \\ C_{YJ/\psi }&=\int _{s^0_{J/\psi }}^\infty \mathrm{{d}}t\frac{\rho _{YJ/\psi }(t,q^2,p^{\prime 2})}{t-p^2}. \end{aligned} \end{aligned}$$

(25)

In calculations, we take the $C_{Y\phi }$ and $C_{YJ/\psi }$ as free parameters, and vary them to eliminate the contaminations to obtain Borel platforms [45, 46].

We carry out the operator product expansion up to the vacuum condensates of dimension 5 and neglect the gluon condensate, which plays a minor important role. We obtain the QCD spectral density through the dispersion relation, take the quark–hadron duality below the continuum thresholds, then set $p^{\prime 2}=p^2$ and take double Borel transforms with respect to the variables $P^2=-p^2$ and $Q^2=-q^2$ respectively to obtain the QCD sum rule

$$\begin{aligned}&\frac{f_{\phi }M_{\phi } f_{J/\psi }M_{J/\psi }\lambda _{Y}G_{YJ/\psi \phi }}{M_{Y}^2-M_{J/\psi }^2} \nonumber \\&\times \left[ \exp \left( -\frac{M_{J/\psi }^2}{T_1^2} \right) -\exp \left( -\frac{M_{Y}^2}{T_1^2} \right) \right] \exp \left( -\frac{M_{\phi }^2}{T_2^2} \right) \nonumber \\&+\;C_{YJ/\psi } \exp \left( -\frac{M_{Y}^2}{T_1^2} -\frac{M_{\phi }^2}{T_2^2} \right) \nonumber \\= & {} -\frac{1}{6\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{Y}} \mathrm{{d}}s \int _{0}^{s^0_{\phi }} \mathrm{{d}}u u\sqrt{1-\frac{4m_c^2}{s}}\nonumber \\&\times \left( m_c-\frac{m_s}{2}-\frac{m_s m_c^2}{s} \right) \exp \left( -\frac{s}{T_1^2} -\frac{u}{T_2^2} \right) \nonumber \\&+\;\frac{4m_s m_c\langle \bar{s}s\rangle }{3\sqrt{2}\pi ^2} \int _{4m_c^2}^{s^0_{Y}} \mathrm{{d}}s \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T_1^2} \right) \nonumber \\&-\;\frac{2\langle \bar{s}g_s\sigma Gs\rangle }{27\sqrt{2}\pi ^2} \int _{4m_c^2}^{s^0_{Y}} \mathrm{{d}}s \sqrt{1-\frac{4m_c^2}{s}}\frac{s+2m_c^2}{s}\nonumber \\&\quad \times \exp \left( -\frac{s}{T_1^2} \right) -\frac{m_s m_c\langle \bar{s}g_s\sigma Gs\rangle }{9\sqrt{2}\pi ^2 T_2^2} \nonumber \\&\quad \times \int _{4m_c^2}^{s^0_{Y}} \mathrm{{d}}s \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T_1^2} \right) , \end{aligned}$$

(26)

where $s^0_{Y}$ and $s^0_{\phi }$ are the continuum threshold parameters for Y(4274) and $\phi (1020)$, respectively.

The hadronic parameters are taken as $M_{\phi }\!=\!1.019461\,\mathrm {GeV}$, $M_{J/\psi }=3.0969\,\mathrm {GeV}$ [33], $f_{J/\psi }=0.418 \,\mathrm {GeV}$ [47], $f_{\phi }=0.253\,\mathrm {GeV}$, $\sqrt{s^0_{\phi }}=1.5\,\mathrm {GeV}$, $\sqrt{s^0_{Y}}=4.8\,\mathrm {GeV}$, $M_Y=4.268\,\mathrm {GeV}$, $\lambda _{Y}=4.674\times 10^{-2}\,\mathrm {GeV}^5$, $T_1^2=(3.1$–$3.5)\,\mathrm {GeV}^2$, $T_2^2=(2.9$–$3.3)\,\mathrm {GeV}^2$ (present work). The unknown parameter is chosen as $C_{YJ/\psi }=0.037\,\mathrm {GeV}^7$ to obtain platforms in the Borel windows $T_1^2=(3.1$–$3.5)\,\mathrm {GeV}^2$ and $T_2^2=(2.$9–$3.3)\,\mathrm {GeV}^2$. The input parameters at the QCD side are chosen as the same in the two-point QCD sum rules for the Y(4274).

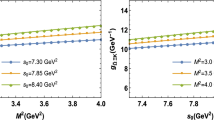
In Fig. 2, we plot the hadronic coupling constant $G_{YJ/\psi \phi }$ with variations of the Borel parameters $T^2_1$ and $T_2^2$, respectively. From the figure, we can see that there appear platforms in the Borel windows $T_1^2=(3.1$–$3.5)\,\mathrm {GeV}^2$ and $T_2^2=(2.9$–$3.3)\,\mathrm {GeV}^2$, respectively. The central value of the hadronic coupling constant $G_{YJ/\psi \phi }$ is

$$\begin{aligned} G_{YJ/\psi \phi }= & {} -6.43. \end{aligned}$$

(27)

If the radiative corrections to the perturbative term of the correlation function $\Pi _{\alpha \mu \nu }(p,q)$ also amount to multiplying a factor about 1.8, as the color octet–octet type current $J_\mu (x)$ is also presented, the value of the quantity $f_{\phi } \,f_{J/\psi }\,\lambda _Y\,G_{YJ/\psi \phi }$ at the hadronic side in the QCD sum rules in Eq. (26) changes according to the rule,

$$\begin{aligned} f_{\phi }\, f_{J/\psi }\,\lambda _Y\, G_{YJ/\psi \phi }\rightarrow & {} f_{\phi }\, f_{J/\psi }\,\lambda _Y\, G_{YJ/\psi \phi }\times 1.8. \end{aligned}$$

(28)

In this article, we take the values $f_{J/\psi }=0.418 \,\mathrm {GeV}$ [47] and $f_{\phi }=0.253\,\mathrm {GeV}$, which include next-to-leading order radiative corrections. The factors 1.8 come from the radiative corrections to the two-point correction function and three-point correlation function cancel out with each other, the net modification of the hadronic coupling constant $G_{YJ/\psi \phi }$ is estimated to be tiny, just like the hadronic coupling constants $D^*D\pi$ and $B^*B\pi$, the net effects of the radiative corrections can be neglected [48].

Now it is easy to obtain the decay width,

$$\begin{aligned}&\Gamma (Y(4274)\rightarrow J/\psi \phi )\nonumber \\&=\frac{p\left( M_{Y},M_{J/\psi },M_{\phi }\right) }{24\pi M_{Y}^2}G_{YJ/\psi \phi }^2 \left\{ \frac{\left( M_{Y}^2-M_{\phi }^2\right) ^2}{2M_{J/\psi }^2}\right. \nonumber \\&\quad \left. +\frac{\left( M_{Y}^2-M_{J/\psi }^2\right) ^2}{2M_{\phi }^2} +4M_Y^2-\frac{M_{J/\psi }^2+M_\phi ^2}{2}\right\} \nonumber \\&=1.8\,\mathrm{{GeV}} \gg 56 \pm 11 ^{+8}_{-11} { \text{ MeV }}\,\,\, \mathrm{Experimental\,\,\,value} \,\,[5, 6] \, ,\nonumber \\ \end{aligned}$$

(29)

where $p(a,b,c)=\frac{\sqrt{[a^2-(b+c)^2][a^2-(b-c)^2]}}{2a}$. It is difficult to assign Y(4274) to the color octet–octet type molecule-like state $\bar{s}\lambda ^a c\bar{c}\lambda ^a s$. In Ref. [23], we assign Y(4140) to the diquark–antidiquark type tetraquark state $cs\bar{c}\bar{s}$ with $J^{PC}=1^{++}$, and we study the mass and pole residue with the QCD sum rules in detail. The predicted mass disfavors assigning Y(4140) to the $J^{PC}=1^{++}$ diquark–antidiquark type tetraquark state $cs\bar{c}\bar{s}$. Y(4140) and Y(4274) have the same quantum numbers except for the masses and widths, the QCD sum rules also disfavor assigning Y(4274) to the $J^{PC}=1^{++}$ diquark–antidiquark type tetraquark state $cs\bar{c}\bar{s}$.

The mass of the $\chi _{c1}(\mathrm 3P)$ state is 4271 and 4317 MeV from the non-relativistic potential model and the relativized Godfrey–Isgur model respectively [49], which are consistent with the experimental value $4273.3~\pm ~8.3 ^{+17.2}_{-3.6} \text{ MeV }$ from the LHCb collaboration [7, 8]. The width of the $\chi _{c1}(\mathrm 3P)$ state is $39\,\mathrm {MeV}$ from the non-relativistic potential model [49], which is consistent with the experimental value $56 \pm 11 ^{+8}_{-11} { \text{ MeV }}$ from the LHCb collaboration [7, 8]. The Y(4274) may be the conventional charmonium $\chi _{c1}(\mathrm 3P)$ state [11, 12], while in Ref. [50], Y(4140) is assigned to the $\chi _{c1}(\mathrm 3P)$ state. In Ref. [51], we study the vector meson transitions among the charmonium and bottomonium states with the heavy quark effective theory in a systematic way. If we assign Y(4274) to the $\chi _{c1}(\mathrm 3P)$ state, the partial decay widths are

$$\begin{aligned} \begin{aligned} \Gamma (Y(4274)\rightarrow J/\psi \omega )&=17.6\times 10^{-2}{\,\mathrm GeV^2}\,\delta (3,1), \\ \Gamma (Y(4274)\rightarrow J/\psi \phi )&=7.0\times 10^{-2}{\,\mathrm GeV^2}\, \delta (3,1), \end{aligned} \end{aligned}$$

(30)

where $\delta (3,1)$ is the hadronic coupling constant describes the transitions between the $\mathrm 3P$ and $\mathrm 1S$ charmonium multiplets [51]. The ratio between the two Okubo-Zweig-Iizuka suppressed decays is

$$\begin{aligned} R= & {} \frac{\Gamma (Y(4274)\rightarrow J/\psi \omega )}{\Gamma (Y(4274)\rightarrow J/\psi \phi )}=2.5, \end{aligned}$$

(31)

the decay to the final state $J/\psi \omega$ is favored due to the more available phase space. Moreover, the decay $Y(4274)\rightarrow D_s^*\bar{D}_s^*$ is Okubo–Zweig–Iizuka allowed and would have much large branching ratio. We can search for Y(4274) in the final states $J/\psi \omega$ and $D_s^*\bar{D}_s^*$ in the future. On the other hand, if we assign Y(4274) to the $cs\bar{c}\bar{s}$ tetraquark state, molecular state or molecule-like state, the decay $Y(4274)\rightarrow J/\psi \omega$ is doubly Okubo–Zweig–Iizuka suppressed. It is important to observe the decay $Y(4274)\rightarrow J/\psi \omega$ to diagnose the nature of Y(4274).

4 Conclusion

In this article, we assign Y(4274) to the color octet–octet type axialvector molecule-like state with $J^{PC}=1^{++}$ tentatively, and construct the color octet–octet type axialvector current to study its mass and width with the QCD sum rules in details. The predicted mass $M_{Y(4274)}=(4.27~\pm ~0.09) \, \mathrm {GeV}$ is consistent with the experimental value $4273.3~\pm ~8.3 ^{+17.2}_{-3.6} \text{ MeV }$ from the LHCb collaboration, and favors assigning Y(4274) to the color octet–octet type molecule-like state $\bar{s}\lambda ^a c\bar{c}\lambda ^a s$. The predicted width $\Gamma (Y(4274)\rightarrow J/\psi \phi )=1.8\,\mathrm{{GeV}}$ is much larger than the experimental value $56 \pm 11 ^{+8}_{-11} { \text{ MeV }}$ from the LHCb collaboration and disfavors assigning the Y(4274) to be the color octet–octet type molecule-like state strongly. The Y(4274) may be the conventional charmonium state $\chi _{c1}(\mathrm 3P)$, and the preferred decays are $Y(4274)\rightarrow D_s^*\bar{D}_s^*$, $J/\psi \omega$. It is important to observe the decay $Y(4274)\rightarrow J/\psi \omega$ to diagnose the nature of the Y(4274). We can search for Y(4274) in the final states $J/\psi \omega$ and $D_s^*\bar{D}_s^*$ in the future.

Appendix

The explicit expressions of the QCD spectral density are

$$\begin{aligned} \rho _{0}(s)= & {} \frac{1}{1152\pi ^6}\int _{y_i}^{y_f} \mathrm{{d}}y \int _{z_i}^{1-y} \mathrm{{d}}z \, yz\,(1-y-z)^3\nonumber \\&\times \left( s-\overline{m}_c^2\right) ^2\left( 35s^2-26s\overline{m}_c^2+3\overline{m}_c^4 \right) \nonumber \\&-\;\frac{m_s m_c}{64\pi ^6}\int _{y_i}^{y_f} \mathrm{{d}}y \int _{z_i}^{1-y} \mathrm{{d}}z \, (y+z)\,(1-y-z)^2\nonumber \\&\times \left( s-\overline{m}_c^2\right) ^2\left( 3s-\overline{m}_c^2\right) , \end{aligned}$$

(32)

$$\begin{aligned} \rho _{3}(s)= & {} -\frac{m_c\langle \bar{s}s\rangle }{24\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \, (y+z)(1-y-z)\nonumber \\&\times \left( s-\overline{m}_c^2\right) \left( 7s-3\overline{m}_c^2 \right) \nonumber \\&-\frac{m_s \langle \bar{s}s\rangle }{12\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \, yz\,(1-y-z)\nonumber \\&\times \left( 15s^2-12s\overline{m}_c^2+3\overline{m}_c^4 \right) \nonumber \\&+\;\frac{m_s m_c^2\langle \bar{s}s\rangle }{3\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \, \left( s-\overline{m}_c^2 \right) , \end{aligned}$$

(33)

$$\begin{aligned} \rho _{4}(s)= & {} -\frac{m_c^2}{864\pi ^4} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \nonumber \\&\times \left( \frac{z}{y^2}+\frac{y}{z^2}\right) (1-y-z)^3\nonumber \\&\times \left\{ 8s-3\overline{m}_c^2+s^2\, \delta \left( s-\overline{m}_c^2\right) \right\} \nonumber \\&-\;\frac{1}{2304\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \nonumber \\&\times \int _{z_i}^{1-y}\mathrm{{d}}z\, (y+z)(1-y-z)^2 \, s\,(5s-4\overline{m}_c^2) \nonumber \\&-\;\frac{m_c^2}{1152\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y} \mathrm{{d}}z \left( s-\overline{m}_c^2 \right) \nonumber \\&\times \left\{ 7-2\left( \frac{1}{y}+ \frac{1}{z}\right) (1-y-z) \right. \nonumber \\&\left. + \frac{7(1-y-z)^2}{2yz} -\frac{7(1-y-z)}{2}\right. \nonumber \\&\left. +\left( \frac{1}{y}+\frac{1}{z} \right) \frac{(1-y-z)^2}{2} -\frac{7(1-y-z)^3}{12yz} \right\} \nonumber \\&+\frac{m_s m_c^3}{192\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z\, (y+z)\nonumber \\&\times \left( \frac{1}{y^3}+\frac{1}{z^3}\right) (1-y-z)^2 \left\{ 1+\frac{2s}{3}\, \delta \left( s-\overline{m}_c^2\right) \right\} \nonumber \\&-\;\frac{m_s m_c }{1152\pi ^4} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \, (1-y-z)\nonumber \\&\times \left[ 1-\frac{7}{4}\left( \frac{1}{y}+\frac{1}{z}\right) (1-y-z) \right. \nonumber \\&\left. + \;6\left( \frac{z}{y^2}+\frac{y}{z^2}\right) (1-y-z)\right] \left( 5s-3\overline{m}_c^2\right) , \end{aligned}$$

(34)

$$\begin{aligned} \rho _{5}(s)= & {} \frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{48\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z \, (y+z) \left( 5s-3\overline{m}_c^2 \right) +\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{192\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \nonumber \\&\times \int _{z_i}^{1-y}\mathrm{{d}}z \left( \frac{y}{z}+\frac{z}{y} \right) (1-y-z) \left( 2s-\overline{m}_c^2 \right) \nonumber \\&-\;\frac{m_c\langle \bar{s}g_s\sigma Gs\rangle }{576\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \left( \frac{y}{z}+\frac{z}{y} \right) \nonumber \\&\times (1-y-z) \left( 5s-3\overline{m}_c^2 \right) +\frac{m_s\langle \bar{s}g_s\sigma Gs\rangle }{36\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \nonumber \\&\times \int _{z_i}^{1-y}\mathrm{{d}}z \,yz \left\{ 8s-3\overline{m}_c^2 +s^2 \delta \left( s-\overline{m}_c^2 \right) \right\} \nonumber \\&-\;\frac{m_s m_c^2\langle \bar{s}g_s\sigma Gs\rangle }{12\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y -\frac{m_s m_c^2\langle \bar{s}g_s\sigma Gs\rangle }{192\pi ^4}\nonumber \\&\times \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \left( \frac{1}{y}+\frac{1}{z} \right) +\frac{m_s\langle \bar{s}g_s\sigma Gs\rangle }{576\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \nonumber \\&\times \int _{z_i}^{1-y}\mathrm{{d}}z\, \left( y+z \right) \left( 5s-3\overline{m}_c^2 \right) , \end{aligned}$$

(35)

$$\begin{aligned} \rho _{6}(s)= & {} \frac{2m_c^2\langle \bar{s}s\rangle ^2}{9\pi ^2}\int _{y_i}^{y_f}\mathrm{{d}}y +\frac{g_s^2\langle \bar{s}s\rangle ^2}{243\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y\nonumber \\&\times \int _{z_i}^{1-y}\mathrm{{d}}z\, yz \left\{ 8s-3\overline{m}_c^2 +s^2\, \delta \left( s-\overline{m}_c^2 \right) \right\} \nonumber \\&+\;\frac{g_s^2\langle \bar{s}s\rangle ^2}{1296\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z\, (1-y-z)\nonumber \\&\times \left\{ \left( \frac{z}{y}+\frac{y}{z} \right) \left( 7s-4\overline{m}_c^2 \right) \right. \nonumber \\&\left. +\;\frac{1}{3}\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_c^2\left[ 7+5s\,\delta \left( s-\overline{m}_c^2 \right) \right] \right. \nonumber \\&\left. -\;\frac{1}{3}(y+z)\left( 4s-3\overline{m}_c^2 \right) \right\} \nonumber \\&-\;\frac{g_s^2\langle \bar{s}s\rangle ^2}{1944\pi ^4}\int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z\,(1-y-z)\nonumber \\&\times \left\{ 3\left( \frac{z}{y}+\frac{y}{z} \right) \left( 2s-\overline{m}_c^2 \right) \right. \nonumber \\&\left. +\;\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_c^2\left[ 1+s\,\delta \left( s-\overline{m}_c^2\right) \right] +2(y+z)\right. \nonumber \\&\left. \times \left[ 8s-3\overline{m}_c^2 +s^2\, \delta \left( s-\overline{m}_c^2\right) \right] \right\} \nonumber \\&+\;\frac{m_s m_c\langle \bar{s}s\rangle ^2}{6\pi ^2}\int _{y_i}^{y_f}\mathrm{{d}}y \left\{ 1+\frac{2s}{3}\delta \left( s-\widetilde{m}_c^2 \right) \right\} , \end{aligned}$$

(36)

$$\begin{aligned} \rho _7(s)= & {} \frac{m_c^3\langle \bar{s}s\rangle }{432\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \,\left( y+z \right) \nonumber \\&\times \left( \frac{1}{y^3}+\frac{1}{z^3}\right) (1-y-z) \left( 1+\frac{2s}{T^2}\right) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{m_c\langle \bar{s}s\rangle }{288\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z\left\{ 1-7\left( \frac{1}{y}+\frac{1}{z}\right) \frac{1-y-z}{2}\right. \left. +12(1-y-z)\right. \nonumber \\&\left. \times \left( \frac{y}{z^2}+\frac{z}{y^2}\right) \right\} \left\{ 1+\frac{2s}{3}\delta \left( s-\overline{m}_c^2\right) \right\} \nonumber \\&-\;\frac{m_c\langle \bar{s}s\rangle }{144\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \left\{ 1+\frac{2s}{3}\delta \left( s-\widetilde{m}_c^2\right) \right\} \nonumber \\&+\;\frac{m_s m_c^2\langle \bar{s}s\rangle }{108\pi ^2T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z \left( \frac{y}{z^2}+\frac{z}{y^2}\right) (1-y-z) \left( s+\frac{s^2}{T^2}\right) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{m_s m_c^4\langle \bar{s}s\rangle }{54\pi ^2T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\mathrm{{d}}z \left( \frac{1}{y^3}+\frac{1}{z^3}\right) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{m_s m_c^2\langle \bar{s}s\rangle }{18\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z \left( \frac{1}{y^2}+\frac{1}{z^2}\right) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{m_s \langle \bar{s}s\rangle }{864\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z \,(y+z)\left( s+\frac{s^2}{2T^2}\right) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{m_s m_c^2\langle \bar{s}s\rangle }{864\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{0}^{1}\mathrm{{d}}y\nonumber \\&\times \left( \frac{1}{y}+\frac{1}{1-y}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{m_s m_c^2 \langle \bar{s}s\rangle }{1728\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\mathrm{{d}}z \left\{ \frac{1}{y^2}+\frac{1}{z^2}\right. \nonumber \\&\left. +\;\frac{14}{yz}-\frac{7(1-y-z)}{yz}\right\} \delta \left( s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{7m_s \langle \bar{s}s\rangle }{288\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{{d}}y \int _{z_i}^{1-y}\nonumber \\&\times \mathrm{{d}}z \left\{ 1+\frac{2s}{3}\delta \left( s-\overline{m}_c^2\right) \right\} +\frac{m_s m_c^2 \langle \bar{s}s\rangle }{108\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \nonumber \\&\times \int _{0}^{1}\mathrm{{d}}y \left( 1+\frac{s}{T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) , \end{aligned}$$

(37)

$$\begin{aligned} \rho _8(s)= & {} -\frac{m_c^2\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{9\pi ^2}\int _0^1 \mathrm{{d}}y \left( 1+\frac{s}{T^2} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{m_c^2\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{144\pi ^2}\int _0^1 \mathrm{{d}}y\nonumber \\&\times \left( \frac{1}{y}+\frac{1}{1-y} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{144\pi ^2}\int _{y_i}^{y_f} \mathrm{{d}}y \left\{ 1+\frac{2s}{3}\delta \left( s-\widetilde{m}_c^2\right) \right\} \nonumber \\&-\; \frac{5 m_s m_c\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{108\pi ^2}\int _0^1 \mathrm{{d}}y \nonumber \\&\times \left( 1+\frac{3s}{2T^2}+\frac{s^2}{T^4} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\; \frac{ m_s m_c\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{288\pi ^2 T^2}\int _0^1 \mathrm{{d}}y \nonumber \\&\times \left( \frac{1-y}{y}+\frac{y}{1-y} \right) \,s\,\delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{ m_s m_c\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle }{864\pi ^2 }\int _0^1 \mathrm{{d}}y\nonumber \\&\times \left( \frac{1-y}{y}+\frac{y}{1-y} \right) \left( 1+\frac{2s}{T^2} \right) \delta \left( s-\widetilde{m}_c^2\right) , \end{aligned}$$

(38)

$$\begin{aligned} \rho _{10}(s)= & {} \frac{m_c^2\langle \bar{s}g_s\sigma Gs\rangle ^2}{72\pi ^2T^6}\int _0^1 \mathrm{{d}}y \,s^2\,\delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{m_c^4\langle \bar{s}s\rangle ^2}{81T^4}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1\mathrm{{d}}y \nonumber \\&\times \left\{ \frac{1}{y^3}+\frac{1}{(1-y)^3}\right\} \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{m_c^2\langle \bar{s}s\rangle ^2}{27T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1\mathrm{{d}}y \nonumber \\&\times \left\{ \frac{1}{y^2}+\frac{1}{(1-y)^2}\right\} \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;7\frac{\langle \bar{s}s\rangle ^2}{1296}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1\mathrm{{d}}y \nonumber \\&\times \left( 1+\frac{2s}{T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{m_c^2\langle \bar{s}g_s\sigma Gs\rangle ^2}{576\pi ^2T^4}\int _0^1 \mathrm{{d}}y \left( \frac{1}{y}+\frac{1}{1-y}\right) \,\nonumber \\&\times s \, \delta \left( s-\widetilde{m}_c^2\right) -\frac{\langle \bar{s}g_s\sigma Gs\rangle ^2}{864\pi ^2}\int _0^1 \mathrm{{d}}y\nonumber \\&\times \left( 1+\frac{3s}{2T^2}+\frac{s^2}{T^4} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{\langle \bar{s}g_s\sigma Gs\rangle ^2}{5832\pi ^2}\int _0^1 \mathrm{{d}}y \left( 1+\frac{2s}{T^2} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{m_c^2\langle \bar{s}s\rangle ^2}{81T^6}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{{d}}y \, s^2 \, \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{ m_s m_c\langle \bar{s}g_s\sigma Gs\rangle ^2}{216\pi ^2T^2}\int _0^1 \mathrm{{d}}y \left( 1+\frac{s}{T^2}\right. \nonumber \\&\left. +\;\frac{s^2}{2T^4} -\frac{s^3}{T^6}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{m_s m_c^3\langle \bar{s}s\rangle ^2}{108T^4}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{{d}}y \left\{ \frac{1}{y^3}+\frac{1}{(1-y)^3}\right\} \nonumber \\&\times \left( 1-\frac{2s}{3T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{m_s m_c \langle \bar{s}s\rangle ^2}{108T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{{d}}y \nonumber \\&\times \left\{ \frac{1-y}{y^2}+\frac{y}{(1-y)^2}\right\} \left( 1-\frac{2s}{T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{7m_s m_c \langle \bar{s}s\rangle ^2}{2592T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{{d}}y \left( \frac{1}{y}+\frac{1}{1-y}\right) \nonumber \\&\times \left( 1-\frac{2s}{T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) -\frac{ m_s m_c\langle \bar{s}g_s\sigma Gs\rangle ^2}{1728\pi ^2T^2}\nonumber \\&\times \int _0^1 \mathrm{{d}}y \, \left( \frac{1-y}{y}+\frac{y}{1-y}\right) \left( 1+\frac{s}{T^2}-\frac{s^2}{T^4} \right) \nonumber \\&\times \delta \left( s-\widetilde{m}_c^2\right) +\frac{ m_s m_c\langle \bar{s}g_s\sigma Gs\rangle ^2}{5184\pi ^2T^2}\int _0^1 \mathrm{{d}}y \, \nonumber \\&\times \left( \frac{1-y}{y}+\frac{y}{1-y}\right) \left( 1+\frac{s}{T^2}-\frac{2s^2}{T^4} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{m_s m_c \langle \bar{s}s\rangle ^2}{324T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{{d}}y \,\nonumber \\&\times \left( 1+\frac{s}{T^2}+\frac{s^2}{2T^4}-\frac{s^3}{T^6}\right) \delta \left( s-\widetilde{m}_c^2\right) ; \end{aligned}$$

(39)

the subscripts 0, 3, 4, 5, 6, 7, 8, 10 denote the dimensions of the vacuum condensates; $y_{f}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $z_{i}=\frac{ym_c^2}{y s -m_c^2}$, $\overline{m}_c^2=\frac{(y+z)m_c^2}{yz}$, $\widetilde{m}_c^2=\frac{m_c^2}{y(1-y)}$, $\int _{y_i}^{y_f}\mathrm{{d}}y \rightarrow \int _{0}^{1}\mathrm{{d}}y$, $\int _{z_i}^{1-y}\mathrm{{d}}z \rightarrow \int _{0}^{1-y}\mathrm{{d}}z$ when the $\delta$ functions $\delta \left( s-\overline{m}_c^2\right)$ and $\delta \left( s-\widetilde{m}_c^2\right)$ appear.