$\varvec{B^0\rightarrow K^{*0}\mu ^+\mu ^-}$ decay in the aligned two-Higgs-doublet model

Abstract

In the aligned two-Higgs-doublet model, we perform a complete one-loop computation of the short-distance Wilson coefficients $C_{7,9,10}^{(\prime )}$, which are the most relevant ones for $b\rightarrow s\ell ^+\ell ^-$ transitions. It is found that, when the model parameter $\left| \varsigma _{u}\right|$ is much smaller than $\left| \varsigma _{d}\right|$, the charged scalar contributes mainly to chirality-flipped $C_{9,10}^\prime$, with the corresponding effects being proportional to $\left| \varsigma _{d}\right| ^2$. Numerically, the charged-scalar effects fit into two categories: (A) $C_{7,9,10}^\mathrm {H^\pm }$ are sizable, but $C_{9,10}^{\prime \mathrm {H^\pm }}\simeq 0$, corresponding to the (large $\left| \varsigma _{u}\right|$, small $\left| \varsigma _{d}\right|$) region; (B) $C_7^\mathrm {H^\pm }$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ are sizable, but $C_{9,10}^\mathrm {H^\pm }\simeq 0$, corresponding to the (small $\left| \varsigma _{u}\right|$, large $\left| \varsigma _{d}\right|$) region. Taking into account phenomenological constraints from the inclusive radiative decay $B\rightarrow X_{s}{\gamma }$, as well as the latest model-independent global analysis of $b\rightarrow s\ell ^+\ell ^-$ data, we obtain the much restricted parameter space of the model. We then study the impact of the allowed model parameters on the angular observables $P_2$ and $P_5'$ of $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ decay, and we find that $P_5'$ could be increased significantly to be consistent with the experimental data in case B.

1 Introduction

The rare $B\rightarrow K^{*}\ell ^+\ell ^-$ decays, being the flavor-changing neutral-current (FCNC) processes, do not arise at tree level and are highly suppressed at higher orders within the Standard Model (SM), due to the Glashow–Iliopoulos–Maiani (GIM) mechanism [1]. However, new TeV-scale particles in many extensions of the SM could affect the decay amplitude at a similar level as the SM does. These decays play, therefore, a crucial role in testing the SM and probing various NP scenarios beyond it [2]. It is particularly interesting to note that, based on these decays, observables with a very limited sensitivity to hadronic uncertainties can be constructed, enhancing therefore the discovery potential for NP [3,4,5,6,7,8,9,10].

Experimentally, several interesting deviations from the SM predictions have been observed in these decays. In 2013, the form-factor-independent angular observable $P'_5$ [8, 9] of $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ decay was measured by the LHCb collaboration [11], showing a $3.7\sigma$ disagreement with the SM expectation [12,13,14,15]. Recently, the LHCb collaboration has released new measurements of the angular observables in this decay, based on the dataset of $3~\mathrm {fb}^{-1}$ of integrated luminosity, and still found a $3.4\sigma$ deviation for $P'_5$ [16]. Moreover, being in agreement with the LHCb measurements, a deviation with a significance of $2.1\sigma$ was also reported by the Belle collaboration [17]. Besides the $P'_5$ anomaly, there are some other slight deviations beyond the $2\sigma$ level, such as the observables $P_2$ in $q^2\in [2,4.3]~\mathrm {GeV}^2$ and $P'_4$ in $q^2\in [14.18,16]~\mathrm {GeV}^2$ [18,19,20]. These anomalies have triggered lots of theoretical studies both within the SM and in various NP models [8,9,10, 12,13,14,15, 18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].

As a minimal extension of the SM scalar sector, the two-Higgs-doublet model (2HDM) [45] can easily satisfy the electroweak (EW) precision data and, at the same time, lead to a very rich phenomenology [46]. The scalar spectrum consists of two charged scalars $H^\pm$ and three neutral ones $h,\,H$, and A, one of which is to be identified with the SM-like Higgs boson found at the LHC [47, 48]. The direct search for these additional scalar states would be an important task for high-energy colliders in the next few years. It should be noted that, complementary to the direct searches, indirect constraints on the 2HDM could also be obtained from the rare FCNC decays like $B\rightarrow K^{*}\ell ^+\ell ^-$, since these scalars can affect these processes through the penguin and box diagrams. These studies are also very helpful to gain further insights into the scalar sector of supersymmetry and other models that have similar scalar contents [49,50,51].

In a generic 2HDM, the non-diagonal couplings of neutral scalars to fermions lead to tree-level FCNC interactions, which can be avoided by imposing on the Lagrangian an ad hoc discrete $\mathcal {Z}_2$ symmetry. Depending on the $\mathcal {Z}_2$ charge assignments to the scalars and fermions, this results in four types of 2HDMs (types I, II, X, Y) [46, 52] under the hypothesis of natural flavor conservation (NFC) [53]. In the aligned two-Higgs-doublet model (A2HDM) [54], on the other hand, the absence of tree-level FCNCs is automatically guaranteed by assuming the alignment in flavor space of the Yukawa matrices for each type of right-handed fermions. Interestingly, the A2HDM can recover as particular cases all known specific implementations of the 2HDMs based on $\mathcal {Z}_2$ symmetries. The model also features possible new sources of CP violation beyond that of the Cabibbo–Kobayashi–Maskawa (CKM) matrix [55, 56]. These features make the A2HDM very attracting both in high-energy collider physics [57,58,59,60,61,62,63] and in low-energy flavor physics [64,65,66,67,68,69,70,71,72,73,74].

In this paper, we will study the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ in the A2HDM. Our paper is organized as follows: in Sect. 2, we give a brief overview of the A2HDM, focusing mainly on the scalar and Yukawa sectors. In Sect. 3, a complete one-loop computation of the short-distance (SD) Wilson coefficients $C_{7,9,10}^{(\prime )}$ is presented, and the final analytical expressions are given both within the SM and in the A2HDM. The angular observables of $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ decay are also introduced in this section. In Sect. 4, taking into account phenomenological constraints from the inclusive radiative decay $B\rightarrow X_s\gamma$ and the latest model-independent global analysis of $b\rightarrow s\ell ^+\ell ^-$ data, we study the impact of the allowed model parameters on the angular observables $P_2$ and $P_5'$ of $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ decay. Finally, our conclusions are drawn in Sect. 5. Some relevant functions for the Wilson coefficients are collected in the appendices.

2 The aligned two-Higgs-doublet model

We consider the minimal version of 2HDM, which is invariant under the SM gauge group and includes, besides the SM matter and gauge fields, two complex scalar ${SU\left( 2\right) _{L}}$ doublets,

$$\begin{aligned} \phi _a^\mathrm{T}\left( x\right) =\frac{\mathrm {e}^{i\theta _a}}{\sqrt{2}}(\sqrt{2}\varphi ^+_a, \,v_a+\rho _a+i\eta _a), \quad \left( a=1,\,2\right) , \end{aligned}$$

(2.1)

with the hypercharge $Y=1/2$. The neutral components of the two scalar doublets acquire the vacuum expectation values (VEVs) $\langle 0|\phi _a^\mathrm{T}\left( x\right) |0\rangle = (0, v_a\mathrm {e}^{i\theta _a}/\sqrt{2})$. Through an appropriate ${U(1)}_Y$ transformation, one can enforce $\theta _1=0$ and leave the relative phase $\theta =\theta _2-\theta _1$ as physical. Using further a global SU(2) transformation in the scalar space, one can rotate the original scalar basis to the so-called Higgs basis [75,76,77],

$$\begin{aligned} \left( \begin{array}{c} \Phi _1 \\ -\Phi _2 \end{array} \right) \equiv \left( \begin{array}{cc} \cos \beta &{} \sin \beta \\ \sin \beta &{} -\cos \beta \end{array} \right) \, \left( \begin{array}{c} \phi _1 \\ \mathrm {e}^{-i\theta }\phi _2 \end{array} \right) , \end{aligned}$$

(2.2)

where the rotation angle (clockwise) $\tan \beta =v_2/v_1$. In the new basis, only the scalar doublet $\Phi _1$ gets a nonzero VEV $\langle 0|\Phi _1^\mathrm{T}\left( x\right) |0\rangle = (0, v/\sqrt{2})$, with $v=\sqrt{v_1^2+v_2^2}=(\sqrt{2} G_F)^{-1/2} \simeq 246~\mathrm {GeV}$, and the two scalar doublets are now parametrized, respectively, by [54]

$$\begin{aligned} \Phi _1=\left( \begin{array}{c} G^+ \\ \frac{1}{\sqrt{2}}\, (v+S_1+iG^0) \end{array} \right) , \quad \Phi _2 = \left( \begin{array}{c} H^+ \\ \frac{1}{\sqrt{2}}\, (S_2+iS_3) \end{array} \right) , \end{aligned}$$

(2.3)

where $G^\pm$ and $G^0$ denote the massless Goldstone fields to be eaten by the $W^\pm$ and $Z^0$ gauge bosons, respectively. The remaining five physical degrees of freedom are given by the two charged fields $H^\pm (x)$ and the three neutral ones $\varphi ^0_i(x) =\{h(x), H(x), A(x)\}=\mathcal {R}_{ij}S_j$, where $\mathcal {R}$ is an orthogonal matrix obtained after diagonalizing the mass terms in the scalar potential. Generally, none of these three neutral scalars can have a definite CP quantum number.

2.1 Scalar sector

The most general scalar potential for the two doublets $\Phi _1$ and $\Phi _2$ that is allowed by the EW gauge symmetry can be written as [75,76,77]

$$\begin{aligned} V&= \mu _{1}\;(\Phi _{1}^{\dagger }\Phi _{1})\,+\,\mu _{2}\;(\Phi _{2}^{\dagger }\Phi _{2})\, +\,[\mu _{3}\;(\Phi _{1}^{\dagger }\Phi _{2})\,+\,\mu _{3}^{*}\;(\Phi _{2}^{\dagger }\Phi _{1} )]\nonumber \\&\quad +\lambda _{1}\,(\Phi _{1}^{\dagger }\Phi _{1})^{2}\,+\,\lambda _{2}\,(\Phi _{2}^{\dagger }\Phi _{2})^{2}\, +\,\lambda _{3}\,(\Phi _{1}^{\dagger }\Phi _{1})(\Phi _{2}^{\dagger }\Phi _{2})\,\nonumber \\&\quad +\,\lambda _{4}\,(\Phi _{1}^{\dagger }\Phi _{2})(\Phi _{2}^{\dagger }\Phi _{1})\nonumber \\&\quad +[(\lambda _{5}\;\Phi _{1}^{\dagger }\Phi _{2}\,+\,\lambda _{6}\;\Phi _{1}^{\dagger }\Phi _{1}\,+\,\lambda _{7}\; \Phi _{2}^{\dagger }\Phi _{2})(\Phi _{1}^{\dagger }\Phi _{2})\,+\,\mathrm {h.c.}]. \end{aligned}$$

(2.4)

The hermiticity of the potential requires the parameters $\mu _{1,2}$ and $\lambda _{1,2,3,4}$ to be real, while $\mu _3$ and $\lambda _{5,6,7}$ could be generally complex. The minimization condition imposes the relations $\mu _1 = -\lambda _1 v^2$ and $\mu _3 = -\frac{1}{2}\,\lambda _6\, v^2$. Since only the relative phases among $\lambda _{5,6,7}$ are physical, the scalar potential is finally fully characterized by 11 real parameters, v, $\mu _2$, $\lambda _{1,2,3,4}$, $|\lambda _{5,6,7}|$, $\mathrm {arg}(\lambda _5\lambda _6^*)$ and $\mathrm {arg}(\lambda _5\lambda _7^*)$, four of which can be determined by the scalar masses $M_{H^\pm ,\,h,\,H,\,A}$. Explicitly, inserting Eq. (2.3) into Eq. (2.4) and imposing the minimization condition, one gets $M_{H^\pm }^2=\mu _2+\frac{1}{2}\lambda _3v^2$, and the mass-squared matrix $\mathcal {M}^{2}$ of $S_{1,2,3}$ fields in terms of v and $\lambda _i$. Using the orthogonal matrix $\mathcal {R}$, one can then obtain the masses of the three neutral scalars, $\mathcal {R}\,\mathcal {M}^2\,\mathcal {R}^\mathrm{T} = \mathrm {diag}\left( M_{h}^2, M_{H}^2,M_A^2\right)$.

In the CP-conserving limit, $\lambda _{5,6,7}$ are all real and the neutral scalars are CP eigenstates. The CP-odd scalar A corresponds to $S_3$, with the mass given by $M_A^2=M_{H^\pm }^2+ v^2\left( \frac{\lambda _4}{2}-\lambda _5\right)$, while the two CP-even scalars h and H are orthogonal combinations of $S_1$ and $S_2$,

$$\begin{aligned} \left( \begin{array}{c} h\\ H \end{array} \right) = \left( \begin{array}{cc} \cos {\tilde{\alpha }} &{} \sin {\tilde{\alpha }} \\ -\sin {\tilde{\alpha }} &{} \cos {\tilde{\alpha }} \end{array}\right) \; \left( \begin{array}{c} S_1\\ S_2 \end{array}\right) , \end{aligned}$$

(2.5)

where the mixing angle $\tilde{\alpha }$ is determined by

$$\begin{aligned} \tan {\tilde{\alpha }} =\frac{M_{h}^2 - 2\lambda _1 v^2}{v^2\lambda _6} =\frac{v^2\lambda _6}{2\lambda _1 v^2- M_{H}^2}. \end{aligned}$$

(2.6)

The masses of the two neutral scalars are given, respectively, by $M_{h}^2=\frac{1}{2}\left( \Sigma -\Delta \right)$ and $M_{H}^2=\frac{1}{2}\left( \Sigma +\Delta \right)$, where

$$\begin{aligned}&\Sigma \, =\, M_{H^\pm }^2\, +\, v^2\,\left( 2\,\lambda _1 +\frac{\lambda _4}{2}+ \lambda _5\right) ,\nonumber \\&\Delta \, =\,\sqrt{\left[ M_{H^\pm }^2\, +\, v^2\,\left( -2\,\lambda _1 +\frac{\lambda _4}{2}+ \lambda _5\right) \right] ^2 + 4 v^4 \lambda _6^2} \nonumber \\&\qquad \!\!\! = \, - \frac{2 v^2\lambda _6}{\sin {(2\tilde{\alpha })}}. \end{aligned}$$

(2.7)

Here $M_{h} \leqslant M_{H}$ by convention and the SM limit is recovered when $\tilde{\alpha }=0$.

2.2 Yukawa sector

The Yukawa Lagrangian of the 2HDM is most generally given by [46, 54]

$$\begin{aligned} \mathcal L_Y= & {} -[ \bar{Q}_{L}' (\Gamma _1 \phi _1 +\Gamma _2 \phi _2) d_R' + \bar{Q}_{L}' (\Delta _1 \tilde{\phi }_1 +\Delta _2 \tilde{\phi }_2) u_R' \nonumber \\&+ \bar{L}_{L}' (\Pi _1 \phi _1 + \Pi _2 \phi _2) \ell _R'] + \mathrm {h.c.}, \end{aligned}$$

(2.8)

where $\tilde{\phi }_a(x)\equiv i\tau _2\phi _a^{*}(x)$ are the charge-conjugated fields with $Y=-\frac{1}{2}$, $\bar{Q}_{L}'$ and $\bar{L}_{L}'$ are the left-handed quark and lepton doublets, and $u'_R$, $d'_R$ and $\ell '_R$ the corresponding right-handed singlets, in the weak-interaction basis. All fermionic fields are written as 3-dimensional vectors and the couplings $\Gamma _a$, $\Delta _a$ and $\Pi _a$ are therefore $3\times 3$ complex matrices in flavor space.

Transforming to the Higgs basis, Eq. (2.8) becomes

$$\begin{aligned} \mathcal {L}_Y= & {} -\frac{\sqrt{2}}{v}\,[\bar{Q}'_{L} (M'_{d} \Phi _1 + Y'_{d} \Phi _2) d'_R + \bar{Q}'_{L} (M'_{u} \tilde{\Phi }_1\nonumber \\&+ Y'_{u} \tilde{\Phi }_2) u'_R + \bar{L}'_{L} (M'_\ell \Phi _1 + Y'_\ell \Phi _2) \ell '_R ] + \mathrm {h.c.} , \end{aligned}$$

(2.9)

where

$$\begin{aligned} M_{d}'&=\frac{1}{\sqrt{2}}(v_1\Gamma _1+v_2\Gamma _2\mathrm {e}^{i\theta }),&Y_{d}'&=\frac{1}{\sqrt{2}}(-v_2\Gamma _1+v_1\Gamma _2\mathrm {e}^{i\theta }),\end{aligned}$$

(2.10)

$$\begin{aligned} M_{u}'&=\frac{1}{\sqrt{2}}(v_1\Delta _1+v_2\Delta _2\mathrm {e}^{-i\theta }),&Y_{u}'&=\frac{1}{\sqrt{2}}(-v_2\Delta _1+v_1\Delta _2\mathrm {e}^{-i\theta }),\end{aligned}$$

(2.11)

$$\begin{aligned} M_\ell '&=\frac{1}{\sqrt{2}}(v_1\Pi _1+v_2\Pi _2\mathrm {e}^{i\theta }),&Y_\ell '&=\frac{1}{\sqrt{2}}(-v_2\Pi _1+v_1\Pi _2\mathrm {e}^{i\theta }). \end{aligned}$$

(2.12)

In general, the Yukawa matrices $M_{f}'$ and $Y_{f}'$ ($f=u,d,\ell$) cannot be simultaneously diagonalized in flavor space. Thus, in the mass-eigenstate basis, with diagonal fermion mass matrices $M_{f}$, the corresponding Yukawa matrices $Y_{f}$ remain non-diagonal, giving rise to tree-level FCNC interactions. The unwanted tree-level FCNCs can be eliminated by requiring the alignment in flavor space of the Yukawa matrices [54]:

$$\begin{aligned}&\Gamma _2 = \xi _{d}\, \mathrm {e}^{-i\theta } \,\Gamma _1 , \quad \Delta _2=\xi _{u}^*\, \mathrm {e}^{i\theta }\Delta _1 , \quad \Pi _2=\xi _\ell \, \mathrm {e}^{-i\theta } \,\Pi _1 , \nonumber \\&Y_{d,\ell }=\varsigma _{d,\ell }\, M_{d,\ell }, \quad Y_{u}=\varsigma ^*_{u}\, M_{u}, \quad \varsigma _{f} \equiv \frac{\xi _{f}-\tan {\beta }}{1+\xi _{f}\tan {\beta }}, \end{aligned}$$

(2.13)

where $\xi _{f}$ ($\varsigma _{f}$) are arbitrary complex parameters and could introduce new sources of CP violation beyond that of the CKM matrix.

The interactions of the charged scalar with the fermion mass-eigenstate fields then read

$$\begin{aligned} \mathcal {L}_{H^\pm }= & {} - \frac{\sqrt{2}}{v}\, H^+\, \{\bar{u} [\varsigma _{d}\,V_{\mathrm {CKM}} M_{d} P_R - \varsigma _{u}\,M_{u}^{\dagger } V_{\mathrm {CKM}} P_{L}] d\nonumber \\&+ \varsigma _\ell \,\bar{\nu } M_\ell P_R \ell \}+ \mathrm {h.c.} , \end{aligned}$$

(2.14)

where $P_{L(R)}\equiv (1\mp \gamma _5)/2$ is the left (right)-handed chirality projector, and $V_{\mathrm {CKM}}$ the CKM matrix [55, 56]. Here we did not give the neutral scalar sector [54] in $\mathcal {L}_Y$ or the FCNC local structures induced beyond tree level (quantum corrections) [64], because their effects are highly suppressed by the muon mass in the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$. The usual NFC models [46, 52], with discrete $\mathcal {Z}_2$ symmetries, are recovered for particular values of $\varsigma _{f}$, as shown in Table 1.

Table 1 The one-to-one correspondence between different specific choices of the couplings $\varsigma _{f}$ and the 2HDMs based on discrete $\mathcal {Z}_2$ symmetries

3 $\varvec{B^0\rightarrow K^{*0}\mu ^+\mu ^-}$ in the A2HDM

3.1 Effective weak Hamiltonian

The rare decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ proceeds through the loop diagrams both within the SM and in the A2HDM. When the heavy degrees of freedom, including the top quark, the weak gauge bosons, as well as the charged scalars, have been integrated out, we obtain the low-energy effective weak Hamiltonian governing the decay [6, 78]:

$$\begin{aligned} \mathcal {H}_{\mathrm {eff}}=-\frac{4G_{F}}{\sqrt{2}}V_{tb}V_{ts}^{*}\sum _{i}(C_{i}O_{i} +C_{i}^{\prime }O_{i}^{\prime }), \end{aligned}$$

(3.1)

where $G_{F}$ is the Fermi coupling constant. Here we neglect the doubly Cabibbo-suppressed contributions to Eq. (3.1) (proportional to $V_{ub}V_{us}^{*}$), and we focus only on the operators [6]

$$\begin{aligned} O_7&= \frac{e}{16\pi ^2}\bar{m}_{b}(\bar{s}\sigma ^{\mu \nu }P_Rb)F_{\mu \nu }, \quad O^{\prime }_7 = \frac{e}{16\pi ^2}\bar{m}_{b}(\bar{s}\sigma ^{\mu \nu }P_{L}b)F_{\mu \nu }, \end{aligned}$$

(3.2)

$$\begin{aligned} O_9&= \frac{e^2}{16\pi ^2}(\bar{s}\gamma ^\mu P_{L}b)(\bar{\mu }\gamma _\mu \mu ), \quad O^{\prime }_9 = \frac{e^2}{16\pi ^2}(\bar{s}\gamma ^\mu P_Rb)(\bar{\mu }\gamma _\mu \mu ), \end{aligned}$$

(3.3)

$$\begin{aligned} O_{10}&= \frac{e^2}{16\pi ^2}(\bar{s}\gamma ^\mu P_{L}b)(\bar{\mu }\gamma _\mu \gamma _5 \mu ), \quad O^{\prime }_{10} = \frac{e^2}{16\pi ^2}(\bar{s}\gamma ^\mu P_Rb)(\bar{\mu }\gamma _\mu \gamma _5 \mu ), \end{aligned}$$

(3.4)

where $\bar{m}_{b}=\bar{m}_{b}(\mu )$ denotes the b-quark running mass in the $\mathrm {\overline{MS}}$ scheme.

Within the SM, the electromagnetic dipole operator $O_7$ and the semileptonic operators $O_{9,10}$ play the leading role in the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$. Besides modifying the values of the SD Wilson coefficients $C_{7,9,10}$, the charged-scalar contributions could also make the chirality-flipped operators $O_{7,9,10}^{\prime }$ defined above to contribute in a significant manner, especially in some regions of the parameter spaces discussed later.

The SD Wilson coefficients $C_i(\mu )$ and $C_i^{\prime }(\mu )$ can be obtained firstly at the matching scale $\mu _{W}\sim M_{W}$ perturbatively, by requiring equality of the one-particle irreducible Green functions calculated in the full and in the effective theory [78]. Using the renormalization group equation, one can then get $C_i(\mu )$ and $C_i^{\prime }(\mu )$ at the lower scale $\mu _{b}\sim m_{b}$. During the calculation, the limit $\bar{m}_{u,c}\rightarrow 0$ and the unitarity of the CKM matrix have been used. For simplicity, we introduce the mass ratios:

$$\begin{aligned} x_{t}=\frac{\bar{m}^2_{t}(\mu _{W})}{M^2_{W}},\quad y_{t}=\frac{\bar{m}^2_{t}(\mu _{W})}{M^2_{H^\pm }}. \end{aligned}$$

(3.5)

Details of the computational method could be found, for example, in Refs. [70, 78].

3.2 Wilson coefficients in the SM

In the SM, the one-loop penguin and box diagrams have been calculated both in the Feynman ($\xi =1$) and in the unitary ($\xi =\infty$) gauge [79,80,81,82,83,84,85,86,87], denoted by the subscript ‘F’ and ‘U’, respectively. The different contributions to $C_i^{\mathrm {SM}}(\mu _{W})$ can be split into the following forms:

$$\begin{aligned} C_{7}^{\mathrm {SM}}= & {} C_{7}^{\gamma \text {-penguin}},\end{aligned}$$

(3.6)

$$\begin{aligned} C_{9}^{\mathrm {SM}}= & {} C_{9}^{W\text {-box}}+C_{9}^{Z\text {-penguin}}+C_{9}^{\gamma \text {-penguin}},\end{aligned}$$

(3.7)

$$\begin{aligned} C_{10}^{\mathrm {SM}}= & {} C_{10}^{W\text {-box}}+C_{10}^{Z\text {-penguin}}, \end{aligned}$$

(3.8)

where the corresponding parts resulting from the W-box, Z-penguin and $\gamma$-penguin diagrams are given, respectively, by

$$\begin{aligned} C_{9,{\mathrm{F(U)}}}^{W\text {-box}}&= -\frac{B_{0,{\mathrm{F(U)}}}}{\sin ^{2}\theta _{W}}, \quad C_{10,{\mathrm{F(U)}}}^{W\text {-box}} = \frac{B_{0,{\mathrm{F(U)}}}}{\sin ^{2}\theta _{W}}, \end{aligned}$$

(3.9)

$$\begin{aligned} C_{9,{\mathrm{F(U)}}}^{Z\text {-penguin}}&= \left( -4+\frac{1}{\sin ^{2}\theta _{W}}\right) C_{0,{\mathrm{F(U)}}}, \quad C_{10,{\mathrm{F(U)}}}^{Z\text {-penguin}} = -\frac{C_{0,{\mathrm{F(U)}}}}{\sin ^{2}\theta _{W}}, \end{aligned}$$

(3.10)

$$\begin{aligned} C_{7,{\mathrm{F(U)}}}^{\gamma \text {-penguin}}&= -\frac{1}{2}D_{0,{\mathrm{F(U)}}}', \quad C_{9,{\mathrm{F(U)}}}^{\gamma \text {-penguin}} = -D_{0,{\mathrm{F(U)}}}+\frac{4}{9}, \end{aligned}$$

(3.11)

where $\theta _W$ is the Weinberg mixing angle, and the Inami–Lim functions [79] are defined as

$$\begin{aligned}&B_{0,\mathrm{F}}=F_{1}\left( x_{t}\right) ,\quad C_{0,\mathrm{F}}=F_{3}\left( x_{t}\right) ,\quad D_{0,\mathrm{F}}'=F_{6}\left( x_{t}\right) ,\quad \nonumber \\&\quad D_{0,\mathrm{F}}=-\frac{4}{9}F_{0}\left( x_{t}\right) +F_{5}\left( x_{t}\right) , \end{aligned}$$

(3.12)

in the Feynman gauge, and

$$\begin{aligned} B_{0,\mathrm{U}}&= -\frac{x_{t}}{16}L_{\epsilon }+F_{4}\left( x_{t}\right) , \quad \nonumber \\ C_{0,{U}}&= -\frac{x_{t}}{16}L_{\epsilon } -F_{1}\left( x_{t}\right) +F_{3}\left( x_{t}\right) +F_{4}\left( x_{t}\right) ,\nonumber \\ D_{0,\mathrm{U}}'&= F_{6}\left( x_{t}\right) ,\nonumber \\ D_{0,\mathrm{U}}&= \frac{x_{t}}{4}L_{\epsilon }-\frac{4}{9}F_{0}\left( x_{t}\right) +4F_{1}\left( x_{t}\right) -4F_{4}\left( x_{t}\right) +F_{5}\left( x_{t}\right) , \end{aligned}$$

(3.13)

in the unitary gauge. Here we introduce the notation $L_{\epsilon }\equiv \frac{1}{\epsilon }+\log \left( \frac{\mu _{W}^{2}}{M_{W}^{2}}\right)$, where $\epsilon =(4-d)/2$ is the dimensional regulator of ultraviolet divergence. Explicit expressions of the basic functions $F_i(x)$ are given by Eqs. (A.1)–(A.9). While each piece on the right-hand side of Eqs. (3.7) and (3.8) depends obviously on $\epsilon$ in the unitary gauge, due to the longitudinal components of the $W^\pm$, $Z^0$ and off-shell photon propagators, the physical quantities $C^{\mathrm {SM}}_{7,9,10}$ are indeed free of $\epsilon$ and are independent of the EW gauge fixings. For a recent review of higher-order corrections to $C^{\mathrm {SM}}_{7,9,10}$, the reader is referred to Ref. [88].

3.3 Wilson coefficients in the A2HDM

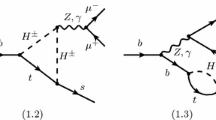
In the A2HDM, the charged-scalar exchanges lead to additional contributions to $C_{7,9,10}$ and could also make the chirality-flipped operators $O^{\prime }_{7,9,10}$ to contribute in a significant manner, through the $Z^0$- and $\gamma$-penguin diagrams shown in Fig. 1. Since we have neglected the light lepton mass, there is no contribution from the SM W-box diagrams with the $W^{\pm }$ bosons replaced by the charged scalars $H^{\pm }$.

Fig. 1

Z- and $\gamma$-penguin diagrams involving the charged-scalar exchanges in the A2HDM

For each Feynman diagram shown in Fig. 1, the contributions are identical in the two gauges. The total Wilson coefficients $C_{7,9,10}$ are split into two parts, one is from the SM contributions $C_{7,9,10}^\mathrm {SM}$, and the other from the charged-scalar ones $C_{7,9,10}^\mathrm {H^\pm }$. For the chirality-flipped operators, $C_{7,9,10}^{\prime }=C_{7,9,10}^{\prime \mathrm {H^\pm }}$, because the SM contributions are well suppressed by the factor $\bar{m}_{s}/\bar{m}_{b}$. For convenience, we decompose these new contributions in such a way as to render explicit their dependence on the couplings $\varsigma _{u}$ and $\varsigma _{d}$:

$$\begin{aligned} C_{7}^\mathrm {H^\pm }&=\left| \varsigma _{u}\right| ^{2}C_{7,\,\mathrm {uu}} +\varsigma _{d}\varsigma _{u}^{*}C_{7,\,\mathrm {ud}}, \end{aligned}$$

(3.14)

$$\begin{aligned} C_{9}^\mathrm {H^\pm }&=\left| \varsigma _{u}\right| ^{2}C_{9,\,\mathrm {uu}}, \end{aligned}$$

(3.15)

$$\begin{aligned} C_{10}^\mathrm {H^\pm }&=\left| \varsigma _{u}\right| ^{2}C_{10,\,\mathrm {uu}}, \end{aligned}$$

(3.16)

$$\begin{aligned} C_{7}^{\prime \mathrm {H^\pm }}&=\frac{\bar{m}_{s}}{\bar{m}_{b}}\left( \left| \varsigma _{u}\right| ^{2}C_{7,\,\mathrm {uu}} +\varsigma _{u}\varsigma _{d}^{*}C_{7,\,\mathrm {ud}}\right) , \end{aligned}$$

(3.17)

$$\begin{aligned} C_{9}^{\prime \mathrm {H^\pm }}&=\left( -1+4\sin ^{2}\theta _{W}\right) C_{10}^{\prime \mathrm {H^\pm }}\nonumber \\&\quad +\frac{\bar{m}_{b}\bar{m}_{s}}{M_{W}^{2}}[\left| \varsigma _{u}\right| ^{2}C_{9,\,\mathrm {uu}}' +2\mathfrak {R}\left( \varsigma _{u}\varsigma _{d}^{*}\right) C_{9,\,\mathrm {ud}}'\nonumber \\&\quad +\left| \varsigma _{d}\right| ^{2}C_{9,\,\mathrm {dd}}'], \end{aligned}$$

(3.18)

$$\begin{aligned} C_{10}^{\prime \mathrm {H^\pm }}&=\frac{\bar{m}_{b}\bar{m}_{s}}{M_{W}^{2}}[\left| \varsigma _{u}\right| ^{2}C_{10,\,\mathrm {uu}}' +2\mathfrak {R}\left( \varsigma _{u}\varsigma _{d}^{*}\right) C_{10,\,\mathrm {ud}}'\nonumber \\&\quad +\left| \varsigma _{d}\right| ^{2} C_{10,\,\mathrm {dd}}'], \end{aligned}$$

(3.19)

where the coefficients of the different combinations of the couplings $\varsigma _{u}$ and $\varsigma _{d}$ are given by Eqs. (B.1)–(B.10). In the particular cases of type II and type Y 2HDMs with large $\tan \beta$, the only terms enhanced by a factor $\tan ^2\beta$ originate from the $\left| \varsigma _{d}\right| ^2$ part contributing only to $C_{9,10}^{\prime \mathrm {H^\pm }}$. The Wilson coefficients $C_{7,9,10}^{(\prime )\mathrm {H^\pm }}$ are found to be invariant under a global U(1) transformation, $\varsigma _{u}\rightarrow \mathrm {e}^{i\chi }\varsigma _{u}$ and $\varsigma _{d}\rightarrow \mathrm {e}^{i\chi }\varsigma _{d}$. This invariance is well anticipated, since it corresponds to an unphysical phase transformation of the second Higgs doublet, $\Phi _2\rightarrow \mathrm {e}^{i\chi }\Phi _2$, a leftover freedom in the Higgs basis [75, 76]. There is an implicit $\mu _{W}$ dependence via the s, b, t-quark masses, which depend on the precise definitions and have to be specified when going beyond the leading logarithm (LL). As we evaluate $C_{7,9,10}^{(\prime )\mathrm {H^\pm }}$ only at the leading order (LO) in $\alpha _{s}$, whether the running masses $\bar{m}_q(\mu _{W})$ or the pole masses $m_q$ are used does not matter too much. As a consequence, we choose the pole masses $m_q$ as input in Eqs. (3.17)–(3.19).

Our results for the chirality-flipped Wilson coefficients $C_{7,9,10}^{\prime \mathrm {H^\pm }}$ are presented for the first time in the A2HDM. In the particular cases of the $\mathcal {Z}_2$ symmetric 2HDMs, our results agree with the ones calculated in Refs. [89,90,91,92]. It is also noted that the next-to-leading order QCD corrections to $C_{7,9,10}^\mathrm {H^\pm }$ in the supersymmetry and type-II 2HDM have already been calculated in Refs. [93,94,95,96,97].

3.4 Angular observables in ${B^0\rightarrow K^{*0}\mu ^+\mu ^-}$ decay

The angular distribution of the $B^0\rightarrow K^{*0}(\rightarrow K^+\pi ^-)\mu ^+\mu ^-$ decay is described by the dimuon invariant mass squared $q^2$ as well as the three angles $\theta _\ell$, $\theta _{K^*}$ and $\phi$, where $\theta _\ell$ is defined as the angle between the flight direction of the $\mu ^+\,(\mu ^-)$ and the opposite direction of the $B^0\,(\bar{B}^0)$ in the rest frame of the dimuon system, and $\theta _{K^*}$ the angle between the flight direction of the $K^+\,(K^-)$ and that of the $B^0\,(\bar{B}^0)$ in the $K^{*0}\,(\bar{K}^{*0})$ rest frame, while $\phi$ is the angle between the plane containing the dimuon pair and the plane containing $K^+$ and $\pi ^-$ mesons in the $B^0\,(\bar{B}^0)$ rest frame. In terms of these four kinematic variables, the full angular decay distribution of the decay is then given by [6, 98]

$$\begin{aligned}&\frac{\mathrm{d}^4 \bar{\Gamma }[B^0\rightarrow K^{*0}\mu ^+\mu ^-]}{\mathrm{d}q^2\, \mathrm{d}\cos \theta _\ell \, \mathrm{d}\cos \theta _{K^*}\, \mathrm{d}\phi }\nonumber \\&\quad =\frac{9}{32\pi }[ \bar{I}_1^s \sin ^2\theta _{K^*} + \bar{I}_1^c \cos ^2\theta _{K^*} \nonumber \\&\qquad + (\bar{I}_2^s \sin ^2\theta _{K^*} + \bar{I}_2^c \cos ^2\theta _{K^*}) \cos 2\theta _\ell \nonumber \\&\qquad + \bar{I}_3 \sin ^2\theta _{K^*} \sin ^2\theta _\ell \cos 2\phi + \bar{I}_4 \sin 2\theta _{K^*} \sin 2\theta _\ell \cos \phi \nonumber \\&\qquad + \bar{I}_5 \sin 2\theta _{K^*} \sin \theta _\ell \cos \phi \nonumber \\&\qquad + \bar{I}_6^s \sin ^2\theta _{K^*} \cos \theta _\ell + \bar{I}_7 \sin 2\theta _{K^*} \sin \theta _\ell \sin \phi \nonumber \\&\qquad + \bar{I}_8 \sin 2\theta _{K^*} \sin 2\theta _\ell \sin \phi + \bar{I}_9 \sin ^2\theta _{K^*} \sin ^2\theta _\ell \sin 2\phi ], \end{aligned}$$

(3.20)

where the angular coefficients $\bar{I}_i^{(a)}$ are functions of $q^2$ only, and the relations $\bar{I}_1^s=3\bar{I}_2^s$, $\bar{I}_1^c=-\bar{I}_2^c$ and $\bar{I}_6^c=0$ hold when the muon mass is neglected. The corresponding expression for the CP-conjugated mode $\bar{B}^0\rightarrow \bar{K}^{*0}(\rightarrow K^-\pi ^+)\mu ^+\mu ^-$ is obtained from Eq. (3.20) by the replacements $\bar{I}_i^{(a)} \rightarrow I_i^{(a)}$ [6, 98]. Explicit forms of the angular coefficients $\bar{I}_i^{(a)}~(I_i^{(a)})$ can be found, for example, in Refs. [6, 10, 16].

The self-tagging property of the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$ makes it possible to determine both the CP-averaged and the CP-asymmetric quantities defined, respectively, by [6]

$$\begin{aligned} S_i^{(a)}= & {} (I_i^{(a)}+\bar{I}_i^{(a)})/\left( \frac{\mathrm{d}\Gamma }{\mathrm{d}q^2}+\frac{\mathrm{d}\bar{\Gamma }}{\mathrm{d}q^2}\right) , \nonumber \\ A_i^{(a)}= & {} (I_i^{(a)}-\bar{I}_i^{(a)})/\left( \frac{\mathrm{d}\Gamma }{\mathrm{d}q^2}+\frac{\mathrm{d}\bar{\Gamma }}{\mathrm{d}q^2}\right) . \end{aligned}$$

(3.21)

The previously studied observables, such as the $q^2$ distributions of the forward–backward asymmetry $A_\mathrm{FB}$ and the CP asymmetry $A_\mathrm{CP}$, can be expressed in terms of these angular observables.

With the structure of the amplitudes at large recoil, it is possible to build clean observables whose sensitivity to the $B\rightarrow K^*$ transition form factors is suppressed by $\alpha _{s}$ or $\Lambda _\mathrm{QCD}/m_{b}$ [9]. These include the so-called $P_i^{\prime }$ and $P_i$ observables defined by [9, 99, 100]

$$\begin{aligned}&P_1=\frac{S_3}{2S_2^s},\quad P_2=\frac{S_6^s}{8S_2^s},\quad P_3=\frac{S_9}{4S_2^s},\end{aligned}$$

(3.22)

$$\begin{aligned}&P_4^{\prime }=\frac{S_4}{2\sqrt{-S_2^sS_2^c}},\quad P_5^{\prime }=\frac{S_5}{2\sqrt{-S_2^sS_2^c}},\nonumber \\&P_6^{\prime }=\frac{S_7}{2\sqrt{-S_2^sS_2^c}},\quad P_8^{\prime }=\frac{S_8}{2\sqrt{-S_2^sS_2^c}}. \end{aligned}$$

(3.23)

The numerical impact of charged-scalar contributions on some of these observables will be discussed in the next section.

4 Numerical results and discussions

4.1 Choice of the model parameters

For the considered decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$, only three model parameters, the charged-scalar mass $M_{H^\pm }$ and the two alignment parameters $\varsigma _{u}$ and $\varsigma _{d}$, are involved. In the following we assume the parameters $\varsigma _{u,d}$ to be real, indicating that the only source of CP violation in the A2HDM is still due to the CKM matrix. Following the previous studies, we now give the preset ranges of these model parameters:

• The charged-scalar mass is assumed to lie in the range $M_{H^{\pm }} \in [80,1000]~\mathrm {GeV}$, where the lower bound comes from the LEP direct search [101], while the upper bound from the unitarity and stability of the scalar potential [102,103,104,105].

• The alignment parameter $\varsigma _{u}$ is assumed to lie in the range $|\varsigma _{u}|\le 2$, to be compatible with the current data of loop-induced processes, such as $Z\rightarrow b\bar{b}$, $b\rightarrow s \gamma$, $B_{s,d}^0$–$\bar{B}_{s,d}^0$ mixings, as well as the h(125) decays [62, 63, 65,66,67,68,69].

• The alignment parameter $\varsigma _{d}$ is only mildly constrained through phenomenological requirements that involve additionally other model parameters. So we let it to be a free parameter.

• In the 2HDMs with discrete $\mathcal {Z}_2$ symmetries, the parameters $\varsigma _{u}$ and $\varsigma _{d}$ are not independent but are related to each other through the ratio of the VEVs $\tan \beta =v_2/v_1$. The upper limit for $\tan \beta$ also comes from the unitarity and stability of the scalar potential [102,103,104,105]; we assume here $\tan \beta \le 50$.

4.2 Constraints on the model parameters

For the other input parameters, we take $M_Z=91.1876~\mathrm {GeV}$, $M_{W}=80.385~\mathrm {GeV}$, $m_{t}=(174.2\pm 1.4)~\mathrm {GeV}$, $m_{b}=(4.78\pm 0.06)~\mathrm {GeV}$, and $\bar{m}_{s}(2~\mathrm {GeV})=(96^{+8}_{-4})~\mathrm {MeV}$ [106]. Since $C_7^{\prime \mathrm {H}^\pm }=\bar{m}_{s}/\bar{m}_{b} C_7^{\mathrm {H}^\pm }$ and $\bar{m}_{s} \ll \bar{m}_{b}$, the contribution from $O_7'$ will be safely neglected.

The Wilson coefficient $C_7^{\mathrm {H}^\pm }$ is severely constrained by the inclusive decay $B\rightarrow X_{s} \gamma$. The branching ratio of $B\rightarrow X_{s} \gamma$ measured by CLEO [107], Belle [108,109,110] and BaBar [111,112,113], lead to the combined average [114]

$$\begin{aligned}&\mathcal {B}^{\mathrm {exp}}(B\rightarrow X_{s} \gamma )\big |_{E_\gamma >1.6~\mathrm {GeV}}\nonumber \\&\quad =\,(3.43\pm 0.21_\mathrm{stat.}\pm 0.07_\mathrm{syst.})\times 10^{-4}, \end{aligned}$$

(4.1)

which is in good agreement with the updated SM prediction [115]

$$\begin{aligned} \mathcal {B}^{\mathrm {SM}}(B\rightarrow X_{s} \gamma )\big |_{E_\gamma >1.6~\mathrm {GeV}}\, =\,\left( 3.36\pm 0.23\right) \times 10^{-4}.\nonumber \\ \end{aligned}$$

(4.2)

It should be noted that the chromomagnetic dipole operator $O_8 = \frac{g_{s}}{16\pi ^2}\bar{m}_{b}\left( \bar{s}\sigma ^{\mu \nu }P_{R}T^a b\right) G_{\mu \nu }^a$ also plays an important role in the decay $B\rightarrow X_{s} \gamma$. However, at the LO in $\alpha _{s}$, this operator contributes to $B\rightarrow X_{s} \gamma$ only via its mixing with $O_7$. It is then found that, at the matching scale $\mu _{W}=160~\mathrm {GeV}$, the Wilson coefficients $C_7^{\mathrm {H}^\pm }$ and $C_8^{\mathrm {H}^\pm }$ should fulfill the constraint [115]:

$$\begin{aligned} -0.0634\le C_7^{\mathrm {H}^\pm }\left( \mu _{W}\right) +0.242\,C_8^{\mathrm {H}^\pm }\left( \mu _{W}\right) \le 0.0464,\nonumber \\ \end{aligned}$$

(4.3)

where $C_8^{\mathrm {H}^\pm }=\left| \varsigma _{u}\right| ^{2}C_{8,\,\mathrm {uu}}+\varsigma _{d}\varsigma _{u}^{*} C_{8,\,\mathrm {ud}}$ [89], with the functions $C_{8,\,\mathrm {uu}}$ and $C_{8,\,\mathrm {ud}}$ given, respectively, by Eqs. (B.11) and (B.12).

Fig. 2

The allowed regions in the $\varsigma _{u}$–$\varsigma _{d}$ plane ($\varsigma _{d}>0$) under the constraint from Eq. (4.3). The blue, red, and green bands correspond to $M_{H^\pm }=80$, 300 and $500~\mathrm {GeV}$, respectively

Under the constraint from Eq. (4.3), we show in Fig. 2 the allowed regions in the $\varsigma _{u}$–$\varsigma _{d}$ plane ($\varsigma _{d}>0$), with three representative values of the charged-scalar mass, $M_{H^\pm }=80$, 300 and $500~\mathrm {GeV}$ as benchmarks. The case with $\varsigma _{d}<0$ is obtained from Fig. 2 with the changes $\varsigma _{u}\rightarrow -\varsigma _{u}$ and $\varsigma _{d}\rightarrow -\varsigma _{d}$. It is observed that the allowed range of $\varsigma _{d}$ becomes quite large when $\varsigma _{u}$ tends to 0; particularly, when $\varsigma _{u}=0$, no constraint on $\varsigma _{d}$ is obtained, because in this limit the SM result is recovered. When $\varsigma _{d}=0$, on the other hand, a bound on $\varsigma _{u}$ can be set with the allowed range of $|\varsigma _{u}|$ further strengthened for smaller values of the charged-scalar mass. These qualitative observations are consistent with those observed previously in Refs. [64,65,66]. However, the allowed regions for $\varsigma _{u}$ and $\varsigma _{d}$ are further reduced compared to those obtained in Refs. [64,65,66], because the updated SM prediction (cf. Eq. (4.2)) becomes now more compatible with the current experimental data (cf. Eq. (4.1)). It is also found that the preset maximum value $\left| \varsigma _{u}\right| =2$ is reached when $\left| \varsigma _{d}\right|$ varies within a range away from 0, rather than at $\varsigma _{d}=0$; for example, taking $M_{H^\pm }=80~\mathrm {GeV}$, we find that $\left| \varsigma _{u}\right|$ approaches 2 when $0.6<\left| \varsigma _{d}\right| <0.8$. This novel observation motivates us to display the $\varsigma _{d}$-axis in the logarithmic coordinate, making clear the correlation between $\varsigma _{u}$ and $\varsigma _{d}$ in the range $\left| \varsigma _{d}\right| <1$. The inversely proportional and parabolic boundary curves in the first quadrant indicate that the NP contribution to $C_{7}^\mathrm {H^\pm }$ (cf. Eq. (3.14)) is dominated by the $\varsigma _{d}\varsigma _{u}^*$ and $\left| \varsigma _{u}\right| ^2$ terms, respectively. As the large same-sign solutions for $\varsigma _{u}$ and $\varsigma _{d}$ obtained in Refs. [64, 65], corresponding to the case when the NP influence is about twice the size of the SM contribution but with an opposite sign, are already excluded by the isospin asymmetry of $B\rightarrow K^*\gamma$ decays [66, 116], they are not shown in Fig. 2.

Motivated by the latest LHCb and Belle measurements of $b \rightarrow s \ell ^+\ell ^-$ decays, there exist several global fits for the NP contributions to the Wilson coefficients $C_{9,10}^{(\prime )}$ [18,19,20, 29]. We use two of these global fit results to further constrain the A2HDM parameters. One is obtained from the combined fit to the $b\rightarrow s\, (\mu ^+\mu ^-, \gamma )$ mesonic decays (at $\mu _{b}=4.8~\mathrm {GeV}$) [19]:

$$\begin{aligned} -2.2&\le C_9^{\mathrm {NP}}\,\le \,-0.4,&-0.5\,\le \,&C_{10}^{\mathrm {NP}}\,\le \,2.0,\nonumber \\ -1.3&\le C_9^{\prime \mathrm {NP}}\,\le \,3.7,&-1.0\,\le \,&C_{10}^{\prime \mathrm {NP}}\,\le \,1.6, \end{aligned}$$

(4.4)

given at the $3\sigma$ level. This fit includes the branching ratios and optimized angular observables of $B\rightarrow K^*\mu ^+\mu ^-$ and $B_{s}\rightarrow \phi \mu ^+\mu ^-$, the branching ratios of $B\rightarrow K\mu ^+\mu ^-$, the branching ratios of $B\rightarrow X_{s}\mu ^+\mu ^-$ (restricted only to the range $1~\mathrm {GeV}^2\le q^2\le 6~\mathrm {GeV}^2$) and $B\rightarrow X_{s}\gamma$, the branching ratio of $B_{s}\rightarrow \mu ^+\mu ^-$, as well as the isospin asymmetry and the time-dependent CP asymmetry of $B\rightarrow K^*\gamma$. Furthermore, both the large- and the low-recoil data are included for the exclusive $b\rightarrow s\mu ^+\mu ^-$ decays, resulting in nearly a hundred observables in total in the analysis [19]. The other global fit includes, besides the time-integrated branching ratio of $B_{s}\rightarrow \mu ^+\mu ^-$ and the branching ratio of $B\rightarrow X_{s}\ell ^+\ell ^-$ integrated over the range $1~\mathrm {GeV}^2\le q^2\le 6~\mathrm {GeV}^2$, the currently available data on $\Lambda _{b}\rightarrow \Lambda (\rightarrow p\pi ^-)\,\mu ^+\mu ^-$ decay, which involves the branching ratio, the rate of longitudinally polarized lepton pair, as well as the leptonic and the hadronic forward–backward asymmetries; numerically, this fit gives (at $\mu _{b}=4.2~\mathrm {GeV}$) [29]

$$\begin{aligned} 0.9\,\le \,&C_9^{\mathrm {NP}}\,\le \,2.5,&1.8\,\le \,&C_{10}^{\mathrm {NP}}\,\le \,4.2,\nonumber \\ -1.3\,\le \,&C_9^{\prime \mathrm {NP}}\,\le \,1.8,&1.0\,\le \,&C_{10}^{\prime \mathrm {NP}}\,\le \,3.1, \end{aligned}$$

(4.5)

at the $1\sigma$ level. It is interesting to note that the latter prefers a shift to $C_9$ that is opposite in sign compared to the former [29]. Since the Wilson coefficients $C_{9,10}^{\mathrm {H^\pm }}(\mu _{W})$ and $C_{9,10}^{\prime \mathrm {H^\pm }}(\mu _{W})$ are calculated only at the LO, they should be evolved to the lower scale $\mu _{b}$ at the LL approximation, which means that they are actually not running [117]. Thus, we can apply directly the bounds given by Eqs. (4.4) and (4.5) to $C_{9,10}^{\mathrm {H^\pm }}$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$. To be more conservative, we require each of these coefficients to lie within the smaller lower and bigger upper bounds of these two global fits. Using these bounds as well as the constraint from Eq. (4.3), we find that the allowed parameter space in the $\varsigma _{u}$–$\varsigma _{d}$ plane are significantly reduced, especially for the model parameter $\varsigma _{u}$, as shown in Fig. 3. This means that $C_{9,10}^\mathrm {H^\pm }$ play a major role in the small $\left| \varsigma _{d}\right|$ region ($\left| \varsigma _{d}\right| <1$) and $C_{9,10}^{\prime \mathrm {H^\pm }}$ can be quite sizable when $\varsigma _{u}$ approaches 0.

Fig. 3

The allowed regions in the $\varsigma _{u}$–$\varsigma _{d}$ plane ($\varsigma _{d}>0$) under the constraint from Eq. (4.3) as well as the bounds on $C_{9,10}^{\mathrm {H^\pm }}$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ from Eqs. (4.4) and (4.5). The other captions are the same as in Fig. 2

Fig. 4

The allowed regions in the $\varsigma _{d}$–$M_{H^\pm }$ plane when $\varsigma _{u}=0$ (a) and in the $\varsigma _{u}$–$M_{H^\pm }$ plane when $\varsigma _d=0$ (b), under the constraint from Eq. (4.3) as well as the bounds on $C_{9,10}^{\mathrm {H^\pm }}$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ from Eqs. (4.4) and (4.5)

Fig. 5

Correlations among the five Wilson coefficients using the allowed values of $\varsigma _{u}$ and $\varsigma _{d}$ with three benchmark values of charged-scalar mass obtained in the previous subsection. The other captions are the same as in Fig. 2

It is also interesting to note that, under the constraint from Eq. (4.3) as well as the bounds on $C_{9,10}^{\mathrm {H^\pm }}$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ from Eqs. (4.4) and (4.5), we could obtain a bound on $\varsigma _{d}$ even when $\varsigma _{u}$ equals 0. Such a bound arises entirely from the information on $C_{9,10}^{\prime \mathrm {H^\pm }}$ due to the $\left| \varsigma _{d}\right| ^2$ terms in these two Wilson coefficients (cf. Eqs. (3.18) and (3.19)). For illustration, the allowed regions in the $\varsigma _{d}$–$M_{H^\pm }$ plane when $\varsigma _{u}=0$ and in the $\varsigma _{u}$–$M_{H^\pm }$ plane when $\varsigma _{d}=0$ are shown in Fig. 4. Numerically, we obtain $\left| \varsigma _{u}\right| \le 0.506$, 0.763 and 0.990, and $\left| \varsigma _{d}\right| \le 212$, 476 and 622, corresponding to $M_{H^\pm }=80$, 300 and $500~\mathrm {GeV}$, respectively. This means that the more accurate $C_{9,10}^{\prime \mathrm{NP}}$ can be better used to restrict the parameter $\varsigma _{d}$.

4.3 $P_2$ and $P_5'$ in the A2HDM

In this subsection, with the constrained parameter space for $\varsigma _{u}$ and $\varsigma _{d}$, we investigate the impact of A2HDM on the angular observables $P_2$ and $P_5'$ in the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$. As there are involved only three model parameters $\varsigma _{u}$, $\varsigma _{d}$ and $M_{H^\pm }$ in Eqs. (3.14)–(3.19), the five Wilson coefficients ($C_7^{\prime \mathrm {H^\pm }}$ is neglected because $\bar{m}_{s} \ll \bar{m}_{b}$) are expected to be highly correlated with each other. Using the allowed values of $\varsigma _{u}$ and $\varsigma _{d}$ with three benchmark values of charged-scalar mass obtained in the previous subsection, we show in Fig. 5 the correlations among these five Wilson coefficients. One can see that, while $C_7^\mathrm {H^\pm }$ is hardly correlated with the other four Wilson coefficients (Fig. 5a–d), $C_9^\mathrm {H^\pm }$ and $C_{10}^\mathrm {H^\pm }$ are obviously linearly correlated with each other and the slope depends only on the charged-scalar mass $M_{H^\pm }$ (Fig. 5e), with the blue, red, and green lines obtained with $M_{H^\pm }=80$, 300, and $500~\mathrm {GeV}$, respectively. In addition, $C_9^{\prime \mathrm {H^\pm }}$ and $C_{10}^{\prime \mathrm {H^\pm }}$ are found to be approximately linearly correlated with each other (Fig. 5f), and the slope starts to be nearly a constant when $M_{H^\pm }\ge 250~\mathrm {GeV}$, which explains why the two lines with $M_{H^\pm }=300$ and $500~\mathrm {GeV}$ almost overlap completely in Fig. 5f. In fact, from the analytic expressions for these Wilson coefficients (cf. Eqs. (3.15)–(3.16) and (3.18)–(3.19), together with (B.3)–(B.10)), we find that $C_{9}^\mathrm {H^\pm }/C_{10}^\mathrm {H^\pm }\rightarrow -1+4\sin ^{2}\theta _{W}\,\left[ 1+4/(9x_{t})\right]$ and $C_{9}^{\prime \mathrm {H^\pm }}/C_{10}^{\prime \mathrm {H^\pm }}\rightarrow -1+4\sin ^{2}\theta _{W}$ when $M_{H^\pm }$ goes to infinity. This explains why the lines shown in Fig. 5e, f get closer to each other with larger $M_{H^\pm }$.

The most interesting results are shown in Fig. 5g–j, which suggest that the charged scalars cannot affect the left- and right-handed semileptonic operators at the same time, under the constraints shown in Figs. 2 and 3. According to Eqs. (3.15) and (3.16), sizable $C_{9,10}^\mathrm {H^\pm }$ need a large $\left| \varsigma _{u}\right|$, which in turn implies that $\left| \varsigma _{d}\right|$ cannot be too large due to the constraints shown in Figs. 2 and 3. Together with the small factor $\bar{m}_{b}\bar{m}_{s}/M_{W}^2$ and the preset range $\left| \varsigma _{u}\right| \le 2$, this renders the coefficients $C_{9,10}^{\prime \mathrm {H^\pm }}$ quite small (cf. Eqs. (3.18)–(3.19)). The same argument applies to the opposite case: sizable $C_{9,10}^{\prime \mathrm {H^\pm }}$ are possible only with a large $\left| \varsigma _{d}\right|$, which then implies a small $\left| \varsigma _{u}\right|$, resulting in quite small $C_{9,10}^\mathrm {H^\pm }$. These qualitative analyses explain the strong correlations observed in Fig. 5g–j, and motivate us to consider the following two specific cases for the NP Wilson coefficients:

$$\begin{aligned}&\text {Case} \,A{:}\, C_{7,9,10}^\mathrm {H^\pm }\, \text {are sizable, but}\, C_{9,10}^{\prime \mathrm {H^\pm }}\simeq 0; \end{aligned}$$

(4.6)

$$\begin{aligned}&\text {Case} \,B{:}\, C_7^\mathrm {H^\pm } \,\text {and}\, C_{9,10}^{\prime \mathrm {H^\pm }} \,\text {are sizable, but}\, C_{9,10}^\mathrm {H^\pm }\simeq 0. \end{aligned}$$

(4.7)

They are associated to the (large $\left| \varsigma _{u}\right|$, small $\left| \varsigma _{d}\right|$) and (small $\left| \varsigma _{u}\right|$, large $\left| \varsigma _{d}\right|$) regions, respectively.

Fig. 6

The $q^2$ dependence of the angular observables $P_2$ and $P_5'$, both within the SM (central value by a red curve and its uncertainty by a yellow band) and in the A2HDM (the green and blue bands correspond to the case A and case B, respectively). The experimental data from the LHCb [11, 16], Belle [17] and BaBar [118] collaborations are represented by the corresponding error bars in different $q^2$ bins

In Fig. 6, we show our predictions for the two angular observables $P_2$ and $P_5'$ at large recoil both within the SM and in the A2HDM, with the Wilson coefficients obtained in the above two cases, together with the experimental data from the LHCb [11, 16], Belle [17] and BaBar [118] collaborations. Here we follow closely the method used in Refs. [6, 13, 18]: Firstly, we take as input the combined LCSR-lattice fit results for the $B\rightarrow K^*$ transition form factors provided in Ref. [13], which allow us to retain all the correlated uncertainties among these form factors. Secondly, we have included the hadronic uncertainties due to non-factorizable power corrections associated with the non-perturbative charm loops [13, 30], the latest discussions of which could be found in Refs. [119, 120]. Finally, these two angular observables are computed within the SM, with their respective uncertainties obtained by adding in quadrature the individual uncertainty due to the $B\rightarrow K^*$ form factors, the non-factorizable charm-loop contributions, and the parametric input (mainly from $m_{b}(\bar{m}_{b})=4.18^{+0.04}_{-0.03}\,\mathrm{GeV}$ and $m_c=1.4\pm 0.2\,\mathrm{GeV}$). For the NP contributions, however, we consider only the uncertainties of the model parameters and perform a random flat scan within their allowed regions. One can see clearly that there is only a small impact on $P_2$ and $P_5'$ in case A, where the chirality-flipped operators $O'_{9,10}$ are absent, while in case B $P_5'$ could be increased significantly to be consistent with the experimental data and reduce $P_2$ when the dimuon invariant mass squared $q^2$ is higher than the zero-crossing point $q_0^2$. Numerical results for the zero-crossing points of $P_2$ (nonzero one) and $P_5'$ are given in Table 2, both within the SM and in the A2HDM. It is observed that the impact on $q_0^2$ in case B is more pronounced than in case A.

Table 2 The zero-crossing points of $P_2$ (nonzero one) and $P_5'$ both within the SM and in the A2HDM

4.4 2HDMs with $\mathcal {Z}_2$ symmetries

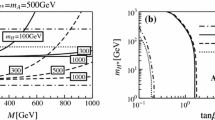
In the generic 2HDMs with discrete $\mathcal {Z}_2$ symmetries, the three alignment parameters $\varsigma _{f}$ will be reduced to a single parameter $\tan \beta =v_2/v_1\ge 0$, as indicated in Table 1. There are, therefore, only two model parameters, $\tan \beta$ and $M_{H^\pm }$, in the Wilson coefficients $C_{7,9,10}^{(\prime )\mathrm {H^\pm }}$. We show in Fig. 7 the allowed regions in the $\tan \beta$–$M_{H^\pm }$ plane corresponding to the four different types of 2HDMs with $\mathcal {Z}_2$ symmetries. As $C_{7,9,10}^{(\prime )\mathrm {H^\pm }}$ do not depend on the parameter $\varsigma _\ell$, the type I (II) and type X (Y) models are indistinguishable from each other. However, one can clearly distinguish types I and X from types II and Y models. As shown in Fig. 7, the bound $M_{H^\pm }>432\,\mathrm{GeV}$ is obtained for types II and Y 2HDMs, while there is no further bound found for $M_{H^\pm }$ in types I and X 2HDMs with sizable $\tan \beta$.

Fig. 7

Allowed regions in the $\tan \beta -M_{H^\pm }$ plane corresponding to different $\mathcal {Z}_2$-symmetric 2HDMs, under the constraint from Eq. (4.3) as well as the bounds on $C_{9,10}^{\mathrm {H^\pm }}$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ from Eqs. (4.4) and (4.5)

Fig. 8

The $q^2$ dependence of the angular observables $P_2$ and $P_5'$ in the types I and X (the green band) and the types II and Y (the blue band) 2HDMs. The other captions are the same as in Fig. 6.

With the constrained model parameters shown in Fig. 7, we then show in Fig. 8 the $q^2$ dependence of $P_2$ and $P_5'$ in the four different types of 2HDMs with $\mathcal {Z}_2$ symmetries. One can see that, compared with the SM predictions, both $P_2$ and $P_5'$ are reduced in the types I and X (the green band), but increased in the types II and Y (the blue band) 2HDMs, only by a small amount. This is because the charged-scalar effect on the left- and right-handed semileptonic operators is controlled by the same parameter $\tan \beta$ and, under the constraint shown in Fig. 7, sizable $C_{9,10}^{\prime \mathrm {H^\pm }}$ are not allowed in these models. It is, therefore, concluded the 2HDMs with $\mathcal {Z}_2$ symmetries cannot explain the so-called $P_5'$ anomaly.

5 Conclusions

In this paper, we have presented a complete one-loop calculation of the SD Wilson coefficients $C_{7,9,10}^{(\prime )\mathrm {H^\pm }}$ due to the charged-scalar exchanges through the $Z^0$- and $\gamma$-penguin diagrams within the A2HDM. For $C_{9,10}^{\prime \mathrm {H^\pm }}$, although being suppressed by the factor $\bar{m}_{b}\,\bar{m}_{s}/M_{W}^2$, they could play an important role in interpreting the observed $P_5'$ anomaly in the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$, when the model parameter $|\varsigma _{d}|$ is large.

Under the constraints from the branching ratio $\mathcal {B}(B\rightarrow X_{s}\gamma )$ and the recent global fit results of $b\rightarrow s\ell ^+\ell ^-$ data, we have obtained the allowed parameter spaces in the $\varsigma _{u}$–$\varsigma _{d}$ plane, corresponding to three representative charged-scalar masses. We found that $C_{9,10}^\mathrm {H^\pm }$ play a major role in the small $\left| \varsigma _{d}\right|$ region ($\left| \varsigma _{d}\right| <1$), while $C_{9,10}^{\prime \mathrm {H^\pm }}$ are most important when the model parameter $\varsigma _{u}$ approaches 0. When $\varsigma _{u}$ is far away from 0 and $\left| \varsigma _{d}\right| \ge 1$, on the other hand, the impact of $C_{7}^\mathrm {H^\pm }$ will become more significant. Within the constrained parameter space, numerically, the effects of these NP Wilson coefficients can be divided into the following two cases: (A) $C_{7,9,10}^\mathrm {H^\pm }$ are sizable, but $C_{9,10}^{\prime \mathrm {H^\pm }}\simeq 0$, corresponding to the (large $\left| \varsigma _{u}\right|$, small $\left| \varsigma _{d}\right|$) region; (B) $C_7^\mathrm {H^\pm }$ and $C_{9,10}^{\prime \mathrm {H^\pm }}$ are sizable, but $C_{9,10}^\mathrm {H^\pm }\simeq 0$, corresponding to the (small $\left| \varsigma _{u}\right|$, large $\left| \varsigma _{d}\right|$) region. We have then discussed their impacts on the angular observables $P_2$ and $P_5'$ in the decay $B^0\rightarrow K^{*0}\mu ^+\mu ^-$. It is found that there is only a small impact on $P_2$ and $P_5'$ in case A, while case B could obviously increase $P_5'$ to be consistent with the experimental data and reduce $P_2$ when the dimuon invariant mass squared $q^2$ is higher than the zero-crossing point.

Finally, we have explored the constraints on $\tan \beta$ and $M_{H^\pm }$ in four types of $\mathcal {Z}_2$-symmetric 2HDMs. The role of chirality-flipped operators $O_{9,10}'$ becomes much more important for large values of $\tan \beta$. Even with the current data, the types I and X and types II and Y could be clearly distinguished from each other. However, the charged-scalar effect on $P_2$ and $P_5'$ in these models is found to be small and does not help to explain the so-called $P_5'$ anomaly.

Future precise measurements of the angular observables in $b\rightarrow s\ell ^+\ell ^-$ decays, especially with a finer binning of $q^2$, would be very helpful to provide a more definite answer concerning the observed anomalies by the LHCb and Belle collaborations, restricting further or even deciphering the NP models.

Appendices

Basic function

The basic functions $F_i(x)$ introduced in Eqs. (3.12) and (3.13) are defined, respectively, as

$$\begin{aligned} F_{0}(x)&=\ln x,\end{aligned}$$

(A.1)

$$\begin{aligned} F_{1}(x)&=\frac{x}{4-4x}+\frac{x\ln x}{4(x-1)^{2}},\end{aligned}$$

(A.2)

$$\begin{aligned} F_{2}(x)&=\frac{x}{96(x-1)}-\frac{x^{2}\ln x}{96(x-1)^{2}},\end{aligned}$$

(A.3)

$$\begin{aligned} F_{3}(x)&=\frac{x}{8}\left[ \frac{x-6}{x-1}+\frac{(3x+2)\ln x}{(x-1)^{2}}\right] ,\end{aligned}$$

(A.4)

$$\begin{aligned} F_{4}(x)&=-\frac{3x(x-3)}{32(x-1)}+\frac{x(x^{2}-8x+4)\ln x}{16(x-1)^{2}},\end{aligned}$$

(A.5)

$$\begin{aligned} F_{5}(x)&=\frac{-19x^{3}+25x^{2}}{36(x-1)^{3}}+\frac{(5x^{2}-2x-6)x^{2}\ln x}{18(x-1)^{4}},\end{aligned}$$

(A.6)

$$\begin{aligned} F_{6}(x)&=\frac{8x^{3}+5x^{2}-7x}{12(x-1)^{3}}-\frac{(3x-2)x^{2}\ln x}{2(x-1)^{4}},\end{aligned}$$

(A.7)

$$\begin{aligned} F_{7}(x)&=\frac{x(53x^{2}+8x-37)}{108(x-1)^{4}}+\frac{x(-3x^{3}-9x^{2}+6x+2)\ln x}{18(x-1)^{5}},\end{aligned}$$

(A.8)

$$\begin{aligned} F_{8}(x)&=\frac{x(18x^{4}+253x^{3}-767x^{2}+853x-417)}{540(x-1)^{5}} \nonumber \\&\quad -\frac{x(3x^{4}-6x^{3}+3x^{2}+2x-3)\ln x}{9(x-1)^{6}}. \end{aligned}$$

(A.9)

Wilson coefficients in A2HDM

The coefficients of the different combinations of the couplings $\varsigma _{u}$ and $\varsigma _{d}$ in Eqs. (3.14)–(3.19) are given, respectively, by

$$\begin{aligned} C_{7,\,\mathrm {uu}}&=-\frac{1}{6}F_{6}(y_{t}),\end{aligned}$$

(B.1)

$$\begin{aligned} C_{7,\,\mathrm {ud}}&=-\frac{4}{3}F_{1}(y_{t})-\frac{80}{17}F_{2}(y_{t}) -\frac{3}{17}F_{5}(y_{t})+\frac{1}{17}F_{6}(y_{t}),\end{aligned}$$

(B.2)

$$\begin{aligned} C_{9,\,\mathrm {uu}}&=\frac{8}{9}F_{1}(y_{t})-\frac{896}{51}F_{2}(y_{t}) -\frac{1}{17}F_{5}(y_{t})-\frac{14}{153}F_{6}(y_{t}) \, \nonumber \\&\quad -\frac{x_{t}}{2}\left( -4+\frac{1}{\sin ^{2} \theta _{W}}\right) F_{1}(y_{t}),\end{aligned}$$

(B.3)

$$\begin{aligned} C_{10,\,\mathrm {uu}}&=\frac{x_{t}}{2\sin ^{2}\theta _{W}}F_{1}(y_{t}),\end{aligned}$$

(B.4)

$$\begin{aligned} C_{9,\,\mathrm {uu}}'&=\frac{y_{t}}{x_{t}}F_{8}(y_{t}),\end{aligned}$$

(B.5)

$$\begin{aligned} C_{9,\,\mathrm {ud}}'&=\frac{y_{t}}{x_{t}}F_{7}(y_{t}),\end{aligned}$$

(B.6)

$$\begin{aligned} C_{9,\,\mathrm {dd}}'&=\frac{y_{t}}{x_{t}}\left[ \frac{2}{9}F_{0}\left( x_{t}\right) +\frac{20}{9}F_{1}(y_{t})+\frac{928}{51}F_{2}(y_{t})\right. \nonumber \\&\qquad \qquad \left. -\frac{2}{17}F_{5}(y_{t})-\frac{11}{153}F_{6}(y_{t})\right] ,\end{aligned}$$

(B.7)

$$\begin{aligned} C_{10,\,\mathrm {uu}}'&=-\frac{1}{17}[80F_{2}(y_{t})+3F_{5}(y_{t}) -F_{6}(y_{t})],\end{aligned}$$

(B.8)

$$\begin{aligned} C_{10,\,\mathrm {ud}}'&=\frac{1}{\sin ^{2}\theta _{W}}\left[ -\frac{1}{12}F_{1}(y_{t}) +\frac{30}{17}F_{2}(y_{t})\right. \nonumber \\&\quad \left. +\frac{9}{136}F_{5}(y_{t}) -\frac{3}{136}F_{6}(y_{t})\right] \, \nonumber \\&\quad -\frac{1}{6}\left( -4+\frac{1}{\sin ^{2}\theta _{W}}\right) F_{1} (y_{t}),\end{aligned}$$

(B.9)

$$\begin{aligned} C_{10,\,\mathrm {dd}}'&=-\frac{1}{\sin ^{2}\theta _{W}}\left[ \frac{1}{2}F_{1}(y_{t}) +F_{2}(y_{t})\right] \nonumber \\&\quad +\left( -4+\frac{1}{\sin ^{2}\theta _{W}}\right) F_{2}(y_{t}), \end{aligned}$$

(B.10)

and for the Wilson coefficient $C_8^\mathrm {H^\pm }$, we have [89]

$$\begin{aligned} C_{8,\,\mathrm {uu}}&=\frac{1}{34}[720F_{2}(y_{t})+27F_{5}(y_{t}) +8F_{6}(y_{t})],\end{aligned}$$

(B.11)

$$\begin{aligned} C_{8,\,\mathrm {ud}}&=2F_{1}(y_{t})-\frac{1}{17}[240F_{2}(y_{t}) +9F_{5}(y_{t})-3F_{6}(y_{t})]. \end{aligned}$$

(B.12)