Soft and diffractive scattering with the cluster model in Herwig

Abstract

We present a new model for soft interactions in the event-generator Herwig. The model consists of two components. One to model diffractive final states on the basis of the cluster hadronization model and a second component that addresses soft multiple interactions as multiple particle production in multiperipheral kinematics. We present much improved results for minimum-bias measurements at various LHC energies.

1 Introduction

With increasingly precise data on observables related to jet physics at the LHC, the impact of soft physics on the accurate modeling of final states plays an increasingly important rôle. While on the one hand there is enormous progress on the perturbative side, soft physics is far from a systematically improvable description and Monte Carlo event generators [1,2,3] merely resort to pure modeling of final states. There is, however, a vast theoretical and phenomenological knowledge on soft physics, accumulated over the last decades that should at least be the benchmark for the modeling in modern event generators.

Still, a large effort is made to model soft aspects of event generation at the LHC [4,5,6,7,8]. With the rise of increasingly accurate data, these aspects become important again as with the increasing precision on the perturbative side of event simulation, non-perturbative aspects become an important part of the uncertainties.

In addition to the interest in modeling collider physics accurately, soft physics is interesting in its own right. Furthermore, it plays an important rôle for the understanding of cosmic ray data [9,10,11].

1.1 The MPI model in Herwig

Minimum-bias interactions at hadron colliders have always been on the edge of physical modeling in Herwig. While there has been a model for the underlying event (UE) that has been an add-on to the Fortran version of the program, the so-called jimmy package [12, 13], a similar model, based on multiple partonic interactions (MPI) had been integrated into the newer C++ version of Herwig later [14, 15]. In addition to the hard multiple interaction model, there have also been soft interactions included in the so-called hot-spot model [16, 17].

Here, semi-hard multiple interactions are included as multiple partonic interactions into the existing framework of partonic scattering with full parton showers and hadronization as for the initial hard process. The interactions are based on the same assumptions as partonic interactions in the usual collinear factorization approach, where for the UE they are modeled in Herwig with parton distribution functions that have the valence quark contribution subtracted. The idea is that the main triggering process usually terminates its parton shower with the extraction of a valence quark and hence the probability to extract yet another valence quark is suppressed. In contrast, the backward evolution of the initial state partons in secondary interactions will always end on a gluon, extracted from the projectile hadron. In this way, the color structure of the secondary scatters is unambiguous, which in turn is mandatory to hook up a hadronization model. There are two important parameters of this model. $p_{\perp }^\mathrm{min}$ is the transverse momentum at which the differential scatting spectrum is cut off in the infrared and $\mu ^2$, which characterizes the inverse proton radius for the transverse spatial distribution of partons within the hadron, which in turn is taken from the dipole form factor.

The additional soft scatters are modeled as another type of multiple interaction with a spatial distribution of the same functional form but another, independent, inverse radius $\mu ^2_\mathrm{soft}$ for soft particles, which are usually broader than the hard partons. Furthermore, the transverse momentum spectrum is modeled with a Gaussian below $p_{\perp }^\mathrm{min}$,

$$\begin{aligned} \frac{\mathrm {d}\sigma }{\mathrm {d}p_{\perp }} = \left( \frac{\mathrm {d}\sigma _\mathrm{hard}}{\mathrm {d}p_{\perp }}\right) _{p_{\perp }=p_{\perp }^\mathrm{min}} \left( \frac{p_{\perp }}{p_{\perp }^\mathrm{min}}\right) e^{-\beta \left( p_{\perp }^2 -p_{\perp }^\mathrm{min}{}^2\right) }\ . \end{aligned}$$

(1)

Here, the spectrum is chosen such that it is continuous at $p_{\perp }^\mathrm{min}$. The two parameters $\mu ^2_\mathrm{soft}$ and $\beta$ are fixed from the additional constraints that the total cross section

$$\begin{aligned} \sigma _\mathrm{tot} = \sigma _\mathrm{hard}^\mathrm{inc} + \sigma _\mathrm{soft}^\mathrm{inc} \end{aligned}$$

(2)

and the elastic slope parameters are given by their known values, of which good parametrizations are available.

With this model for hard and soft MPI in Herwig it has always been possible to give a good description of the UE, i.e. the presences of multiple interactions within one triggered hard scattering. In addition, also minimum-bias interactions have been modeled. Here, due to the setup of Herwig that every event is being triggered by one hard interaction, a dummy process is set up, where two quarks with zero transverse momentum are pulled out of the proton, such that then secondary hard and soft scatters give rise to a description of a minimum-bias event. This model gives satisfactory results whenever the hard contributions dominate. Measurements of fiducial cross sections at the LHC here then cut either on low transverse momentum particles or require a minimum number of charged particles in order to suppress contributions from typical diffractive final state signatures.

1.2 Breakdown of the MPI model in Herwig

When applied to fiducial measurements, where these cuts are loosened, the description of minimum-bias events with Herwig is bound to fail. The reason is that in particular the model for soft interactions is very much ad hoc. It will give the production of soft particles in a way that the ’turn-on regions’ in the UE measurements are well described, but not the correlations among them or with other hard particles. So, the soft model is limited to describe the average soft activity that accompanies a hard event.

This failure is clearly visible, when our model for minimum-bias events is applied to observables which have prominent contributions from diffractive events or are even designed to emphasize contributions of these. This can of course be done, albeit there has never been a claim from the Herwig authors that these measurements could be described, as, clearly, there has so far not been a model for diffractive events.

The prominent example is the so-called ‘bump’ problem, which was first observed by ATLAS [18]. The measurement finds the distribution of large gaps in pseudorapidity $\Delta \eta _F$ in the forward region of the detector in events with a minimal trigger. $\Delta \eta _F$ is the larger of the pseudorapidity gaps from either end of the tracker to the track with the largest (smallest, resp.) pseudorapidity. Herwig is found to over-emphasize the region of large gaps which is mostly attributed to diffractive event topologies. Closer inspection has shown that these events stem from high-mass clusters that stretch out into the forward regions and can be attributed to the color assignment of non-perturbative partons that are produced in the decay of the proton remnants [19].

1.3 New model for soft interactions

The bump problem together with other shortcomings of the simulation of relatively soft particle production lead us to rethink the model of soft interactions in Herwig. There is on the one hand the lack of simulation of diffractive final states and on the other hand the model for soft interactions which seems to be very ad hoc. More hints for problems with soft interactions can be seen in the soft part of transverse momentum spectra of charged particles or identified hadrons which show a pronounced structure of a suppression of soft particles in the region of $p_{\perp }\sim 1\,$GeV.

In this paper we introduce a model for diffractive final states, based on the cluster hadronization model. The idea is to make use of the phenomenological parametrization of diffractive cross sections in a Gribov–Regge factorization approach in order to produce diffractive systems with certain momentum transfer t and diffractive mass M and couple these with the cluster hadronization.

The second new model concerns the production of soft particles. From observations we expect soft particle production to be connected with a particle production which is flat in rapidity and quite narrow in transverse momentum. These requirements are fulfilled by the usual models for soft gluon production, based on small-x dynamics [20,21,22,23,24,25].

In Sect. 2 we introduce the new diffraction model, followed by the model for soft particle production in Sect. 3. We tune the parameters of these models in conjunction with other sensitive parameters of the remaining parts of the MPI model and describe this procedure in Sect. 4, before we present first results in Sect. 5.

2 Diffraction model

In this section we describe in more detail the implementation of high-mass diffraction dissociation within the cluster model which was initially presented in [19]. Events are generated utilizing differential cross sections for single and double diffraction only, where central diffraction remains to be implemented in the future. These cross sections can be derived from Regge theory and the generalized optical theorem, or the so-called Mueller’s theorem [26] (for a review see for example [27]). Let us consider the single diffractive dissociation process $A+B\rightarrow X+B$ first, where A and B are hadrons and X is some hadronic final state, in the limit $s\gg M^2\gg |t|$. s is the total center of mass energy of the incoming particles, M is the invariant mass of the state X and $-t$ is the momentum transfer. In this work we focus only in the case where both hadrons A and B are protons. By considering the amplitude for a single Pomeron exchange, linearity of Regge trajectory and generalized optical theorem, we can write for single diffraction:

$$\begin{aligned} \frac{\mathrm{d}^2\sigma ^\mathrm{SD}}{\mathrm{d}M^2\mathrm{d}t}&= \frac{g_{3{P}}(0)}{16\pi ^2 s}|g_\mathbb {P}(t)|^2 g_\mathbb {P}(0) \nonumber \\&\quad \times \left( \frac{s}{M^2}\right) ^{2\alpha _\mathbb {P}(t)-1}(M^2)^{\alpha _\mathbb {P}(0)-1}, \end{aligned}$$

(3)

where $g_\mathbb {P}$ and $g_{3\mathbb {P}}$ are the proton–pomeron and the triple pomeron coupling, respectively, and they are in general t dependent. For small values of |t|,

$$\begin{aligned} \frac{\mathrm{d}^2\sigma ^\mathrm{SD}}{\mathrm{d}M^2\mathrm{d}t} = N \left( \frac{s}{M^2}\right) ^{\alpha _\mathbb {P}(0)} e^{\left( B_0 + 2 \alpha ' \ln \frac{s}{M^2}\right) t}, \end{aligned}$$

(4)

where $B_0 \approx 10.1\,\mathrm {GeV}^{-2}$ is the so-called proton–pomeron slope; the normalization constant depends on the proton–pomeron and triple pomeron coupling. We have also used the linearity of the Regge trajectory, $\alpha _{\mathbb {P}}(t)=\alpha _{\mathbb {P}}(0)+\alpha ' t$, where $\alpha '$ and $\alpha (0)$ are the pomeron slope and intercept, respectively.

For double diffraction $A+B\rightarrow X_A + X_B$, one can derive the differential cross section using the factorization property of Regge amplitudes and then use the results for single diffraction and elastic cross sections. For details see the references mentioned above. The result is

$$\begin{aligned} \frac{\mathrm{d}^3\sigma ^{DD}}{\mathrm{d}M_A^2\mathrm{d}M_B^2\mathrm{d}t}&= \frac{1}{16\pi ^3 s} g_\mathbb {P}^2(0) g_{3\mathbb {P}}^2(0) \left( \frac{s}{M_A^2M_B^2}\right) ^{2\alpha _\mathbb {P}(t)-1}\nonumber \\&\quad \times \left( M_A^2\right) ^{\alpha _\mathbb {P}(0)-1}(M_B^2)^{\alpha _\mathbb {P}(0)-1}. \end{aligned}$$

(5)

Similarly, for small momentum exchange one can write

$$\begin{aligned} \frac{\mathrm{d}^3\sigma ^{DD}}{\mathrm{d}M_A^2\mathrm{d}M_B^2\mathrm{d}t}&= N \left( \frac{s}{M_A^2}\right) ^{\alpha _\mathbb {P}(0)}\left( \frac{s_0}{M_B^2}\right) ^{\alpha _\mathbb {P}(0)} \nonumber \\&\quad \times e^{\left( b + 2 \alpha ' \ln \frac{s s_0}{M_A^2M_B^2}\right) t}, \end{aligned}$$

(6)

where $s_0$ is fixed in the total normalization and b is a constant set to ${\sim } 0.1$. The total and relative normalization between single and double diffraction is not fixed and it is chosen roughly according to measurements of total cross sections in [28].

In order to integrate the diffractive model into the MPI model in Herwig, we have to ensure that the cross sections for hard and soft interactions only sum up to a fraction of the total cross section when we fix the model parameters of the soft interaction [1, 17]. We assume that the diffractive events come at a rate of about 20–25% of the total event rate. Then we can generate the diffractive processes as an independent sample.

Fig. 1

Diffraction dissociation for single (top) and double (bottom) diffraction

The implementation of diffractive dissociation in Herwig is illustrated in the matrix element shown in Fig. 1 where the upper figure shows single diffraction and the one at the bottom double diffraction. We are dealing here with a two-to-two body problem with the incoming proton momenta being $p_A$ and $p_B$ and the outgoing ones $p'_A$ and $p'_B$. In order to construct the kinematics, we first sample t, $M_A$ and $M_B$ (for single diffraction one of them is the proton mass $m_p$) and make sure that one of the masses is larger. We can then compute the scattering angle in the usual way:

$$\begin{aligned} \cos \theta = \frac{s(s+2t-2m_p^2-M_A^2-M_B^2)}{\sqrt{\lambda (s,M_A^2,M_B^2)\lambda (s,m_p^2,m_p^2)}}, \end{aligned}$$

(7)

where

$$\begin{aligned} \lambda (x,y,z)=x^2+y^2+z^2-2(xy+yz+xz) \end{aligned}$$

(8)

is the so-called Källén function. Knowing the invariant masses and the scattering angle it is straightforward to construct the outgoing momenta. The dissociated proton is then decayed further into a quark–diquark pair that moves collinear to the original hadron. This pair in turn is converted into a cluster and taken over by the hadronization model, where the cluster will eventually decay into two or more hadrons.

Fig. 2

Multiperipheral particle production

We should point out that a fraction of the diffractive events, for very low diffractive mass, are modeled with the $\Delta$ baryon as a final state instead of quark–antiquark pair. Namely, $p \ p \rightarrow \Delta \ p$ for single and $p \ p \rightarrow \Delta \ \Delta$ for double diffraction. The $\Delta$ in turn is handled by the decay handler. For the time being this gives satisfactory results and is only a precautionary measure to avoid exceptional kinematics with very light clusters. Eventually this part shall be taken over from the low mass end of the cluster spectrum.

3 Soft particle production model

We describe in this section the implementation of a new model for soft interactions in Herwig. With this model some of the shortcomings of the simple model for soft interactions presented above are addressed and the description of many minimum-bias observables is significantly improved.

The kinematics of soft scatterers is constructed along the lines of the so-called multiperipheral particle production introduced in [29] and we especially follow the approach taken in [30]. For the case $s\gg m^2$, where m is the typical mass of a final state particle, the intermediate states depicted in Fig. 2 via unitarity give rise to a Reggeized amplitude. We briefly recall the main features of the intermediate state amplitudes: (i) the amplitude of N particle production, as shown in Fig. 2, falls off rapidly when there is no ordering in the longitudinal momenta for which the momentum transfer is small; (ii) the correlation between particle momenta decreases rapidly with distance in the ladder (i.e. momenta $p_i$ and $p_j$, where $|i-j| \gg 1$); (iii) for sub-energies $s_{i,i+1}\equiv (p_i+p_{i+1})^2$ of the neighboring pairs much larger than $m^2$ the amplitude is not large. Large sub-energies correspond to diffractive processes. Some remarks are in order. The assumptions above lead to a fall off of the amplitude for configurations with large rapidity separation. This gives hope that the model will fix the so-called “bump” problem mentioned in the introduction. Also, regarding point (iii), we only consider amplitudes with small sub-energies of neighboring particles, because we implement diffraction using a different method as explained in the previous section.

The model we present now uses many of the features of the old soft MPI model, namely the eikonal model for calculating the number of soft interactions, but implements the assumptions listed above. It should be noted that in Herwig 7, the final particles whose kinematics is constructed using this model, will be partons, more precisely proton remnants, sea quarks and gluons. In the following we explain the algorithm for deriving the kinematics of final particles in more detail. First, as in the previous versions of Herwig, the soft process starts from a quasi-hard process, where a valence quark with only longitudinal momentum is selected from the proton and the remnant takes the rest of the momentum. This is illustrated in Fig. 3 by the dashed lines, where a pomeron is exchanged between quasi-hard quarks. The total energy available to perform the multiperipheral particle production is given in the energy of the remnants. The incoming momenta of the remnants are denoted by $p_{r1}$ and $p_{r2}$ in Fig. 3. According to [30] the number N of the final particles in the ladder is drawn from a Poissionian distribution with mean

$$\begin{aligned} \left\langle N \right\rangle = n_\mathrm{ladder} \ln \frac{(p_{r1}+p_{r2})^2}{m_{\mathrm {rem}}^2}, \end{aligned}$$

(9)

where $m_{\mathrm {rem}}$ is the constituent mass of the remnant and $n_\mathrm{ladder}$ is a constant which is very close to one and will be tuned below to minimum-bias data. Figure 3 illustrates a case with $N=6$, where we have two remnants, a sea quark and an antiquark and two gluons.

Fig. 3

Cluster formation in the multiperipheral final state

In the following we adopt the algorithm described in [30] for generating the kinematics of final state partons, which give diagrams with amplitudes satisfying the assumptions above. The momenta are separated into their longitudinal and transverse parts, namely

$$\begin{aligned} p_i=(p_{0i}, \varvec{p}_{i\perp }, p_{iz}). \end{aligned}$$

(10)

It was shown in [30] that, for the case

$$\begin{aligned} p_{iz}^2 \gg m_i^2+p_{i\perp }^2 \end{aligned}$$

(11)

where $p_i^2=m_i^2$, and assuming the same holds for momentum transfer between neighboring elements in Fig. 2, the longitudinal momenta can be generated by the following rule:

$$\begin{aligned}&p_{1+}=x_1 p_{r1+}, \quad p_{2+}=(1-x_1)x_2 p_{r1+}, \ldots , \nonumber \\&p_{i+}=(1-x_1)(1-x_2)\cdots (1-x_{i-1})x_ip_{r1+}. \end{aligned}$$

(12)

where $p_{i\pm }\equiv p_{i0}\pm p_{iz}$ and $x_i$ take values between 0 and 1. We want to ensure partons are separated equally in rapidity. We assume all $x_i\approx x$ to have roughly the same value. Consider the total rapidity between remnants $\Delta Y$. The spacing in rapidity between partons, after the number N is sampled, is

$$\begin{aligned} \Delta y = \frac{1}{N-1}\Delta Y\simeq \ln \frac{p_{(i-1)+}}{p_{i+}}. \end{aligned}$$

(13)

Using (12) and (13), we can compute

$$\begin{aligned} x=1-e^{-\Delta y}=1-e^{-\frac{1}{N-1}\Delta Y}. \end{aligned}$$

(14)

Longitudinal momenta are thus generated from (12) and (14). Note, that the $x_i$ values do not remain exactly constant. We compute the average $\langle x\rangle$ across the ladder from N (cf. (9)) and smear the actual $x_i$ around these values in order to introduce some fluctuation in the kinematics. Transverse momenta are sampled from (1). In order to facilitate the proper color flow, we have to introduce a pair of quark–antiquark as shown in Fig. 3.

Let us explain in a bit more detail the picture in Fig. 3. The initial quark extracted from the proton is color connected with the remnant and form a cluster (clusters are denoted by gray blobs in the figure). The same holds on the other end for the other proton. The sea quark, denoted by q is color connected to the first gluon, denoted by g. The subsequent gluons are connected with their neighbors. The same holds for the other proton where instead of a quark, we have an antiquark (also denoted by q). Since the first quark is extracted from the proton using a parton distribution function (PDF), we have to make sure that its rapidity is close to the rapidity of second particle in the ladder, which in our case is the sea quark. This can be done by choosing the proper value of $x_{\mathrm {min}}$ of this PDF.

The algorithm presented in this section guarantees exponential fall off of the amplitude for large values of rapidity separation $\Delta \eta$. Also, it gives a roughly flat distribution in rapidity of the clusters and the subsequently produced particles.

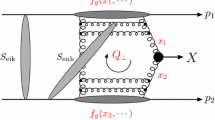
Finally, it should be noted that we take into account also soft multiple parton interactions. This would correspond to intermediate amplitudes with many multiperipheral final states for a given event. The probability for having k soft interactions is computed from the existing model in Herwig (see [1]). The implementation of such a final state is shown in Fig. 4.

Fig. 4

Cluster formation in the multiperipheral final state with multiple interactions

Fig. 5

Comparison of the new model prediction for soft interactions and diffraction with the old model from Herwig 7 to ATLAS rapidity gap measurement at $\sqrt{s} = 7 \, \mathrm {TeV}$ with $p_{t}>200\, \mathrm {MeV}$. In the left panel we compare to ATLAS data in the range $|\eta | \le 4.9$ [18]. In the right panel we compare to data from CMS in the range $|\eta |\le 4.7$ [34]

4 Tuning

In order to model minimum-bias one must also include single and double-diffractive events which makes minimum-bias modeling more complicated than the modeling of the UE. With the new model for diffraction and soft particle interaction the new model can be tuned to fit minimum-bias data. In this section we describe the tuning of the new model to data from hadron colliders. The main part of the tuning is achieved by using the Professor framework [31]. Since we changed the soft part of the MPI model we need to re-tune all parameters that affect this model. The main parameters of the MPI model are the parameters of the $p_{\perp }^\mathrm{min}$ parametrization, $p_{\perp ,0}^\mathrm{min}$ and b, presented in Ref. [32] and the inverse proton radius squared $\mu ^2$. Also considered in the tuning is the color reconnection probability $p_{\mathrm {reco}}$ and the only new parameter of the model, the ladder multiplicity $n_\mathrm{ladder}$ introduced in expression (9) above. At the same time we get rid of the parameter $P_\mathrm{disrupt}$ from the old soft interaction model, that described the probability of choosing a disrupted color connection. Hence, in total we keep the number of tunable parameters fixed with introducing the new model for soft interactions.

Fig. 6

Comparison of the default tune from Herwig 7.0 with the new model to minimum-bias data from ATLAS [33] at $\sqrt{s} = 7 \, \mathrm {TeV}$. The new model was tuned to all data points in this figure

Fig. 7

Comparison of the default tune from Herwig 7.0 with the new model to minimum-bias data from ATLAS [33] at $\sqrt{s} = 7 \, \mathrm {TeV}$. The new model was tuned to all data points in these plots

Fig. 8

Comparison of the default tune from Herwig 7 with the new model to minimum-bias data from ATLAS [33] at $\sqrt{s} = 7 \, \mathrm {TeV}$. The new model was tuned to the data points in the left panel

The parameters governing hadronization were tuned to LEP data [1] and are left untouched. We tune the model to minimum-bias data from the ATLAS collaboration at $\sqrt{s}=900 \, \mathrm {GeV}$ and $\sqrt{s}=7 \, \mathrm {TeV}$ [33]. For the tuning procedure we use the following eight observables with equal weights:

• the pseudorapidity distributions for $N_{\mathrm {ch}} \ge 1$, $N_{\mathrm {ch}} \ge 2$ , $N_{\mathrm {ch}} \ge 6$, $N_{\mathrm {ch}} \ge 20$,

• the transverse momentum of charged particles for $N_{\mathrm {ch}} \ge 1$, $N_{\mathrm {ch}} \ge 2$ , $N_{\mathrm {ch}} \ge 6$,

• the charged transverse momentum vs. number of charged particles for $N_{\mathrm {ch}}\ge 1$.

For the tuning of 5 parameters with a 4-dimensional interpolation we generate 500 runs consisting of 500,000 events each with randomly selected parameter values within a specified range. A subset of these 500 runs is then used 350 times in order to interpolate the generator response. This also serves as a cross check if the interpolation does indeed find the minimum value. For each of these run combinations the $\chi ^2/N_{\mathrm {dof}}$ is calculated and real Monte Carlo runs were performed in order to verify if the interpolation did predict the right value of $\chi ^2/N_{\mathrm {dof}}$. The set of parameters that resulted in the smallest value of $\chi ^2/N_{\mathrm {dof}}$ was then used for further analyses.

Fig. 9

Multiplicity distributions for the very central region $|\eta |<0.5$ (a) and the most inclusive measurement by CMS [35] (b). In order to compare to the data only non-single-diffractive events were simulated with the new model while H7.0 uses the old model for MPI and lacks a model for diffraction completely. The data points in these plots were not used to tune the new model

Fig. 10

$p_{\perp }$ distributions for $|\eta |<2.4$ and $|\eta |=1.9$ measured by CMS [39]. In order to compare to the data only non-single-diffractive events were simulated with the new model while H7.0 uses the old model for MPI and lacks a model for diffraction completely. The data points shown were not included in the new model tune

The tuning to minimum-bias data resulted in two slightly different sets of parameters for $\sqrt{s}=900 \, \mathrm {GeV}$ and $\sqrt{s}=7000 \, \mathrm {GeV}$. The 7000 GeV tune will serve as the default minimum-bias tune for now. We note that the parameters of the $p_{\perp }^\mathrm{min}$ parametrization have approximately the same value in both tunes, which indicates that the parametrization is stable with respect to energy extrapolation, which gets confirmed with our runs at 13 TeV.

The new model with the tuned parameters clearly improves the description of all observables which were considered in the tuning itself. This will be shown in the next section.

5 Results

5.1 Rapidity gap analysis

In Refs. [18, 34] the differential cross section with respect to the forward pseudorapidity gap $\Delta \eta ^F$ is measured. $\Delta \eta ^F$ is defined as the larger of the two pseudorapidity regions extending to the boundary of the detector in which no particles are produced. The acceptance in pseudorapidity $\eta$ ranges from $-4.9$ to $+4.9$ at ATLAS and from $-4.7$ to $+4.7$ at CMS, which is restricted by the geometry of the detectors. All particles with $p_{\perp }>p_{\perp }^{\mathrm {cut}}$ are analyzed where $p_{\perp }^{\mathrm {cut}}$ is varied from 200 to $800 \, \mathrm {MeV}$. The total cross section is usually decomposed into the non-diffractive (ND), single/double-diffractive dissociation (SD/DD) and central-diffractive (CD) parts. The latter is suppressed with respect to other contributions. Events with small pseudorapidity gaps are mainly dominated by ND contributions and for a small $p_{\perp }^{\mathrm {cut}}$ the large rapidity gap region is dominated by SD and DD events. The ND part is characterized by the experimental observation that the average rapidity difference between neighboring particles is around 0.15 with larger rapidity gaps due to fluctuations in the hadronization process. This leads to a cross section that decreases exponentially with larger rapidity gaps $\sigma _\mathrm{ND} \sim \exp (-a\Delta \eta ^F)$ where a is some constant. Events with large pseudorapidity gaps, dominated by diffractive events which result from pomeron exchange as briefly reviewed above, at large energies give rise to a constant cross section $\sigma _{D} \approx \mathrm {const}.$ in $\Delta \eta ^F$.

By combining the model for the simulation of diffractive events, as reviewed in Sect. 2, with the new model for soft particle production proposed in 3, we can describe quite well the measurement of the rapidity gap cross section from ATLAS [18] and CMS [34]. Results for $p_{\perp }>200$ MeV are shown in Fig. 5. It should be noted that while the data from CMS is described very well, the simulation overestimates the data provided by ATLAS despite quite similar cuts. It is very unlikely that our prediction is unstable against the slight opening of rapidity range of ATLAS with respect to CMS, hence we conclude that there is some additional systematic uncertainty in one or both data sets that is not reflected by the quoted error bars.

Fig. 11

Average transverse momentum $\langle p_{\perp }\rangle$ as a function of $p_{\perp }^{\mathrm {lead}}$ for the transverse, forward and away region compared to ATLAS data [40]. The underlying event data were not used in the new model tune

Fig. 12

Average transverse momentum $p_{\perp }$ over number of charged particles $N_\mathrm{ch}$ for the transverse, toward and away region. The data [40] is compared with the new model and Herwig 7. The underlying event data was not used in the new model tune

Fig. 13

Comparison of the default tune from Herwig 7 with the new model to minimum-bias data from ATLAS [33] at $\sqrt{s} = 7 \, \mathrm {TeV}$. The underlying event data was not used in the new model tune

5.2 Minimum-bias data

We further test the new model versus many different minimum-bias measurements. Most observables are significantly improved, although we only tuned to a small subset of available observables. The results for the Monte Carlo runs with the tuned parameters for $7\, \mathrm {TeV}$ are shown in Fig. 6. Here we show all $\eta$ distributions, and we notice that the overall description is quite good. The distribution for the charged particle $p_{\perp }$ versus the number of charged particles is shown in Fig. 7, for different cuts. We notice that for small $p_\perp$ cut the model fails to describe the data. This observable is very sensitive to models of color reconnection that add correlations to final state particles from previously uncorrelated events of MPI models [12]. Overall, it is especially noteworthy to mention that the new model fits the charged particle $p_{\perp }$ distribution almost perfectly in the range where we expect it to contribute significantly. Also the onset of the charged particle $p_{\perp }$ versus the number of charged particles improves which is due to diffraction. The tail of this distribution seems to underestimate the $p_{\perp }$ value but the tune results in an overall better description of the observables.

In Fig. 8 the average charged particle $p_{\perp }$ versus the number of charged particles $N_\mathrm{ch}$ is shown. While there is an improvement for low $N_\mathrm{ch}$ due to perhaps the diffractive model, the overall result is unsatisfactory for very soft particles ($p_\perp > 100\,$MeV). Here, the color reconnection of soft particles appears to have too small an effect in order to result in a rise of this observable for larger $N_\mathrm{ch}$. We note that the transverse momentum spectra of charged particles are much improved in our model with respect to our old model. This is interesting, as sometimes a failure to describe these spectra in older models has been attributed to a lack of collective effects.

5.3 Analysis of non-single-diffractive events

The analysis presented in Ref. [35] is based on an event selection which is corrected according to the SD, DD and ND events predicted by Pythia 6 [36]. Therefore this analysis is automatically biased by these predictions. In particular, single diffractive events have been subtracted from the data set, based on the model prediction. The large error at low multiplicities is dominated by the sizable difference in predictions for SD only final states from Pythia 6 and Phojet [11, 37, 38]. Here, the quoted error bars might be underestimated at low multiplicities and have to be judged accordingly.

It is nonetheless useful to see how our new model performs with respect to these observables. Although we note significant improvement in the region of low multiplicity the new model fails to describe the data correctly (see Fig. 9). It is interesting to note that in Ref. [35] it was found that the event generators systematically underestimated the increase of the multiplicity distribution, while our model (and also the old default model) overestimate it. The multiplicity distribution is mainly influenced by the mass distribution of the clusters. The higher the cluster mass, the more particles get produced from the cluster. We expect a change in the color reconnection model to have significant impact on these distributions which will be studied in more detail in the near future.

Fig. 14

Most inclusive $\eta$ distribution for $p_{\perp }>500 \, \mathrm {MeV}$ and average $p_{\perp }$ distribution for all particles with $p_{\perp }>500 \, \mathrm {MeV}$ measured by ATLAS [41] at $\sqrt{s} = 13 \, \mathrm {TeV}$. The runs for the new model were simulated with the set of parameters from the tune at $7 \, \mathrm {TeV}$, i.e. the energy extrapolation is predicted. H7.0 uses the old model for MPI

In Ref. [39] a similar analysis was performed in order to study the transverse momentum distributions of non-single-diffractive events using the same corrections according to the predictions by Pythia. The new model shows a significant improvement and seems to describe the data correctly except for the ultra low $p_{\perp }<0.4 \,\mathrm {GeV}$ region (see Fig. 10).

5.4 Underlying event

With the model for diffraction and the new model for soft interactions at hand, Herwig 7 for the first time attempts to give a satisfactory description of minimum-bias data. Before that we were limited to diffraction reduced data samples. The next important question is whether the new model affects our previous description of the UE data and possibly improve it. The UE is described as “everything except the hard scattering process” and consists of contributions from the initial- and final state radiation and hard and soft multiparticle interactions. The measurements are made relative to a leading object which is in this case the hardest charged track. In UE analyses three regions of interest are usually considered. The three regions are defined according to their azimuthal angle with respect to the leading track: the toward region, where $\phi <\pi /3$; the away region, where $\phi >2\pi /3$, and the transverse region, where $\pi /3< \phi < 2\pi /3$. The toward and the away regions are usually the regions which are dominated by the activity of the triggered hard scattering process. The transverse region on the other hand contains little contribution from the hard process and is therefore sensitive to interactions coming from the UE.

In Figs. 11 and 12 we show the $\langle p_{\perp }\rangle$ distributions as a function of $p_{\perp }^{\mathrm {lead}}$ and $N_{\mathrm {chg}}$. We see that in all three regions, transverse, toward and away, the data is described fairly well. In Fig. 13 we show more comparisons with UE measurements from ATLAS. This time we compare the number of charged particles and the sum of transverse momenta in the three different regions against data and our old model. We find that the description has improved for all observables.

5.5 Extrapolation to 13 TeV

With the energy update of the LHC to $13\, \mathrm {TeV}$ in 2015 new sets of data are available. This data at the new energy frontier serves as an excellent cross check for our new model. In order to test the energy extrapolation we compare it to data provided by the ATLAS collaboration [41] at $\sqrt{s} = 13 \, \mathrm {TeV}$. We used the same set of parameters as for $\sqrt{s} = 7\, \mathrm {TeV}$, and we did not tune the model parameters to any data taken at this energy, the new model improves the description of the data compared to the old model significantly as shown in Fig. 14.

As a cross check, we have tuned the model exclusively to 13 TeV data instead of 7 TeV data. As this resulted in almost identical values for the parameters as for $7 \, \mathrm {TeV}$, we have an excellent indication of a stable overall energy scaling of our model.

6 Summary and outlook

We have implemented a completely new model for soft physics in Herwig, which will become available with the next release of the program. A simple model for diffractive final states, based on the cluster model is implemented in combination with a new model for multiparticle production in soft interactions, based on multiperipheral particle production. We tuned the free parameters to data from minimum-bias measurements at 900 and 7 TeV and obtained good results in all observables for charged particles. Particularly the rapidity gap observable, which has revealed a peculiar bump structure in our previous model, is now well described. The quality of other observables not considered in the tuning procedure is significantly improved as well. We note that with these new models, Herwig 7 is for the first time able to describe the full range of minimum-bias analyses completely. A stable extrapolation of our model to higher energies is implied by a good description of 13 TeV data albeit we did not tune to data taken at this energy.

Remaining shortcomings of our model include the failure to describe the average transverse momentum of all charged particles versus the event multiplicity for very soft particles. This hints at problematic particle correlations via color reconnections for very soft particles or a problematic assignment of color connections in the first place. These shortcomings will be addressed in future work.

Despite these remaining problems we regard this work as an important first step forward in order to be able to describe collider phenomena involving very soft particles for the first time.