1 Introduction

Astrophysics and theories regarding gravity bear two emerging issues: the aftermath of gravitational collapse and exploration regarding the stability of celestial bodies. The collapse of a star depends on the availability of its fuel, and exhaustion of all of its fuel makes the gravitational collapse indispensable because inward gravitational pull meanwhile overpowers the outward drawn force [1]. Undoubtedly, the size of a collapsing star determines the end state of the evolution, the life span of huge stars having a mass equivalent to 10 to 20 solar masses is not comparable to that of stars assuming sufficiently little mass. Moreover, the more massive stars are the more vulnerable to instability due to heat flux emanating because of high energy dissipation during the collapse phenomenon [2, 3].

The astronomical bodies deserve attention only if they show resistance against fluctuations and remain stable. In 1964, Chandrasekhar [4] presented investigations of a primary level on the dynamical stability of spherical bodies. He pinpointed the instability range of a star assuming mass M and radius r with the help of the adiabatic index \(\Gamma \) using the inequality \(\Gamma \ge {\frac{4}{3}+n\frac{M}{r}}\). The adiabatic index is a tool which is defined as the pressure to density ratio and used to determine the stability range of celestial objects. It imposes some conditions on the physical parameters to meet a stability criterion which is defined for stellar objects. Instability problems in the theory of general relativity (GR) coupled with dissipation, shear, zero expansion, radiation, isotropy, and local anisotropy were addressed by Herrera et al. in [5,6,7,8,9,10]. They established the fact that the instability range is vulnerable to drastic changes if slight variations take place in isotropic profile and shearing effects. Sharif and Abbas [11, 12] analyzed the collapse of charged cylindrical celestial bodies for a non-adiabatic and perfect fluid. Sharif and Azam [13, 14] presented a stability analysis for cylindrically symmetric thin-shell wormholes.

Researchers contributed substantially in addressing the instability problems with the help of GR but it is no longer helpful to explain the cosmological and astrophysical phenomena in a satisfactory way in the presence of dark matter. The concept of exotic matter, like dark energy, and observational evidence of the expanding universe have put theoretical cosmology into a crisis. Due to the limitations of GR on large scales, gravitational modified theories have drawn the attention of astrophysicists. With the help of these theories, they made many efforts to analyze the collapse phenomenon and the stability of astronomical bodies. Among different modified theories, f(R) gravity admits one of the basic modifications in the Einstein–Hilbert action, which includes high order curvature R to explain the above mentioned exotic matter. With the help of various observations like the cosmic microwave background, clustering spectrum, and weak lensing [15,16,17,18], it was concluded that the stability range is increased by the inclusion of curvature terms of higher order.

In modified theories of gravity, the collapse phenomenon has been widely studied. The collapse of self-gravitating dust particles has been discussed in [19], where the authors found that analysis of gravitational collapse is an important tool to constrain the modified models that present late time cosmological acceleration. Meanwhile, Gosh and Maharaj [20] established exact solutions of a null dust non-static cluster of particles in f(R) gravity, constrained by constant curvature describing an anti de Sitter background. Some highly important prospects of celestial collapse for f(R) theory are worked out in [21,22,23,24]. Sharif and Bhatti [25] discussed the instability conditions for cylindrically symmetric self-gravitating objects surrounded by a charged expansion-free anisotropic environment. Kausar and Noureen [26] discussed the evolution of gravitating sources in the context of f(R) theory and concluded that the adiabatic index has a dependence upon the electromagnetic background, mass, and radius of spherically symmetric bodies.

In 2011, another modification to the theory of GR was introduced by Harko et al. in [27], which is an extension of f(R) theory, and such a theory is named f(R, T) theory. The f(R, T) theory of gravity covers curvature and matter coupling and its action includes an arbitrary function of the Ricci scalar R and the trace of the energy-momentum tensor T. After its introduction, this gained significant attention and authors discussed its various properties including reconstructions schemes, energy conditions, cosmological and thermodynamical implications, neutron stars, scalar perturbations, wormholes and analysis of anisotropic universe models, stability, etc. in [28,29,30,31,32,33,34,35,36,37,38,39,40]. Shabani and Farhoudi [41] applied a dynamical system approach to the elaboration of the weak field limit and presented an analysis of cosmological implications of f(R, T) models with various cosmological parameters like Hubble parameter, equation of state parameter, and the snap parameter.

Recently, a dynamical analysis of self-gravitating sources has been discussed in f(R, T) theory. Noureen and Zubair [42] discussed the dynamical instability of a spherically symmetric collapsing star in the presence of an anisotropic fluid. The implications of shear-free and expansion-free conditions on dynamical instability are also discussed in the framework of f(R, T) [43, 44]. Motivated by the significance of non-spherical symmetries, the impact of axially symmetric gravitating sources has also been explored in the context of f(R) and f(R, T) [45, 46]. Yousaf and Bhatti [47] identified dynamical instability conditions of a self-gravitating cylindrical object in f(R, T) theory of gravity.

In this paper, we have chosen the model defined by \(f(R,T)=R+\alpha R^2+\gamma R^n+\lambda T\) to present the dynamical analysis of the cylindrically symmetric object. In order to present this analysis we employ a perturbation approach to the collapse equations and explore the instability range of the model under consideration with the help of the adiabatic index \(\Gamma \) in both the Newtonian and the post-Newtonian regimes. The paper has been organized as follows: the next section contains modified field equations and dynamical equations. In Sect. 3, we provide the adopted f(R, T) model and present perturbation scheme along with the corresponding collapse equation. A discussion of the instability in the form of adiabatic index in both the Newtonian and the post-Newtonian regimes is also presented in the same section. Section 4 concludes our main findings; it is followed by Appendix A.

2 Dynamical equations in f(R, T)

The f(R, T) modification of the Einstein–Hilbert action is given by

$$\begin{aligned} \int \mathrm{d}x^4\sqrt{-g}\left[ \frac{f(R, T)}{16\pi G}+\mathcal {L} _ {(m)}\right] . \end{aligned}$$
(1)

Here, the action due to the matter is described by \(\mathcal {L} _ {(m)}\), whose different choices can be taken into account, each of which leads to a particular form of fluid.

The variation of the above modified action with respect to the metric \(g_{\alpha \beta }\) leads to the following set of field equations:

$$\begin{aligned}&R_{\alpha \beta } f_R(R,T)-\frac{1}{2}g_{\alpha \beta } f(R,T)\nonumber \\&\qquad +(g_{\alpha \beta }\Box -\nabla _{\alpha }\nabla _{\beta })f_R(R,T)\nonumber \\&\quad =8\pi GT_{\alpha \beta }^{(m)}-f_T(R,T)T_{\alpha \beta }^{(m)} -f_T(R,T)\Theta _{\alpha \beta }, \end{aligned}$$
(2)

where \(f_R(R,T)=\frac{\partial f(R,T)}{\partial R}\), \(f_T(R,T)=\frac{\partial f(R,T)}{\partial T}\), while \(\nabla _{\beta }\) and \(\Box \) are derivative operators and represent covariant derivative and four-dimensional Levi-Civita covariant derivative, respectively. The term \(\Theta _{\alpha \beta }\) is defined as

$$\begin{aligned} \Theta _{\alpha \beta }=\frac{g^{\mu \nu }\delta T_{\mu \nu }}{\delta g^{\alpha \beta }}= -2T_{\alpha \beta }+g_{\alpha \beta }\mathcal {L} _ {(m)}-2g^{\mu \nu }\frac{\partial ^2\mathcal {L} _ {(m)}}{\partial g^{\alpha \beta }\partial g^{\mu \nu }}.\nonumber \\ \end{aligned}$$
(3)

Here, we have chosen \(\mathcal {L} _ {(m)}= \mu \), \(8\pi G = 1\), then the expression \(\Theta _{\alpha \beta }\) becomes

$$\begin{aligned} \Theta _{\alpha \beta }=-2T_{\alpha \beta }+\mu g_{\alpha \beta }. \end{aligned}$$
(4)

For the aforementioned choice of the matter Lagrangian and Eq. (3), the modified field equations (2) will be as follows:

$$\begin{aligned} G_{\alpha \beta }= & {} T_{\alpha \beta }^\mathrm{eff}, \end{aligned}$$
(5)

where

$$\begin{aligned} T^\mathrm{eff}_{\alpha \beta }= & {} \frac{1}{f_R}\left[ (f_T+1)T^{(m)}_{\alpha \beta }-\mu g_{\alpha \beta }f_T\right. \nonumber \\&+\left. \frac{f-Rf_R}{2}g_{\alpha \beta }(\nabla _\alpha \nabla _\beta -g_{\alpha \beta }\Box )f_R\right] , \end{aligned}$$
(6)

where \(T^{(m)}_{\alpha \beta }\) represents the energy-momentum tensor for ordinary matter.

The system that we have chosen for analysis is a cylindrically symmetric object which consists of a timelike three dimensional boundary surface \(\Sigma \). The boundary surface under consideration, \(\Sigma \), constitutes two regions termed the interior and the exterior regions. The interior region inside the boundary [48] is

$$\begin{aligned} \mathrm{d}s^2_-=A^2(t,r)\mathrm{d}t^{2}-B^2(t,r)\mathrm{d}r^{2}-C^2(t,r)\mathrm{d}\phi ^{2}-\mathrm{d}z^{2},\nonumber \\ \end{aligned}$$
(7)

whereas the line element for the exterior region [49] can be defined with the help of the following diagonal form:

$$\begin{aligned} \mathrm{d}s^2_+=\left( -\frac{2M}{r}\right) \mathrm{d}\nu ^2+2\mathrm{d}r\mathrm{d}\nu -r^2(\mathrm{d}\phi ^2+\zeta ^{2} \mathrm{d}z^{2}), \end{aligned}$$
(8)

where \(\nu \) is the retarded time, M is the total gravitating mass and \(\zeta \) represents an arbitrary constant. The fluid can be described through configurations of the mathematical form [50]

$$\begin{aligned}&T^{(m)}_{\alpha \beta }=(\mu +P_r)V_{\alpha }V_{\beta }-P_rg_{\alpha \beta }\nonumber \\&\quad +(P_z-P_r)S_{\alpha }S_{\beta }+(P_\phi -P_r)K_{\alpha }K_{\beta }, \end{aligned}$$
(9)

where \(\mu \) represent energy density, \(P_r\), \(P_\phi \), and \(P_z\) are the principal stresses, while \(V_{\beta }\), \(S_{\beta }\), and \(K_{\beta }\) denote four-velocity and four-vectors, respectively. Under co-moving relative motion, these four-vectors and four-velocity are defined as

$$\begin{aligned} V_{\beta }=A\delta ^{0}_{\beta },\quad S_{\beta }=S\delta ^3_{\beta },\quad K_\beta =C\delta ^{2}_\beta , \end{aligned}$$
(10)

and satisfy the following relations:

$$\begin{aligned}&V^{\beta }V_{\beta }=-1,\quad K^{\beta }K_{\beta }=S^{\beta }S_\beta =1,\nonumber \\&\quad V^{\beta }K_\beta =S^{\beta }K_\beta =V^{\beta }S_\beta =0. \end{aligned}$$

The expansion scalar \(\Theta \) defines the rate of change of the matter distribution and it is given by the following mathematical formula:

$$\begin{aligned} \Theta =V^\alpha _{;\alpha }=\frac{1}{A}\left( \frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) , \end{aligned}$$
(11)

where a ‘dot’ indicates a partial derivative w.r.t. the time coordinate.

The Ricci invariant corresponding to the interior region given in (7) is

$$\begin{aligned} R(r,t)= & {} \frac{2}{B^{2}}\left[ \frac{A''}{A}+\frac{C''}{C}+\frac{A'}{A}\left( \frac{C'}{C}-\frac{B'}{B}\right) -\frac{B'C'}{BC}\right] \nonumber \\&-\frac{2}{B^{2}}\left[ \frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}-\frac{\dot{A}}{A}\left( \frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) +\frac{\dot{B}\dot{C}}{BC}\right] , \end{aligned}$$
(12)

where a ‘prime’ represents partial derivatives w.r.t. the radial coordinate.

The f(R, T) field equations for the interior of the cylindrically symmetric system are

$$\begin{aligned}&G_{00}=\frac{A^{2}}{f_R}\left[ \mu +\frac{f-Rf_R}{2}+\eta _{00}\right] ,\nonumber \\&G_{01}=\frac{1}{f_R}\left( \dot{f'_R}-\frac{A'}{A}\dot{f_R}-\frac{\dot{B}}{B}f'_R\right) ,\end{aligned}$$
(13)
$$\begin{aligned}&G_{11}=\frac{B^{2}}{f_R}\left[ P_r(1+f_T)+\mu f_T-\frac{f-Rf_R}{2}+\eta _{11}\right] ,\nonumber \\&G_{22}=\frac{C^{2}}{f_R}\left[ P_{\phi }(1+f_T)+\mu f_T-\frac{f-Rf_R}{2}+\eta _{22}\right] ,\nonumber \\\end{aligned}$$
(14)
$$\begin{aligned}&G_{33}=\frac{1}{f_R}\left[ P_z(1+f_T)+\mu f_T-\frac{f-Rf_R}{2}+\eta _{33}\right] ,\nonumber \\ \end{aligned}$$
(15)

where

$$\begin{aligned} \eta _{00}= & {} \frac{f''_R}{B^2}-\frac{\dot{f_R}}{A^2}\left( \frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) -\frac{f_R'}{B^2}\left( \frac{B'}{B}-\frac{C'}{C}\right) ,\nonumber \\ \eta _{11}= & {} \frac{\ddot{f_R}}{A^{2}}+\frac{\dot{f_R}}{A^{2}}\left( \frac{\dot{C}}{C}-\frac{\dot{A}}{A}\right) -\frac{f'_R}{B^{2}}\left( \frac{A'}{A}+\frac{C'}{C}\right) ,\end{aligned}$$
(16)
$$\begin{aligned} \eta _{22}= & {} \frac{\ddot{f_R}}{A^{2}}-\frac{f''_R}{B^{2}}-\frac{\dot{f_R}}{A^{2}}\left( \frac{\dot{A}}{A}-\frac{\dot{B}}{B}\right) -\frac{f'_R}{B^{2}}\left( \frac{A'}{A}-\frac{B'}{B}\right) ,\nonumber \\\end{aligned}$$
(17)
$$\begin{aligned} \eta _{33}= & {} \frac{\ddot{f_R}}{A^{2}}-\frac{f''_R}{B^{2}}-\frac{\dot{f_R}}{A^{2}}\left( \frac{\dot{A}}{A}-\frac{\dot{B}}{B}-\frac{\dot{C}}{C}\right) \nonumber \\&-\frac{f'_R}{B^{2}}\left( \frac{A'}{A}-\frac{B'}{B}+\frac{C'}{C}\right) . \end{aligned}$$
(18)

The dynamical equations are significant for the establishment of the stability range of relativistic bodies, so we are interested in their construction. In f(R, T) framework, it is observed that the divergence of the energy-momentum tensor is non-vanishing and is found to be

$$\begin{aligned}&\nabla {^{\alpha }}T_{\alpha \beta }\nonumber \\&\quad =\frac{f_T}{1-f_T}\left[ (\Theta _{\alpha \beta }-T_{\alpha \beta })\nabla {^{\alpha }}ln f_T{-}\frac{1}{2}g_{\alpha \beta }\nabla {^{\alpha }}{+}\nabla ^{^{\alpha }}\Theta _{\alpha \beta }\right] .\nonumber \\ \end{aligned}$$
(19)

The divergence of the effective energy-momentum tensor which is mentioned in the above expression yields the following two equations:

$$\begin{aligned}&\dot{\mu }\left( \frac{1-f_T+f_R f_T}{f_R(1-f_T)}\right) -\mu \frac{\dot{f_R}}{f_R}+ \frac{\dot{B}}{B}\frac{1}{f_R}(1+f_T)(\mu +P_r)\nonumber \\&\quad +\frac{\dot{C}}{C}\frac{1}{f_R}(1+f_T)(\mu +P_\phi ) +\frac{\dot{T}}{2}\frac{f_T}{1-f_T}+H_0(r,t)=0,\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned}&P'_r\left( \frac{1-f^{2}_T+2f_R f_T}{f_R(1-f_T)}\right) +\frac{P_r}{f_R}\left( f'_T-\frac{f'_R(1+f_T)}{f_R}\right) \nonumber \\&\quad +\mu '\frac{f_T}{f_R}+ \frac{\mu }{f_R}\left( f'_T-\frac{f_T f'_R}{f_R}\right) \nonumber \\&\quad +\frac{A'}{A}\frac{1}{f_R}(1+f_T)(\mu +P_r)\nonumber \\&\quad +\frac{C'}{C}\frac{1}{f_R}(1+f_T)(P_r-P_\phi )\nonumber \\&\quad +\frac{f'_T}{1-f_T}(\mu +P_r)+\frac{f_T}{1-f_T}\frac{T'}{2}\nonumber \\&\quad +\frac{f_T}{1-f_T}\mu '+H_1(r,t)=0. \end{aligned}$$
(21)

These are the required dynamical equations that will lead to the collapse equation. Here, \(H_0(r,t)\) and \(H_1(r,t)\) represent extra curvature dark source terms emerging from the f(R, T) gravitational field and these quantities are given in the appendix. The variation of the physical parameters of the gravitating system with the passage of time can be observed with the help of a perturbation scheme as given in the following section.

3 f(R, T) model and perturbation scheme

The perturbation scheme is a mathematical tool that is used to find an approximate solution of a differential equation. After applying the perturbation scheme, the corresponding equation can be broken into parts, i.e., static and perturbed parts. We employ this theory to analyze the effects of the f(R, T) model on the evolution of the celestial body under consideration. We have applied perturbation theory in such a way that initially all the quantities are in static equilibrium but with the passage of time the perturbed quantities have both radial and time dependence. The selection of the model is very important for the analysis. The f(R, T) model we have considered for the evolution analysis is a combination of the extended Starobinsky model [51] and a linear term of trace T, written mathematically as

$$\begin{aligned}&f(R, T)= R+\alpha R^2+\gamma R^n+\lambda T, \end{aligned}$$
(22)

where \(n\ge 3\), \(\alpha \) and \(\gamma \) corresponds to the positive real values, while \(\lambda \) is a coupling parameter and \(\lambda T\) represents a modification to f(R) gravity. Assuming \(0<\varepsilon \ll 1\), the functions may be written in the following form:

$$\begin{aligned}&A(t,r)=A_0(r)+\varepsilon D(t)a(r),\end{aligned}$$
(23)
$$\begin{aligned}&B(t,r)=B_0(r)+\varepsilon D(t)b(r),\end{aligned}$$
(24)
$$\begin{aligned}&C(t,r)=C_0(r)+\varepsilon D(t)\bar{c}(r),\end{aligned}$$
(25)
$$\begin{aligned}&\mu (t,r)=\mu _0(r)+\varepsilon {\bar{\mu }}(t,r),\end{aligned}$$
(26)
$$\begin{aligned}&P_r(t,r)=P_{r0}(r)+\varepsilon {\bar{P_r}}(t,r),\end{aligned}$$
(27)
$$\begin{aligned}&P_\phi (t,r)=P_{\phi 0}(r)+\varepsilon {\bar{P_\phi }}(t,r), \end{aligned}$$
(28)
$$\begin{aligned}&P_z(t,r)=P_{z0}(r)+\varepsilon {\bar{P_z}}(t,r)\end{aligned}$$
(29)
$$\begin{aligned}&m(t,r)=m_0(r)+\varepsilon {\bar{m}}(t,r),\end{aligned}$$
(30)
$$\begin{aligned}&R(t,r)=R_0(r)+\varepsilon D_1(t)e_1(r),\end{aligned}$$
(31)
$$\begin{aligned}&T(t,r)=T_0(r)+\varepsilon D_2(t)e_2(r),\end{aligned}$$
(32)
$$\begin{aligned}&f(R, T)=[R_0(r)+\alpha R_0^2(r)+\gamma R^n(r)\nonumber \\&\qquad \qquad +\lambda T_0]+\varepsilon D_1(t)e_1(r)\nonumber \\&\qquad \qquad \times [1+2\alpha R_0(r)+\gamma nR_0^{n-1}]+\varepsilon \lambda D_2(t)e_2(r),\end{aligned}$$
(33)
$$\begin{aligned}&f_R=(1+2\alpha R_0(r)+\gamma nR_0^{n-1})+\varepsilon D_1(t)e_1(r)\nonumber \\&\quad \quad \times (2\alpha +\gamma n(n-1)R_0^{n-2}),\end{aligned}$$
(34)
$$\begin{aligned}&f_T=\lambda , \end{aligned}$$
(35)
$$\begin{aligned}&\Theta (t,r)=\varepsilon \bar{\Theta }. \end{aligned}$$
(36)

In the above equations, \(R_0\) represents the static part of the Ricci scalar whose value is given below

$$\begin{aligned} R_{0}(r)=\frac{2}{B_0^{2}}\left[ \frac{A''_0}{A_0}+\frac{B'_0}{B_0r} +\frac{A'_0}{A_0}\left( \frac{1}{r}-\frac{B'_0}{B_0}\right) \right] , \end{aligned}$$
(37)

while the value of perturbed part of the Ricci scalar is given as

$$\begin{aligned} -\mathrm{De}= & {} \frac{2\ddot{D}}{A_0^{2}}\left( \frac{b}{B_0}+\frac{\bar{c}}{r}\right) \nonumber \\&+D\left[ \frac{4b}{B_0^{3}}R_0-\frac{2}{B_0^{2}}\left\{ \frac{a''}{A_0}-\frac{aA''_0}{A_0^{2}}+\frac{c''}{r}-\frac{A'_0}{A_0}\nonumber \right. \right. \\&\times \left. \left. \left\{ \left( \frac{b}{B_0}\right) '-\left( \frac{\bar{c}}{r}\right) '\right\} +\left( \frac{a}{A_0}\right) ' \left( \frac{1}{r}-\frac{B'_0}{B_0}\right) \right. \right. \nonumber \\&-\left. \left. \frac{B'_0}{B_0}\left( \frac{\bar{c}}{r}\right) '-\frac{1}{r} \left( \frac{b}{B_0}\right) '\right\} \right] . \end{aligned}$$
(38)

The static configuration of the f(R, T) field equations (13)–(14) with the assumption \(C_0(r)=r\) is

$$\begin{aligned}&\frac{1}{B_0^{2}}\frac{B'_0}{B_0}\nonumber \\&\quad =\frac{1}{Z}\left( \mu _0+\frac{\lambda T_0-\alpha R_0^{2}-\gamma (n-1)R_0^{n}}{2}+\eta _{00}^{(s)}\right) ,\end{aligned}$$
(39)
$$\begin{aligned}&\qquad \times \frac{1}{rB_0^{2}}\frac{A'_0}{A_0}=\frac{1}{Z}\left( P_{r0}+\lambda (P_{r0}+\mu _0)\right. \nonumber \\&\qquad \left. -\frac{\lambda T_0-\alpha R_0^{2}-\gamma (n-1)R_0^{n}}{2}+\eta _{11}^{(s)}\right) ,\end{aligned}$$
(40)
$$\begin{aligned}&\qquad \times \frac{1}{B_0^{2}}\frac{A'_0}{A_0}\left( \frac{A''_0}{A'_0}-\frac{B'_0}{B_0}\right) =\frac{1}{Z}\left( P_{\phi 0}+\lambda (P_{\phi 0}+\mu _0)\right. \nonumber \\&\qquad \left. -\frac{\lambda T_0-\alpha R_0^{2}-\gamma (n-1)R_0^{n}}{2}+\eta _{22}^{(s)}\right) ,\end{aligned}$$
(41)
$$\begin{aligned}&\qquad \times \frac{1}{B_0^{2}} \left( \frac{A''_0}{A_0}-\frac{A'_0}{rA_0}\right) -\frac{B'_0}{B_0^{3}}\left( \frac{1}{r}+\frac{A'_0}{A_0}\right) \nonumber \\&\quad =\frac{1}{Z}\left( P_{z0}+\lambda (P_{z0}+\mu _0)\right. \nonumber \\&\qquad \left. -\frac{\lambda T_0-\alpha R_0^{2}-\gamma (n-1)R_0^{n}}{2}+\eta _{33}^{(s)}\right) , \end{aligned}$$
(42)

where

$$\begin{aligned} \eta _{00}^{(s)}= & {} \frac{Z_{R_0}}{B_0^{2}}\left[ R''_0-R'_0\left( \frac{B'_0}{B_0}-\frac{1}{r}\right) \right] +\frac{Z_{R_0R_0}(R'_0)^{2}}{B_0^{2}},\nonumber \\ \eta _{11}^{(s)}= & {} -\frac{Z_{R_0}R_0'}{B_0^{2}}\left( \frac{A'_0}{A_0}+\frac{1}{r}\right) ,\end{aligned}$$
(43)
$$\begin{aligned} \eta _{22}^{(s)}= & {} \frac{Z_{R_0}}{B_0^{2}}\left[ R'_0\left( \frac{B'_0}{B_0}-\frac{A'_0}{A_0}\right) -R''_0\right] +\frac{Z_{R_0R_0}(R'_0)^{2}}{B_0^{2}},\nonumber \\ \eta _{33}^{(s)}= & {} \frac{Z_{R_0}}{B_0^{2}}\left[ R'_0\left( \frac{B'_0}{B_0}-\frac{A'_0}{A_0}-\frac{1}{r}\right) -R''_0\right] \nonumber \\&+\frac{Z_{R_0R_0}(R'_0)^{2}}{B_0^{2}}. \end{aligned}$$
(44)

After applying the static configuration, the first dynamical equation (20) is identically satisfied, while the second equation (21) has the following form:

$$\begin{aligned}&\frac{1}{Z}\left[ \frac{1-\lambda ^{2}{+}2\lambda Z}{1-\lambda }P'_{r0}{-}\frac{(1+\lambda )Z'}{Z}P_{r0}{+}\lambda \left( \mu '_0-\frac{Z'}{Z}\mu _0\right) \right. \nonumber \\&\quad +\left. (1+\lambda ){\frac{A'_0}{A_0}(\mu _0+P_{r0})+\frac{1+\lambda }{r}(P_{r0}-P_{\phi 0})}\right] \nonumber \\&\quad +\frac{\lambda }{1-\lambda }\left( \frac{T'_0}{2} +\mu '_0\right) +H_1^{(s)}=0, \end{aligned}$$
(45)

where \(H_1^{(s)}\) represents the static part of \(H_1\) and is given by

$$\begin{aligned} H_1^{(s)}= & {} \left[ \frac{1}{Z}\left( \frac{\lambda T_0+\alpha R_0^{2}+\gamma (n-1)R_0^{n}}{2}+\eta _{11}^{(s)}\right) \right] _{,1}\nonumber \\&+\frac{1}{Z} \left[ \frac{A'_0}{A_0}\left( \eta _{00}^{(s)}+\eta _{11}^{(s)} \right) +\frac{1}{r}\left( \eta _{11}^{(s)}-\eta _{22}^{(s)}\right) \right] . \end{aligned}$$
(46)

After the application of perturbation scheme, the dynamical equations (20) and (21) obtained through the non-zero divergence of the effective energy-momentum tensor in f(R, T) gravity turn out to be

$$\begin{aligned}&\frac{1}{Z}\left[ \frac{\dot{\bar{\mu }}(1-\lambda +\lambda Z)}{1-\lambda }+\left\{ \mu _0 eZ_{R_0}+\frac{b}{B_0}(1+\lambda )(\mu _0+P_{r0})\right. \right. \nonumber \\&\quad +\left. \left. \frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})\right. \right. \nonumber \\&\quad \left. \left. +\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p_1)}\right\} \dot{D}\right] =0,\end{aligned}$$
(47)
$$\begin{aligned}&\quad \times \frac{\ddot{D}}{A_0^2}\left[ e'-\frac{1}{Z}\left\{ Z_{R_0}\left( e'-\frac{A'_0}{A_0}e-\frac{b}{B_0}R_0\right) \right. \right. \nonumber \\&\quad \left. \left. \!+Z_{R_0R_0}eR'_0\right\} - e\frac{A'_0}{A_0}\right] +\bar{P'_r}\left( \frac{1-\lambda ^{2}+2\lambda Z}{Z(1-\lambda )}\right) \nonumber \\&\quad +\bar{\mu '}\left( \frac{\lambda -\lambda ^{2}+\lambda Z}{Z(1-\lambda )}\right) +\frac{1+\lambda }{Z}\left( \frac{Z_{R_0}R'_0}{Z}+\frac{A'_0}{A_0}+\frac{1}{r}\right) \bar{P_r}\nonumber \\&\quad +\bar{\mu } \left( \frac{\lambda }{Z^{2}}Z_{R_0}R'_0+\frac{1+\lambda }{Z}\frac{A'_0}{A_0}\right) \nonumber \\&\quad -\frac{1+\lambda }{Zr}\bar{P_\phi } +\left[ \frac{eZ_{R_0}}{Z(1-\lambda )}\left\{ \left( 2\lambda -\frac{1-\lambda ^{2}+2\lambda Z}{Z}\right) P'_{r0}\right. \right. \nonumber \\&\quad +\left. \left. \left( \lambda -\frac{\lambda -\lambda ^{2}+\lambda Z}{Z}\right) \mu '_0\right\} \right. \nonumber \\&\quad \left. -\frac{2eZ_{R_0}^{2}R'_0}{Z^{3}}\left\{ (1+\lambda )P_{r_0} +\lambda \mu _0\right\} \right. \nonumber \\&\quad +\left. \frac{1}{Z^{2}} (e'Z_{R_0}+eZ_{R_0R_0}R'_0)\left\{ (1+\lambda )P_{r_0}+\lambda \mu _0\right\} \right. \nonumber \\&\quad +\left. \frac{1+\lambda }{Z}(\mu _0+P_{r0}) \left\{ \left( \frac{a}{A_0}\right) '-\frac{eZ_{R_0}}{Z}\frac{A'_0}{A_0}\right\} \right. \nonumber \\&\quad +\left. \frac{1+\lambda }{Z}(P_{r0}-P_{\phi 0})\left\{ \left( \frac{\bar{c}}{r}\right) '-\frac{eZ_{R_0}}{Z}\frac{1}{r}\right\} +\frac{\lambda e'}{2(1-\lambda )}\right. \nonumber \\&\quad +\left. H_1^{(p)}\right] D=0, \end{aligned}$$
(48)

where \(Z=1+2\alpha R_0+\gamma nR^{n-1}_0\), \(Z_{R_0}=\frac{\partial Z}{\partial R_0}\), \(Z_{R_0R_0}=\frac{\partial ^2 Z}{\partial R_0^2}\), and \(H_0^{(p)}\), \(H_1^{(p)}\) represent perturbed parts of \(H_0\) and \(H_1\), respectively, which are addressed in the appendix. It is also assumed that \(D_1=D_2=D\) and \(e_1=e_2=e\).

Eliminating \(\dot{\bar{\mu }}\) from the perturbed equation (47) and integrating this with respect to t, we get

$$\begin{aligned} \bar{\mu }= & {} \frac{\lambda -1}{1-\lambda +\lambda Z}\left[ \mu _0 eZ_{R_0}+\frac{b}{B_0}(1+\lambda )(\mu _0+P_{r0})\right. \nonumber \\&+\left. \frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})+\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right] D.\nonumber \\ \end{aligned}$$
(49)

The second law of thermodynamics relates \(\bar{\mu }\) and \(\bar{P_r}\) as the ratio of specific heat with the assumption of a Harrison–Wheeler type equation of state expressed by [52]

$$\begin{aligned} \bar{P_r}= & {} \Gamma \frac{P_{r0}}{\mu _0+P_{r0}}\bar{\mu }. \end{aligned}$$
(50)

The adiabatic index is a measure for the variation of the pressure with changing density. Substituting the value of \(\bar{\mu }\) given in Eq. (47) in the above equation, we obtain

$$\begin{aligned}&\bar{P_r}=\left[ \frac{\lambda ^2-1}{1-\lambda +\lambda Z}\Gamma \left\{ \frac{b}{B_0}P_{r0}+ \frac{\bar{c}}{r}P_{r0}\frac{\mu _0+P_{\phi 0}}{\mu _0+P_{r0}}\right\} \right. \nonumber \\&\qquad +\left. \Gamma \frac{P_{r0}}{\mu _0+P_{r0}}\left( \frac{\lambda -1}{1-\lambda +\lambda Z}\right) \right. \nonumber \\&\qquad +\left. \quad \left\{ \mu _0 eZ_{R_0}+\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right\} \right] D. \end{aligned}$$
(51)

The expressions for \(\bar{P_\phi }\) and \(\bar{P_z}\) can be obtained from the perturbed forms of the last two field equations. Applying a perturbation on the field equations and eliminating \(\bar{P_\phi }\) and \(\bar{P_z}\) lead to

$$\begin{aligned}&\bar{P_\phi }=-\ddot{D}\frac{Z}{(1+\lambda )A_0^2}\left( e+\frac{b}{r^2B_0}\right) -\frac{\lambda }{1+\lambda }\bar{\mu }+\mathrm{DH}_2,\nonumber \\ \end{aligned}$$
(52)
$$\begin{aligned}&\bar{P_z}=-\ddot{D}\frac{Z}{(1+\lambda )A_0^{2}}\left( e+\frac{b}{B_0}+\frac{\bar{c}}{r}\right) -\frac{\lambda }{1+\lambda }\bar{\mu }+\mathrm{DH}_3,\nonumber \\ \end{aligned}$$
(53)

where \(H_2\) and \(H_3\) are presented in the appendix.

After substitution of the values of \(\bar{\mu }, \bar{P_r}, \bar{P_\phi }\), the second dynamical equation takes the form

$$\begin{aligned}&\frac{\ddot{D}}{A_0^2}\left[ e'+e\left( \frac{1}{r}-\frac{A'_0}{A_0}\right) -\frac{1}{Z}\left\{ Z_{R_0}\left( e'-\frac{A'_0}{A_0}e-\frac{b}{B_0}R_0\right) \right. \right. \nonumber \\&\quad +\left. \left. Z_{R_0R_0}eR'_0\right\} + \frac{b}{B_0r^{3}}\right] +\left[ \frac{\lambda }{Zr}\left[ \left( \frac{\lambda -1}{1-\lambda +\lambda Z}\right) \left\{ \mu _0 eZ_{R_0}\right. \right. \right. \nonumber \\&\quad +\left. \left. \left. \frac{b}{B_0}(1+\lambda )(\mu _0+P_{r0})+ \frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})\right. \right. \right. \nonumber \\&\quad +\left. \left. \left. \frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right\} \right] +\left( \frac{\lambda -\lambda ^{2}+\lambda Z}{(\lambda -1)Z}\right) \left[ \left( \frac{\lambda -1}{1-\lambda +\lambda Z}\right) \right. \right. \nonumber \\&\quad \times \left. \left. \left\{ \mu _0 eZ_{R_0}+\frac{b}{B_0}(1+\lambda )(\mu _0+P_{r0}) +\frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})\right. \right. \right. \nonumber \\&\quad +\left. \left. \left. \frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right\} \right] '+\left( \frac{\lambda }{Z^{2}}Z_{R_0}R'_0 +\frac{1+\lambda }{Z}\times \frac{A'_0}{A_0}\right) \right. \nonumber \\&\quad \times \left. \left[ \left( \frac{\lambda -1}{1-\lambda +\lambda Z}\right) \left\{ \mu eZ_{R_0}+\frac{b}{B_0}(1+\lambda )(\mu _0+P_{r0})\right. \right. \right. \nonumber \\&\quad +\left. \left. \left. \frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})+\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right\} \right] -\Gamma \right. \nonumber \\&\quad \times \left. \left( \frac{1-\lambda ^{2}+2\lambda Z}{Z}\right) \left\{ \frac{P_{r0}}{\mu _0+P_{r0}}\left( \frac{1}{1-\lambda +\lambda Z}\right) \right. \right. \nonumber \\&\quad \times \left. \left. \left( \mu _0 eZ_{R_0}+\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right) \right\} '-\Gamma \left( \frac{1-\lambda ^{2}+2\lambda Z}{Z}\right) \right. \nonumber \\&\quad \times \left. \left\{ \left( \frac{1+\lambda }{1-\lambda +\lambda Z}\right) \left( \frac{b}{B_0}P_{r0}+\frac{\bar{c}}{r}\frac{\mu _0+P_{\phi 0}}{\mu _0+P_{r0}}P_{r0}\right) \right\} '\right. \nonumber \\&\quad -\left. \Gamma \frac{1-\lambda ^{2}}{Z} \left( \frac{Z_{R_0}R'_0}{Z}+\frac{A'_0}{A_0}+\frac{1}{r}\right) \left\{ \frac{P_{r0}}{\mu _0+P_{r0}}\left( \frac{1}{1-\lambda +\lambda Z}\right) \right. \right. \nonumber \\&\quad \times \left. \left. \left( \mu _0 eZ_{R_0}+\frac{\lambda eZ}{2(1-\lambda )}+ZH_0^{(p)}\right) \right\} \right. \nonumber \\&\quad -\left. \Gamma \frac{1-\lambda ^{2}}{Z} \left( \frac{Z_{R_0}R'_0}{Z}+\frac{A'_0}{A_0}+\frac{1}{r}\right) \right. \nonumber \\&\quad \times \left. \left\{ \left( \frac{1+\lambda }{1-\lambda +\lambda Z}\right) \left( \frac{b}{B_0}P_{r0}+\frac{\bar{c}}{r}\frac{\mu _0+P_{\phi 0}}{\mu _0+P_{r0}}P_{r0}\right) \right\} \right. \nonumber \\&\quad +\left. \frac{eZ_{R_0}}{Z(1-\lambda )}\left\{ \left( 2\lambda -\frac{1-\lambda ^2+2\lambda Z}{Z}\right) P'_{r0}\right. \right. \nonumber \\&\quad +\left. \left. \left( \lambda -\frac{\lambda -\lambda ^2+2\lambda Z}{Z}\right) \mu _0'\right\} \right. \nonumber \\&\quad +\left. \frac{(1+\lambda )P_{r0}+\lambda \mu _0}{Z^{2}}\left\{ e'Z_{R_0} +eZ_{R_0R_0}R'_0\right. \right. \nonumber \\&\quad -\left. \left. \frac{2eZ_{R_0}^{2}R'_0}{Z}\right\} +\frac{1+\lambda }{Z}(\mu _0+P_{r0})\left\{ \left( \frac{a}{A_0}\right) '-\frac{eZ_{R_0}}{Z}\frac{A'_0}{A_0}\right\} \right. \nonumber \\&\quad +\left. \frac{1+\lambda }{Z}(P_{r0}-P_{\phi 0})\left\{ \left( \frac{\bar{c}}{r}\right) ' -\frac{eZ_{R_0}}{Zr}\right\} +\frac{\lambda e'}{2(1-\lambda )}\right. \nonumber \\&\quad -\left. \frac{1+\lambda }{Zr}H_{2}+H_1^{(p)}\right] D=0. \end{aligned}$$
(54)

A second order differential equation is obtained after some manipulation in the perturbed part of the Ricci scalar, which takes the form

$$\begin{aligned} \ddot{D(t)}-H_4(r)D(t)=0, \end{aligned}$$
(55)

where \(H_4\) is addressed in the appendix. Here, it is presumed that all the terms in \(H_4\) are positive. The solution of the above differential equation is of the form

$$\begin{aligned} D(t)=-e^{\sqrt{H_4}t}. \end{aligned}$$
(56)

To estimate the instability range in the Newtonian and the post-Newtonian regimes, Eq. (56) can be used in Eq. (53). The subsections following this section provide the dynamical analysis in both regimes.

3.1 Newtonian regime

To arrive at the Newtonian approximation, we assume \(\mu _0\gg P_{r0}\), \(\mu _0\gg P_{\phi 0}\), \(\mu _0\gg P_{z0}\), and \(A_0=1\), \(B_0=1\). Insertion of these assumptions along with Eqs. (55) and (56) leads to the following stability conditions:

$$\begin{aligned} \Gamma< & {} \frac{H_4U+V+\frac{\lambda -\lambda ^{2}+\lambda Z}{Z(\lambda -1)}W'+\lambda \left( \frac{1}{Zr}+\frac{Z_{R0}R'_0}{Z^{2}}\right) W +\left\{ (1+\lambda )P_{r0}+\lambda \mu _0\right\} X+\mu _0\frac{(1+\lambda )a'}{Z}+(P_{r0}-P_{\phi 0})Y+H_5}{\frac{(1-\lambda ^2+\lambda Z)}{(1-\lambda )Z}J'+\frac{1+\lambda }{Z}\left( \frac{Z_{R0}R'_0}{Z}+\frac{1}{r}\right) J}, \end{aligned}$$
(57)

where \(H_{2N}\), \(H_{0N}^{(p)}\), and \(H_{1N}^{(p)}\) are the terms of \(H_2\), \(H_0^{(p)}\) and \(H_1^{(p)}\), respectively, that belong to the Newtonian approximation, and

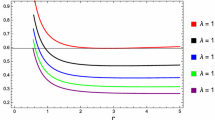
$$\begin{aligned} U= & {} e'+\frac{e}{r}-\frac{1}{Z}\{Z_{R_0}(e'-bR_0)+eZ_{R_0R_0}R'_0\}+\frac{b}{r^{3}},\\ V= & {} \frac{eZ_{R_0}}{Z(1-\lambda )}\left\{ \left( 2\lambda -\frac{1-\lambda ^{2}+2\lambda Z}{Z}\right) P'_{r0}\right. \\&+\left. \left( \lambda -\frac{\lambda -\lambda ^{2}+\lambda Z}{Z}\right) \mu '_0\right\} ,\\ W= & {} \frac{\mu _0(\lambda -1)}{1-\lambda +\lambda Z}\left\{ eZ_{R_0}+(1+\lambda )\left( b+\frac{\bar{c}}{r}\right) \right\} ,\nonumber \\ X= & {} \frac{1}{Z^{2}}\left( e'Z_{R_0}+eZ_{R_0R_0}R'_0-\frac{2eZ_{R_0}^{2}R'_0}{Z}\right) ,\\ Y= & {} \frac{1+\lambda }{Z}\left\{ \left( \frac{\bar{c}}{r}\right) '-\frac{eZ_{R_0}}{Zr}\right\} ,\nonumber \\ J= & {} P_{r0}\frac{1-\lambda ^{2}}{1-\lambda +\lambda Z}\left( b+\frac{\bar{c}}{r}\right) . \end{aligned}$$

The above condition describes the stability range of gravitating sources. All terms mentioned in the above inequality are presumed in a way that whole expression on right side of the adiabatic index \(\Gamma \) remains positive. For the maintenance of the positivity, the following constraints must be satisfied:

$$\begin{aligned} eZ_{R_0R_0}R'_0<Z_{R_0}(bR_0-e'),\quad \left( \frac{\bar{c}}{r}\right) '>\frac{eZ_{R_0}}{Zr},\end{aligned}$$
(58)
$$\begin{aligned} e'Z_{R_0}+eZ_{R_0R_0}R'_0>\frac{2eZ_{R_0}^2R'_0}{Z},\quad p_{r0}>p_{\phi 0}. \end{aligned}$$
(59)

3.2 Post-Newtonian regime

In the post-Newtonian approximation, we choose

$$\begin{aligned} A_0=1-\frac{m_0}{r}\quad and\quad B_0=1+\frac{m_0}{r},\quad then\\ \frac{A'_0}{A_0}=\frac{m_0}{r(r-m_0)},\quad \frac{B'_0}{B_0}=-\frac{m_0}{r(r+m_0)}. \end{aligned}$$

Substitution of the above relations in Eq. (51) leads to the following inequality:

$$\begin{aligned} \Gamma< & {} \frac{H_4H_{8}+V+\frac{\lambda -\lambda ^{2}+\lambda Z}{(\lambda -1)Z}H'_6+\left( \frac{\lambda }{Zr}+\frac{\lambda }{Z^{2}}Z_{R_0}R'_0+\frac{m_0}{r(r-m_0)}\times \frac{1+\lambda }{Z}\right) H_6}{\frac{1-\lambda ^{2}+2\lambda Z}{Z(1-\lambda )}\left( \frac{P_{r0}}{\mu _0+P_{r0}}H_6\right) '+\frac{1+\lambda }{Z}\left( \frac{Z_{R0}R'_0}{Z}+\frac{m_0}{r(r-m_0)} +\frac{1}{r}\right) \left( \frac{P_{r0}}{\mu _0+P_{r0}}H_6\right) }\nonumber \\&+\frac{\left( (1+\lambda )P_{r0}+\lambda \mu _0\right) X+H_7-\frac{1+\lambda }{Zr}H_{2(pN)}+H_{1(pN)}^{(p)}}{\frac{1-\lambda ^{2}+2\lambda Z}{Z(1-\lambda )}\left( \frac{P_{r0}}{\mu _0+P_{r0}}H_6\right) '+\frac{1+\lambda }{Z}\left( \frac{Z_{R0}R'_0}{Z}+\frac{m_0}{r(r-m_0)} +\frac{1}{r}\right) \left( \frac{P_{r0}}{\mu _0+P_{r0}}H_6\right) }, \end{aligned}$$
(60)

where \(H_{2pN}\), \(H_{0pN}^{(p)}\), and \(H_{1pN}^{(p)}\) are the terms of \(H_2\), \(H_0^{(p)}\), and \(H_1^{(p)}\) that lie in the post-Newtonian era. We have

$$\begin{aligned} H_6= & {} \left( \frac{\lambda -1}{1{-}\lambda +\lambda Z}\right) \left( \mu _0 eZ_{R_0}{+}\frac{rb}{r+m_0}(1{+}\lambda )(\mu _0{+}P_{r0})\right. \\&+\left. \frac{\bar{c}}{r}(1+\lambda )(\mu _0+P_{\phi 0})+\frac{\lambda eZ}{2(1-\lambda )}+ZH_{0(pN)}^{(P)}\right) ,\\ H_7= & {} \frac{1{+}\lambda }{Z}\left[ (\mu _0{+}P_{r0})\left( (\frac{ra}{r-m_0})'{-}\frac{eZ_{R_0}}{Z}{\times }\frac{m_0}{r(r-m_0)}\right) \right. \\&+\left. (P_{r0} {-}P_{\phi 0})\left( (\frac{\bar{c}}{r})'{-}\frac{eZ_{R_0}}{Zr}\right) \right] {+}\frac{\lambda e'}{2(1-\lambda )},\\ H_8= & {} \frac{r^2}{(r-m_0)^2}\left[ e'+\frac{e}{r}+\frac{b}{r^2(r+m_0)}\right. \\&-\left. \left\{ \frac{Z_{R_0}}{Z}\left( e'-e\frac{m_0}{r(r-m_0)} -\frac{br}{r-m_0}R'_0\right) \right. \right. \\&+\left. \left. \frac{Z_{R_0R_0}eR'_0}{Z}\right\} -\frac{em_0}{r(r-m_0)}\right] . \end{aligned}$$

Again, to maintain the positivity of the right side of the inequality (60), the following conditions must be fulfilled:

$$\begin{aligned}&\left( \frac{ra}{r-m_0}\right) '>\frac{eZ_{R_0}}{Z}\times \frac{m_0}{r(r-m_0)},\quad \left( \frac{\bar{c}}{r}\right) '>\frac{eZ_{R_0}}{Zr},\\&e'+\frac{e}{r}+\frac{b}{r^2(r+m_0)}>\frac{Z_{R_0}}{Z}\nonumber \\&\quad \times \left( e'-e\frac{m_0}{r(r-m_0)}-\frac{br}{r-m_0}R'_0\right) \\&\quad +\frac{Z_{R_0R_0}eR'_0}{Z} -\frac{em_0}{r(r-m_0)}. \end{aligned}$$

4 Summary

The cosmological observations from recent data-sets like the cosmic microwave background, clustering spectrum, weak lensing, Planck data, and supernovae type Ia revealed that the universe is expanding at an accelerated rate. Alternative gravitational theories have become a paradigm in the description of the gravitational interaction and its impact on the expansion of the universe. The alternative theories of gravity can be categorized as theories with extra gravitational fields, extra spatial dimension, and higher derivatives. A large number of mechanisms have been presented to interpret the accelerated expansion of the universe based on improvement of Einstein theory.

The f(R, T) theory of gravity, being a generalization of f(R) gravity, representing alternative gravitation theory constituting non-minimal curvature matter coupling has gained increasing attention in recent years. Its gravitational action includes an additional scalar force (trace of energy-momentum tensor) together with the function f(R) of the Ricci scalar, which further modifies the gravitational interaction. A scalar force is always appealing because it can reduce the time of collapse, so the addition of an extra scalar term of T in a modified Einstein–Hilbert action provides a better description of the so-called exotic matter.

The exploration of the instability range in extended theories of gravity provides insight of gravitational interaction in the current era, which is one of expansion of the universe. In this paper, we have studied the impact of the f(R, T) model on the dynamical instability of cylindrically symmetric objects. The selection of the f(R, T) model for dynamical analysis is restricted to the form \(f(R,T)=f(R)+\lambda T\), where \(\lambda \) is an arbitrary positive constant. The f(R, T) model under consideration constitutes a combination of the extended Starobinsky model i.e., \(f(R)=R+\alpha R^2+\gamma R^n\) for positive real values of \(\alpha \), \(\gamma \) and the trace T, which provides a suitable replacement for dark source entities. The gravitating system chosen for analysis is assumed to be filled with an anisotropic fluid in the interior.

For dynamical analysis, we have started with the construction of modified field equations within the framework of f(R, T) gravity for cylindrically symmetric gravitating system evolved under locally anisotropic background. A covariant divergence of the effective energy-momentum tensor is taken into account to arrive at dynamical equations. The gravitating field equations describe a set of non-linear differential equations which are complex enough and their solutions are still unknown. That is why we have chosen a perturbation approach to counter this problem and considered the perturbation scheme proposed by Herrera et al. [53]. The system is assumed to be static at the initial stage, then gradually enters into the non-static phase depending on the radial and time coordinates constituting the same time dependence of the parameter.

In order to count with the issue of the instability in a gravitating system, one may utilize numerical techniques or employ an analytic approach. Highly complicated non-linear modified field equations can be tackled essentially by implementing some numerical techniques and this is of great importance in numerical relativity. The numerical design of a Jeans analysis devised in [54,55,56] can be adopted for gaining deep insight in the dynamical analysis of a particular gravitating source. However, a numerical analysis may be confined to some particular model with some specific ranges of physical parameters and so these turn out to be model dependent. We have chosen an analytic approach to discuss the dynamics of a stellar evolution for a class of models and presented general results of the gravitational interaction.

A linear perturbation has been applied to the field equations and dynamical equations. The expressions for the energy density \(\bar{\mu }\) and principal stresses \(\bar{P}_\phi \) and \(\bar{P_z}\) are obtained from perturbed forms of the dynamical equation (20) and field equations (13) and (14), respectively, while \(\bar{P_r}\) is extracted from a Harrison–Wheeler type equation. Perturbed dynamical equations together with perturbed differential equations lead to an evolution equation that provides a comprehensive description of the celestial body of cylindrical shape for a dynamical analysis. An analytic description of evolving stars can be carried through with an estimation of the evolution equation constituting an expression for the adiabatic index \(\Gamma \). The adiabatic index describes the stiffness in the fluid distribution which is helpful in the estimation of the instability eras for gravitational bodies in the presence of the expansion scalar.

It is significant to mention here that the results of any gravitational theory must meet with the well-tested results of Newtonian (N) and post-Newtonian (pN) theories. Although the gravitational field is thought to be weak in the N and pN regimes, testing the outcome in these eras is of fundamental importance. Corrections to the N and pN regimes can be settled in f(R, T) gravity that must be negligible or coincide with N and pN approximations. The adiabatic index \(\Gamma \) requires positivity of the terms for the maintenance of stability of the celestial objects in both the N and the pN regimes. Physical parameters involved in the evolution equation are constrained to meet with the requirement of positive terms in expression for \(\Gamma \) discussed in Sects. 3.1 and 3.2; see Sect. 3.

It is observed that the terms appearing in \(\Gamma \) are less constrained in the weak field regimes than the terms that appear in the case of f(R) gravity; thus f(R, T) gravity represents a wider class of viable models. Thus corrections to GR can be made by assuming \(\alpha \rightarrow {0}\), \(\gamma \rightarrow {0}\), \(\lambda \rightarrow {0}\), while only \(\lambda \rightarrow {0}\) leads to the correction of f(R) gravity. The local isotropy can be established by considering pressures to be the same in the r, \(\phi \), and z directions.