Low-lying charmed and charmed-strange baryon states

Abstract

In this work, we systematically study the mass spectra and strong decays of 1P and 2S charmed and charmed-strange baryons in the framework of non-relativistic constituent quark models. With the light quark cluster–heavy quark picture, the masses are simply calculated by a potential model. The strong decays are studied by the Eichten–Hill–Quigg decay formula. Masses and decay properties of the well-established 1S and 1P states can be reproduced by our method. $\Sigma _c(2800)^{0,+,++}$ can be assigned as a $\Sigma _{c2}(3/2^-)$ or $\Sigma _{c2}(5/2^-)$ state. We prefer to interpret the signal $\Sigma _c(2850)^0$ as a $2S(1/2^+)$ state although at present we cannot thoroughly exclude the possibility that this is the same state as $\Sigma _c(2800)^0$. $\Lambda _c(2765)^+$ or $\Sigma _c(2765)^+$ could be explained as the $\Lambda _c^+(2S)$ state or $\Sigma ^+_{c1}(1/2^-)$ state, respectively. We propose to measure the branching ratio of $\mathcal {B}(\Sigma _c(2455)\pi )/\mathcal {B}(\Sigma _c(2520)\pi )$ in the future, which may disentangle the puzzle of this state. Our results support $\Xi _c(2980)^{0,+}$ as the first radial excited state of $\Xi _c(2470)^{0,+}$ with $J^P=1/2^+$. The assignment of $\Xi _c(2930)^0$ is analogous to $\Sigma _c(2800)^{0,+,++}$, i.e., a $\Xi ^\prime _{c2}(3/2^-)$ or $\Xi ^\prime _{c2}(5/2^-)$ state. In addition, we predict some typical ratios among partial decay widths, which are valuable for experimental search for these missing charmed and charmed-strange baryons.

1 Introduction

At present, the particle data group (PDG) lists nine charmed and ten charmed-strange baryons [1]. They are $\Lambda _c(2286)^+$, $\Lambda _c(2595)^+$, $\Lambda _c(2625)^+$, $\Lambda _c(2765)^+$ (or $\Sigma _c(2765)^+$), $\Lambda _c(2880)^+$, $\Lambda _c(2940)^+$, $\Sigma _c(2800)^{0,+,++}$, $\Sigma _c(2455)^{0,+,++}$, $\Sigma _c(2520)^{0,+,++}$, $\Xi _c(2470)^{0,+}$, $\Xi ^{\prime }_c(2580)^{0,+}$, $\Xi ^\prime _c(2645)^{0,+}$, $\Xi _c(2790)^{0,+}$, $\Xi _c(2815)^{0,+}$, $\Xi ^{(\prime )}_c(2930)^0$, $\Xi _c(2980)^{0,+}$, $\Xi _c(3055)^{0,+}$, $\Xi _c(3080)^{0,+}$, and $\Xi ^{(\prime )}_c(3123)^+$. For brevity, we call these charmed and charmed-strange baryons just charmed baryons in the following. Among these observed states, some new measurements have been performed by experiments in the past several years. The masses and widths of $\Sigma _c(2455)^{0,+,++}$, $\Sigma _c(2520)^{0,+,++}$, $\Lambda _c(2595)^+$, and $\Lambda _c(2625)^+$ have been measured with significantly small uncertainties with the efforts of CDF [2] and Belle [3]. Very recently, the Belle Collaboration updated the measurements of $\Xi ^{\prime }_c(2580)^{0,+}$, $\Xi ^\prime _c(2645)^{0,+}$, $\Xi _c(2790)^{0,+}$, $\Xi _c(2815)^{0,+}$, and $\Xi _c(2980)^{0,+}$ [4]. On the other hand, new decay modes for the higher excited charmed baryon states have been found by experiment. For instance, the decay channel of $\Lambda D^+$ was first found for $\Xi _c(3055)^+$ and $\Xi _c(3080)^+$, and the following ratios of branching fractions were first reported by Belle several months ago [5]:

$$\begin{aligned} \frac{\mathcal {B}(\Xi _c(3055)^+\rightarrow \Lambda D^+)}{\mathcal {B}(\Xi _c(3055)^+\rightarrow \Sigma _c(2455)^{++}K^-)}=5.09\pm 1.01\pm 0.76, \end{aligned}$$

$$\begin{aligned} \frac{\mathcal {B}(\Xi _c(3080)^+\rightarrow \Lambda D^+)}{\mathcal {B}(\Xi _c(3080)^+\rightarrow \Sigma _c(2455)^{++}K^-)}=1.29\pm 0.30\pm 0.15, \end{aligned}$$

and

$$\begin{aligned} \frac{\mathcal {B}(\Xi _c(3080)^+\rightarrow \Sigma _c(2520)^{++}K^-)}{\mathcal {B}(\Xi _c(3055)^+\rightarrow \Sigma _c(2455)^{++}K^-)}=1.07\pm 0.27\pm 0.01, \end{aligned}$$

where the uncertainties are statistical and systematic. Obviously, these new measurements are very useful to understand the nature of these excited charmed baryon states.

Theoretically, the charmed baryons which contain one heavy quark and two light quarks occupy a particular position in the baryon physics. Since the chiral symmetry and heavy quark symmetry (HQS) can provide some qualitative insight into the dynamics of charmed baryons, the investigation of charmed baryons should be more helpful for improving our understanding of the confinement mechanism. The spectroscopy of charmed baryons has been investigated in various models. So far, the several kinds of quark potential models [6,7,8,9,10], the relativistic flux tube (RFT) model [11, 12], the coupled channel model [13], the QCD sum rule [14,15,16], and the Regge phenomenology [17] have been applied to study the mass spectra of excited charmed baryons, and so did lattice QCD [18, 19]. The strong decay behaviors of charmed baryons have been studied by several methods, such as the heavy hadron chiral perturbation theory (HHChPT) [20, 21], the chiral quark model [22, 23], the $^3P_0$ model [24], and a non-relativistic quark model [25]. The decays of 1P $\Lambda _c$ and $\Xi _c$ baryons have also been investigated by a light front quark model [26, 27], a relativistic three-quark model [28], and the QCD sum rule [29].

Although many experimental and theoretical efforts have been made for the research of charmed baryons, most of the 1P and 2S charmed baryons are not yet established. Several candidates, including $\Lambda _c(2765)^+$, $\Sigma _c(2800)^{0,+,++}$, $\Xi _c(2930)^0$, and $\Xi _c(2980)^{0,+}$ are still in controversy. $\Lambda _c(2765)^+$ was first observed by the CLEO Collaboration in the decay channel of $\Lambda _c(2765)^+\rightarrow \Lambda _c^+\pi ^+\pi ^-$ [30], and confirmed by Belle in the $\Sigma _c(2455)\pi$ mode [31, 32]. Because both $\Lambda _c^+$ and $\Sigma _c^+$ excitations can decay through $\Lambda _c^+\pi ^+\pi ^-$ and $\Sigma _c(2455)\pi$, we even do not know whether the observed charmed baryon signal around 2765 MeV is the $\Lambda _c^+$ or $\Sigma _c^+$ state, or their overlapping structure [33]. In the $e^+e^-$ annihilation process, an isotriplet state, $\Sigma _c(2800)^{0,+,++}$, was observed by Belle in the channel of $\Lambda _c^+\pi$, and it was tentatively identified as the $\Sigma _{c2}$ state with $J^P=3/2^-$ [34]. Interestingly, another neutral resonance was later found by BaBar in the process of $B^-\rightarrow \Sigma _c^{*0}\bar{p}\rightarrow \Lambda _c^+\pi ^-\bar{p}$ with the mass $2846\pm 8\pm 10$ MeV and decay width $86^{+33}_{-22}$ MeV [35]. The higher mass and the weak evidence of $J=1/2$ indicate that the signal observed by BaBar might be different from the Belle observation. In this paper, we denote the signal discovered by BaBar by $\Sigma _c(2850)^0$. $\Xi _c(2930)^0$, which was only seen by BaBar in the decay mode $\Lambda ^+_cK^-$ [36], still needs more confirmation. $\Xi _c(2980)^{0,+}$ was first reported by Belle in the channels $\Lambda _c^+K^-\pi ^+$ and $\Lambda _c^+K_S^0\pi ^-$ [37], and was later confirmed by Belle [4, 38] and BaBar [39] in the channels $\Xi ^\prime _c(2580)\pi$, $\Xi _c(2645)\pi$ and $\Sigma _c(2455)K$, respectively. However, the decay widths reported by Refs. [4, 37,38,39] were quite different from each other. More experimental information as regards the charmed baryons can be found in Refs. [40,41,42,43].

Obviously, a systematic study of masses and decays is required for these unestablished charmed baryons. More importantly, most of 2S and 1P charmed baryons have not yet been detected by any experiments. Such a research can also help the future experiments to find them. In the present work, we will focus on both the mass spectra and the strong decays of low-lying 1P and 2S charmed baryons. We pay attention to only the charmed baryons inside of which degrees of freedom of two light quarks are frozen. It means that two light quarks are not considered to be excited, neither radially nor orbitally. As illustrated in Ref. [44], these kinds of charmed excitations carry lower-excited energies, which means these excited charmed baryons may more likely be detected by experiments. Fortunately, our results indicate that most of the observed charmed baryons can be accommodated in this way.

The paper is arranged as follows. In Sect. 2, the masses of low-excited charmed baryons are calculated by the non-relativistic quark potential model. In Sect. 3, the Eichten–Hill–Quigg (EHQ) decay formula, which is employed to study the strong decays of excited charmed baryons, is introduced. The properties of low-lying charmed baryon states are fully discussed in Sect. 4. Finally, the paper ends with a conclusion and an outlook. Some detailed calculations and definitions are collected in the appendices.

2 The deduction of mass spectra

2.1 Treating charmed baryon system as a two-body problem

To study the baryon dynamics, one crucial question which should be answered is “What are the relevant degrees of freedom in a baryon?” [45]. In constituent quark models, a baryon system consists of three confined quarks. Thus the dynamics of a baryon resonance is surely more complex than a meson. Due to the HQS, however, the dynamics of charmed baryons could be greatly simplified. The HQS suggests that the couplings between a c quark and two light quarks are weak [46]. Therefore, two light quarks in a charmed baryon could first couple with each other to form a light quark cluster.¹ Then the light quark cluster couples with a charm quark, and a charmed baryon resonance forms. With this assumption, two light quarks have the same status to a c quark, including the average distances to a c quark. In the light cluster–heavy quark picture, the dynamics of heavy baryon can be simplified. In the non-relativistic constituent quark model, the spin-independent part of the Hamiltonian is

$$\begin{aligned} H = \sum \limits _{i=1}^{3}\left( \frac{p_i^2}{2m_i}+m_i\right) + \sum \limits _{i<j}\left( -\frac{2\alpha }{3r_{ij}}+\frac{b}{2}r_{ij}\right) , \end{aligned}$$

(1)

where the Cornell potential [47] is used as a phenomenological confining term. The Jacobi coordinates are usually taken to deal with the three-body problem for baryons. $\rho$, $\lambda$, and R are related to the quark positions by

$$\begin{aligned} \vec {\rho }= & {} \vec {r}_1-\vec {r}_2,~~~~\\ \vec {\lambda }= & {} \frac{m_1\vec {r}_1+m_2\vec {r}_2}{m_1+m_2}-\vec {r}_Q,~~~~\\ \vec {R}= & {} \frac{m_1\vec {r}_1+m_2\vec {r}_2+m_Q\vec {r}_Q}{m_1+m_2+m_Q} , \end{aligned}$$

where the indices, 1, 2, and Q, are for two light quarks and a heavy quark, respectively. The momenta $\vec {p}_\rho$, $\vec {p}_\lambda$ and $\vec {p}_R$, which are conjugate to the Jacobi coordinates above, can be defined easily. Now the spin-independent Hamiltonian becomes

$$\begin{aligned} H= & {} \frac{p^2_\rho }{2m_\rho } + \frac{p^2_\lambda }{2m_\lambda } + \frac{p^2_R}{2M} + M + \left( -\frac{2\alpha }{3r_{12}}+\frac{b}{2}r_{12}\right) \nonumber \\&+ \left( -\frac{2\alpha }{3r_{1Q}}+\frac{b}{2}r_{1Q}\right) + \left( -\frac{2\alpha }{3r_{2Q}}+\frac{b}{2}r_{2Q}\right) , \end{aligned}$$

(2)

where $m_\rho =m_1m_2/(m_1+m_2)$, $m_\lambda =(m_1+m_2)m_Q/M$, and $M=m_1+m_2+m_Q$. According to the definitions above, the relative motion between two light quarks is usually called the $\rho$-mode, while the one between the center of mass of the two light quarks and the heavy quark is called the $\lambda$-mode.

Fig. 1

A single heavy baryon in the light cluster–heavy quark picture. With the SU(3) flavor symmetry, the relation of $\tau =\sqrt{\lambda ^2+\rho ^2/4}$ is obvious

As emphasized above, the average distances to c quark should be equal for two light quarks in a cluster, i.e., $\tau \equiv r_{1Q}=r_{2Q}$ (see Fig. 1). In practice, we should solve the following Schrödinger equation for the mass of a heavy baryon:

$$\begin{aligned}&\left[ -\frac{\nabla _\rho ^2}{2m_\rho }-\frac{\nabla _\lambda ^2}{2m_\lambda }+\left( \frac{b\rho }{2}-\frac{2\alpha }{3\rho }\right) +\left( b\tau -\frac{4\alpha }{3\tau }\right) +C\right] \nonumber \\&\quad \times \quad \psi = E\psi . \end{aligned}$$

(3)

Since the excited mode between two light quarks is not considered in this paper, the light quark cluster can be treated as a block with the antitriplet color structure and peculiar size. Specifically, a color singlet baryon system should be formed as $3_{q_1}\otimes 3_{q_2}\otimes 3_Q\ni \bar{3}_{\mathrm{cl.}}\otimes 3_Q\ni \bar{1}_{\mathrm{Q-cl.}}$. In this way, a heavy baryon could be treated as a quasi-two-body system. In the light quark cluster–heavy quark picture, Isgur has discussed the similarity of dynamics between heavy baryons and heavy–light mesons [48]. It should be stressed that the scenario of a light cluster–heavy quark picture is not contradictory to the one-gluon exchange interaction. Since the color–spin interaction is proportional to the inverse of the quark masses, two light quarks in the heavy-baryon system are expected to strongly couple to each other [49]. Thus, they may develop into a quark cluster. In fact, the existence of a light quark cluster correlations was partly confirmed by the lattice QCD [50] and the Bethe–Salpeter equation [51].

Thus, we expect the light quark cluster to be an effective degree of freedom for a charmed baryon. Since the $\rho$ mode of a cluster is not considered here, the Schrödinger equation (3) is simplified as

$$\begin{aligned} \left( -\frac{\nabla _\lambda ^2}{2m_\lambda }-\frac{4\alpha }{3\tau }+b\tau +C \right) \psi = E\psi . \end{aligned}$$

(4)

2.2 Adopted effective potentials

As a whole, the light quark cluster which occupies an antitriplet color structure interacts with the c quark. Then we would like to substitute $\lambda$ (distance between light cluster and c quark) for $\tau$ (distance between light quark and c quark). To this end, the effective potential [52]

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{conf}}(\lambda )=-\frac{4}{3}\frac{\alpha _s}{\lambda }+b\lambda ^\nu -C_{Qqq'} \end{aligned}$$

(5)

describes the interaction between the cluster and c quark, where $\nu$ is an adjustable parameter. This approximation can greatly decrease the computational complexity. As shown in Tables 2 and 3, the mass spectra given in this way are reasonable for the low-lying excited charmed baryons.

As a two-body problem, we treat the masses of different kinds of clusters as parameters and first fix them before calculating the masses of the low-lying charmed baryons. According to the flavor and spin, the light cluster can be classified into two kinds: one is the “scalar” cluster, and another is the “vector” cluster. Constrained by the Pauli exclusion principle, the total wave function of the light quark cluster should be antisymmetric in the exchange of two quarks. Because the spatial and color parts of this light quark cluster are always symmetric and antisymmetric, respectively, the function $|\mathrm {flavor}\rangle \times |\mathrm {spin}\rangle$ should be symmetric. Therefore, the scalar light quark cluster $[qq]~(S =0)$ is always flavor antisymmetric, and the axial-vector light quark cluster $\{qq\}~(S =1)$ is flavor symmetric. In Jaffe’s terminology [49], the “scalar” and “vector” quark clusters are named the “good” and “bad” quark clusters, respectively. The masses of the “good” light quark cluster [qq] and [qs] are taken from our previous work where $m_{[qq]}$ and $m_{[qs]}$ were fixed as 450 and 630 MeV by the RFT model [11], respectively. Following Jaffe’s method [49], the bad light quark cluster masses can be evaluated by the following relationships:

$$\begin{aligned} \frac{4\times \Sigma _c(2520)+2\times \Sigma _c(2455)}{6}-\Lambda _c(2286)\approx & {} 210~\mathrm {MeV},\\ \frac{4\times \Xi ^*_c(2645)+2\times \Xi '_c(2580)}{6}-\Xi _c(2470)\approx & {} 150~\mathrm {MeV}. \end{aligned}$$

Evidently, the masses of $\{qq\}$ and $\{qs\}$ are about 660 MeV and 780 MeV, respectively. Henceforth, we will call the $\Lambda _c^+$ and $\Xi _c^{0,+}$ baryons the $\mathcal {G}$-type baryons, and $\Sigma _c^{0,+,++}$ and $\Xi _c^{\prime 0,+}$ the $\mathcal {B}$-type baryons for convenience.

Due to an antitriplet color structure, the spin-dependent interactions between light cluster and c quark are expected to be the same as the meson systems. In a constituent quark model [53], the spin-dependent interaction is written as

$$\begin{aligned} H_S = H_{\mathrm{Q-cl.}}^{\mathrm{cont}}+H_{\mathrm{Q-cl.}}^{\mathrm{ten}}+H_{\mathrm{Q-cl.}}^{SO}. \end{aligned}$$

(6)

The color contact interaction $H_{\mathrm{Q-cl.}}^{\mathrm{cont}}$ is usually given by the following form:

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{cont}}=\frac{32\pi }{9}\frac{\alpha _s}{m_Qm_{\mathrm{cl.}}}\tilde{\delta }_{\sigma }(\lambda )\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}, \end{aligned}$$

(7)

where $\vec {S}_Q$ and $\vec {S}_{\mathrm{cl.}}$ refer to the heavy quark and light cluster spins. A Gaussian-smeared function $({\sigma }/\sqrt{\pi })^3e^{-{\sigma }^2\lambda ^2}$ is normally used for $\tilde{\delta }_{\sigma }(\lambda )$ [54]. If the SU(3) flavor symmetry is kept for the charmed baryons, we may modify the color contact interaction as

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{cont}}=\frac{32}{9\sqrt{\pi }}\frac{\alpha _s\sigma ^3}{m_Q}e^{-\sigma ^2\lambda ^2}\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}, \end{aligned}$$

(8)

where the mass of a light quark cluster is just replaced by a unit. This assumption is supported by the mass differences of the 1S $\mathcal {B}$-type charmed baryons,

$$\begin{aligned}&\Sigma _c(2520)^{++}-\Sigma _c(2455)^{++}=64.44^{+0.25}_{-0.24}~\mathrm {MeV},~~~~\\&\Xi _c(2645)^{+}~-\Xi '_c(2580)^{+}=70.2\pm 3.0~\mathrm {MeV},~~~~\\&\Omega _c(2770)^0~-\Omega _c(2695)^0=70.7\pm 2.6~\mathrm {MeV}. \end{aligned}$$

The mass differences shown above are mainly due to the color contact interaction in the quark potential model. Clearly, these values are almost independent of the light quark cluster masses. The color tensor interaction in Eq. (6) is

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{ten}}=\frac{4}{3}\frac{\alpha _s}{m_Qm_{\mathrm{cl.}}}\frac{1}{\lambda ^3}\left( \frac{3\left( \vec {S}_Q\cdot \vec {\lambda }\right) \left( \vec {S}_{\mathrm{cl.}}\cdot \vec {\lambda }\right) }{\lambda ^2}-\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}\right) .\nonumber \\ \end{aligned}$$

(9)

Finally, $H_{\mathrm{Q-cl.}}^{\mathrm{SO}}$ denotes the spin–orbit interaction which contains two terms. One is the color magnetic interaction which arises from one-gluon exchange,

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{SO(cm)}}=\frac{4}{3}\frac{\alpha _s}{\lambda ^3}\left( \frac{\vec {S}\cdot \vec {L}}{m_Qm_{\mathrm{cl.}}}+\frac{\vec {S}_Q\cdot \vec {L}}{m_Q^2}+\frac{\vec {S}_{\mathrm{cl.}}\cdot \vec {L}}{m_{\mathrm{cl.}}^2}\right) , \end{aligned}$$

(10)

where $\vec {S}$ denotes the spin of a baryon, $\vec {S}=\vec {S}_Q+\vec {S}_{\mathrm{cl.}}$. Another spin–orbit interaction is the Thomas-precession term,

$$\begin{aligned} H_{\mathrm{Q-cl.}}^{\mathrm{SO(tp)}}=-\frac{1}{2\lambda }\frac{\partial H_{\mathrm{Q-cl.}}^{\mathrm{conf}}}{\partial \lambda }\left( \frac{\vec {S}_Q\cdot \vec {L}}{m_Q^2}+\frac{\vec {S}_{\mathrm{cl.}}\cdot \vec {L}}{m_{\mathrm{cl.}}^2}\right) . \end{aligned}$$

(11)

To reflect the importance of the heavy quark symmetry, we rewrite the spin-dependent interactions as

$$\begin{aligned} H_S=V_{ss}~\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}+V_1~\vec {S}_{\mathrm{cl.}}\cdot \vec {L}+V_2~\vec {S}_Q\cdot \vec {j}_{\mathrm{cl.}}+V_t~\hat{S}_{12}.\nonumber \\ \end{aligned}$$

(12)

The degrees of freedom of the light quark cluster are characterized by its total angular momentum $\vec {j}_{\mathrm{cl.}}$, i.e., $\vec {j}_{\mathrm{cl.}}=\vec {S}_{\mathrm{cl.}}+\vec {L}$. Obviously, the orbital angular momentum $\vec {L}$ of a charmed baryon in the present picture is defined by the angular momentum between light quark cluster and c quark, i.e., $\vec L=\vec L_\lambda$. The tensor operator is defined as $\hat{S}_{12}=3\left( \vec {S}_Q\cdot \vec {\lambda }\right) \left( \vec {S}_{\mathrm{cl.}}\cdot \vec {\lambda }\right) /\lambda ^2-\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}$.

With the confining term of Eq. (5), the coefficients $V_{ss}$, $V_1$, $V_2$, and $V_t$ in Eq. (12) are defined by

$$\begin{aligned} V_{ss}= & {} \frac{1}{m_Q}\left[ \frac{32\alpha _s}{9\sqrt{\pi }}\sigma ^3e^{-\sigma ^2\lambda ^2}-\frac{1}{m_Q}\left( \frac{2\alpha _s}{3\lambda ^3}-\frac{b\nu }{2}\lambda ^{\nu -2}\right) \right. \nonumber \\&\left. -\frac{4\alpha _s}{3\lambda ^3}\frac{1}{m_{\mathrm{cl.}}}\right] ,~~~~\nonumber \\ V_1= & {} \frac{1}{m_{\mathrm{cl.}}}\left[ \frac{1}{m_{\mathrm{cl.}}}\left( \frac{2\alpha _s}{3\lambda ^3}-\frac{b\nu }{2}\lambda ^{\nu -2}\right) +\frac{4\alpha _s}{3\lambda ^3}\frac{1}{m_{Q}}\right] ,~~~~\nonumber \\ V_2= & {} \frac{1}{m_Q}\left[ \frac{1}{m_Q}\left( \frac{2\alpha _s}{3\lambda ^3}-\frac{b\nu }{2}\lambda ^{\nu -2}\right) +\frac{4\alpha _s}{3\lambda ^3}\frac{1}{m_{\mathrm{cl.}}}\right] ,~~~~\nonumber \\ V_t= & {} \frac{4\alpha _s}{3\lambda ^3}\frac{1}{m_Qm_{\mathrm{cl.}}}. \end{aligned}$$

(13)

2.3 Getting masses of charmed baryons

In our calculation, the following Schrödinger equation is solved for the nS state:

$$\begin{aligned} \left( -\frac{\nabla _\lambda ^2}{2m_\lambda }+H_{\mathrm{Q-cl.}}^{\mathrm{conf}}+H_{\mathrm{Q-cl.}}^{\mathrm{cont}}\right) \Psi =E\Psi . \end{aligned}$$

(14)

The confining and contact terms have been given by Eqs. (5) and (8). For the orbital excitations, all spin-dependent interactions are treated as the leading-order perturbations. Our calculation indicates that the color contact interaction can be ignored for the orbital excitations.

Two bases are employed to extract the mass matrix elements. One is defined by the eigenstates $|S_{\mathrm{cl.}}, L, j_{\mathrm{cl.}}, S_Q, J\rangle$ (jj coupling scheme) and the other is by $|S_{\mathrm{cl.}}, S_Q, S, L, J\rangle$ (LS coupling scheme). The relation between these two bases is

$$\begin{aligned} \begin{array}{ll} |[S_{\mathrm{cl.}}, L]_{j_{\mathrm{cl.}}}, S_Q\rangle _J&{}=\sum \limits _S(-1)^{S_{\mathrm{cl.}}+S_Q+L+J}\\ &{}\quad \times \sqrt{(2J_{\mathrm{cl.}}+1)(2S+1)}\\ &{}\quad \times \left\{ \begin{array}{ccc} s_{\mathrm{cl.}} &{} L &{} j_{\mathrm{cl.}}\\ J &{} S_Q &{} S\\ \end{array} \right\} |[S_{\mathrm{cl.}}, S_Q]_S, L\rangle _J. \end{array} \end{aligned}$$

(15)

Due to $S_{\mathrm{cl.}}=0$, only $V_2~\vec {S}_Q\cdot \vec {j}_{\mathrm{cl.}}$ contributes to the masses of $\mathcal {G}$-type charmed baryons. With a bad light quark cluster, however, $\mathcal {B}$-type charmed baryons have more complicated splitting structures. Within the framework of the heavy quark effective theory, the spin of an axial-vector light quark cluster, $S_{\mathrm{cl.}}$, first couples with the orbital angular momentum L. As illustrated in Fig. 2, in the heavy quark limit $m_c\rightarrow \infty$, there are only three states which are characterized by $j_{\mathrm{cl.}}$ for 1P charmed baryons. When the heavy quark spin $S_Q$ couples with $j_{\mathrm{cl.}}$, the degeneracy is resolved and the five states appear. These are two $J^P=1/2^-$, two $J^P=3/2^-$, and one $J^P=5/2^-$ states. Lastly, the states with the same $J^P$ mix with each other by the interactions of $V_{ss}~\vec {S}_Q\cdot \vec {S}_{\mathrm{cl.}}$ and $V_t~\hat{S}_{12}$, and physical states are formed.

Fig. 2

A schematic diagram for the splittings of p-wave $\Sigma _c$ and $\Xi '_c$. Here $\vec j_l=\vec L+\vec j_{\mathrm{cl.}}$ and subindices $\ell$ and h of the last column mean low and high states in mass after including $\tilde{V}_{ss}$ and $\tilde{V}_t$ interactions

We now turn to a calculation of the mass matrix in the jj coupling scheme. For 1P states with $J^P=1/2^-$, the mass matrix is given by

$$\begin{aligned} \langle \Phi _{1/2}\mid H_S\mid \Phi _{1/2}\rangle =\left( \begin{array}{ccc} -2V_1-4V_t &{}\quad \frac{V_{ss}-4V_t}{\sqrt{2}}\\ \frac{V_{ss}-4V_t}{\sqrt{2}} &{}\quad -V_1-V_2-\frac{V_{ss}}{2}-2V_t \\ \end{array} \right) . \end{aligned}$$

Similarly, for two states with $J^P=3/2^-$,

$$\begin{aligned} \begin{array}{ll} &{}\langle \Phi _{3/2} \mid H_S\mid \Phi _{3/2}\rangle \\ &{}\quad =\left( \begin{array}{ccc} -V_1+\frac{V_2}{2}+\frac{V_{ss}}{4}+4V_t &{}\quad \frac{5V_{ss}+16V_t}{4\sqrt{5}}\\ \frac{5V_{ss}+16V_t}{4\sqrt{5}} &{}\quad V_1-\frac{3V_2}{2}-\frac{3V_{ss}}{4}+\frac{4V_t}{5} \\ \end{array} \right) . \end{array} \end{aligned}$$

For the $J^P=5/2^-$ state,

$$\begin{aligned}&\langle j_l=2, J^P=5/2^- \mid H_S\mid j_l=2, J^P=5/2^-\rangle \\&\quad =V_1+V_2+\frac{1}{2}V_{ss}-\frac{6}{5}V_{t}. \end{aligned}$$

In the following, we denote $|S_{\mathrm{cl.}}, L, j_{\mathrm{cl.}}, S_Q, J\rangle$ as $|j_{\mathrm{cl.}}, J^P\rangle$ for brevity. Then the notations $\mid \Phi _{1/2}\rangle$ and $\mid \Phi _{3/2}\rangle$ appearing above are defined by

$$\begin{aligned} \begin{array}{l} \mid \Phi _J\rangle =\left( \begin{array}{cc} \mid j_l=J-1/2, J^P\rangle \\ \mid j_l=J+1/2, J^P\rangle \\ \end{array} \right) . \end{array} \end{aligned}$$

The mass matrix of 1D states can also be obtained by the similar procedure. As shown above, there are seven parameters in the non-relativistic quark potential model, which are $m_Q$, $m_{\mathrm{cl.}}$, b, $\alpha$, $\gamma$, $\nu$, and $C_{Qqq'}$. All values of parameters are listed in Table 1. If the SU(3) flavor symmetry is taken into account for the charmed and charmed-strange baryons, the dynamics of $\Lambda _c^+$ states should be like $\Xi _c$. The case of $\Sigma _c$ and $\Xi '_c$ is alike. Accordingly, the same value of $\gamma$ is selected for the $\mathcal {G}$-type charmed baryons, as well as the case of $\mathcal {B}$-type.

Table 1 Values of the parameters of the non-relativistic quark potential model. The unit of b is GeV$^{\nu +1}$ which varies depending on each value of $\nu$

We have adopted the typical values in the quark potential models for $m_c$, b, $\alpha$, and $\nu$ (see Table 1). It is an effective method to investigate charmed baryons in the heavy quark–light quark cluster picture. We do not expect the values of $\nu$ to be the same for $\mathcal {G}$-type and $\mathcal {B}$-type baryons. Here, $\nu$ of $\Lambda _c^+/\Xi _c$ is slightly larger than $\Sigma _c/\Xi '_c$. The predicted masses of the low-excited charmed baryons are collected in Tables 2 and 3.

Table 2 Predicted masses for $\Lambda _c^+$ and $\Xi _c$ states of ours and other approaches in Refs. [10, 11, 56, 57] compared to experimental data [1] (in MeV)

Table 3 Predicted masses for $\Sigma _c$ and $\Xi '_c$ states of ours and other approaches in Refs. [9, 10, 56, 58] compared to experimental data [1] (in MeV)

As mentioned earlier, the nonzero off-diagonal elements in mass matrices of $\langle \Phi _{1/2}\mid H_S\mid \Phi _{1/2}\rangle$ and $\langle \Phi _{3/2}\mid H_S\mid \Phi _{3/2}\rangle$ cause the mixing between two states with the same $J^P$ but different $j_{cl.}$. However, the mechanism of mixing effects in hadron physics is still unclear. In principle, a physical hadron state with a specific $J^P$ comprises all possible Fock states with the same total spin and parity. As the most famous member of the XYZ family, X(3872) may be explained as a mixture of charmonium and the molecular state with $J^{PC}=1^{++}$ [55]. Here we take the $|j_{cl.}, J^P\rangle$ basis to describe the mixing for the $\mathcal {B}$-type baryons. Then two physical states characterized by different masses can be denoted

$$\begin{aligned} \begin{array}{ll} \left( \begin{array}{c} |\mathrm{High}, J^P\rangle \\ |\mathrm{Low}, J^P\rangle \\ \end{array} \right) &{}=\left( \begin{array}{cc} ~\cos \phi &{}\quad \sin \phi \\ -\sin \phi &{}\quad \cos \phi \\ \end{array} \right) \left( \begin{array}{c} |J-1/2, J^P\rangle \\ |J+1/2, J^P\rangle \\ \end{array} \right) . \end{array}\nonumber \\ \end{aligned}$$

(16)

For example, two 1P $\Sigma _c$ states with $J^P=1/2^-$ can be represented as

$$\begin{aligned} \begin{array}{ll} \left( \begin{array}{c} \Sigma _c(2765)\\ \Sigma _c(2702)\\ \end{array} \right) &{}=\left( \begin{array}{cc} ~\cos 125.4^\circ &{}\quad \sin 125.4^\circ \\ -\sin 125.4^\circ &{}\quad \cos 125.4^\circ \\ \end{array} \right) \\ &{}\quad \times \left( \begin{array}{c} |0, 1/2^-\rangle \\ |1, 1/2^-\rangle \\ \end{array} \right) . \end{array} \end{aligned}$$

(17)

Here we have denoted the physical states by their masses (see Table 3). The mixing angles for other states in Table 3 with the same $J^P$ are listed in Table 4.

Our results of the mixing angles in Table 4 indicate that the heavier $1/2^-$ state, $\Sigma _c(2765)$, is dominated by a $|1, 1/2^-\rangle$ component, while $\Sigma _c(2702)$ is dominated by a $|0, 1/2^-\rangle$ component. For two $3/2^-$ states, the light $\Sigma _c(2785)$ is dominated by $|2, 1/2^-\rangle$, and the heavy $\Sigma _c(2798)$ by $|1, 1/2^-\rangle$. The mixing of 2P states is similar to the 1P states. For the 1D states, one notices that both $3/2^+$ and $5/2^+$, with heavier masses, are dominated by smaller $j_{\mathrm{cl.}}$ components.

Table 4 The mixing angles for the 1P, 2P, and 1D $\Sigma _c/\Xi '_c$ states

The uncertainty may exist in the mixing angles. Firstly, the loop corrections to the spin-dependent one-gluon-exchange potential may be important for the heavy–light hadrons. As an example, the lower mass of $D_s(2317)^\pm$ compared with the old calculations [53] can be well explained by the corrected spin-dependent potential [59, 60]. If we use this type of potential in our calculation, of course, the mixing angle will change. Secondly, the mixing angles depend on the parameters. Thirdly, there are other mechanisms, e.g., hadron loop effects [61], which may contribute to the mixing phenomenon in hadron physics. Anyway, we expect that the mixing angles in Table 4 reflect the main features of the mixing states. Due to the uncertainties of the mixing angles, however, we ignore the mixing effects as the first step to the study of the decays of charmed excitations in the next subsection. Obviously, it is a good approximation only when the mixing effects are not large. Fortunately, this crude procedure is partially supported by the former analysis of charmed mesons [62,63,64]. If the decay properties obtained in this way describe the principal characteristics of the mixing states, the angles obtained by the potential model may be overestimated.

2.4 Simple harmonic oscillator (SHO) $\beta$ values

In the next section, the Okubo–Zweig–Iizuka (OZI) allowed decays will be calculated for the 1P and 2S charmed baryons where the SHO wave functions are used to evaluate the transition factors via the $^3P_0$ model. We will also discuss the mixing effects for the decays of the relevant states. Following the method of Ref. [65], all values of the SHO wave function scale, denoted $\beta$ in the following, are calculated (see Table 5). The values of $\beta$ reflect the distances between the light quark cluster and the c quark.

Table 5 The meson effective $\beta$ values in GeV

In our calculation of strong decays, we will consider the structures of light diquarks. What is more important is that the possible final states of an excited charmed baryon may contain a light flavor meson, a charmed meson, a light flavor baryon, e.g., $\pi$, K, D, p, and $\Lambda$. For the $\beta$ of these hadrons, the following potential will be used:

(18)

where

Here, the parameters $\alpha _s$ and b are taken as 0.45 and 0.145 GeV$^{\nu +1}$ as in Table 1, respectively. To reproduce the masses of the light quark clusters in Table 1, the masses of u / d, s are fixed as 0.195 and 0.380 GeV. While $\sigma$ and C are treated as adjustable parameters, the masses of the $\pi /\rho$, $K/K^*$, $D/D^*$, $p/\Delta$, and $\Lambda$ families are fitted with experimental data. Meanwhile, the values of $\beta$ for the corresponding states are also obtained; they are collected in Table 6.

Table 6 The effective $\beta$ values in GeV for the light quark cluster and various hadrons (the second row). The values of $\sigma$ and C are given in the square brackets for various hadron structures (the third row)

Before ending this section, we briefly summarize the complicated deduction presented here. Firstly, the dynamics of heavy baryon is simplified as a two-body system when the symmetric configuration is considered. Secondly, the mass matrices were calculated in the jj coupling scheme. By solving the Schrödinger equation, we obtain the mass spectra and mixing angles for the relevant states. For estimating the two-body strong decays in the next section, finally, we also present the values of the SHO wave function scale for all initial and final states.

3 Strong decays

In this section, we will use the formula provided by Eichten, Hill, and Quigg (EHQ) [66] to extract the decay widths of excited charmed baryons. Since the dynamical behavior of the heavy–light hadrons is governed by the light degrees of freedom in the limit of heavy quark symmetry, a doublet formed by two states with the same ${j}_{\mathrm{cl.}}$ but different J shall have similar decay properties. More specifically, the transitions between two doublets should be determined by a single amplitude which is proportional to the products of four Clebsch–Gordan coefficients [46]. Some typical ratios of excited charmed baryons with negative parity were predicted by this law [46]. Later, a more concise formula (the EHQ formula) was proposed for the widths of heavy–light mesons [66]. The EHQ formula has been applied systematically to the decays of excited open-charm mesons [62,63,64]. Recently, the EHQ formula has been extended to the study of the decay properties of 1D $\Lambda _c$ and $\Xi _c$ states [11].

Fig. 3

The two topological diagrams for an excited charmed baryon A decaying into the final states B and C. The brown line 3 denotes a charm quark

For the charmed baryons, the EHQ formula can be written as

$$\begin{aligned} \Gamma ^{A\rightarrow BC}_{j_C,\ell } = \xi \,\left( \mathcal {C}^{s_Q,j_B,J_B}_{j_C,j_A,J_A}\right) ^2\left| \mathcal {M}^{j_A,j_B}_{j_C,\ell }(q)\right| ^2 \,q^{2\ell +1}\, e^{-q^2/\tilde{\beta }^2},\nonumber \\ \end{aligned}$$

(20)

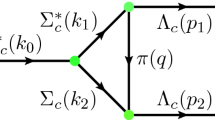
where $\xi$ is the flavor factor given in Table 13 in Appendix B. $q=|\vec q|$ denotes the three-momentum of a final state in the rest frame of an initial state. A and B represent the initial and final heavy–light hadrons, respectively. C denotes the light flavor hadron (see Fig. 3). The explicit expression of $\tilde{\beta }$ is given in Eq. (A.11) in Appendix A. In addition, $\mathcal {C}^{s_Q,j_B,J_B}_{j_C,j_A,J_A}$ is a normalized coefficient given by the following equation:

$$\begin{aligned} \begin{array}{ll} \mathcal {C}^{s_Q,j_B,J_B}_{j_C,j_A,J_A}&{}=(-1)^{J_A+j_B+j_C+s_Q}~\sqrt{(2j_A+1)(2J_B+1)}\\ &{}\quad \times \left\{ \begin{array}{ccc} s_Q &{} j_B &{} J_B\\ j_C &{} J_A &{} j_A\\ \end{array} \right\} , \end{array} \end{aligned}$$

(21)

where $\vec {j}_C \equiv \vec {s}_C + \vec {\ell }$. The symbols $s_C$ and $\ell$ represent the spin of the light hadron C and the orbital angular momentum relative to B, respectively. The transition factors $\mathcal {M}^{j_A,j_B}_{j_C,\ell }(q)$ involved in the concrete dynamics can only be calculated by various phenomenological models. For the decays of heavy–light mesons, transition factors have been calculated by the relativistic chiral quark model [67] and the $^3P_0$ model [62, 64, 68]. In our work, we will employ the $^3P_0$ model [69,70,71] to obtain the transition factors. More details of an estimate of the transition factors are given in Appendix A.

4 Discussion

4.1 Experimentally well-established 1S and 1P states

Table 7 The masses and widths (in units of MeV) of $\Sigma _c(2455)^{++}$ and $\Sigma _c(2520)^{++}$ measured by CDF [2] and Belle [3]

At present, all the ground states and 1P $\mathcal {G}$-type charmed states have been experimentally established [1]. These states have been observed, at least, by two different collaborations, and their properties including masses and decays have been well determined. With good precision, the strong decays of these states provide a crucial test of our method.

Among the 1S charmed baryons, the measurements of $\Sigma _c(2455)$ and $\Sigma _c(2520)$ have been largely improved [2, 3] (see Table 7). In our calculation, the mass and decay width of $\Sigma _c(2520)^{++}$ measured by CDF will be taken as input data to fix the constant $\gamma$ peculiar to the $^3P_0$ model. With the transition factor for the process $\Sigma _c(2520)\rightarrow \Lambda _c(2286)+\pi$ [see Eq. (A.12) in Appendix A], the value of $\gamma$ is fixed as 1.296.²

As shown in Tables 8 and 9, the predicted widths of other ground and $1P\, \mathcal {G}$-type charmed baryons are well consistent with experiments. Our results of mass spectra and decay widths indicate that $\Lambda _c(2595)^+$, $\Lambda _c(2625)^+$, $\Xi _c(2790)^{0,+}$, and $\Xi _c(2815)^{0,+}$ can be accommodated with the 1P $\mathcal {G}$-type charmed baryons. $\Lambda _c(2595)^+$ and $\Xi _c(2790)^{0,+}$ can be classified into the $1/2^-$ states while $\Lambda _c(2625)^+$ and $\Xi _c(2815)^{0,+}$ into the $3/2^-$ states. The predicted mass splittings between the 1P $1/2^-$ and $3/2^-$ states are 25 MeV and 27 MeV for the $\Lambda _c$ and $\Xi _c$ baryons, respectively, which are also consistent with the experiments. The assignments of $\Lambda _c(2595)^+$, $\Lambda _c(2625)^+$, $\Xi _c(2790)^{0,+}$, and $\Xi _c(2815)^{0,+}$ are also supported by other work [9,10,11,12] in which the light quark cluster scenario was also employed. In addition, the mass spectra obtained by different types of the quark potential models in the three-body picture also support these assignments [7, 8, 56,57,58]. However, the investigations by QCD sum rules indicate that these 1P candidates may have more complicated structures [14,15,16]. Especially, the work by Chen et al. suggested that $\Lambda _c(2595)^+$ and $\Lambda _c(2625)^+$ form the heavy doublet $\tilde{\Lambda }_{c1}(1/2^-, 3/2^-)$ (the same assignments as the case of $\Xi _c(2790)^{0,+}$ and $\Xi _c(2815)^{0,+}$) [16], which is different from our conclusion. Since the quantum numbers of $J^P$ have not yet been determined for these 1P charmed states, more experiments are required in the future.

Table 8 Open-flavor strong decay widths of 1S $\Sigma _c$ and $\Xi '_c$ in MeV

Table 9 Open-flavor strong decay widths of 1P $\Lambda _c$ and $\Xi _c$ in MeV

4.2 1P $\Sigma _c^{~0,+,++}$ states

Table 10 The partial and total decay widths of 1P $\Sigma _c$ states in MeV

As shown in Tables 2 and 3, the masses of 1P $\Sigma _c$ states are predicted in the range of 2700–2800 MeV. Then $\Sigma _c(2765)^+$ and $\Sigma _c(2800)^{0,+,++}$ can be grouped into the candidates of 1P $\Sigma _c$ family. The predicted mass of the $|1P,1/2^-\rangle _h$ state is about 2765 MeV, which is in good agreement with the measured mass of $\Sigma _c(2765)^+$. In addition, the theoretical result for the decay width of the $\Sigma _{c1}(1/2^-)$ state in Table 10 is about 63.52 MeV, which is also in agreement with the measurements [30,31,32]. Furthermore, the signal of $\Sigma _c(2765)^+$ has been observed in the $\Sigma _c(2455)\pi$ intermediate state, while there is no clear evidence for the decay of $\Sigma _c(2765)^+$ through $\Sigma _c(2520)\pi$ [31, 32]. This is also consistent with our results of the $|1P,1/2^-\rangle _h$. Based on the combined analysis of the mass spectrum and strong decays, we therefore conclude that $\Sigma _c(2765)^+$ could be regarded as a good candidate of $\Sigma _{c1}(1/2^-)$. Considering the uncertainties of the quark potential models, the masses obtained by Refs. [9, 10, 56] are not contradictory to our assignment to $\Sigma _c(2765)^+$.

According to the predicted masses in Table 3, $\Sigma _c(2800)^{0,+,++}$ could be assigned to either the $|1P,3/2^-\rangle _l$, or the $|1P,3/2^-\rangle _h$, or the $|1P,5/2^-\rangle$ states. When we consider the decay properties of these three states (see Table 10), the possibility of assignment to the $|1P,3/2^-\rangle _l$ state can be excluded since the Belle Collaboration observed this state in the $\Lambda _c^+\pi$ mode.³ At present, the Belle Collaboration tentatively identified $\Sigma _c(2800)^{0,+,++}$ as members of the $\Sigma _{c2}(3/2^-)$ isospin triplet, which agrees with our results of both mass spectrum and strong decays. When the measured mass of $\Sigma _c(2800)^0$ (2806 MeV) is used for the $\Sigma _{c2}(3/2^-)$ state, the predicted width is about 40.1 MeV, which is comparable with the experiment [34]. However, we notice that the quantum number $J^P$ of $\Sigma _c(2800)^{0,+,++}$ has not yet been measured. Then the possibility of this state as the $\Sigma _{c2}(5/2^-)$ candidate cannot be excluded by our results since the decay mode of $\Lambda _c^+\pi$ is dominant for this state. In addition, the predicted mass and total width of the $\Sigma _{c2}(5/2^-)$ state are also compatible with experimental data of the $\Sigma _c(2800)^{0,+,++}$ baryon. Therefore, we would like to point out that the signal of $\Sigma _c(2800)^{0,+,++}$ found by Belle might be their overlapping structure. We hope the future experiments measure the following branching ratios to disentangle this state.

Table 11 The partial and total decay widths of 1P $\Xi ^\prime _c$ states in MeV

For the $\Sigma _{c2}(3/2^-)$ state,

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _{c2}(3/2^-)\rightarrow \Sigma _c(2455)~\pi )}{\mathcal {B}(\Sigma _{c2}(3/2^-)\rightarrow \Sigma _c(2520)~\pi )}~=~1.90; \end{aligned}$$

(22)

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _{c2}(3/2^-)\rightarrow \Lambda _c(2286)~\pi )}{\mathcal {B}(\Sigma _{c2}(3/2^-)\rightarrow \Sigma _c(2455)~\pi )}~=~4.07. \end{aligned}$$

(23)

For the $\Sigma _{c2}(5/2^-)$ state,

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _{c2}(5/2^-)\rightarrow \Sigma _c(2455)~\pi )}{\mathcal {B}(\Sigma _{c2}(5/2^-)\rightarrow \Sigma _c(2520)~\pi )}~=~0.58; \end{aligned}$$

(24)

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _{c2}(5/2^-)\rightarrow \Lambda _c(2286)~\pi )}{\mathcal {B}(\Sigma _{c2}(5/2^-)\rightarrow \Sigma _c(2455)~\pi )}~=~9.85. \end{aligned}$$

(25)

As mentioned earlier, the signal $\Sigma _c(2850)^0$ discovered by the BaBar Collaboration may be a $J=1/2$ state. If $\Sigma _c(2850)^0$ is the $1/2^+(2S)$ state, the corresponding ratios (see Sect. 4.5) are different from Eqs. (22)–(25). So the measurements of these ratios of branching fractions can help us understand the nature of $\Sigma _c(2800)^{0,+,++}$ and $\Sigma _c(2850)^0$.

Although, at present, the $\Sigma _{c0}(1/2^-)$ and $\Sigma _{c1}(3/2^-)$ states are still missing in the experiments, our results indicate that the $\Sigma _{c0}(1/2^-)$ state may be a narrow resonance and its predominant decay channel $\Lambda _c^+\pi$ is only about 3.64 MeV (see Table 10). Since the decay mode of $\Sigma _c(2520)~\pi$ is the largest for the $\Sigma _{c1}(3/2^-)$ state, we suggest to search this channel for this state in future experiments. In the heavy quark limit, the branching ratio for the $\Sigma _{c1}(3/2^-)$ state,

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _{c1}(3/2^-)\rightarrow \Sigma _c(2455)~\pi )}{\mathcal {B}(\Sigma _{c1}(3/2^-)\rightarrow \Sigma _c(2520)~\pi )}~=~0.04, \end{aligned}$$

(26)

is much smaller than $\Sigma _{c2}(3/2^-)$ (Eq. 22).

4.3 1P $\Xi _c^{\prime ~0,+}$ states

As shown in Table 3, the predicted mass of 1P $\Xi _c^\prime$ is in the range from 2840 to 2930 MeV. Then the resonance structure observed by BaBar [36] in the decay channel $B^-\rightarrow \Xi _c^{\prime }(2930)^0\bar{\Lambda }_c^-\rightarrow \Lambda ^+_cK^-\bar{\Lambda }_c^-$ with an invariant mass of 2.93 GeV could be a good candidate of 1P $\Xi _c^\prime$ members. The results of the decays in Table 11 favor $\Xi _c^{\prime }(2930)^0$ as the $\Xi '_{c2}(3/2^-)$ or $\Xi '_{c2}(5/2^-)$ state. Then $\Xi _c^{\prime }(2930)^0$ might be regarded as the strange partner of $\Sigma _c(2800)^{0,+,++}$ by our results. Interestingly, the mass difference between $\Xi _c^{\prime }(2930)^0$ and $\Sigma _c(2800)^{0,+,++}$ is about 130 MeV, which is comparable with the mass differences among sextet states of the ground charmed baryons [21]. With a chiral quark model, Liu et al. also analyzed the $\Xi _c^{\prime }(2930)^0$ by the two-body strong decays [23]. Their results support $\Xi _c^{\prime }(2930)^0$ as the $|\Xi _c^{\prime 2}P_\lambda ,~1/2^-\rangle$ or $|\Xi _c^{\prime 4}P_\lambda ,~1/2^-\rangle$ state. Since the heavy quark symmetry was not considered in Ref. [23], the notations of charm-strange baryons in Ref [23] are different from our $\Xi '_{c0}(1/2^-)$ and $\Xi '_{c1}(1/2^-)$. Although the results in Table 11 indicate that the $\Lambda _c^+K$ decay mode dominates the decay of $\Xi ^\prime _{c0}(1/2^-)$ state, the mass of this state is predicted to be about 2840 MeV, which is much smaller than $\Xi _c^{\prime 0}(2930)$. In addition, the $\Lambda _c^+K$ decay mode is forbidden for the $\Xi ^\prime _{c1}(1/2^-)$ state. Thus, according to our results, $\Xi _c^{\prime 0}(2930)$ is unlikely to be a 1P state with $J^P=1/2^-$.

Another charm-strange baryon, $\Xi _c(2980)^{0,+}$, is slightly higher than the predicted mass range of 1P $\Xi _c^\prime$ states. This state has been observed in $\Sigma _c(2455)K$, $\Xi ^\prime _c(2580)\pi$, $\Xi ^\prime _c(2645)\pi$, and nonresonant $\Lambda ^+_c\bar{K}\pi$ decay channels. However, it was not seen in the decay modes of $\Lambda ^+_c\bar{K}$ and $\Xi _c\pi$ [37,38,39]. Comparing the mass and decay properties of $\Xi _c(2980)^{0,+}$ with our results, the possibility of a 1P $\Xi ^\prime _c$ state might be excluded. As shown in the next subsection, $\Xi _c(2980)^{0,+}$ could be a good 2S $\Xi _c$ candidate. Based on our results on strong decays, we find that the $\Xi ^\prime _{c1}(1/2^-)$ and $\Xi ^\prime _{c1}(3/2^-)$ are quite narrow (see Table 11).

Table 12 The partial and total decay widths of 2S $\Lambda _c^+$ and $\Xi _c^{+,0}$ states in MeV

4.4 2S $\Lambda _c^+$ and $\Xi _c^{0,+}$ states

According to the mass spectrum (see Table 2), $\Lambda _c/\Sigma _c(2765)^+$ can also be regarded as the first radial (2S) excitation of the $\Lambda _c(2286)^+$ with $J^P=1/2^+$. Interestingly, the results of strong decays in Table 12 do not contradict this assignment. Our calculation indicates that the decay channel $\Sigma _c(2455)\pi$ is a dominant decay channel for the $\Lambda _c^+(2S)$ state. This is in line with the observations by Belle [31, 32]. At present, both $1/2^+(2S)$ $\Lambda _c^+$ and $1/2^-(1P)$ $\Sigma _c^+$ are possible for the assignment of $\Lambda _c/\Sigma _c(2765)^+$. However, there is the very important feature for experiments to distinguish these two assignments in future. Specifically, we suggest to search $\Lambda _c/\Sigma _c(2765)^+$ in the channel of $\Sigma _c(2520)\pi$. As shown in Table 12, the channel $\Sigma _c(2520)\pi$ is large enough to find the $\Lambda _c^+(2S)$ state. On the other hand, this mode seems to be too small to be detected for the $\Sigma _{c1}(1/2^-)$ (see Table 10). Explaining the criteria concretely, we give the following branching ratios for these two states.

For the $\Lambda _c(2S)$ state,

$$\begin{aligned} \frac{\mathcal {B}(\Lambda _c(2765)\rightarrow \Sigma _c(2520)~\pi )}{\mathcal {B}(\Lambda _c(2765)\rightarrow \Sigma _c(2455)~\pi )}~=~0.74. \end{aligned}$$

(27)

For the $\Sigma _{c1}(1/2^-)$ state,

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _c(2765)\rightarrow \Sigma _c(2520)~\pi )}{\mathcal {B}(\Sigma _c(2765)\rightarrow \Sigma _c(2455)~\pi )}~=~0.03. \end{aligned}$$

(28)

The branching ratio of $\mathcal {B}(\Sigma _c(2520)\pi )/\mathcal {B}(\Sigma _c(2455)\pi )$ for the $\Sigma _{c1}(1/2^-)$ state is roughly an order of magnitude smaller than $\Lambda _c(2S)$. If $\Lambda _c(2765)$ is the 2S excitation, $\Xi _c(2980)$ could be a good candidate as its charm-strange analog [21] as seen in Table 12. The mass difference between $\Lambda _c(2765)$ and $\Xi _c(2980)$ is about 200 MeV, which nearly equals the mass difference between $\Lambda _c(2287)$ and $\Xi _c(2470)$. The predicted width of $\Xi _c(2980)$ is 27.44 MeV which is in good agreement with the experimental data [4, 39]. As the 2S excitation of $\Xi _c(2470)$, the branching ratio

$$\begin{aligned} \frac{\mathcal {B}(\Xi _c(2980)\rightarrow \Xi ^\prime _c(2580)~\pi )}{\mathcal {B}(\Xi _c(2980)\rightarrow \Xi _c(2645)~\pi )}~=~0.89 \end{aligned}$$

(29)

is predicted for $\Xi _c(2980)$, which can be tested by future experiments. Recently, the ratio of branching fractions

$$\begin{aligned} \frac{\mathcal {B}(\Xi _c(2980)^+\rightarrow \Xi ^\prime _c(2580)^0\pi ^+)}{\mathcal {B}(\Xi _c(2815)^+\rightarrow \Xi _c(2645)^0\pi ^+\rightarrow \Xi _c^+\pi ^-\pi ^+)}~\approx ~75\%\nonumber \\ \end{aligned}$$

(30)

has been estimated by the Belle Collaboration [4]. Combining this with the predicted partial widths of $\Xi _c(2815)$ and $\Xi _c(2645)$ in Tables 8 and 9, the branching fraction $\mathcal {B}(\Xi _c(2980)^+\rightarrow \Xi ^\prime _c(2580)^0\pi ^+)$ is evaluated to be about $40\%$, which is consistent with our direct result of $41.8\%$.

4.5 2S $\Sigma _c^{0,+,++}$ and $\Xi _c^{\prime ~0,+}$ states

In Table 3, masses of the 2S $\Sigma _c(1/2^+,3/2^+)$ states are predicted as 2850 and 2876 MeV, respectively. The neutral $\Sigma _c(2850)^0$ found by the BaBar Collaboration in the decay channel $B^-\rightarrow \Sigma _c(2850)^0\bar{p}\rightarrow \Lambda _c^+\pi ^-\bar{p}$ [35] can be regarded as the 2S $\Sigma _c$ state with $J^P=1/2^+$. The mass and width of the neutral $\Sigma _c(2800)^0$ and $\Sigma _c(2850)^0$ are collected here:

$$\begin{aligned} \begin{array}{ll} \Sigma _c(2800)^0:~~~m~&{}=~2806^{+5}_{-7}~\mathrm {MeV},~~~\Gamma ~=~72^{+22}_{-15}~\mathrm {MeV};\\ \Sigma _c(2850)^0:~~~m~&{}=~2846\pm 8\pm 10~\mathrm {MeV},~~~\Gamma ~=~86^{+33}_{-22}~\mathrm {MeV}. \end{array} \end{aligned}$$

For lack of experimental information, at present, PDG treated $\Sigma _c(2850)^0$ and $\Sigma _c(2800)^{0,+,++}$ as the same state [1]. As pointed out by the BaBar Collaboration [35], however, there are indications that these two signals detected by Belle [34] and BaBar [35] are two different $\Sigma _c^*$ states. The main reasons are listed as follows:

• 1. Although the widths of $\Sigma _c(2800)^{0,+,++}$ and $\Sigma _c(2850)^0$ are consistent with each other, their masses are $3\sigma$ apart.

• 2. The Belle Collaboration tentatively identified the $\Sigma _c(2800)^{0,+,++}$ as the $J=3/2$ isospin triple, while the BaBar Collaboration found weak evidence of $\Sigma _c(2850)^0$ as a $J=1/2$ state.

Our results also indicate that $\Sigma _c(2800)^{0,+,++}$ and $\Sigma _c(2850)^0$ are the different $\Sigma _c$ excited states. One notices that the predicted mass of $1/2^+(2S)$ $\Sigma _c$ state in this work and in Ref. [9] are around 2850 MeV. Even the results in Refs. [10, 56] are only about 50 MeV larger than the measurements. Due to the intrinsic uncertainties of the quark potential model, it is appropriate to assign $\Sigma _c(2850)^0$ as a 2S $1/2^+$ state. More importantly, the predicted decay width of $\Sigma _c(1/2^+,~2S)$ state is 118.36 MeV, which is comparable with the measurement by BaBar [35]. The partial width of $\Lambda _c\pi$ is 35.11 MeV, which can explain why $\Sigma _c(2850)^0$ was first found in this channel. We find that the decay modes of $\Sigma _c(2455)\pi$ and $\Sigma _c(2520)\pi$ are also large. Finally, we give the following branching ratios:

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _c(2850)\rightarrow \Sigma _c(2455)~\pi )}{\mathcal {B}(\Sigma _c(2850)\rightarrow \Sigma _c(2520)~\pi )}~=~3.26, \end{aligned}$$

(31)

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _c(2850)\rightarrow \Sigma _c(2286)~\pi )}{\mathcal {B}(\Sigma _c(2850)\rightarrow \Sigma _c(2455)~\pi )}~=~0.61, \end{aligned}$$

(32)

which can be tested by future experiments. If $\Sigma _c(2850)^0$ is the $1/2^+(2S)$ state, the mass of its doublet partner in the heavy quark effective theory is predicted as 2876 MeV (denoted $\Sigma _c(2880)$). According to the predicted decay widths in Table 12, this state might also be broad. $\Lambda _c^+\pi$, $\Sigma _c(2455)\pi$, and $\Sigma _c(2520)\pi$ are also dominant for the decay of $\Sigma _c(2880)$. The ratio of $\Gamma (\Sigma _c(2455)\pi )/\Gamma (\Sigma _c(2520)\pi )$ for $\Sigma _c(2880)$ is different from $\Sigma _c(2850)$, whose numerical value is given by

$$\begin{aligned} \frac{\mathcal {B}(\Sigma _c(2880)\rightarrow \Sigma _c(2455)~\pi )}{\mathcal {B}(\Sigma _c(2880)\rightarrow \Sigma _c(2520)~\pi )}~=~0.29. \end{aligned}$$

(33)

Even though the strange partners of $\Sigma _c(2850)$ and $\Sigma _c(2880)$ have not been found by any experiments, their decay properties are calculated and presented in Table 12. Our results indicate that $\Lambda _c^+K$, $\Xi _c^\prime (2580)\pi$, and $\Sigma _c(2455)K$ are the dominant decay modes of the $\Xi _c^\prime (3000)$ state with $J^P=1/2^+$, while $\Lambda _c^+K$ and $\Xi _c^\prime (2645)\pi$ are those of the $\Xi _c^\prime (3030)$.⁴ Besides the masses and decay widths, the following branching ratios may also be valuable for future experiments:

$$\begin{aligned} \frac{\mathcal {B}(\Xi ^\prime _c(3000)\rightarrow \Xi ^\prime _c(2580)~\pi )}{\mathcal {B}(\Xi ^\prime _c(3000)\rightarrow \Xi ^\prime _c(2645)~\pi )}~=~3.04, \end{aligned}$$

(34)

$$\begin{aligned} \frac{\mathcal {B}(\Xi ^\prime _c(3030)\rightarrow \Xi ^\prime _c(2580)~\pi )}{\mathcal {B}(\Xi ^\prime _c(3030)\rightarrow \Xi ^\prime _c(2645)~\pi )}~=~0.27. \end{aligned}$$

(35)

5 Summary and outlook

In principle, both $\rho$ and $\lambda$ modes can be excited in a baryon system. For charmed baryons, the excitation energies of the $\rho$ and $\lambda$ modes are different due to the heavier mass of a c quark. For the ordinary confining potential, such as the linear or harmonic form, the excited energy of the $\rho$ mode is larger than the $\lambda$ mode [44]. Hence the low-excited charmed baryons may be dominated by the $\lambda$ mode excitations. Recently, the investigation by Yoshida et al. confirmed this point [75]. Furthermore, they find that the $\rho$ and $\lambda$ modes are well separated for the charmed and bottom baryons, which means the component of the $\rho$ mode can be ignored for the low-excited charmed baryons. Interestingly, Refs. [9,10,11] have also shown that the masses of existing charmed baryons can be explained by the $\lambda$ mode. Hence, our study of strong decays of the low-excited charmed baryons is an important complement to this work [9,10,11, 75].

Up to now, several candidates of the 1P and 2S charm and charm-strange baryons have been found by experiments, and some of them are still open to debate. To better understand these low-excited charmed baryons, in this paper, we carry out a systematical study of the mass spectra and strong decays for the 1P and 2S charmed baryon states in the framework of the non-relativistic constituent quark model. The masses have been calculated in the potential model where the charmed baryons are simply treated as a quasi-two-body system in a light quark cluster picture. The strong decays are computed by the EHQ decay formula where the transition factors are determined by the $^3P_0$ model. When calculating the decays, the inner structure of a light quark cluster has also been considered. Except for the unique parameter $\gamma$ of the QPC model, the parameters in the potential model and in the EHQ decay formula have the same values.

The well-established ground and 1P $\mathcal {G}$-type charmed baryons provide a good test to our method. The experimental properties including both masses and widths for these states can be well explained by our results. This success has made us more confident of our predictions for other 1P and 2S states. Our main conclusions are as follows.

The broad state $\Lambda _c(2765)^+$ (or $\Sigma _c(2765)^+$) which is still ambiguous could be assigned to the $1/2^+(2S)$ $\Lambda _c^+$, or the $1/2^-(1P)$ $\Sigma _{c1}^+$ state. The branching ratio $\mathcal {B}(\Sigma _c(2455)\pi )/\mathcal {B}(\Sigma _c(2520)\pi )$ is found to be different for these two assignments, which may help us understand the nature of this state.

$\Sigma _c(2800)^{0,+,++}$ observed by the Belle Collaboration in $e^+e^-$ annihilation processes [34] can be regarded as a negative-parity state with $J^P=3/2^-$, or $5/2^-$, or their overlapping structure. We suggest to measure the $\mathcal {B}(\Sigma _c(2455)\pi )/\mathcal {B}(\Sigma _c(2520)\pi )$ in the future. Another neutral state, $\Sigma _c(2850)^0$, which was found in the $B^-$ meson decay [35] could be a good candidate for the first radial excited state of $\Sigma _c(2455)$. With the above assignments, the ratios of $\mathcal {B}(\Lambda _c(2287)\pi )/\mathcal {B}(\Sigma _c(2455)\pi )$ shall be very different for $\Sigma _c(2800)^{0,+,++}$ and $\Sigma _c(2850)^0$, i.e., 4.07 for $\Sigma _c(2800)^{0,+,++}$ and 0.61 for $\Sigma _c(2850)^0$. The puzzle of $\Sigma _c(2800)^{0,+,++}$ and $\Sigma _c(2850)^0$ may be disentangled if these branching ratios are measured in the future. In addition, the ratio of branching fractions $\mathcal {B}(\Sigma _c(2455)\pi )/\mathcal {B}(\Sigma _c(2520)\pi )$ for $\Sigma _c(2850)^0$ is predicted to be 3.26.

The analysis of the mass and decay properties supports that $\Xi _c(2980)^{0,+}$ is the 2S excitation (the first radial excited state of $\Xi _c(2470)$). The existence of $\Xi _c(2930)^0$ is still in dispute. If it exists, the assignments of $\Xi _{c2}^\prime (3/2^-)$ and $\Xi _{c2}^\prime (5/2^-)$ are possible. In other words, it could be regarded as a strange partner of $\Sigma _c(2800)^{0,+,++}$. Some useful ratios of partial decay widths are also presented for $\Xi _c(2980)^{0,+}$ and $\Xi _c(2930)^0$.

Although both the masses and the strong decays have been explained in the heavy quark–light quark cluster picture for the observed 2S and 1P candidates, it is not the end of the story of the study of the excited charmed baryon states. Investigation of the $\rho$ mode excited states with higher energies are also important to identify the effective degrees of freedom of charmed baryons. However, this topic needs much laborious work and is beyond the scope of the present work. In addition, the quark model employed here neglects the effect of virtual hadronic loops. In the future, a more reasonable scheme for studying the properties of heavy baryons will be obtained by the unquenched quark model. Another topic which is left as a future task is to calculate the sum rules among the branching fractions of charmed baryons by applying the technique found in Ref. [76].

Appendices

Appendix A: Transition factor $\mathcal {M}^{j_A,j_B}_{j_C,\ell }(q)$ in the QPC model

In the following, we will show how to obtain the partial wave amplitudes by the $^3P_0$ strong decay model for the decays of excited charmed baryons. As an example, the process $\Sigma _c(2520)\rightarrow \Lambda _c(2280)\pi$ will be constructed and the transition factor for the EHQ formula will be extracted.

As pointed out in Sect. 3, there are two possible decay processes for an excited charmed baryon state (see Fig. 3). The final states of the left figure contain a charmed baryon and a light meson. The right one contains a charmed meson and a light baryon. If a baryon decays via the so-called $^3P_0$ mechanism, a quark–antiquark pair is created from the vacuum and then regroups two outgoing hadrons by a quark rearrangement process. In the non-relativistic limit, the transition operator $\mathcal {\hat{T}}$ of the $^3P_0$ model is given by

$$\begin{aligned} \mathcal {\hat{T}}= & {} -3\gamma \sum _{\text {m }}\langle 1,m;1,-m|0,0\rangle \iint d^3\vec {k}_4d^3\vec {k}_5\delta ^3(\vec {k}_4+\vec {k}_5)\nonumber \\&\times \mathcal {Y}_1^m(\frac{\vec {k}_4-\vec {k}_5}{2})\omega ^{(4,5)}\varphi ^{(4,5)}_0\chi ^{(4,5)}_{1,-m}d^\dag _{4}(\vec {k}_4)d^\dag _{5}(\vec {k}_5), \end{aligned}$$

(A.1)

where $\omega ^{(4,5)}$ and $\varphi ^{(4,5)}_0$ are the color and flavor wave functions of the $q_4\bar{q}_5$ pair created from the vacuum. Thus, $\omega ^{(4,5)}=(R\bar{R}+G\bar{G}+B\bar{B})/\sqrt{3}$ and $\varphi ^{(4,5)}_0=(u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3}$ are color and flavor singlets. The pair is also assumed to carry the quantum number of $0^{++}$, suggesting that they are in a $^3P_0$ state. The $\chi ^{(4,5)}_{1,-m}$ represents the pair production in a spin triplet state. The solid harmonic polynomial $\mathcal {Y}_1^m(\vec {k})\equiv |\vec {k}|\mathcal {Y}_1^m(\theta _k,\phi _k)$ reflects the momentum-space distribution of the $q_4\bar{q}_5$. $\gamma$ is a dimensionless constant which expresses the strength of the quark–antiquark pair created from the vacuum. The value of $\gamma$ is usually fixed by fitting the well-measured partial decay widths.

When the mock state [77] is adopted to describe the spatial wave function of a meson, the helicity amplitude $\mathcal {M}^{j_A,j_B,j_C}(q)$ can easily be constructed in the LS basis [71]. The mock state for an A meson is

$$\begin{aligned}&\Big |A\left( {n_A}^{2S_A+1}L_A^{J_Aj_A}\left. \left( \vec {P}_A\right) \right) \right\rangle \nonumber \\&\quad \equiv \omega _A^{123}\phi _A^{123}\prod _A\int d^3\vec {k}_1d^3\vec {k}_2d^3\vec {k}_3\delta ^3\left( \vec {k}_1+\vec {k}_2+\vec {k}_3-\vec {P}_A\right) \nonumber \\&\qquad \times \Psi _{n_A}^{L_Al_A}\left( \vec {k}_1,\vec {k}_2,\vec {k}_3\right) \Big |q_1\left( \vec {k}_1\right) q_2\left( \vec {k}_2\right) q_3\left. \left( \vec {k}_3\right) \right\rangle . \end{aligned}$$

(A.2)

As for the left decay process in Fig. 3, the wave function of a B baryon can be constructed in the same way. The wave function of a C meson is

$$\begin{aligned}&\left| C\left( {n_C}^{2S_C+1} L_C^{J_Cj_C}\left( \vec {P}_C\right) \right) \right\rangle \nonumber \\&\quad \equiv \omega _C^{15}\phi _C^{15}\prod _C \int d^3\vec {k}_1d^3\vec {k}_5\delta ^3\left( \vec {k}_1+\vec {k}_5-\vec {P}_C\right) \nonumber \\&\qquad \times \,\left. \left. \Psi _{n_C}^{L_Cl_C}\left( \vec {k}_1,\vec {k}_5\right) \right| q_1\left( \vec {k}_1\right) \bar{q}_5\left( \vec {k}_5\right) \right\rangle .\nonumber \\ \end{aligned}$$

(A.3)

Here, the symbols of $\prod _i~(i=A, B$, and C) represent the Clebsch–Gordan coefficients for the initial and final hadrons, which arise from the couplings among the orbital, spin, and total angular momentum and their projection of $l_z$ and $s_z$ to $j_z$. More specifically, $\prod _i~(i=A, B$, and C) are given by

$$\begin{aligned} \prod \nolimits _A= & {} \big \langle s_{1}m_{1}, s_{2}m_{2}\big |s_{12}m_{12}\big \rangle \big \langle s_{12}m_{12}, s_{3}m_{3}\big |S_{A}s_{A}\big \rangle \\&\times \big \langle L_{A}l_{A}, S_{A}s_{A}\big |J_{A}j_{A}\big \rangle ,\\ \prod \nolimits _B= & {} \big \langle s_{2}m_{2}, s_{5}m_{5}\big |s_{25}m_{25}\big \rangle \big \langle s_{25}m_{25}, s_{3}m_{3}\big |S_{B}s_{B}\big \rangle \\&\times \big \langle L_{B}l_{B}, S_{B}s_{B}\big |J_{B}j_{B}\big \rangle ,\\ \prod \nolimits _C= & {} \big \langle s_{1}m_{1}, s_{4}m_{4}\big |S_{C}s_{C}\big \rangle \big \langle L_{C}l_{C}, S_{C}s_{C}\big |J_{C}j_{C}\big \rangle , \end{aligned}$$

respectively.

The helicity amplitude $\mathcal {M}^{j_A,j_B,j_C}(q)$ is defined by

$$\begin{aligned} \langle BC|\mathcal {\hat{T}}|A\rangle = \delta ^3(\vec {P}_A-\vec {P}_B-\vec {P}_C)\mathcal {M}^{j_A,j_B,j_C}(q), \end{aligned}$$

(A.4)

where q represents the momentum of an outgoing meson in the rest frame of a meson A. For comparison with experiments, one obtains the partial wave amplitudes $\mathcal {M}_{LS}(q)$ via the Jacob–Wick formula [78],

$$\begin{aligned} \mathcal {M}_{LS}(q)= & {} \frac{\sqrt{2L+1}}{2J_A+1}\sum _{{j_B,j_C}}\langle L0Jj_A|J_Aj_A\rangle \nonumber \\&\times \langle J_Bj_B,J_Cj_C|Jj_A\rangle \mathcal {M}^{j_A,j_B,j_C}(q). \end{aligned}$$

(A.5)

Then the decay width $\Gamma (A\rightarrow BC)$ is derived analytically in terms of the partial wave amplitudes in the A rest frame,

$$\begin{aligned} \begin{array}{ll} \Gamma (A\rightarrow BC)=2\pi \frac{E_BE_C}{M_A}q\sum _{L,S}|\mathcal {M}_{LS}(q)|^2. \end{array} \end{aligned}$$

(A.6)

Finally, the full expression of $\mathcal {M}_{LS}(q)$ in the rest frame of the baryon A is

$$\begin{aligned}&\mathcal {M}_{LS}(q)=-3\gamma \sum _{l_i,m_j}\langle L0;Jj|J_Aj_A\rangle \langle J_Bj_B;J_Cj_C|Jj\rangle \nonumber \\&\quad \times \langle s_1m_1;s_2m_2|s_{dA}m_{12}\rangle \langle s_{dA}m_{12};s_3m_3|S_As_A\rangle \nonumber \\&\quad \times \langle S_As_A;L_Al_A|J_Aj_A\rangle \langle s_2m_2;s_5m_5|s_{dB}m_{25}\rangle \nonumber \\&\quad \times \langle s_{dB}m_{25};s_3m_3|S_Bs_B\rangle \langle S_Bs_B;L_Bl_B|J_Bj_B\rangle \nonumber \\&\quad \times \langle s_1m_1;s_4m_4|S_Cs_C\rangle \nonumber \\&\quad \times \langle S_Cs_C;L_Cl_C|J_Cj_C\rangle \langle s_4m_4;s_5m_5|1-m\rangle \nonumber \\&\quad \times \langle 1,m;1,-m|0,0\rangle \nonumber \\&\quad \times \langle \varphi ^{235}_B\varphi ^{14}_C|\varphi ^{45}_0\varphi ^{123}_A\rangle \langle \omega ^{235}_B\omega ^{14}_C|\omega ^{45}_0\omega ^{123}_A\rangle \int \cdots \int d^3\vec {k}_1\cdots \nonumber \\&\quad \times d^3\vec {k}_5\delta ^3(\vec {k}_1+\vec {k}_2+\vec {k}_3)\delta ^3(\vec {q}-\vec {k}_1-\vec {k}_4)\delta ^3(\vec {q}+\vec {k}_2+\vec {k}_3+\vec {k}_5)\nonumber \\&\quad \times \delta ^3(\vec {k}_4+\vec {k}_5)\Psi _A(\vec {k}_1,\vec {k}_2,\vec {k}_3)\Psi ^*_B(\vec {k}_1,\vec {k}_2,\vec {k}_4)\nonumber \\&\quad \times \psi ^*_C(\vec {k}_3,\vec {k}_5)\mathcal {Y}_1^m\left( \frac{\vec {k}_3-\vec {k}_4}{2}\right) , \end{aligned}$$

(A.7)

where $i=A, B, C$ and $j=1, 2, \ldots , 5$. The color matrix element $\langle \omega ^{235}_B\omega ^{14}_C|\omega ^{45}_0\omega ^{123}_A\rangle$ is a constant which can be absorbed into the parameter $\gamma$. The flavor matrix element $\xi =\langle \varphi ^{235}_B\varphi ^{14}_C|\varphi ^{45}_0\varphi ^{123}_A\rangle$ will be presented in the next subsection. To obtain the analytical amplitudes, the SHO wave functions are employed to describe the spatial wave function of a hadron. In the momentum space, the SHO radial wave function, $\psi ^n_{Lm}(\mathbf q )$, is given by

$$\begin{aligned} \begin{array}{ll} &{}\psi ^n_{Lm}(\mathbf q ) \\ &{}\quad =\frac{(-1)^n}{\beta ^{3/2}}\sqrt{\frac{2(2n-1)!}{\Gamma (n+L+\frac{1}{2})}}\left( \frac{q}{\beta }\right) ^L e^{-\frac{q^2}{2\beta ^2}}L^{L+1/2}_{n-1}\left( \frac{q^2}{\beta ^2}\right) \mathcal {Y}_{Lm}(\mathbf q ), \end{array}\nonumber \\ \end{aligned}$$

(A.8)

with $\mathbf q =(m_i\vec {k}_j-m_j\vec {k}_i)/(m_i+m_j)$ and $\mathcal {Y}_{Lm}(\mathbf q )=|\mathbf q |^LY_{Lm}(\Omega _\mathbf q )$. $L^{L+1/2}_{n-1}(q^2/\beta ^2)$ is an associated Laguerre polynomial. The values of the SHO wave function scale parameter $\beta$ have been given in Tables 5 and 6. In the light quark cluster picture, the wave function of a charmed baryon can easily be constructed. Taking the A baryon as an example, the wave functions corresponding to the 1S, 2S, and 1P states are given as follows, respectively:

$$\begin{aligned} \Psi ^0_{00}=\frac{3^{3/4}}{\pi ^{3/2}\beta _{dA}^{3/2}\beta _{A}^{3/2}}e^{-\frac{1}{2\beta _{dA}^2}\left( \frac{m_1\vec {k}_2-m_2\vec {k}_1}{m_1+m_2}\right) ^2-\frac{1}{2\beta _A^2}\left[ \frac{(m_1+m_2)\vec {k}_3-m_Q(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_Q}\right] ^2}; \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} \Psi ^1_{00}=&{}-\frac{3^{3/4}}{\sqrt{6}\pi ^{3/2}\beta _{dA}^{3/2}\beta _{A}^{3/2}}e^{-\frac{1}{2\beta _{dA}^2}\left( \frac{m_1\vec {k}_2-m_2\vec {k}_1}{m_1+m_2}\right) ^2-\frac{1}{2\beta _A^2}\left[ \frac{(m_1+m_2)\vec {k}_3-m_Q(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_Q}\right] ^2}\\ &{}\times \left\{ 3-\frac{2}{\beta ^2_A}\left[ \frac{(m_1+m_2)\vec {k}_3-m_Q(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_Q}\right] ^2\right\} ; \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} \Psi ^0_{1m}=&{}\frac{3^{3/4}\times 2\sqrt{2/3}}{\pi \beta _{dA}^{3/2}\beta _{A}^{5/2}}e^{-\frac{1}{2\beta _{dA}^2}\left( \frac{m_1\vec {k}_2-m_2\vec {k}_1}{m_1+m_2}\right) ^2-\frac{1}{2\beta _A^2}\left[ \frac{(m_1+m_2)\vec {p}_3-m_Q(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_Q}\right] ^2}\\ &{}\times \mathcal {Y}_{1m}\left( \frac{(m_1+m_2)\vec {k}_3-m_Q(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_Q}\right) . \end{array} \end{aligned}$$

With the help of Eq. (A.7), the transition amplitude can be obtained. In the following, we take the process $\Sigma _c(2520)\rightarrow \Lambda _c(2280)^+\pi$ as an example. The wave functions of initial and final states are

$$\begin{aligned} \begin{array}{ll} &{}\Psi _A=\frac{3^{3/4}}{\pi ^{3/2}\beta _{dA}^{3/2}\beta _{A}^{3/2}}e^{-\frac{1}{2\beta _{dA}^2}\left( \frac{m_1\vec {k}_2-m_2\vec {k}_1}{m_1+m_2}\right) ^2-\frac{1}{2\beta _A^2}\left[ \frac{(m_1+m_2)\vec {k}_3-m_3(\vec {k}_1+\vec {k}_2)}{m_1+m_2+m_3}\right] ^2};\\ &{}\Psi _B=\frac{3^{3/4}}{\pi ^{3/2}\beta _{dB}^{3/2}\beta _{B}^{3/2}}e^{-\frac{1}{2\beta _{dB}^2}\left( \frac{m_5\vec {k}_2-m_2\vec {k}_5}{m_2+m_5}\right) ^2-\frac{1}{2\beta _B^2}\left[ \frac{(m_2+m_5)\vec {k}_3-m_Q(\vec {p}_2+\vec {k}_5)}{m_2+m_3+m_5}\right] ^2};\\ &{} \psi _C=-\frac{1}{\pi ^{3/4}\beta _C^{3/2}}e^{-\frac{1}{2\beta _C^2}\left( \frac{m_1\vec {k}_4-m_4\vec {k}_1}{m_1+m_2}\right) ^2}. \end{array} \end{aligned}$$

Based on Eq. (A.7), we obtain the amplitude:

$$\begin{aligned} \mathcal {M}_{1\frac{1}{2}}(q)=-\frac{3g}{8\pi ^{5/4}f^{5/2}\lambda ^{3/2}\beta _A^{3/2}\beta _{dA}^{3/2}\beta _B^{3/2}\beta _{dB}^{3/2}\beta _C^{3/2}}pe^{-\frac{4fg-g^2}{4f}q^2},\nonumber \\ \end{aligned}$$

(A.9)

where

$$\begin{aligned}&f=\frac{1}{2\beta _{dA}^2}+\frac{1}{2\beta _{dB}^2}+\frac{1}{2\beta _M^2}-\frac{\mu ^2}{4\lambda };\\&g=\frac{1}{\beta _{dA}^2}+\frac{\varepsilon _3}{\beta _{dB}^2}+\frac{\varepsilon _4}{\beta _M^2}-\frac{\mu \nu }{2\lambda };\\&h=\frac{1}{2\beta _{dA}^2}+\frac{\varepsilon _2^2}{2\beta _B^2}+\frac{\varepsilon _3^2}{2\beta _{dB}^2}+\frac{\varepsilon _4^2}{2\beta _M^2}-\frac{\nu ^2}{4\lambda };\\&\lambda =\frac{1}{2\beta _A^2}+\frac{1}{2\beta _B^2}+\frac{\varepsilon _1^2}{2\beta _{dA}^2}+\frac{\varepsilon _3^2}{2\beta _{dB}^2};\\&\mu =\frac{\varepsilon _1}{\beta _{dA}^2}+\frac{\varepsilon _3}{\beta _{dB}^2};~~\nu =\frac{\varepsilon _1}{\beta _{dA}^2}+\frac{\varepsilon _3}{\beta _B^2}+\frac{\varepsilon _3^2}{\beta _{dB}^2};\\&\varepsilon _1=\frac{m_1}{m_1+m_2};~~\varepsilon _2=\frac{m_3}{m_1+m_3+m_5};\\&\varepsilon _3=\frac{m_5}{m_2+m_5};~~\varepsilon _4=\frac{m_4}{m_1+m_4}, \end{aligned}$$

and

$$\begin{aligned} q=\frac{\sqrt{[M_A^2-(M_B+M_C)^2][M_A^2-(M_B-M_C)^2]}}{2M_A}.\nonumber \\ \end{aligned}$$

(A.10)

Here, $M_A$, $M_B$, and $M_C$ are the masses of hadrons A, B, and C, respectively. Then the $\tilde{\beta }$ in Eq. (20) is given by

$$\begin{aligned} \tilde{\beta }=2\sqrt{\frac{f}{4fg-g^2}}, \end{aligned}$$

(A.11)

where f and g have been defined above. For the decay channel of $\Sigma _c(2520)\rightarrow \Lambda _c(2280)\pi$, the value of $\mathcal {C}^{s_Q,j_B,J_B}_{j_C,j_A,J_A}$ is $-1$. Therefore, we obtain

$$\begin{aligned} \mathcal {M}^{1,0}_{11}(q)=\frac{3g}{8\pi ^{5/4}f^{5/2}\lambda ^{3/2}\beta _A^{3/2}\beta _{dA}^{3/2}\beta _B^{3/2}\beta _{dB}^{3/2}\beta _C^{3/2}},\nonumber \\ \end{aligned}$$

(A.12)

where a phase space factor $(2\pi E_BE_C/M_A)^{1/2}\gamma$ is omitted. One notices that the unitary rotation between the LS coupling and jj coupling (Eq. (15)) should be performed to reduce the transition factors of 1P state with the same $J^P$. More details for calculating the decay amplitudes of an excited baryon in the $^3P_0$ model can be found in Refs. [24, 79].

Appendix B: Flavor factors

Based on the light SU(3) flavor symmetry, the flavor wave functions of charmed and charmed-strange baryons are given by [57]

$$\begin{aligned} \begin{array}{ll} \Lambda _c^+&{}=\frac{1}{\sqrt{2}}(ud-du)c;\quad \Sigma _c^{++}=uuc;\\ \Xi _c^+&{}=\frac{1}{\sqrt{2}}(us-su)c;\quad \Sigma _c^+=\frac{1}{\sqrt{2}}(ud+du)c;\\ \Xi _c^0&{}=\frac{1}{\sqrt{2}}(ds-sd)c;\quad \Sigma _c^0=ddc;\\ \Xi ^{'+}_c&{}=\frac{1}{\sqrt{2}}(us+su)c;\quad \Xi ^{'0}_c=\frac{1}{\sqrt{2}}(ds+sd)c. \end{array} \end{aligned}$$

As shown in Fig. 3, the final states of an excited charmed baryons may contain a light meson and a low energy charmed baryon or a light baryon and a charmed meson. The flavor wave functions for the final states are collected in the following:

$$\begin{aligned} \begin{array}{ll} \pi ^+&{}=u\bar{d};~~~~\pi ^-=d\bar{u};~~~~\pi ^0=(u\bar{u}-d\bar{d})/\sqrt{2};\\ K^-&{}=\bar{u}s;~~~~~\bar{K}^0=\bar{d}s;~~~~~D^+=\bar{d}c;~~~~~D^0=\bar{u}c;\\ p&{}=\frac{1}{\sqrt{2}}(du-ud)u;~~~~~n=\frac{1}{\sqrt{2}}(du-ud)d;\\ \Lambda ^0&{}=\frac{1}{\sqrt{2}}(du-ud)s. \end{array} \end{aligned}$$

Table 13 The flavor matrix element $\xi$ for different decay channels of the charmed baryons

With the above flavor wave functions, the flavor matrix elements $\xi$ for different decay processes are presented in Table 13.