1 Introduction

Recent experimental data have shown deviations from standard model (SM) predictions in the ratio of \(R(D^{(*)}) = \mathrm{Br}({\bar{B}} \rightarrow D^{(*)} \tau \nu )/\mathrm{Br}({\bar{B}} \rightarrow D^{(*)} l \nu )\) with \(l = e,\;\mu \) and also in \(b\rightarrow s \mu ^+ \mu ^-\) induced B decays. The experimental values for \(R(D^{(*)})\) [1,2,3,4,5] are larger than the SM predictions [6, 7]. This anomalous effect is significant, at about 4\(\sigma \) level [8]. The anomalies due to the \(b\rightarrow s \mu ^+\mu ^-\) induced processes show up in [9,10,11,12,13] \(B \rightarrow (K,K^*,\phi )\mu ^+\mu ^-\) decays. The observed branching ratios in these decays are lower than the SM predictions [14, 15]. Also a deficit is shown in the ratio \(R_K = \mathrm{Br}(B\rightarrow K\mu ^+\mu ^-)/\mathrm{Br}(B\rightarrow K e^+ e^-)\) [16]. The SM predicts \(R_K\) to be close to 1 [17, 18], but experimental data give [16] \({\varvec{R}}_{\varvec{K}} = 0.745^{+0.090}_{-0.074}\pm 0.036\). These effects are at 2\(\sigma \) to 3\(\sigma \). Needless to say that these anomalies need to be further confirmed experimentally. One also needs to understand the SM predictions better. The processes induced by \(b\rightarrow s\mu ^+\mu ^-\) are rare processes and therefore are sensitive to new physics [15]. The anomaly in \(R(D^{(*)})\) is related to tree level processes, which indicates that there may exist new physics at the tree level already. The anomalies mentioned above have attracted a lot of theoretical attention in trying to solve the problems using new physics beyond SM [6, 7, 14, 15, 19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55, 55,56,57,58,59]. In this work we study the possibility of using the R-parity violating interaction to explain these anomalies. Previously, R-parity violation was invoked to explain [33] \(R(D^{(*)})\) and to explain [56] \(b\rightarrow s \mu ^+\mu ^-\) anomalies separately. The exchange of down type right-handed squark coupled to quarks and leptons yield interactions which are similar to the leptoquark induced interactions that have been proposed to explain the \({\bar{B}} \rightarrow D^{(*)}\rightarrow \tau {\bar{\nu }}\) and \(b\rightarrow s \mu ^+\mu ^-\) induced anomalies simultaneously [59]. However, the Yukawa couplings have severe constraints from other rare processes in B and D decays. We found that this interaction can provide a viable solution to the \(R^{(*)}\) anomaly. But with the severe constraint from \({\bar{B}} \rightarrow K \nu {\bar{\nu }}\), it proves to be impossible to explain the anomalies induced by the \(b\rightarrow s \mu ^+\mu ^-\) process.

The most general renomalizable R-parity violating terms in the superpotentials are [60]

$$\begin{aligned} W_\mathrm{RPV}= & {} \mu _i L_i H_u + {1\over 2} \lambda _{ijk}L_i L_j E^c_k + \lambda ^\prime _{ijk}L_i Q_j D^c_k\nonumber \\&+ {1\over 2} \lambda {''}_{ijk}U^c_iD^c_jD^c_k. \end{aligned}$$
(1)

We will assume that the \(\lambda ''\) term is zero to ensure proton stability. Since the processes we discuss involve leptons and quarks, the \(\lambda '\) term should remain. In fact the interactions induced by this term at the tree and one loop level can contribute to the \({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }}\) and \(b\rightarrow s \mu ^+\mu ^-\) induced processes. It is tempting to see if these interactions can explain the related anomalies already. Although a combination of \(\lambda '\) and \(\lambda \) terms can also contribute, the resulting operators are disfavored by the \({\bar{B}}\rightarrow D^{(*)} \tau {\bar{\nu }}\) process.

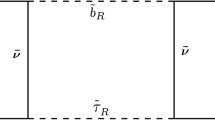
We shall limit ourselves to exchange of the right-handed down type squark, \({\tilde{d}}^k_R\), which are expected to have the necessary ingredients to explain the anomalies in B decays. This model is similar to the leptoquark exchange discussed by many authors [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55], except a general leptoquark also has a right-handed coupling to \(SU(2)_L\) singlets, which is forbidden in SUSY. These additional right-handed couplings turn out to be important for explaining the \(g-2\) anomaly of the muon, but they do not play an essential role in explaining the B anomalies that we are discussing. The object of our paper is a careful consideration of the constraints from various B and D decays and the structure of Yukawa couplings \(\lambda ^\prime _{ijk}\) to see if the B anomalies can be resolved simultaneously. The paper by Bauer and Neubert [59] is closest in spirit to our paper, but we are able to show the tension between different experimental constraints, and we find that it is impossible to solve the \(R(D^{(*)})\) and \(b \rightarrow s \mu ^+\mu ^-\) anomalies simultaneously.

The \(R(D^{(*)})\) and \(b\rightarrow s\mu ^+\mu ^-\) anomalies occur at tree level and loop level in the SM, respectively. To simultaneously solve these anomalous problems using a simple set of beyond SM interactions one faces more constraints [55, 57,58,59] than just solving one of them, as has been done in most of the studies. We find that by exchanging a right-handed down type of squark, it is possible to solve the \(R(D^{(*)})\) anomaly with tree interaction provided \(\lambda ^\prime _{33k}\) is sizable, of order \({\sim } 3\). For anomalies induced by \(b\rightarrow s \mu ^+\mu ^-\), to obtain the right chirality for operators \(O_9\), one needs to go to one loop level. The allowed couplings \(\lambda ^\prime _{ijk}\) are constrained from various experimental data, such as \(K \rightarrow \pi \nu {\bar{\nu }}\), \({\bar{B}} \rightarrow K(K^*) \nu {\bar{\nu }}\), and \(D^0 \rightarrow \mu ^+\mu ^-\). The strongest constraint comes from \({\bar{B}} \rightarrow K(K^*) \nu {\bar{\nu }}\) making it impossible to explain anomalies induced by \(b\rightarrow s \mu ^+\mu ^-\).

2 R-parity violating interactions and \({\bar{B}}\rightarrow D^{(*)} \tau {\bar{\nu }}\)

Expanding the \(\lambda '\) term in terms of fermions and sfermions, we have

$$\begin{aligned} L= & {} \lambda ^{\prime }_{ijk}\big [ {\tilde{\nu }}^i_L {\bar{d}}^k_R d^j_L + {\tilde{d}}^j_L {\bar{d}}^k_R\nu ^i_L + {\tilde{d}}^{k*}_R {\bar{\nu }}^{ci}_L d^j_L\nonumber \\&- {\tilde{l}}^i_L {\bar{d}}^k_R u^j_L - {\tilde{u}}^j_L {\bar{d}}^k_R l^i_L - {\tilde{d}}^{k*}_R {\bar{l}}^{ci}_L u^j_L\big ], \end{aligned}$$
(2)

where the tilde indicates the sparticles, and c indicates charge conjugated fields.

Working in the basis where the down quarks are in their mass eigenstates, \(Q^T = (V^{\mathrm{KM}\dagger }u_L, d_l)\), one replaces \(u^j_L\) in the above by \((V^{\mathrm{KM}\dagger }u_L)^j\). Here \(V^\mathrm{KM}\) is the Kobayashi–Maskawa (KM) mixing matrix for quarks. If experimentally, the mass eigenstate of the neutrino is not identified, one does not need to insert the PMNS mixing matrix for the lepton sector. The neutrinos in the above equation are thus in the weak eigenstates. For leptoquark interactions discussed in Eq. (6) in Ref. [59], the reference seems to indicate that new parameters are involved due to the rotation matrix \(U_e\) in the lepton sector. However, since neutrinos are not in the mass basis in our work, it seems that, provided we are always in the weak basis, no matrix is required in the lepton sector. We will assume that the sfermions are in their mass eigenstate basis. For a discussion of the choice of basis, see Ref. [60]

Exchanging sparticles, one obtains the following four fermion operators at the tree level:

$$\begin{aligned} \mathcal{L}_\mathrm{eff}= & {} {\lambda '_{ijk}\lambda ^{'*}_{i'j'k}\over 2 m^2_{{\tilde{d}}^k_R}} \big [ {\bar{\nu }}^{i'}_L \gamma ^\mu \nu ^i_L {\bar{d}}^{j'}_L \gamma _\mu d_L^j + {\bar{e}}^{i'}_L \gamma ^\mu e^i_L ({\bar{u}}_L V^\mathrm{KM})^{j'}\nonumber \\&\times \gamma _\mu (V^{\mathrm{KM}\dagger }u_L)^j -\nu ^{i'}_L \gamma ^\mu e^i_L {\bar{d}}^{j'}_L \gamma _\mu (V^{\mathrm{KM}\dagger }u_L)^j\nonumber \\&-{\bar{e}}^{i'}_L \gamma ^\mu \nu ^i_L ({\bar{u}}_LV^\mathrm{KM})^{j'} \gamma _\mu d^j_L\big ]\nonumber \\&-{\lambda '_{ijk}\lambda ^{'*}_{i'jk'}\over 2m^2_{{\tilde{d}}^j_L} } {\bar{\nu }}^{i'}_L \gamma ^\mu \nu ^i_L {\bar{d}}^k_R \gamma _\mu d^{k'}_R\nonumber \\&-{\lambda '_{ijk}\lambda ^{'*}_{i'jk'}\over 2m^2_{{\tilde{u}}^j_L}} {\bar{e}}^{i'}_L \gamma ^\mu e^i_L {\bar{d}}^k_R \gamma _\mu d^{k'}_R \nonumber \\&-{\lambda '_{ijk}\lambda ^{'*}_{ij'k'}\over 2m^2_{{\tilde{e}}^i_L}} ({\bar{u}}_{L\beta } V^\mathrm{KM})^{j'} \gamma ^\mu (V^{\mathrm{KM}\dagger }u_{L\alpha })^j \nonumber \\&\times {\bar{d}}^k_{R\alpha } \gamma _\mu d^{k'}_{R\beta } - {\lambda '_{ijk}\lambda ^{'*}_{ij'k'}\over 2m^2_{{\tilde{\nu }}^i_L}} {\bar{d}}^{j'}_{L\beta } \gamma ^\mu d^j_{L\alpha } {\bar{d}}^k_{R\alpha } \gamma _\mu d^{k'}_{R\beta }. \end{aligned}$$
(3)

In the above \(\alpha \) and \(\beta \) are color indices.

At the tree level, besides the SM contributions to \({\bar{B}}\rightarrow D^{(*)} l {\bar{\nu }}\), there are also R-parity violating contributions, they are given by the term proportional to \( - (\lambda '_{l3k}\lambda ^{\prime *}_{l'mk}/2 m^2_{{\tilde{d}}^k_R}){\bar{l}}_L \gamma ^\mu \nu ^{l'}_L ({\bar{u}}_LV^\mathrm{KM})^{m} \gamma _\mu b_L\) in the above equation. Including the SM contributions one obtains [33]

$$\begin{aligned} H_\mathrm{eff}= & {} -{4G_F\over \sqrt{2}}V_{m3} (\delta ^{l'}_l + \Delta ^{l'm}_l) {\bar{l}} \gamma ^\mu P_L \nu _{l'} {\bar{u}}^m\gamma _\mu P_L b_L,\nonumber \\ \Delta ^{l,m}_{l'}= & {} {\sqrt{2}\over 4 G_F} {\lambda ^\prime _{l3k} \lambda ^{\prime *}_{l' j' k}\over 2 m^2_{{\tilde{d}}^k_R}}{V_{mj'}\over V_{m3}}, \end{aligned}$$
(4)

where \(V_{ij}\) are elements in \(V^\mathrm{KM}\).

Identifying different charged leptons in the final states, we find the ratio \(R^\mathrm{SM}_l(c) = \mathrm{Br}({\bar{B}}\rightarrow D^{(*)} l \nu )/\mathrm{Br}({\bar{B}} \rightarrow D^{(*)} l \nu )_\mathrm{SM}\) of branching ratios compared with SM predictions to be given by

$$\begin{aligned}&R^\mathrm{SM}_\tau (c) = \vert \Delta _1^{3,2}\vert ^2 + \vert \Delta _2^{3,2}\vert ^2 + \vert 1+\Delta _3^{3,2}\vert ^2,\nonumber \\&R^\mathrm{SM}_\mu (c) = \vert \Delta _1^{2,2}\vert ^2 + \vert 1+\Delta _2^{2,2}\vert ^2 + \vert \Delta _3^{2,2}\vert ^2,\nonumber \\&R^\mathrm{SM}_e(c) = \vert 1+\Delta _1^{1,2}\vert ^2+\vert \Delta _2^{1,2}\vert ^2 +\vert \Delta _3^{1,2}\vert ^2. \end{aligned}$$
(5)

One can define a similar quantity \(R^\mathrm{SM}_l(u)\) for \(\mathrm{Br}({\bar{B}}\rightarrow (\rho , \pi ) l \nu )/\mathrm{Br}({\bar{B}} \rightarrow (\rho , \pi ) l \nu )_\mathrm{SM}\) and \(\mathrm{Br}({\bar{B}}\rightarrow l \nu )/\mathrm{Br}({\bar{B}} \rightarrow l \nu )_\mathrm{SM}\), and we have

$$\begin{aligned} R^\mathrm{SM}_l(u)={\mathrm{Br}({\bar{B}}\rightarrow (\rho , \pi ) l \nu )\over \mathrm{Br}({\bar{B}} \rightarrow (\rho , \pi ) l \nu )_\mathrm{SM}}={\mathrm{Br}({\bar{B}}\rightarrow l \nu )\over \mathrm{Br}({\bar{B}} \rightarrow l \nu )_\mathrm{SM}}. \end{aligned}$$
(6)

Experimentally, the deviation of \(R^\mathrm{SM}_{e}\) from the SM prediction is small, that is, \(R^\mathrm{SM}_{e} \approx 1\), therefore we require \(\Delta _i^{1,2}\) to be close to zero, which can be achieved by setting \(\lambda ^\prime _{1jk} = 0\), so that no linear terms in \(\Delta ^{i,j}_k\) contribute to \({\bar{B}}\rightarrow D^{(*)} e {\bar{\nu }}_e\). No large deviation has been observed in \(R^\mathrm{SM}_\mu \). However, \(b\rightarrow s\mu ^+\mu ^-\) induced anomalies involve \(\mu \) couplings and therefore \(R^\mathrm{SM}_\mu (c)\) will be affected at some level. One may even contemplate that a somewhat enhanced \({\bar{B}}\rightarrow D^{(*)} \mu {\bar{\nu }}_\mu \) must be there if one tries to solve the \(b\rightarrow s \mu ^+\mu ^-\) anomalies simultaneously. Although such a large deviation has not been observed, theoretical calculations for the absolute values for the SM predictions and the experimental measurements may have some errors, so a certain level of deviation can be tolerated. We will take a conservative attitude to only allow up to 10% deviation from the SM value in \(R^\mathrm{SM}_\mu (c)\). We find that even such a modest requirement puts a stringent constraint, making the attempt of simultaneously solving the two types of anomalies difficult.

Defining \(r({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }}) = R({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }})/R({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }})_\mathrm{SM}\), we have

$$\begin{aligned} r({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }}) = {2R^\mathrm{SM}_\tau (c)\over R^\mathrm{SM}_\mu (c)+R^\mathrm{SM}_e(c)}. \end{aligned}$$
(7)

Changing c to u, one can obtain the R-parity violating contributions to \(R({\bar{B}} \rightarrow (\rho , \pi ) \tau \nu )\). With the same approximation as above, we have

$$\begin{aligned} r({\bar{B}} \rightarrow \tau {\bar{\nu }})=r({\bar{B}} \rightarrow (\rho , \pi ) \tau {\bar{\nu }})={2R^\mathrm{SM}_\tau (u)\over R^\mathrm{SM}_\mu (u)+R^\mathrm{SM}_e(u)}.\nonumber \\ \end{aligned}$$
(8)

The linear terms in \(r({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }})\) and \(r({\bar{B}} \rightarrow \tau {\bar{\nu }})\) are proportional to

$$\begin{aligned}&(2 \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{31k} - \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{21k}){V_{cd}\over V_{cb}}+ (2\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32k}- \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{22k}){V_{cs}\over V_{cb}}\\&\quad +(2 \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{33k} - \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{23k}) \end{aligned}$$

and

$$\begin{aligned}&(2 \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{31k} - \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{21k}){V_{ud}\over V_{ub}}+ (2\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32k}- \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{22k}){V_{us}\over V_{ub}}\\&\quad +(2 \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{33k} - \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{23k}), \end{aligned}$$

respectively. Note that there is a large enhancement factor \((V_{ud}/V_{ub})/(V_{cb}/V_{cd})\) for the first term in the expression for \(r({\bar{B}} \rightarrow \tau {\bar{\nu }})\) compared with \(r({\bar{B}} \rightarrow D^{(*)}\tau {\bar{\nu }})\). This may cause a problem for a small deviation from 1 in \(r({\bar{B}} \rightarrow D^{(*)}\tau {\bar{\nu }})\) to a large deviation in \(r({\bar{B}} \rightarrow \tau {\bar{\nu }})\). One can avoid such a large enhancement by setting \(\lambda ^{\prime }_{31k, 21k}\) to be much smaller than other terms. In our later discussions we will set \(\lambda ^{\prime }_{31k}\) to be zero. The \(\lambda ^{\prime }_{21k}\) is also constrained to be small from \(D^0 \rightarrow \mu ^+\mu ^-\) decay, as to be discussed in the following. But it may play an important role in \(b\rightarrow s \mu ^+\mu ^-\) decay. We will consider it in our discussions.

The SM predictions and experimental measurements for \(R(D^{(*)})\) are [8]

$$\begin{aligned}&R(D)_\mathrm{SM} = 0.300\pm 0.008, \nonumber \\&R(D) = 0.397 \pm 0.040 \pm 0.028,\nonumber \\&R(D^*)_\mathrm{SM} = 0.252\pm 0.003,\nonumber \\&R(D^*) = 0.316 \pm 0.016 \pm 0.010. \end{aligned}$$
(9)

The R-parity violating contributions to both R(D) and \(R(D^*)\) occur in a similar way, we use the averaged \(r({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }})_\mathrm{ave} = 1.266\pm 0.070\) of \(r({\bar{B}}\rightarrow D \tau {\bar{\nu }})\) and \(r({\bar{B}} \rightarrow D^* \tau {\bar{\nu }})\) to represent the anomaly. In the SM, \(r_\mathrm{ave} = 1\). To obtain a \(r_\mathrm{ave}\) within the \(1\sigma \) region, \(\lambda ^\prime _{33k}\) is typically required to be of order \({\sim } 3\). This large coupling makes it worrisome for this scenario from a unitarity consideration. In more general terms, the unitarity limits concern the upper bound constraints on the coupling constants imposed by the condition of a scale evolution between the electroweak and the unification scales, free of divergences or Landau poles for the entire set of coupling constants. If so, the R-parity couplings are constrained to be about 1 at the TeV scale [60]. A value of 3 is not consistent. The requirement of there being no Landau pole up to the unification scale may not be necessary if some new physics appears. One cannot for sure rule out the possibility of reaching the unitarity bound of \(\sqrt{4\pi }\) at a lower energy. However, when attempting to also solve \(b\rightarrow s \mu ^+\mu ^-\) induced anomalies, the model becomes much more constrained.

3 Constraints from other tree level processes

Several other rare processes may receive tree level R-parity violating contributions. The constraints from these processes should be taken into account. We now study a few of the relevant ones: \(K \rightarrow \pi \nu {\bar{\nu }}\), \({\bar{B}} \rightarrow K (K^{*}) \nu {\bar{\nu }}\), and \(D^0 \rightarrow \mu ^+\mu ^-\).

The possible terms generating these decays are

$$\begin{aligned}&{\lambda '_{ijk}\lambda ^{'*}_{i'j'k}\over 2 m^2_{{\tilde{d}}^k_R}} {\bar{\nu }}^{i'}_L \gamma ^\mu \nu ^i_L {\bar{d}}^{j'}_L \gamma _\mu d_L^j,\nonumber \\&\quad {\lambda '_{ijk}\lambda ^{'*}_{i'j'k}\over 2 m^2_{{\tilde{d}}^k_R}} {\bar{e}}^{i'}_L \gamma ^\mu e^i_L ({\bar{u}}_L V^\mathrm{KM})^{j'}\gamma _\mu (V^{\mathrm{KM}\dagger }u_L)^j,\nonumber \\&{\lambda '_{ijk}\lambda ^{'*}_{i'jk'}\over 2m^2_{{\tilde{d}}^j_L} } {\bar{\nu }}^{i'}_L \gamma ^\mu \nu ^i_L {\bar{d}}^k_R \gamma _\mu d^{k'}_R,\quad {\lambda '_{ijk}\lambda ^{'*}_{i'jk'}\over 2m^2_{{\tilde{u}}^j_L}} {\bar{e}}^{i'}_L \gamma ^\mu e^i_L {\bar{d}}^k_R \gamma _\mu d^{k'}_R.\nonumber \\ \end{aligned}$$
(10)

If \(\lambda ^\prime _{ijk}\) is non-zero for k restricted to only one value, the two terms on the second line in the above equation will not induce the unwanted decays in question. For simplicity, we will work with this assumption.Footnote 1

\(D^0\rightarrow \mu ^+\mu ^-\) decay in the SM is extremely small. In our case, there are tree contributions. The effective Hamiltonian is given by

$$\begin{aligned} H_\mathrm{eff}= & {} - {1\over 2 m^2_{{\tilde{d}}^k_R}} C^k_{D\mu \mu }\mu _L\gamma _\mu \mu _L {\bar{u}}_L \gamma ^\mu c_L,\nonumber \\ C^k_{D\mu \mu }= & {} \lambda ^\prime _{2jk}\lambda ^{\prime *}_{2j'k}V_{1j'}V^*_{2j}\nonumber \\= & {} ( \lambda ^\prime _{21k}V^*_{21} + \lambda ^\prime _{22k}V^*_{22} + \lambda ^\prime _{23k}V^*_{23} )\nonumber \\&\times (\lambda ^{\prime *}_{21k}V_{11} + \lambda ^{\prime *}_{22k}V_{12} + \lambda ^{\prime *}_{23k}V_{13}). \end{aligned}$$
(11)

The decay width is given by

$$\begin{aligned} \Gamma (D^0\rightarrow \mu ^+\mu ^-) = {1 \over 128 \pi } \left| {C^k_{D\mu \mu }\over m^2_{{\tilde{d}}^3_R}} \right| ^2 f_D^2 m_D m^2_\mu \sqrt{1-{4 m^2_\mu \over m^2_D}},\nonumber \\ \end{aligned}$$
(12)

where \(f_D = 212(1)\) MeV [61] is the \(D^0\) decay constant.

Using an experimental upper bound on the branching ratio [62] \(6.2\times 10^{-9}\) at 90% C.L. for \(D^0\rightarrow \mu ^+\mu ^-\), we have \(\vert C^k_{D\mu \mu }{(1\,\text{ TeV })^2 /m^2_{{\tilde{d}}^k_R}}\vert < 6.1\times 10^{-2}\). With \(\lambda ^\prime _{21k, 22k}\) set to zero, \(C^k_{D\mu \nu }\) is given by \(C^k_{D\mu \mu } = \lambda ^{\prime }_{23k}\lambda ^{\prime *}_{23k}V_{ub}V_{cb}^*\). We have \(\lambda ^\prime _{23k} \lambda ^{\prime *}_{23k}(1\,\text{ TeV })^2 / m^2_{{\tilde{d}}^k_R} < (20)^2\). \(\lambda ^\prime _{23k}\) is only very loosely constrained from \(D^0\rightarrow \mu +\mu ^-\). If just \(\lambda ^\prime _{21k}\) or \(\lambda ^\prime _{22k}\) is non-zero, they are constrained to be

$$\begin{aligned} \lambda ^\prime _{21k} \lambda ^{\prime *}_{21k}{(1\,\text{ TeV })^2 \over m^2_{{\tilde{d}}^k_R}},\quad \lambda ^\prime _{22k} \lambda ^{\prime *}_{22k}{(1\,\text{ TeV })^2 \over m^2_{{\tilde{d}}^k_R}} < 0.28. \end{aligned}$$
(13)

These constraints on \(\lambda ^\prime _{21k}\) and \(\lambda ^\prime _{22k}\) make their effects on \(b\rightarrow s\mu ^+\mu ^-\) small. Later we will show that even a small \(\lambda ^\prime _{22k}\) may play some important role for the \(R(D^{(*)})\) and \(b\rightarrow s \mu ^+\mu ^-\) anomalies.

For \(K \rightarrow \pi \nu {\bar{\nu }}\), the ratio of \(R_{K\rightarrow \pi \nu {\bar{\nu }}} =\Gamma _\mathrm{RPV}/\Gamma _\mathrm{SM}\) is given by [63]

$$\begin{aligned} R_{K\rightarrow \pi \nu {\bar{\nu }}}= & {} \sum _{i=,e,\mu ,\tau }{1\over 3}\left| 1 +{\Delta ^\mathrm{RPV}_{\nu _i{\bar{\nu }}_i}\over X_0(x_t) V_{ts}V^*_{td}} \right| ^2\nonumber \\&+ {1\over 3} \sum _{i\ne i'} \left| {\Delta ^\mathrm{RPV}_{\nu _i{\bar{\nu }}_{i'} }\over X_0(x_t)V_{ts}V^*_{td} }\right| ^2,\nonumber \\ \Delta ^\mathrm{RPV}_{\nu _i {\bar{\nu }}_{i'}}= & {} {\pi s^2_W \over \sqrt{2} G_F \alpha } \left| -{\lambda ^{\prime }_{i2k}\lambda ^{\prime *}_{i' 1 k} \over 2 m^2_{{\tilde{d}}^k_R}} \right| ^2,\nonumber \\ X_0(x)= & {} {x(2+x)\over 8(x - 1)} + {3x(x-2)\over 8(x-1)^2}\ln x, \end{aligned}$$
(14)

where \(x_t = m^2_t/m^2_W\).

Combining the SM prediction [64] for the branching ratio and experimental information [62] \(\mathrm{Br} = (1.7\pm 1.1)\times 10^{-10}\), at \(2\sigma \) level, \(\lambda ^{\prime }_{i2k}\lambda ^{\prime *}_{i'1k}\) are constrained to be less than a few times of \(10^{-3} (m^2_{d^k_R}/ (1\,\text{ TeV })^2)\). Since we will set \(\lambda ^{\prime *}_{i1k}=0\), this process is not affected at tree level.

The expressions for \(R_{{\bar{B}} \rightarrow \pi \nu {\bar{\nu }}}\) and \(R_{{\bar{B}} \rightarrow K(K^*)\nu {\bar{\nu }}}\) of \({\bar{B}}\rightarrow \pi \nu {\bar{\nu }}\) and \({\bar{B}} \rightarrow K(K^*)\nu {\bar{\nu }}\) can be obtained from Eq. (14) by replacing \(V_{ts}V^*_{td}\) to \(V_{tb}V^*_{td}\) and \(V_{tb}V^*_{ts}\), respectively. The corresponding \(\Delta ^\mathrm{RPV}_{\nu _i {\bar{\nu }}_{i'}}\) are as follows:

$$\begin{aligned}&\text{ For }\; {\bar{B}}\rightarrow \pi \nu {\bar{\nu }}: \quad \Delta ^\mathrm{RPV}_{\nu _i {\bar{\nu }}_{i'}} = {\pi s^2_W \over \sqrt{2} G_F \alpha } \left| -{\lambda ^{\prime }_{i3k}\lambda ^{\prime *}_{i' 1 k} \over 2 m^2_{{\tilde{d}}^k_R}} \right| ^2.\nonumber \\&\text{ For }\; {\bar{B}}\rightarrow K(K^*) \nu {\bar{\nu }}: \quad \Delta ^\mathrm{RPV}_{\nu _i {\bar{\nu }}_{i'}} = {\pi s^2_W \over \sqrt{2} G_F \alpha } \left| -{\lambda ^{\prime }_{i3k}\lambda ^{\prime *}_{i' 2 k} \over 2 m^2_{{\tilde{d}}^k_R}} \right| ^2.\nonumber \\ \end{aligned}$$
(15)

For \(B\rightarrow \pi \nu {\bar{\nu }}\), since we have set \(\lambda ^\prime _{i1k} = 0\), it is again not affected by R-parity violating interactions in this model.

The process \({\bar{B}}\rightarrow K(K^{*}) \nu {\bar{\nu }}\) will be affected. We have the following non-zero \(\Delta ^\mathrm{RPV}_{\nu {\bar{\nu }}}\):

$$\begin{aligned}&\Delta ^\mathrm{RPV}_{\nu _\mu {\bar{\nu }}_\mu } = -{\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{22k} \over 2 m^2_{d^k_R}}{\pi s^2_W\over \sqrt{2} G_F \alpha },\quad \Delta ^\mathrm{RPV}_{\nu _\tau {\bar{\nu }}_\tau } = -{\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32k} \over 2 m^2_{d^k_R}}{\pi s^2_W\over \sqrt{2} G_F \alpha },\nonumber \\&\Delta ^\mathrm{RPV}_{\nu _\tau {\bar{\nu }}_\mu } = -{\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{22k} \over 2 m^2_{d^k_R}}{\pi s^2_W\over \sqrt{2} G_F \alpha },\quad \Delta ^\mathrm{RPV}_{\nu _\mu {\bar{\nu }}_\tau } = -{\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{32k} \over 2 m^2_{d^k_R}}{\pi s^2_W\over \sqrt{2} G_F \alpha }.\nonumber \\ \end{aligned}$$
(16)

Experimental data from BaBar [65] and Belle [66] give \(R_{B\rightarrow K(K^*) \nu {\bar{\nu }}} <4.3 (4.4)\), implying that \(\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{22k}\), \(\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32k}\), \(\lambda ^{\prime }_{33k}\lambda ^{\prime *}_{22k}\), and \(\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{32k}\) are constrained from \({\bar{B}}\rightarrow K(K^*)\nu {\bar{\nu }}\). We shall return to this later.

4 Loop contributions for \(b\rightarrow s \mu ^+\mu ^-\) induced anomalies

The anomalous effects in \(b\rightarrow s\mu ^+\mu ^-\) induced processes are only 2\(\sigma \) to 3\(\sigma \) effects and need to be confirmed further. They may be due to our poor understanding of the hadronic matrix elements involved, and they may also be caused by new physics beyond SM. We now discuss how the R-parity violating interaction may help to solve the problems.

New physics contributing to \(b\rightarrow s l {\bar{l}}\) can be parametrized as \(H^\mathrm{NP}_\mathrm{eff} = \sum C^\mathrm{NP}_i O_i\). Some of the most studied operators \(O_i\) are

$$\begin{aligned}&O_9 = {\alpha \over {4\pi } }{\bar{s}} \gamma ^\mu P_L b {\bar{\mu }}\gamma _\mu \mu ,\quad O^{\prime }_9 = {\alpha \over {4\pi }} {\bar{s}} \gamma ^\mu P_R b {\bar{\mu }}\gamma _\mu \mu ,\nonumber \\&O_{10} = {\alpha \over {4\pi }} {\bar{s}} \gamma ^\mu P_L b {\bar{\mu }}\gamma _\mu \gamma _5 \mu ,\quad O^{\prime }_{10} = {\alpha \over {4\pi }} {\bar{s}} \gamma ^\mu P_R b {\bar{\mu }}\gamma _\mu \gamma _5 \mu ,\nonumber \\ \end{aligned}$$
(17)

where \(P_{L,R} = (1\mp \gamma _5)/2\).

The SM predictions are \(C^\mathrm{SM}_9 \approx - C^\mathrm{SM}_{10} = 4.1\). A global analysis shows that to explain the anomalies in decays induced by \(b\rightarrow s \mu ^+\mu ^-\), there are few scenarios where the anomalies can be explained with high confidence level and all cases \(C^\mathrm{NP}_9\) need to be around −1 [14]. For example with \(C^\mathrm{NP}_9 = -1.09\) and \(C^\mathrm{NP}_{10}\), \(C^{\prime , \mathrm{NP}}_{9,10} = 0\) with a 4.5 pull, the cases with \(C^\mathrm{NP}_9 = - C^{\prime , \mathrm{NP}}_{9}\), the best fit values are \(C^\mathrm{NP}_{9} = -C^{\prime , \mathrm{NP}}_{9} = -1.06\) and the others equal to zero with a 4.8 pull; and the case with \(C^\mathrm{NP}_9 = - C^\mathrm{NP}_{10}\), the best fit values are \(C^\mathrm{NP}_{9} = -C^\mathrm{NP}_{10} = -0.68\) and others equal to zero with a 4.2 pull. Here the number of “pulls” indicates by how many sigmas the best fit point is preferred over the SM point for a given scenario. The higher the pull, the better fit between theory and experimental data is reached. In our case, the R-parity violating contribution to be discussed belongs to the last case. For this case, the \(1\sigma \) allowed range is [14] −0.85 to −0.5. With a negative value for \(C^\mathrm{NP}_9\), the new physics contribution reduces the strength of the \(b\rightarrow s \mu ^+\mu ^-\) interaction and therefore helps to explain why \(B \rightarrow (K,K^*,\phi )\mu ^+\mu ^-\) branching ratios and \(R_K\) are smaller than those predicted by SM.

There is a potential contribution to \(b\rightarrow s \mu ^+\mu ^-\) at tree level due to a term proportional to \(\lambda '_{ijk}\lambda ^{'*}_{i'jk'}/2m^2_{{\tilde{u}}^j_L} {\bar{e}}^{i'}_L \gamma ^\mu e^i_L {\bar{d}}^k_R \gamma _\mu d^{k'}_R\). However, since we assume that there is only one non-vanishing value for k, \(b\rightarrow s \mu ^+\mu ^-\) is not induced by this contribution.

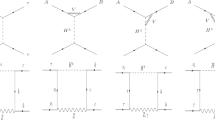
One needs to include one loop contributions. At one loop level, exchanging \({\tilde{d}}^k_R\) in the loop, the contribution for \(C^\mathrm{NP}_{9}\) with \(C^\mathrm{NP}_{9} = -C^\mathrm{NP}_{10}\) can be generated with

$$\begin{aligned}&C^{\mathrm{NP},l {\bar{l}}'}_{9} \approx {m^2_q\over 8\pi \alpha } {1\over m^2_{{\tilde{d}}^k_R}} \lambda ^{\prime }_{ l b k}\lambda ^{\prime *}_{{\bar{l}}' m k} {V_{qm}V^{ *}_{ts}\over V_{tb} V^{ *}_{ts}}\nonumber \\&\quad -{\sqrt{2}\over 64 \pi \alpha G_F} {\ln (m^2_{{\tilde{d}}^k_R}/m^2_{{\tilde{d}}^{k'}_R}) \over m^2_{{\tilde{d}}^k_R} - m^2_{{\tilde{d}}^{k'}_R}} \lambda ^{\prime }_{ibk}\lambda ^{\prime *}_{is k'} \lambda ^{\prime }_{l j k'}\lambda ^{\prime *}_{{\bar{l}}' j k} {1 \over V_{tb} V^{*}_{ts}},\nonumber \\ \end{aligned}$$
(18)

where \(m_q\) is the up type quark mass. The first term is induced by exchanging a W boson and a sparticle \({\tilde{d}}^k_R\), and the second term is induced by exchanging two sparticles \({\tilde{d}}^k_R\) in the loops. The term of interest corresponds to \(l=2\), \({\bar{l}}'=2\), \(s=2\), and \(b=3\) for the process \(b\rightarrow s \mu ^+ \mu ^-\). One can relabel them with different numbers for other processes.

The first term is dominated by \(q=t\), its contribution to \(C_9^{\mathrm{NP},\mu {\bar{\mu }}}\) is about \(0.16 \lambda ^\prime _{23k}\lambda ^{\prime *}_{23k}(1\,\text{ TeV }/m_{{\tilde{d}}^k_R})^2\). This is a “wrong sign” contribution to explain the \(b\rightarrow s\mu ^+\mu ^-\) induced anomalies.Footnote 2 With \(\lambda ^\prime _{1jk} = 0\) and \(\lambda ^\prime _{i1k} =0\) from the considerations of no processes with electrons one has shown anomalies and a \(K\rightarrow \pi \nu {\bar{\nu }}\) constraint, and restricting k to have only one value, we have

$$\begin{aligned} C^{\mathrm{NP}, l {\bar{l}}'}_{9}\approx & {} {m^2_t\over 8\pi \alpha } {1\over m^2_{{\tilde{d}}^k_R}} \lambda ^{\prime }_{ l3 k}\lambda ^{\prime *}_{{\bar{l}}' 3 k} \nonumber \\&-{\sqrt{2}\over 64 \pi \alpha G_F} {1\over m^2_{{\tilde{d}}^3_R}} (\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{22 k}+ \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32 k})\nonumber \\&\times (\lambda ^\prime _{l2k}\lambda ^{\prime *}_{{\bar{l}}' 2k}+\lambda ^\prime _{l3k}\lambda ^{\prime *}_{{\bar{l}}' 3k} ) {1 \over V_{tb} V^{*}_{ts}}\nonumber \\= & {} \big (0.157 \lambda ^{\prime }_{ l3 k}\lambda ^{\prime *}_{{\bar{l}}'3 k} +2.0 (\lambda ^{\prime }_{23k}\lambda ^{\prime *}_{2 2 k}+ \lambda ^{\prime }_{33k}\lambda ^{\prime *}_{32 k})\nonumber \\&\times (\lambda ^\prime _{l2k}\lambda ^{\prime *}_{{\bar{l}}'2k}+\lambda ^\prime _{l 3k}\lambda ^{\prime *}_{{\bar{l}}' 3k} )\big ){(1\,\text{ TeV })^2\over m^2_{{\tilde{d}}^k_R}}. \end{aligned}$$
(19)
Fig. 1
figure 1

\(C^\mathrm{NP}_9\), \(r_\mathrm{ave}\) and \(R^\mathrm{SM}_{\mu }(c)\) as functions of \(\lambda ^\prime _{23k}\) from left to right, respectively. To get \(R^\mathrm{SM}_{\mu }(c)-1\) down to 10%, one needs to go to the lower range, the \(3{\sigma }\) range for \(C^\mathrm{NP}_9\), to about −0.18 [14]. However, in that case, \(r_\mathrm{ave}\) also gets lower and cannot explain the observed \(R(D^{(*)})\) anomaly

Full size image

5 Numerical analysis

We are now in a position to put things together to see if R-parity violating interactions may be able to explain the \(R(D^{(*)})\) and \(b\rightarrow s \mu ^+\mu ^-\) anomalies simultaneously. For the KM parameters we use those given in Particle Data Group [62]. The aim is to produce values for \(r({\bar{B}}\rightarrow D^{(*)}\tau {\bar{\nu }})_\mathrm{ave}\) and \(C_{9}^\mathrm{NP}\) as close as possible to their central values, 1.266 and \(-0.68\). At the same time we have to restrict \(R_{{\bar{B}} \rightarrow K(K^*)\nu {\bar{\nu }}}\) to be less than 4.3 to satisfy experimental bound.

If one just needs to solve the \(R(D^{(*)})\) anomaly, one can easily obtain the central value of \(r_\mathrm{ave}-1 = 0.266\) by setting all other \(\lambda ^\prime _{ijk}\) to zero except \(\lambda ^\prime _{33k}\) with its value given by \(2.95(m_{{\tilde{d}}^k_B}/1\,\text{ TeV })\). If \(m_{{\tilde{d}}^k_R}\) is way above TeV, then the coupling will violate the unitarity bound of \(\sqrt{4\pi }\). Therefore for the theory to work perturbatively, one expects the squark mass to be less than a TeV or so and it can be looked for at the LHC. With this choice of \(\lambda ^\prime \) the SM predictions for \(R_{{\bar{B}}\rightarrow K \nu {\bar{\nu }},\;K\rightarrow \pi \nu {\bar{\nu }}}\) and \(\Gamma (D^0\rightarrow \mu ^+\mu ^-)\) will not be affected, and \(R^\mathrm{SM}_{e,\mu }(c,u) = 1\). One also predicts \(r({\bar{B}} \rightarrow D^{(*)}\tau {\bar{\nu }}) = r({\bar{B}}\rightarrow \tau {\bar{\nu }})=1.26\). This can be tested by future experimental data. This is the scenario discussed in Ref. [33]. One can try to ease the unitarity bound by including the \(\lambda ^\prime _{33k}\lambda ^{\prime *}_{32k}\) term with positive sign so that a smaller \(\lambda ^\prime _{33k}\) value is allowed.

We now discuss the contributions to \(C^\mathrm{NP}_9\) from Eq. (19). Note that the first term in that equation is always positive; one needs a larger second term with negative sign to produce the required value. If one just needs to satisfy this equation, one can easily find solutions. For example, taking \(\lambda ^\prime _{23k} = 3.0\), one just needs to have \(\lambda ^\prime _{23k}\lambda ^{\prime *}_{22k} + \lambda ^\prime _{33k}\lambda ^{\prime *}_{32k}\) to be about −0.046 to produce \(C^\mathrm{NP}_9\sim -0.68\).

One, however, has to consider other constraints. A particularly important constraint is from Eq. (16), \(R_{{\bar{B}}\rightarrow K \nu {\bar{\nu }}} <4.3\). To produce a negative \(C^\mathrm{NP}_9\), \(\lambda ^\prime _{23k}\lambda ^{\prime *}_{22k} + \lambda ^\prime _{33k}\lambda ^{\prime *}_{32k}\) needs to be negative. From the \(R_{{\bar{B}} \rightarrow K \nu {\bar{\nu }}}\) constraint, each of \(r_{2322}=\lambda ^\prime _{23k}\lambda ^{\prime *}_{22k}\) and \(r_{3332}=\lambda ^\prime _{33k}\lambda ^{\prime *}_{32k}\) is constrained to be larger than \(-0.09\). But in general they appear together in order to produce the value required for \(C^\mathrm{NP}_9\). This also leads to non-zero values for \(r_{2332}=\lambda ^\prime _{23k}\lambda ^{\prime *}_{32k}\) and \(r_{3322}=\lambda ^\prime _{33k}\lambda ^{\prime *}_{22k}\), increasing the value for \(R_{{\bar{B}} \rightarrow K \nu {\bar{\nu }}}\). We find that all \(r_{ijkl}=-0.0436\) having the same value maximizes the size of \(C^\mathrm{NP}_9\), while it minimizes \(R_{{\bar{B}}\rightarrow K\nu {\bar{\nu }}}\). For this case, using \(C^\mathrm{NP}_9 = -0.68\) and \(R_{{\bar{B}} \rightarrow K \nu {\bar{\nu }}} <4.3\), we find \(\lambda ^\prime _{33k,23k} = 6.3\) and a small value for \(\lambda ^\prime _{22,32} =-0.0068\). With the above values for \(\lambda ^\prime \), the constraints from \(D^0\rightarrow \mu ^+\mu ^-\) can be satisfied. However, the predicted value for \(r_\mathrm{ave}\) becomes 1.48 and \(R^\mathrm{SM}_\mu (c)\) is about 2.9. These values are ruled out by existing data. Also the solution with \(\lambda ^\prime _{33k,23k} = 6.3\) is problematic because it violates the unitarity bound and therefore is not a viable solution either. In Fig. 1, we show \(C^\mathrm{NP}_9\), \(r_\mathrm{ave}\) and \(R^\mathrm{SM}_{\mu }(c)\) as functions of \(\lambda ^\prime _{23k}\). We see a smaller \(C^\mathrm{NP}_9\) in size may relax the situation, but within 1\(\sigma \) range for \(C^\mathrm{NP}_9\), the values for \(R^\mathrm{SM}_{\mu ,\tau }(c)\) are too large to allow the model to be viable.

We have searched a wide range of parameter space for \(\lambda ^\prime \) including the case with complex numbers and found no solutions which can simultaneously satisfy the bounds on \(R_{{\bar{B}} \rightarrow K\nu {\bar{\nu }}}\) and \(R^\mathrm{SM}_\mu (c)\), and at the same time to solve anomalies in \(R(D^{(*)})\) and \(b\rightarrow s \mu ^+\mu ^-\).

6 Conclusions

We have studied the possibility of explaining the enhancement in semileptonic decays of \({\bar{B}} \rightarrow D^{(*)} \tau {\bar{\nu }}\) and the anomalies induced by \(b\rightarrow s\mu ^+\mu ^-\) within the framework of R-parity violating (RPV) MSSM. The exchange of the down type right-handed squark coupled to quarks and leptons yields interactions which are similar to leptoquark induced interactions which have been proposed to explain the \({\bar{B}} \rightarrow D^{(*)}\rightarrow \tau {\bar{\nu }}\) by tree level interactions and \(b\rightarrow s \mu ^+\mu ^-\) induced anomalies by loop interactions, simultaneously. However, we find that the Yukawa couplings have severe constraints from other rare processes in B and D decays. This interaction can provide a viable solution to the \(\varvec{R}({\varvec{D}(*)})\) anomaly. But with the severe constraint from \({\bar{B}} \rightarrow K \nu {\bar{\nu }}\), it proves impossible to explain the anomalies induced by \(b\rightarrow s \mu ^+\mu ^-\). This conclusion also applies equally to the leptoquark model proposed in Ref. [59].