1 Introduction

Many astronomical observations (type Ia supernova, large scale structure, and cosmic microwave background radiation) predict that our universe is expanding at an accelerating rate in its present stage [1,2,3]. These observations suggest two cosmic phases, i.e., the cosmic state before radiation (the primordial inflationary era) and ultimately the present cosmos phase after the matter dominated era. In the last couple of decades, it has been speculated that the source for this observed cosmic acceleration with an unusual anti-gravitational force may be an unknown energy component, dubbed dark energy (DE). The existence of this energy with large negative pressure can be recognized by its distinctive nature from ordinary matter which may lead to cosmic expansion. The study of the dominant contents of matter distribution in the universe has remained one of the most challenging issues. Recent observations show that the visible part of our universe is made up of baryonic matter contributing only \(5\%\) of the total budget, while the remaining ingredients yield the total energy density composed of non-baryonic fluids (\(68\%\) DE and \(27\%\) dark matter) [4, 5].

Several cosmological proposals have been introduced in the literature to explore the ambiguous nature of DE. The cosmological constant (\(\Lambda \)) governed by a negative equation of state (EoS) parameter (\(\gamma =-1\)) is taken to be the simplest characterization of DE. However, this identification has two well-known problems, i.e., fine-tuning and cosmic coincidence. In addition, there are several cosmological models which can be considered as an alternative to a \(\Lambda \) like scalar field model [6, 7], a phantom model [8], a tachyon field [9] and k-essence [10], which also suggest expanding behavior of the universe. Another approach involves the generalization of simple barotropic EoS to more exotic forms such as the Chaplygin gas [11] and its modification [12]. It has also been demonstrated that a fluid with the bulk viscosity may cause accelerated expansion of the model of the universe without cosmological constant or scalar field [13, 14]. Our main concern is to find another approach which can minimize exotic forms of matter by introducing dissipation through viscous effects of fluids.

During the last few years, cosmological models including nonlinear electromagnetic fields have attained remarkable interest. The application of this electrodynamics to different models of the universe may lead to many significant results. Nonlinear electrodynamics (NLED) is the generalization of Maxwell theory which is considered as the most viable theory to remove the initial singularities. Vollick [15] considered the FRW model of the universe with NLED and found that the model entailed will show a period of late-time acceleration for \(E^2<3B^2\). Kruglov [16] found that the universe tends to accelerate in a magnetic background at the early era due to NLED model. Ovgun [17] formulated an analytical nonsingular extension of isotropic and homogeneous solutions by presenting a new mathematical model in nonlinear magnetic monopole fields.

The study of possible stable late-time attractors has attained remarkable significance for different models of the universe. A phase space analysis manifests dynamical behavior of a cosmological model through a global view by reducing the complexity of the equations (converting the system of equations to an autonomous system) which may help to understand the different stages of the evolution. Copeland et al. [18] studied a phase plane analysis of standard inflationary models and found that these models cannot solve the density problem. Guo et al. [19] explored a phase space analysis of the FRW model of the universe filled with barotropic fluid and phantom scalar field in which a phantom dominated solution is found to be a stable late-time attractor.

Garcia-Salcedo [20] examined the dynamics of the FRW universe with NLED and found that the critical points have no effects. Yang and Gao [21] discussed a phase space analysis of k-essence cosmology in which critical points play an important role for the final state of the universe. Xiao and Zhu [22] analyzed the stability of the FRW model of the universe in loop quantum gravity via phase space portraits by taking barotropic fluid as well as positive field potential. Acquaviva and Beesham [23] made a phase space analysis of the FRW spacetime filled with a noninteracting mixture of fluids (dust and viscous radiation) and found that the nonlinear viscous model shows the possibility of current cosmic expansion.

This paper is devoted to the phase space analysis of the FRW model of the universe with nonlinear viscous fluid. The plan of the paper is as follows. In Sect. 2, we provide a basic formalism for NLED and general equations as well as a nonlinear model for the bulk viscosity. An autonomous system of equations is established to analyze the stability of the system by introducing normalized dimensionless variables in Sect. 3. Section 4 provides the formulation of power-law scale factor. Finally, we conclude our results in the last section.

2 Nonlinear electrodynamics and general equations

The standard cosmological model is successful in resolving many issues but still there are some issues which remain to be solved. One of them is the initial singularity which leads to a troubling state of affairs, because at this point all known physical theories break down. If the early universe is governed by Maxwell’s equations, then there will be a spacelike initial singularity in the past. However, if Maxwell’s equations become modified in the early universe, when the electromagnetic field is large, it might help avoiding the occurrence of cosmic singularities [24]. For the situations where a strong electromagnetic field occurs, it makes sense to couple gravitation with NLED. The coupling of Einstein gravity with NLED is defined by the action

$$\begin{aligned} S=\frac{1}{16\pi }\int \sqrt{-g}[R-{\mathcal {L}}(F,F^*)]\mathrm{d}^4x. \end{aligned}$$
(1)

We consider a nonlinear extension of the Maxwell Lagrangian density up to second order terms in the field invariants \(F=F_{\mu \nu }F^{\mu \nu }\) and \(F^*=F^*_{\mu \nu }F^{\mu \nu }\) given by [15]

$$\begin{aligned} {\mathcal {L}}={\mathcal {L}}(F,F^*)=-\frac{1}{4\mu _{0}}F+\alpha F^2+\beta F^{*2}, \end{aligned}$$
(2)

where \(\mu _{0}\) denotes the magnetic permeability, \(\alpha ,\beta >0\) are arbitrary constants which yield a linear density for \(\alpha ,\beta \rightarrow 0\), and \(F^*_{\mu \nu }\) is the dual of the electromagnetic field tensor. We do not consider the term \(FF^*\) involving \(F^*\) in order to preserve the parity [25, 26]. The linear term of this Lagrangian dominates during a radiation dominated era, while the quadratic terms dominate in the early universe, which corresponds to the bouncing behavior of the universe to avoid initial singularity [27]. The mechanisms behind the bounce have been demonstrated in [28, 29]. The energy-momentum tensor associated with this Lagrangian has the following form:

$$\begin{aligned} T_{\mu \nu (EM)}=-4\partial _{F}{\mathcal {L}}F^{\eta }_{\mu }F_{\eta \nu }+ (\partial _{F^*}{\mathcal {L}}F^*-{\mathcal {L}})g_{\mu \nu }. \end{aligned}$$
(3)

In order to fulfill the requirement of isotropic and homogeneous universe, i.e., the electromagnetic field to act as its source, the energy density and the pressure corresponding to the electromagnetic field can be computed by averaging over volume [26, 28]. It is assumed that the electric and magnetic fields have coherent lengths that are much shorter than the cosmological horizon scales. After posing several conditions, the energy momentum tensor of the electromagnetic field associated with \({\mathcal {L}}(F,F^*)\) can be written as that of a perfect fluid,

$$\begin{aligned} T_{\mu \nu }=(\rho +p)u_{\mu }u_{\nu }+pg_{\mu \nu }, \end{aligned}$$
(4)

such that

$$\begin{aligned} \rho _{EM}= & {} -{\mathcal {L}}-4E^2\partial _{F}{\mathcal {L}},\end{aligned}$$
(5)
$$\begin{aligned} p_{EM}= & {} {\mathcal {L}}-\frac{4}{3}(2B^2-E^2)\partial _{F}{\mathcal {L}}, \end{aligned}$$
(6)

where \(\partial _{F}\) represents a partial derivative with respect to \(F=F_{\mu \nu }F^{\mu \nu }=2(B^2-E^2)\), and E and B denote the averaged electric and magnetic fields, respectively.

We consider an isotropic and homogeneous model of the universe given by

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a(t)(\mathrm{d}r^2+r^2\mathrm{d}\theta ^2+r^2\sin ^2\theta \mathrm{d}\phi ^2), \end{aligned}$$
(7)

where a(t) is the scale factor. We assume the model of the universe to be filled with two cosmic fluids, i.e., a noninteracting electromagnetic fluid with energy density \(\rho _{EM}\) as well as pressure \(p_{EM}\) and a viscous fluid having energy density \(\rho _{v}\) as well as pressure \(p=p_{v}(\rho _{v})+\Psi \). Here \(p_{v}\) represents the equilibrium part of viscous pressure whereas \(\Psi \) is the non-equilibrium part, i.e., the bulk viscous pressure satisfying an evolution equation. The bulk viscosity plays an important role in stabilizing the density evolution and overcomes rapid changes in cosmos. It also promotes a negative energy field in the fluid and hence can play the role of dark energy to describe the dynamics of cosmos. It has been suggested that a fluid with bulk viscosity may cause an accelerated expansion of the model of the universe without cosmological constant or scalar field [14]. The main contribution of the bulk viscosity to the effective pressure is its dissipative effect. We obtain the Raychaudhuri and constraint equations from the field equations given by

$$\begin{aligned} \dot{\Theta }= & {} -\frac{1}{3}\Theta ^2-\frac{1}{2}\left[ \rho _{EM}+ \rho _{v}+3(p_{EM}+p_{v}+\Psi )\right] ,\end{aligned}$$
(8)
$$\begin{aligned} 0= & {} \rho _{EM}+\rho _{v}-\frac{1}{3}\Theta ^2, \end{aligned}$$
(9)

where a dot means the derivative with respect to time. The conservation of the energy-momentum tensor yields the following evolution equations for the viscous and electromagnetic field components:

$$\begin{aligned} \dot{\rho }_{v}= & {} -[\rho _{v}+p_{v}+\Psi ]\Theta , \end{aligned}$$
(10)
$$\begin{aligned} \dot{\rho }_{EM}= & {} -[\rho _{EM}+p_{EM}]\Theta . \end{aligned}$$
(11)

We consider a barotropic EoS for a viscous fluid defined by

$$\begin{aligned} p_{v}=(\gamma -1)\rho _{v}, \end{aligned}$$
(12)

where \(1\le \gamma \le 2\). Using Eqs. (8) and (9), the Raychaudhuri and conservation equations for viscous fluid turn out to be

$$\begin{aligned} \dot{\Theta }= & {} -\frac{1}{2}\Theta ^2-\frac{3}{2}[p_{EM}+(\gamma -1) \rho _{v}+\Psi ],\end{aligned}$$
(13)
$$\begin{aligned} \dot{\rho }_{v}= & {} -[\gamma \rho _{v}+\Psi ]\Theta . \end{aligned}$$
(14)

We characterize the viscous pressure variable by the following evolution equation [30]:

$$\begin{aligned} \tau \dot{\Psi }= & {} -\zeta \Theta -\Psi \left( 1+\frac{\tau _{*}}{\zeta }\Psi \right) ^{-1}\nonumber \\&-\frac{1}{2}\tau \Psi \left[ \Theta +\frac{\dot{\tau }}{\tau }-\,\frac{\dot{\zeta }}{\zeta }-\frac{\dot{T}}{T}\right] , \end{aligned}$$
(15)

where \(\zeta \), T, \(\tau \), and \(\tau _{*}\) denote the bulk viscosity, local equilibrium temperature, linear relaxation time, and the characteristic time in the nonlinear background, respectively. This equation is derived by using a nonlinear model describing a relationship between thermodynamic flux \(\Psi \) and the thermodynamic force \(\chi \) in the form

$$\begin{aligned} \Psi =-\frac{\zeta \chi }{1+\tau _{*}\chi }. \end{aligned}$$
(16)

This is a nonlinear extension of the Israel–Stewart equation, which reduces to its linear form as \(\tau _{*}\rightarrow 0\). The nonlinear term in Eq. (15) must be positive for thermodynamic consistency and positivity of entropy production rate. The parameters involved in Eq. (15) can be defined by the relations \(\zeta =\zeta _{0}\Theta \) \((\zeta >0)\), \(\tau =\frac{\zeta }{\gamma \nu ^2\rho _{v}}\), \(\tau _{*}=k^2\tau \), and \(T=T_{0}\rho ^{(\gamma -1)/\gamma }\). Here k is a constant such that \(k=0\) gives the linear (Israel–Stewart) case, while \(T_{0}\) represents a constant temperature. Also, \(\nu \) corresponds to the dissipative effect of the speed of sound V such that \(V^2=c^2_{s}+\nu ^2\), where \(c^2_{s}\) is its adiabatic contribution. By causality, \(V\le 1\) and \(c^2_{s}=\gamma -1\), which yields

$$\begin{aligned} \nu ^2\le 2-\gamma , \quad 1\le \gamma \le 2. \end{aligned}$$
(17)

The explicit form of the evolution equation by using the above relations yields

$$\begin{aligned} \dot{\Psi }= & {} -\gamma \nu ^2\rho _{v}\Theta -\frac{\gamma \nu ^2\Psi \rho _{v}}{\zeta _{0}\Theta } \left( 1+\frac{k^2\Psi }{\gamma \nu ^2\rho _{v}}\right) ^{-1}\nonumber \\&-\,\frac{1}{2} \Psi \left[ \Theta -\left( \frac{2\gamma -1}{\gamma }\right) \frac{\dot{\rho _{v}}}{\rho _{v}}\right] . \end{aligned}$$
(18)

3 Phase space analysis

In this section, we discuss the phase space analysis of the isotropic and homogeneous model of the universe for the radiation case. Due to there being many arbitrary parameters, it seems difficult to find an analytical solution of the evolution equation. In this context, we define normalized dimensionless variables \(\Omega =\frac{3\rho _{v}}{\Theta ^2}\) and \(\tilde{\Psi }=\frac{3\Psi }{\Theta ^2}\) such that the corresponding dynamical system can be reduced to autonomous one. We also define a new variable \(\tilde{\tau }\) for the time for which the corresponding derivative is represented by a prime such that \(\frac{\mathrm{d}t}{\mathrm{d}\tilde{\tau }}=\frac{3}{\Theta }\). Here each term is associated with some physical explicit background, since the chosen dimensionless variables \(\Omega \) and \(\tilde{\Psi }\) occur due to the physical impact of the viscous energy density and pressure, respectively. The system of Eqs. (13) and (14) in terms of these normalized variables takes the form

$$\begin{aligned} \frac{\Theta '}{\Theta }= & {} -\frac{3}{2}[1+p_{EM}+(\gamma -1)\Omega + \tilde{\Psi }],\end{aligned}$$
(19)
$$\begin{aligned} \frac{3\rho _{v}'}{\Theta ^2}= & {} - 3[\gamma \Omega +\tilde{\Psi }]. \end{aligned}$$
(20)

Differentiation of the dimensionless variable for the energy density gives

$$\begin{aligned} \Omega '=\frac{3\rho _{v}'}{\Theta ^2} -2\Omega \frac{\Theta '}{\Theta }. \end{aligned}$$
(21)

Using Eqs. (19) and (20), this equation turns out to be

$$\begin{aligned} \Omega '=3(\Omega -1)[\Omega (\gamma -1)+\tilde{\Psi }+3p_{EM}]. \end{aligned}$$
(22)

Now we introduce the concept of a new evolution equation for \(\tilde{\Psi }\). The first derivative of \(\tilde{\Psi }\) with respect to \(\tilde{\tau }\) through Eq. (19) leads to an evolution equation of the form

$$\begin{aligned} \tilde{\Psi }'= & {} -3\gamma \nu ^2\Omega \left[ 1+\frac{\tilde{\Psi }}{3\zeta _{0}}\left( 1+\frac{k^2\tilde{\Psi }}{\gamma \nu ^2\Omega } \right) ^{-1}\right] \nonumber \\&+\,3\tilde{\Psi }\left[ 1+3p_{EM} \left( 1-\frac{3}{\Omega }\frac{2\gamma -1}{2\gamma }\right) \right] \nonumber \\&-\,3(\gamma -1)\tilde{\Psi }(1-\Omega ). \end{aligned}$$
(23)

It is mentioned here that Eqs. (22) and (23) play a remarkable role in describing the dynamical system entailed for the phase space analysis.

In order to find the critical points \(\{\Omega _{c},\tilde{\Psi }_{c}\}\), we need to solve the dynamical system by imposing the condition \(\Omega '=\tilde{\Psi }'=0\). The stability of the FRW model of the universe can be analyzed according to the nature of the critical points. Here we restrict the phase space region by a condition which is necessary for the positivity of the entropy production rate given by [23, 30]

$$\begin{aligned} \tilde{\Psi }>-\frac{\gamma \nu ^2\Omega }{k^2}. \end{aligned}$$
(24)

This condition makes the possible negative values of \(\tilde{\Psi }\) tend toward zero for \(k^2\gg \nu ^2\). Contrarily, the bulk pressure will be less restrictive if \(k^2\ll \nu ^2\). It is noted that finite values of k allow only positive values of the bulk pressure in the limit \(\nu \rightarrow 0\). It would be more convenient to consider \(k^2\le \nu ^2\) along with \(\nu ^2\le 2-\gamma \) and \(\tau _{*}=k^2\tau \), which leads to the fact that the characteristic time for nonlinear effects \(\tau _{*}\) does not exceed the characteristic time in linear background \(\tau \). We characterize the critical points by the deceleration parameter \(q=-1-\frac{\Theta '}{\Theta }\) and the effective EoS parameter \(\gamma _{\mathrm{eff}}=-\frac{2\Theta '}{3\Theta }\), which yield

$$\begin{aligned} q= & {} \frac{1}{2}[1+9p_{EM}+3(\gamma -1)\Omega +3\tilde{\Psi }],\end{aligned}$$
(25)
$$\begin{aligned} \gamma _{\mathrm{eff}}= & {} 1+3p_{EM}+(\gamma -1)\Omega +\tilde{\Psi }. \end{aligned}$$
(26)

To examine a region of phase space undergoing accelerated expansion, we impose \(q<0\) in Eq. (25) which gives

$$\begin{aligned} \tilde{\Psi }<-\frac{1}{3}-3p_{EM}-(\gamma -1)\Omega . \end{aligned}$$
(27)

The possibility of the accelerated expansion in the physical phase space is determined by comparing Eqs. (24) and (25) through \(q<0\) given by

$$\begin{aligned} \frac{\nu ^2}{k^2}>\frac{1+9p_{EM}+3(\gamma -1)\Omega }{3\gamma \Omega }. \end{aligned}$$
(28)

Substituting \(\Omega '=0\) in Eq. (22), we find the following conditions:

$$\begin{aligned}&\Omega _{c}=1,\end{aligned}$$
(29)
$$\begin{aligned}&(\gamma -1)\Omega _{c}+\tilde{\Psi }_{c}+3p_{EM}=0. \end{aligned}$$
(30)

We insert these conditions in \(\tilde{\Psi }'\) to find the location of critical points. This analysis is carried out by characterizing the viscous fluid through the choice of its EoS parameter \(\gamma \) (radiation). We consider \(0<k^2=\nu ^2\le 2-\gamma \) for which the case of stiff matter (\(\gamma =2\)) is excluded from the analysis as it yields \(\nu ^2=0\).

3.1 Radiation case \((\gamma =\frac{4}{3})\)

We consider the radiation case for the phase space analysis by taking \(\gamma =\frac{4}{3}\). Imposing the condition (29) and \(\tilde{\Psi }'=0\) in Eq. (23), we have

$$\begin{aligned}&\frac{3\nu ^2}{4\zeta _{0}}\tilde{\Psi }^3- \frac{\nu ^2}{\zeta _{0}}\tilde{\Psi }^2-3\tilde{\Psi }\left( 1-\frac{4\nu ^2}{9\zeta _{0}}-\frac{21p_{EM}}{8}\right) +4\nu ^2=0.\nonumber \\ \end{aligned}$$
(31)

This cubic equation yields three roots among which we retain only those roots that lie in the physical phase space. The general form of the dynamical system is given by

$$\begin{aligned} \Omega '=X(\Omega , \tilde{\Psi }),\quad \tilde{\Psi }'=Y(\Omega , \tilde{\Psi }). \end{aligned}$$
(32)

The eigenvalues of the system can be determined by the Jacobian matrix

$$\begin{aligned} Z=\left( \begin{array}{cc} \frac{\partial X}{\partial \Omega }&{}\frac{\partial X}{\partial \tilde{\Psi }}\\ \frac{\partial Y}{\partial \Omega }&{}\frac{\partial Y}{\partial \tilde{\Psi }}\\ \end{array} \right) _{|P_i^{\pm }}. \end{aligned}$$
(33)

The eigenvalues for the above stability matrix corresponding to the points \(P^{\pm }_{r}\) are given by

$$\begin{aligned} \lambda _{1}= & {} 1+3\tilde{\Psi }+9p_{EM},\end{aligned}$$
(34)
$$\begin{aligned} \lambda _{2}= & {} -\frac{16\nu ^2}{3\zeta _{0}}\left[ \frac{1}{4 +\tilde{\Psi }}-\frac{\tilde{\Psi }}{(4+\tilde{\Psi })^2}\right] -\frac{63p_{EM}}{8}+6\tilde{\Psi }+3.\nonumber \\ \end{aligned}$$
(35)

The fixed point is called a source (respectively, a sink) if both eigenvalues consist of positive (respectively, negative) real parts. In the case of a viscous radiating fluid, we can explore source and sink according to the sign of eigenvalues as well as direction of the trajectories. We investigate two critical points \(P_{r}^+=\{1, \tilde{\Psi }_{c}^+\}\) and \(P_{r}^-=\{1, \tilde{\Psi }_{c}^-\}\) corresponding to positive \((\tilde{\Psi }_{c}^+)\) and negative \((\tilde{\Psi }_{c}^-)\) roots, respectively. By taking \(\Omega _{c}=0\) and the second condition (30) with \(\tilde{\Psi }_{c}=-\frac{\Omega _{c}}{3}-3p_{EM}\), we obtain \(P^0_{r}=\{0,-3p_{EM}\}\).

Fig. 1
figure 1

Plots for the phase plane evolution of viscous radiating fluid with \(\gamma =4/3\), \(\nu =k=\sqrt{1/5}\), \(\zeta _{0}=0.2\), \(\alpha =0.01\), and different values of B and E

Full size image
Fig. 2
figure 2

Plots for the phase plane evolution of viscous radiating fluid with \(\gamma =4/3\), \(\nu =k=1\), \(\zeta _{0}=1\), \(\alpha =0.01\), and different values of B and E

Full size image
Fig. 3
figure 3

Plots for the phase plane evolution of viscous radiating fluid with \(\gamma =4/3\), \(\nu =k=\sqrt{2/3}\), \(\zeta _{0}=1\), \(\alpha =0.01\), and \(B=0.2,0.8\)

Full size image

3.1.1 Case I

We are interested in analyzing the impact of the electromagnetic field on the stability of the critical points in the presence of the nonlinear bulk viscosity. The energy density (5) and pressure (6) are given by

$$\begin{aligned} \rho _{EM}= & {} \frac{1}{2\mu _{0}}(B^2+E^2)-4\alpha (B^2-E^2)(B^2+3E^2),\end{aligned}$$
(36)
$$\begin{aligned} p_{EM}= & {} \frac{1}{6\mu _{0}}(B^2+E^2)-\frac{4\alpha }{3}(B^2-E^2)(5B^2-E^2). \end{aligned}$$
(37)

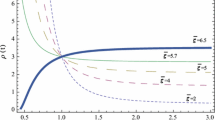
The dynamical behavior of critical points for different values of electric and magnetic fields as well as other parameters is shown in Figs. 1 and 2. The green trajectory depicts a flow from the point \(P^{+}_{d}\) toward \(P^{-}_{d}\). The white region corresponds to the negative entropy production rate that diverges on its boundary whereas the green region shows accelerated expansion of the universe (\(q<0\)). Here the point \(P^{0}_{d}\) shows varying behavior, i.e., either it is a saddle point or a sink, depending on the values of the different parameters.

In these plots, we have taken \(\zeta _{0}=0.2,1\) by varying \(\nu ,k,B\) and E. For \(\nu =k=\sqrt{1/5}\) and \(\zeta _{0}=0.2\), it is found that the global attractor \(P_{d}^-\) lies in the green region showing accelerated expansion for the same values of B and E. This region tends to decrease by increasing E such that the point \(P_{d}^-\) lies in the deceleration region. By increasing \(\zeta _{0}\), we find accelerated expansion with different values of B, E and larger values of the parameters \(\nu \) and k. For \(\nu =k=1\) and \(\zeta _{0}=1\), we find accelerated expansion of the model of the universe for all choices of electric and magnetic fields. The point \(P^{0}_{d}\) behaves as a sink for \(\zeta _{0}=0.2\) which becomes a saddle point for larger values of \(\zeta _{0}\). We observe that the increasing value of the bulk viscosity increases the region for accelerated expansion in the presence of NLED. In the following, we discuss two different cases for the electric as well as the magnetic universe.

3.1.2 Case II (\(E=0\))

It is well known that NLED helps to diminish the initial singularity in the early universe where only the primordial plasma identifies matter [31]. Some recent results indicate that a magnetic universe is appropriate to avoid the initial singularity and ultimately shows late-time accelerated expansion [25, 28, 32]. Here we assume the squared electric field \(\left<E^2\right>\) to be zero such that the magnetic field \((F=2B^2)\) rules over the universe; this is known as a magnetized universe. Thus the energy density (5) and pressure (6) take the form

$$\begin{aligned} \rho _{B}= & {} \frac{B^2}{2\mu _{0}}(1-8\mu _{0}\alpha B^2),\end{aligned}$$
(38)
$$\begin{aligned} p_{B}= & {} \frac{B^2}{6\mu _{0}}(1-40\mu _{0}\alpha B^2). \end{aligned}$$
(39)

The respective evolution plots are given in Fig. 3. For \(\nu =k=\sqrt{2/3}\) and \(\zeta _{0}=1\), we find that the sink lies in the green region showing the stability of the accelerated expansion for the magnetized universe. This region tends to decrease by increasing the value of magnetic field B. The point \(P^{0}_{d}\) behaves as a saddle for small values of magnetic field. It is mentioned here that increasing values of the bulk viscosity and the parameters \(\nu \) as well as k with different values of B give rise to the stability of the accelerated expansion of the universe for different choices of B. We also find that a smaller value of the bulk viscosity shows decelerated expansion with increasing values of B.

3.1.3 Case III (\(B=0\))

Here, we deal with the electric universe by setting \(\langle B^2\rangle =0\). The corresponding energy density and pressure are given by

$$\begin{aligned} \rho _{E}= & {} \frac{E^2}{2\mu _{0}}(1+24\mu _{0}\alpha E^2),\end{aligned}$$
(40)
$$\begin{aligned} p_{E}= & {} \frac{E^2}{6\mu _{0}}(1-8\mu _{0}\alpha E^2). \end{aligned}$$
(41)
Fig. 4
figure 4

Plots for the phase plane evolution of viscous radiating fluid with \(\gamma =4/3\), \(\nu =k=\sqrt{2/3}\), \(\zeta _{0}=1\), \(\alpha =0.01\) and \(E=0.2,0.8\)

Full size image

The plots corresponding to different choices of electric field E are shown in Fig. 4. For \(\nu =k=\sqrt{2/3}\) and \(\zeta _{0}=1\), we analyze the sink \(P^{-}_{d}\) in the green region showing accelerated expansion of the universe for different values of E. The point \(P^{0}_{d}\) behaves as a saddle for small values of the magnetic field. We find that the region for accelerated expansion tends to decrease by increasing electric field E. It is observed that an accelerated expanding region exists for increasing values of the bulk viscosity and parameters \(\nu \) as well as k with all choices of E. It supports the fact that the role of the bulk viscosity and electric field is to increase the stability of the accelerated expansion of the model of the universe. The summary of our results filled with viscous radiating fluid is given in Table 1.

Table 1 Stability analysis of critical points for radiation dominated fluid
Full size table

4 Power-law scale factor

In this section, we discuss the power-law behavior of the scale factor corresponding to the critical points. For this purpose, we integrate Eq. (19), which leads to

$$\begin{aligned} \dot{\Theta }=-\frac{1}{2}[1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }]\Theta ^2. \end{aligned}$$
(42)

For \(\Theta \ne 0\), we formulate a power-law scale factor whenever \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }\ne 0\). Solving \(\Theta =\frac{3\dot{a}}{a}\) for a(t), we obtain the generic critical point as

$$\begin{aligned} a=a_{0}(t-t_{0})^{\frac{2}{3[1+3p_{EM}+(\gamma -1)\Omega _{c} +\tilde{\Psi _{c}}]}}. \end{aligned}$$
(43)

The following condition must hold for exponentially expanding models (identified by the condition \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }=0\)) to be present in the physical phase space region (bounded by Eq. (24)):

$$\begin{aligned} (1-\gamma )\Omega _{c}-3p_{EM}-1>-\frac{\gamma \nu ^2}{k^2}\Omega . \end{aligned}$$
(44)

This condition is not satisfied in the physical phase space for \(\nu ^2=k^2\). If \(\nu ^2>k^2\), the above inequality must be satisfied in the following physical phase space region:

$$\begin{aligned} (1+3p_{EM})\left[ 1-\gamma \left( 1-\frac{\nu ^2}{k^2}\right) \right] ^{-1} <\Omega \le 1. \end{aligned}$$
(45)
Fig. 5
figure 5

Plot of qualitative phase space analysis for power-law scale factor with \(v^2>k^2\). Yellow and dark gray regions indicate the accelerated and exponential expansion of the model of the universe, respectively

Full size image

It is mentioned here that the sign of the term \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }\) is quite important in evaluating different cosmological stages. If \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }=0\), it corresponds to the exponential expansion of the model of the universe. Also, \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }\gtrless 0\) yields accelerated expansion or contraction of the cosmological model, respectively. If \(\nu ^2<k^2\), the possibility of having accelerated expansion will narrow down. Figure 5 shows the physical phase space region (excluding the white region with negative entropy production rate) whereas yellow and dark gray regions correspond to accelerated and exponential expansion of the model of the universe for \(v^2>k^2\), respectively. Table 2 provides the polynomial behavior of power-law scale factor for different critical points with \(1+3p_{EM} +(\gamma -1)\Omega +\tilde{\Psi }\ne 0\).

Table 2 Power-law scale factors for different critical points
Full size table

5 Outlook

In this paper, we have discussed the impact of NLED on the phase space analysis of isotropic and homogeneous model of the universe by taking noninteracting mixture of the electromagnetic and viscous radiating fluids. This analysis has been proved to be a remarkable technique for the stability of dynamical system. An autonomous system of equations has been developed by defining normalized dimensionless variables. We have evaluated the corresponding critical points for different values of the parameters to discuss stability of the system. We have also calculated eigenvalues which characterize these critical points. We summarize our results as follows.

Firstly, we have discussed stability of critical points through their eigenvalues corresponding to different values of E and B for viscous radiation dominated model of the universe. It is found that the critical points \(P^{+}_{d}\) and \(P^{-}_{d}\) correspond to source (unstable) and sink (stable), respectively (Figs. 1 and 2). It is mentioned here that the green region corresponds to an accelerated expansion of the universe. The point \(P_{d}^-\) is a global attractor in the physical phase space region which leads to an expanding model dominated by viscous matter for various choices of the cosmological parameters. In the presence of both electric and magnetic fields, we find that the bulk viscosity increases the region for accelerated expansion, while the increasing values of E show a deceleration region for smaller values of the bulk viscosity. It is mentioned here that large values of the bulk viscosity as well as other parameters correspond to accelerated expansion of the ensuing model of the universe for all choices of electric and magnetic fields.

We have also studied the electric and magnetic cases for the universe separately. It is found that a sink lies in the green region showing accelerated expansion of the magnetized universe for smaller values of the bulk viscosity and the other parameters, while an increasing value of magnetic field decreases this region. For \(B=0\), we have analyzed accelerated expansion of the model of the universe corresponding to large values of the parameters, which tends to decrease by increasing E. It is worth mentioning here that the role of the bulk viscosity is to increase the green region for accelerated expansion with different choices of E and B for both electric as well as magnetic universe. Moreover, we have also studied the behavior of a power-law scale factor corresponding to the critical points. It is found that the power-law scale factor indicates various phases of the evolution (accelerated or exponential expansion) of the model of the universe entailed.