1 Introduction

The inflationary scenario provides a model able to explain many of the observational features of the observed Universe, such as the cosmic microwave background radiation isotropy or the spatial flatness. An alternative scenario to solve the horizon problem is the possibility that the Universe underwent a contraction phase before the big-bang, i.e. a bounce. Several attempts have been made to understand if the bounce could be of a fully consistent cosmological model [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], and could indeed lead to viable alternatives to inflation.

In this paper we study the general conditions to realize the bounce with a K-essence type scalar field, without introducing any additional field. At the background level we impose the existence of two turning points where the derivative of the Hubble parameter H changes sign and of a bounce point where the Hubble parameter vanishes. We first obtain some general conditions on the function K(X) and the potential \(V(\phi )\) and then give the examples of two models constructed according to these conditions. One is based on a quadratic K(X), and the other on a K(X) which is always avoiding divergences of the second time derivative of the scalar field, which may otherwise occur. We integrate numerically the classical equations of motion for these models, verifying that they indeed have the expected evolution and can produce a bounce.

In the region where these models have a constant potential they became adiabatic on any scale, i.e. globally adiabatic, and because of this they may not conserve curvature perturbations on super-horizon scales. We then study the stability of the perturbations, focusing attention on the presence of ghosts and gradient instabilities. We confirm that gradient instabilities can arise around the bounce because the ghost free condition implies that the sign of the squared speed of sound is opposite to the sign of the time derivative of H. Finally we discuss how this kind of instabilities could be avoided by modifying the Lagrangian by introducing Galilean terms in order to prevent a negative squared speed of sound around the bounce.

2 K(X)-bounce

We will consider a scalar field with Lagrangian

$$\begin{aligned} L_{\phi }=\sqrt{-g}\left[ K(X)-V(\phi )\right] ,\quad X=\frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi . \end{aligned}$$
(1)

We denote the Planck mass with \(m_p=(8\pi G)^{-1/2}\), and we adopt units in which \(8\pi G/3=1\), so that the Einstein equation takes the form

$$\begin{aligned} H^2=\rho , \quad \dot{H}=-\frac{3}{2}(\rho +P)=\frac{3}{2}(K+T)=-3K'X \,, \end{aligned}$$
(2)

where the energy density and pressure are

$$\begin{aligned} \rho= & {} 2K' X-K+V=T+V,\end{aligned}$$
(3)
$$\begin{aligned} P= & {} K-V. \end{aligned}$$
(4)

In the above equations we have introduced the function T(X)

$$\begin{aligned} T(X)= & {} 2K'X-K, \end{aligned}$$
(5)

because it is convenient to express the equations of motion in terms of it, and it plays a crucial role in defining the conditions for avoiding singularities in the solutions of the classical equations of motion. The energy conservation equations can then give the equation of motion of the scalar field,

$$\begin{aligned} T' \ddot{\phi }+ 3 H K' \dot{\phi } +V'= & {} 0. \end{aligned}$$
(6)

The minimally coupled scalar field equation of motion corresponds to the case when \(K(X)=T(X)=X\).

Another important quantity to determine the dynamics of the Universe is the second derivative of H,

$$\begin{aligned} \ddot{H}= & {} -\left( 3 K' \dot{\phi }\ddot{\phi }+\frac{3}{2} \dot{\phi }^3 K'' \ddot{\phi }\right) , \end{aligned}$$
(7)

which after substituting the equation of motion for \(\ddot{\phi }\) gives

$$\begin{aligned} \ddot{H}= & {} \frac{3 \left( \dot{\phi }^3 K''+2 \dot{\phi } K'\right) \left( 3H \dot{\phi } K'+V'\right) }{2 \left( \dot{\phi }^2 K''+K'\right) }. \end{aligned}$$
(8)

We now define turning points the local extrema of H(t), where \(\dot{H}=0\). From the Einstein equations we know that \(\dot{H}\) can be zero either because \(K'=0\) or \(X=0\), and the corresponding value of the second order time derivative \(\ddot{H}\) will play a crucial role in determining if these are actual extrema or flex points. From the previous equation after substituting, respectively, \(K'=0\) or \(X=0\) we get

$$\begin{aligned}&X=0 \, : \ \ddot{H}=0 \,,\end{aligned}$$
(9)
$$\begin{aligned}&K'=0 \, : \ \ddot{H}=\frac{3}{2} V' \dot{\phi }. \end{aligned}$$
(10)

This implies that \(X=0\) is a flex point and consequently can never be a turning point, while points at which \(K'=0\) can be either local maxima or minima depending on the relative sign of \(V'\) and \(\dot{\phi }\).

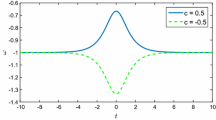
For a bounce with dynamics similar to the one shown in Fig. 1 to occur, the following three critical points are necessary:

$$\begin{aligned}&t_1 \,: \dot{H}=0, \ddot{H}>0 \rightarrow K'_1=0\,, V'_1 \dot{\phi }_1>0 \,, \end{aligned}$$
(11)
$$\begin{aligned}&t_b \,: \dot{H}>0, H=0 , \rightarrow K'_b<0\,,\rho =0 \,, \end{aligned}$$
(12)
$$\begin{aligned}&t_2 \,: \dot{H}=0,\ddot{H}<0 \rightarrow K'_2=0\,, V'_2 \dot{\phi }_2<0 \,, \end{aligned}$$
(13)

where we have defined

$$\begin{aligned} K'_i=K'(X(t_i)), V'_i=V'(\phi (t_i)), \dot{\phi }_i=\dot{\phi }(t_i) , \end{aligned}$$
(14)

and \(\{t_1,t_2\}\) correspond to the first and second turning point times, while \(t_b\) is the bounce time. The construction of models satisfying the above conditions will be studied in the following sections.

Fig. 1
figure 1

Schematic representation of the evolution of H(t) around the bounce. There are two turning points at which the derivative \(\dot{H}(t_1)=\dot{H}(t_2)\) is zero, and a bounce point where \(H(t_b)=0\)

Full size image

2.1 Phase space dynamic of the bounce

In the previous section we have derived the conditions which have to be satisfied at the turning and bounce points, in Eqs. (11)–(13). In order to give a qualitative description of the phase space behavior of the models is convenient to define \({\mathcal H}^2_0\) as the phase space locus of the points where the energy density is zero, i.e. the set of points satisfying the equation

$$\begin{aligned} 3H^2=\rho (X,\phi )=&T(X)+V(\phi )=0. \end{aligned}$$
(15)

The bounce occurs when the phase space trajectory reaches \({\mathcal H}^2_0\), and as shown in Appendix A, the trajectory is always tangent to \({\mathcal H}^2_0\).

The other important points are the ones where \(K'=0\), which can correspond to a local minimum or maximum of H, depending on the sign of \(V' \dot{\phi }\), according to Eqs. (11) and (13).

It should be noted that even if the trajectory does not reach \({\mathcal H}^2_0\), the conditions for the local extrema of H could be satisfied. This can lead to an oscillating H as shown in Fig. 9, with oscillations that can continue even after the bounce. In phase space this behavior corresponds to oscillations around the turning point \(X_T\) where \(K'(X_T)=0\). The conditions in Eqs. (11) and (13) by them self do not guarantee the bounce, but only the existence of local extrema of H, which can produce oscillations of H. If somewhere between the turning points also the condition in Eq. (12) is satisfied, than there can be a bounce, or a sequence of bounces as shown in Fig. 9. The particular choice of K(X), \(V(\phi )\) and the initial conditions can determine different phase space behaviors, but we can use the conditions in Eqs. (11)–(13) in order to design models appropriately. In order to have turning points we need a kinetic term with at least one local extrema where \(K'=0\), while for the choice of the potential there is more freedom as long as \(V' \dot{\phi }\) has the right sign at the turning points according to Eqs. (11)–(13).

A more detailed analytical study of the phase space trajectories and their dependence on the initial conditions goes beyond the scope of the present paper, which is mainly focusing on deriving the general conditions for the bounce and turning points contained in the previous section. We devote the rest of the paper to the construction of models specifically designed to satisfy those conditions and show by numerical integration of the differential equations that the expected phase space behavior is realized. It should be noted that the conditions we obtained in Eqs. (11)–(13) are completely general since we do not assume any specific form of K(X) contrary to the analysis performed in previous work such as [17, 18], where it was assumed \(K(X)=X^n\). Another important difference is that we consider models with only one scalar field, without any additional matter field or perfect fluid, and find the most general conditions for a bounce uniquely driven by the scalar field with a dynamics depicted schematically in Fig. 1.

3 An example: quadratic bounce

Based on the background conditions derived in the previous section we can introduce a quadratic kinetic term model and an appropriate potential which will give the correct dynamic for H(t):

$$\begin{aligned} K(X)= & {} (X-X_T)^2,\end{aligned}$$
(16)
$$\begin{aligned} V(\phi )= & {} \frac{1}{2}\left[ \alpha _1 e^{\beta _1 x^2}+\alpha _2 e^{\beta _2 x^2}\right] . \end{aligned}$$
(17)

In the rest of the paper we will consider a model with \(\{\alpha _1=-\beta _1=1,\alpha _2=-0.2,\beta _2=-0.25\}\), which is plotted in Fig. 2.

Fig. 2
figure 2

The potential for the model in Eq. (17) is plotted as a function of the \(\phi \) in units of \(m_p^2\)

Full size image
Fig. 3
figure 3

The zero energy locus \({\mathcal H}^2_0\) locus is plotted for the model defined in Eq. (17). The region below this curve is physically impossible, since it corresponds to \(H^2<0\). Physical phase space trajectories can only be above this line, or be tangent to it at the time of the bounce, as proved in the appendix

Full size image
Fig. 4
figure 4

The phase space trajectory of the solution of the differential equations for the model defined in Eq. (17) is plotted in blue. The red line corresponds to the \({\mathcal H}^2_0\) locus where the energy is zero. As can be seen, the phase space trajectory is tangent to \({\mathcal H}^2_0\) at the bounce time, as proved in the appendix. The scalar field is plotted in units of \(m_p^2\) and X in units of \(m_p^4\)

Full size image
Fig. 5
figure 5

H is plotted as a function of time in units of \(m_p^{-1}\) for the model defined in Eq. (17)

Full size image
Fig. 6
figure 6

The scalar field \(\phi \) is plotted as a function of time in units of \(m_p^{-1}\) for the model defined in Eq. (17)

Full size image
Fig. 7
figure 7

X(t) is plotted as a function of time in units of \(m_p^2\) for the model defined in Eq. (17)

Full size image

The phase space behavior of the model defined in Eq. (17) is shown in Figs. 2, 3, 4, 5, 6, and 7. As can be seen in Fig. 4 the phase space trajectory is tangent to the zero energy locus \({\mathcal H}^2_0\) at the bounce time, as proved in the appendix. The turning points correspond to \(X=X_T=X(t_1)=X(t_2)\), and the sign of \(V'_i \dot{\phi }_i\) determine, according to Eqs. (11) and (13), if the turning point is a local minimum or maximum for H(t).

4 Possible divergences of the second derivative of \(\phi \)

In this section we will try to construct some other model satisfying the conditions in Eq. (14). Let us consider models of the type

$$\begin{aligned} K(X)= & {} (X-X_T)^2 ,\end{aligned}$$
(18)
$$\begin{aligned} V(\phi )= & {} \frac{1}{2} m^2 \phi ^2, \end{aligned}$$
(19)

where \(X_T\) is the value of X at which the turning point for H should occur, i.e. where \(K'(X_T)=0\), based on the considerations in the previous sections. Note that in this case we have \(X_T=X(t_1)=X(t_2)\), but \(V_1\dot{\phi _1}\ne V_2\dot{\phi _2}\) in order to satisfy the conditions for the turning points given in Eqs. (11) and (13). The problem with this kind of model is that there is a line in phase space plane where \(T'(X_c)=0\), which corresponds to a divergence of the second derivative of \(\phi \). At that point the equation of motion becomes a first order equation, which correspond to a constraint of the value of the field \(\phi _c\) when \(X=X_c\). This critical point in phase space is defined by the following conditions:

$$\begin{aligned}&T'(X_c)= 0,\end{aligned}$$
(20)
$$\begin{aligned}&\frac{3 [K(X_c)+T(X_c)] \sqrt{T(X_c)+V(\phi _c)} }{\sqrt{2 X_c}} +V_c'=0. \end{aligned}$$
(21)

These equations can be solved to give

$$\begin{aligned} X_c= & {} \frac{X_T}{3},\end{aligned}$$
(22)
$$\begin{aligned} \phi _c= & {} -\frac{8 \sqrt{\frac{2}{3}} {X_T}^{5/2}}{\sqrt{-3+16 {X_T}^3}}. \end{aligned}$$
(23)

To avoid this kind of divergence we will introduce a new class of models in the next section.

5 Models avoiding the divergence of the second derivative

In order to avoid the degenerate solutions encountered in the model studied in the previous section we consider a class of models for which \(T'(X)\) is never zero

$$\begin{aligned} T'(X)=a , \end{aligned}$$
(24)

where a is a constant. Solving for K(X) the above differential equation we get

$$\begin{aligned} K(X)= & {} a X + b \sqrt{X}+c, \end{aligned}$$
(25)

where b and c are two arbitrary integration constants. The so-called cuscuton model [19] corresponds to the case in which \(a=0\). In this case both T and \(T'\) vanish. In order to obtain a K(X) with a local minimum we need a negative \(b<0\), leading to a minimum at

$$\begin{aligned} X_T= & {} \frac{b^2}{4}. \end{aligned}$$
(26)

Note that an oscillatory H(t) can be obtained for an appropriate choice of the initial conditions, leading to a sequence of consecutive bounces, or to an oscillating H(t).

The linear part of K(X) can give an ekpyrotic phase, and it arises naturally by imposing the condition \(T'(X)=a>0\). The phase space behavior of the model defined in Eq. (17) is shown in Figs. 9, 8, 10, and 11. As can be seen in Figs. 9 and 8 the phase space trajectory is tangent to the zero energy locus \({\mathcal H}2_0\) at the bounce time, as proved in the appendix. As in the case of the model defined in Eq. (17) the turning points correspond to \(X=X_T=X(t_1)=X(t_2)\), and the sign of \(V'_i \dot{\phi }_i\) determine, according to Eqs. (11) and (13), if the turning point is a local minimum or maximum for H(t). For the purpose of integrating numerically the equations of motion we consider this specific model

$$\begin{aligned}&K(X)=X-\sqrt{X},\end{aligned}$$
(27)
$$\begin{aligned}&K'(X_T)=0 \,; X_T=\frac{1}{4}, \end{aligned}$$
(28)
$$\begin{aligned}&V_2(\phi )=V_0+\frac{1}{2}\phi ^2. \end{aligned}$$
(29)
Fig. 8
figure 8

Space phase trajectory of the solution of the differential equations for the scalar field \(\phi \) is plotted in blue for the model in Eq. (28), with \(V_0=-0.41 m_p^4\). The red line corresponds to the zero energy locus \({\mathcal H}^2_0\). The vertical line is for \(X=X_t\), the minimum of K where \(K'(X_T)=0\), which corresponds to a turning point for H(t). The points at which the field trajectory is touching the zero energy locus correspond to the bounce times. The scalar field is plotted in units of \(m_p^2\) and X in units of \(m_p^4\)

Full size image
Fig. 9
figure 9

H is plotted as a function of time in units of \(m_p^{-1}\) for the model defined in Eq. (28)

Full size image
Fig. 10
figure 10

The scalar field \(\phi \) is plotted as a function of time in units of \(m_p^{-1}\) for the model defined in Eq. (28)

Full size image
Fig. 11
figure 11

X(t) is plotted as a function of time in units of \(m_p^4\) for the model defined in Eq. (28)

Full size image

6 Stability of cosmological perturbations and adiabaticity

So far we have focused on the conditions to realize the bounce at the background level, but in order for these models to be viable cosmological models which could provide an alternative to inflation, we need to check if the cosmological perturbations are stable. In particular there could be problems with the growth of anisotropies [14] and gradient instabilities or ghosts [20] could arise. The quadratic action for scalar perturbations in the comoving slice gauge for a general Lagrangian of the form \(K(X,\phi )+G(\phi ) \Box \) can be written as [20]

$$\begin{aligned} S^{(2)}=\int \mathrm {d}^3x\mathrm {d}t a^3 {A\over 2} \left[\dot{\zeta }^2 - {c_\mathrm {s}^2 \over a^2} (\partial _i\zeta )^2 \right], \end{aligned}$$
(30)

where we have defined

$$\begin{aligned} A= & {} {2XD\over (H-\dot{\phi }XG_X)^2},\end{aligned}$$
(31)
$$\begin{aligned} D= & {} K_X+2XK_{XX}- 2G_\phi - 2XG_{X\phi }\nonumber \\&+6\dot{\phi }H(G_X+XG_{XX})+6X^2G_X^2, \end{aligned}$$
(32)

and the squared sound speed for the scalar perturbations is

$$\begin{aligned} c_\mathrm {s}^2 = \frac{K_X-2G_\phi + 2XG_{\phi X} + 2\ddot{\phi }(G_X+XG_{XX}) + 4\dot{\phi }HG_X - 2X^2G_X^2}{D}. \end{aligned}$$
(33)

The condition for absence of ghosts [20] is \(A>0\), while gradient instabilities are avoided when the square of speed of propagation of perturbations \(c_s^2\) is always positive. For the class of models we considered, corresponding to \(G=0\), these conditions imply

$$\begin{aligned} D= & {} K_X+2XK_{XX}=T'(X),\end{aligned}$$
(34)
$$\begin{aligned} A= & {} {2XD\over H^2}>0 \rightarrow T'(X)>0,\end{aligned}$$
(35)
$$\begin{aligned} c_s^2= & {} \frac{K_X}{D}>0 \rightarrow K_X>0 ,\end{aligned}$$
(36)
$$\begin{aligned} \dot{H}= & {} -3K_X(X)X=-3 D X c_s^2 =-3 T'(X) X c_s^2. \end{aligned}$$
(37)

We can see that an additional advantage of the class of models satisfying \(T'(X)=a>0\) given in Eq. (28) is that they are ghost free by construction, beside avoiding a singularity of the classical equations since as discussed previously \(T'(X)\) is also the coefficient of \(\ddot{\phi }\) in Eq. (6). Nevertheless around the bounce time, when \(\dot{a}(t_b)=0\), gradient instabilities could arise [21] because \(\dot{a}\) is negative before and positive after \(t_b\), which implies \(\dot{H}>0\) in some neighborhood of \(t_b\). From the Einstein equation (2) we can then immediately deduce that gradient instabilities will necessarily arise in any K(X) model which is also ghost free, i.e. also satisfy \(T'(X)>0\), because in this case the sign of \(\dot{H}\) is the opposite of the sign of \(c_s^2\),

$$\begin{aligned} \mathop {\mathrm {sgn}}{\dot{H}}=-\mathop {\mathrm {sgn}}{c_s^2}. \end{aligned}$$
(38)

These kinds of instabilities could be healed by adding Galilean terms of the form \(G(X,\phi )\Box \phi \), to the Lagrangian [20], because in this case the above relation would not be valid anymore. Here we can note that a modification consisting in adding terms of the type \(G(\phi ) \Box \) would not be sufficient because in this case we have

$$\begin{aligned} \rho= & {} 2 X(K_X-G_{,\phi })-K; \quad P=K-2 X G_{,\phi }, \end{aligned}$$
(39)
$$\begin{aligned} A= & {} {2XD\over H^2}>0 \rightarrow D>0, \end{aligned}$$
(40)
$$\begin{aligned} D= & {} K_X+2XK_{XX}- 2G_\phi =T'(X)-2G_\phi , \end{aligned}$$
(41)
$$\begin{aligned} c_s^2= & {} \frac{K_X-2G_{,\phi }}{D}, \end{aligned}$$
(42)
$$\begin{aligned} \dot{H}= & {} -\frac{3}{2}(\rho +P) = -3 X(K_X-2G_{,\phi })=-3 D X c_s^2. \end{aligned}$$
(43)

The last equation implies that also in this case \(c_s^2\) must be negative around the bounce, since \(\dot{H}\) is positive around the bounce and \(D>0\) in order to avoid ghosts. Consequently also for these models, the ghosts free condition implies the relation \(\mathop {\mathrm {sgn}}{\dot{H}}=-\mathop {\mathrm {sgn}}{c_s^2}\), and gradient instabilities are unavoidable around the bounce. Only introducing a general \(G(X,\phi )\), which is also a function of the kinetic term X, the gradient instabilities can be avoided, but even in this case a careful analysis is necessary [24,25,26].

Another general problem of K(X) models related to the sign of \(c_s^2\) is that around the bounce the Hamiltonian could be not positive definite when the gradient term dominates the kinetic term. Also this problem could be avoided by adding a Galilean term of the form \(G(X,\phi )\Box \phi \) to the Lagrangian in order to avoid a negative sound speed, according to Eq. (33), while still realizing the conditions for the bounce. We will leave to a future upcoming work a detailed study of the stability of cosmological perturbation for K(X) models with the addition of general Galilean terms, since the purpose of the present paper is mainly the derivation of general conditions to realize the bounce at the background level with a K(X) model. It should be noted nevertheless that these types of instabilities are general for any K(X) driven bounce model [21], and can arise also for the other models which were previously studied in [17, 18].

7 Adiabaticity

Due to the form of the Lagrangian we can anticipate that the behavior of curvature perturbations for these models requires a careful treatment. The non-adiabatic pressure perturbation for these kind of scalar field models is in fact zero on any scales [23] in the region where the potential is constant, because in that regime they are equivalent to a barotropic fluid with equation of state \(P(\rho )\) so that

$$\begin{aligned} \delta P_{nad}=\delta P-\frac{\dot{P}}{\dot{\rho }}=0. \end{aligned}$$
(44)

For this reason they are called globally adiabatic(GA) models, to distinguish them from attractor models which are adiabatic only on super-horizon scales (SHA).

After defining the perturbed metric as

$$\begin{aligned} \mathrm{d}s^2= & {} a^2\Bigl [-(1+2A)\mathrm{d}\eta ^2+2\partial _jB \mathrm{d}x^j\mathrm{d}\eta \nonumber \\&+\left\{ \delta _{ij}(1+2{\mathcal R})+2\partial _i\partial _j E\}\mathrm{d}x^i\mathrm{d}x^j\right\} \Bigr ]\,, \end{aligned}$$
(45)

in [24] it was shown that in general relativity, in absence of anisotropies, the conservation of the perturbed energy momentum tensor gives

$$\begin{aligned} \delta P_{ nad}= \left[ \left( \frac{c_w}{c_s}\right) ^2-1\right] (\rho +P)\frac{\dot{{\mathcal R}_c}}{H}, \end{aligned}$$
(46)

which is true on any scale, and is not based on neglecting any gradient term. For GA models the adiabatic sound speed \(c_s=\left( \frac{\delta P}{\partial \rho }\right) _c\) is equal to the phase speed \(c_w=\frac{\dot{P}}{\dot{\rho }}\) and for this reason, despite \(\delta P_{nad}=0\), nothing can be inferred about the behavior of \(\dot{{\mathcal R}_c}\), otherwise \({\mathcal R}_c\) should be constant on any scale. Since in ekpyrotic models the potential is not constant during the bouncing phase, \(c_s\ne c_w\). The exponential growth of \({\mathcal R}_c\) [14] then implies that \(\delta P_{ nad}\ne 0\), i.e. the bounce is strongly non-adiabatic. This large non-adiabaticity is in fact the cause of the growth of anisotropies during the bouncing phase.

On the contrary, in the region where the potential asymptotes a constant value, these models could enter a phase of ultra-slow inflation in which curvature perturbations may not be conserved on super-horizon scales [23]. This is due to the fact that when the potential is constant \(c_s=c_w\) and conservation of curvature perturbation on super-horizon scales is not guaranteed anymore [24] despite adiabaticity. A similar ultra-slow phase could occur for the model defined in Eq. (17), in the region where the potential tends to a constant value.

8 Conclusion

We have derived the general conditions to obtain a bounce with a scalar field model with generalized kinetic term of the form K(X) in general relativity. The requirement of the existence of a bounce point and of two turning points for H(t) give some conditions which K(X) and the potential \(V(\phi )\) have to satisfy. We have given the examples of two models constructed according to these conditions. One is based on a quadratic K(X), and the other on a K(X) which is always avoiding divergences of the second time derivative of the scalar field, which may otherwise occur. An appropriate choice of the initial conditions can lead to a sequence of consecutive bounces.

While at the perturbation level one class of models is free from ghosts, in general gradient instabilities are present around the bounce time, and they could be avoided only by modifying the Lagrangian. In the future it will be interesting to add Galilean type terms to the Lagrangian and study in detail the cosmological perturbations during and after the bounce, and the effects of global adiabaticity in the region where the potential tends to a constant value.