1 Introduction

A large number of cosmological and astrophysical observations provide strong evidence for the existence of dark matter (DM) in the universe. The amount of cold dark matter (CDM) has been precisely estimated from the measurements of the Planck satellite to be \(\Omega _{\mathrm{DM}} h^{2} = 0.1198 \pm 0.0015\) [1]. The nature of DM particles and their properties is the subject of intense investigation. One of the main physics programmes at the Large Hadron Collider (LHC) is devoted to the detection of DM, where there is the real possibility of the production of DM particles of any spin at 13 TeV centre-of-mass energy. As such, the ATLAS and the CMS collaborations are closely examining several DM signatures involving missing energy, , accompanied by a single or two jet events [2]. In addition there are direct detection experiments, which measure the nuclear-recoil energy and its spectrum in DM-nucleon elastic scattering. The indirect detection experiments look for signals of DM annihilation into Standard Model (SM) particles in cosmic rays, and have detection instruments mounted on satellites and ground based telescopes [3, 4].

Effective field theories (EFT) in which the DM-SM interactions are mediated by heavy particles, which are not accessible at the LHC energies, have been analysed in detail with limits from direct and indirect searches. Recently the need to go beyond these EFT models has been pointed out, in light of the large energy accessible at the LHC [5]. Simplified models of DM with interactions to SM particles have emerged as attractive alternatives to EFT models. In these models the interaction between the DM and SM particles are mediated by spin-0 and spin-1 particles in the s-channel, whereas in the t-channel models the mediator can be a scalar, a fermion or a vector particle, which will typically also carry colour or lepton number [5].

In this paper we consider a minimal SM singlet spin-3/2 fermion, \(\chi \), as a DM candidate, interacting with the SM particles through the exchange of a spin-1 mediator, \(Z^{\prime }\), in a minimal flavour violation (MFV) s-channel model. Spin-3/2 particles exist in several models beyond the SM, namely in models of supergravity where the graviton is accompanied by spin-3/2 gravitino superpartner. Spin-3/2 fermions also exist in Kaluza–Klein models, in string theory, and in models of composite fermions [6,7,8,9,10,11]. Recently spin-3/2 CDM has been studied in EFT models, and constraints from direct and indirect observations obtained [12,13,14,15]. Spin-3/2, 7.1 keV warm dark matter (WDM) has also been considered as a means to provide a viable explanation from the anomalous 3.1 KeV X-ray line observed by the XMM Newton [16]. As such we shall introduce the spin-3/2 CDM in an MFV s-channel model in Sect. 2. Whilst in Sect. 3 we discuss all relevant experimental constraints including the relic density and the signatures of these DM particles at the LHC. In Sect. 4 we summarise our main results.

2 Spin-3/2 singlet DM model

In this paper we extend the SM by including a spin-3/2 particle \(\chi \). We further let \(\chi \) to be a SM singlet which interacts with the SM particles through the exchange of a vector particle \(Z^{\prime }\) in the s-channel. Note that this can be done, for example, by extending the SM gauge symmetry with a new \(U(1)^{\prime }\) gauge symmetry which is spontaneously broken, such that the mediator obtains a mass \(m_{Z^{\prime }}\). We also invoke a discrete \({Z}_{2}\) symmetry under which the spin-3/2 DM particle \(\chi \) is odd, whereas all other SM particles, including the vector mediator \( Z^{\prime }\), are even. The spin-3/2 free Lagrangian is given by [17]:

$$\begin{aligned} \mathscr {L} = \bar{\chi }_{\mu } \Lambda ^{\mu \nu } \chi _{\nu }, \end{aligned}$$
(1)

with

(2)

Note that \(\chi _{\mu }\) satisfies \(\Lambda ^{\mu \nu }\chi _{\nu } = 0\), and with \(\chi _\mu \) being on mass-shell we have

(3)

The spin sum for spin-3/2 fermions

$$\begin{aligned} S_{\mu \nu }^{+}(p) = \sum _{i = -3/2}^{3/2} u^{i}_{\mu }(p)\bar{u}^{i}_{\nu }(p) \end{aligned}$$
(4)

and

$$\begin{aligned} S_{\mu \nu }^{-}(p) = \sum _{i = -3/2}^{3/2} v^{i}_{\mu }(p)\bar{v}^{i}_{\nu }(p), \end{aligned}$$
(5)

are given by [17]:

(6)

In view of the non-renormalisable nature of interacting spin-3/2 theories, we can only write a generic set of interactions respecting the SM gauge symmetry between the singlet Dirac-vector spinor, \(\chi _{\mu }\), with SM fermions mediated by a vector particle \(Z^{\prime }_{\mu }\) as (see for example [18])

$$\begin{aligned} \mathscr {L}_{\chi , Z^\prime } + \mathscr {L}_{f, Z^\prime }&\supset \bar{\chi }_{\alpha } \gamma ^{\mu } (g_{\chi }^{V} - \gamma ^{5} g_{\chi }^{A}) \chi _{\beta } Z_{\mu }^{\prime } g^{\alpha \beta } \nonumber \\&\quad + \sum _{f = q, l, \nu } \bar{f} \gamma ^{\mu } ( g_{f}^{V} - \gamma ^{5} g_{f}^{A} ) f Z_{\mu }^{\prime }, \end{aligned}$$
(7)

where the sum is over all quarks, charged leptons and neutrinos. The interaction is not restricted by MFV to be either a pure vector or axial-vector. Although the form of the low energy interactions of spin-3/2 particles should arise from an underlying theory at high energies, such as string theory, we follow the approach of simplified model theories. The purpose of a simplified model approach is to characterise the DM production present in a complete theory, without having to specify the complete theory. In these theories the mediator provides the link between the SM and DM candidate. In general this interaction will induce flavour-changing neutral currents, which are strongly constrained by low energy phenomenology. The constraints can be avoided by imposing a MFV structure on the couplings, or by restricting the interactions to one generation.

There exists an extensive range of models with an extra \(U(1)^{\prime }\) symmetry (for a review see [19]). The most stringent indirect constraints on \(m_{Z^{\prime }}\) arise from the effect of a \(Z^{\prime }\) coupling to SM fermions in precision electro-weak observables from low energy weak neutral current experiments [20, 21], and gives a lower limit on \(m_{Z^{\prime }}\) of \(\mathscr {O}\)(1 TeV); where LHC experiments set strong bounds on the \(Z^{\prime }\) mass. For a \(Z^{\prime }\) coupling with SM particles to be of the order of SM - Z electro-weak coupling this bound is typically \(m_Z^{\prime }\ge \) 2 TeV [5]. This bound is somewhat relaxed (depending on the model) when \(Z^{\prime }\) is allowed to decay into DM candidate [20, 22].

Fig. 1
figure 1

Ratio of the mediator decay width to its mass \(\Gamma /{m_{Z^{\prime }}}\) as a functions of \(m_{\chi }/{m_{Z^{\prime }}}\) for a few benchmark values of the couplings: 0.1, 0.5 and 1.0. The left panel is for the vector couplings \(g^{V}_{\chi ,f}\), and the middle panel is for the chiral couplings (\(g^{V}_{\chi ,f} = \pm \,g^{A}_{\chi ,f}\)). The right panel is for the axial-vector couplings \(g^{A}_{\chi ,f}\)

Full size image

The decay width \(\Gamma (Z^{\prime }\rightarrow f\bar{f} + \chi _{\alpha }\bar{\chi }_{\alpha })\) is given by

$$\begin{aligned}&\Gamma (Z^{\prime }\rightarrow f\bar{f} + \chi _{\alpha }\bar{\chi }_{\alpha })\nonumber \\&\quad = \sum _{f}\frac{N_{c}}{12\pi }m_{Z^{\prime }}\sqrt{1-\frac{4m_{f}^{2}}{m^{2}_{Z^{\prime }}}} \nonumber \\&\quad \times \left[ ( (g^{V}_{f})^{2} + (g^{A}_{f})^{2}) + \frac{2m^{2}_{f}}{m^{2}_{Z^{\prime }}} ( (g^{V}_{f})^{2} - 2 (g^{A}_{f})^{2}) \right] \nonumber \\&\quad + \frac{m_{Z^{\prime }}}{108\pi } \left( \frac{m^{2}_{\chi }}{m^{2}_{Z^{\prime }}}\right) \sqrt{1-\frac{4m_{\chi }^{2}}{m^{2}_{Z^{\prime }}}} \nonumber \\&\quad \times \left[ (g_{\chi }^{V})^{2}\left( 36 - 2\frac{m^{2}_{Z^{\prime }}}{m^{2}_{\chi }}- 2\frac{m^{4}_{Z^{\prime }}}{m^{4}_{\chi }} + \frac{m^{6}_{Z^{\prime }}}{m^{6}_{\chi }}\right) \right. \nonumber \\&\left. \quad +\, (g_{\chi }^{A})^{2} \left( -40 + 26\frac{m^{2}_{Z^{\prime }}}{m^{2}_{\chi }} - 8 \frac{m^{4}_{Z^{\prime }}}{m^{4}_{\chi }} + \frac{m^{6}_{Z^{\prime }}}{m^{6}_{\chi }}\right) \right] . \end{aligned}$$
(8)

The sum extends over all SM fermions f that are above the threshold, \(N_{c} = 3\) for quarks and 1 for leptons.

There are several interesting consequences on the DM mass and couplings arising from the above decay width expressions. If the DM mass \(m_{\chi } > m_{Z^{\prime }}/2\), the only decay channel available to the mediator \(Z^{\prime }\) is into SM fermions. Since \(\Gamma (Z^{\prime }) < \, m_{Z^{\prime }}\) is required for the mediator description to be perturbatively valid, the vector coupling, for example, should satisfy

$$\begin{aligned} \frac{8 m_{Z^{\prime }}}{12\pi }\left( g_{f}^{V}\right) ^{2}< m_{Z^{\prime }} \quad \Rightarrow \quad \left( g_{f}^{V}\right) ^{2} < \frac{3\pi }{2}. \end{aligned}$$
(9)

Here we consider the coupling to be only to one generation for the purposes of illustration. The qualitative result remains essentially unchanged if all three generations are taken, except that the top quark mass may not be neglected in comparison to the mediator mass. This gives \(\Gamma _{Z^{\prime }}/m_{Z^{\prime }} \simeq \frac{2}{3\pi }(g_{f}^{V})^{2}\), and we have the narrow width approximation being applicable for \(g_{f}^{V}\le 1\). However, if the DM mass \(m_{\chi } < m_{Z^{\prime }}/2\), the mediator can decay into DM pairs, and there exists a minimum limit on the DM mass \(\chi \) for a given value of the mediator mass with the coupling given roughly by

$$\begin{aligned} \frac{1}{108\pi }\left( \frac{m_{Z^{\prime }}}{m_{\chi }}\right) ^{4} \left( g_{\chi }^{V,A}\right) ^{2} < 1. \end{aligned}$$
(10)

If the DM mass is below this value, the decay width would exceed the mediator mass.

In the following we consider universal couplings for simplicity, \(g_{\chi }^{V} = g_{f}^{V}\) and \(g_{\chi }^{A} = g_{f}^{A}\), and restrict ourselves to one generation of SM fermions. In Fig. 1 we have plotted the mediator \(Z^{\prime }\) decay width as a function of \(m_{\chi }\) for some benchmark values of pure vector couplings \(g_{\chi , f}^{V}\), chiral couplings \(g_{\chi , f}^{V} = \pm \,g_{\chi , f}^{A}\) and pure axial couplings \(g_{\chi , f}^{A}\). It can be seen from Fig. 1 that there exists a minimum \(m_\chi \) for a given coupling, where a mass of \(\chi \) less than the limit given in Eq. 10, results the value of decay width more than the value of \(m_\chi \). This feature is peculiar to the spin-3/2 nature of the DM.

Fig. 2
figure 2

The contour plots between the \(m_{Z^{\prime }}\) and \(m_{\chi }\), where we have assumed that the DM \(\chi \) saturates the observed DM density. The left and the right panels are for benchmark values of vector and axial-vector couplings, respectively. The middle panel is for the chiral coupling

Full size image

3 Constraints

3.1 Relic density

In the early universe the DM particles were kept in thermal equilibrium with the rest of the plasma through the creation and annihilation of \(\chi \)’s. The cross section of the annihilation process \(\chi \bar{\chi } \rightarrow f \bar{f}\) proceeds through \(Z^{\prime }\), and the spin averaged cross section is given by

$$\begin{aligned}&\sigma (\chi \bar{\chi }\rightarrow f \bar{f} ) \nonumber \\&\quad = \sum _{f}\frac{N_{c}\,\sqrt{s-4m_{f}^{2}}}{ 432 \,\pi \, m_\chi ^4 \,m_{Z^\prime }^4\, s }\frac{1}{\sqrt{s-4m_{\chi }^{2}}} \left[ \frac{1}{(s - m_{Z^\prime }^2)^2 + \Gamma ^2 m_{Z^\prime }^2 }\right] \nonumber \\&\qquad \times [ ( g^{A}_{f})^{2} \{ ( g^{A}_{\chi } )^{2} \{ 4m_{f}^{2} \{ 10\, m_{\chi }^{6} (7m_{Z^{\prime }}^{4} - 6 m_{Z^{\prime }}^{2}s + 3s^{2} ) \nonumber \\&\qquad - 2 \, m_{\chi }^{4} \,s (16 \,m_{Z^{\prime }}^{4} - 6\,m_{Z^{\prime }}^{2}\,s + 3\,s^{2}) \nonumber \\&\qquad + m_{\chi }^{2}\,s^{2}(11\,m_{Z^{\prime }}^{4}- 6\,m_{Z^{\prime }}^{2}\,s + 3\,s^{2}) - m_{Z^{\prime }}^{4}\,s^{3}\} \nonumber \\&\qquad + m_{Z^{\prime }}^{4} \,s (- 40 \,m_{\chi }^{6} + 26\, m_{\chi }^{4} \,s - 8 \,m_{\chi }^{2} \,s^{2} + s^{3})\} \nonumber \\&\qquad - (g^{V}_{\chi })^{2} m_{Z^{\prime }}^{4} (4m_{f}^{2}-s) ( 36\,m_{\chi }^{6} - 2\,m_{\chi }^{4}\,s - 2\,m_{\chi }^{2}\,s^{2} + s^{3})\} \nonumber \\&\qquad + ( g^{V}_{f})^{2} m_{Z^{\prime }}^{4} (2 m_{f}^{2} + s) \nonumber \\&\qquad \times \{ (g_{\chi }^{A})^{2} (-40 \,m_{\chi }^{6} + 26 \,m_{\chi }^{4}s - 8\,m_{\chi }^{2} \,s^{2} + s^{3}) \nonumber \\&\qquad + (g^{V}_{\chi })^{2} ( 36\,m_{\chi }^{6} - 2\,m_{\chi }^{4}\,s - 2\,m_{\chi }^{2}\,s^{2} + s^{3})\}]. \end{aligned}$$
(11)

Freeze-out occurs when the \(\chi \)’s are non-relativistic \((v \ll c)\). We then have

$$\begin{aligned} s \simeq 4\,m_{\chi }^{2} + m_{\chi }^{2} v^{2} + \mathscr {O}(v^{4}) \end{aligned}$$
(12)

in the lab frame. The cross section can be expanded in powers of \(v^{2}\) as

$$\begin{aligned} \sigma v = a + b v^{2} + \mathscr {O}(v^{4}). \end{aligned}$$
(13)

The relic-density contributions of the DM particles can be obtained by numerically solving the Boltzmann equation:

$$\begin{aligned} \frac{\mathrm{d} n_{\chi }}{\mathrm{d} t} + 3 H n_{\chi } = -\langle \sigma |v|\rangle (n^{2}_{\chi } - (n^{eq}_{\chi })^{2}), \end{aligned}$$
(14)

where \(\langle \sigma |v\rangle \) is the thermally averaged \(\chi \)-annihilation cross section \(\langle \sigma (\chi \bar{\chi } \rightarrow f\bar{f})|v\rangle \), and \(n_{\chi }\) is the number density of the \(\chi \)’s. When we have thermal equilibrium the number density is given by

$$\begin{aligned} n^{eq}_{\chi } = 4\left( \frac{m_{\chi }\, T}{2\pi }\right) ^{3/2} \exp \left( -\frac{m_{\chi }}{T}\right) . \end{aligned}$$
(15)

The Hubble expansion rate is given by

$$\begin{aligned} H = \sqrt{\frac{8\pi \rho }{3M_{\text {pl}}^{2}}}, \end{aligned}$$
(16)

where \( M_{\text {pl}} = 1.22\times 10^{19}\) GeV is the Planck mass. The Boltzmann equation is solved numerically to yield [23]

$$\begin{aligned} \Omega _\mathrm{DM} h^{2}\simeq \frac{2\times 1.07\times 10^{9}X_{F}}{M_\mathrm{pl}\sqrt{g_{*}}(a + \frac{3b}{X_{F}})}, \end{aligned}$$
(17)

where \(g_{*}\) is the number of degrees of freedom at freeze-out temperature \(T_{F}\), and is taken to be 92 for \(m_{b}< T_{F} < m_{Z^{\prime }}\), \(X_{F} = m_{\chi }/{T_{F}}\). The freeze-out temperature is obtained by solving

$$\begin{aligned} X_{F} = \ln \left[ c(c+2)\sqrt{\frac{45}{8}}\frac{g M_\mathrm{pl} m_{\chi }(a + \frac{6b}{X_{F}})}{2\pi ^{3}\sqrt{g_{*}(X_{F})}\sqrt{X_{F}}}\right] , \end{aligned}$$
(18)

where c is taken to be 1 / 2. For spin-3/2 DM \(g = 4\).

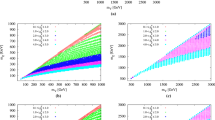
In Fig. 2 we show the contour graphs between the mass of the mediator \(m_{Z^{\prime }}\) and the DM mass \(m_{\chi }\), by assuming that the DM \(\chi \) saturates the observed DM density. From the graphs we see that, for small couplings \(g \le 0.1\), the parameter space \((m_{\chi }, m_{Z^{\prime }})\) is consistent with the observed relic density and is thus independent of the coupling. This can be understood by noting that the leading term in the thermally averaged DM annihilation cross section into SM fermions is given by

$$\begin{aligned} \langle \sigma (\chi \bar{\chi } \rightarrow f\bar{f})|v\rangle&\simeq \frac{20\, g^{4}}{9\, \pi \, m^{2}_{Z^{\prime }}}\frac{m^{2}_{\chi }}{ m^{2}_{Z^{\prime }}}\frac{1}{\left( 1- \frac{4m^{2}_{\chi }}{m^{2}_{Z^{\prime }}}\right) ^{2}+ \left( \frac{\Gamma ^{2}}{m^{2}_{Z^{\prime }}}\right) }\nonumber \\&\simeq \frac{8 \times 10^{-24}}{(m_{Z^{\prime }}/1 TeV)^{2}}\frac{g^{4}}{\left( 1- \frac{4m^{2}_{\chi }}{m^{2}_{Z^{\prime }}}\right) ^{2}+ \left( \frac{\Gamma ^{2}}{m^{2}_{Z^{\prime }}}\right) }\nonumber \\&\quad \times \left( \frac{m_{\chi }}{m_{Z^{\prime }}}\right) ^{2}\,\mathrm{cm}^{3}\,\mathrm{s}^{-1}. \end{aligned}$$
(19)

The annihilation cross section, being proportional to the fourth power in coupling, falls rapidly for couplings \(\le \)0.1, and the freeze-out occurs early when the temperature is high. This will result in the relic density falling below the observed value. The annihilation rate, however, receives resonant enhancement at \(m_{\chi } \simeq \frac{1}{2} m_{Z^{\prime }}\), in which case the \(\Gamma /m_{Z^{\prime }}\) term dominates over the pole term in the denominator. Thus near resonance the annihilation cross section becomes independent of the coupling and we get the relic-density contour curves almost independent of coupling. In this situation the observed relic density is obtained for \(m_{\chi } \simeq \frac{1}{2} m_{Z^{\prime }}\) as is evident from the graphs.

Fig. 3
figure 3

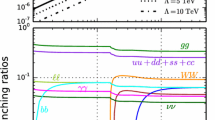
The spin-independent nucleon–DM cross section \(\sigma ^\mathrm{SI}\) (left panel) and spin-dependent nucleon–DM cross section \(\sigma ^\mathrm{SD}\) (right panel). The predicted cross section is shown here for different values of the coupling, and are in agreement with the relic-density constraints. In the plots we show the recent XENON1T data for \(\sigma ^\mathrm{SI}\), and the XENON 100 neutron bounds for \(\sigma ^\mathrm{SD}\). For the vector coupling almost the entire parameter space \((m_{\chi }, m_{Z^{\prime }})\) is consistent with the relic-density constraints and is ruled out from the XENON1T bound. In contrast for the axial-vector coupling, the parameter space consistent with the observed relic density is also allowed by the direct XENON 100 neutron bound

Full size image

3.2 Direct detection

Constraints from DM detection experiments can be obtained from the elastic DM-nucleon cross section. In the present case, owing to the presence of both vector and axial-vector couplings, the DM-nucleon scattering has both spin-independent and spin-dependent components. The corresponding cross section at zero momentum transfer can easily be computed [24,25,26]. The spin-independent and spin-dependent sub-dominant cross sections are given by [27]

$$\begin{aligned} \sigma _{\chi N}^\mathrm{SI}&= \frac{\mu ^{2} f^{2}_{N}}{\pi m^{4}_{Z^{\prime }}} = \frac{9\mu ^{2}(g_{f}^{V} g_{\chi }^{V})^{2}}{\pi m^{4}_{Z^{\prime }}} \nonumber \\&\simeq 1.4\times 10^{-37} (g_{f}^{V} g_{\chi }^{V})^{2} \left( \frac{\mu }{1\, \mathrm{GeV}}\right) ^{2} \left( \frac{300 \,\mathrm GeV}{m_{Z^{\prime }}}\right) ^{4} \mathrm{cm}^{2}, \end{aligned}$$
(20)

and

$$\begin{aligned} \sigma _{\chi N}^\mathrm{SD}&= \frac{5\mu ^{2}}{3\pi m^{4}_{Z^{\prime }}}a^{2}_{N} = \frac{5\mu ^{2}(g_{f}^{A} g_{\chi }^{A} )^{2}}{3\pi m^{4}_{Z^{\prime }}} ( \Delta u^{N} + \Delta d^{N} + \Delta s^{N})^{2} \nonumber \\&\simeq 4.7\times 10^{-39}( g_{\chi }^{A} g_{f}^{A})^{2} \left( \frac{\mu }{1\,\mathrm{GeV}}\right) ^{2} \left( \frac{300 \,\mathrm GeV}{m_{Z^{\prime }}}\right) ^{4} \mathrm{cm}^{2}, \end{aligned}$$
(21)

where

$$\begin{aligned} \mu = \frac{m_{\chi }m_{N}}{m_{\chi } + m_{N}} \end{aligned}$$
(22)

is the reduced mass. \(m_{N} = (m_{p}+m_{n})/2\simeq 0.939\) GeV is the nucleon mass for direct detection, with \(f_{p}\), \(f_{n}\) and \(a_{p,n}\) being given by

$$\begin{aligned} f_{p} = g_{\chi }^{V} (2 g_{u}^{V} + g_{d}^{V}),\quad f_{n} = g_{\chi }^{V}(2g_{d}^{V} + g_{u}^{V}) \end{aligned}$$
(23)

and

$$\begin{aligned} a_{p,n} = \sum _{q= u,d,s} g_{\chi }^{A} \Delta q^{p,n} g_{q}^{A}. \end{aligned}$$
(24)

The coefficients \(\Delta q^{p,n}\) depend on the light quark contributions to the nucleon spin [27];

$$\begin{aligned} \Delta u^{p} =&\Delta d^{n} = 0.84\pm 0.02,\nonumber \\ \Delta d^{p} =&\Delta u^{n} = -0.43\pm 0.02, \\ \Delta s^{p} =&\Delta s^{n} = -0.09\pm 0.02. \nonumber \end{aligned}$$
(25)

The axial-vector term is suppressed by the momentum transfer, or by the DM velocity, and has been neglected. In Fig. 3 we show the predictions for the spin-independent \(\sigma ^{SI}\) and spin-dependent \(\sigma ^{SD}\) cross sections for benchmark values of the vector and axial-vector couplings, as a function of DM mass \(m_{\chi }\). The corresponding experimental bounds from XENON1T [28] and XENON100 [29] are also displayed. The mediator mass \(m_{Z^{\prime }}\) is set to give the observed relic density for all values of \(m_{\chi }\) and the couplings. We find that for the vector coupling almost the entire parameter space \((m_{\chi }, m_{Z^{\prime }})\) consistent with the observed relic density, is ruled out from the XENON1T bound on spin-independent nucleon–DM elastic scattering cross sections. The XENON100 data on the spin-dependent cross section on the other hand does not place severe constraints on the parameter space, and as such the allowed parameter space is consistent with the observe relic density.

Fig. 4
figure 4

The prediction for the DM \(\chi \) annihilation rate into \(b\bar{b}\) and \(\tau ^{+}\tau ^{-}\) for benchmark values of couplings. The top, middle and bottom panels are for pure vector, chiral and axial couplings, respectively. The cross sections are obtained for \((m_{\chi }, m_{Z^{\prime }})\) values consistent with the observed relic density. Bounds from the Fermi-LAT experiments are also shown

Full size image

3.3 Indirect Detection

DM annihilation in the universe would result in cosmic ray fluxes which can be observed by dedicated detectors. The Fermi Large Area Telescope (LAT) collaboration [30, 31] has produced constraints on the DM annihilation cross section into some final states, namely \(e^{+}e^{-}\), \(\mu ^{+}\mu ^{-}\), \(\tau ^{+}\tau ^{-}\), \(b\bar{b}\), \(u\bar{u}\), \(W^{+}W^{-}\) etc. [31, 32].

In Fig. 4 we show the prediction for the DM annihilation into \(b\bar{b}\) and \(\tau ^+ \tau ^-\) for vector, axial-vector and chiral couplings, as a function of \(m_{\chi }\). The predictions shown here are for benchmark values of couplings and for the DM mass \(m_{\chi }\) consistent with the observed relic density. The same is true for the chiral couplings. We have also shown the bounds from the Fermi-LAT experiments. It can be seen from these figures that the Fermi-LAT data on the DM annihilation cross section, \(\langle \sigma (\chi \bar{\chi } \rightarrow b\bar{b}, \tau ^{+}\tau ^{-})|v\rangle \), is consistent with the benchmark vector and axial-vector couplings, and for \((m_{\chi }, m_{Z^{\prime }})\) parameters obtained from the observed relic density. However, for the chiral couplings considered in this work there is only a narrow window in the high DM mass (\(m_{\chi } \ge \) 400 GeV) range for the coupling \(g \simeq 1\). For small values of the coupling (\(g \le 0.1\)) Fermi-LAT data does not provide any stringent bounds on the \((m_{\chi }, m_{Z^{\prime }})\) parameter space.

Fig. 5
figure 5

The monojet cross section in (pb) at the LHC with missing transverse energy + 1 jet signal, through \(pp \rightarrow Z^{\prime } \rightarrow \chi \bar{\chi }+ 1 j\). The cross sections are obtained by considering values of \((m_{Z^{\prime }}, m_\chi )\) consistent with the observed relic density for the benchmark couplings. The allowed parameter space for spin-3/2 DM candidates lies below the CMS bound of \(\sigma _\mathrm{monojet} = 7.8\) fb, as explained in the text. The left, central and middle panels are for pure vector, chiral and axial-vector couplings respectively

Full size image

3.4 Collider constraints

Monojet searches at the LHC with missing transverse energy, , have been used by CMS at 8 TeV, based on an integrated luminosity of 19.7 \(\mathrm fb^{-1}\) [33], to put constraints on the interaction of quarks and DM particles. In the context of a spin-1/2 DM particle interacting through a vector mediator, with vector and axial-vector couplings, constraints on the DM mass \(m_{\chi }\) and the mediator mass \(m_{Z^{\prime }}\) for some representative values of the coupling have been obtained in the literature [34,35,36,37,38,39].

For monojet constraints at the LHC, we use the parameter space \((m_{\chi }, m_{Z^{\prime }})\) for the spin-3/2 DM, consistent with the observed DM density for benchmark couplings. To obtain the cross section for monojets we generate parton level events of the process \(p p \rightarrow \chi \bar{\chi }+ 1 j\) using MadGraph5 [40], where the required model file for the Lagrangian (7) is obtained from FeynRules [41]. The cross sections are calculated here to obtain bounds by requiring GeV, for which the CMS results exclude new contributions to the monojet cross section exceeding 7.8 \(\mathrm fb\) at 95\(\%\) CL. The resulting monojet cross section for the vector, axial-vector and chiral couplings are shown in Fig. 5, where we find that the vector coupling results are in agreement with the bounds from the direct detection experiments. In the case of axial-vector couplings, the monojet search places stronger constraints on the parameters, in comparison to the constraints from direct and indirect searches, albeit for \(g^{A}_{\chi , f} \sim 1\).

4 Summary

In this paper we have considered a spin-3/2 DM particle interacting with SM fermions through a vector mediator in the s-channel. Assuming MFV we used universal vector and axial-vector couplings and restricted ourselves to one generation. The main observations are the following:

  • In view of the spin-3/2 nature of the DM, in addition to the restriction on the coupling arising from the decay width, there also exists a minimum value of the DM mass for a given coupling and mediator mass.

  • For the case of vector and chiral couplings, almost the entire parameter space \((m_{\chi }, m_{Z^{\prime }})\) consistent with the observed relic density, is ruled out by direct detection through nucleon–DM elastic scattering bounds given by XENON1T data.

  • The case of a vector mediator with pure axial-vector coupling is, in contrast, different from the vector coupling. The parameter space is consistent with the observed relic density and is also allowed by the indirect and direct (XENON100 neutron) observations.

  • For the benchmark couplings considered here there are no strong bounds on vector and chiral couplings from the monojet searches at the LHC, and the results are in broad agreement with the direct detection experiments.

  • The case of pure axial coupling is, however, different. Here the monojet search place stronger constraints on the parameters in comparison to the constraints obtained from the XENON100 neutron observations.

  • The Fermi-LAT data on the DM annihilation cross section is consistent with the vector and axial-vector couplings considered here, and for the \((m_{\chi }, m_{Z^{\prime }})\) parameter values obtained from the relic density. For couplings \(g \le 0.1\) the Fermi-LAT data does not provide stringent bounds on the \((m_{\chi }, m_{Z^{\prime }})\) parameters. For chiral couplings the data allows only a narrow window in the DM mass (\(m_{\chi } \ge \,\)400  GeV) and \(g \simeq 1\).

  • In the EFT frame work for pure vector couplings [12, 13] the entire parameter space 10 GeV \(< m_{\chi }<\) 1 TeV, and an effective interaction scale of the order of a few tens of TeV, though consistent with the observed relic density, is ruled out from the direct detection observations. For the case of pure axial coupling, bounds from direct detection do not forbid the DM mass to lie in this range. This is in agreement with our study in a simple s-channel mediator model, except that in the mediator model the minimum allowed DM mass is consistent with the observed relic density, and it is of order of 100 GeV. In the case of couplings with chiral SM fermions \((g_{f}^{V} = g_{f}^{A})\) it was found [14] that, for a spin-3/2 DM mass up to 1 TeV, the entire parameter space is ruled out from direct detection. 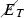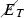The monojet + searches at ATLAS rules out DM masses up to 200 GeV. In contrast the s-channel mediator model monojet searches at ATLAS are more stringent, and the allowed DM mass limit is raised to greater than 500 GeV. For DM masses exceeding 1 TeV, there are no direct detection constraints, but collider and indirect observation constraints still exist.