Open charm production in double parton scattering processes in the forward kinematics

Abstract

We calculate the rate of double open charm production in the forward kinematics studied recently in the LHCb experiment. We find that the mean field approximation for the double parton GPD (generalized parton distributions), which neglects parton–parton correlations, underestimates the rate by a factor of 2. The enhancement due to the perturbative QCD correlation $1\otimes 2$ mechanism which explains the rate of double parton interactions at the central rapidities is found to explain 60 $\div$ 80% of the discrepancy. We argue that the nonperturbative fluctuations leading to non-factorized (correlated) contributions to the initial conditions for the DGLAP collinear evolution of the double parton GPD play an important role in this kinematics. Combined, the two correlation mechanisms provide a good description of the rate of double charm production reported by the LHCb. We also give predictions for the variation of the $\sigma _{\text {eff}}\,$(i.e. the ratio of double and square of single inclusive rates) in the discussed kinematics as a function of $p_t$. The account for two correlation mechanisms strongly reduces the sensitivity of the results to the starting point of the QCD evolution.

1 Introduction

It is widely realized now that hard Multiple Parton Interactions (MPI) play an important role in the description of inelastic proton–proton (pp) collisions at the LHC energies where MPIs occur with probability of the order 1 in typical inelastic collisions.

Hence after years of relatively sparse theoretical activities after pioneering papers of the 1980s [1, 2] studies of the MPI became a field of very active theoretical research; see e.g. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] and references therein.

Also, in the past several years a number of double parton scattering (DPS) measurements in different channels in the central rapidity kinematics were carried out [18,19,20,21,22,23], while many Monte Carlo (MC) event generators now incorporate MPIs.

The recent discovery by the LHCb of the double charm DPS production attracted a lot of attention since it expands the study of multiparton dynamics into a new kinematics region of large rapidities [24,25,26,27], and since the background from the leading twist processes is very strongly suppressed in this kinematics [28,29,30].

The LHCb data are available for the $J/\psi$ DPS production: $J/\psi$–$D\bar{D}$ and for the DPS production of two $D\bar{D}$ pairs. According to the LHCb experiment results, the DPS rate in the studied kinematics, which is customarily parameterized by 1/$\sigma _{\text {eff}}\,$ is practically the same for all channels and $\sigma _{\text {eff}}\,$ $\sim$ 20 mb (see Fig. 10 in [25]). The observed universality of $\sigma _{\text {eff}}\,$is consistent with expectations of the approximation outlined below. Here, as usual, $\sigma _{\text {eff}}\,$is defined as

$$\begin{aligned} \sigma _\mathrm{eff}=\sigma _1\sigma _2/\sigma _4 \end{aligned}$$

(1)

where $\sigma _{1,2}$ are cross sections of elementary $2\rightarrow 2$ processes and $\sigma _4$ is a cross section of a process $pp\rightarrow 1+2$ final state. We will focus on the production of two $D\bar{D}$ pairs since the data for this channel have the smallest errors [31]. Also, more complicated mechanisms than the $gg \rightarrow J/\psi +X$ process may contribute in the case of $J/\psi$ production, i.e. $ggg\rightarrow J/\psi$ (see e.g. [32] for a recent discussion).

It was pointed out starting with [5, 33, 34] that the rate of DPS calculated under assumption that partons in nucleons are uncorrelated (and using information as regards the gluon GPDs available from the analysis [33, 34] of the HERA data) is too low to explain the data. It was pointed out in [11, 12, 16, 17, 35] that correlations generated in the course of the DGLAP evolution—the $1\otimes 2$ mechanism—explain the DPS rates in the central rapidity region [11, 12, 16, 17, 35] provided the starting scale for the QCD evolution—$Q_0^2= 0.5 \div 1 \mathrm{GeV}^2$ is chosen. The remaining problem seems to be a strong enhancement of the processes involving $J/\Psi$ production [36, 37] at $\sqrt{s}$ = 2TeV, which does not show up in the LHCb data.

In this letter we demonstrate that the new LHCb data [24,25,26,27] corresponding to the forward kinematics can be explained by taking into account two effects: buildup with increase of $Q^2$ of the perturbative correlations—the $1\otimes 2$ mechanism, calculated using DGLAP formalism [5, 8, 10, 11] and soft small x parton–parton correlations in the nucleon wave function which result in a non-factorized contribution to the initial conditions of the double parton GPD which can be estimated using information on diffraction in lepton/hadron–nucleon scattering following the ideas first presented in [8].

The paper is organized as follows. In Sect. 2 we describe the kinematics of the LHCb experiment. In the Sect. 3 we show the mean field approximation results for the rate of DD production and demonstrate that they are a factor of 2 lower than the data. In Sect. 4 we present results for the $1\otimes 2$ mechanism contribution (see Fig. 2) to the cross section. In Sect. 5 we discuss the Reggeon model based estimate of the non-factorized contribution to the initial conditions at $Q_0^2\sim 0.5-1\mathrm{GeV}^2$, and its $Q^2$ evolution. In Sect. 6 we present a general formula for $\sigma _{\text {eff}}\,$ combining the mean field,$1\otimes 2$ and nonperturbative non-factorized contributions. In Sect. 7 we demonstrate that the simultaneous account of all three DPS mechanisms leads to the $\sigma _\mathrm{eff}$ values consistent with the data. The results are summarized in Sect. 8.

2 Kinematics of the LHCb study of the double charm production

So far the LHCb experiment has presented results for $\sigma _{\text {eff}}\,$ integrated over a significant range of rapidities and transverse momenta. So in our analysis we will first perform calculations for the typical LHCb kinematics and later on present the results for the variation of $\sigma _{\text {eff}}\,$ within the LHCb kinematic range which turns out to be pretty weak.

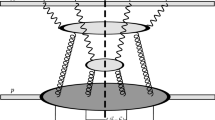
In the case of production of two D-mesons, the main mechanism is production of two pairs of $D\bar{D}$-mesons in two hard process (DPS) (see Fig. 1) with two D ($D_s$)-mesons originating from two $D\bar{D}$ pairs. D-mesons are observed in the rapidity interval $y= 2 \div 5$, the average rapidity interval between D- and $\bar{D}$-meson is of the order $\Delta y = 0.5$. A cutoff of $p_t\ge 3 \mathrm{GeV}$ was introduced in the DPS analysis leading to the average transverse momenta of the D-mesons of the order of $p_t\sim 4$ GeV. Hence D-mesons are created in the interaction of two gluons with virtualities $Q^2\sim (2p_t^2+m_c^2)\sim 34$ GeV$^2$. The factor of 2 takes into account the fragmentation of $c\rightarrow D$ in which D-mesons carry, on average, $\sim 0.75$ fraction of the jet momentum [31] (see Fig. 1).

The invariant mass squared of the created D-meson pair is $x_1x_3s=4(p_t^2+0.5*m_c^2)\times 2\sim 136$GeV$^2$, where the factor 2 roughly accounts for the fragmentation of the charmed quark into D-meson, and spread of D and $\bar{D}$ over rapidities, and $s=4.9\times 10^7$ GeV$^2$. The Bjorken x of the colliding gluon belonging to the proton moving in positive direction is determined from the condition $x_3\sim p_t\exp (y)/(\sqrt{s}/2)\sim 0.01$–0.02, where $y\sim 3$ is the D-meson rapidity. The Bjorken x of the gluon emitted by the nucleon moving in negative direction is given by $x_1\cdot x_3 s=136$ GeV$^2$ and is 0.0001–0.0002 (in our notation $x_1, x_2$ correspond to small $\times$ gluons, and $x_3, x_4$ to large $\times$ ones). The effective cross section was determined for several channels

$$\begin{aligned} \sigma _{\mathrm{eff\,\, 2D 2}\bar{D}}=\frac{\sigma _1\sigma _2}{\sigma _4(D\bar{D})}\sim 20~ \mathrm{mb}, \end{aligned}$$

(2)

with a small uncertainty for the channels with the highest statistics.

Fig. 1

Kinematics of double charm production at LHCb

The important advantage of these processes as compared to the processes experimentally studied before is that in this kinematics the SPS production of D-meson pairs is practically negligible [28,29,30] and the dominant process is the DPS production of $c\bar{c}$ pairs by gluons, thus permitting to use the methods developed in [5, 8, 10, 11].

Similar calculations can be carried out for double $b\bar{b}$ pair production and $b\bar{b} c \bar{c}$ pair production. The only difference is that the corresponding transverse scale for b-pairs is $Q^2=m^2_b+1.5p_t^2\sim 50$ GeV$^2$ where we shall take $p_t\sim 4$ GeV below as characteristic momenta. The corresponding invariant mass squared is of order 200 GeV$^2$ and $x_1\sim 0.003,x_3\sim 0.014$.

Fig. 2

Sketch of the two considered DPS mechanisms: $2 \otimes 2$ (left) and $1\otimes 2$ (right) mechanism

3 Mean field approximation estimate of $\sigma _{\text {eff}}\,$

Recall that in the mean field approach (see Fig. 2 left) double parton GPDs, describing the DPS, are

$$\begin{aligned} _2D(x_1,x_2,Q_1^2,Q_2^2,\Delta )= & {} _1D(x_1,Q_1^2,\Delta _1) \nonumber \\&\cdot _1D(x_2,Q_2^2,\Delta _2), \end{aligned}$$

(3)

where the one particle GPDs $_1D$ are known from the analyses [33, 38] of exclusive $J/\Psi$ photoproduction at HERA. They are parametrized as

$$\begin{aligned} D_1(x,Q^2,\Delta )=D(x,Q^2) F_{2g}(\Delta ,x). \end{aligned}$$

(4)

Here $D(x,Q^2)$ is the conventional gluon PDF of the nucleon, and $F_{2g}(\Delta ,x)$ is the two gluon nucleon form factor. The effective cross section $\sigma _{\text {eff}}\,$ is then given by

$$\begin{aligned} 1/\sigma _\mathrm{eff}=\int \frac{\mathrm{d}^2\Delta }{(2\pi )^2}F^4_{2g}(\Delta ). \end{aligned}$$

(5)

We shall use exponential parametrization [38]

$$\begin{aligned} F_{2g}(\Delta ,x)=\exp (-B_g(x)\Delta ^2/2), \end{aligned}$$

(6)

where $B_g$(x)= $B_0$ + 2$K_Q\cdot \log (x_{0}/x)$, with $x_0\sim 0.0012$, $B_0=4.1$ GeV$^{-2}$, and $K_Q=0.14$ GeV$^{-2}$ (very weak $Q^2$ dependence of $B_g$ is neglected). (The dipole fit to $F_{2g}(\Delta ,x)$ gives a very similar numerical result for $\sigma _{\text {eff}}\,$  in our kinematics, decreasing $\sigma _{\text {eff}}\,$by 4–5$\%$, which is well within the uncertainties of the current knowledge of the t-dependence of the gluon GPD in the studied $x,Q^2$ range.)

Integrating over $\Delta ^2$, we obtain for $\sigma _{\text {eff}}\,$ in the mean field approximation

$$\begin{aligned} \frac{1}{\sigma ^{(MF)}_{\text {eff}}}=\frac{1}{2\pi }\frac{1}{B_g(x_1)+B_g(x_2)+B_g(x_3)+B_g(x_4)}, \end{aligned}$$

(7)

where $x_{i}$ are the longitudinal momentum fractions of the four partons involved in the $2 \otimes 2$ mechanism. Hence we find for the mean field value of $\sigma _\mathrm{eff}$  in the LHCb kinematics $x_2\sim x_4=0.02,x_3\sim x_4\sim 0.0001$:

$$\begin{aligned} \sigma ^{MF}_\mathrm{eff}\approx 40~\mathrm{mb}, \end{aligned}$$

(8)

which, as we already mentioned, is a factor of 2 larger than the value reported by the LHCb.

Fig. 3

$_2$GPD as a two Pomeron exchange

Fig. 4

$2I\!\!P$ contribution to $_2$D and Reggeon diagrams

4 3–4 Mechanism

The mechanism for the enhancement of the rate of DPS (increase of $1/\sigma _\mathrm{eff}$) as compared to its mean field value was suggested in [5, 8, 10, 11], where it was shown that taking into account the pQCD DGLAP ladder splits leads to a decrease of $\sigma _\mathrm{eff}$—the $1\otimes 2$ mechanism; see the right hand side of Fig. 2.

We calculate R by solving by iterations the evolution equation for $_2GPD$ [8, 11, 12]. The cross section due to the $1\otimes 2$ mechanism is calculated as [8]

$$\begin{aligned} \frac{1}{\sigma _{\text {eff}}}\equiv & {} \int \frac{\mathrm{d}^2\vec {\Delta }}{(2\pi )^2} _{2}D_2(x_1,x_2, Q_1^2,Q_2^2;\vec \Delta )\nonumber \\&\cdot {}_2D_2(x_3,x_4, Q_1^2,Q_2^2; -\vec \Delta )\nonumber \\&+_2D_1 (x_1,x_2, Q_1^2,Q_2^2;\vec \Delta ) \cdot {}_2D_2(x_3,x_4, Q_1^2,Q_2^2;-\vec \Delta )\nonumber \\&+ {}_{2}D_2(x_1,x_2, Q_1^2,Q_2^2;\vec \Delta )\cdot {}_{2}D_1(x_3,x_4, Q_1^2,Q_2^2;-\vec \Delta ).\nonumber \\ \end{aligned}$$

(9)

Note here that the $1 \otimes 1$mechanism contribution must be excluded [8]. Here $_2D_1$ corresponds to $1\otimes 2$ mechanism, while $_2D_2$ to $2 \otimes 2$ contribution (with generic initial conditions—either factorized, or including non-factorized terms).

The distribution $_2D_1$ corresponding to Fig. 2 (the right hand side) is obtained by solving by iterations of the evolution equation for $_2GPD$ [8, 10, 12]. The mean field distribution $_2D_2$ gets corrections from the QCD evolution due to $1\otimes 2$ mechanism. The DPS effective cross section is then parametrized as

$$\begin{aligned} \sigma _{DPS}=\sigma _\mathrm{MF}/(1+R_\mathrm{pQCD}). \end{aligned}$$

(10)

In [8, 10] it was assumed that the factorized form given by Eq. (3) is valid at the starting point of the evolution, $Q_0^2$, which is essentially the parameter separating soft and hard dynamics. The enhancement coefficient increases with decrease of $Q_0^2$.

Numerical results for the enhancement coefficient $R_\mathrm{pQCD}$ for charm pair production are given in Figs. 6 and 7 below. The direct calculations of $\sigma _{\text {eff}}\,$ $_\mathrm{pQCD}=\sigma _{MF}/(1+R_\mathrm{pQCD})$ show that the pQCD correlation leads to a decrease of $\sigma _{\mathrm{eff}}$ to 24–28 mb for the double charm production, slightly larger reduction for charm + bottom, and a more significant reduction for double bottom.

Thus the $1\otimes 2$ mechanism significantly improves the agreement with the experimental data, but its relative contribution is smaller than in the central rapidity range covered by the ATLAS and CMS experiments.

5 Non-factorized contribution to $_2D$ at the initial $Q_0$ scale

There is an additional contribution to the DPS at small x which is absent in the case of processes involving $x_i \ge 0.01$ (production of jets, etc at the central rapidities). This contribution was first discussed in [10]. It results in a non-factorized contribution to $_2$GPD at the initial scale $Q_0^2$ that separates soft and hard physics and which we consider as the starting scale for the DGLAP evolution. In the previous sections we assumed that at this scale $_2$GPD factorizes into the product of two $_1$GPDs. It is natural to expect that the transition from soft to hard QCD regime is smooth and occurs at scales $Q^2 \sim 0.5$–$1\, \mathrm{GeV}^2$. In this case one expects that at such a scale the single parton distributions at small x below $10^{-3}$ are given by the soft Pomeron exchange. In this picture the two soft partons may originate from two independent “multiperipheral ladders” represented by cut Pomerons; see Fig. 3.

The soft Pomeron amplitude is practically pure imaginary [39] see also [40] for the most recent experimental measurements. As a result, this amplitude equals the amplitude of the diffractive cut of the two Pomeron diagram of Fig. 4. The two contributions to the cut are the elastic and diffractive intermediate states. The elastic intermediate state obviously corresponds to the uncorrelated contribution to $_2$D, while the inelastic diffractive cut encodes correlations.

Note here that, different from the conventional situation of diffraction into large masses, the rapidity intervals occupied by the Pomeron ladders from which partons with fractions $x_1, x_2$ are taken are different.

In the case of soft diffraction the ladder corresponding to diffraction to masses $M^2$ occupies the interval of rapidities $\sim \ln (M^2/m_0^2)$ where $m_0^2\sim m^2_N$ is a soft scale. Hence the ladders associated with the transition $p\rightarrow ``diffractive\, \, state$” carry the fraction of the nucleon momentum $x \sim m_0^2/M^2$.

It is convenient to consider first the ratio of non-factorized (correlated) and factorized (uncorrelated) contributions at the zero momentum transfer $t=-\Delta ^2=0$:

$$\begin{aligned} \rho (x_1,x_2, Q_0^2)= & {} {_2D_{nf}(x_1,x_2,Q_0^2)\over D_{f} (x_1,x_2, Q_0^2)}\nonumber \\= & {} {_2D_{nf}(x_1,x_2,Q_0^2)\over D_N(x_1,Q_0^2)D_N(x_2,Q_0^2)}. \end{aligned}$$

(11)

We can write

$$\begin{aligned}&\rho (x_1,x_2, Q_0^2)\nonumber \\&\quad = \int \mathrm{d}M^2 S(M^2) {D_N(x_1/x,Q_0^2)D_N(x_2/x,Q_0^2)\over D_N(x_1,Q_0^2)D_N(x_2,Q_0^2)}, \end{aligned}$$

(12)

where the factors $x_i/x$ take into account a smaller rapidity intervals occupied by the ladders in the case of transition to inelastic diffractive states. The factor

$$\begin{aligned} S(M^2)=C_{3I\!\!P}(M^2/m_0^2)^{\alpha _{I\!\!P}(0) } \end{aligned}$$

(13)

corresponds to the cut Pomeron that splits into two Pomerons in diagram 4. It is equal to the product of the triple Pomeron vertex and the square of proton–Pomeron residues, cf. [39, 41]. Here we use $\alpha _{I\!\!P}(0)=1.1$, corresponding to a soft effective Pomeron [42].

If $x_1=x_2$ the right hand side of Eq. (12) is equal to

$$\begin{aligned} \int \mathrm{d} M^2 {{\mathrm{d}\sigma _\mathrm{in \, diff} (M^2) \over \mathrm{d}t \mathrm{d}M^2}\over {\mathrm{d} \sigma _\mathrm{el} \over \mathrm{d} t}}{\left. \right| _{t=0} }, \end{aligned}$$

(14)

that is, to the ratio of inelastic and elastic diffraction in DIS for the invariant $\gamma p$ energy $s=m_0^2/x$.

Using the triple Reggeon parametrization of the cross section we can determine normalization of the three Pomeron vertex $C_{3I\!\!P}$ in Eq. (13) from the HERA data [43, 44] for the ratio of inelastic and elastic diffraction at $t=0$ in the processes of vector meson production:

$$\begin{aligned} \omega \equiv { {\mathrm{d}\sigma _{in.\, dif.}\over \mathrm{d} t}\over {\mathrm{d}\sigma _{el}\over \mathrm{d} t}}{\left. \right| _{t=0} } =0.25 \pm 0.05. \end{aligned}$$

(15)

The constant $C_{3I\!\!P}$ is roughly the same for diffractive production of light mesons and $J/\psi$ in a wide range of $Q^2$, thus confirming the hypothesis of a smooth transition between soft and hard regimes. It is determined from the condition $\rho (x_1,x_1,Q_0^2)=\omega$, where $x_1\sim 0.001$, which corresponds to HERA data in [43, 44]. Note here that to have a smooth connection with the low $Q^2$ gluon density model of GRV we take the x-dependence of the gluon density at small x from this model. This may correspond to a relatively hard effective Pomeron in the lower legs though a priori the density of partons in the Pomeron may grow more rapidly at small x than the overall Pomeron dominated amplitude.

In the Reggeon calculus [39] the effective triple Pomeron coupling is expected to decrease slowly with energy due to screening corrections, somewhat reducing the rate of the increase of $\omega$ expected in the unscreened triple Pomeron model.

In any case, our procedure involves normalizing parameters of the model for $x\sim 10^{-3}$ and studying a relatively narrow x range $10^{-4}< x < 10^{-2}$. As a result our results are not sensitive to the variation of the Pomeron intercept between the soft and hard values.

Accordingly, for the parton density in the ladder we use

$$\begin{aligned} xD(x,Q_0^2)=\frac{1-x}{x^{\lambda (Q_0^2)}}, \end{aligned}$$

(16)

where the small x intercept of the parton density $\lambda$ is taken from the GRV parametrization [45] for the nucleon gluon pdf at $Q_0^2$ at small x. Numerically $\lambda (0.5 \,\,\mathrm{GeV}^2)\sim 0.27$, $\lambda (1.0 \,\,\mathrm{GeV}^2)\sim 0.31$

Using Eqs. (12), (13), and (15), and the above values of $\lambda (Q_0^2)$ we obtain $C_{3I\!\!P}=0.125\pm 0.025$ GeV$^{-2}$ for $Q_0^2=0.5$ GeV$^2$, and $C_{3I\!\!P}=0.14\pm 0.025$ GeV$^{-2}$ for $Q_0^2=1$ GeV$^2$.

As a result we can estimate $_2D(x_1,x_2,Q_0^2)_{nf}$ to be

$$\begin{aligned} _2D(x_1,x_2,Q_0^2)_{nf}= & {} c_{3I\!\!P}\int ^1_{x_m/a} \frac{\mathrm{d}x}{ x^{2+\alpha _{I\!\!P}}} D(x_1/x,Q_0^2)\nonumber \\&\times D(x_2/x,Q_0^2), \end{aligned}$$

(17)

where we introduced an additional factor of $a=0.1$ in the limit of integration over x (or, equivalently, the limit of integration over diffraction masses $M^2$) to take into account that the Pomeron exchanges should occupy at least two units in rapidity, i.e. $x>max(x_1,x_2)/0.1$. The dependence on rapidity gap cutoff is weak, of order 10%, and is present in all inelastic diffraction calculations [41].

The constant $c_{3I\!\!P}=m_0^2C_{3I\!\!P}$, where $m_0^2=m_N^2=1$ GeV$^2$ is the low limit of integration over diffraction masses.

Consider now the $t= - \Delta ^2$ dependence of the above expressions. Strictly speaking Eqs. (11), (12), and (17 have to include the explicit dependence on t. Here we shall, however, assume the factorization of the t-dependence, which reveals itself in the form

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}\sim U(x_1,x_2,Q_0^2)F(t), \end{aligned}$$

(18)

where the function U does not depend on t and all t-dependence is given by the form factor F(t), for which we will use the exponential parametrization. Then we can use Eqs. (11), (12), and (17) at $t=0$ (with corresponding functions, given by these equations, and the t-dependence given by the exponential form factors F(t)). Note that these form factors depend on x and the resolution scale only weakly and the scale dependence can be neglected while performing the integrations in Eqs. (12) and (17). Such a factorization is well known to work well for a pure diffraction case (diagram 4 for $x_1=x_2$, and we expect it to work in the general case as well).

The t-dependence of elastic diffraction is given by

$$\begin{aligned} F(t)=F_{2g}^2(x_1,t)=\exp (B_\mathrm{el}(x_1)t). \end{aligned}$$

(19)

Thus the t dependence of the factorized contribution to $_2D_f$ is given by

$$\begin{aligned} F(t)= & {} F_{2g}(x_1,t)\cdot F_{2g}(x_2,t)\nonumber \\= & {} \exp ((B_\mathrm{el}(x_1)+B_\mathrm{el}(x_2))t/2), \end{aligned}$$

(20)

where $F_{2g}$ is the two gluon nucleon form factor.

The t-dependence of the non-factorized term Eq. (17) is given by the t-dependence of the inelastic diffraction: $\exp ((B_\mathrm{in}(x_1)+B_\mathrm{in}(x_2))t/2.)$.

Studies of various diffractive processes, both “soft” ($pp\rightarrow p +M_X$) and “hard” ($\gamma +p\rightarrow J/\psi +p$, $\gamma ^*+p\rightarrow V+p$ with $V=\rho ,\omega ,\phi , J/\psi$) indicate that the t-dependence of the differential cross section is dominated by the elastic vertex $ppI\!\!P\propto \exp (B_\mathrm{el}t)$ with $B_\mathrm{el}=5\div 6\> \text{ GeV }^2$ for $x<10^{-3}$.

Using the exponential parameterization $\exp (B_\mathrm{in}t)$ for the t-dependence of the square of the inelastic vertex $pM_X\!I\!\!P$, the experimentally measured ratio of the slopes $B_\mathrm{in}/B_\mathrm{el} \simeq 0.28$ [43] translates into the absolute value $B_\mathrm{in} = 1.4 \div 1.7\, \mathrm{GeV}^2$. A much weaker t-dependence of the inelastic diffractive residue as compared to the elastic vertex is observed also for the reaction $pp\rightarrow p +M_X$; see e.g. [46].

In the language of the Reggeon calculus this is a consequence of the well-known observation that the t-dependence of the three Pomeron vertex is much weaker than of the square of the $ppI\!\!P$ vertex; see e.g. [41].

The evolution of the initial conditions, Eq. (17), is given then by

$$\begin{aligned} _2D(x_1,x_2,Q_1^2,Q_2^2)= & {} \int _{x_1}^{1}\frac{\mathrm{d}z_1}{z_1}\int _{x_2}^{1}\frac{\mathrm{d}z_2}{z_2}G(x_1/z_1,Q_1^2,Q_0^2)\nonumber \\&G(x_2/z_2,Q_2^2,Q_0^2) _2D(z_1,z_2,Q_0^2),\nonumber \\ \end{aligned}$$

(21)

where $G(x_1/z_1,Q_1^2,Q_0^2)$ is the conventional DGLAP gluon–gluon kernel [47] describing the evolution from $Q_0^2$ to $Q_1^2,Q_2^2$. In our calculations we neglect initial sea quark densities in the Pomeron at scale $Q_0^2$ (obviously the Pomeron does not get a contribution from the valence quarks).

Let us define the quantity K (generalizing $\rho$ from Eqs. (11) and (12) to arbitrary $Q_1^2,Q_2^2$):

$$\begin{aligned} K(x_1,x_2,Q_1^2,Q_2^2,Q_0^2)\equiv \frac{D(x_1,x_2,Q_1^2,Q_2^2,Q_0^2)}{D(x_1,Q_1^2)D(x_2,Q_2^2)}. \end{aligned}$$

(22)

The nominator of this quantity is given by the integral (21), while the denominator is a product of the conventional PDFs. We carried out the numerical calculation of K for $Q_0^2=0.5$ GeV$^2$ and $Q_0^2=1.0$ GeV$^2$. The typical results are presented in Fig. 5. (the corresponding $x_i$ are taken in accordance with analysis of Sect. 2, and the calculations are carried out at $t=0$).

Fig. 5

Transverse momentum dependence of the K factor of Eq. (22) for $_2$GPD for regimes of small and large x in kinematics of Sect. 2 ($Q_0^2=0.5$ GeV$^2$)

One can see that K grows with the increase of $Q_0^2$ and that the QCD evolution leads to the suppression of the nonperturbative contribution. We perform the calculation neglecting the PPR (Pomeron–Pomeron–Reggeon) contribution. Inclusion of this term would increase the result by $\sim$ 10%. Overall we estimate that the errors in the K-factor due to uncertainties in the input parameters are $\sim$25–35%.

Fig. 6

$R_\mathrm{tot}$ and contributions to $R_\mathrm{tot}$ due to $R_\mathrm{pQCD},R_\mathrm{soft}$ as a function of the D-meson transverse momentum $p_t$ for 3.5 $\times$ 3.5 TeV run

The characteristic feature of the K-factor is its increase as one considers more forward kinematics for charm production. Moreover, if we start from a smaller $x_1,x_2$ the rate of decrease of K with the increase of transverse momenta decreases. We illustrate these features in Fig. 5, where we consider K for the charm production kinematics described in Sect. 2; in Fig. 5 $Q_0^2=0.5$ GeV$^2$, the behavior for $Q_0^2=1$ GeV$^2$ is similar. The upper curve is K for the $_2$GPD with small x $\sim 10^{-4}$ gluons and the lower one for larger x $\sim 10^{-2}$. We can see that the main non-factorizable contribution originates from a smaller x gluon pair. The same is true for production of $c\bar{c} b\bar{b}$ and $b\bar{b} b\bar{b}$.

One can see from Fig. 5 that $K(x,Q^2)$ decreases strongly with increase of $Q^2$. This reflects the increase of typical x at $Q_0^2$ scale contributing to $K(x,Q^2)$ with increase of $Q^2$ and a fast decrease of $K(x,Q_0^2)$ with increase of x (remember that $K(x\ge 0.05$–$10^{-1},Q_0^2)\approx 0$ and grows strongly with a decrease of x less than $10^{-2}$.

6 Contribution of the correlated term in the initial conditions to DPS

We can now write the general expression for $\sigma _{\text {eff}}\,$ taking into account non-factorized contribution to the initial conditions, the $1\otimes 2$ mechanism and the mean field contribution. We have

$$\begin{aligned} \frac{1}{\sigma _\mathrm{eff}}= & {} \int \frac{\mathrm{d}^2\Delta }{(2\pi )^2}(\exp (-(B_{1\mathrm el}+B_{2\mathrm el})\Delta ^2/2)+S_{12\, \mathrm pQCD}\nonumber \\&+K_{12}\exp (-(B_{1\mathrm in}+B_{2 \mathrm in})\Delta ^2/2.))\nonumber \\&\times \,(\exp (-(B_{3\,\mathrm el}+B_{4\,\mathrm el})\Delta ^2/2)+S_{34\, \mathrm pQCD}\nonumber \\&+K_{34}\exp (-(B_{3\mathrm in}+B_{4\mathrm in})\Delta ^2/2))). \end{aligned}$$

(23)

Here $B_i\equiv B(x_i)$, and

$$\begin{aligned} S_{ij\, \mathrm pQCD}\equiv S(x_i,x_j,Q_i^2,Q_j^2)=\frac{_2D_1(x_i,x_j,Q_i^2,Q_j^2)}{D(x_i,Q_i^2)D(x_j,Q_j^2)}.\nonumber \\ \end{aligned}$$

(24)

Also

$$\begin{aligned} K_{ij}\equiv \frac{_2D(x_i,x_j,Q_i^2,Q_j^2)_\mathrm{nf}}{D(x_i,Q_i^2)D(x_j,Q_j^2)} \end{aligned}$$

(25)

is the ratio of $_2$GPD obtained from non-factorized and factorized terms at the scale $Q_1^2,Q_2^2$. After carrying out the integration over $\Delta ^2$ we obtain the expression for $\sigma _{\text {eff}}\,$ in terms of $R_\mathrm{pQCD}$, K, $B_\mathrm{el}$ and $B_\mathrm{in}$. For simplicity we will write it only for the case of kinematics under considerations where the K term enters only for the partons with smaller x’s.

7 $\sigma _{\text {eff}}\,$ for production of the heavy quark pairs

We can now return to the analysis of the process of production of two charmed pairs. We consider the symmetric kinematics, i.e. $x_1\sim x_2; x_3\sim x_4$.

In this case we can ignore terms proportional to $K_{34}$ since it corresponds to a negligible Regge mechanism contributions at $x_3,x_4\sim 0.01\div 0.1$, and in particular we ignore $S_{12}$–$K_{34}$ interference terms). Then we have

$$\begin{aligned} \frac{1}{\sigma _\mathrm{eff}}= & {} \int \frac{\mathrm{d}^2\Delta }{(2\pi )^2}((\exp (-B_{1\mathrm el}\Delta ^2)+K_{12}\exp (-B_{1\mathrm in}\Delta ^2)+S_{12})\nonumber \\&\times (\exp (-B_{3 \mathrm el}\Delta ^2)+S_{34})-S_{12}S_{34}) . \end{aligned}$$

(26)

Carrying out the integration we obtain for the full rescaling of $\sigma _{\text {eff}}\,$ including all three mechanisms discussed above:

$$\begin{aligned} R_\mathrm{tot}=R_\mathrm{pQCD}+R_\mathrm{soft}, \end{aligned}$$

(27)

where $R_\mathrm{pQCD}$ is the cross section enhancement due to $1\otimes 2$ mechanism, i.e. proportional to $S_{34}exp(-B_{1\mathrm el}\Delta ^2)$, see Sect. 3, while

$$\begin{aligned} R_\mathrm{soft}=K_{12}\left( \frac{B_{1 \mathrm el}+B_{3 \mathrm el}}{B_{3 \mathrm el}+B_{1 \mathrm in}}+R_{ \mathrm pQCD}\frac{B_{1 \mathrm el}}{B_{1 \mathrm in}}\right) \end{aligned}$$

(28)

is the enhancement due to nonperturbative correlations and interference of nonperturbative and perturbative contributions.

Note that the main sources of large $R_{tot}$ are the presence of the pQCD enhancement—$1\otimes 2$ for two partons with larger x and nonperturbative enhancement for smaller x’s. The latter enhancement is amplified by the fact that the only $\Delta ^2$ dependence in this case is due to $\exp (-B_{ \mathrm in}\Delta ^2)$, whose slope is almost three times smaller than that of the mean field term, leading to the major enhancement of the corresponding contribution, compensating for a relatively small K (the smallness of K is connected with a rapid decrease of the effect of nonperturbative correlations with the increase of $Q^2$). Thus the enhancement we obtain is essentially due to asymmetric (between upper and lower parts of diagram Fig. 2) kinematics of two pairs of x’s.

Numerically, $B_{1 \mathrm el}+B_{2 \mathrm el}\sim 8.2$ GeV$^{-2}$, $B_{1 \mathrm el}/B_{1 \mathrm in}\sim 2.8$. Thus for example for $p_t=4 GeV$ altogether the Regge type contribution to R is $\sim 0.3$, $R_{ \mathrm pQCD}\sim 0.7$ For $Q_0^2=1 GeV^2$ we find the Regge contribution to R to be larger–$\sim 0.4$, while $R_{ \mathrm pQCD}\sim 0.4$. As a result for both choices of the initial conditions we obtain $R\sim 1.8$–2., leading to

$$\begin{aligned} \sigma _\mathrm{eff}\sim 20\text {--}22\,\mathrm{mb}. \end{aligned}$$

(29)

Note that numerically variation of the values of $R_{ \mathrm pQCD}$, with a choice of the starting point of the $Q^2$ evolution is practically completely compensated for by the variation of the soft non-factorizable contribution.

Note that Eq. (29) does not include additional uncertainties in the Reggeon calculation. For example, the uncertainty in the ratio of inelastic and elastic diffraction of order 25% will lead to 19–23 mb in Eq. (29) and so on. There is a similar uncertainty due to the input t-dependence of the gluon GPDs.

The same calculation for the production of two bottom and two charm pairs in the LHCb kinematics [24, 25] also gives $R\sim$ 1.9–2. In this case $\sigma _\mathrm{eff \, mean \, field}\sim 38$ mb, and we find $\sigma _{\text {eff}}\,$ $\sim 19$ mb, in good agreement with the LHCb data.

We show different contributions to $\sigma _{\text {eff}}\,$ enhancement as a function of the transverse momentum of D-meson $p_t$ for 3.5 and 6.5 TeV runs in Figs. 6 and 7.

Fig. 7

$R_\mathrm{tot}$ and contributions to $R_\mathrm{tot}$ due to $R_\mathrm{pQCD},R_\mathrm{soft}$ as a function of the D-meson transverse momentum $p_t$ for 6.5 $\times$ 6.5 TeV run

We see that the $R_\mathrm{pQCD}$ slowly decreases with energy, but this is compensated with increase of $R_\mathrm{soft}$, whose relative contribution also increases with the increase of energy.

The corresponding $\sigma _{\text {eff}}\,$for two LHC runs are depicted in Fig. 8.

Fig. 8

$\sigma _{\text {eff}}\,$ as a function of the D-meson transverse momentum $p_t$ for $Q_0^2=0.5,1$ GeV$^2$ and for 3.5 $\times$ 3.5 TeV and 6.5 $\times$ 6.5 TeV runs

Fig. 9

$\sigma _{\text {eff}}\,$ as a function of the B-meson transverse momentum $p_t$ for $Q_0^2=0.5,1$ GeV$^2$ and for 3.5 $\times$ 3.5 TeV and 6.5 $\times$ 6.5 TeV runs

We see that $\sigma _{\text {eff}}\,$increases by less than 1 mb for small $p_t$ when we move from 3.5 to 6.5 TeV, i.e. it effectively remains constant with the increase of energy, due to the increase of the soft correlation contribution compensating the decrease of the pQCD contribution and an increase of the mean field $\sigma _\mathrm{eff}^{MF}$. In fact of course such small changes are beyond the accuracy of our model, and we can only conclude that $\sigma _{\text {eff}}\,$are approximately constant in this interval of energies for the given transverse momenta $p_t$. We obtain very similar results for the production of two pairs of $b\bar{b}$ (Fig. 9). Note that in our approach the same $\sigma _{\text {eff}}\,$are expected for the production of two $\Upsilon$ and $\Upsilon b\bar{b}$; cf. discussion in Sect. 2 of the case of charm production.

8 Conclusions

We have demonstrated that the rate of DPS of the production of two pairs of D-mesons in the pp collisions in the forward kinematics studied by the LHCb can be explained by taking into account two types of correlations in the nucleon double GPD—the pQCD mechanism of [5, 8, 10, 11] which allowed us previously to describe the rate of DPS at the central rapidities and a new nonperturbative correlation mechanism specific for small x, which is related to the phenomenon of the inelastic diffraction.

The account for the two correlation mechanisms significantly reduces the sensitivity of the results to the starting point of the QCD evolution, both for forward and for central kinematics.

Though the estimates of the nonperturbative correlations are only semiquantitative, we naturally obtain $\sigma _{\mathrm{eff}}\sim 20$–22 mb for the D-meson pair production (see Figs. 7, 8) which is in a good agreement with experimental data for 3.6 and 4 TeV runs (see Fig. 10 in [25]). We obtain similar results for other charm DPS production processes (2 J / Psi, $J/\Psi$, and $D\bar{D}$ pair), and this is indeed observed in experiment [24] in the forward kinematics (within experimental accuracy). For the DPS production of the bottom quarks we find (see Fig. 9) $\sigma _{\text {eff}}\,$ $\sim$ 21–23 mb, which is nearly a factor of 2 smaller than the mean field estimate of $\sigma _{\text {eff}}\,$=38 mb. Thus we observe that combining the pQCD correlation mechanism and the Regge inspired model for the initial conditions we find approximately constant $\sigma _{\text {eff}}\,$, of order 20–22 mb for the LHCb kinematics.

Our calculations of $\sigma _{\text {eff}}\,$ were performed both for the $3.5\times 3.5 \mathrm \, TeV$ $6.5 \times 6.5 \mathrm \, TeV$ runs. (The corresponding differences with 4 and 7 TeV runs, respectively, are negligible.) We obtain practically the same values of $\sigma _{\text {eff}}\,$, since the decrease of $R_\mathrm{pQCD}$ is compensated by an increase of $R_\mathrm{soft}$. The actual difference is of order 1mb, slightly increasing to 2 mb ($\sigma _{\text {eff}}\,$slightly decreases with increase of energy, but this change may be an artifact of our model assumptions, i.e. it is obviously beyond the accuracy of our model).

Clearly, the role of soft correlations increases with the decrease of the typical Bjorken x in the process. The same is true for the transverse scale where the soft correlations start to be relevant, and we see that it increases with energy. On the other hand the changes in the scale of pQCD and soft correlations tend to compensate each other with the increase of energy. This means that from the theoretical point of view it will be extremely helpful to carry out the measurement of $\sigma _{\text {eff}}\,$ for new 6.5 TeV run at LHCb, as well as to measure the dependence of $\sigma _{\text {eff}}\,$ on the rapidity of the forward quark pair.

Obviously the calculations of soft correlations presented in this paper can be considered only as a semi-quantitative estimate. In particular this is connected with a large uncertainty in the parameters of the model (see Sect. 4), which are known with the accuracy of 25–30%, leading to a corresponding inaccuracy in $R_\mathrm{soft}$. Additional inaccuracy (although significantly reduced) is due to the choice of the $Q_0^2$ scale. Nevertheless, our estimate clearly reveals the importance of soft correlations in forward kinematics and the increase of their contribution with the energy of the collision.

Finally, let us note that our model can be used also for the central kinematics, where in particular it can be applied to calculate $\sigma _{\text {eff}}\,$ in the underlying event (UE). Preliminary results show that it will not influence significantly the MC simulations of UE given in [16, 17], although it may lead to stabilization of $\sigma _{\text {eff}}\,$ in the region of small $p_t$ characteristic for UE. The detailed results for the central kinematics, as well as comparison of our predictions for $\sigma _{\text {eff}}\,$ with that of [48], which developed a different model also based on observations of [10] and applied it to the central kinematics, will be given elsewhere [49].