1 Introduction

Precise astronomical measurements of the universe indicate that nearly \(25\%\) of its content is in the form of dark matter (DM), the key ingredient necessary to explain large scale structure formation, and \(70\%\) dark energy (DE), the unknown component driving the recent cosmic acceleration.

In this context, the best model to describe almost all the observational data is a mixture of elements from the standard cosmological model plus a cosmological constant, the so-called “concordance” \(\Lambda \)CDM model. Although successful in fitting the observational data, from a theoretical point of view the model seems too arbitrary. First, there is no clue about where this cosmological constant came from, and with it, why its value is so close to the critical energy density, and second, why we live in a very special epoch where the contributions from DM and DE are of the same order of magnitude, the well-known “cosmic coincidence problem” (CCP).

Physicists have proposed different ways to overcome this dilemma. The first was to adopt a dynamical cosmological constant, trying to adjust the dynamics of it to alleviate the CCP. This is the idea behind quintessence [1,2,3,4,5,6], where a scalar field is responsible for driving the current cosmic acceleration. The second was to modify the left-hand side of Einstein’s equations, trying to explain the presence of a cosmological constant as a non-standard geometric effect [7,8,9]. The third was to violate the Copernican Principle, i.e., by assuming we live in an inhomogeneous universe [10,11,12,13,14,15]. Although some success has been obtained in each of these alternative scenarios, there is so far no clear evidence of a preference compared to the \(\Lambda \)CDM model.

Since Einstein’s field equations link the geometric properties of the universe with its total content, there is a well-known degeneracy between these two components; DM and DE. This is in fact one good reason to consider unified dark models. Of course the simplicity of considering a single component acting as both DM and DE is also a good reason.

In this letter, we show that a new class of scalar field models that exhibit a non-trivial response to geometry, dubbed stealth, serves as a unified model of the dark sector.

The idea of considering unified scalar field models (see [16] for a review) to describe DM and DE emerges as a natural way to alleviate the so-called “coincidence problem”, namely, to explain why the energy densities of these two dark components are of the same order of magnitude today. Models of this type have been proposed in the past, assuming the stress-energy tensor of the scalar field to back-react to the geometry according to Einstein’s equations. Among them we can mention the model of [17], where a potential \(V(\phi )=V_0 (\cosh \lambda \phi - 1)^p\) is considered, the Chaplygin gas [18], the generalized Chaplygin gas model [19], and models with a non-canonical kinetic term called k-essence models [20].

On the other hand, it is well-known that in the General theory of Relativity gravity is understood as a manifestation of the curvature of space-time and the latter is caused by the presence of matter. This fundamental principle is codified in the equations proposed by Einstein. So the slightest presence of matter on the right-hand side of Einstein’s equations is sufficient to alter the geometry of space-time. However, the stealth is a kind of matter that remains present in the space-time without altering or changing its geometry. The stealth appears only for a scalar field non-minimally coupled to gravity, and its origins date back to the improved energy-momentum tensor considered first in [21], where the authors showed the possibility of this new tensor becoming the source of the gravitational field; meanwhile, the dynamic of the scalar field is dictated by the Klein–Gordon equation.

The original proposal of the stealth was reported for a three-dimensional BTZ black hole in [22], in higher dimensions in Minkowski space-time [23] and (anti-)de Sitter [(A)dS] space [25]. Also in Lifshitz space-time in [26], for a four dimensional black hole [27], for an AdS black hole in Lovelock gravity [28], in Einstein–Gauss–Bonnet gravity for topological black hole [29], for a rotating AdS black hole in new massive gravity [30], and finally for a BTZ rotating black hole present two solutions in [31]. Lately, as was shown in [32], there were stealth fields during the cosmological evolution and some cosmological solutions are given in order to have a LCDM cosmology, in particular those with polynomials and power-law evolution are analyzed. Also, the general solutions for de Sitter cosmologies and inhomogeneous stealths have been studied, concluding that only for de Sitter backgrounds a full dependence on the space-time coordinates is allowed.

In this letter, we examine the case of a cosmological model coming from a non-minimal coupling with a stealth scalar field as a unified component describing both DM and DE, and thus mimicking the \(\Lambda \)CDM model.

1.1 Stealths as a unified dark model

In the present work we study a cosmological model coming from a non-minimal coupling with a stealth scalar field, described by the action:

$$\begin{aligned} S=\int \mathrm{d}^4x \sqrt{-g}\left[ \frac{R}{2\kappa } + L_m - \frac{1}{2}\zeta R \phi ^2 -\frac{1}{2}\partial _{\mu } \phi \partial ^{\mu } \phi - V(\phi )\right] .\nonumber \\ \end{aligned}$$
(1)

Here, \(L_m\) is the Lagrangian matter. Clearly, for \(\zeta =0\) the scalar field stress tensor reduces to the usual case of a minimally coupled field. By varying the action (1), the field equations are written as

$$\begin{aligned} G_{\mu \nu }-\kappa T^{(m)}_{\mu \nu }= \kappa T^{(S)}_{\mu \nu }, \end{aligned}$$
(2)

where \(T^{(m)}_{\mu \nu }\) is the stress-energy tensor of matter, and \(T^{(S)}_{\mu \nu }\) is the stress-energy tensor of the stealth field \(\phi \), given by

$$\begin{aligned} T^{S}_{\mu \nu }= & {} \nabla _\mu \phi \nabla _\nu \phi -\left( V(\phi )+ \frac{1}{2}\nabla _\alpha \phi \nabla ^\alpha \phi \right) g_{\mu \nu } \nonumber \\&+\, \zeta (G_{\mu \nu }\phi ^2-\nabla _\mu \nabla _\nu \phi ^2 +g_{\mu \nu } \nabla ^\alpha \nabla _\alpha \phi ^2 ). \end{aligned}$$
(3)

It is worth noting that, for \(\zeta \ne 0\), the variation on \(g_{\mu \nu }\) produces the stealth stress tensor \(T^{(S)}_{\mu \nu }\) to get a contribution from the Einstein tensor.

The stealth configuration emerges once we set both sides of Eq. (2) to zero: the left-hand side is the Einstein equation for a universe with a matter content described by \(T^{(m)}_{\mu \nu }\), and the right-hand side is the stealth equations \(T^{(S)}_{\mu \nu }=0\). Once a solution to the right side is found, the stealth obeys the dynamics dictated by the space-time and at the same time it is invisible to it.

While on the one hand the existence of gravitational stealth is a fact, and its feature of not having back-reaction on the gravitational field is of interest, the gravitational field equations say very little about their interaction with matter.

There are a few works on this topic; some remarkable results in that direction are given in [33], where the interaction between ordinary matter and stealth is shown and [34], where a relation with the axionic field is shown. Furthermore, it is possible to show the ability of the stealth fields to mimic any kind of matter, which is another surprising characteristic of these fields [35].

As was demonstrated in [24], there is a stealth solution in the context of a Friedmann–Lemaître–Robertson–Walker (FLRW) space-time. Now we obtain our cosmological model by coupling

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}t^2 + a(t)^2 \left[ \frac{\mathrm{d}r^2}{1-k r^2} +r^2 \mathrm{d}\Omega ^2 \right] , \end{aligned}$$
(4)

to a perfect fluid with zero pressure, i.e., the dust case, and when the scalar field depend only on time.

On the left-hand side of (2) we use the stress-energy tensor for a perfect fluid as the DM contribution, leading to the usual \(\Lambda \)CDM model, where the DM density \(\rho \) and the cosmological constant \(\Lambda \) determine the cosmic evolution a(t). At the same time, from the right-hand side of (2), the stealth field \(\phi \) and its self-interacting potential \(V(\phi )\) determines completely the cosmic evolution a(t). As a consequence of this—the evolution must be the same as that of the \(\Lambda \)CDM model—the stealth here works as a unifying field simultaneously describing the effects of the action of both DM and DE. We get

$$\begin{aligned} 3\left( \frac{\dot{a}}{a}\right) ^2 + 3\frac{k}{a^2} = -6\frac{\dot{\phi }}{\phi }\frac{\dot{a}}{a} -\frac{1}{2\zeta } \left( \frac{\dot{\phi }}{\phi }\right) ^2-\frac{V}{\zeta \phi ^2}, \end{aligned}$$
(5)

and

$$\begin{aligned} \frac{2V}{3\zeta \phi ^2}+ \frac{6\zeta -2}{3\zeta }\left( \frac{\dot{\phi }}{\phi }\right) ^2 +2\frac{\dot{\phi }}{\phi }\frac{\dot{a}}{a}+ 2\frac{\ddot{a}}{a}+2\frac{\ddot{\phi }}{\phi }=0. \end{aligned}$$
(6)

2 Specific stealth realizations

As is well known, the \(\Lambda \)CDM model is so far the best fit model for a large set of astronomical observations, such as type Ia supernovae (SNIa), baryon acoustic oscillations (BAO), cosmic microwave background radiation (CMBR), growth of structure, etc. [36]. In this setup the cosmological constant \(\Lambda \) drives the current accelerated expansion of the universe, detected for the first time using type Ia supernovae [37, 38].

As we mentioned in the introduction, although the stealth field does not back-react to the geometry, the existence of a non-zero coupling \(\zeta \) enables the stealth to appear dynamically coupled to the matter content. In this section we characterize the stealth field associated with this cosmological model.

In order to give a complete description of the model we are presenting, we display the features of the \(\Lambda \)CDM model. The Friedmann equation is

$$\begin{aligned} H^2+\frac{k}{a^2} = \frac{\kappa }{3} \rho + \frac{\Lambda }{3}, \end{aligned}$$
(7)

and the stress-energy conservation equation implies

$$\begin{aligned} \dot{\rho }+3H\rho =0, \end{aligned}$$
(8)

where we have assumed explicitly an equation of state \(p=0\) for the matter content (cold dark matter). From Eq. (8) we obtain the energy density, which evolves as \(\rho = \rho _0 a^{-3}\). This simple model fits several observational probes quite well. The best fit parameters so far, assuming a curved FRLW metric, are those from the Planck Collaboration [39]: \(\Omega _{\Lambda }=0.685 \pm 0.018\), \(\Omega _m=0.315\pm 0.018\), and \(H_0=67.3 \pm 1.2\), where \(\Omega _{\Lambda }=\Lambda /(3H_0^2)\), \(\Omega _k=-k/H_0^2\), and \(\Omega _m=\kappa \rho _0/(3H_0^2)\).

On the other hand, from the vanishing of the stealth stress-energy tensor, Eqs. (5) and (6), we can read the equivalence relations between the set \([\rho , \Lambda ]\) for the \(\Lambda \)CDM model, and the set \([\phi , V(\phi )]\) for the stealths.

It is easy to show that an equivalence can be met by proposing the following relation:

$$\begin{aligned} -\frac{V}{\zeta \phi ^2}=\Lambda . \end{aligned}$$
(9)

This means that the self-interacting potential is related only algebraically to the cosmological constant. Using this relation and after some manipulations, the equivalence is complete after we impose

$$\begin{aligned} - \frac{\dot{\phi }}{\phi } \frac{\mathrm{d}}{\mathrm{d}t}\ln [\phi ^{1/2\zeta } a^6] = \kappa \rho , \end{aligned}$$
(10)

as well as

$$\begin{aligned} \frac{\dot{\phi }}{\phi } = - \frac{c}{\phi ^{\beta }a^2 }, \end{aligned}$$
(11)

where \(\beta = (8\zeta -1)/4\zeta \) and c is an integration constant.

What we have obtained here is a stealth field \(\phi \)—given by the solution of (11)—with self-interaction (9) that (by construction) generates an evolution—a(t)—totally indistinguishable from that obtained from the \(\Lambda \)CDM model.

The equivalence enables us to use cosmological observations to fix the values (and the uncertainties) of the model parameters. Using (11) in the equation for \(\rho \) we get for the Hubble function

$$\begin{aligned} H = \frac{\kappa \rho _0}{6a}\frac{\phi ^{\beta }}{c} + \frac{1}{12\zeta a^2}\frac{c}{\phi ^{\beta }}. \end{aligned}$$
(12)

Before testing the model, we have to write it in terms of the redshift z. Recalling that \(a=(1+z)^{-1}\), Eq. (11) can be written as

$$\begin{aligned} E(z) \varphi ^{\delta }\varphi ' = \frac{(1+z)\Omega _{m}}{\Xi }, \end{aligned}$$
(13)

where \(E(z)=H(z)/H_0\), \(\varphi =\phi /\phi _0\), \(\delta =\beta -1\), and \(\Xi =1 \pm \sqrt{1-\Omega _m/6\zeta }\). On the other hand, Eq. (12) can be written as

$$\begin{aligned} E(z) = \frac{(1+z)}{2}\varphi ^{\beta } \Xi + \frac{(1+z)^2}{12\zeta }\frac{\Omega _m}{\varphi ^{\beta } \Xi }. \end{aligned}$$
(14)
Fig. 1
figure 1

Here we display the confidence level contours, at \(1 \sigma \) and \(2 \sigma \), for the parameters of the model

Full size image

The free parameters to constrain are clearly \(\zeta \) and \(\Omega _m\). There is no way to constrain \(H_0\) based on the sets (13) and (14). However, if we test the model using H(z) measurements, we can get a number for \(H_0\) just by minimizing the residuals of

$$\begin{aligned} \left[ H^{\mathrm{obs}}(z_i) - H_0 E(z_i | \zeta ,\Omega _m)\right] . \end{aligned}$$
(15)

In practice we solve the differential equation (13) numerically with the initial condition \(\varphi (z=0)=1\), and by making use of (14) to get E(z). Then we compute the residuals. In the following, we use observational measurements of H(z) extracted from [40]—consisting of 30 data points—to constrain the free parameters in the model.

In addition to the parameters \(\zeta \), \(\Omega _m\), and \(H_0\), we must also consider the parameters associated with the stealth potential \(V(\phi )\). Given our choice of (9), the potential can be described by just one parameter that is fixed by relation (9). In fact, by writing \(V=V_0 \phi ^2\), from (9) we find that \(V_0=-3H_0^2\zeta \Omega _{\Lambda }\). In this way, it is not necessary to fit it along with the other three, because it depends on the best fit value of \(\zeta \) and \(H_0\), and it should be consistent with the known value of \(\Omega _{\Lambda }\).

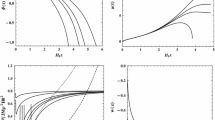
Along these lines, it is clear that our stealth have more free parameters than the original \(\Lambda \)CDM model (the former has four and the latter three). However, as we just mentioned, the only free parameters that we can fix using (13) and (14) are \(\zeta \), \(\Omega _m\), and \(H_0\). After the fit (assuming the plus sign in \(\Xi \)), we get \(h=0.59 \pm 0.02\), \(\Omega _m = 0.10 \pm 0.05\), and \( \zeta = 0.10 \,{\pm }\,0.12\). In Fig. 1 we show the \(1 \sigma \) and \(2 \sigma \) C.L. among the free parameters. In Fig. 2 we display the data points used to constrain the model along with the best theoretical curve.

The reduced Hubble parameter (\(h=H_0/100\)) is the most sensitive parameter in the fit. As we mentioned in the last paragraph, this parameter essentially controls the amplitude of the theoretical curve displayed in Fig. 2. By contrast the parameters \(\Omega _m\) and \(\zeta \) are not very sensitive to changes, so it was very difficult to find a best fit set based on the H(z) data. A close study of the system of Eqs. (13) and (14) enables us to understand this behavior. In fact, the use of observational data for each value of E(z)—instead of using an analytical expression for it—renders these two parameters highly correlated.

Fig. 2
figure 2

We display the theoretical curve together with the data points for the H(z) measurements obtained from [40]

Full size image

3 Conclusions

In this paper we have shown an example of how the stealth can operate during the cosmological evolution describing the \(\Lambda \)CDM model. This example make use of an explicit quadratic potential for the stealth, and opens the possibility of extends this finding using other forms of \(V(\phi )\). We have also re-write the stealth equations in a way to find explicitly the equivalence between the \(\Lambda \)CDM content—non-relativistic matter and a cosmological constant—and the stealth field and its potential. It was through this philosophy—working with the stealth equivalent of the \(\Lambda \)CDM—that we have found the example we studied.

To put our model to the test, considering the special features of the current cosmological model, we opt not to use an ansatz for the scale factor a(t); instead, we make use of observational data directly to constrain the free parameters of the stealth.

What we have shown here is the observationally induced stealth that best describes the \(\Lambda \)CDM model. Here, the stealth field with its self-interacting potential enables us to describe both the dark matter and the cosmological constant contributions, thus being a unified scalar field model. The best fit curve—i.e., the function E(z) extracted from (14)—together with the data is shown in Fig. 2, showing the capacity of the stealth to describe the observational data directly.

Although by construction the stealth mimics the evolution of the \(\Lambda \)CDM model, we have performed a direct test of the model against observational data, and we have found that in this case the best fit modifies the value for \(\Omega _m\) (instead of the typical \(\simeq 0.27\), by our value \(\simeq 0.1\)) at the expense of fixing an extra parameter, \(\zeta \), which is absent in the \(\Lambda \)CDM model.

Finally, we would like to emphasize the importance of understanding the potential role the stealth may play in cosmic evolution. As we have shown, although stealth does not back-react to the space-time, it can describe both dark contributions at once, accounting for almost 95% of the matter content of the universe. There is no doubt that we must continue to explore the consequences of the stealth in the recent cosmic evolution as well as in the early ages of the universe.