1 Introduction

The Higgs particle seems to be unnaturally light if there is new particle physics at higher scales to which the Higgs may couple. Barring a Copernican perspective on nature and the conclusion that our generation has completed the discovery of particle physics of the visible world, this puzzle – known as the “electroweak hierarchy problem” – constitutes a pressing question.

The persistent absence of evidence for new resonances in the vicinity of the electroweak scale calls for an in-depth exploration of beyond the Standard Model (BSM) theories which may separate and isolate the Higgs mass from the putative scale of exotic BSM resonances. Pseudo-Nambu–Goldstone bosons (PNGB) are naturally lighter than and decoupled from the rest of the spectrum of their mother theory. This suggested decades ago that the Higgs particle could be identified with the PNGB of some BSM high-energy theory [1,2,3].

In the initial proposal [1] a global SU(5) symmetry was considered for the high-energy strong dynamics. Recent attempts tend to start instead from a global SO(5) symmetry [4, 5] at a high scale \(\Lambda \), spontaneously broken to SO(4) and producing at this stage an ancestor of the Higgs particle in the form of one of the resulting massless Goldstone bosons, with characteristic scale f and \(\Lambda \le 4 \pi f\) [6]. The coset SO(5) / SO(4) represents the minimal possibility to interpret the Higgs as a pseudo-Goldstone boson in the presence of a custodial symmetry. The explicit breaking of the global symmetry needed to generate the electroweak scale \(v\ne f\) and a mass for the Higgs usually stems from soft couplings of the high-energy dynamics to the Standard Model (SM) gauge bosons and fermions.

Most of the literature on composite Higgs models based on (or containing) SO(5) assumes from the start a strong dynamics and uses an effective non-linear formulation of the models [5, 7,8,9,10,11,12,13], often denominated “composite Higgs” scenario. The ratio

$$\begin{aligned} \xi \equiv \frac{v^2}{f^2}\, \end{aligned}$$
(1)

encodes the degree of non-linearity of a given model and is a measure of the fine-tuning required to accommodate data.

A complete renormalizable model was instead constructed in Refs. [14, 15] (see also Refs. [9, 16] for related results), which in its scalar part is a linear sigma model including a new singlet scalar \(\sigma \). Furthermore, in Ref. [15] the procedure and first steps to obtain the non-linear effective Lagrangian were developed. Later work has impact on interesting phenomenological consequences [17, 18] and other aspects [19, 20]. That minimal sigma model allows one to gain intuition on the dependence on the ultraviolet (UV) completion scale: it can be considered either as an ultimate model made out of elementary fields, or as a renormalizable version of a deeper dynamics, much as the linear \(\sigma \) model [21] is to QCD. Upon spontaneous breaking of the electroweak symmetry, the Higgs and the \(\sigma \) field mix, and the resulting scalar sector is that of a system with two “Higgs-like” particles.Footnote 1 The implications on low-energy precision data and the expected signals at LHC have also been developed in Refs. [15, 17, 18], leading to a lower bound \(m_\sigma \gtrsim 550\) GeV and interesting \(\sigma \) decay channels into gauge bosons and \(t\bar{t}\) pairs at LHC.

The linear–non-linear divide will be further explored here by varying the mass of the extra scalarFootnote 2 \(\sigma \): a light \(\sigma \) particle corresponds to a weakly coupled regime, while in the high mass limit the theory should fall back onto a usual effective non-linear construction. The effective low-energy Lagrangian for non-linear realizations of electroweak symmetry breaking has been determined previously, but the number of couplings is very large in the most general case [22,23,24,25]. For the generic SO(5) / SO(4) construction, a very reduced subset of those couplings, constituting a complete basis of bosonic operators, was first established in Ref. [26]. This served to generically parametrize scenarios of electroweak symmetry breaking in which the Higgs particle is a low-energy remnant of some dynamics based on or containing SO(5) as a global symmetry. Here we will focus on the particular case of the minimal SO(5) sigma model, leading to an even more reduced subset of operators – the benchmark low-energy effective Lagrangian – which are expected to be common to the non-linear limit of any construction containing the SO(5) / SO(4) spontaneous breaking. We will consider here both bosonic and fermionic operators, though. The leading linear corrections and the leading dependence on the explicit SO(5)-breaking mechanism will be determined as well in this work.

While the bosonic couplings should be universal, the fermionic part may instead be quite model-dependent. Many different choices of exotic fermions have been explored in the literature, mainly within non-linear realizations of the global symmetry (see e.g. Ref. [8]). Nevertheless, a common characteristic of the so-called “partial compositeness” framework is that SM tree-level Yukawa couplings are forbidden by the global symmetry, while instead vertices coupling one or two heavy exotic fermions to the Higgs field are allowed. Effective Yukawa couplings between the SM and the Higgs field are thus induced at low energies, with a generic Seesaw-like pattern for the mass generation of SM fermions, whose masses are then inversely proportional to those of the heavy fermions. We will analyze the problem in two approaches:

  • A rather model-independent one in which the field content of the SM is augmented exclusively by a singlet scalar within the minimal SO(5) setup mentioned, while the leading phenomenological impact of heavy fermions is encoded in an effective Yukawa coupling of the SM fields that we will define. This effective operator will serve to parametrize and disentangle among different choices of BSM fermion embeddings.

  • In a second step, a concrete choice for the heavy-fermion representations will be considered [15]. This sector will be integrated out explicitly.

Note that in Ref. [15] we had already integrated out the specific BSM heavy fermion mentioned in this second step, although leaving fully dynamical the scalar sector. That is, the effective Lagrangian made out of SM fields plus the \(\sigma \) particle was established. It was also proposed there to next integrate out the latter, which is a straightforward procedure starting from that result. This task will be completed here in order to compare with the case in which the order of integration of the heavy fields (bosons versus fermions) is inverted. The resulting benchmark couplings will also be compared with those stemming from the procedure indicated in the first bullet above.

By furthermore keeping track of the linear and heavy-fermion corrections, the analysis will provide candles to identify whether a renormalizable ultraviolet completion exists in nature or alternatively an underlying “composite” mechanism is at work at high energy, analogous to QCD for the chiral dynamics involving pions.

Note that the results may be relevant as well for other scenarios based on global groups larger than SO(5). Furthermore, a Goldstone-boson parenthood for the Higgs is not exclusive of strong interacting dynamical setups, but is also embedded in other constructions such as “little Higgs” models, extra-dimensional scenarios and others; our results will then apply as well to those constructions.

The structure of the paper can easily be inferred from the Table of Contents.

2 Model-independent analysis

Consider a Lagrangian

$$\begin{aligned} \mathcal {L}=\mathcal {L}_s+\mathcal {L}_\mathrm{{f}}\, +\mathcal {L}_g, \end{aligned}$$
(2)

comprising, in its scalar sector \(\mathcal {L}_s\), a linear sigma model which exhibits a global SO(5) symmetry broken to SO(4) and includes a new scalar, \(\sigma \), singlet under the SM gauge group [15]

$$\begin{aligned} \mathcal {L}_s= & {} \frac{1}{2}D_\mu \phi ^T D^\mu \phi - \lambda (\phi ^T\phi -f^2)^2-\alpha f^3 \sigma \nonumber \\&+\, 2\beta f^2 H^\dagger H, \end{aligned}$$
(3)

where \(\phi =(\widetilde{H},H,\sqrt{2}\sigma )/\sqrt{2}\) is a \(\mathbf{5}\)-plet of SO(5) encompassing the Higgs doublet degrees of freedom H in addition to \(\sigma \). The terms which break softlyFootnote 3 the SO(5) symmetry – proportional to \(\alpha \) and \(\beta \) – endow the Higgs particle with a PNGB character, remaining naturally light as long as \(\alpha , \beta \ll \lambda \). The embedding of the gauge group \(SU(2)_L\times U(1)_Y\) inside SO(5) is purely conventional. \(\mathcal {L}_s\) contains as well the scalar interactions with gauge bosons, with the \(SU(2)_L\times U(1)_Y\) covariant derivative given by

$$\begin{aligned} D_\mu \phi =\left( \partial _\mu + i g \Sigma _L^i W_\mu ^i+ig'\Sigma _R^3B_\mu \right) \phi , \end{aligned}$$
(4)

where \(\Sigma _L^i\) and \(\Sigma _R^i\) denote, respectively, the generators of the \(SU(2)_L\) and \(SU(2)_R\) subgroups of the custodial SO(4) group contained in SO(5). Both h and \(\sigma \) acquire a vacuum expectation value (vev), leaving unbroken an \(SO(4)'\) subgroup which is rotated with respect to the group \(SO(4)\approx SU(2)_L\times SU(2)_R\) containing \(SU(2)_L\times U(1)_Y\). \(\mathcal {L}_g\) in Eq. (2) encodes the kinetic terms for gauge bosons.

Consider now the fermion sector. A generic feature is that the phenomenological constraints on partial compositeness require additional vector-like fermions, which couple and act as mediators among the SM fields. The exact form of the effective coupling is model-dependent and varies according to how the SM fermions are embedded in SO(5). We will obviate until Sect. 3 the details of the heavy-fermion spectrum and use instead in this section a simplified – effective – approach to the dominant fermion-induced effects.

The fermionic part of the Lagrangian in Eq. (2) will be written as the sum of two terms,

$$\begin{aligned} \mathcal {L}_\mathrm{{f}}= \mathcal {L}_{\mathrm{{f}}, \mathrm SM}^\mathrm{kin} + \mathcal {L}_\mathrm{{f}}^\mathrm{Yuk}, \end{aligned}$$
(5)

where \(\mathcal {L}_{\mathrm{{f}}, \mathrm SM}^\mathrm{kin}\) comprises the kinetic terms for only SM fermions. All what is needed here in addition is the fact that, in frameworks akin to “partial compositeness”, the global symmetry is explicitly broken by couplings between the SM fermions and heavy exotic fermions, which are the source of: (1) non-zero values for the soft SO(5) breaking parameters \(\alpha \) and \(\beta \) at one loop, inducing a potential and mass for the Higgs particle; (2) effective Yukawa couplings for the SM fermions and thus the generation of SM fermion masses.

Fig. 1
figure 1

Schematic fermion mass operator at low scales with arbitrary insertions of the scalar fields

Full size image

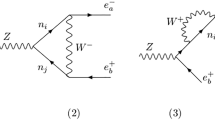
The schematic effective Yukawa coupling in the presence of the \(\sigma \) particle is presented in Fig. 1. It follows that at low energies it is possible to write an effective Yukawa Lagrangian in terms of only the SM fermions, plus h and \(\sigma \), which respects electroweak gauge invariance but not SO(5) invariance,

$$\begin{aligned} \mathcal {L}_\mathrm{{f}}^\text {Yuk} \equiv - y_\mathrm{{f}}^0\, \mathcal {O}_{\mathrm{Yuk},\mathrm{{f}}}^{(n,m)} + \dots + \mathrm{h.c.}, \end{aligned}$$
(6)

where the constant \(y_\mathrm{{f}}^0\) is a model-dependent coefficientFootnote 4 and we define the effective Yukawa operator for a given fermion \(\mathrm {f}\) as

$$\begin{aligned} \mathcal {O}_{\mathrm{Yuk},\mathrm {f}}^{(n,m)} \equiv \bar{q}_L\widetilde{H}\, \mathrm{f}_R \left( \frac{\sigma }{f}\right) ^n \left( \frac{2H^\dagger H}{f^2}\right) ^m, \end{aligned}$$
(7)

with \(\widetilde{H}\equiv i\sigma ^2 H^*\). The ellipses in Eq. (6) refer to other SM fermion operators and possibly extra model-dependent terms coming from the heavy-fermion sector.

In the literature of composite Higgs models the notation MCHM\(_\mathrm{{A-B-C}}\) is often used to indicate their fermion composition, with \(\mathrm {A, B, C}\) indicating the SO(5) representation in which the SM doublet \(q_L\), up-type right-handed and down-type right-handed fermions are embedded, respectively; else, when only one subindex appears as in MCHM\(_\mathrm{{A}}\) it is understood to be of the type MCHM\(_\mathrm{{A-A-A}}\). Table 1 summarizes the \(\{n, m\}\) parameter values for different models.Footnote 5

Equation (7) assumes that a given fermion mass corresponds to a single set of \(\{n, m\}\) values. This is often the case; for instance, the top and bottom Yukawa couplings in the MCHM\(_{5-1-1}\) model [15] correspond to \(\mathcal {O}_{\mathrm{Yuk}}^{(0,0)}\), while in the MCHM\(_5\) scenario they both correspond to \(\mathcal {O}_{\mathrm{Yuk}}^{(1,0)}\) (see e.g. Ref. [27]). Notice that, for the cases with a single Yukawa operator, the global coefficients and suppression scales in Eqs. (6), (7) are constrained by the fermion masses and therefore do not constitute any additional model dependence.

Table 1 Yukawa operators corresponding to particular embeddings (see e.g. Ref. [8]) of a SM quark doublet \(q_L\) and right-handed \(q_R\) fermion (either up-type or down-type right-handed quark) into SO(5). The coefficients y, \(y'\) refer to distinct possible relative weights of SO(5) invariant operators allowed by the models
Full size table

Nevertheless, in some scenarios a given fermion mass results instead from combining several operators of the type in Eq. (7) with different \(\{n,m\}\) values. The procedure derived can easily be extended to encompass it. A model-dependence remains then in the relative size of the y and \(y'\) weights in Table 1. An example is the MCHM\(_{14-14-10}\) scenario [8] in which different sets of \(\{n, m\}\) values are involved in generating the top mass, while the bottom mass only requires set \(\{n,m\}=\{1,0\}\). The cases of single and of multiple Yukawa operators contributing to a given mass will be further considered explicitly below. We focus in the following on the top Yukawa coupling unless otherwise explicitly stated, while the conclusions to be obtained are easily generalized to all light fermions.

2.1 Polar coordinates

Armed with the tools described, it is quite straightforward to derive the benchmark bosonic Lagrangian as well as the leading couplings involving fermions. To this aim, it is convenient to rewrite the scalar degrees of freedom in polar coordinates,

$$\begin{aligned} \sigma\equiv & {} \rho \, c_\varphi , \end{aligned}$$
(8)
$$\begin{aligned} H\equiv & {} \frac{1}{\sqrt{2}}\,\rho \,\,U\,s_\varphi , \end{aligned}$$
(9)

with \(c_\varphi {\equiv } \cos \varphi {/}f\), \(s_\varphi {\equiv } \sin \varphi {/}f\), and \(U(x) \equiv \exp \{2 i \Pi (x)/f\}\), where \(\Pi (x)\) denotes the Goldstone matrix corresponding to the longitudinal components of the electroweak gauge bosons. In this notation the scalar Lagrangian in Eq. (2) reads

$$\begin{aligned} \mathcal {L}_s= & {} \frac{1}{2}\partial _\mu \rho \,\partial ^\mu \rho + \frac{\rho ^2}{2f^2}\left[ \partial _\mu \varphi \,\partial ^\mu \varphi - \frac{f^2}{2}s_\varphi ^2 \langle V_\mu V^\mu \rangle \right] \nonumber \\&-\lambda (\rho ^2-f^2)^2 - \alpha f^3 \rho \, c_\varphi + \beta f^2\rho ^2 s_\varphi ^2, \end{aligned}$$
(10)

where \(\langle \, \rangle \) denotes the trace and \(V_\mu \equiv (D_\mu U)U^\dagger \) as is customary. The effective top Yukawa operator in Eqs. (6) and (7) is then given by

$$\begin{aligned} y_t^0\, \mathcal {O}_{\mathrm{Yuk},t}^{(n,m)}=\frac{y_t^0}{\sqrt{2}}(\bar{q}_LU P_+ \mathbf {q}_R)\rho \left( \frac{\rho }{f}\right) ^{n+2m}c_\varphi ^n s_\varphi ^{2m+1}, \end{aligned}$$
(11)

where the right-handed SM fermions have been gathered in a formal doublet \(\mathbf {q}_R\equiv (t_R,\,\,b_R)\), with \(P_+\equiv \mathrm{diag}(1,\,\,0)\) (\(P_-=\mathrm{diag}(0,\,\,1)\)) being a projector onto the up-type (down-type) right-handed SM fermions.

The \(\rho \) and \(\varphi \) fields will develop vevs,

$$\begin{aligned} \rho \rightarrow \rho +\langle \rho \rangle ,\quad \varphi \rightarrow h + \langle \varphi \rangle , \end{aligned}$$
(12)

where at the minimum of the potential the \(\varphi \) field corresponds to

$$\begin{aligned} \cos \left( \frac{\langle \varphi \rangle }{f}\right) =-\frac{\alpha }{2\beta }\,{\left( 1 +\frac{\beta }{2\lambda }\right) ^{-1/2}}. \end{aligned}$$
(13)

The connection between the vevs of the fields in the linear and polar parametrizations is

$$\begin{aligned} \langle \rho \rangle = \sqrt{\langle \sigma \rangle ^2+2\langle H \rangle ^2 }, \quad \langle \varphi \rangle =\,f\,\tan ^{-1}\left( \frac{\sqrt{2}\langle H \rangle }{\langle \sigma \rangle } \right) .\nonumber \\ \end{aligned}$$
(14)

The scalar resonance, which in the linear parametrization is customarily denoted \(\sigma \), is traded by \(\rho \) in the polar parametrization, with \(m_\rho =m_\sigma \) exactly as expected for a physical observable, while the Higgs resonance h corresponds now to the excitation of the \(\varphi \) field; see Eq. 12.

Finally, as the pure gauge Lagrangian \(\mathcal {L}_g\) and the weak coupling to fermions are not modified, the coefficient of the \(W_\mu \) mass term in Eq. (10) allows one to identify the electroweak scale v in terms of the Lagrangian parameters:

$$\begin{aligned} v^2=\langle \rho \rangle ^2\, \sin ^2\left( \frac{\langle \varphi \rangle }{f}\right) . \end{aligned}$$
(15)

2.2 Expansion in \(1/\lambda \)

The scalar quartic coupling \(\lambda \) can be conventionally traded by the \(\rho \) mass, given by \(m_\rho ^2\simeq 8 \lambda f^2\) for negligible \(\alpha \) and \(\beta \), see Ref. [15] and further below; the non-linear model would be recovered in the limit \(m_\rho \gg f\), that is, \(\lambda \rightarrow \infty \). Varying the \(\rho \) mass (that is, \(\lambda \)) allows one to sweep from the regime of perturbative ultraviolet completion to the non-linear one assumed in models in which the Higgs particle is a low-energy remnant of some strong dynamics. We will explore this limit next.

The exact equation of motion for \(\rho \) reads

$$\begin{aligned}&\square \rho - \frac{\rho }{f^2}\left[ \partial _\mu \varphi \,\partial ^\mu \varphi - \frac{f^2}{2}s_\varphi ^2 \langle V_\mu V^\mu \rangle \right] \nonumber \\&\qquad +\,4\lambda \rho (\rho ^2-f^2) + \alpha f^3 c_\varphi - 2\beta \rho f^2 s_\varphi ^2\nonumber \\&\qquad +\, (n+2m+1)\left( \frac{y_t^0}{\sqrt{2}}\bar{q}_LU P_+ \mathbf {q}_R+\mathrm{h.c.}\right) c_\varphi ^n s_\varphi ^{2m+1}\nonumber \\&\qquad \times \,\left( \frac{\rho }{f}\right) ^{n+2m}=0, \end{aligned}$$
(16)

where \(\square \equiv \partial _\mu \,\partial ^\mu \). In a \(1/\lambda \) expansion, the \(\rho \) field can be expressed as

$$\begin{aligned} \rho \equiv \rho _0 + \rho _1/\lambda + \rho _2/\lambda ^2+\cdots \end{aligned}$$

where the leading terms are given by

$$\begin{aligned} \rho _0&= f,\end{aligned}$$
(17)
$$\begin{aligned} \rho _1&= \frac{f}{4} \Big [\frac{1}{2f^4}\partial _\mu \varphi \,\partial ^\mu \varphi -\frac{1}{4f^2}\langle V_\mu V^\mu \rangle s_\varphi ^2 - \frac{1}{2}\alpha c_\varphi + \beta s_\varphi ^2\nonumber \\&\quad - \frac{(n+2m+1)}{2f^3}\left( \frac{y_t^0}{\sqrt{2}}\bar{q}_LU P_+ \mathbf {q}_R+\mathrm{h.c.}\right) c_\varphi ^n s_\varphi ^{2m+1}\Big ], \end{aligned}$$
(18)

and subsequent ones can be written as polynomial functions of \(\rho _1\). Substituting these in Eq. (10) yields the \(1/\lambda ^n\) Lagrangian corrections,

$$\begin{aligned} \mathcal {L} = \mathcal {L}_0 + \mathcal {L}_1/\lambda + \mathcal {L}_2/\lambda ^2+\cdots , \end{aligned}$$
(19)

where the different terms in this equation are given by

$$\begin{aligned} \mathcal {L}_0= & {} \frac{1}{2}\partial _\mu \varphi \,\partial ^\mu \varphi -\frac{f^2 }{4}\langle V_\mu V^\mu \rangle s_\varphi ^2 - \alpha f^4 c_\varphi \nonumber \\&+ \beta f^4 s_\varphi ^2 - f\,\frac{y_t^0}{\sqrt{2}}\bar{q}_LU P_+ \mathbf {q}_Rc_\varphi ^n s_\varphi ^{2m+1}, \end{aligned}$$
(20)
$$\begin{aligned} \mathcal {L}_1= & {} 4f^2 \rho _1^2, \end{aligned}$$
(21)
$$\begin{aligned} \mathcal {L}_2= & {} \frac{1}{2}\Bigg \{(\partial _\mu \rho _1)^2 +\bigg [\alpha f^2c_\varphi +\left( 1-(n\!+\!2m)^2\right) \nonumber \\&\times \frac{1}{f}\left( \frac{y_t^0}{\sqrt{2}}\bar{q}_LUP_+\mathbf {q}_R+\mathrm{h.c.}\right) c_\varphi ^ns_\varphi ^{2m+1})\bigg ]\rho _1^2\Bigg \}. \end{aligned}$$
(22)

\(\mathcal {L}_0\) coincides with the leading-order Lagrangian for the scalar sector of the minimal composite Higgs model [4], as expected. The expressions obtained for \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are remarkably compact and a similar pattern holds for higher orders in \(1/\lambda \).

The maximum number of derivatives of \(\mathcal {L}_n\) is \(2+2n\), although not all \(2+2n\) derivative operators are generated at order n. This is as foreseen, as for large \(\lambda \) the non-linear regime is approached and ordering the operators by their \(1/\lambda \) dependence does not coincide with the ordering given by mass dimensions. The ordering in which the operators appear is akin to the power counting of non-linear Higgs effective theory [6, 28,29,30].

Table 2 Effective operators before electroweak symmetry breaking, including two- and four-derivative couplings, together with their coefficients up to their first corrections in the \(1/\lambda \) expansion. The bosonic contributions from SO(5) breaking contributions (\(\alpha \ne 0\) and/or \(\beta \ne 0\)) are also shown. The right-hand column indicates the order in \(1/\lambda \) at which a given couplings first appears. The Higgs field h is defined as the excitation of the field \(\varphi \); see Eq. (12)
Full size table

Equations (18) and (21) suggest interesting correlations between operators involving the Higgs boson, gauge bosons and fermions. In particular, operators such as \((\partial _\mu h)^2\bar{\psi }\psi \) or \(\langle V_\mu V^\mu \rangle \bar{\psi }\psi \), where \(\psi \) denotes a generic fermion, are weighted by the fermion mass and also bear a dependence on the SM embedding into SO(5), parametrized by the set \(\{n,m\}\) in Eq. (11). From those equations emerges the low-energy effective Lagrangian in terms of SM fields at a given order in \(1/\lambda \),

$$\begin{aligned} \mathcal {L}_\mathrm{eff}=\mathcal {L}_g + \mathcal {L}_{\mathrm{{f}}, \mathrm SM}^\mathrm{kin} +\sum _i \mathcal {P}_i \,\mathcal {F}_i(\varphi ), \end{aligned}$$
(23)

where the first two terms in the right-hand side contain, respectively, the kinetic terms for gauge bosons and fermions as in Eqs. (2) and (5), and the index i runs over all operator labels and coefficient functions \(\mathcal {F}_i(\varphi )\) in Table 2. The table collects all couplings corresponding to two and four “derivatives”, where plain derivatives and gauge boson insertions are counted with equal weight, as they come together in the covariant derivative. The notation/basis for the purely bosonic operators was chosen according to Ref. [26] to facilitate the comparison with a model-independent approach. From this tree-level analysis we draw the following conclusions:

  • Up to first order in the linear corrections, the benchmark effective Lagrangian is determined to be composed of ten operators, five of them bosonic and the rest fermionicFootnote 6 including that responsible for Yukawa couplings. The coefficients of those operators are not free but intimately correlated by the coefficient functions explicitly determined in this work, and they are shown in the table.

  • Among the couplings which first appear at \(\mathcal {O}(1/\lambda )\), three bosonic operators are singled out in the SO(5)-invariant limit (\(\alpha =\beta =0\), massless SM fermions): \(\mathcal {P}_6\), \(\mathcal {P}_{20}\) and \(\mathcal {P}_{DH}\). The two latter ones involve multiple Higgs insertions and are out of present experimental reach while the strength of \(\mathcal {P}_6\), which involves vertices with four gauge bosons, is already tested directly by data, although the present sensitivity is very weak [31, 32].Footnote 7

  • Operators involving SM fermions have an implicit dependence on the symmetry-breaking terms in the Lagrangian – they are weighted by the fermion masses in a pattern alike to that of the Minimal Flavor Violation setup [33,34,35]. Most interestingly, the corresponding \(\mathcal {F}_i(\varphi )\) coefficients, written as a function of the \(\{n,m\}\) parameters, allow one to differentiate the expected impact of different fermionic ultraviolet completions in the literature.

  • All operators derived from Eqs. (20)–(22) are at most four-derivative ones, and they are all shown in Table 2, including the only one appearing at \(\mathcal {O}(1/\lambda ^3)\).

  • The gauge field dependence is present only through powers of \(\langle V_\mu V^\mu \rangle \), consistent with its exclusively scalar covariant-derivative origin; see Eqs. (3) and (10). Other Lorentz contractions such as \(\langle V_\mu V_\nu \rangle ^2\) would be loop-induced, and thus expected to be subleading.

  • The scalar functions \(\mathcal {F}_i(\varphi )\) obtained as operator weights of bosonic couplings are in agreement with those derived in Ref. [26] in the SO(5) invariant limit, for the subset of operators identified here as benchmarks; see their Eqs. (2.5)–(2.8). Table 2 provides in addition the leading deviations due to the presence of explicit SO(5)-breaking parameters \(\alpha \) and \(\beta \).

2.3 Impact on Higgs observables

2.3.1 Bosonic sector

From Eqs. (20) and (21), the potential at order \(1/\lambda \) reads

$$\begin{aligned} \frac{V}{f^4} =\alpha c_\varphi - \beta s_\varphi ^2 - \frac{1}{16\lambda }\left( \alpha c_\varphi -2\beta s_\varphi ^2\right) ^2 + \mathcal {O}\left( \frac{1}{\lambda ^{2}}\right) ,\quad \end{aligned}$$
(24)

with minimum at \( \cos \left( \frac{\langle \varphi \rangle }{f}\right) \simeq -\frac{\alpha }{2\beta }\left( 1-\frac{\beta }{4\lambda }\right) \), see Eq. (13). The kinetic energy of the physical Higgs excitation h (see Eq. (12)) gets then a correction given by

$$\begin{aligned} \frac{1}{2}\left( 1+\frac{\beta }{2\lambda }\right) \partial _\mu h\,\partial ^\mu h, \end{aligned}$$
(25)

which is reabsorbed by a field redefinition

$$\begin{aligned} h\rightarrow (1+Z_h)\, h, \quad \mathrm{{with}} \quad Z_h = -\frac{\beta }{4\lambda }. \end{aligned}$$
(26)

Renormalization The four independent parameters of the scalar Lagrangian Eq. (3), f, \(\lambda \), \(\alpha \) and \(\beta \), can be expressed in terms of the following observables [15]:

$$\begin{aligned} G_F\equiv (\sqrt{2} v^2)^{-1},\quad m_h,\quad \kappa _V, \quad m_\rho \, \end{aligned}$$
(27)

with the Fermi constant \(G_F\) as measured from muon decay, while \(\kappa _V\) can be extracted from deviations of the Higgs couplings to two gauge bosons, for instance

$$\begin{aligned} \Gamma (h\rightarrow W W^*) \equiv \Gamma _\mathrm{SM}(h\rightarrow WW^*)\,\kappa _V^2. \end{aligned}$$

\(m_h\) is determined from the Higgs pole mass and \(m_\rho \) could in turn be determined from future measurements of the \(\rho \) mass, identifying them, respectively, with the light and heavy mass eigenvalues of the scalar sector [15]

$$\begin{aligned}&m^2_\mathrm{heavy, light}\nonumber \\&\quad = 4\lambda f^2\left\{ \left( 1+\frac{3}{4}\frac{\beta }{\lambda } \right) \pm \left[ 1+ \frac{\beta }{2 \lambda }\left( 1 +\frac{\alpha ^2}{2 \beta ^2} +\frac{\beta }{8 \lambda }\right) \right] ^{1/2} \right\} ,\nonumber \\ \end{aligned}$$
(28)

where the plus sign refers to the heavier eigenstate. Assuming the SO(5) explicit breaking to be small, \({|\beta |}/{4\lambda }\ll 1\), the mass eigenvalues read

$$\begin{aligned} m_\rho ^2=&~ 8\lambda f^2 + 2\beta (3 f^2 - v^2) +\mathcal {O}\left( \frac{\beta }{4\lambda } \right) ,\end{aligned}$$
(29)
$$\begin{aligned} m_h^2=&~ 2\beta v^2+\mathcal {O}\left( \frac{\beta }{4\lambda } \right) . \end{aligned}$$
(30)

with the measured value of \(m_h\) implying \(\beta \simeq 0.13\). In the non-linear limit \(\lambda \rightarrow \infty \) the \(\rho \) field decouples from the spectrum and the scalar sector would depend on just three renormalized parameters. It is now possible to foresee the impact of the linear corrections in terms of mass dependence. Precisely because the large \(\lambda \) and \(m_\rho \) limits are in correspondence, dimensional arguments suggest the equivalence

$$\begin{aligned} \frac{1}{\lambda } \Rightarrow \frac{m_h^2}{m_\rho ^2}\,\simeq \frac{\beta \xi }{4\lambda }, \end{aligned}$$
(31)

as expansion parameter; see Eqs. (29) and (30). In other words, the linear corrections are expected to be proportional to the two small parameters \(\beta \) and \(\xi \) and thus doubly suppressed.

Extending the renormalization scheme to the gauge sector, we choose the two extra observables needed to be the mass of the Z boson and the fine structure constant,

$$\begin{aligned} M_Z, \quad \alpha _{em}=\frac{e^2}{4\pi }, \end{aligned}$$
(32)

with \(M_Z\) and \( \alpha _{em}\) as determined from Z-pole mass measurements and from Thompson scattering, respectively [36]. In terms of the ensemble of renormalized parameters discussed above, predictions can now be made. For instance the relation between the gauge boson masses remains the same than that in the SM,

$$\begin{aligned} M_W=\cos \theta _W M_Z \, ,\end{aligned}$$
(33)

where the weak angle is given at tree-level by

$$\begin{aligned} \sin ^2\theta _W=\frac{1}{2}\left( 1-\sqrt{1-\frac{4\pi \alpha _{em}}{\sqrt{2}G_FM_Z^2}} \right) . \end{aligned}$$
(34)

As another example, the prediction for the Higgs\(\rightarrow ZZ\) width is modified with respect to the SM expectation by

$$\begin{aligned} \Gamma (h\rightarrow ZZ^*) =\Gamma _\mathrm{SM}(h\rightarrow ZZ^*)\,\kappa _V^2. \end{aligned}$$
(35)

A generic expectation is the departure of \(\kappa _V\) from 1. Indeed, the coupling between the Higgs and the gauge bosons which stems from the Lagrangian Eqs. (19)–(22) at order \(1/\lambda \) is that encoded in the operator \(\mathcal {P}_C\) in Table 2 and reads

$$\begin{aligned} \mathcal {L}_{hVV} = -\left( \frac{1}{2}\sqrt{1-\xi } +\frac{\beta }{8\lambda }\frac{(2-\xi )\xi }{\sqrt{1-\xi }} \right) \langle V_\mu V^\mu \rangle vh, \end{aligned}$$
(36)

or in other words

$$\begin{aligned} \kappa _V = \sqrt{1-\xi } + \frac{\beta \xi }{2\lambda }\frac{(1-\xi /2)}{\sqrt{1-\xi }}. \end{aligned}$$
(37)

Assuming for illustrative purposes \(\mathcal {O}(\xi )\sim \mathcal {O}(1/\lambda )\) and expanding up to second order in these parameters, the result simplifies to

$$\begin{aligned} \kappa _V\simeq \sqrt{1-\xi }+\frac{\beta \xi }{2\lambda }. \end{aligned}$$
(38)

The first term on the right-hand side of this equation is the well-known correction present in non-linear scenarios [4], while the second term encodes the linear correction linked to the scale of ultraviolet completion, which in terms of physical parameters we predict to be given by

$$\begin{aligned} \kappa _V^2\simeq 1-\xi +4\frac{m_h^2}{m_\rho ^2}, \end{aligned}$$
(39)

where Eq. (31) has been used. Higher-order corrections are expected to be very small, as they will stem from operators with at least four derivatives. For instance, the first extra tree-level contribution to \(\kappa _V\) is the \(1/\lambda ^2\) weight of the operator \(\mathcal {P}_7\) in Table 2,

$$\begin{aligned} \delta \kappa _V^2 \simeq \frac{1}{2\sqrt{2} G_F}\frac{m_h^2}{m_\rho ^4}. \end{aligned}$$

2.3.2 Fermionic sector

Consider first the case in which the fermion mass is generated by a single Yukawa operator \(\mathcal {O}_{\mathrm{Yuk},f}^{(n,m)}\); see Eqs. (6) and (7). From the Lagrangian in Eqs. (19)–(22), and more specifically from the Yukawa operator in the third line of Table 2, an expression for the fermion mass follows after applying Eqs. (12) and (26),

$$\begin{aligned}&\mathcal {L}_\mathrm{{f}}^\mathrm{{Yuk}}\supset -m_{\mathrm{f}}\, \bar{\mathrm{f}}_L \mathrm{f}_R+\mathrm{h.c.}, \nonumber \\&m_{\mathrm{f}}\simeq \frac{y_{\mathrm{f}}^0}{\sqrt{2}}\,f\,\sqrt{\xi }\,(1-\xi )^{n/2}\xi ^m\left( 1+n\, \frac{1}{\xi (1-\xi )}\,\frac{m_h^2}{m_\rho ^2}\right) .\nonumber \\ \end{aligned}$$
(40)

Renormalization The renormalization scheme is now enlarged to the fermion sector choosing as observable precisely the fermion masses. The prediction that follows for the Higgs coupling to a given fermion \(\mathrm{f}\),

$$\begin{aligned} \mathcal {L}_{h{\mathrm{f}}{\mathrm{f}}} \equiv - g_{h{\mathrm{f}}{\mathrm{f}}} \, h \, {\bar{\mathrm{f}}_L} \mathrm{f}_R+\mathrm{h.c.}, \end{aligned}$$
(41)

then takes the form

$$\begin{aligned} g_{h{\mathrm{f}}{\mathrm{f}}}&\simeq \frac{y_{\mathrm{f}}^0}{\sqrt{2}} (1-\xi )^{\frac{n-1}{2}}\xi ^m\Big \{ (1+2m)(1-\xi )-n\xi \nonumber \\&\quad + \frac{\beta }{\xi (1-\xi )}\frac{m_h^2}{m_\rho ^2} \times \big [ (1+2m+n)\xi (1-\xi ) \nonumber \\&\quad \times (2-\xi ) + n\left( 1+2m(1-\xi )-n\xi \right) \big ] \Big \}.\end{aligned}$$
(42)

Encoding the deviations with respect to the SM expectations through the conventional \(\kappa _{\mathrm{f}}\) parameter,

$$\begin{aligned} \kappa _{\mathrm{f}}\equiv g_{h{\mathrm{f}}{\mathrm{f}}}/g_{h{\mathrm{f}}{\mathrm{f}}}^\mathrm{SM}, \end{aligned}$$
(43)

where \(g_{h{\mathrm{f}}{\mathrm{f}}}^\mathrm{SM}=m_{\mathrm{f}}/v\), the exact and somewhat lengthy expression for \(\kappa _{\mathrm{f}}\) up to order \(1/\lambda \) follows. The latter can be simply recast assuming again \(\mathcal {O}(\xi )\sim \mathcal {O}(1/\lambda )\), leading to

$$\begin{aligned} \kappa _{\mathrm{f}}\simeq \frac{(1+2m)(1-\xi )-n\xi }{\sqrt{1-\xi }}+(2+4m+3n)\,\frac{m_h^2}{m_\rho ^2}, \end{aligned}$$
(44)

where once again Eq. (31) has been used. It is straightforward to check that the first term on the right-hand side of this equation reproduces well-known \(\kappa _{\mathrm{f}}\) results for different models in the literature, which assume a non-linear realization. The second term gives instead the leading linear corrections. For instance, this equation leads to the following results for the MCHM\(_{5-1-1}\) (corresponding to \(n=m=0\) in our parametrization) and MCHM\(_5\) (corresponding to \(n=1\), \(m=0\)):

$$\begin{aligned} \kappa _{\mathrm{f}}^{\mathrm{MCHM}_{5-1-1}}\simeq \sqrt{1-\xi }+2\frac{m_h^2}{m_\rho ^2},\quad \kappa _{\mathrm{f}}^{\mathrm{MCHM}_5}\simeq \frac{1-2\xi }{\sqrt{1-\xi }}+5\frac{m_h^2}{m_\rho ^2}, \end{aligned}$$
(45)

obtaining again at order \(1/\lambda \) a correction doubly suppressed as proportional to both \(\beta \) and \(\xi \); see Eq. (31).

Consider next the case in which a given fermion mass corresponds to the combination of several SO(5) invariant Yukawa operators, instead of just one as developed above,

$$\begin{aligned} \mathcal {L}_{\mathrm{f}}^\text {Yuk} =-\,c_{(n,m)}\, \mathcal {O}_{\mathrm{Yuk},{\mathrm{f}}}^{(n,m)} + \dots + \mathrm{h.c.}, \end{aligned}$$
(46)

where \(c_{(n,m)}\) are related to the generators of SO(5) and the fermion embedding in a given model. The procedure is still quite straightforward. The fermion mass will be a sum of contributions similar to that in Eq. (40) weighted by the coefficients \(c_{(n,m)}\), and a similar combination protocol will apply to the obtention of the fermion-Higgs coupling \(g_{h{\mathrm{f}}{\mathrm{f}}}\) and \(\kappa _{\mathrm{f}}\). As an example, consider the MCHM\(_{14-14-10}\) scenario [8], in which the third family quark doublet and the right-handed top are embedded each in a \(\mathbf {14}\)-plet of SO(5), denoted \(Q_L\) and \(U_R\), respectively, while the right-handed bottom is included in a \(\mathbf {10}\)-plet representation denoted \(D_R\). Two SO(5) invariant operators [8] contribute in this case to the top quark mass,

$$\begin{aligned}&y_u\phi ^\dagger \bar{Q}_LU_R\phi - \tilde{y}_u(\phi ^\dagger \bar{Q}_L\phi )(\phi ^\dagger U_R\phi ) \rightarrow 3y_u\mathcal {O}_\mathrm{Yuk}^{(1,0)} \nonumber \\&\quad - \tilde{y}_u\left( 2\mathcal {O}_\mathrm{Yuk}^{(1,1)} -8\mathcal {O}_\mathrm{Yuk}^{(3,0)}\right) , \end{aligned}$$
(47)

leading to

$$\begin{aligned} \kappa _\mathrm{t}^{\mathrm{{MCHM}}_{14-14-10}}\simeq & {} \frac{y_u(3-6\xi )+2\tilde{y}_u(4-23\xi +20\xi ^2)}{\sqrt{1-\xi }\left( 3y_u+2\tilde{y}_u(4-5\xi )\right) }\nonumber \\&+\frac{15y_u^2+32\tilde{y}_u(8\tilde{y}_u-3y_u)}{(8\tilde{y}_u-3y_u)^2}\frac{3m_h^2}{m_\rho ^2}. \end{aligned}$$
(48)

In contrast, in this same scenario only one effective Yukawa operator contributes to the bottom quark mass,

$$\begin{aligned} y_d\phi ^\dagger \bar{Q}_LD_R\phi \rightarrow y_d\mathcal {O}_\mathrm{Yuk}^{(1,0)} , \end{aligned}$$
(49)

and consequently

$$\begin{aligned} \kappa _\mathrm{b}^{\mathrm{{MCHM}}_{14-14-10}}\simeq \frac{1-2\xi }{\sqrt{1-\xi }}+\frac{5\beta \xi }{4\lambda } \simeq \frac{1-2\xi }{\sqrt{1-\xi }}+\frac{5m_h^2}{m_\rho ^2} . \end{aligned}$$
(50)

All \(\mathcal {O}(1/\lambda )\) corrections considered above show again the double suppression in \(\xi \) and \(\beta \), which after Eq. (31) is tantamount to a \(m_h^2/m_\rho ^2\) suppression factor, as expected.

3 Explicit fermion sector

In the previous section, the infinite mass limit for the heavy-fermion sector was assumed from the start, while the corrections due to the heavy scalar singlets were explored. In this section we start instead of a complete (bosons plus fermions) renormalizable model, so as to estimate the impact of a fermionic ultraviolet completion beyond that related to the Yukawa couplings discussed earlier. The low-energy effective Lagrangian made out of SM fields will then be explicitly determined up to the leading corrections stemming from the heavy scalar and fermion sectors: respectively, up to \(\mathcal {O}(1/\lambda )\sim \mathcal {O}(m_h^2/m_{\rho }^2)\) and \(\mathcal {O}(f/\mathcal {M}_i)\), where \(\mathcal {M}_i\) denotes generically the heavy-fermion masses.

The details of the fermion mass Lagrangian are quite model-dependent and derived from the specific SO(5) embedding of the light and heavy fermions. Many choices of fermion representations are possible. In addition to the use of heavy vectorial representations, a common trend is to avoid by construction direct Yukawa couplings of the Higgs field to the SM fermions, leading to a generalized see-saw pattern for light fermions with masses inversely proportional to those for the heavy fermions.

The fermionic Lagrangian \(\mathcal {L}_\mathrm{f}\) in Eq. (2) needs to be redefined,

$$\begin{aligned} \mathcal {L}_{\mathrm{f}}= \mathcal {L}_{{\mathrm{f}}}^\mathrm{kin} + \mathcal {L}_{\mathrm{f}}^\mathrm{Yuk}, \end{aligned}$$
(51)

where \(\mathcal {L}_{{\mathrm{f}}}^\mathrm{kin}\) contains now kinetic terms for all fermions, light and heavy, and the fermion mass Lagrangian denoted by \(\mathcal {L}_{\mathrm{f}}^\mathrm{Yuk}\) needs to be specified for a particular ultraviolet fermion completion. The model developed in Ref. [15] will be analyzed as an illustration, recalling first its main ingredients. In order to obtain the correct hypercharge assignments, the symmetry of the Lagrangian needs to be enlarged as customary to \(SO(5) \times U(1)_X\) which is broken down to \(SU(2)_L \times SU(2)_R \times U(1)_X\), where the hypercharge corresponds to \(Y = \Sigma ^{(3)}_R + X\). The fermion fields that will generate the top mass are

$$\begin{aligned}&\psi ^{(2/3)} \sim (X,Q,T^{(5)}) \sim (\mathbf {2}_{+7/6},\mathbf {2}_{+1/6},\mathbf {1}_{+2/3}),\nonumber \\&\chi ^{(2/3)} \sim T^{(1)}\sim (\mathbf {1}_{+2/3}), \nonumber \\&\psi ^{(-1/3)} \sim (Q',X',B^{(5)})\sim (\mathbf {2}_{+1/6},\mathbf {2}_{-5/6},\mathbf {1}_{-1/3}),\nonumber \\&\chi ^{(-1/3)} \sim B^{(1)}\sim (\mathbf {1}_{-1/3}),\nonumber \end{aligned}$$

where \(\psi ^{(x)}\) and \(\chi ^{(x)}\) belong, respectively, to the \(\mathbf {5}\) and \(\mathbf {1}\) representations of SO(5) with \(U(1)_X\) charge x; their decomposition in terms of \(SU(2)_L\times U(1)_Y\) charges is also shown. This choice of heavy-fermion representations corresponds to the MCHM\(_{5-1-1}\) scenario, that is, to the entry 5–1 in the first row of Table 1, and thus to the effective Yukawa operator \(\mathcal {O}_{\mathrm{Yuk},\mathrm {f}}^{(n,m)}\) in Eq. (7) with \(\{n,m\}=\{0,0\}\).

The fermionic Lagrangian for that field content reads

(52)

where \(\Delta ^{(x)}_{n\times m}\) are spurion fields that break explicitly SO(5), while all other terms are SO(5) invariant. In terms of \(SU(2)_L\) fields, the Yukawa and spurion terms in Eq. (52) provide now an explicit realization of the Lagrangian \(\mathcal {L}_{\mathrm{f}}^{\mathrm{Yuk}}\) in Eq. (51):

$$\begin{aligned} \mathcal {L}_{\mathrm{f}}^\mathrm{Yuk} =&-\Big [y_1 \left( \bar{X}_L H{} T_R^{(1)} +\bar{Q}_L \widetilde{H}{} T_R^{(1)} +\bar{T}_L^{(5)}\sigma T_R^{(1)} \right) \nonumber \\&+y_2\,\left( \bar{T}_L^{(1)} H{}^\dagger X_R +\bar{T}_L^{(1)}\widetilde{H}{}^\dagger Q_R+\bar{T}_L^{(1)}\sigma T_R^{(5)} \right) \nonumber \\&+y'_1 \left( \bar{X'}_L \widetilde{H} B_R^{(1)} +\bar{Q'}_L H B_R^{(1)} +\bar{B}_L^{(5)}\sigma B_R^{(1)} \right) \nonumber \\&+ y'_2\,\left( \bar{B}_L^{(1)} \widetilde{H}^\dagger X'_R +\bar{B}_L^{(1)} H^\dagger Q'_R+\bar{B}_L^{(1)}\sigma B_R^{(5)} \right) \nonumber \\&+\Lambda _1\bar{q}_L Q_R+ \Lambda _1'\bar{q}_L Q_R'+\Lambda _2\bar{T}_L^{(5)} t_R+\Lambda _3\bar{T}_L^{(1)} t_R\nonumber \\&+\Lambda '_2\bar{B}_L^{(5)} b_R+\Lambda '_3\bar{B}_L^{(1)} b_R + h.c.\Big ]. \end{aligned}$$
(53)

In Ref. [15] we had first integrated out the heavy fermions of this Lagrangian, determining then the effective Lagrangian made out of SM fields plus the singlet scalar present in the minimal SO(5) sigma model. Here we reverse the order of integration of the heavy fields, taking first the limit of heavy \(\rho \) and then that of heavy BSM fermions. We have explicitly checked that the final low-energy effective Lagrangian made out only of SM fields is independent of the order in which those limits are taken.

Using polar coordinates and integrating out the radial mode \(\rho \) does not bring about any novel complication with respect to the procedure carried out in the previous section, except for lengthier expressions. Nevertheless, \(\mathcal {L}_F^\mathrm{Yuk}\) can be compactly written prior to any integration procedure as

$$\begin{aligned} \mathcal {L}_F^\mathrm{Yuk}&=-\Big [\rho \left( s_\varphi \mathcal {O}^F_s + c_\varphi \mathcal {O}^F_c\right) +\Lambda _1\bar{q}_L Q_R+ \Lambda _1'\bar{q}_L Q_R'\nonumber \nonumber \\&\quad +\Lambda _2\bar{T}_L^{(5)} t_R+\Lambda _3\bar{T}_L^{(1)} t_R +\Lambda '_2\bar{B}_L^{(5)} b_R \nonumber \\&\quad +\Lambda '_3\bar{B}_L^{(1)} b_R + h.c.\Big ], \end{aligned}$$
(54)

where \(\mathcal {O}^F_s\) and \(\mathcal {O}^F_c\) are heavy-fermion bilinears corresponding to the first four lines in Eq. (53):

$$\begin{aligned} \mathcal {O}^F_s&\equiv -\frac{1}{\sqrt{2}}\Big [y_1\! \left( \bar{X}_L U e_- T_R^{(1)} +\bar{Q}_L U e_+ T_R^{(1)} \right) \nonumber \\&\quad +y_2\left( \bar{T}_L^{(1)} U e_- X_R+\bar{T}_L^{(1)} U e_+ Q_R \right) \nonumber \\&\quad +y'_1\left( \bar{X}'_L U e_+ B_R^{(1)} +\bar{Q}'_L U e_- B_R^{(1)} \right) \nonumber \\&\quad + y'_2\left( \bar{B}_L^{(1)} U e_+ X'_R+\bar{B}_L^{(1)} U e_- Q'_R \right) \Big ],\end{aligned}$$
(55)
$$\begin{aligned} \mathcal {O}^F_c&\equiv -\frac{1}{\sqrt{2}}\Big [y_1\bar{T}_L^{(5)} T_R^{(1)}+y_2\bar{T}_L^{(1)} T_R^{(5)}\nonumber \\&\qquad \qquad \qquad +y'_1 \bar{B}_L^{(5)} B_R^{(1)}+ y'_2\bar{B}_L^{(1)} B_R^{(5)}\Big ], \end{aligned}$$
(56)

where \(e_+ = (1,0)\) and \(e_-=(0,1)\).

Table 3 Effective operators, up to order \(f/\mathcal {M}_i\) and \(1/\lambda \), after integrating out the radial mode \(\rho \) and the heavy fermions in a UV realization of partial compositeness. The coefficients \(a_{\sigma 1}^f\), with \(f=t,b\) can be found in Ref. [15]; see footnote 6. The Hermitian conjugate should be included for all operators here. The Higgs field h is defined as the excitation of the field \(\varphi \); see Eq. (12)
Full size table

Consider next the limit of very large scalar mass \(m_\rho \) (that is, \(\lambda \rightarrow \infty \)) and very heavy fermions. Implementing first the \(1/\lambda \) corrections, the effective Lagrangian at this order takes exactly the form in Eq. (21), although \(\rho _1\) shows now an explicit dependence on the heavy-fermion spectrum,

$$\begin{aligned} \rho _1= & {} \frac{f}{4} \left[ \frac{1}{2f^4}\partial _\mu \varphi \,\partial ^\mu \varphi -\frac{1}{4f^2}\langle V_\mu V^\mu \rangle s_\varphi ^2 - \frac{1}{2}\alpha c_\varphi + \beta s_\varphi ^2\right. \nonumber \\&\left. -\left\{ \frac{1}{2f^3}\mathcal {O}^F_c c_\varphi +\frac{1}{2f^3}\mathcal {O}^F_s s_\varphi \,+\,h.c.\right\} \,\right] ,\nonumber \end{aligned}$$

instead of the effective dependence in Eq. (18). New operators beyond those previously considered appear, such as

$$\begin{aligned}&-\frac{1}{8\lambda f^3}\partial _\mu \varphi \,\partial ^\mu \varphi \,\left( \mathcal {O}^F_c c_\varphi +\mathcal {O}^F_s s_\varphi \right) ,\end{aligned}$$
(57)
$$\begin{aligned}&\frac{1}{16\lambda f}\langle V_\mu V^\mu \rangle s_\varphi ^2 \left( \mathcal {O}^F_c c_\varphi +\mathcal {O}^F_s s_\varphi \right) ,\end{aligned}$$
(58)
$$\begin{aligned}&\frac{1}{16\lambda f^2}\left( \mathcal {O}^F_c c_\varphi +\mathcal {O}^F_s s_\varphi \right) ^2. \end{aligned}$$
(59)

They are higher-order operators made out of both SM and heavy BSM fermions and related to the explicit fermionic ultraviolet completion. Furthermore, it is again easy to verify that the counting rule matches the NDA rule [6, 30] by identifying \(\lambda f\sim \Lambda \).

Consider next the integration of the heavy-fermion sector in the results just obtained.

This is an elaborated task, and the procedure and an explicit computation is described in Ref. [15]. To estimate the corrections, we adopt here a universal heavy-fermion mass scale \(\mathcal {M}_i\) associated with the mass generation mechanism of a given SM fermion, so that \(M_1\sim M_5\sim \Lambda _1\sim \dots \sim \mathcal {M}_t\). Assuming this scale to be larger than f, \(f/\mathcal {M}_i\) is a good expansion parameter. The final set of five effective operators resulting up to first order in the \(1/\lambda \) and \(f/\mathcal {M}_i\) expansions is shown in Table 3, where the \(a_{\sigma 1}^i\) operator coefficients weighting the \(f/\mathcal {M}_i\) corrections are expected to be \(\mathcal {O}(1)\) and their exact expressions can be found in Ref. [15].Footnote 8 Noteworthy consequences include:

  • At tree level, the heavy fermions have no impact on the gauge-Higgs coupling and \(\kappa _V\) is still given by Eq. (37). The coupling to top quarks, on the contrary, will receive fermionic contributions from the first operator in Table 3,

    $$\begin{aligned} \kappa _\mathrm{t}=\sqrt{1-\xi }+2\,\frac{m_h^2}{m_\rho ^2}+a_{\sigma 1}^t\frac{f}{\mathcal {M}_t}\xi +\dots \end{aligned}$$
    (60)

    Again, a double suppression acts on the leading heavy-fermion corrections \(\sim \xi f/\mathcal {M}_t\), alike to the case for the bosonic ones in \(\sim \beta \xi /(2\lambda )\). It is important to note, though, that the tree-level fermionic contributions found may be larger than those induced by the scalar sector if \(f/\mathcal {M}_t > \beta /\lambda \); this may occur specially for the top quark since the top partners, with characteristic mass scale \(\mathcal {M}_t\), should be light enough in order not to generate a hierarchy problem.

  • On top of the above, higher-order effective operators involving SM fields are singled out at low scales: the dominant ones are the last three presented in Table 3. For these operators, the inclusion of an explicit heavy-fermion sector does not change much the conclusions obtained previously by using an effective Yukawa coupling as defined in Eq. (7).

  • In the limit \(f/\mathcal {M}_i\rightarrow 0\), the operators in Table 3 coincide as expected with the fermion-Higgs and four fermion operators given previously in Table 2 using the effective Yukawa operator \(\mathcal {O}^{(0,0)}_\mathrm{Yuk}\).

4 Conclusions

The linear sigma model for QCD allows one to monitor the transition from a completely renormalizable model in a weakly interacting regime to a non-linear regime in the high mass (\(\lambda \rightarrow \infty \)) limit. In this work we have carried out an analogous exploration assuming that the Higgs particle may correspond to a pseudo-Goldstone boson of a spontaneously SO(5) global symmetry (or containing SO(5)) at high energies, completing the procedure first proposed and started in Ref. [15].

The minimal sigma model for SO(5) has been used as starting point. The results are independent of the relative order in which the high mass limit for the heavy boson \(\rho \) and for the heavy fermions are taken. In a first stage, the bosonic sector was left fully dynamical while we defined an effective Yukawa operator characterized by two parameters, which depend only on how the light SM fermion fields are embedded in representations of the SO(5) symmetry for any given model. Armed with this tool, the benchmark effective Lagrangian has been derived for the large \(m_\rho \) limit, see Table 2. Up to first order in the linear corrections, it is shown to be composed of ten operators, five of them bosonic and the rest fermionic including that responsible for the usual fermion Yukawa coupling; for the fermionic operators the coefficients are given as an explicit function of the two parameters which define the effective Yukawa operator. Their simple form allows a direct prediction and comparison of the many models in the literature which differ by their fermionic embedding. It is straightforward to obtain from this result the expressions of the Higgs couplings to fermions, \(\kappa _\mathrm{{f}}\), in general.

Among the \(\mathcal {O}(1/\lambda )\) corrections, three bosonic operators have coefficients which are independent of the global symmetry-breaking mechanism and should thus be of special relevance; among them a four-gauge boson vertex is already being directed probed by present data, while the other two involve vertices with at least two Higgs fields. We have also proved that the leading phenomenological couplings of the Higgs particle to gauge bosons and SM fermions, \(\kappa _V\) and \(\kappa _{\mathrm{f}}\), are quite universal, the reason being that the linear corrections must be doubly suppressed as proportional to both \(1/\lambda \) and to the explicit symmetry-breaking parameters, in a combination corresponding to a \(m_h^2/m_\rho ^2\) suppression.

The tower of higher-order operators obtained is shown to correspond to only a small subset of the most general non-linear Lagrangian [26] for a generic non-linear realization of electroweak symmetry breaking. It is also consistent with the results for general SO(5) / SO(4) constructions in Ref. [26], singling out a fraction of operators found in the latter, with its expected coefficients. The minimal set identified here could serve to focus model-independent searches of a dynamical nature for the Higgs particle.

In a second stage, we have explored a complete renormalizable model with an explicit heavy-fermion ultraviolet completion and repeated the integration procedure; the leading corrections stemming both from the heavy-boson and from the heavy-fermion sector were then identified and their coefficients determined. New higher-order operators related to the specific fermion ultraviolet completion, made out of SM and heavy fermions and containing vertices with at least four fields, were identified as an intermediate step. Finally, the set of operators made out of SM fields and involving fermions was determined to consist of only five operators at the leading order in both expansions: one coupling contains the usual SM Yukawa coupling, two are fermion-boson operators and the remaining two correspond to four fermion couplings. The results match those obtained in the first part using the effective Yukawa operator; interestingly, they show that deviations to the SM value for \(\kappa _{\mathrm{f}}\) due to tree-level exchange of heavy fermions may dominate over those stemming from the scalar (e.g. \(1/\lambda \)) linear corrections.

The starting point of the analysis in this work is a minimal renormalizable sigma model for SO(5). Other renormalizable – more complicated – realizations are conceivable, in the same way that the linear sigma model for QCD could be extended. Although additional effective operators could be sourced in such constructions [26], the operators identified here are expected to be the tell-tale of a Goldstone-boson origin for the Higgs field and as such common to all realizations.