1 Introduction

Several years ago, some three-body hadronic \(B \rightarrow 3h^{(')}\) (\(h,h'=\pi , K\)) decays have been measured by BaBar and Belle Collaborations [1,2,3,4] and studied by using the Dalitz-plot analysis. The LHCb Collaboration reported, very recently, their experimental measurements for the branching ratios and sizable direct CP asymmetries for some three-body charmless hadronic decays \(B^+ \rightarrow K^+ K^+K^-, K^+ K^+\pi ^-, K^+ \pi ^+\pi ^-\), and \(\pi ^+ \pi ^+\pi ^-\) [5,6,7], the three-body charmed hadronic decays \(B^0\rightarrow J/\psi \pi ^+\pi ^-\) [8,9,10,11,12,13] and \(B^+\rightarrow J/\psi \phi K^+\) [14, 15], or the decays \(B_s^0\rightarrow J/\psi K^+K^-\), \(J/\psi \phi \phi \), \(\bar{D}^0 K^- \pi ^+\) [10,11,12, 16]. The large localized CP asymmetry observed by LHCb brings about new challenges to experimentalists and their traditional models to fit data, and it also has invoked more theoretical studies on how to understand these very interesting three-body \(B/B_s\) meson decays.

On the theory side, the three-body hadronic decays of the heavy \(B/B_s\) meson are much more complicated to be described theoretically than those two-body \(B/B_s \rightarrow h_1 h_2\) (here \(h_i\) refer to light mesons \(\pi , K, \rho \), etc.) decays. During the past two decades, such two-body hadronic \(B/B_s\) meson decays have been studied systematically and successfully by employing various kinds of factorizations approaches. The three major factorization approaches are the QCD-improved factorization (QCDF) [17,18,19,20,21,22], the perturbative QCD (PQCD) factorization approach [23,24,25,26,27,28,29,30,31,32,33,34] and the soft-collinear-effective theory (SCET) [35,36,37,38,39]. For most \(B/B_s \rightarrow h_1 h_2\) decay channels, the theoretical predictions obtained by using these different factorization approaches agree well with each other and also turn out to be well consistent with the data within errors.

Fig. 1
figure 1

Typical Feynman diagrams for the three-body decays \(B^0_q \rightarrow \eta _c\pi ^+\pi ^-\) with \(q=(d,s)\), and the symbol \(\bullet \) denotes the weak vertex

Full size image

For \(B/B_s\) three-body hadronic decays, however, they do receive both the resonant and the non-resonant contributions, as well as the possible final state interactions (FSIs), while the relative strength of these contributions are varying significantly for different decay modes. They are known experimentally to be dominated by the low-energy resonances on \(\pi \pi \), KK and \(K\pi \) channels on Dalitz plot, usually analyzed by employing the isobar model in which the decay amplitudes are parameterized by sums of the Breit–Wigner terms and a background, but without the inclusion of the possible contributions from the coupled channels and the three-body effects such as the FSIs. In fact, the three-body hadronic \(B/B_s\) meson decays have been studied for many years for example in Refs. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55] by employing the isobar model and/or other rather different theoretical approaches, but it is still in the early stage for both the theoretical studies and the experimental measurements of such kinds of three-body decays. For example, the factorization for such three-body decays has not been verified yet, and many important issues remain to be resolved.

In Ref. [45], for instance, the authors studied the decays of \(B \rightarrow K \pi \pi \) by assuming the validity of factorization for the quasi-two-body \(B \rightarrow (K \pi )_{S,P} \pi \rightarrow K\pi \pi \) and introducing the scalar \(f_0^{K\pi }(q^2)\) and vector \(f_1^{K,\pi }(q^2)\) form factors to describe the matrix element \(<K^- \pi ^+|(\bar{s} d)_{V-A}|0>\). From the viewpoint of the authors of Ref. [46], a suitable scalar form factor could be developed by the chiral dynamics of low-energy hadron–hadron interactions, which is rather different from the Breit–Wigner form adopted to study \(B \rightarrow \sigma \pi \).

In Refs. [47,48,49], the authors calculated the branching ratios and direct CP violation for the charmless three-body hadronic decays \(B \rightarrow 3h\) with \(h=(\pi ,K)\) by using a simple model based on the factorization approach. They evaluated the non-resonant contributions to the considered decays in the framework of heavy meson chiral perturbation theory (HMChPT) with some modifications, while describing the resonant contributions by using the isobar model in terms of the usual Breit–Wigner formalism. The strong phase \(\phi \), the parameter \(\alpha _\mathrm{NR}\) and the exponential factor \(e^{-\alpha _\mathrm{NR} p_B\cdot (p_i+p_j)}\) are introduced in their work [49] in order to accommodate the data.

In PQCD factorization approach, however, we study the three-body hadronic decays of the B meson by introducing the crucial non-perturbative input of the two-hadron distribution amplitude (DA) \(\Phi _{h_1 h_2}\) [56] and use the time-like form factors to parameterize these two-hadron DAs. In our opinion, a direct evaluation of hard b-quark decay kernels, which contain two virtual gluons at leading order (LO), is power-suppressed and not important. When there is at least one pair of light mesons having an invariant mass below \(O(\bar{\Lambda }m_B)\) [40] (here \(\bar{\Lambda }=m_B-m_b\) being the B meson and b quark mass difference), the contribution from this region is dominant. The configuration involves two energetic mesons almost collimating to each other, in which three-body interactions are expected to be suppressed. However, the relative importance of the contributions from the two hard gluon exchanges and from the configuration with two collimating mesons still depend on specific decay channels and kinematic regions considered. It seems reasonable that the dynamics associated with the pair of mesons can be factorized into a two-meson distribution amplitude \(\Phi _{h_1h_2}\) [56]. One can describe the typical PQCD factorization formula for a \(B\rightarrow h_1h_2h_3\) decay amplitude as the form of  [40, 41]

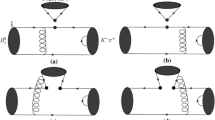
$$\begin{aligned} \mathcal {A}=\Phi _B\otimes H\otimes \Phi _{h_1h_2}\otimes \Phi _{h_3}, \end{aligned}$$
(1)

where the hard kernel H describes the dynamics of the strong and electroweak interactions in three-body hadronic decays in a similar way as the one for the two-body hadronic \(B\rightarrow h_1 h_2\) decays, the functions \(\Phi _B\), \(\Phi _{h_1h_2}\) and \(\Phi _{h_3}\) are the wave functions for the B meson and the final state mesons, which absorbs the non-perturbative dynamics in the process. Specifically, \(\Phi _{h_1h_2}\) is the two-hadron (\(h_1\) and \(h_2\)) DAs proposed for example in Refs. [56,57,58,59], which describes the structure of the final state \(h_1-h_2\) pair, as illustrated explicitly in Fig. 1.

By employing the PQCD approach, the authors of Ref. [60] studied the \(B^\pm \rightarrow \pi ^\pm \pi ^+ \pi ^-\) and \( K^\pm \pi ^+\pi ^-\) decays, evaluated the direct CP asymmetries by fitting the time-like form factors and the rescattering phases contained in the two-pion distribution amplitudes to relevant experimental data, the resulted PQCD predictions agree well with the LHCb measurements [5, 6]. In Ref. [60], however, only the non-resonant contributions to the time-like form factors were taken into account, the regions involving intermediate resonances are not considered. In the new work [61], by parameterizing the complex time-like form factors which include both resonant and non-resonant contributions, the authors studied the three-body decays \(B_s\rightarrow J/\psi f_0(980)[f_0(980)\rightarrow \pi ^+\pi ^-]\) and \(B_s\rightarrow f_0(980)[f_0(980)\rightarrow \pi ^+\pi ^-]\mu ^+\mu ^-\) decays by using the S-wave two-pion DAs.

In recent years, significant improvements for understanding the heavy quarkonium production mechanism have been achieved [62]. The meson \(\eta _c\) and \(J/\psi \) have the same quark content but with different spin angular momentum. Following Ref. [61], we here will study the three-body hadronic decays \(B^0_{(s)} \rightarrow \eta _c f_0\rightarrow \eta _c [f_0\rightarrow \pi ^+\pi ^-]\). We will consider the S-wave resonant contributions to the decay \(B^0\rightarrow \eta _c f_0(500)\rightarrow \eta _c (\pi ^+\pi ^-)\), as well as the decays \(B^0_s\rightarrow \eta _c f_0(X)\rightarrow \eta _c (\pi ^+\pi ^-)\) with \(f_0(X)=(f_0(980),f_0(1500),f_0(1790))\). Apart from the leading-order factorizable contributions, we also take into account the NLO vertex corrections to the Wilson coefficients. In Sect. 2, we give a brief introduction for the theoretical framework and present the expressions of the decay amplitudes. The numerical values, some discussions, and the conclusions will be given in the final two sections.

2 The theoretical framework

By introducing the two-pion DAs, the \(B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-\) decays can proceed mainly via quasi-two-body channels which contain scalar or vector resonant states as argued in Refs. [40, 60]. We first derive the PQCD factorization formulas for the \(B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-\) decays with the input of the S-wave two-pion DAs. We made an hypothesis that the leading-order hard kernel for three-body B meson decays contain only one hard gluon exchange as depicted in Fig. 1, where the \(B^0\) or \(B^0_s\) meson transits into a pair of the \(\pi ^+\) and \(\pi ^-\) mesons through an intermediate resonance. Figure 1a, b represent the factorizable contributions, while the Fig. 1c, d denote the spectator contributions.

In the light-cone coordinates, we assume that the light final state “two pions” and \(\eta _c\) is moving along the direction of \(n_+=(1,0,0_ \mathrm{T})\) and \(n_-=(0,1,0_ \mathrm{T})\), respectively. The \(B^0_{(s)}\) meson momentum \(p_{B}\), the total momentum of the two pions, \(p=p_1+p_2\), and the \(\eta _c\) momentum \(p_3\) are chosen as

$$\begin{aligned}&p_{B}=\frac{m_{B}}{\sqrt{2}}(1,1,0_ \mathrm{T}),\quad p=\frac{m_{B}}{\sqrt{2}}(1-r^2,\eta ,0_ \mathrm{T}),\nonumber \\&p_3=\frac{m_{B}}{\sqrt{2}}(r^2,\bar{\eta },0_ \mathrm{T}), \end{aligned}$$
(2)

where \(m_{B}\) denotes the \(B^0_{(s)}\) meson mass, the variable \(\eta \) is defined as \(\eta =\omega ^2/[(1-r^2)m^2_{B}]\) with the mass ratio \(r=m_{\eta _c}/m_{B}\), the variable \(\bar{\eta } =1-\eta \) and the invariant mass squared \(\omega ^2=p^2=m^2(\pi ^+\pi ^-)\) of the pion pair. As shown in Fig. 1a, the momentum \(k_B\) of the spectator quark in the B meson, the momentum \(k=z p^+\) and \(k_3=x_3 p_3\) are of the form of

$$\begin{aligned} k_{B}= & {} \left( 0,\frac{m_{B}}{\sqrt{2}} x_B,k_{BT}\right) ,\nonumber \\ k= & {} zp^+=\left( \frac{m_{B}}{\sqrt{2}} z(1-r^2),0,k_ \mathrm{T}\right) ,\nonumber \\ k_3= & {} x_3p_3=\left( \frac{m_{B}}{\sqrt{2}} r^2x_3,\frac{m_{B}}{\sqrt{2}} \bar{\eta } x_3,k_{3 \mathrm{T}}\right) , \end{aligned}$$
(3)

where the momentum fraction \(x_{B}\), z, and \(x_3\) run between zero and unity. The wave function of \(B/B_s\) meson can be written as [23,24,25,26, 63]

$$\begin{aligned} \Phi _B= \frac{i}{\sqrt{2N_c}} ( p / _B +m_B) \gamma _5 \phi _B (\mathbf{k_1}). \end{aligned}$$
(4)

Here we adopt the B meson distribution amplitude \(\phi _B(x,b)\) in the PQCD approach widely used since 2001 [23,24,25,26, 63]

$$\begin{aligned} \phi _B(x,b)= & {} N_B x^2(1-x)^2\mathrm {exp} \left[ -\frac{M_B^2\ x^2}{2 \omega _{B}^2} -\frac{1}{2} (\omega _{B}\; b)^2\right] , \nonumber \\ \end{aligned}$$
(5)

where the normalization factor \(N_B\) depends on the value of \(\omega _B\) and \(f_B\) and defined through the normalization relation \(\int _0^1\mathrm{d}x \; \phi _B(x,b=0)=f_B/(2\sqrt{6})\). \(\omega _B\) is a free parameter and we take \(\omega _B = 0.40 \pm 0.04\) GeV and \(\omega _{B_s}=0.50 \pm 0.05\) GeV in the numerical calculations.

For the pseudoscalar meson \(\eta _c\), its wave function can be written as

$$\begin{aligned} \Psi _{\eta _c}=\frac{1}{\sqrt{2N_c}}{\gamma _5}\left[ p / _3\psi _v+m_{\eta _c}\psi _s\right] , \end{aligned}$$
(6)

here the twist-2 distribution amplitude \(\psi _v\) and the twist-3 distribution amplitude \(\psi _s\) take the form of [64]

$$\begin{aligned} \psi _v(x)= & {} 9.58\frac{f_{\eta _c}}{2\sqrt{2N_c}}x(1-x)\left[ \frac{x(1-x)}{1-2.8x(1-x)}\right] ^{0.7},\nonumber \\ \psi _s(x)= & {} 1.97\frac{f_{\eta _c}}{2\sqrt{2N_c}}\left[ \frac{x(1-x)}{1-2.8x(1-x)}\right] ^{0.7}, \end{aligned}$$
(7)

where \(f_{\eta _c}\) is the decay constant of \(\eta _c\) meson.

The S-wave two-pion distribution amplitude \(\Phi _{\pi \pi }^\mathrm{S}\) have been defined in Ref. [65]

$$\begin{aligned} \Phi _{\pi \pi }^\mathrm{S}= & {} \frac{1}{\sqrt{2N_c}}\left[ p / \Phi _{v\nu =-}^{I=0}(z,\zeta ,\omega ^2)\right. \nonumber \\&\left. +\omega \Phi _{s}^{I=0}(z,\zeta ,\omega ^2)+\omega ( n / _+ n / _--1)\Phi _{t\nu =+}^{I=0}(z,\zeta ,\omega ^2) \right] ,\nonumber \\ \end{aligned}$$
(8)

where \(\zeta =p_1^+/p^+\) is the momentum fraction of the \(\pi ^+\) in the pion pair, the asymptotic forms of the individual DAs in Eq. (8) have been parameterized as [56,57,58,59]

$$\begin{aligned} \Phi _{v\nu =-}^{I=0}= & {} \phi _0=\frac{9F_{s}(\omega ^2)}{\sqrt{2N_c}}a_2^{I=0}z(1-z)(1-2z),\nonumber \\ \Phi _{s}^{I=0}= & {} \phi _s=\frac{F_{s}(\omega ^2)}{2\sqrt{2N_c}},\nonumber \\ \Phi _{t\nu =+}^{I=0}= & {} \phi _t=\frac{F_{s}(\omega ^2)}{2\sqrt{2N_c}}(1-2z), \end{aligned}$$
(9)

with the time-like scalar form factor \(F_{s}(\omega ^2)\) and the Gegenbauer coefficient \(a_2^{I=0}\). For simplicity, we here denote the distribution amplitudes \(\Phi _{v\nu =-}^{I=0}(z,\zeta ,\omega ^2)\), \(\Phi _{s}^{I=0}(z,\zeta ,\omega ^2)\) and \(\Phi _{t\nu =+}^{I=0}(z,\zeta ,\omega ^2)\) by \(\phi _0\), \(\phi _s\) and \(\phi _t\), respectively.

Following the LHCb Collaboration,[8,9,10, 13]Footnote 1 we also introduce the S-wave resonances into the parametrization of the function \(F_{s}(\omega ^2)\), so that both resonant and non-resonant contributions are included into the S-wave two-pion wave function \(\Phi _{\pi \pi }^\mathrm{S}\). For the \(s\bar{s}\) component in the \(B_s\rightarrow \eta _c\pi ^+\pi ^-\) decay, we take into account the contributions from the intermediate resonant \(f_0(980), f_0(1500)\) and \(f_0(1790)\) as in Ref. [13]. We use the Flatté model [66] for \(f_0(980)\) as given in Eq. [18] of Ref. [13], and the Breit–Wigner model for \(f_0(1500)\) and \(f_0(1790)\). The \(s\bar{s}\) component of the time-like scalar form factor \(F_{s}(\omega ^2)\), consequently, can be written as the form of

$$\begin{aligned} F_s^{s\bar{s}}(\omega ^2)= & {} \frac{c_1m_{f_0(980)}^2e^{i\theta _1}}{m_{f_0(980)}^2-\omega ^2-im_{f_0(980)} (g_{\pi \pi }\rho _{\pi \pi }+g_{KK}\rho _{KK})} \nonumber \\&+\frac{c_2m_{f_0(1500)}^2e^{i\theta _2}}{m_{f_0(1500)}^2-\omega ^2-im_{f_0(1500)}\Gamma _{f_0(1500)}(\omega ^2)}\nonumber \\&+\frac{c_3m_{f_0(1790)}^2e^{i\theta _3}}{m_{f_0(1790)}^2-\omega ^2-im_{f_0(1790)}\Gamma _{f_0(1790)}(\omega ^2)}, \end{aligned}$$
(10)

here the three terms describe the contributions from \(f_0(980)\), \(f_0(1500)\), and \(f_0(1790)\), respectively. All relevant parameters in the above equation are the same as those having been defined previously in Refs. [13, 61, 67], such as

$$\begin{aligned} m_{f_0(980)}= & {} 0.97 \,\mathrm{GeV}, \quad g_{\pi \pi }=0.167, \quad g_{KK}=3.47 g_{\pi \pi }, \nonumber \\ m_{f_0(1500)}= & {} 1.50\, \mathrm{GeV}, \quad m_{f_0(1790)} = 1.81\, \mathrm{GeV}. \end{aligned}$$
(11)

We assume that the energy-dependent width \(\Gamma _S(\omega ^2)\) for a S-wave resonance decaying into two pions is parameterized in the same way as in Ref. [68],

$$\begin{aligned} \Gamma _S(\omega ^2)=\Gamma _S \; \frac{m_S}{\omega }\; \left( \frac{\omega ^2-4m_{\pi }^2}{m_S^2-4m_{\pi }^2} \right) ^{\frac{1}{2}} F_R^2, \end{aligned}$$
(12)

with the pion mass \(m_{\pi }=0.13\) GeV, the constant width \(\Gamma _S\) with \(\Gamma _S =0.12, 0.32\) GeV for \(f_0(1500)\) and \(f_0(1790)\), respectively, and the Blatt–Weisskopf barrier factor \(F_R=1\) in this case [10].

For the \(d\bar{d}\) component \(F_s^{d\bar{d}}(\omega ^2)\), only the resonance \(f_0(500)\) or the so-called \(\sigma \) meson in the literature is relevant. Because the resonance \(f_0(500)\) is complicated and has a wide width, we here parameterize the \(f_0(500)\) contribution to the scalar form factor for the \(d\bar{d}\) component in two different ways: the Breit–Wigner and the Bugg model [69], respectively. Following Refs. [8, 9, 67], we first adopt the Breit–Wigner model with the pole mass \(m_{f_0(500)}=0.50\) GeV and the width \(\Gamma _{f_0(500)}=0.40\) GeV,

$$\begin{aligned} F_s^{d\bar{d}}(\omega ^2)=\frac{c m_{f_0(500)}^2}{m_{f_0(500)}^2-\omega ^2 -im_{f_0(500)}\Gamma _{f_0(500)}(\omega ^2)}. \end{aligned}$$
(13)

The parameters c, \(c_i\), and \(\theta _i\) with \(i=(1,2,3)\) appeared in Eqs. (10) and (13) have been extracted from the LHCb data [13],

$$\begin{aligned} c_1= & {} 0.900,\quad c_2=0.106, \quad c_3=0.066, \quad c=3.500,\nonumber \\ \theta _1= & {} -\frac{\pi }{2}, \quad \theta _2=\frac{\pi }{4}, \quad \theta _3=0. \end{aligned}$$
(14)

Second, we parameterize the form factor of \(f_0(500)\) with the Bugg resonant lineshape [69] in the same way as in Ref. [70]

$$\begin{aligned} T_{11}(s)= & {} M \; \Gamma _1(s) \left[ M^2 - s - g^2_1 \frac{s-s_A}{M^2-s_A} \left[ j_1(s) - j_1(M^2) \right] \right. \nonumber \\&\qquad \qquad \qquad \left. - iM \sum _{i=1}^4 \Gamma _i(s) \right] ^{-1}, \end{aligned}$$
(15)

where \(s=\omega ^2 =m^2(\pi ^+\pi ^-)\), \(j_1(s) = \frac{1}{\pi }\left[ 2 + \rho _1 \ln \left( \frac{1 - \rho _1}{1 + \rho _1}\right) \right] \), the functions \(g^2_1(s)\), \(\Gamma _i(s)\) and other relevant functions in Eq. (15) are the following:

$$\begin{aligned} g^2_1(s)= & {} M(b_1 + b_2s)\exp [-(s - M^2)/A],\nonumber \\ M\; \Gamma _1(s)= & {} g^2_1(s)\frac{s-s_A}{M^2-s_A}\rho _1(s), \nonumber \\ M\; \Gamma _2(s)= & {} 0.6g^2_1(s)(s/M^2)\exp (-\alpha |s-4m^2_K|)\rho _2(s),\nonumber \\ M\;\Gamma _3(s)= & {} 0.2g^2_1(s)(s/M^2)\exp (-\alpha |s-4m^2_\eta |)\rho _3(s), \nonumber \\ M\;\Gamma _4(s)= & {} M\; g_{4\pi }\; \rho _{4\pi }(s)/\rho _{4\pi }(M^2), \ \ \mathrm{with} \ \ \rho _{4\pi }(s)\nonumber \\= & {} 1.0/[1 + \exp (7.082 - 2.845s)]. \end{aligned}$$
(16)

For the parameters in Eqs. (15) and (16), we use their values as given in the fourth column of Table I in Ref. [69]:

$$\begin{aligned} M= & {} 0.953\, \mathrm{GeV}, \quad s_A = 0.41 \ m_{\pi }^2, \quad b_1 = 1.302\, \mathrm{GeV}^2,\nonumber \\ b_2= & {} 0.340, \quad A = 2.426 \,\mathrm{GeV}^2, \quad g_{4\pi } = 0.011\, \mathrm{GeV}. \end{aligned}$$
(17)

The parameters \(\rho _{1,2,3}\) in Eq. (16) are the phase-space factors of the decay channels \(\pi \pi \), KK and \(\eta \eta \), respectively, and have been defined as [69]

$$\begin{aligned} \rho _i(s) = \sqrt{1 - 4\frac{m^2_i }{s} }, \end{aligned}$$
(18)

with \(m_1=m_\pi , m_2=m_K\) and \(m_3=m_\eta \).

The differential decay rate for the \(B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-\) decay can be written as [67]

$$\begin{aligned} \frac{\mathrm{d}\mathcal{B}}{\mathrm{d}\omega }=\tau _{B}\frac{\omega |\mathbf {p}_1| |\mathbf {p}_3 | }{4(2\pi )^3m^3_{B}}|\mathcal{A}|^2, \end{aligned}$$
(19)

where \(\omega =m(\pi ^+\pi ^-)\), \(|\mathbf {p}_1|\) and \(|\mathbf {p}_3|\) denote the magnitudes of the \(\pi ^+\) and \(\eta _c\) momenta in the center-of-mass frame of the pion pair,

$$\begin{aligned} |\mathbf {p}_1|= & {} \frac{1}{2}\sqrt{\omega ^2-4m^2_{\pi ^{\pm }}}, \nonumber \\ |\mathbf {p}_3|= & {} \frac{1}{2\omega } \sqrt{\left[ m^2_{B}-(\omega +m_{\eta _c})^2 \right] \left[ m^2_{B}-(\omega -m_{\eta _c})^2 \right] }. \end{aligned}$$
(20)

The decay amplitude for the decay \(B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-\) is of the form

$$\begin{aligned} \mathcal {A}({B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-})= & {} V^*_{cb}V_{cd(cs)}\left( F^{LL}+M^{LL}\right) \nonumber \\&-V^*_{tb}V_{td(ts)}\left( F^{\prime LL}+F^{LR} \right. \nonumber \\&+ \left. M^{\prime LL} +M^{SP} \right) , \end{aligned}$$
(21)

where the functions \(F^{LL}, F^{\prime LL}\) and \(F^{LR}\) (\(M^{LL}, M^{\prime LL}\) and \(M^{LR}\)) denote the amplitudes for the \(B/B_s\) meson transition into two pions as illustrated by Fig. 1a, b (Fig. 1c, d):

$$\begin{aligned} F^{LL}= & {} 8\pi C_F m^4_B f_{\eta _c}\int _0^1 \mathrm{d}x_B \mathrm{d}z \int _0^\infty b_B\; \mathrm{d}b_B\; b\; \mathrm{d}b\; \phi _B(x_B,b_B)\nonumber \\&\times \bigg \{\bigg [\sqrt{\eta (1-r^2)}\big [[(1-2z)\bar{\eta } +r^2(1+2z \bar{\eta } ) ]\phi _s \nonumber \\&-(r^2(1-2z\bar{\eta } )+(2z-1)\bar{\eta } )\phi _t\big ]\nonumber \\&-\big [ -(1+z)\bar{\eta } + r^2(1+2z\bar{\eta } -2\eta ) -r^4z\bar{\eta } \big ] \phi _0\bigg ] \nonumber \\&\times a_1(t_a)\; E_e(t_a)\; h_a(x_B,z,b_B,b)\nonumber \\&+\bigg [2\sqrt{\eta (1-r^2)}\big [r^2(\eta -x_B)+(1-r^2) \bar{\eta } \big ]\phi _s \nonumber \\&-(1-r^2)\big [ \eta \bar{\eta } + r^2(\eta -x_B)\big ] \phi _0\bigg ] \nonumber \\&\times a_1(t_b)\; E_e(t_b)\; h_b(x_B,z,b_B,b) \bigg \}, \end{aligned}$$
(22)
$$\begin{aligned} F^{\prime LL}= & {} F^{LL}|_{a_1\rightarrow a_2},\quad F^{LR}=-F^{LL}|_{a_1\rightarrow a_3}, \end{aligned}$$
(23)
$$\begin{aligned} M^{LL}= & {} 32\pi C_F m^4_B/\sqrt{6} \int _0^1 \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3 \nonumber \\&\times \int _0^\infty b_B \mathrm{d}b_B\; b_3 \mathrm{d}b_3\; \phi _B(x_B,b_B)\nonumber \\&\times \bigg \{\bigg [\sqrt{\eta (1-r^2)}\Big [ \big [r^2x_B+(1-\eta )(1-r^2)z \big ]\phi _t\psi _v\nonumber \\&- \big [ 2r^2 (1-x_3) \bar{\eta } +(1-r^2)z\bar{\eta } -r^2x_B \big ]\psi _v \phi _s -4rr_c\psi _s \phi _s \Big ]\nonumber \\&+ (\bar{\eta } +r^2)\big [(1-r^2)(1-x_3-x_B)+ x_3(1-2r^2)\eta \nonumber \\&-(1-r^2)(1-z)\eta +r^2\eta \big ]\psi _v \phi _0 \nonumber \\&-rr_c(1-r^2+\eta )\psi _s \phi _0\bigg ] C_2(t_c)\; E_n(t_c)\; h_c(x_B,z,x_3,b_B,b_3)\nonumber \\&+\bigg [\sqrt{\eta (1-r^2)}\Big [ \big [2r^2x_3 \bar{\eta } -r^2x_B+ z(1-r^2)\bar{\eta } \big ] \psi _v\phi _s \nonumber \\&+\big [ z(1-r^2)\bar{\eta } +r^2x_B \big ]\psi _v\phi _t\Big ]\nonumber \\&-[ \bar{\eta } +r^2(\eta -\bar{\eta } ) ] \big [x_3 \bar{\eta } -x_B+r^2x_3 +z(1-r^2)\big ]\psi _v\phi _0\bigg ]\nonumber \\&\times C_2(t_d)\; E_n(t_d)\;h_d(x_B,z,x_3,b_B,b_3)\bigg \},\end{aligned}$$
(24)
$$\begin{aligned} M^{\prime LL}= & {} M^{LL}|_{C_{2}\rightarrow C_4+C_{10}}, \end{aligned}$$
(25)
$$\begin{aligned} M^{SP}= & {} 32\pi C_F m^4_B/\sqrt{6} \int _0^1 \mathrm{d}x_B\; \mathrm{d}z\; \mathrm{d}x_3\nonumber \\&\times \int _0^\infty b_B \mathrm{d}b_B\; b_3 \mathrm{d}b_3\; \phi _B(x_B,b_B)\nonumber \\&\times \bigg \{ \bigg [\sqrt{\eta (1-r^2)}\Big [ \big [ 2r^2(1-x_3)\bar{\eta } +z(1-r^2)\bar{\eta } \nonumber \\&- r^2x_B \big ]\psi _v\phi _s -4rr_c\psi _s \phi _s \Big ]\nonumber \\&+\sqrt{\eta (1-r^2)}\left[ z(1-r^2)\bar{\eta } + r^2x_B\right] \psi _v\phi _t\nonumber \\&-\Big [ \left( -r^2+\bar{\eta } + 2r^2\eta \right) \big [ (1-x_3)r^2+z(1-r^2)\nonumber \\&+(1-x_3)\bar{\eta } -x_B \big ]\psi _v \phi _0\nonumber \\&- rr_c(1+\eta -r^2)\psi _s\phi _0 \Big ] \bigg ] \left[ C_6(t_c)+C_8(t_c)\right] \; \nonumber \\&\times E_n(t_c)\; h_c(x_B,z,x_3,b_B,b_3)\nonumber \\&-\bigg [ \sqrt{\eta (1-r^2)}\Big [ \big [ 2r^2x_3 \bar{\eta } +(1-r^2)z\bar{\eta } -r^2x_B \big ] \psi _v \phi _s \nonumber \\&- \big [ z(1-r^2)\bar{\eta } +r^2x_B \big ]\psi _v \phi _t\Big ]\nonumber \\&-(r^2 +\bar{\eta } )\Big [(1-r^2)( x_3\bar{\eta } -x_B)+x_3r^2\eta \nonumber \\&+\eta z(1-r^2)\Big ]\psi _v\phi _0\bigg ] \nonumber \\&\times \left[ C_6(t_d)+C_8(t_d)\right] \; E_n(t_d)\; h_d(x_B,z,x_3,b_B,b_3) \bigg \}, \nonumber \\ \end{aligned}$$
(26)

where \(C_F=4/3\), \(r_c=m_c/m_B\), and \(a_i\) are the combinations of the Wilson coefficients \(C_i\):

$$\begin{aligned} a_1= & {} C_1+\frac{C_2}{3}, \quad a_2=C_3+C_9+ \frac{C_4 +C_{10}}{3},\nonumber \\ a_3= & {} C_5+C_7+\frac{C_6+C_8}{3}. \end{aligned}$$
(27)

The explicit expressions of the evolution factors \((E_e(t_a),E_e(t_b),E_n(t_c),E_n(t_d))\), the hard functions \((h_a,h_b,h_c,h_d)\) and the hard scales \((t_a,t_b,t_c,t_d)\), appeared in Eqs. (22)–(26), can be found in the appendix of Ref. [61].

Fig. 2
figure 2

The \(m(\pi ^+\pi ^-)\)-dependence of the differential decay rates \(d\mathcal{B}/d\omega \) for a the contribution from the resonance \(f_0(980)\), \(f_0(1500)\) and \(f_0(1790)\) to \(B^0_s\rightarrow \eta _c\pi ^+\pi ^-\) decay, and b the contribution from \(f_0(500)\) to \(B^0\rightarrow \eta _c\pi ^+\pi ^-\) decay in the BW model (red curve) or the Bugg model (blue curve)

Full size image

For the factorizable emission diagrams Fig.1a, b, the NLO vertex corrections can be taken into account through the inclusion of additional terms to the Wilson coefficients [17,18,19, 71, 72]. After the inclusion of the NLO vertex corrections, the Wilson coefficients \(a_1\), \(a_2\), and \(a_3\) as defined in Eq. (27) will be modified to the following form:

$$\begin{aligned} a_1(\mu )= & {} C_1(\mu ) +\frac{C_2(\mu )}{3} \left\{ 1+ \frac{2 \alpha _s(\mu ) }{3\pi } \left[ 6\ln \frac{m_b}{\mu }-9\right. \right. \nonumber \\&+\left. \left. \frac{ \sqrt{6} }{f_{\eta _c} } \int _0^1 \mathrm{d}x\psi _v(x) g(x) \right] \right\} , \end{aligned}$$
(28)
$$\begin{aligned} a_2(\mu )= & {} C_3(\mu ) + C_9(\mu ) +\frac{C_4(\mu )+C_{10}(\mu )}{3}\nonumber \\&\times \left\{ 1+ \frac{2 \alpha _s(\mu ) }{3\pi } \left[ 6\ln \frac{m_b}{\mu }-9\right. \right. \nonumber \\&+\left. \left. \frac{ \sqrt{6} }{f_{\eta _c} } \int _0^1 \mathrm{d}x\psi _v(x) g(x) \right] \right\} , \end{aligned}$$
(29)
$$\begin{aligned} a_3(\mu )= & {} C_5(\mu ) + C_7(\mu ) +\frac{C_6(\mu )+C_{8}(\mu )}{3}\nonumber \\&\times \left\{ 1 - \frac{2 \alpha _s(\mu ) }{3\pi } \left[ 6\ln \frac{m_b}{\mu }-3\nonumber \right. \right. \\&+\left. \left. \frac{ \sqrt{6} }{f_{\eta _c} } \int _0^1 \mathrm{d}x\psi _v(x) g(1-x) \right] \right\} . \end{aligned}$$
(30)

Since the emitted meson \(\eta _c\) is heavy, the terms proportional to the factor \(z=m^2_{\eta _c}/m^2_B\) cannot be neglected. One therefore should use the hard-scattering functions g(x) as given in Ref. [73] instead of the one in Ref. [71],

$$\begin{aligned} g(x)= & {} \frac{3(1-2x)}{1-x}\ln [x]+3 \left[ \ln (1-z)-i \pi \right] -\frac{2z (1-x)}{1-z x}\nonumber \\&- \frac{2 x z(\ln [1 - z]-i \pi )}{1 - (1 - x) z} - \frac{ x^2 z^2 (\ln [1 - z]-i \pi )}{(1 - (1 - x) z)^2}\nonumber \\&+ x z^2 \ln [x z]\left[ \frac{x}{(1-(1 - x) z)^2}-\frac{1-x}{(1-x z)^2}\right] \nonumber \\&+ 2 x z \ln [x z] \left[ \frac{1}{1-(1 - x) z} -\frac{1}{1-x z}\right] , \end{aligned}$$
(31)

where \(z=m^2_{\eta _c}/m^2_B\). For \(B_s \rightarrow \eta _c \pi ^+\pi ^-\) decay, the mass \(m_B\) in the above equations should be replaced by the mass \(m_{B_s}\).

3 Numerical results

In numerical calculations, besides the quantities specified before, the following input parameters (the masses, decay constants, and QCD scale are in units of GeV) will be used [60, 67]

$$\begin{aligned} \Lambda ^{(f=4)}_{ \overline{MS} }= & {} 0.326, \quad m_{B^0}=5.280, \quad m_{B_s}=5.367, \nonumber \\ m_{\eta _c}= & {} 2.9836, \nonumber \\ m_{\pi ^\pm }= & {} 0.140, \quad m_{\pi ^0}=0.135, \quad m_{b}=4.8, \quad m_c=1.275, \nonumber \\ m_s= & {} 0.095, \nonumber \\ f_B= & {} 0.19\pm 0.02, \quad f_{B_s}=0.236, \quad \tau _{B^0}=1.519\; ps,\nonumber \\ \tau _{B_{s}}= & {} 1.512\; ps. \end{aligned}$$
(32)

The values of the Wolfenstein parameters are the same as given in Ref. [67]: \(A=0.814^{+0.023}_{-0.024}, \lambda =0.22537\pm 0.00061\), \(\bar{\rho } = 0.117\pm 0.021, \bar{\eta }= 0.353\pm 0.013\). For the Gegenbauer coefficient we use \(a_2^{I=0}=0.2\).

In Fig. 2a, we show the contributions to the differential decay rate \(d\mathcal{B}(B_s\rightarrow \eta _c \pi ^+\pi ^-)/\mathrm{d}\omega \) from each resonance \(f_0(980)\) (the blue solid curve), \(f_0(1500)\) (the red solid curve) and \(f_0(1790)\) (the dots curve), as a function of the pion-pair invariant mass \(\omega =m(\pi ^+\pi ^-)\). For the considered \(B_s\) decay, the allowed region of \(\omega \) is \(4m_\pi ^2 \le \omega ^2 \le (M_{B_s}-m_{\eta _c})^2\). In Fig. 2b, furthermore, we show the contribution to the differential decay rate \(\mathrm{d}\mathcal{B}(B^0\rightarrow \eta _c \pi ^+\pi ^-)/\mathrm{d}\omega \) from the resonance \(f_0(500)\) as a function of \(m(\pi ^+\pi ^-)\) too, where the red and blue lines show the prediction obtained by using the Breit–Wigner model and the Bugg model, respectively. For \(B\rightarrow \eta _c \pi ^+\pi ^-\) decay, the dynamical limit on the value of \(\omega \) is \(4m_\pi ^2 \le \omega ^2 \le ( M_B-m_{\eta _c} )^2\).

For the decay \(B \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+\pi ^-\), the PQCD prediction for its branching ratio with Breit–Wigner form is

$$\begin{aligned}&\mathcal{B}(B^0\rightarrow \eta _c f_0(500)[\pi ^+\pi ^-])\nonumber \\&\quad =\left[ 1.53 ^{+0.44}_{-0.35}(\omega _{B})^{+0.62}_{-0.00}(a^{I=0}_2)^{+0.00}_{-0.01}(m_c)\right] \times 10^{-6}. \end{aligned}$$
(33)

When we use the method of Bugg, the PQCD prediction for its branching ratio is of the form

$$\begin{aligned}&\mathcal{B}(B^0\rightarrow \eta _c f_0(500)[\pi ^+\pi ^-])\nonumber \\&\quad = \left[ 2.31 ^{+0.63}_{-0.48}(\omega _{B})^{+0.73}_{-0.00}(a^{I=0}_2)^{+0.00}_{-0.01}(m_c)\right] \times 10^{-6}, \end{aligned}$$
(34)

where the three major errors are induced by the uncertainties of \(\omega _{B}=(0.40\pm 0.04)\) GeV, \(a_2^{I=0}=0.2\pm 0.2\) and \(m_c=(1.275\pm 0.025)\) GeV, respectively.

For the decay mode \(B_s \rightarrow \eta _c f_0(X) \rightarrow \eta _c (\pi ^+\pi ^-)_S\), when the contribution from each resonance \(f_0(980)\), \(f_0(1500)\) and \(f_0(1790)\) are included, respectively, the PQCD predictions for the branching ratios for each case are the following:

$$\begin{aligned}&\mathcal{B}(B_s\rightarrow \eta _c f_0(980)[\pi ^+\pi ^-])\nonumber \\&\quad =\left[ 3.37 ^{+0.98}_{-0.77}(\omega _{B_s})^{+0.38}_{-0.00}(a^{I=0}_2)^{+0.03}_{-0.00}(m_c)\right] \times 10^{-5}, \end{aligned}$$
(35)
$$\begin{aligned}&\mathcal{B}(B_s\rightarrow \eta _c f_0(1500)[\pi ^+\pi ^-])\nonumber \\&\quad =\left[ 6.76 ^{+1.50}_{-1.21}(\omega _{B_s})^{+0.60}_{-0.00}(a^{I=0}_2)^{+0.09}_{-0.00}(m_c)\right] \times 10^{-6}, \end{aligned}$$
(36)
$$\begin{aligned}&\mathcal{B}(B_s\rightarrow \eta _c f_0(1790)[\pi ^+\pi ^-])\nonumber \\&\quad =\left[ 1.97 ^{+0.59}_{-0.44}(\omega _{B_s})^{+0.21}_{-0.00}(a^{I=0}_2)^{+0.01}_{-0.01}(m_c)\right] \times 10^{-6}, \end{aligned}$$
(37)

where the three major errors are induced by the uncertainties of \(\omega _{B_s}=(0.50\pm 0.05)\) GeV, \(a_2^{I=0}=0.2\pm 0.2\) and \(m_c=(1.275\pm 0.025)\) GeV, respectively. The errors induced by the variations of the Wolfenstein parameters and the other input are very small and have been neglected. If we take into account the interference between different scalars \(f_0(X)\), we found the total branching ratio:

$$\begin{aligned}&\mathcal{B}(B_s\rightarrow \eta _c f_0(X)[\pi ^+\pi ^-])\nonumber \\&\quad =\left[ 5.02^{+1.37}_{-1.08} (\omega _{B_s})^{+0.58}_{-0.00}(a^{I=0}_2)^{+0.03}_{-0.02}(m_c)\right] \times 10^{-5}. \end{aligned}$$
(38)

The interference between \(f_0(980)\) and \(f_0(1500)\), \(f_0(980)\) and \(f_0(1790)\), as well as \(f_0(1500)\) and \(f_0(1790)\), will provide a contribution of \(3.29\times 10^{-6}, 5.59\times 10^{-6}\) and \(-1.16\times 10^{-6}\) to the total decay rate, respectively.

From the curves in Fig. 2 and the PQCD predictions for the decay rates as given in Eqs. (33)–(38), one can see the following points:

  1. (i)

    For \(B_s \rightarrow \eta _c f_0(X) \rightarrow \eta _c (f_0(X)\rightarrow \pi ^+\pi ^-) \) decay, as illustrated clearly by Fig. 2a, the contribution from the resonance \(f_0(980)\) is dominant (\(\sim 70\%\)), while the contribution from \(f_0(1790)\) is very small (\(\sim 4\%\) only). The interference between \(f_0(980)\) and \(f_0(1500)\), as well as \(f_0(980)\) and \(f_0(1790)\), are constructive and can provide \(\sim \)20% enhancement to the total decay rate. The interference between \(f_0(1500)\) and \(f_0(1790)\), however, is destructive, but very small (less than \(-2\%\)) in size.

  2. (ii)

    For \(B \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+\pi ^-\) decay, the PQCD predictions for its branching ratios are around \(2\times 10^{-6}\) in magnitude when we use the Breit–Wigner or the Bugg model to parameterize the wide \(f_0(500)\) meson. The model-dependence of the differential decay rate \(dB/d\omega (B \rightarrow \eta _c f_0(500)(\pi ^+\pi ^-))\), as illustrated in Fig. 2b, are indeed not significant. Although the central value of PQCD predictions based on the Bugg model are moderately larger than the one from the Breit–Wigner model, but they are still consistent within errors.

  3. (iii)

    The \(B/B_s \rightarrow \eta _c f_0(X) \rightarrow \eta _c (\pi ^+\pi ^-)\) decays are similar in nature with the decays \(B/B_s \rightarrow J/\psi f_0(X) \rightarrow J/\psi (\pi ^+\pi ^-)\) studied previously in Ref. [61]. We find numerically \(\mathcal{B}(B \rightarrow \eta _c \pi ^+\pi ^-):\mathcal{B}(B \rightarrow J/\psi \pi ^+\pi ^-)\approx 0.3:1\).

4 Summary

In this paper, we studied the contributions from the S-wave resonant states \(f_0(X)\) to the \(B^0_{(s)}\rightarrow \eta _c\pi ^+\pi ^-\) decays by employing the PQCD factorization approach. We calculated the differential decay rates and the branching ratios of the decay \(B^0\rightarrow \eta _c f_0(500)\rightarrow \eta _c (\pi ^+\pi ^-)\), the decays \(B^0_{s}\rightarrow \eta _c f_0(X) \rightarrow \eta _c (\pi ^+\pi ^-)\) with \(f_0(X)=f_0(980), f_0(1500)\), and \(f_0(1790)\), respectively. By using the S-wave two-pion wave function \(\Phi _{\pi \pi }^\mathrm{S}\) the resonant and non-resonant contributions to the considered decays are taken into account. The NLO vertex corrections are also included through the redefinition of the relevant Wilson coefficients.

From analytical analysis and numerical calculations we found the following points:

  1. (i)

    For the branching ratios, we found

    $$\begin{aligned}&\mathcal{B}^{BW}(B^0\rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+\pi ^-)\nonumber \\&\quad = \left( 1.53 ^{+0.76}_{-0.35} \right) \times 10^{-6}, \end{aligned}$$
    (39)
    $$\begin{aligned}&\mathcal{B}^{Bugg}(B^0\rightarrow \eta _c f_0(500)\rightarrow \eta _c \pi ^+\pi ^-)\nonumber \\&\quad = \left( 2.31^{+0.96}_{-0.48}\right) \times 10^{-6},\end{aligned}$$
    (40)
    $$\begin{aligned}&\mathcal{B}(B_s\rightarrow \eta _c f_0(X)\rightarrow \eta _c \pi ^+\pi ^-] ) \nonumber \\&\quad =\left( 5.02^{+1.49}_{-1.08} \right) \times 10^{-5}, \end{aligned}$$
    (41)

    where the individual errors have been added in quadrature. For the decay rate \(\mathcal{B}(B_s\rightarrow \eta _c \pi ^+\pi ^-)\), the contribution from the resonance \(f_0(980)\) is dominant.

  2. (ii)

    For \(B \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+\pi ^-\) decay, we used the Breit–Wigner and the Bugg model to parameterize the wide \(f_0(500)\) meson, respectively, but found that the model-dependence of the PQCD predictions are not significant.

  3. (iii)

    The considered decays with the branching ratio at the order of \(10^{-6}\sim 10^{-5}\) could be measured at the ongoing LHCb experiment. The formalism of two-hadron distribution amplitudes, consequently, could be tested by such experiments.