1 Introduction

The process of structure formation in the universe unavoidably leads to the production of radiation. Electromagnetic radiation is emitted during star formation, which started in small halos at redshifts of order \(z\sim 20\) and then peaked at \(z\sim 2\) [1]. Dust absorbs part of the UV radiation produced, which is then re-radiated at IR frequencies [2]. Photons are also emitted through a variety of late-time astrophysical processes such as accreting black holes, spinning neutron stars and supernova explosions. In the latter case large amounts of relativistic neutrinos are produced [3].

Radiation is also created in the form of gravitational waves, which are emitted both on large scales during the mergers of the supermassive black holes at the centers of galaxies and on small scales during black hole/neutron star mergers and supernova explosions. For example, the two recent gravitational-wave detections from LIGO [4] showed that roughly 5% of the total black hole mass has been converted into gravitational radiation. In addition, there is also the possibility that dark matter is made of primordial black holes [5,6,7,8] which again could radiate gravitational waves. Finally, gravitational radiation may be produced by the backreaction of small-scale inhomogeneities on the dynamics of the background metric [9].

To a first approximation one can model the radiation produced during the process of structure formation as a uniform (astrophysical) radiation background (ARB). The cosmic microwave background (CMB) – the fossil blackbody radiation from big bang – is not part of ARB. This energy transfer from matter to radiation could affect the expansion rate of the universe and the growth of perturbations. The aim of the present work is to understand to which level one can constraint the ARB using cosmological observations. Here, we answer this question by modeling the energy transfer discussed above through an effective interaction between matter and astrophysical radiation. We will consider future data from the Large Synoptic Survey Telescope (LSST [10]) and Euclid [11]; our results, therefore, should give the best possible cosmological constraints – at least in the near future – on the ARB.

2 Model

The (twice contracted) Bianchi identity, within General Relativity, implies that the total energy-momentum tensor is conserved. Hence, a possible interaction between matter and astrophysical radiation can be modeled through an interaction current \(Q^{\beta }\) which transfers energy and momentum from one source to the other with opposite direction:

$$\begin{aligned} \nabla _{\alpha } T_{m}^{\alpha \beta }= Q^{\beta } ,\qquad \nabla _{\alpha } T_{\mathrm{ar}}^{\alpha \beta }=- Q^{\beta } \,. \end{aligned}$$
(1)

We will consider a phenomenological description for the effective interaction between matter and radiation. In particular, we will consider the following simple interaction:Footnote 1

$$\begin{aligned} Q^{\beta }&= \Gamma \, T_{m} \, u^{\beta }_{m} \,, \end{aligned}$$
(2)

where \(T_{m}=-\rho _{m}\) is the trace of the matter energy-momentum tensor so that the temporal component is \(Q^{0} = \Gamma \, \rho _{m}\). For the interaction rate we will consider \(\Gamma = \alpha \, H\), that is, we use the Hubble function \(H=\dot{a}/a\) in order to parametrize the time dependence of the interaction.Footnote 2 Since the energy goes from \(\rho _m\) to \(\rho _{\mathrm{ar}}\) we set \(\alpha >0\). Moreover, as the production of astrophysical radiation is a recent phenomenon we will demand that \(\alpha =0\) for \(z \ge \bar{z}\) where \(\bar{z} \sim 5\text {--}10\). In other words, the interaction is switched off at early times. An advantage of the interaction above is that it is possible to obtain analytical solutions.

2.1 Background

The dynamical equations for the background are (a dot denotes a derivative with respect to cosmic time t):

$$\begin{aligned}&H^2 =\frac{8\pi G}{3} \left( \rho _m + \rho _{\gamma } + \rho _{\mathrm{ar}} \right) +\frac{\varLambda }{3} \,, \end{aligned}$$
(3)
$$\begin{aligned}&\dot{\rho }_m +3H\rho _m = - \alpha \, H \, \rho _m \,, \end{aligned}$$
(4)
$$\begin{aligned}&\dot{\rho }_{\mathrm{ar}} +4H\rho _{\mathrm{ar}} = \alpha \, H \, \rho _m \,, \end{aligned}$$
(5)
$$\begin{aligned}&\dot{\rho }_{\gamma } +4H\rho _{\gamma }=0 , \end{aligned}$$
(6)

where Eqs. (4–6) are the conservation equations for matter, astrophysical radiation, and CMB photons, respectively, \(\varLambda \) is the cosmological constant and we have assumed spatial flatness, in agreement with recent cosmological observations (see [14] and references therein).

It is clear that this model is but a rough approximation to the actual process of production of radiation. An important approximation is the use of an overall coupling constant to describe different processes which may or may not involve both dark matter and baryons. Another approximation comes from the fact that the time dependence of the interaction rate \(\Gamma \) is parametrized using the Hubble rate – i.e. according to a cosmological time scale – while astrophysical processes could evolve on a shorter time scales. For example, the interaction rate could be modeled as being proportional to the matter density contrast, \(\Gamma = \alpha \, \delta _m \, H_0\), as proposed in [15]. However, the aim of this work is to understand if future observations can constrain the effective coupling \(\alpha \) or, equivalently, the energy density of ARB. More precisely, we would like to know if cosmological observations can constrain astrophysical radiation to the level predicted by astrophysical models of star formation, IR background and gravitational-wave production. For such a goal the simple model above should be adequate.

As we will confirm a posteriori, for the forecasted observations we consider it is \(\rho _{\mathrm{ar}}\gg \rho _{\gamma }\). Consequently, we will neglect the well understood CMB photons from the remaining of this analysis. For the same reason we neglect the contribution from a possibly massless neutrino.

Equations (3–5) can be solved analytically:

$$\begin{aligned}&\rho _m = \rho _{m_0} (1+z)^{3+\alpha } \,, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{\mathrm{ar}} = \rho _{\mathrm{ar}_0} (1+z)^4 +\frac{\alpha }{\alpha -1} \rho _{m_0} \left[ (1+z)^4 - (1+z)^{3+\alpha } \right] , \end{aligned}$$
(8)
$$\begin{aligned} E^2(z)&= \left[ \varOmega _{\mathrm{ar}_0} + \frac{\alpha }{\alpha - 1} \varOmega _{m_0}\right] \left( 1+z\right) ^4 \nonumber \\&\quad +\frac{1}{1-\alpha } \varOmega _{m_0} (1+z)^{3+\alpha } +\varOmega _{\varLambda _0} , \end{aligned}$$
(9)

where \(\rho _{m_0}\) and \(\rho _{\mathrm{ar}_0}\) are the matter and astrophysical radiation energy densities today, respectively, \(E(z)=H(z)/H_0\), and \(\varOmega _{\varLambda _0}=1-\varOmega _{m_0}-\varOmega _{\mathrm{ar}_0}\). The corresponding density parameters are:

$$\begin{aligned}&\varOmega _m(z)= \frac{ \varOmega _{m_0}(1+z)^{(3+\alpha )}}{E^2(z)} \,, \end{aligned}$$
(10)
$$\begin{aligned}&\varOmega _{\mathrm{ar}}(z) = \frac{\varOmega _{ar_0}(1+z)^4 +\frac{\alpha }{\alpha -1} \varOmega _{m_0}\left[ (1+z)^4 -(1+z)^{3+\alpha }\right] }{E^2(z)} , \end{aligned}$$
(11)

so that one has \( \varOmega _m + \varOmega _{\mathrm{ar}} +\varOmega _{\varLambda } =1\).

As discussed earlier, the energy exchange from \(\rho _m\) to \(\rho _{ar}\) is a recent phenomenon which we model as starting at a redshift \(\bar{z} \sim 5\text {--}10\). Consequently, for \(z \ge \bar{z}\) it is \(\alpha =\rho _{\mathrm{ar}}=0\). Using this initial condition and equations (8) one then finds the present-day astrophysical density parameter as a function of initial redshift and coupling:

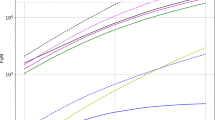
$$\begin{aligned}&\varOmega _{\mathrm{ar}_0} = \left( \frac{\alpha }{\alpha -1}\right) \left[ (1+\bar{z})^{\alpha -1}-1\right] \varOmega _{m_0} . \end{aligned}$$
(12)

As expected, \(\varOmega _{\mathrm{ar}_0}\) is proportional to both the coupling parameter and the matter density. One expects a small \(\alpha \) and so \(\varOmega _{ar_0} \ll \varOmega _{m_0}\). For illustration purposes, the left panel of Fig. 1 shows the evolution of the background energy densities for the case \(\alpha = 0.2\).

2.2 Perturbations

In Eq. (2) \(u^{\beta }_{m}\) is the four-velocity of the matter component. As discussed in [16] this kind of interaction does not alter the Euler equation as there is no momentum transfer in the matter rest frame. This choice should be reasonable as one does not expect a fifth force for the phenomenology discussed in this paper. The perturbation equation for sub-horizon scales is then

$$\begin{aligned} \ddot{\delta }_m +2 H \dot{\delta }_m + H^2 \left( \frac{\alpha -3}{2} \right) \varOmega _m \delta _m \approx 0 \,, \end{aligned}$$
(13)

where we made the approximation \(\varOmega _{\mathrm{ar}} \theta _{\mathrm{ar}}\ll \varOmega _{m} \theta _m\) and \(\varOmega _{\mathrm{ar}} \delta _{\mathrm{ar}}\ll \varOmega _{m} \delta _m\), and we neglected terms quadratic (or higher) in combinations of \(\alpha \) and \(\varOmega _{\mathrm{ar}}/\varOmega _{m}\). This means that \(\theta _\mathrm{tot} \approx \theta _m\). In the previous equations \(\delta \) is the density contrast, \(\theta = \nabla _i v^i \) is the divergence of the velocity field, and the total divergence is given by:

$$\begin{aligned} \theta _\mathrm{tot}=\frac{3\varOmega _m \theta _m + 3\varOmega _{\mathrm{ar}} \theta _{\mathrm{ar}}}{3\varOmega _m +4\varOmega _{\mathrm{ar}}} \ . \end{aligned}$$
(14)

We will denote with \(G(t)=\delta _m(t)/\delta _m(t_0)\) the growth function normalized to unity at the present time. In obtaining (13) we have perturbed the expansion rate in \(\Gamma = \alpha \, H\) as done in [17, 18] in order to preserve gauge invariance. The right panel of Fig. 1 shows the evolution of the growth rate \(f=\frac{\mathrm{d}\ln \delta _m}{\mathrm{d}\ln a}\) for the case \(\alpha = 0.2\). For the sake of comparison, the growth rate of the \(\varLambda \)CDM with the same present-day matter density is also shown.

Fig. 1
figure 1

Top evolution of the background energy densities for \(\alpha =0.2\). At \(\bar{z}\) the interaction is turned off and \(\varOmega _{\mathrm{ar}} = 0\). Bottom growth rate for the model of this paper with \(\alpha = 0.2\) and for the \(\varLambda \)CDM with the same present-day matter density. In both plots the interaction induces larger changes for redshifts between 0 and \(\bar{z}=5\) (vertical line). Indeed for \(z\ge \bar{z}\) the interaction is switched off and for redshifts close to zero the cosmological constant dominates. See Sect. 2 for more details

Full size image

3 Comparison to observations

3.1 SN data

At the background level, we will use the forecasted supernova Ia sample relative to ten years of observations by the LSST. This dataset features a total of \(10^{6}\) supernovae with intrinsic dispersion of 0.12 mag in the redshift range \(z=0.1\)–1.0 with the redshift distribution as given in [10].

The predicted theoretical magnitudes are related to the luminosity distance \(d_{L}\) by

$$\begin{aligned} m(z)=5\log _{10}\frac{d_{L}(z)}{10\,\text {pc}}\,, \end{aligned}$$
(15)

which is computed under the assumption of spatial flatness:

$$\begin{aligned} d_{L}(z)=(1+z)\int _{0}^{z}\frac{\mathrm{d}\tilde{z}}{H(\tilde{z})}\,. \end{aligned}$$
(16)
Fig. 2
figure 2

Marginalized 1-, 2- and 3\(\sigma \) constraints and correlations on the parameters \(\alpha \), \(\varOmega _{m0}\), and \(\sigma _8\) using the total likelihood built from the \(\chi ^2\) function of Eq. (25). The starting redshift of \(\bar{z} =5\) has been adopted. See Sect. 4 for more details

Full size image

The \(\chi ^{2}\) function is then

$$\begin{aligned} \chi _\mathrm{SNe}^{'2}=\sum _{i}\frac{[m_{i}-m(z_{i})+\xi ]^{2}}{\sigma ^{2}}\,, \end{aligned}$$
(17)

where the index i labels the forecasted supernovae and \(\sigma =0.12\) mag. The parameter \(\xi \) is an unknown offset sum of the supernova absolute magnitude and other possible systematics. As usual, we marginalize the likelihood \(L'_\mathrm{SNe}=\exp (-\chi _\mathrm{SNe}^{'2}/2)\) over \(\xi \), such that \(L_\mathrm{SNe}=\int \mathrm{d}\xi \, L'_\mathrm{SNe}\), leading to a new marginalized \(\chi ^{2}\) function:

$$\begin{aligned} \chi _\mathrm{SNe}^{2}=S_{2}-\frac{S_{1}^{2}}{S_{0}}\,, \end{aligned}$$
(18)

where we neglected a cosmology-independent normalizing constant, and the auxiliary quantities \(S_{n}\) are defined as

$$\begin{aligned} S_{n}\equiv \sum _{i}\frac{\left[ m_{i}-m(z_{i})\right] ^{n}}{\sigma _{i}^{2}}\,. \end{aligned}$$
(19)

Note that, as \(\xi \) is degenerate with \(\log _{10}H_{0}\), we are effectively marginalizing also over the Hubble constant.

3.2 Growth-rate data

At the linear perturbation level, we will build the growth-rate likelihood using the forecast accuracy of a future Euclid-like mission as obtained in [19]. Growth-rate data are given as a set of values \(d_{i}\) where

$$\begin{aligned} d=f\sigma _{8}(z)=f(z) G(z) \sigma _{8} \,. \end{aligned}$$
(20)

The \(\chi ^{2}\) function is then

$$\begin{aligned} \chi _{f\sigma _{8}}^{2}=\sum _{i}\frac{[d_{i}-d(z_{i})]^{2}}{\sigma _{i}^{2}}\,, \end{aligned}$$
(21)

where the index i labels the redshift bins which span the redshift range \(0.5<z<2.1\). The uncertainties \(\sigma _i\) are as given in [19] (Table II).

3.3 Planck prior

The \(\chi ^{2}\) functions above depend on three parameters: \(\alpha \), \(\varOmega _{m_0}\), and \(\sigma _8\). It is useful to consider a prior on the latter two parameters in order to reduce possible degeneracies. As the interaction we are considering is absent at earlier times – and so the cosmology is unchanged for \(z\ge \bar{z}\) – we can use a prior on \(\varOmega _{m_0}\) and \(\sigma _8\) from the CMB. However, as the evolution for \(z< \bar{z}\) is different, we have to adopt effective present-day parameters in building the prior. Specifically, by demanding \(\varOmega _m^{\varLambda }(\bar{z}) = \varOmega _m(\bar{z})\) and \(\sigma ^{\varLambda }_8(\bar{z}) =\sigma _8(\bar{z})\) we find that the effective parameters that we have to use are:

$$\begin{aligned}&\varOmega _{m_0}^{\varLambda } =\varOmega _{m_0}(1+\bar{z})^{\alpha } \left[ \frac{E^{\varLambda }(\bar{z})}{E(\bar{z})}\right] ^2 \,,\end{aligned}$$
(22)
$$\begin{aligned}&\sigma _{8}^{\varLambda } = \sigma _{8} \frac{G^{\varLambda }(\bar{z})}{G(\bar{z})} \,, \end{aligned}$$
(23)

where \(E^{\varLambda }(z)\) and \(G^{\varLambda }(z)\) are the corresponding functions in the \(\varLambda \)CDM case (i.e. with \(\alpha =0\)).

From Figure 19 (TT, TE, EE+lowP) of Planck 2015 XIII [14] one can deduce the covariance matrix between \(\varOmega _{m_0}\) and \(\sigma _8\) (we approximate the posterior as Gaussian): \(\sigma _{\varOmega _m}=0.009\), \(\sigma _{\sigma _8}=0.014\), and \(\rho \simeq 0\). Consequently, the \(\chi ^{2}\) function of the CMB prior is

$$\begin{aligned} \chi _\mathrm{cmb}^{2}= & {} \left[ \frac{\varOmega _{m_0}^\mathrm{fid} -\varOmega _{m_0}^{\varLambda }}{\sigma _{\varOmega _m}}\right] ^2 + \left[ \frac{\sigma _{8}^\mathrm{fid} -\sigma _{8}^{\varLambda }}{\sigma _{\sigma _8}}\right] ^2 \,. \end{aligned}$$
(24)

3.4 Full likelihood

The full likelihood is based on the total \(\chi ^{2}\), which is

$$\begin{aligned} \chi _{\mathrm{tot}}^{2}=\chi _\mathrm{SNe}^{2}+\chi _{f\sigma _{8}}^{2} + \chi _\mathrm{cmb}^{2}\,. \end{aligned}$$
(25)

Furthermore, since energy is transferred from \(\rho _m\) to \(\rho _{\mathrm{ar}}\), we adopt the following flat prior on the coupling constant: \(\alpha \ge 0\). Our fiducial model is specified by the following values of the parameters: \(\alpha =0\), \(\varOmega _{m0}=0.3\), and \(\sigma _8=0.8\).

The datasets we consider should give the tightest constraints – at least for the near future – as far as background and perturbation observables are concerned. One way to improve the results of the next section could be to place a low-redshift prior on \(\sigma _8\), for which one has to extend the theory of nonlinear structure formation (mass function, bias, etc.) to the case of the interaction here considered.

4 Results

Figure 2 shows marginalized 1-, 2- and 3\(\sigma \) constraints and correlations on the parameters \(\alpha \), \(\varOmega _{m_0}\), and \(\sigma _8\) using the total likelihood built from the \(\chi ^2\) function of equation (25). The left panel of Fig. 3 shows the marginalized 1- and 2\(\sigma \) constraints on \(\alpha \) and \(\varOmega _{m_0}\) for each of the three individual likelihoods (LSST supernovae, Euclid growth-rate data and Planck prior). It is clear that the strong degeneracy between \(\alpha \) and \(\varOmega _{m_0}\) comes from the supernova likelihood, and that growth data and CMB prior marginally help at constraining \(\varOmega _{m_0}\). At 95% confidence level we find that \(\alpha < 0.035\).

In the analysis of Figs. 2 and 3 (left panel) the starting redshift of \(\bar{z} =5\) has been adopted. In the right panel of Fig. 3 we present constraints on \(\alpha \) and \(\varOmega _{m_0}\) for the case \(\bar{z} =10\). The 95% confidence level constraint on the coupling is now slightly tighter: \(\alpha < 0.03\). As one can see, the results do not depend strongly on \(\bar{z}\). As the processes contributing to the ARB start and take place at different redshifts, the fact that our results do not depend strongly on \(\bar{z}\) means that our modeling and approximations are consistent.

Fig. 3
figure 3

Top marginalized 1- and 2\(\sigma \) constraints on \(\alpha \) and \(\varOmega _{m0}\) for the SN likelihood of (18) (yellow contours), the growth-rate likelihood of (21) (green contours) and the CMB prior of (24) (blue contours). The combination of these constraints give the corresponding panel of Fig. 2. Bottom the dashed empty contours show the constraints on \(\alpha \) and \(\varOmega _{m0}\) for the case \(\bar{z} = 10\). For comparison-sake, the red-to-orange contours from Fig. 2 corresponding to the case \(\bar{z} =5\) are also shown. See Sect. 4 for more details

Full size image

5 Discussion

In order to make contact with astrophysical bounds on the ARB it is useful to express our results not with respect to the coupling constant \(\alpha \) but with respect to the present-day density of astrophysical radiation \(\varOmega _{\mathrm{ar}_0}\). Using Eq. (12) it is easy to make this change of variable and obtain from the results of the previous section that, at the 95% confidence level, it is \(\varOmega _{\mathrm{ar}_0}<0.008\). The latter constraint depends weakly on \(\bar{z}\).

The total extra galactic background light (EBL) has a density parameter of the order of \(\varOmega _\mathrm{ebl} \sim 5 \times 10^{-6}\), roughly a factor 10 times smaller than the density parameter relative to the CMB photons [2].

Regarding the stochastic gravitational-wave background, one usually defines the density parameter \(\varOmega _\mathrm{gw}(f)\) within the logarithmic frequency interval between f and \(f+\mathrm{d}f\). For \(f<100\) Hz the spectrum is well approximated by a power law, \(\varOmega _\mathrm{gw}(f)\propto f^{2/3}\), while for \(f>100\) Hz it quickly drops. Using the normalization \(\varOmega _\mathrm{gw} (f=25 \text { Hz}) \sim 10^{-9}\) [20] one can then integrate \(\varOmega _\mathrm{gw}(f)\) and obtain \(\varOmega _\mathrm{gw}\sim 5 \times 10^{-9}\). The latter estimate only considers gravitational waves from binary black holes. Therefore, the total energy density in the stochastic gravitational-wave background is somewhat larger, see [21, 22] for a comprehensive reviews. If a fraction of dark matter is made of primordial black holes, one would expect an additional gravitational-wave background coming from their stochastic mergers [5,6,7]. However, this background is supposed to be subdominant as compared to the one produced by black holes which were the result of star formation and evolution [23]. Moreover, the merger rate of primordial black holes is not negligible in the past, contrary to our assumption that \(\alpha =0\) for \(z \ge \bar{z}\).

A sizable contribution to the ARB comes from the diffuse supernova neutrino background (DSNB). The cosmic energy density in neutrinos from core-collapse supernovae is expected to be comparable to that in photons from stars [3]. Indeed, one single core-collapse supernova produces \({\sim } 3 \times 10^{53}\) erg in MeV neutrinos and such supernovae occur approximately every 100 years in the Milky Way. One can then conclude that the average neutrino power of our Galaxy is \({\sim }10^{44}\) erg/s, similar to its IR-optical luminosity.Footnote 3 One can then estimate that \(\varOmega _\mathrm{dsnb} \sim 5 \times 10^{-6}\).

Finally, as discussed in the Introduction, backreaction could contribute to the ARB at not-well understood rates [9]. Summing up, one expects the ARB to have a density parameter of the order of \(\varOmega _{\mathrm{ar}_0}\sim 10^{-5}\).

6 Conclusions

We have computed how well future cosmological observations can constrain the energy density of the astrophysical radiation background (ARB). ARB is the (to a first approximation) uniform radiation density produced during the process of structure formation in the recent universe. We modeled the energy transfer from matter to radiation through an effective interaction between matter and astrophysical radiation, which is set to be zero at a redshift of about 5–10. Using forecasted supernovas from the LSST and growth-rate data from Euclid we found that the coupling constant \(\alpha \) is constrained to be \(\alpha < 0.035\) and the present-day density of astrophysical radiation to be \(\varOmega _{\mathrm{ar}_0}<0.008\) (both at the 95% confidence level).

Estimates of the energy density produced by well-known astrophysical processes give roughly \(\varOmega _{\mathrm{ar}_0}\sim 10^{-5}\), almost three orders of magnitude smaller than the upper limit that can be obtained with LSST and Euclid. Therefore, we conclude that cosmological observations will be able to constrain only exotic not-well understood sources of radiation such as the backreaction of small-scale inhomogeneities on the dynamics of the universe.