Semileptonic decays of $B_c$ meson to S-wave charmonium states in the perturbative QCD approach

Abstract

Inspired by the recent measurement of the ratio of $B_c$ branching fractions to $J/\psi \pi ^+$ and $J/\psi \mu ^+\nu _{\mu }$ final states at the LHCb detector, we study the semileptonic decays of $B_c$ meson to the S-wave ground and radially excited 2S and 3S charmonium states with the perturbative QCD approach. After evaluating the form factors for the transitions $B_c\rightarrow P,V$, where P and V denote pseudoscalar and vector S-wave charmonia, respectively, we calculate the branching ratios for all these semileptonic decays. The theoretical uncertainty of hadronic input parameters are reduced by utilizing the light-cone wave function for the $B_c$ meson. It is found that the predicted branching ratios range from $10^{-7}$ up to $10^{-2}$ and could be measured by the future LHCb experiment. Our prediction for the ratio of branching fractions $\frac{\mathcal {BR}(B_c^+\rightarrow J/\Psi \pi ^+)}{\mathcal {BR}(B_c^+\rightarrow J/\Psi \mu ^+\nu _{\mu })}$ is in good agreement with the data. For $B_c\rightarrow V l \nu _l$ decays, the relative contributions of the longitudinal and transverse polarization are discussed in different momentum transfer squared regions. These predictions will be tested on the ongoing and forthcoming experiments.

1 Introduction

Recently, the LHCb Collaboration has measured the semileptonic and hadronic decay rates of the $B_c$ meson and obtained $\frac{\mathcal {BR}(B_c^+\rightarrow J/\Psi \pi ^+)}{\mathcal {BR}(B_c^+\rightarrow J/\Psi \mu ^+\nu _{\mu })}=0.0469\pm 0.0028(\mathrm{stat})\pm 0.0046(\mathrm{syst})$ [1]. It is a motivation to investigate the $B_c$ meson semileptonic decays to charmonium, which are easier to identify in experiment. Indeed, both the CDF and the D0 Collaboration have measured the lifetime of the $B_c$ meson through its semileptonic decays [2–4]. More recently, the LHCb Collaboration gave a more precise measurement of its lifetime using semileptonic $B_c\rightarrow J/\psi \mu \nu _{\mu } X$ decays [5], where X denotes any possible additional particles in the final states. At the quark level, the semileptonic decays of the $B_c$ meson driven by a $b\rightarrow c$ transitions, where the effects of the strong interaction can be separated from the effects of the weak interaction into a set of Lorentz-invariant form factors. It may provide us with the information as regards the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements $V_{cb}$ and the weak $B_c$ to charmonia transition form factors.

There are many theoretical approaches to the calculation of $B_c$ meson semileptonic decays to charmonium. Some of them are: the nonrelativistic QCD [6, 7], the Bethe–Salpeter relativistic quark model [8], the relativistic quark model [9–11], the light-cone QCD sum rules approach [12, 13], the covariant light-front model [14], the nonrelativistic quark model [15], the QCD potential model [16–18], and the light-front quark model [19]. The perturbative QCD (pQCD) [20, 21] is one of the recently developed theoretical tools based on QCD to deal with the nonleptonic and semileptonic B decays. So far the semileptonic $B_{u,d,s,c}$ decays have been studied systematically in the pQCD approach [22–25]. One may refer to the review paper [26] and the references therein.

Fig. 1

The leading-order Feynman diagrams for the semileptonic decays $B^+_c\rightarrow P/V l^+ \nu _l$ with $l=(e,\mu ,\tau )$

In our previous work [27, 28], we analyzed the two-body nonleptonic decays of the $B_c$ meson with the final states involving one S-wave charmonium using the perturbative QCD based on $k_T$ factorization. By using the harmonic-osillator wave functions for the charmonium states, the obtained ratios of the branching fractions are consistent with the data and other studies. Especially some of our predictions were well tested by the recent experiments at ATLAS [29] and LHCb [30], which may indicate that the harmonic-oscillator wave functions for S-wave charmonium work well.

In this paper, we extend our previous pQCD analysis to the semileptonic $B_c$ decay such as $B_c\rightarrow (\eta _c(nS), \psi (nS))l \nu$ (here l stands for the leptons e, $\mu$, and $\tau$) with the radial quantum number $n=1,2,3$, while the higher 4S charmonia are not included here since their properties are still not understood well. The semileptonic decays $B_c\rightarrow (J/\psi ,\eta _c)l \nu$ have been studied in pQCD [31], compared to which the new ingredients of this paper are the following.

(1) Instead of the traditional zero-point wave function for the $B_c$ meson, the light-cone wave function which was well developed in Ref. [32] is employed in order to reduce the uncertainties caused by the hadronic parameters. In addition, the charmonium distribution amplitudes are also extracted from the correspond Schrödinger states for the harmonic-oscillator potential. (2) Here, the momentum of the spectator charm quark is proportional to the corresponding meson momentum. In Ref. [31], the charm quark in the $B_c$ meson carries a momentum with only the minus component. That is, its invariant mass vanishes, while the charm quark in the final states is proportional to the charmonium meson momentum and its invariant mass does not vanish. This substantial revision will render our analysis more consistent. (3) We updated some input hadronic parameters according to the Particle Data Group 2014 [33]. (4) Besides including the $B_c\rightarrow (J/\psi , \eta _c) l \nu$ decays, the $B_c\rightarrow P/V(2S,3S) l \nu$ decays are also investigated, where it is theoretically easier compared with that of nonleptonic decays. Our goal is to provide a ready reference to the existing and forthcoming experiments to compare their data with the predictions in the pQCD approach.

The paper is organized as follows. In Sect. 2 we define kinematics and describe the wave functions of the initial and final states, while the analytic expressions for the transition form factors and the differential decay rate of the considered decay modes are given in Sect. 3. The numerical results and relevant discussions are given in Sect. 4. The final section is the conclusion. The evaluation of the 3S charmonium distribution amplitudes is relegated to the appendix.

2 Kinematics and the wave functions

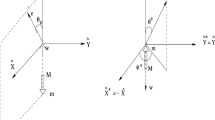
It is convenient to work at the $B_c$ meson rest frame and the light cone coordinate. The $B_c$ meson momentum $P_1$ and the charmonium meson momentum $P_2$ are chosen as [34]

$$\begin{aligned} P_1=\frac{M}{\sqrt{2}}(1,1,\mathbf 0 _{T}),\quad P_2=\frac{M}{\sqrt{2}}(r\eta ^+,r\eta ^-,\mathbf 0 _{T}), \end{aligned}$$

(1)

with the ratio $r=m/M$ and m(M) is the mass of the charmonium ($B_c$) meson. The factors $\eta ^{\pm }=\eta \pm \sqrt{\eta ^2-1}$ come with the definition of the $\eta$ of the form [34]

$$\begin{aligned} \eta =\frac{1+r^2}{2r}-\frac{q^2}{2rM^2}, \end{aligned}$$

(2)

with the momentum transfer $q=P_1-P_2$. When the final state is a vector meson, the longitudinal and transverse polarization vector $\epsilon _{L,T}$ can be written as

$$\begin{aligned} \epsilon _L=\frac{1}{\sqrt{2}}(\eta ^+,-\eta ^-,\mathbf 0 _{T}),\quad \epsilon _T=(0,0,1). \end{aligned}$$

(3)

The momentum of the valence quarks $k_{1,2}$, whose notation is displayed in Fig. 1, is parametrized as

$$\begin{aligned} k_1= & {} \left( x_1\frac{M}{\sqrt{2}},x_1\frac{M}{\sqrt{2}},\mathbf k _{1T}\right) ,\quad \nonumber \\ k_2= & {} \left( \frac{M}{\sqrt{2}}x_2r\eta ^+,\frac{M}{\sqrt{2}}x_2r\eta ^-,\mathbf k _{2T}\right) , \end{aligned}$$

(4)

the $k_{1T,2T}$, $x_{1,2}$ represent the transverse momentum and longitudinal momentum fraction of the charm quark inside the meson, respectively. One should note that there is no end-point singularity in the $B_c$ meson decays and the integral is still convergent without the parton transverse momentum $k_{1T}$ of $B_c$ meson in the collinear factorization. However, we here still keep it to suppress some non-physical contributions near the singularity (for example the singularity at $x_1=0.1923$ for $B_c\rightarrow J/\psi$ decay).

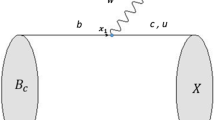
There are three typical scales of the $B_c$ to charmonium decays: M, m, and the heavy-meson and heavy-quark mass difference $\bar{\Lambda }$. These three scales allow for a consistent power expansion in m / M and in $\bar{\Lambda }/m$ under the hierarchy of $M\gg m \gg \bar{\Lambda }$. In the heavy-quark and large-recoil limits, based on the $k_T$ factorization theorem, the corresponding form factors can be expressed as the convolution of the hard amplitude with $B_c$ and charmonium meson wave functions. The hard amplitude can be treated by perturbative QCD at the leading order in an $\alpha _s$ expansion (single gluon exchange as depicted in Fig. 1). The higher-order radiative corrections generate the logarithm divergences, which can be absorbed into the meson wave functions. One also encounters double logarithm divergences when collinear and soft divergences overlap, which can be summed to all orders to give a Sudakov factor. After absorbing all the soft dynamics, the initial and final state meson wave functions can be treated as nonperturbative inputs, which are not calculable but universal.

Similar to the situation of the B meson [35], under above hierarchy, at leading order in 1 / M, the $B_c$ meson light-cone matrix element can be decomposed as [36–40]

(5)

with the unit vectors $v=(0,1,0_T)$ on the light cone. Here, we only consider the contribution from $\Phi _{B_c}$, while the contribution of $\bar{\Phi }_{B_c}$ starting from the next-to-leading-power $\bar{\Lambda }/M$ is numerically neglected [41, 42]. In coordinate space $\Phi _{B_c}$ can be expressed by

(6)

The distribution amplitude $\phi _{B_c}$ is adopted in the form [32]

$$\begin{aligned} \phi _{B_c}(x)=N x(1-x)\exp \left[ -\frac{m_b+m_c}{8m_bm_c \omega }\left( \frac{m_c^2}{x}+\frac{m_b^2}{1-x}\right) \right] ,\nonumber \\ \end{aligned}$$

(7)

with shape parameters $\omega =0.5\pm 0.1$ GeV and the normalization conditions

$$\begin{aligned} \int _0^1\phi _{B_c}(x)\mathrm{d}x=1. \end{aligned}$$

(8)

N is the normalization constant.

For the charmonium meson, because of its large mass, the higher-twist contributions are important. The light-cone wave functions are obtained in powers of m / E or $\bar{\Lambda }/E$ where $E(\approx M)$ is the energy of the charmonium meson. In terms of the notation in Ref. [43], we decompose the nonlocal matrix elements for the longitudinally and transversely polarized vector mesons ($V=J/\psi , \psi (2S), \psi (3S)$) and pseudoscalar mesons ($P=\eta _c, \eta _c(2S), \eta _c(3S)$) into

(9)

respectively. For the distribution amplitudes of the 1S and 2S states, the same form and parameters are adopted as in [27, 28]. The distribution amplitudes of 3S states will be derived in the appendix.

3 Form factors and semileptonic differential decay rates

The two factorizable emission Feynman diagrams for the semileptonic $B_c$ decays are given in Fig. 1. The transition form factors, $F_+(q^2)$, $F_0(q^2)$, $V(q^2)$, and $A_{0,1,2}(q^2)$ are defined via the matrix element [44, 45],

$$\begin{aligned}&\langle P(P_2)|\bar{c}\gamma ^{\mu }b|B_c(P_1)\rangle =\left[ (P_1+P_2)^{\mu } \right. \nonumber \\&\left. \quad -\;\frac{M^2-m^2}{q^2}q^{\mu }\right] F_+(q^2) +\frac{M^2-m^2}{q^2}q^{\mu }F_0(q^2), \end{aligned}$$

(10)

$$\begin{aligned} \langle V(P_2)|\bar{c}\gamma ^{\mu }b|B_c(P_1)\rangle =\frac{2iV(q^2)}{M+m}\epsilon ^{\mu \nu \rho \sigma } \epsilon ^*_{\nu }P_{2\rho }P_{1\sigma }, \end{aligned}$$

(11)

$$\begin{aligned}&\langle V(P_2)|\bar{c}\gamma ^{\mu }\gamma _5b|B_c(P_1)\rangle =2mA_0(q^2)\frac{\epsilon ^*\cdot q}{q^2}q^{\mu } \nonumber \\&\quad + (M+m)A_1(q^2)\left[ \epsilon ^{*\mu }-\frac{\epsilon ^*\cdot q}{q^2}q^{\mu }\right] \nonumber \\&\quad -A_2(q^2)\frac{\epsilon ^*\cdot q}{M+m}\left[ (P_1+P_2)^{\mu }-\frac{M^2-m^2}{q^2}q^{\mu }\right] , \end{aligned}$$

(12)

with $\epsilon ^{0123}=+1$. In the large-recoil limit ($q^2=0$), the following relations should hold to cancel the poles:

$$\begin{aligned} F_0(0)=F_+(0),\quad A_0(0)=\frac{1+r}{2r}A_1(0)-\frac{1-r}{2r}A_2(0).\nonumber \\ \end{aligned}$$

(13)

In the pQCD framework, it is convenient to compute the other equivalent auxiliary form factors $f_1(q^2)$ and $f_2(q^2)$, which are related to $F_+(q^2)$ and $F_0(q^2)$ by [31]

$$\begin{aligned} F_+= & {} \frac{1}{2}(f_1+f_2),\nonumber \\ F_0= & {} \frac{1}{2}f_1\left[ 1+\frac{q^2}{M^2-m^2}\right] +\frac{1}{2}f_2\left[ 1-\frac{q^2}{M^2-m^2}\right] .\nonumber \\ \end{aligned}$$

(14)

Following the derivation of the factorization formula for the $B\rightarrow P$, $B\rightarrow V$ transitions [46], we obtain these form factors as follows:

$$\begin{aligned}&f_1(q^2)=4 \sqrt{\frac{2}{3}} \pi M^2 f_B C_f r \int _0^1\mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\quad \times \int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\quad \times [\psi ^L(x_2,b_2) r(x_2-1)-\psi ^t(x_2,b_2)(r_b-2)] \nonumber \\&\quad \times E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&\quad - [\psi ^L(x_2,b_2)(r-2\eta x_1)+\psi ^t(x_2,b_2)2(x_1-r_c)] \nonumber \\&\quad \times E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1), \end{aligned}$$

(15)

$$\begin{aligned}&f_2(q^2)=4 \sqrt{\frac{2}{3}} \pi M^2 f_B C_f \int _0^1\mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\quad \times \int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\quad \times [\psi ^L(x_2,b_2)(2r_b-1-2r\eta (x_2-1)) \nonumber \\&\quad +\psi ^t(x_2,b_2)2r(x_2-1)]E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&\quad -[\psi ^L(x_2,b_2)(r_c+x_1)-\psi ^t(x_2,b_2)2r] \nonumber \\&\quad \times E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1), \end{aligned}$$

(16)

$$\begin{aligned} A_0(q^2)= & {} -2 \sqrt{\frac{2}{3}} \pi M^2 f_B C_f \int _0^1\mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\times \;\int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\times \;[\psi ^L(x_2,b_2) \left( 1-2 r_b-r(x_2-1)(r-2\eta )\right) \nonumber \\&-\psi ^t(x_2,b_2)r \left( 2 x_2-r_b\right) ]E_{ab}(t_a)\nonumber \\&\times h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&- \psi ^L(x_2,b_2)[r_c+r^2+x_1(1-2r\eta )] \nonumber \\&\times E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1), \end{aligned}$$

(17)

$$\begin{aligned} A_1(q^2)= & {} 4 \sqrt{\frac{2}{3}}\frac{r}{1+r} \pi M^2 f_B C_f\int _0^1\mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\times \int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\times [\psi ^V(x_2,b_2) \left( -2 r_b+\eta r (x_2-1)+1\right) \nonumber \\&+\;\psi ^T(x_2,b_2)[\eta r_b-2 (\eta +r (x_2-1))]]\nonumber \\&\times \;E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&-\;\psi ^V(x_2,b_2)[r_c-x_1+\eta r] \nonumber \\&\times E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1), \end{aligned}$$

(18)

$$\begin{aligned} A_2(q^2)= & {} -A_1\frac{(1+r)^2(r-\eta )}{2r(\eta ^2-1)}-2 \pi M^2 f_B C_f\sqrt{\frac{2}{3}}\frac{1+r}{\eta ^2-1} \nonumber \\&\times \int _0^1\mathrm{d}x_1\mathrm{d}x_2\int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\times [\psi ^t(x_2,b_2)(r_b (1-\eta r)+2 r^2 (x_2-1) \nonumber \\&-2 \eta r (x_2-2)-2)\nonumber \\&-\psi ^L(x_2,b_2)(2 r_b (\eta -r)-\eta +r (\eta r (x_2-1) \nonumber \\&-2 \eta ^2 (x_2-1)+x_2))] \nonumber \\&\times E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&+\psi ^L(x_2,b_2)[r_c (r-\eta )+\eta r^2 \nonumber \\&+r \left( -2 \eta ^2 x_1+x_1-1\right) +\eta x_1] \nonumber \\&\times E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1), \end{aligned}$$

(19)

$$\begin{aligned} V(q^2)= & {} 2\sqrt{\frac{2}{3}}\pi M^2 f_B C_f (1+r) \nonumber \\&\times \int _0^1\mathrm{d}x_1\mathrm{d}x_2\int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2\phi _{B_c}(x_1)\nonumber \\&\times [\psi ^V(x_2,b_2) r\left( 1-x_2\right) +\psi ^T(x_2,b_2)(r_b-2)] \nonumber \\&\times E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&-\psi ^V(x_2,b_2)rE_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1),\nonumber \\ \end{aligned}$$

(20)

with $r_{b,c}=\frac{m_{b,c}}{M}$. $\alpha _e$ and $\beta _{a,b}$ are the virtuality of the internal gluon and quark, respectively. Their expressions are

$$\begin{aligned} \alpha _e= & {} -M^2[x_1+\eta ^+r(x_2-1)][x_1+\eta ^-r(x_2-1)],\nonumber \\ \beta _{a}= & {} m_b^2-M^2[1+\eta ^+r(x_2-1)][1+\eta ^-r(x_2-1)],\nonumber \\ \beta _{b}= & {} m_c^2-M^2[\eta ^+r-x_1][\eta ^-r-x_1]. \end{aligned}$$

(21)

The explicit expressions of the functions $E_{ab}$, the scales $t_{a,b}$, and the hard functions h are referred to [27]. In fact, if we take $q^2\rightarrow 0$, these expressions are agree with the results in Ref. [28]. At the quark level, the charged current $B_c\rightarrow P(V)l \nu$ decays occur via the $b\rightarrow c l \nu _l$ transition. The effective Hamiltonian for the $b\rightarrow c l \nu _l$ transition is written as [47]

$$\begin{aligned} \mathcal {H}_\mathrm{eff}=\frac{G_F}{\sqrt{2}}V^*_{cb}\bar{b}\gamma _{\mu } (1-\gamma _5)c\otimes \bar{\nu _l}\gamma ^{\mu }(1-\gamma _5)l, \end{aligned}$$

(22)

where $G_F=1.16637 \times 10^{-5} \mathrm{GeV}^{-2}$ is the Fermi coupling constant and $V_{cb}$ is one of the CKM matrix elements.

Table 1 The values of the input parameters for numerical analysis. The tensor decay constant $f^{T}_V$ are determined through the assumption $f^T_V m_V=2 f_V m_c$, which has been used in [48]

The differential decay rate of $B_c\rightarrow P l \nu$ reads [14]

$$\begin{aligned}&\frac{\mathrm{d}\Gamma }{\mathrm{d}q^2}(B_c\rightarrow P l \nu )=\frac{G_F^2|V_{cb}|^2}{384\pi ^3M^3q^2}\sqrt{\lambda (q^2)} \left( 1-\frac{m_l^2}{q^2}\right) ^2 \nonumber \\&\quad \times \; [3m_l^2(M^2-m^2)^2|F_0(q^2)|^2\nonumber \\&\quad + \;(m_l^2+2q^2)\lambda (q^2)|F_+(q^2)|^2], \end{aligned}$$

(23)

where $m_l$ is the mass of the leptons and $\lambda (q^2)=(M^2+m^2-q^2)^2-4M^2m^2$. Since the electron and muon are very light compared with the charm quark, we can safely neglect the masses of these two kinds of leptons in the analysis. For the channel of $B_c\rightarrow V l \nu$, the decay rates in the transverse and longitudinal polarization of the vector charmonium can be formulated as [14]

$$\begin{aligned}&\frac{\mathrm{d}\Gamma _{\pm }}{\mathrm{d}q^2}(B_c\rightarrow V l \nu )=\frac{G_F^2|V_{cb}|^2}{384\pi ^3M^3}\lambda ^{3/2}(q^2) \left( 1-\frac{m_l^2}{q^2}\right) ^2 \nonumber \\&\quad \times (m_l^2+2q^2)\left[ \frac{V(q^2)}{M+m} \mp \frac{(M+m)A_1(q^2)}{\sqrt{\lambda (q^2)}}\right] ^2,\nonumber \\&\frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^2}(B_c\rightarrow V l \nu )=\frac{G_F^2|V_{cb}|^2}{384\pi ^3M^3q^2}\sqrt{\lambda (q^2)} \left( 1-\frac{m_l^2}{q^2}\right) ^2\nonumber \\&\quad \times \left\{ 3m_l^2\lambda (q^2)A_0^2(q^2) +\frac{m_l^2+2q^2}{4m^2}\left[ (M^2\right. \right. \nonumber \\&\left. \left. \quad \times -m^2-q^2)(M+m) A_1(q^2)- \frac{\lambda (q^2)}{M+m}A_2(q^2)\right] ^2\right\} .\nonumber \\ \end{aligned}$$

(24)

The combined transverse and total differential decay widths are defined as

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^2}=\frac{\mathrm{d}\Gamma _{+}}{\mathrm{d}q^2}+ \frac{\mathrm{d}\Gamma _{-}}{\mathrm{d}q^2},\quad \frac{\mathrm{d}\Gamma }{\mathrm{d}q^2}=\frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^2}+ \frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^2}. \end{aligned}$$

(25)

4 Numerical results and discussions

In our calculations, some parameters are used as inputs, which are listed in Table 1.

As known, the pQCD results of these form factors are reliable only in the small $q^2$ region. For the form factors in the large $q^2$ region, the fast rise of the pQCD results indicates that the perturbative calculation gradually becomes unreliable. In order to extend our results to the whole physical region, we first perform the pQCD calculations to these form factors in the lower $q^2$ region ($q^2\in (0,\xi (M-m)^2)$ with $\xi =0.2(0.5)$ for the $B_c\rightarrow 1S(2S/3S)$ transition), and then we make an extrapolation for them to the larger $q^2$ region ($q^2\in (\xi (M-m)^2,(M-m)^2)$). There exist in the literature several different approaches for extrapolating the form factors from the small $q^2$ region to the large $q^2$ region. The three-parameter form is one of the pervasive models, where the fit function is chosen as

$$\begin{aligned} \mathcal {F}_i(q^2)=\mathcal {F}_i(0)\exp \left[ a\frac{q^2}{M^2}+b\left( \frac{q^2}{M^2}\right) ^2\right] , \end{aligned}$$

(26)

where $\mathcal {F}_i$ denotes any of the form factors, and a, b are the fitted parameters.

Table 2 The fit parameters a, b, and the pQCD predictions of $F_{0,+}(0)$, $A_{0,1,2}(0)$, and V(0) for $B_c\rightarrow nS(n=1,2,3)$ decays, where the uncertainties come from the hadronic parameters including shape parameters $\omega$ in the initial and final state wave functions and charm-quark mass $m_c$, decay constants, and the hard scale t, respectively

Our results of the transition form factors at the scale $q^2=0$ together with the fitted parameters a, b are collected in Table 2, where the theoretical uncertainties are estimated including three aspects.

The first kind of uncertainties is from the shape parameters $\omega$ in the initial and final states and the charm-quark mass $m_c$. In the evaluation, we vary the values of $\omega$ within a 20 % range and $m_c=1.275$ GeV by $\pm 0.025$  GeV. We find that, in this work, the form factors are less sensitive to these hadronic parameters than our previous studies [27, 28]. For example, the error induced by $m_c$ is just a few percent here, while in Ref. [28] this can reach 10–20  %. This can be understood from the $B_c$ meson wave function. In Ref. [28], the $\delta$ function depends strongly on the mass of charm quark which results in a relative large uncertainty. The second error comes from the decay constants of the final charmonium meson, which are shown in Table 1. Due to the low accuracy measurement of the decay width of the double photons decay of the pseudoscalar charmonia, the relevant uncertainty of $F_{0.+}$ is large. The last one is caused by the variation of the hard scale from 0.75 to 1.25 t. Most of this uncertainty is less than $10\%$, which means the next-to-leading-order contributions can be safely neglected. The errors from the uncertainty of the CKM matrix elements are very small, and they have been neglected.

It shows that the $B_c\rightarrow P/V(1S, 2S)$ transition form factors are a bit larger than our previous calculations [27, 28]. It is because, here, instead of the traditional zero-point wave function, we have used the light-cone wave function for the $B_c$ meson [32]. The shape of the leading twist distribution amplitude of the $B_c$ meson together with the final S-wave charmonium states are displayed in Fig. 2. It is easy to see that the dashed line is broader in shape than that of the zero-point wave function ($\phi _{B_c}(x)\propto \delta (x-r_c)$). The overlap between the initial and final state wave functions becomes larger in this work, which certainly induces larger form factors. We also can see that the form factors of the $B_c$ weak transitions to the 2S charmonium states at zero momentum transfer are comparable with the corresponding values of $B_c$ decays to the 1S charmonium states in Table 2. Since one of the peaks of the 2S charmonium states wave function is so close to the peak of the $B_c$ meson wave function, the overlaps between them are large, which enhances the values of the $B_c\rightarrow P/V(2S)$ form factors. However, due to the presence of the nodes in the 3S states wave function and the smaller decay constants, the corresponding form factors of the $B_c$ decays to the 3S states are slightly suppressed.

Fig. 2

The overlap of the leading twist distribution amplitudes of the initial and final state at $b=0$. Dashed, dotted, solid and short dash dotted lines correspond to $B_c$, 1S, 2S, and 3S states, respectively

Fig. 3

Form factors of the $B_c$ decays to the S-wave charmonium states defined as in Eq. (26). The left panel is for the $B_c\rightarrow P$ processes, while the right panel for $B_c\rightarrow V$ processes

We plot the $q^2$ dependence of the weak form factors with center values without theoretical uncertainties in Fig. 3 for the six decay processes in their physical kinematic range. We can see the different $q^2$ dependence of the form factors among the $B_c$ decays to different S-wave charmonia clearly. For example, the form factors for the $B_c\rightarrow P/V(1S)$ transition have a relatively strong $q^2$ dependence, but those of the $B_c\rightarrow P/V(2S/3S)$ transition show a little weaker $q^2$ dependence. In addition, most of these form factors become larger with increasing $q^2$. However, this behavior is not universal. For instance, from Fig. 3 some of the form factors for $B_c\rightarrow P/V(2S/3S)$ decays decreases with the increasing $q^2$ in the large region. A similar situation also exists in the light-front quark model [19] and in the ISGW2 quark model [49]. This behavior of the difference for the corresponding final states is the consequence of their different nodal structure in the wave functions.

Table 3 Branching ratios (in units of %) of $B_c\rightarrow P/Vl\nu _l$ decays evaluated by pQCD and by other methods in the literature. The errors induced by the same sources as in Table 2

Table 4 Some of the ratios among the branching fractions of the $B_c$ decays in comparison with the data and other theoretical estimates, Here l stands for $l=e,\mu$. The errors correspond to the combined uncertainty in the hadronic parameters, decay constants, and the hard scale

Integrating the expressions in Eqs. (23) and (24) over the variable $q^2$ in the physical kinematical region, one obtains the relevant decay widths. Then it is straightforward to calculate the branching ratios. The results of our evaluation of the branching ratios for all the considered decays appear in Table 3 in comparison with predictions of other approaches. For the $B_c\rightarrow P/V(1S)$ decays, our results are comparable to those of [6, 7] within the error bars, but larger than the results from other models due to the values of the weak form factors.

For the $B_c\rightarrow P/V(2S,3S)$ decays our predictions are generally close to the light-cone QCD sum rules results of [12]. However, the relativistic quark model predictions for the $B_c\rightarrow P/V(3S)$ decays in Refs. [9, 10] are typically smaller, which can be discriminated by the future LHC experiments.

From Table 3, we can see the former four processes have a relatively large branching ratio ($10^{-2}$), while the branching ratios of the last four processes are comparatively small ($10^{-7}\sim 10^{-3}$). They have the following hierarchy:

$$\begin{aligned} \mathcal {BR}(B_c\rightarrow P/V (3S))<&\mathcal {BR}(B_c\rightarrow P/V (2S)) \nonumber \\< & {} \mathcal {BR}(B_c\rightarrow P/V(1S)). \end{aligned}$$

(27)

This is due to the tighter phase space, smaller decay constants, and the less sensitive dependence of the form factors on the momentum transfer $q^2$ for the higher excited state, which can be seen in Fig. 3. The combined effect above suppresses the branching ratios of the semileptonic $B_c$ decays to radially excited charmonia. For decays to higher charmonium excitations such a suppression should be more pronounced. In order to reduce the theoretical uncertainties from the hadronic parameters and the decay constants, we defined six ratios between the electron and tau branching ratios, i.e.

$$\begin{aligned} \mathcal {R}(P/V)=\frac{\mathcal {BR}(B_c^+\rightarrow P/V e^+ \nu _e)}{\mathcal {BR}(B_c^+\rightarrow P/V \tau ^+\nu _{\tau })}. \end{aligned}$$

(28)

From our numerical values listed in Table 3, we obtain

$$\begin{aligned}&\mathcal {R}(J/\psi ) =3.4^{+0.1}_{-0.1},\quad \mathcal {R}(\psi (2S)) =14.3^{+0.9}_{-1.4},\nonumber \\&\mathcal {R}(\psi (3S)) =947.4^{+71.1}_{-0.0},\nonumber \\&\mathcal {R}(\eta _c) =1.6^{+0.0}_{-0.0},\quad \mathcal {R}(\eta _c(2S)) =14.5^{+0.0}_{-0.3},\nonumber \\&\mathcal {R}(\eta _c(3S)) =736.8^{+21.8}_{-9.5}, \end{aligned}$$

(29)

where the errors correspond to the combined uncertainty in the hadronic parameters, decay constants, and the hard scale. Since these parameter dependences canceled out in Eq. (28), the total theoretical errors of these ratios are only a few percent, much smaller than those for the branching ratios. In general, these ratios are of the same order of magnitude in the different approaches except the light-cone QCD sum rules [12], where it is obtained the smallest values of $\mathcal {R}(\eta _c(3S))=33.3$.

For a more direct comparison with the available experimental data [1], we need to recalculate some of the nonleptonic $B_c$ decays by using the same wave functions and input parameters as this paper, whose results are

$$\begin{aligned}&\mathcal {BR}(B^+_c\rightarrow J/\psi \pi ^+)=2.6^{+0.6+0.2+0.8}_{-0.4-0.2-0.2}\times 10^{-3}, \nonumber \\&\mathcal {BR}(B^+_c\rightarrow \eta _c \pi ^+)=5.2^{+1.3+1.3+1.8}_{-0.6-1.2-0.2} \times 10^{-3},\nonumber \\&\mathcal {BR}(B^+_c\rightarrow \psi (2S) \pi ^+)=8.2^{+2.1+0.2+2.7}_{-2.4-0.1-0.7} \times 10^{-4}, \nonumber \\&\mathcal {BR}(B^+_c\rightarrow \eta _c(2S) \pi ^+)=1.3^{+0.5+0.9+0.7}_{-0.1-0.9-0.0} \times 10^{-3},\nonumber \\&\mathcal {BR}(B^+_c\rightarrow \psi (3S) \pi ^+)=4.8^{+2.0+0.5+1.5}_{-1.7-0.5-0.3} \times 10^{-4}, \nonumber \\&\mathcal {BR}(B^+_c\rightarrow \eta _c(3S) \pi ^+)=1.4^{+0.4+0.4+0.4}_{-0.5-0.4-0.1} \times 10^{-3}, \end{aligned}$$

(30)

where the errors induced by the same sources as in Table 2.

Table 5 The partial branching ratios and polarizations $\frac{\Gamma _L}{\Gamma _T}$ of $B_c\rightarrow V l\nu _l$ decays in different $q^2$ regions

The ratios among the branching fractions are shown explicitly in Table 4, from which we can see that the ratios $\frac{\mathcal {BR}(B_c^+\rightarrow J/\psi \pi ^+)}{\mathcal {BR}(B_c^+\rightarrow J/\psi l^+\nu _{l})}$ and $\frac{\mathcal {BR}(B_c^+\rightarrow \psi (2S) \pi ^+)}{\mathcal {BR}(B_c^+\rightarrow J/\psi \pi ^+)}$ are well consistent with the recent data [1, 30], and also comparable with the prediction of the NRQCD [6, 7]. Furthermore the latter still agree with the previous pQCD calculations [28] 0.29, although both $\mathcal {BR}(B_c^+\rightarrow \psi (2S) \pi ^+)$ and $\mathcal {BR}(B_c^+\rightarrow J/\psi \pi ^+)$ are enhanced compared with the corresponding values of [27, 28].

We now investigate the relative importance of the longitudinal ($\Gamma _L$) and transverse ($\Gamma _T$) polarizations contributions to the branching ratios of $B_c\rightarrow V l\nu _l$ decays within Region (1), Region (2), and the whole physical region, whose results and the ratios $\frac{\Gamma _L}{\Gamma _T}$ are displayed separately in Table 5. For light electron and muon, the regions are defined as: Region (1): $0<q^2<(M-m)^2/2$; Region (2): $(M-m)^2/2<q^2<(M-m)^2$. For the heavy lepton $\tau$, The first region is $m^2_{\tau }<q^2<[(M-m)^2+m^2_{\tau }]/2$ while the second region is $[(M-m)^2+m^2_{\tau }]/2<q^2<(M-m)^2$. From Table 5, all of $\frac{\Gamma _L}{\Gamma _T}$ are $<1$ in Region (2), which means that the transverse polarization dominates the branching ratios in this region. It can be understood as follows. For the $B_c\rightarrow 1S,2S$ decays, the form factor V as shown in Fig. 3 increase as the $q^2$ increases, which enhances the transverse polarization contribution in the large $q^2$ region, while for the $B_c\rightarrow 3S$ decay, although the value of V decreases gradually with increasing $q^2$, the form factor $A_1$, which gives a dominant contribution to $\Gamma _L$, is significantly suppressed in the large region, and as a results the dominant contributions to the branching ratios of $B_c\rightarrow \psi (2S)$ decays come from Region (1).

For $B_c\rightarrow \psi (2S,3S)e\nu _e$ decays $\Gamma _L$ is comparable with $\Gamma _T$ in the whole physical region. These results will be tested by LHCb and the forthcoming Super-B experiments.

5 Conclusion

We calculate the transition form factors and obtain the branching ratios of the semileptonic decays of $B_c$ meson to S-wave charmonium states by employing the pQCD factorization approach. By using the light-cone wave function for the $B_c$ meson, the theoretical uncertainties from the nonperturbative hadronic parameters are largely reduced. It is found that the processes of $B_c$ to the ground state charmonium have comparatively large branching ratios ($10^{-2}$), while the branching ratios of other processes are relatively small owing to the phase space suppression, smaller decay constants, and the weaker $q^2$ dependence of the form factors. The theoretically evaluated ratio $\frac{\mathcal {BR}(B_c^+\rightarrow J/\Psi \pi ^+)}{\mathcal {BR}(B_c^+\rightarrow J/\Psi \mu ^+\nu _{\mu })}=0.046^{+0.003}_{-0.002}$ is consistent with the recent data from LHCb. In addition, some interesting ratios among these branching fractions are discussed and compared with other studies. In general, these ratios in the different approaches are of the same order of magnitude, while there are also large discrepancies for specific decay modes. The partial branching ratios for transverse and longitudinal polarizations were investigated separately in $B_c \rightarrow V l\nu _l$ decays. We found that the transverse polarization gives a large contribution in the large $q^2$ region. For the semileptonic $B_c\rightarrow \psi (2S,3S)e\nu _e$ decays the longitudinal contribution is comparable with the transverse contribution in the whole physical region. These theoretical predictions could be tested at the ongoing and forthcoming experiments.

Appendix A: Wave functions of the 3S state

In the quark model, $\eta _c(3S)$ and $\psi (3S)$ are the second excited states of $\eta _c$ and $J/\psi$, respectively. The 3S means that, for these states, we have the radial quantum number $n = 3$ and the orbital angular momentum $l=0$. The radial wave function of the corresponding Schrödinger state for the harmonic-oscillator potential is given by

$$\begin{aligned} \Psi _{(3S)}(\mathbf r )\propto \left( \frac{15}{4}-5\alpha ^2r^2+\alpha ^4 r^4\right) e^{-\frac{\alpha ^2r^2}{2}}, \end{aligned}$$

(A1)

where $\alpha ^2=\frac{m\omega }{2}$ and $\omega$ is the frequency of oscillations or the quantum of energy. We perform the Fourier transformation to the momentum space to get $\Psi _{3S}(\mathbf{k})$ as

$$\begin{aligned} \Psi _{(3S)}({\mathbf {k}})\propto (15\alpha ^4-20 \alpha ^2 k^2+4 k^4)e^{-\frac{k^2}{2\alpha ^2}}, \end{aligned}$$

(A2)

with $k^2$ being the square of the three momentum. In terms of the substitution assumption,

$$\begin{aligned} {\mathbf {k}}_{\perp }\rightarrow {\mathbf {k}}_{\perp },\quad k_z\rightarrow \frac{m_0}{2}(x-\bar{x}), \quad m_0^2=\frac{m_c^2+ {\mathbf {k}}^2_{\perp }}{x\bar{x}}, \end{aligned}$$

(A3)

with $m_c$ the c-quark mass and $\bar{x}=1-x$. We should make the following replacement as regards the variable $k^2$:

$$\begin{aligned} k^{2}\rightarrow \frac{{\mathbf {k}}^2_{\perp }+(x-\bar{x})^2m_c^2}{4x\bar{x}}. \end{aligned}$$

(A4)

Then the wave function can be taken as

$$\begin{aligned}&\Psi _{(3S)}({\mathbf {k}})\rightarrow \Psi _{(3S)}(x,{\mathbf {k}}_{\perp }) \propto \left[ 15\alpha ^4 \right. \nonumber \\&\quad -\frac{5\alpha ^2({\mathbf {k}}^2_{\perp }+m_c^2(x-\bar{x})^2)}{x\bar{x}}\nonumber \\&\quad \left. +\left( \frac{{\mathbf {k}}^2_{\perp }+m_c^2(x-\bar{x})^2}{2x\bar{x}}\right) ^2\right] e^{-\frac{{\mathbf {k}}^2_{\perp }+ m_c^2(x-\bar{x})^2}{8x\bar{x}\alpha ^2}}. \end{aligned}$$

(A5)

Applying the Fourier transform to replace the transverse momentum $\mathbf k _{\perp }$ with its conjugate variable b, the 3S oscillator wave function can be taken as

$$\begin{aligned} \Psi _{(3S)}(x,\mathbf b )\sim & {} \int \mathbf d ^2\mathbf k _{\perp }e^{-i\mathbf k _{\perp } \cdot \mathbf b }\Psi _{(2S)}(x,\mathbf k _{\perp })\nonumber \\\propto & {} x\bar{x}\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(A6)

with

$$\begin{aligned}&\mathcal {T}(x)=7-2\frac{m_c(x-\bar{x})^2}{\omega x\bar{x}}-24m_c \omega b^2x(1-x) \nonumber \\&\quad + \left( \frac{m_c(x-\bar{x})^2}{\omega x\bar{x}}-4b^2m_c\omega x\bar{x}\right) ^2. \end{aligned}$$

(A7)

We then propose the 3S states distribution amplitudes inferred from Eq. (A6),

$$\begin{aligned} \Psi _{(3S)}(x,b) \propto \Phi ^{asy}(x)\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(A8)

with the $\Phi ^{asy}(x)$ being the asymptotic models, which are given in [50]. Therefore, we have the distribution amplitudes for the radially excited charmonium mesons $\eta _c(3S)$ and $\psi (3S)$:

$$\begin{aligned} \Psi ^{L,T,v}(x,b)= & {} \frac{f^{(T)}_{3S}}{2\sqrt{2N_c}}N^{L} x\bar{x}\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\ \Psi ^t(x,b)= & {} \frac{f^{T}_{3S}}{2\sqrt{2N_c}}N^t (x-\bar{x})^2\mathcal {T}(x)\nonumber \\&\times e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\ \Psi ^V(x,b)= & {} \frac{f_{3S}}{2\sqrt{2N_c}}N^V [1+(x-\bar{x})^2]\mathcal {T}(x)\nonumber \\&\times e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\ \Psi ^s(x,b)= & {} \frac{f_{3S}}{2\sqrt{2N_c}}N^s \mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(A9)

with the normalization conditions

$$\begin{aligned} \int _0^1\Psi ^{i}(x,0)d x= & {} \frac{f^{(T)}_{3S}}{2\sqrt{2N_c}}\;. \end{aligned}$$

(A10)

$N_c$ above is the color number, $N^{i}(i=L,t,V,s)$ are the normalization constants. $f_{3S}$ and $f^T_{3S}$ are the vector and tensor decay constants, respectively. Since the energy spectrum of a three-dimensional harmonic oscillator is given by $E_{nl}=[2(n-1)+l+\frac{3}{2}]\omega$, the value of the frequency $\omega$ can be determined by the difference between the two adjacent energy states. Here, the parameter $\omega \approx (m_{4S}-m_{3S})/2\approx 0.1$ GeV.