1 Introduction

The dynamics of a particles (massless or massive, neutral or charged) in the vicinity of a black hole (BH) is the most intriguing problems in the BH astrophysics. The geometrical structure of spacetime in the surrounding of BH could be studied better by these phenomena [1, 2]. The motion of a particle helps us to understand gravitational fields of BHs experimentally and to compare them with observational data. The magnetic field in the vicinity of BH is due to the presence of a plasma [3]. Magnetic fields cannot change the geometry of a BH but its interaction with plasma and charged particles is very important [4, 5]. The transfer of energy to particles moving around in a BH geometry is due to the magnetic field, so that there is a possibility of their escape to spatial infinity [6]. Hence, a high energy may be produced by a charged particles collision in the presence of a magnetic field rather than its absence.

Recent observations have also provided hints about connecting magnetars with very massive progenitor stars, for example an infrared elliptical ring or shell was discovered surrounding the magnetar SGR 1900\(+\)14 [7]. The explanation of magnetic white dwarfs was first proposed in the scenario of a fossil-field for magnetism of compact objects [8–10]. Magnetic white dwarfs may be created as a result of a rebound shock explosion [10] and may further give rise to novel magnetic modes of global stellar oscillations [11]. This fossil-field scenario is supported by the statistics for the mass and magnetic field distributions of magnetic white dwarfs. Magnetized massive progenitor stars with a quasi-spherical general polytropic magneto fluid under the self-gravity are modeled by [12]. Over recent years methods were developed to detect truly cosmologically magnetic fields, not associated with any virilized structure. The spectral energy distribution of some tera-electronvolt range (TeV) blazers in the TeV and giga-electronvolt (GeV) range hint at the presence of a cosmological magnetic field pervading all space [13, 14].

The authors [15–17] investigated the effects on charged particles in the presence of a magnetic field near BHs. The motion of charged particles was discussed by Jamil et al. [18] around weakly magnetized BHs in Janis-Newman-Winicour (JNW) spacetime. Many aspects of the motion of particles around an SH and a Reissner–Nordstrom BH have been studied and a detailed review is given in Refs. [19, 20]. An important question may rise in the studies of these important problems: what will happen in the dynamics of a particles (neutral or charged) around BHs with respect to time? Particles moving in circular orbits around BHs in an equatorial plane may show a drastic change with respect to time. Following the work done by Al Zahrani et al. [20], we show under what conditions a particle may escape to infinity after collision. At some specific time interval, we study the dynamics of neutral and charged particles around a time conformal Schwarzschild BH.

The purpose of our work is to investigate under which circumstances the particle moving initially would escape from an innermost stable circular orbit (ISCO) or would remain bounded, captured by the BH or escape to infinity after collision with another particle. We calculate the escape velocity of a particle and investigate some important characteristics such as the effective potential and the effective force of particle motions around the BH with respect to time. Initially, we will find attraction in the particle motion but after some specific time we see repulsion. The comparison of the stability orbits of a particle with the help of a Lyapunov exponent is also established.

The outline of paper is as follows: in Sect. 2, we discuss the Noether and approximate Noether symmetries for a Schwarzschild BH and a time conformal Schwarzschild BH and find the corresponding conservation laws. In Sect. 3, we investigate the dynamics of a neutral particle through the effective potential, effective force, and escape velocity. In Sect. 4, the motion of the charged particle is discussed, the behavior of the effective potential, effective force and escape velocity is analyzed in the presence of a magnetic field. In Sect. 5, the Lyapunov exponent is discussed. Conclusion and observations are given in the last section.

2 Noether and approximate Noether symmetries and corresponding conservation laws

The one to one correspondence between conservation laws and symmetries of a Lagrangian (Noether symmetries) has been first pointed out by Emmy Noether [21–23]. She suggested that there exists a conservation law for every Noether symmetry. One can obtain the approximate Noether symmetries of a Schwarzschild solution by considering its first order perturbation and investigating the energy-momentum of corresponding spacetime.

2.1 Schwarzschild black hole

The line element of the Schwarzschild solution is

$$\begin{aligned} \mathrm{d}s^{2}_e= & {} \left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\nonumber \\&\times \,\mathrm{d}r^{2}- r^2({\mathrm{d}\theta }^{2}+\sin \theta {\mathrm{d}\phi }^{2}), \end{aligned}$$
(1)

the corresponding Lagrangian is

$$\begin{aligned} L_e=\left( 1-\frac{2M}{r}\right) \dot{t}^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\dot{r}^{2} -r^2(\dot{\theta }^{2}+\sin \theta \dot{\phi }^{2}). \end{aligned}$$
(2)

The symmetry generator

$$\begin{aligned} \mathbf X ^{1}_e=\xi _e\frac{\partial }{\partial s} +\eta ^{i}_e\frac{\partial }{\partial x^i}+\eta ^i_{es}\frac{\partial }{\partial \dot{x}^i},\quad i=0,1,2,3, \end{aligned}$$
(3)

is the first order prolongation of

$$\begin{aligned} \mathbf X _e=\xi _e\frac{\partial }{\partial s} +\eta ^{i}_e\frac{\partial }{\partial x^i}. \end{aligned}$$
(4)

\(\mathbf X _e\) is the Noether symmetry if it satisfies the equation

$$\begin{aligned} \mathbf X ^{1}_eL_e+(D\xi _e)L_e=DA_e, \end{aligned}$$
(5)

where D is differential operator of the form

$$\begin{aligned} D=\frac{\partial }{\partial s}+\dot{x}^i\frac{\partial }{\partial x^i}, \end{aligned}$$
(6)

and \(A_e\) is a gauge function.

The solution of the system (5) is

$$\begin{aligned} A_e= & {} {C_2},\quad \eta _e^0 =C_3,\nonumber \\ \eta ^1_e= & {} 0,\quad \eta ^2_e = -C_5\cos \phi +C_6\sin \phi ,\nonumber \\ \eta ^3_e= & {} C_4+ \frac{\cos \theta \left( C_5\sin \phi +C_6\cos \phi \right) }{\sin \theta },\nonumber \\ \xi ^0= & {} C_1. \end{aligned}$$
(7)

The corresponding Noether symmetries generators are

$$\begin{aligned} \mathbf {X_1}= & {} \frac{\partial }{\partial t}, \quad \mathbf {X_2}=\frac{\partial }{\partial s}, \quad \mathbf {X_3}=\frac{\partial }{\partial \phi }, \nonumber \\ \mathbf {X_4}= & {} \cos \phi \frac{\partial }{\partial \theta } -\cot \theta \sin \phi \frac{\partial }{\partial \phi }, \nonumber \\ \mathbf {X_5}= & {} \sin \phi \frac{\partial }{\partial \theta }+\cot \theta \cos \phi \frac{\partial }{\partial \phi }. \end{aligned}$$
(8)

For the conservation laws given in the Table 1 we use the equation

$$\begin{aligned} \phi =\frac{\partial \mathcal {L}}{\partial \dot{x}^i}(\eta ^i-\xi \dot{x}^i) +\xi \mathcal {L}-A, \end{aligned}$$
(9)

for example, let us show the calculation for the symmetry \(\mathbf {X_1}\). In this symmetry \(\xi =0\) and \(\eta ^0=1\) and we have the above Lagrangian from Eq. (9), \(\frac{\partial \mathcal {L}}{\partial \dot{t}}=2(1-\frac{2M}{r})\dot{t}\); putting these values in Eq. (9) we have

$$\begin{aligned} \phi =2\left( 1-\frac{2M}{r}\right) \dot{t}(1-0)+0-0=2\left( 1-\frac{2M}{r}\right) \dot{t}. \end{aligned}$$

Similarly for the other symmetries. The corresponding conservation laws are

3 Perturbed metric

Perturbing the metric given by (1) we use the general time conformal factor \(e^{\epsilon f(t)}\), which gives

$$\begin{aligned} \mathrm{d}s^{2}=e^{\epsilon f(t)}\mathrm{d}s^{2}_e=(1+\epsilon f(t)+\frac{\epsilon ^2 f(t)^2}{2}+\cdots \cdots )\mathrm{d}s^2_e. \end{aligned}$$
(10)

Picking the first order terms in \(\epsilon \) and neglecting the higher order terms we have

$$\begin{aligned} \mathrm{d}s^{2}=e^{\epsilon f(t)}\mathrm{d}s^{2}_e=(1+\epsilon f(t))\mathrm{d}s^2_e=\mathrm{d}s^2_e+\epsilon f(t)\mathrm{d}s^2_e,\nonumber \\ \end{aligned}$$
(11)

or in expanded form

$$\begin{aligned} \mathrm{d}s^{2}= & {} \left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\nonumber \\&\times \,\mathrm{d}r^{2}-r^2 ({\mathrm{d}\theta }^{2}+\sin \theta {\mathrm{d}\phi }^{2})\nonumber \\&+\,\epsilon {f}(t)\bigg (\left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\nonumber \\&\times \,\mathrm{d}r^{2} -r^2({\mathrm{d}\theta }^{2}+\sin \theta {\mathrm{d}\phi }^{2})\bigg ),\nonumber \\ L= & {} \left( 1-\frac{2M}{r}\right) \dot{t}^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\dot{r}^{2}-r^2\nonumber \\&\times \,(\dot{\theta }^{2}+\sin \theta \dot{\phi }^{2})\nonumber \\&+\,\epsilon {f}(t)\bigg (\left( 1-\frac{2M}{r}\right) \dot{t}^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\nonumber \\&\times \,\dot{r}^{2}-r^2(\dot{\theta }^{2}+\sin \theta \dot{\phi }^{2})\bigg ), \end{aligned}$$
(12)

where \( \dot{} \) denotes differentiation with respect to s, \(L_e\) is defined in Eq. (2), and

$$\begin{aligned} L_a&=f(t)\bigg (\left( 1-\frac{2M}{r}\right) \dot{t}^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\\&\quad \times \dot{r}^{2}-r^2(\dot{\theta }^{2}+\sin \theta \dot{\phi }^{2})\bigg ). \end{aligned}$$

We define the first order approximate Noether symmetries by [24]

$$\begin{aligned} \mathbf {X}=\mathbf {X}_e+ \epsilon \mathbf {X}_a, \end{aligned}$$
(13)

up to the gauge \( A=A_e+\epsilon A_a.\) Here

$$\begin{aligned} \mathbf {X}_a=\xi _a\frac{\partial }{\partial s}+\eta ^{i}_a\frac{\partial }{\partial x^i}, \quad i=4,5,6,7, \end{aligned}$$
(14)

is the approximate Noether symmetry and \(A_a\) is the approximate part of the gauge function.

Now \(\mathbf X \) is the first order approximate Noether symmetry if it satisfies the equation

$$\begin{aligned} \mathbf {X}^1L+(D\xi )L=DA, \end{aligned}$$
(15)

where \(\mathbf {X}^1\) is the first order prolongation of the first order approximate Noether symmetry \(\mathbf X \) given in Eq. (13).

Equation (15) splits into two parts, that is,

$$\begin{aligned} \mathbf {X}_eL_e+(D\xi _e)L_e=DA_e, \end{aligned}$$
(16)
$$\begin{aligned} \mathbf X ^{1}_aL_e+\mathbf X ^{1}_eL_a+(D\xi _e)L_a+(D\xi _a)L_e=DA_a. \end{aligned}$$
(17)
Table 1 First integrals
Full size table

All of \(\eta ^{i}_e,\) \(\eta ^{i}_a,\) \(\xi _e,\) \(\xi _a,\) \( A_e\), and \(A_a\) are functions of \(s,t,r,\theta ,\phi \), and \(\dot{\eta ^{i}_e},\) \(\dot{\eta ^{i}_a}\) are functions of \(s,t,r,\theta ,\phi ,\dot{t},\dot{r},\dot{\theta },\dot{\phi }\). From Eq. (17) we obtained a system of 19 partial differential equations whose solution will provide us the cases where the approximate Noether symmetry(ies) exist(s). By putting the exact solution given in Eq. (7) in Eq. (17) we have the following system of 19 PDEs:

$$\begin{aligned}&\xi ^1_t=\xi ^1_r=\xi ^1_\theta =\xi ^1_\phi =A_{as}=0,\quad 2\eta ^4_s\left( 1-\frac{2M}{r}\right) -A_{at}=0,\nonumber \\&2\eta ^5_s\left( 1-\frac{2M}{r}\right) ^{-1}+A_{ar}=0,\quad 2\eta ^6_sr^2+A_{a\theta }=0,\nonumber \\&2\eta ^7_sr^2\sin ^2\theta +A_{a\phi }=0,\quad \eta ^4_\phi \left( 1-\frac{2M}{r}\right) -r^2\sin ^2\theta \eta ^7_t=0,\nonumber \\&\eta ^4_\theta \left( 1-\frac{2M}{r}\right) -r^2\eta ^6_t=0,\quad \eta ^4_r\left( 1-\frac{2M}{r}\right) ^2-\eta ^5_t=0,\nonumber \\&\eta ^5_\phi \left( 1-\frac{2M}{r}\right) ^{-1}-r^2\sin ^2\theta \eta ^7_r=0,\quad \eta ^5_\theta \left( 1-\frac{2M}{r}\right) ^{-1}-r^2\eta ^6_r=0,\nonumber \\&\eta ^6_\phi -\sin ^2\theta \eta ^7_\theta =0,\quad C_3f_t(t)+\frac{2}{r}\eta ^5+2\eta ^5_r-\xi ^1_s=0,\nonumber \\&C_3f_t(t)-\frac{2M}{r^2\left( 1-\frac{2M}{r}\right) }\eta ^5+2\eta ^5_r-\xi ^1_s=0,\nonumber \\&C_3f_t(t)+\frac{2M}{r^2\left( 1-\frac{2M}{r}\right) }\eta ^5+2\eta ^5_r-\xi ^1_s=0,\nonumber \\&C_3f_t(t)+\frac{2}{r}\eta ^5+2\cot \theta \eta ^6+2\eta ^7_\phi -\xi ^1_s=0. \end{aligned}$$
(18)

We see that the system (18) have \(C_3\) and f(t) in it. The solution of this system (18) is

$$\begin{aligned}&A_a ={C_2}^{'},\quad \eta _a^4 =C_3^{'},\nonumber \\&\eta ^5_a =0,\quad \eta ^6_a = -C_5^{'}\cos \phi +C_6^{'}\sin \phi ,\nonumber \\&\eta ^7_a =C_4^{'}+ \frac{\cos \theta \left( C_5^{'}\sin \phi +C_6^{'}\cos \phi \right) }{\sin \theta },\nonumber \\&\xi ^0 =C_1^{'}+C_3\frac{s}{\alpha }, \quad f(t)=\frac{t}{\alpha }. \end{aligned}$$
(19)

Combining the solution (7) and (19) we have the following solution of Eq. (15):

$$\begin{aligned}&A_e+\epsilon A_a ={C_2}+\epsilon C_2^{'},\quad \eta _e^0+\epsilon \eta ^4_a =C_3+\epsilon C_3^{'},\nonumber \\&\eta ^1_e+\epsilon \eta ^{{5}}_a =0,\quad \eta ^2_e+\epsilon \eta ^{{6}}_a\nonumber \\&\quad = -(C_5+\epsilon C_5^{'})\cos \left( \phi \right) +(C_6+\epsilon C_6^{'})\sin \left( \phi \right) ,\nonumber \\&\eta ^3_e+\epsilon \eta ^{{7}}_a =(C_4+\epsilon C_4^{'})\nonumber \\&\qquad + \frac{\cos \left( \theta \right) \left( (C_5+\epsilon C_5^{'})\sin \left( \phi \right) +(C_6+\epsilon C_6^{'})\cos \left( \phi \right) \right) }{\sin \left( \theta \right) },\nonumber \\&\xi ^0+\epsilon \xi _{{1}} =\epsilon {\frac{ C_3s}{\alpha }}+(C_1+\epsilon C_1^{'}),\quad f(t)=\frac{t}{\alpha }. \end{aligned}$$
(20)

In symmetry generator form we have

$$\begin{aligned}&\mathbf {X_1}=\frac{\partial }{\partial t}+\epsilon \frac{s}{\alpha }\frac{\partial }{\partial s}, \quad \mathbf {X_2}=\frac{\partial }{\partial s}, \quad \mathbf {X_3}=\frac{\partial }{\partial \phi }, \nonumber \\&\mathbf {X_4}=\cos \phi \frac{\partial }{\partial \theta }-\cot \theta \sin \phi \frac{\partial }{\partial \phi }, \nonumber \\&\mathbf {X_5} =\sin \phi \frac{\partial }{\partial \theta }+\cot \theta \cos \phi \frac{\partial }{\partial \phi }. \end{aligned}$$
(21)

We see that only the symmetry \(\mathbf {X_1}\) got the non-trivial approximate part which re-scales the energy content of the Schwarzschild spacetime. The corresponding conservation laws are

3.1 Existence and location of horizon

Consider the line element of a time conformal Schwarzschild BH

$$\begin{aligned} \mathrm{d}s^{2}= & {} \left( 1+\frac{\epsilon {t}}{\alpha }\right) \bigg ( \left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}\nonumber \\&\times \,\mathrm{d}r^{2}-r^2 ({\mathrm{d}\theta }^{2} +\sin \theta {\mathrm{d}\phi }^{2})\bigg ). \end{aligned}$$
(22)

The parameter \(\epsilon \) is a dimensionless small parameter that causes the perturbation in the spacetime and \(\alpha \) is a constant with dimension equal to that of time t so as to make the term \(\frac{t}{\alpha }\) dimensionless. M is the mass of the black hole. In order to discuss the trapped surfaces and apparent horizon of the above metric, we use the definitions of [25–28] and Eqs. (13) and (14) of [28]. Here, we define the mean curvature one-form by

$$\begin{aligned} H_{\mu }=\delta ^{a}_{\mu }(U,{\mu }-\mathrm{div}{\vec {g}}_{a}). \end{aligned}$$
(23)

Also, the scalar defining the trapped surface of a given spacetime is

$$\begin{aligned} \kappa =-g^{bc}H_{b}H_{c}. \end{aligned}$$
(24)

In the notation of [28], the quantities in the above equations are defined as \(G\equiv e^{U}=\sqrt{\mathrm{det}g_{AB}}\) and \({\vec {g}}_{a}=g_{aA}\mathrm{d}x^{A}\). The coordinates are defined by \(\{x^a\}=\{t,r\}\) and \(\{x^A\}=\{\theta ,\phi \}\). By using these coordinates, we obtain

$$\begin{aligned}&{\vec {g}}_{t}=0 , \qquad {\vec {g}}_{r}=0\end{aligned}$$
(25)
$$\begin{aligned}&e^{U}=\sqrt{\mathrm{det}g_{AB}}=\left( 1+\frac{\epsilon t}{\alpha }\right) r^2 \mathrm{sin} \theta . \end{aligned}$$
(26)

Hence, using given the metric (22), Eqs. (23)–(26), we get the following form for the trapping scalar:

$$\begin{aligned} \kappa =\frac{-\left( \frac{\epsilon }{\alpha }\right) ^2r^2+4\left( 1-\frac{2m}{r}\right) ^2\left( 1+ \frac{\epsilon {t}}{\alpha }\right) ^2}{\left( 1-\frac{2m}{r}\right) \left( 1+\frac{\epsilon t}{\alpha }\right) ^3r^2}. \end{aligned}$$
(27)

Now the surface of the given geometry (22), will be trapped, marginally trapped, and absolutely non-trapped if \(\kappa \) is positive, zero, and negative, respectively. In order to analyze the nature of trapped surfaces and the location of the horizons, we solve Eq. (27) for r by imposing a restriction on \(\kappa \) such that \(\kappa >0\), \(\kappa =0\), and \(\kappa <0\). In the following we discuss these situations in detail.

  • \(\kappa >0\) leads to two positive real values of r, \(r_+>\frac{(\alpha +\epsilon {t})\big (1+\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon {t})}}\big )}{\epsilon }\) and \(r_-< \frac{(\alpha +\epsilon {t})\big (1-\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon t)}}\big )}{\epsilon }\) such that \(\alpha >\epsilon (4m-t)\). Here \(r_+\) and \(r_-\) correspond to outer and inner horizons for trapping surface, respectively.

  • \(\kappa =0\) leads to two positive real values of r, \(r_+=\frac{(\alpha +\epsilon t)\big (1+\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon t)}}\big )}{\epsilon }\) and \(r_-=\frac{(\alpha +\epsilon t)\big (1-\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon t)}}\big )}{\epsilon }\) such that \(\alpha >\epsilon (4m-t)\). Here \(r_+\) and \(r_-\) correspond to outer and inner horizons for marginally trapping surface, respectively.

  • \(\kappa <0\) leads to two positive real values of r, \(r_+<\frac{(\alpha +\epsilon t)\big (1+\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon t)}}\big )}{\epsilon }\) and \(r_->\frac{(\alpha +\epsilon t)\big (1-\sqrt{1-\frac{4m\epsilon }{(\alpha +\epsilon t)}}\big )}{\epsilon }\) such that \(\alpha >\epsilon (4m-t)\). Here \(r_+\) and \(r_-\) correspond to outer and inner absolutely non-trapping points on the given surface, respectively. We would like to mention that we have considered the denominator of Eq. (27) as positive for the arbitrary value of parameters and coordinates.

3.2 Thermal stability

The time conformal Schwarzschild metric is

$$\begin{aligned} \mathrm{d}s^{2}= & {} \left( 1+\frac{\epsilon {t}}{\alpha }\right) \left( f(r)\mathrm{d}t^{2} -(f(r))^{-1}\mathrm{d}r^{2}\right. \nonumber \\&\left. -\,r^2({\mathrm{d}\theta }^{2} +\sin \theta {\mathrm{d}\phi }^{2})\right) , \end{aligned}$$
(28)

where \(f(r)=1-\frac{r_{*}}{r}\) with \(r_{*}=2M\). Further suppose that \(v(r,t)=\big (1+\frac{\epsilon t}{\alpha }\big )f(r)\). Clearly, for values of \(r>r_{*}\) this solution is positive definite and a coordinate singularity occurs at \(r=r_{*}\). The coordinate t is identified periodically with period

$$\begin{aligned} \beta =\frac{4 \pi }{v'(r,t)}|_{r=r_{*}}=\left( 1-\frac{\epsilon t}{\alpha }\right) (4 \pi r_{*}). \end{aligned}$$
(29)

In the limit of large r, the Killing vector \(\frac{\partial }{\partial t}\) is normalized to 1. The temperature measure to infinity may be formally identified with inverse of this period. Hence by the Tolman law, for any self gravitating system in thermal equilibrium, a local observer will measure a local temperature T which scales as \(g_{11}^{-\frac{1}{2}}\) [29]. The constant of proportionality in the present context is

$$\begin{aligned} T_{\infty }=\frac{1}{\beta }=\left( 1+\frac{\epsilon t}{\alpha }\right) (4 \pi r_{*})^{-1}. \end{aligned}$$
(30)

The wall temperature \(T_W\) and surface area \(A_W=4\pi r_W^2\) are defined by York [30]. One topologically regular solution to the Einstein equation with these boundary conditions is a hot flat space with uniform temperature \(T_W\). Another solution is the Schwarzschild metric. If a BH of horizon \(r_{*}<r_W\) does exist then the wall temperature from the Tolman law must satisfy

$$\begin{aligned} T_W=\left( 1+\frac{\epsilon t}{\alpha }\right) (4 \pi r_{*})^{-1}\left( 1-\frac{r_{*}}{r_W}\right) ^{-\frac{1}{2}}. \end{aligned}$$
(31)

In terms of \(r_W\) and \(T_W\), this equation may be solved for \(r_{*}\). There is no real positive root for \(r_{*}\), if \(r_W T_W<\frac{\sqrt{27}}{8 \pi }\) [29].

For any value of \(r_W\) and \(T_W\), the entropy of the BH solution to Eq. (31) is \(S=\pi r_{*}^2\). The heat capacity of a constant surface for any solution is

$$\begin{aligned} C_A=T_W \frac{\partial S}{\partial T_W}|_{A_W}=-2 \pi r_{ast}^2 \left( 1-\frac{r_{*}}{r_W}\right) \left( 1-\frac{3r_{*}}{2r_W}\right) ^{-1}. \end{aligned}$$
(32)

The heat capacity is positive and the equilibrium configuration is locally thermally stable if \(r_{*}<r_W<\frac{3r_{*}}{2}\).

3.3 Energy conditions

Consider the line element of time conformal Schwarzschild BH of Eq. (22). Let us suppose that the matter distribution is isotropic in nature, whose energy-momentum tensor is given by

$$\begin{aligned} T_{\mu \nu }= (\rho + p)u_{\mu } u_{\nu }-p g_{\mu \nu }. \end{aligned}$$
(33)

Here the vector \(u_i\) is the fluid four-velocity with \(u_i=(\sqrt{g_{11}},0,0,0)\), \(\rho \) is the matter density, and p is the pressure.

Table 2 First integrals
Full size table

Taking \(G=1=c\), from the Einstein field equations one can deduce that

$$\begin{aligned} 8 \pi \rho= & {} \frac{\epsilon t}{\alpha r^2} ,\end{aligned}$$
(34)
$$\begin{aligned} 8 \pi p= & {} -\frac{\epsilon t}{\alpha r^2}. \end{aligned}$$
(35)

Now, we want to check the energy conditions for a time conformal Schwarzschild BH. For the null energy condition (NEC), the weak energy condition (WEC), the strong energy condition (SEC), and the dominant energy condition (DEC), the following inequalities must be satisfied:

NEC: \(\rho + p \ge 0\).

WEC: \(\rho + p \ge 0\), \(\rho \ge 0\).

SEC: \(\rho + p \ge 0\), \(\rho + 3p \ge 0\).

DEC: \(\rho \ge |p|\).

From Eqs. (34) and (35), we can see that the NEC, WEC, and DEC satisfy by time conformal Schwarzschild BH, on the other hand, SEC violates it.

4 Dynamics of the neutral particle

We discuss the dynamics of a neutral particle around the time conformal Schwarzschild BH defined by (1). The approximate energy \(E_\mathrm{approx}\) and the approximate angular momentum \(L_{z}\) are given in Table 2. The total angular momentum in the \((\theta , \phi )\) plane can be calculated from \(\phi _4\) and \(\phi _5\) and it has the value

$$\begin{aligned}&E_\mathrm{approx}=\left( 1+\frac{\epsilon t}{\alpha }\right) \left( E-\frac{\epsilon s}{\alpha }\right) ,\\&L^2=\left( 1+\frac{\epsilon {t}}{\alpha }\right) \left( r^2v_{\bot }+ \frac{L_z^2}{\sin ^2\theta }\right) , \end{aligned}$$

where

$$\begin{aligned} v_{\bot }=r^2\dot{\theta }^2,\quad E=\left( 1-\frac{2M}{r}\right) \dot{t},\quad \dot{x}^\mu \dot{x}_\mu =1. \end{aligned}$$
(36)

Using the normalization condition given in Eq. (36), we can get the approximate equation of motion of the neutral particle,

$$\begin{aligned} \dot{r}^2=E^2-\left( 1-\frac{2M}{r}\right) \left( \left( 1-\frac{\epsilon t}{\alpha }\right) +\frac{L_z^2\left( 1-\frac{2\epsilon t}{\alpha }\right) }{r^2\sin ^2\theta }\right) . \end{aligned}$$
(37)

For \(\dot{r}=0\) and \(\theta =\frac{\pi }{2}\), the effective potential turns out to be

$$\begin{aligned} {E}^2=\left( 1-\frac{2M}{r}\right) \left( 1-\frac{\epsilon t}{\alpha } +\frac{L_z^2\left( 1-\frac{2\epsilon t}{\alpha }\right) }{r^2}\right) =U_\mathrm{eff}. \end{aligned}$$
(38)

The effective potential extreme values are obtained by \(\frac{\mathrm{d}U_\mathrm{eff}}{\mathrm{d}r}=0.\) The convolution point of the effective potential lies in the inner most circular orbit (ISCO);

$$\begin{aligned} r_0= & {} \frac{L}{2M}\bigg (\left( \frac{t \epsilon }{\alpha }-1\right) \pm \left( 1-\frac{\epsilon t}{\alpha }\right) \nonumber \\&\times \sqrt{(L^2+12M^2)-(L^2+9M^2)\frac{4 t \epsilon }{\alpha }} \bigg ). \end{aligned}$$
(39)

The corresponding azimuthal angular momentum and the energy of the particle at the ISCO are

$$\begin{aligned}&L_{Z_0}^2=\frac{Mr\left( 1+\frac{\epsilon t}{\alpha }\right) }{1-\frac{3m}{r}},\\&E^2_{0}=\frac{(r-2M)^2\left( 1-\frac{\epsilon t}{\alpha }\right) }{r(r-3m)}. \end{aligned}$$
Fig. 1
figure 1

The plot of the effective potential (\(U_\mathrm{eff}\)) versus r and t for \(\alpha = \epsilon = 1\), \(M = 10^{-16}\)

Full size image

Consider the circular orbit \(r = r_0\) of a particle, where \(r_0\) is for the local minimum of the effective potential. This orbit exists for \(r_0 \in (4M,\infty )\). The convolution point of the effective potential for ISCO is defined by \(r_0=4M\) [31]. Now suppose that the particle collides with another particle which is in ISCO. There are three possibilities after collision: (i) bounded around BH, (ii) captured by the BH, and (iii) escape to \(\infty \). The results depend upon the process of the collision. The orbit of a particle is slightly changed but remains bounded for small changes in energy and momentum. Otherwise, it can be moved from initial position and captured by the BH or escape to infinity. After collision, the energy and both angular momenta (total and azimuthal) change [3]. Before simplifying the situation, one can apply some conditions, i.e., the azimuthal angular momentum and initial radial velocity do not change but the energy can change, by which we determine the motion of the particle. Hence the effective potential becomes

$$\begin{aligned} {E}^2=f(r)\left( \left( 1-\frac{\epsilon t}{\alpha }\right) + \frac{(L_z+rv_{\bot })^2\left( 1-\frac{2\epsilon t}{\alpha }\right) }{r^2\sin ^2\theta }\right) =U_\mathrm{eff}. \end{aligned}$$
(40)

This energy is greater than the energy of the particle before collision, because after collision the colliding particle gives some of its energy to the orbiting particle. Simplifying Eq. (40), we obtain the escape velocity as follows:

$$\begin{aligned} v_{\bot }=\left( \frac{rE^2\left( 1+\frac{2\epsilon t}{\alpha }\right) -(r-2M) \left( 1+\frac{\epsilon {t}}{\alpha }\right) }{r-2M}\right) ^{ \frac{1}{2}}-\frac{L_z}{r}. \end{aligned}$$
(41)
Fig. 2
figure 2

Plot of effective force versus r and t for \(\alpha = \epsilon = 1\), \(M = 10^{-16}\)

Full size image

4.1 Behavior of the effective potential of the neutral particle

We analyze the trajectories of the effective potential and explain the conditions on energy required for bound motion or escape to infinity around the Schwarzschild BH. Figure 1 represents the behavior of the effective potential of a particle moving around the Schwarzschild BH for different values of the angular momentum. We can see from Fig. 1 that the maxima of the effective potential for \(L_z = 5, 10, 15\) are at \(r \approx 0.5, 1, 1.5\) for the time interval [0, 0.5). Similarly, the minima of the effective potential for \(L_z = 5, 10, 15\) are at \(r \approx 0.5, 1, 1.5\) for the time interval (0.5, 1]. Hence, it is concluded that maxima and minima are shifting forward for large values of the angular momentum. Also the repulsion and attraction of effective force depends upon time. For the time interval [0, 0.5), there is a strong attraction near the BH and it vanishes when the radial coordinate approaches infinity. Moreover, for the time interval (0.5, 1] there is strong repulsion near the BH and it vanishes for r approaching infinity. For \(t=0.5\), we find the equilibrium i.e. there is no attraction and repulsion in the effective potential. Hence, the effective potential is shifting from attraction to repulsion when time increases and the shifting point of time is \(t = 0.5\). Hence, it is concluded that the effective potential is attractive and repulsive with respect to time, maxima and minima of the effective potential shifting forward in radial coordinate for large values of the angular momentum.

4.2 Behavior of effective force of the neutral particle

The effective force is

$$\begin{aligned} F_\mathrm{eff}&=-\frac{1}{2}\frac{\mathrm{d}U_\mathrm{eff}}{\mathrm{d}t}=-\frac{M}{r^2}\left( 1- \frac{\epsilon t}{\alpha }+\frac{L_z^2\left( 1-2\frac{\epsilon t}{\alpha }\right) }{r^2}\right) \nonumber \\&\quad +\left( 1-\frac{2M}{r}\right) \frac{L_z^2\left( 1-2 \frac{\epsilon t}{\alpha }\right) }{r^3}. \end{aligned}$$
(42)

We are studying the motion of the neutral particle in the surrounding of a Schwarzschild BH where attractive and repulsive gravitational forces are produced by a scalar vector tensor field which prevents a particle to fall into the singularity [32]. The comparison of the effective force on the particle around the Schwarzschild BH as a function of the radial coordinate for different values of the angular momentum is shown in Fig. 2. We can see from this figure that, at time interval [0, 0.5), the attraction of a particle to reach the singularity is higher for \(L_z=15\) as compared to \(L_z = 5, 10\). Similarly, at time interval (0.5, 1], the repulsion of a particle to reach the singularity is higher for \(L_z=15\) as compared to \(L_z=5, 10\). Also, at \(t=0.5\) there is no effective force. \(t=0.5\) acts as a shifting point, i.e., the effective force is shifting from attraction to repulsion at \(t=0.5\). We can conclude that the attraction and repulsion of a particle to reach and escape from the singularity is higher for large values of the angular momentum but it mainly depends upon time.

4.3 Trajectories of escape velocity of neutral particle

Figure 3 represents the trajectories of the escape velocity for different values of \(L_z\) as a function of r. It is evident that if the angular momentum is positive then the escape velocity is repulsive while it is attractive for negative values of the angular momentum. Also, the repulsion of the escape velocity for large values of \(L_z\) is strong as compared to the small values of \(L_z\). On the other hand, the attraction of the escape velocity for \(L_z = -15\) is strong as compared to \(L_z=-5, -15\). We can conclude that the escape velocity of a particle increases as the angular momentum increases, but it becomes almost constant away from the BH. Also it is interesting that the trajectories of the escape velocity do not vary with respect to time.

Fig. 3
figure 3

Plot of escape velocity versus r and t for \(E = \alpha = \epsilon = 1\), \(M = 10^{-16}\)

Full size image

5 Dynamics of the charge particle

Now we consider the dynamics of the charged particle around the time conformal Schwarzschild BH defined by (1). We assume that a particle has electric charge and its motion is affected by the magnetic field in BH exterior. Also, we assume that there exists a magnetic field of strength \((\mathbb {B})\) in the neighborhood of BH which is homogeneous, static, and axisymmetric at spatial infinity. Next, we follow the procedure of [33] to construct the magnetic field. Using metric (1), the general Killing vector is [34]

$$\begin{aligned} \Box \xi ^{\mu }=0, \end{aligned}$$
(43)

where \(\xi ^{\mu }\) is the Killing vector. Using the above equation in the Maxwell equation for the 4-potential \(A^{\mu }\) in Lorenz gauge \(A^{\mu }_{;\mu }=0\), we have [35]

$$\begin{aligned} A^{\mu }=\frac{\mathbb {B}}{2}\xi ^{\mu }_{(\phi )}. \end{aligned}$$
(44)

The Killing vectors correspond to a 4-potential which is invariant under symmetries as follows:

$$\begin{aligned} L_{\xi }A_{\mu } = A_{\mu ,\nu } \xi ^{\nu }+A_{\nu }\xi ^{\nu }_{,\mu }=0. \end{aligned}$$
(45)

Using the magnetic field vector [20]

$$\begin{aligned} \mathbb {B}^{\mu } = -\frac{1}{2}e^{\mu \nu \lambda \sigma } F_{\lambda \sigma }u_{\nu }, \end{aligned}$$
(46)

where \(e^{\mu \nu \lambda \sigma }=\frac{\epsilon ^{\mu \nu \lambda \sigma }}{\sqrt{-g}}\), \(\epsilon _{0123}=1\), \(g=\mathrm{det}(g_{\mu \nu })\), and \(\epsilon ^{\mu \nu \lambda \sigma }\) is the Levi-Civita symbol. The Maxwell tensor is

$$\begin{aligned} F_{\mu \nu } = A_{\nu ,\mu }-A_{\mu ,\nu }. \end{aligned}$$
(47)

In the metric (1), for a local observer at rest, we have

$$\begin{aligned} u^{\mu }_{0} = \left( 1-\frac{2M}{r}\right) ^{-\frac{1}{2}} \xi ^{\mu }_{(t)}, u^{\mu }_{3} = (r \mathrm{sin}\theta )^{-1}\xi ^{\mu }_{(\phi )}. \end{aligned}$$
(48)

The remaining two components are zero at \(\dot{r}=0\) (turning point). From Eqs. (44) and (46), we get

$$\begin{aligned} \mathbb {B}^{\mu } =\mathbb {B}\left( 1-\frac{2M}{r}\right) ^{- \frac{1}{2}}\left( \mathrm{cos}\theta \delta ^{\mu }_{r}-\frac{\mathrm{sin}\theta \delta ^{\mu }_{\theta }}{r}\right) , \end{aligned}$$
(49)

here the magnetic field is directed along the z-axis (vertical direction). Since the field is directed upward, we have \(\mathbb {B}>0\).

The Lagrangian of a particle moving in curved spacetime is given by [36]

$$\begin{aligned} L = \frac{1}{2}g_{\mu \nu }u^{\mu }u^{\nu }+\frac{qA}{m}u^{\mu }, \end{aligned}$$
(50)

where m and q are the mass and electric charge of the particle respectively. The generalized 4-momentum of a particle is

$$\begin{aligned} P_{\mu }=m u_{\mu }+q A_{\mu }. \end{aligned}$$
(51)

The new constants of motion are defined as

$$\begin{aligned} \dot{t}=\frac{E\left( 1-\frac{\epsilon t}{\alpha }\right) }{\left( 1-\frac{2M}{r}\right) },\quad \dot{\phi }=\frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2\sin ^2\theta }-B, \end{aligned}$$
(52)

where \(B=\frac{q \mathbb {B}}{2m}\). Using the constraints in the Lagrangian (12) the dynamical equations for \(\theta \) and r become

$$\begin{aligned} \ddot{\theta }&=\frac{\cos \theta \left( L_z\left( 1-\frac{\epsilon t}{\alpha }\right) -B\right) ^2}{r^4\sin ^3\theta }-2\frac{\epsilon \dot{\theta }Er}{\alpha (r-2M)} -4\frac{\dot{r}\dot{\theta }}{r},\end{aligned}$$
(53)
$$\begin{aligned} \ddot{r}&=\frac{3M\dot{r}^2}{r(r-2M)}- \frac{2\epsilon Er\dot{r}}{\alpha (r-2M)}-\frac{ME^2(1-\frac{2\epsilon t}{\alpha })}{r(r-2M)}\nonumber \\&\quad +(r-2M)\left( \dot{\theta }^2+\sin ^2\theta \left( \frac{L_z(1- \frac{\epsilon {t}}{\alpha })}{r^2\sin ^2\theta }-B\right) ^2\right) . \end{aligned}$$
(54)

Using the normalization condition, we obtain

$$\begin{aligned} E^2&=\dot{r}^2+r^2\left( 1-\frac{2M}{r}\right) \dot{\theta }^2+\left( 1-\frac{2M}{r}\right) \bigg (\bigg (1-\frac{\epsilon t}{\alpha }\bigg )\nonumber \\&\quad +r^2\sin ^2\theta \bigg (\frac{L_z(1-\frac{\epsilon t}{\alpha })}{r^2\sin ^2\theta }-B\bigg )^2\bigg ). \end{aligned}$$
(55)

The effective potential takes the form

$$\begin{aligned} U_\mathrm{eff}=\left( 1-\frac{2M}{r}\right) \left( \left( 1-\frac{\epsilon t}{\alpha }\right) +r^2\sin ^2\theta \left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2\sin ^2\theta }-B\right) ^2\right) . \end{aligned}$$
(56)

The energy of the particle moving around the BH in orbit r at the equatorial plane is

$$\begin{aligned} U_\mathrm{eff}=\left( 1-\frac{2M}{r}\right) \left( \left( 1-\frac{\epsilon t}{\alpha }\right) +r^2\left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) ^2\right) . \end{aligned}$$
(57)

This is a constraint equation i.e. it is always valid if it is satisfied at initial time. Let us discuss the symmetric properties of Eq. (53) which are invariant under the transformation as follows:

$$\begin{aligned} \phi \rightarrow - \phi ,\quad L_z \rightarrow -L_z,\quad B \rightarrow -B. \end{aligned}$$
(58)

Therefore, without the loss of generality, we consider \(B>0\) and for \(B<0\) we should apply transformation (58) because both negative and positive charges are inter related by the above transformation. However, if one chooses a positive electric charge \((B>0)\) then both cases of \(L_z\) (positive and negative) must be studied. They are physically different: the change of sign of \(L_z\) corresponds to the change in direction of the Lorentz force acting on the particle [20].

The system (52)–(54) is also invariant with respect to reflection, \(\theta \rightarrow \pi - \theta .\) This transformation preserves the initial position of the particle and changes \(v_{\bot }\rightarrow -v_{\bot }.\) Therefore it is sufficient to consider the positive value of escape velocity \((v_{\bot })\) [20]. By differentiating Eq. (57) with respect to r, we obtain

$$\begin{aligned} \frac{dU_\mathrm{eff}}{dr}&=\frac{2M}{r^2}\left( 1-\frac{\epsilon t}{\alpha }+r^2\left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) ^2\right) \nonumber \\&\quad \ -2rB\left( 1-\frac{2M}{r}\right) \left( \frac{L_z(1-\frac{\epsilon t}{\alpha })}{r^2}-B\right) . \end{aligned}$$
(59)

The effective potential after the collision when the body in the magnetic field (\(\theta =\frac{\pi }{2}\) and \(\dot{r}=0\)) is

$$\begin{aligned} E^2&=U_\mathrm{eff}=f(r)\nonumber \\&\quad \times \left( \left( 1-\frac{\epsilon t}{\alpha }\right) +r^2\left( \frac{(L_z+v_{\bot }r)\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) ^2\right) . \end{aligned}$$
(60)

The escape velocity of the particle takes the form

$$\begin{aligned} v_{\bot }&=\left[ \left( \frac{rE^2-(r-2M)\left( 1-\frac{\epsilon t}{\alpha }\right) }{r-2M}\right) ^{\frac{1}{2}}+rB\right] \nonumber \\&\quad \times \left( 1+\frac{\epsilon t}{\alpha }\right) -\frac{L_z}{r}. \end{aligned}$$
(61)

Differentiating Eq. (59) again with respect to r we have

$$\begin{aligned} \frac{\mathrm{d}^2U_\mathrm{eff}}{\mathrm{d}r^2}=\frac{2M}{r^2}\left( 1-\frac{\epsilon t}{\alpha }\right) +(4M-r)\left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) ^2. \end{aligned}$$
(62)
Fig. 4
figure 4

Graph of the effective potential versus r and t given in Eq. (57) for \(\alpha = \epsilon = 1\), \(M = 10^{-16}\) and \(L_z = 3\)

Full size image

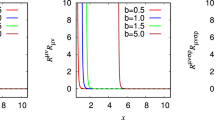
5.1 Behavior of the effective potential of the charged particle

Figure 4 represents the behavior of the effective potential as a function of radial coordinate for different values of magnetic field B. The minimum of the effective potential at \(B=0.5\) is approximately at \(r=2\) initially but as time increases it is shifting near the BH. Hence the presence of a magnetic field increases the possibility for a particle to move in a stable orbit. Similarly, initially the minimum of the effective potential at \(B=1, 1.5\) is approximately at \(r=1.5, 1.25\), respectively; as time increases it approaches near the BH. One may notice that in the presence of a low magnetic field, the minimum of the effective potential is shifted away from the horizon and the width of ISCO is also decreased as compared to a high magnetic field. These results are in agreement with [17, 33]. Therefore we can say that an increase in magnetic field acts as an increase of the instable orbits of a particle. Another aspect of the figure is that, at initial time, we have the possibility of a stable orbit but as time increases the possibility of ISCO gets low and at \(t=1\), the stable orbit is lost. Hence it is possible that the particle is captured by the BH or it escapes to infinity.

5.2 Behavior of effective force of the charged particle

The effective force on the particle can be defined as

$$\begin{aligned} F_\mathrm{eff}&=-\frac{1}{2}\frac{\mathrm{d}U_\mathrm{eff}}{\mathrm{d}r}=-\frac{M}{r^2}\left( 1-\frac{\epsilon t}{\alpha }+r^2\left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) ^2\right) \nonumber \\&\quad +rB\left( 1-\frac{2M}{r}\right) \left( \frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2}-B\right) . \end{aligned}$$
(63)

We have plotted the effective force for different values of B as a function of r. We see from Fig. 5 that the effective force is more attractive for large values of a magnetic field as compared to small values. We can conclude that the effective force of a particle increases as the strength of a magnetic field increases near the BH initially but with the passage of time, the particle moves away from the BH and it becomes almost constant.

5.3 Trajectories of escape velocity of the charged particle

From Eq. (52), for the angular variable we have

$$\begin{aligned} \dot{\phi }=\frac{L_z\left( 1-\frac{\epsilon t}{\alpha }\right) }{r^2\sin ^2\theta }-B. \end{aligned}$$
(64)

If the Lorentz force on a particle is attractive then the left hand side of the above equation is negative [37] and vice versa. The motion of the charged particles is in the clockwise direction. Our main focus on the magnetic field acting on a particle, the large value of the magnetic field deforms the orbital motion of a particle as compared to small values. Hence, we can conclude that the possibility to escape for the particle from the ISCO is greater for large values of the magnetic field. We also explain the behavior of the escape velocity for different values of a magnetic field in Fig. 6 graphically. The escape velocity of a particle increases for large values of the magnetic field as compared to small values. We can conclude that the presence of a magnetic field provides more energy to the particle to escape from the vicinity of BH. Figure 7 represents the escape velocity against r for different values of the angular momentum. The possibility of the particle to escape is low for large values of the angular momentum. Also as time increases the possibility for a particle to escape is decreasing drastically.

Fig. 5
figure 5

Graph of effective force versus r and t given in Eq. (63) for \(\alpha = \epsilon = 1\), \(M = 10^{-16}\), and \(L_z = 3\)

Full size image
Fig. 6
figure 6

Plot of escape velocity versus r and t given in Eq. (61) for \(E = \alpha = \epsilon = 1\), \(M = 10^{-16}\), and \(L_z = 5\)

Full size image
Fig. 7
figure 7

Plot of escape velocity versus r and t given in Eq. (61) for \(E = \alpha = \epsilon = 1\), \(M = 10^{-16}\), and \(B=0.5\)

Full size image

6 Stability orbit

The Lyapunov function is defined as [38]

$$\begin{aligned} \lambda =\left( \frac{-U_\mathrm{eff}^{''}(r_0)}{2\dot{t}^2(r_0)}\right) ^{\frac{1}{2}}. \end{aligned}$$
(65)

Using Eq. (62) we can get the Lyapunov function as

$$\begin{aligned} \lambda&=\frac{\left( 1+\frac{\epsilon {t}}{2\alpha }\right) (r-2M)}{r^{ \frac{5}{2}}E}\bigg [2M\bigg (1+2L_z\bigg (\frac{\big (1-\frac{\epsilon t}{\alpha }\big )L_z}{r^2}-B\bigg )\bigg )\\&\quad +B\bigg (rL_z-r^3B\bigg (1+\frac{\epsilon t}{\alpha }\bigg ) -2L_z(r-2M)\bigg )\bigg ]^{\frac{1}{2}}. \end{aligned}$$
Fig. 8
figure 8

Lyapunov exponent as a function for \(\alpha \) for \(B = \epsilon = 1\), \(M = 10^{-16}\), \(L_z = 3\), \(r = 1\), and \(t=1\)

Full size image

The behavior of \(\lambda \) as a function of \(\alpha \) is analyzed Fig. 8. We can see from the figure that an instability of the circular orbit increases as \(\alpha \) increases but it becomes constant

7 Conclusion and observations

In the present work, we found that one of the Noether symmetries admits an approximate part. This symmetry is the translation in time which means that the energy of the spacetime is re-scaling. We also found the conservation laws corresponding to the exact Schwarzschild spacetime and the time conformal Schwarzschild spacetime and compare their numerical solutions. The geodesic deviation has also presented. The perturbation in the spacetime has perturbed the geodesic. The numerical solutions showed how much they deviated from each other.

Using Noether symmetries, we have calculated the equation of motion. We have found three types of approximate Noether symmetries which correspond to energy, scaling, and Lorentz transformation in the conformal plane symmetric spacetimes. These symmetries approximate the corresponding quantities in the respective spacetimes. We have not seen approximate Noether symmetries corresponding to linear momentum, angular momentum, and galilean transformation in our calculations. This shows that these quantities are conserved for plane symmetric spacetimes. The spacetime section of zero curvature does not admit an approximate Noether symmetry [39] which shows that the approximate symmetries disappeared whenever we have a section of zero curvature in the spacetimes. However, the approximate Noether symmetry does not exist in flat spacetimes (Minkowski spacetime).

In addition, we have investigated the motion of neutral and charged particles in the absence and presence of a magnetic field around the time conformal Schwarzschild BH. The behavior of the effective potential, effective force, and escape velocity of neutral and charged particles with respect to time are discussed. In the case of neutral particle, for large values of the angular momentum, we have found attraction and repulsion with respect to time as shown in Figs. 1, 2, and 3. This effect decreases far away from the BH with respect to time. The more aggressive attraction and repulsion of a particle to reach and escape from the BH have been observed for large values of the angular momentum due to the time dependence. The escape velocity increases as the angular momentum increases but it does not vary with respect to time.

In the case of the charged particle, the presence of a high magnetic field shifted the minimum of the effective potential toward the horizon and the width of the stable region is increased as compared to a low magnetic field. The escape velocity for different values of the angular momentum and magnetic field is shown in Figs. 6 and 7. It is found that the presence of a magnetic field provided more energy to the particle to escape. The possibility for a particle to escape is low for a large angular momentum and as time increases it decreases continuously.