Abstract
We study the Faddeev–Jackiw symplectic Hamiltonian reduction for \(3+1\)-dimensional free and Abelian gauged Rarita–Schwinger theories that comprise Grassmannian fermionic fields. We obtain the relevant fundamental brackets and find that they are in convenient forms for quantization. The brackets are independent of whether the theories contain mass or gauge fields, and the structures of constraints and symplectic potentials largely determine characteristic behaviors of the theories. We also note that, in contrast to the free massive theory, the Dirac field equations for free massless Rarita–Schwinger theory cannot be obtained in a covariant way.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 1941, Rarita and Schwinger constructed a theory of spin-\(\frac{3}{2}\) vector–spinor fields which has a local fermionic gauge invariance [1]. However, this symmetry is lost when the vector–spinor field has mass or couples to the other lower spin fields. More precisely, in 1961, Johnson and Sudarshan studied massive Rarita–Schwinger field minimally coupled to an external electromagnetic field, and they showed that the equal-time commutators and relativistic covariance of the theory are in conflict, which makes the quantization a rather subtle issue [2]. In 1969, Velo and Zwanziger found that the massive gauged extension of the theory also admits superluminal wave propagation. Thus, the causality principle is also violated in the theory [3]. Despite these persistent problems, the massless theory keeps its importance particularly in two respects. First, the massless (Majorana) Rarita–Schwinger field plays a central role in the construction of covariantly interacting supergravity theory [4–6]. The theory describes a generalization of the Rarita–Schwinger fermionic gauge invariance and the vector–spinor fields are fermionic superpartner of gravitons, namely gravitinos of the supergravity. By this concept, Das and Freedman showed that the massless theory is free from the non-causal wave propagation and has a unitary propagator structure [7]. Second, the massless Rarita–Schwinger theory is valuable for the cancelation of SU(8) gauge anomalies. Unlike the generic anomaly cancelation mechanisms in which the anomalies are supposed to be canceled withing the lower spin fermionic fields, it was shown by Marcus [8] and later studied by Adler [9] that a complete SU(8) gauge theory can be constructed via Rarita–Schwinger fields. In this set-up, the vector–spinor field acquires a crucial role in canceling anomalies arising in the gauge theory. Thus, it is left to determine whether the gauged Rarita–Schwinger fields describe well-behaved, complete classical or quantum field theories. For this purpose, Adler has recently studied minimally gauged massless Rarita–Schwinger theories at both classical and quantum levels in detail [10, 11]. He showed that, unlike the massive case, the massless gauged Rarita–Schwinger theory provides consistent classical and quantum theories with a generalized fermionic gauge invariance.
Taking the above mentioned observations as inspiration points and noting the hard task of getting proper brackets of constrained systems providing viable quantization, we study the Faddeev–Jackiw (FJ) symplectic Hamiltonian reduction [12, 13] for free and gauged Rarita–Schwinger theories. Unlike Dirac’s approach for constrained systems [14], the FJ symplectic first-order formalism does not require any classification of constraints.Footnote 1 In other words, the method avoids analyzing systems by evaluating all commutation relations among the constraints and classifying them accordingly. Apparently, the FJ approach supplies a rather economical way of quantizing constrained systems. In doing so, we find the fundamental brackets for the free and gauged Rarita–Schwinger theories for both massless and massive versions. Here, the brackets are in admissible structures to be quantized. We also observe that the brackets are identical for all kinds of the theories; the brackets are independent of whether the theory is massive or interacting with external electromagnetic field or not. The differences between the theories arise among the constraints they have. We also notice that, in contrast to the massive case, the Dirac field equations for free massless Rarita–Schwinger theory cannot be obtained in a covariant way.
The layout of the paper is as follows: In Sect. 2, we recapitulate the fundamental properties of free massless Rarita–Schwinger theory and apply FJ Hamiltonian reduction to the theory. In Sect. 3, we turn our attention to the FJ Hamiltonian reduction for free massive Rarita–Schwinger theory. Sections 4 and 5 are devoted to the first-order symplectic analysis for Abelian gauged extensions of massless and massive Rarita–Schwinger theories. In Sect. 6, we conclude our results. In Appendix A, the derivation of the transverse and traceless decomposition of the fields in the free massless Rarita–Schwinger theory is given as a sample. In the Appendix B, we briefly review the FJ approach for constrained and unconstrained systems. We also give an example of the application of symplectic method to anti-commuting spin-\(\frac{1}{2}\) Dirac theory.
2 Free massless Rarita–Schwinger theory
The \(3+1\)-dimensional free massless Rarita–Schwinger theory is described by the Lagrangian
where \(\psi _\mu \) and \(\bar{\psi }_\mu \) are vector–spinor fields with spinor indices suppressed. We work in the metric signature \((+, -, -, -)\), \( \gamma _5=\mathrm {i} \gamma ^0 \gamma ^1 \gamma ^2 \gamma ^3\), and \( \{\gamma ^\mu , \gamma ^\nu \}=2 \eta ^{\mu \nu } \). We consider the fermionic fields as independent anti-commuting Grassmannian variables. Recall that, unlike the complex Dirac field, for the Grassmannian variables there is no such relation as \(\bar{\psi }_\mu =\gamma ^0 \psi ^+_\mu \). Instead, \( \psi _\mu \) and \(\bar{\psi }_\mu \) are independent generators in the Grassmann algebra. Thus, one can define the conjugation as follows:
Notice that this does not mean that Eq. (2) produces a new element in the Grassmannian algebra. This is merely the conjugation of independent variables. Therefore, with the help of the conjugation of the Grassmannian variables \((\theta _1 \theta _2)^*=\theta ^*_2 \theta ^*_1 \), one can show that the Lagrangian in Eq. (1) is self-adjoint up to a boundary term:
such that the total derivative term naturally drops at the action level. Moreover, variations with respect to independent variables, respectively, yield
which are the corresponding field equations. From now on, we will work with the first of Eq. (4). But, by following the same steps, one could easily obtain similar results for the second equation. Notice that by using the identity
one can recast the field equation in Eq. (4) as follows:

Here  and \( \gamma \cdot \psi =\gamma ^\mu \psi _\mu \). Contracting Eq. (6) with \(\gamma _\lambda \) gives
and \( \gamma \cdot \psi =\gamma ^\mu \psi _\mu \). Contracting Eq. (6) with \(\gamma _\lambda \) gives

Finally, by plugging this result in Eq. (6), the field equation reduces to

To obtain the real propagating degrees of freedom, let us now study gauge transformation and corresponding gauge conditions. For this purpose, let us recall that under the local Rarita–Schwinger fermionic gauge transformation
the Lagrangian in Eq. (1) transforms as
Here \(\epsilon \) is an arbitrary four-component spinor field. As is seen in Eq. (10), the free massless Rarita–Schwinger Lagrangian changes by a total derivative under the Rarita–Schwinger gauge transformation, which drops at the action level and thus we have a completely gauge-invariant theory. This means that the theory admits a gauge redundancy. To find the correct physical degrees of freedom of the theory, one needs to fix this gauge freedom. For this purpose, let us assume the Coulomb-like gauge condition
where \(i=1,2,3\). In fact, this is a reasonable gauge choice: Any initial data \(\psi ^{'}_i(\mathbf{x}, t)\) that does not satisfy Eq. (11) can be tuned to the desired form viaFootnote 2
(See [7, 18] for further discussions.) For the sake of the self-completeness, one needs to examine the theory further to see whether Eq. (11) imposes any additional conditions or not. For this purpose, note that \(\psi _0\) component does not have a time derivative, so it is a Lagrange multiplier. In other words, as in the electromagnetic case, the zeroth component of the vector–spinor field is a zero mode which is followed with a constraint. More precisely, the \(\lambda =0\) component of the field equation in Eq. (8) reads
One can also get a secondary constraint by contracting the field equation with \(\partial _\lambda \). But since our primary aim is not analyzing the system by examining all the existing constraints, we leave it as a comment. As is seen in Eq. (13), gauge-fixing condition \(\gamma ^i \psi _i=0 \) imposes \( \gamma ^i \partial _i \psi _0=0 \). Here, since the operator is not invertible, we are not allowed to have \(\psi _0=0\) as a corollary of \(\gamma ^i \psi _i=0 \); yet we assume an additional condition of \(\psi _0=0\). Furthermore, splitting the fully contracted equation in Eq. (7) into its space and time components yields
In Eq. (14), one should notice that the gauge-fixing condition \(\gamma ^i \psi _i=0\) together with the assumed condition \( \psi _0 =0\) impose \( \partial ^i \psi _i=0 \). As a consequence of this, we obtain the set of consistency conditions
Observe that Eq. (15) can also be written in covariant forms as follows:
which are the Rarita–Schwinger gauge-fixing conditions. Thus, with the gauge choices in Eq. (16), the field equation for the free massless Rarita–Schwinger theory in Eq. (8) turns into the Dirac field equation for massless spin-\(\frac{3}{2}\) vector–spinor field,

2.1 Symplectic reduction for free massless Rarita–Schwinger theory
In this section, we study the FJ Hamiltonian reduction for the free massless Rarita–Schwinger theory which will lead us to the fundamental brackets of the theory. For this purpose, let us recast the Lagrangian in Eq. (1) in a more symmetric form:
To study the theory in the first-order symplectic formalism, one needs to convert Eq. (18) into the desired symplectic form. That is, one needs to split the Lagrangian into its space and time components. After a straightforward decomposition, one gets
where the symplectic coefficients are
and the corresponding symplectic potential reads
As expected, all the non-dynamical components have been relegated into the Hamiltonian part of the system. In analyzing the theory, one could also choose the conjugate momenta of \(\bar{\psi }_k\) as a dynamical variable. But in our analysis, we will not work with it. Instead, we consider \(\psi _\mu \) and \(\bar{\psi }_\mu \) as the independent variables. Note that \(\psi _0\) and \(\bar{\psi }_0\) are not dynamical components, so they are Lagrange multipliers. Following [12, 13], the elimination of constraints gives the equations
To solve the constraint equations, one can decompose the independent fields into its local transverse and \(\gamma \)-traceless parts as
where “T” and “\({}^\wedge \)” stand for the transverse and traceless parts, respectively. Here the \(\gamma \)-traceless parts are
such that \( \gamma ^i \hat{\psi }_i=0 \) and \(\gamma ^i \hat{\bar{\psi }}_i=0 \). Then, by using the identity
as well as the constraints in Eq. (22), one can show that the transverse and traceless decomposition of the fields in Eq. (23) can actually be written as follows:
where  and \(\nabla ^2=\partial _i \partial ^i\). As a side comment, one should note that as is done in [13], without addressing the transverse and \(\gamma \)-traceless parts Eq. (23), one could also directly start with Eq. (26). Here, we further provide what the explicit form of the Longitudinal part is. (See Appendix A for the derivation of Eq. (26).) Accordingly, the constraint equations in Eq. (22) turn into completely transverse ones
and \(\nabla ^2=\partial _i \partial ^i\). As a side comment, one should note that as is done in [13], without addressing the transverse and \(\gamma \)-traceless parts Eq. (23), one could also directly start with Eq. (26). Here, we further provide what the explicit form of the Longitudinal part is. (See Appendix A for the derivation of Eq. (26).) Accordingly, the constraint equations in Eq. (22) turn into completely transverse ones
Finally, by inserting Eqs. (26) and (27) in the Eq. (19), up to a boundary term, one gets a completely transverse Lagrangian
Here the transverse symplectic coefficients and potential are
Thus, by defining the symplectic variables as \( (\xi _1, \xi _2)=(\psi ^T_k, \bar{\psi }^T_k) \), one gets the corresponding symplectic matrix,
which is clearly non-singular. Notice that the minus sign in the sub-block is due to the anti-symmetric \(\epsilon \) tensor. Therefore, by taking care of the epsilons contraction in the current signature, one can easily show that the inverse symplectic matrix is
Once the inverse symplectic matrix is found, one can evaluate the fundamental brackets. That is, by using the definition of the FJ equal-time brackets for the Grassmann variables,
one gets the fundamental brackets for free massless Rarita–Schwinger theory as follows:
Note that, with the help of the identity in Eq. (25), the non-vanishing bracket can also be rewritten as
which is identical to the one found in [19].
3 Free massive Rarita–Schwinger theory
The Lagrangian that describes the \(3+1\)-dimensional free massive Rarita–Schwinger theory is
where \(\sigma ^{\lambda \rho }=\frac{i}{2} [\gamma ^\lambda , \gamma ^\rho ]=\mathrm {i}(\eta ^{\lambda \rho }-\gamma ^\rho \gamma ^\lambda ) \). Recall that the fermionic fields are anti-commuting Grassmannian variables. Accordingly, the field equations of the independent variables, respectively, read
In dealing with the fundamental properties of the theory, as we did in the massless theory, we will work only with the first field equation in Eq. (34). Notice that by using the identity in Eq. (5), one can recast the field equation as follows:

Observe that the contraction of Eq. (35) with \( \gamma _\lambda \) yields

and the contraction of Eq. (35) with \( \partial _\lambda \) gives

Combining both contracted field equations Eqs. (36) and (37), one obtains
With these gauge-fixing conditions, the equation in Eq. (35) turns into the Dirac field equation for a massive spin-\(\frac{3}{2}\) vector–spinor field,

Note that, unlike the massless theory, one obtains the Dirac field equation in Eq. (39) without addressing the space and time decompositions of the field equations. On the other hand, due to the mass term, the Rarita–Schwinger gauge invariance is inevitably lost.
3.1 Symplectic reduction for free massive Rarita–Schwinger lagrangian
Let us now study the symplectic Hamiltonian reduction of the free massive Rarita–Schwinger theory. For this purpose, let us recall that the Lagrangian in Eq. (33), up to a boundary term, can be written as
In order to proceed the FJ symplectic reduction of Eq. (40), one needs to separate the dynamical components from the non-dynamical ones so that the non-dynamical components can be relegated to Hamiltonian part of the Lagrangian. Therefore, by splitting the Lagrangian into its space and time components, one will obtain
where the coefficient of the dynamical parts are
and the explicit form of the symplectic potential is
Like the free massless theory, \(\psi _0\) and \(\bar{\psi }_0\) are zero modes of the system whose eliminations give rise the constraints
As was done in the previous section, by decomposing the fields into the local transverse and \(\gamma \)-traceless parts as in the Eq. (23), the constraints in Eq. (44) turn into completely transverse ones,
In this case, the longitudinal part reads  . Thus, by plugging Eq. (23) and the transverse constraints Eq. (45) into the Eq. (41), up to a boundary term, the Lagrangian turns into
. Thus, by plugging Eq. (23) and the transverse constraints Eq. (45) into the Eq. (41), up to a boundary term, the Lagrangian turns into
where the transverse symplectic coefficients and potential, respectively, are
Observe that the middle two terms in Eq. (46) are not in the symplectic forms. Therefore, by assuming the Darboux transformation
with an additional assumption of
the undesired terms in Eq. (46) drop and thus we are left with a completely transverse Lagrangian
Note that the extra condition Eq. (49) is enforced by the Darboux transformation and the constraint equations; otherwise, the coupled terms in the symplectic part could not be decoupled. In fact, it seems there is a lack in the physical interpretation of Eq. (49). Therefore, it will be particularly interesting if one can show that it has a relation with the real constraints or not. Here, as is mentioned in Eq. (117), the remaining variables (i.e., the longitudinal components) are called the Lagrange multipliers
such that
As noted in [12, 13], since the last two terms in Eq. (50) cannot be dropped via elimination of constraints anymore, Eq. (52) corresponds to the true constraints of the system. Note also that the true constraints cannot be rewritten as linear combinations of the ones that are obtained during the eliminations of the constraints; otherwise, they would also drop when the eliminations of constraint was performed. These are the constraints that cannot be eliminated anymore. Therefore, setting \(\phi ^k(\psi ^T_k, \bar{\psi }^T_k) \) and \(\bar{\phi }^i(\psi ^T_k, \bar{\psi }^T_k) \) to zero provides an unconstrained fully traceless Lagrangian
Thus, with the definition of the dynamical variables \( (\xi _1, \xi _2)=(\psi ^T_k,\,\bar{\psi }^T_k) \), the non-vanishing equal-time FJ bracket for the free massive Rarita–Schwinger theory becomes
which is the same as the one found in [20].
4 Gauged massless Rarita–Schwinger theory
In this section, we study the massless Rarita–Schwinger field minimally coupled to an external electromagnetic field which is described by the Lagrangian
Here the gauge-covariant derivative is \( \mathcal{D}_\nu =\partial _\nu +g A_\nu \), where g is the relevant coupling constant and \(A_\mu \) is an Abelian gauge field. The field equations read
As in the free massless and massive theories, while deducing the some basic properties of the theory, we will only deal with the first of Eq. (56). Notice that with the help of the identity in Eq. (5), Eq. (56) turns into

Moreover, contracting Eq. (57) with \(\gamma _\lambda \) yields

Finally, substituting Eq. (58) in Eq. (57) gives

On the other side, contracting Eq. (56) with \(\mathcal{D}_\lambda \) becomes
which is a secondary constraint in the theory and does not provide any further simplification in the field equation in Eq. (59).
4.1 Symplectic reduction for gauged massless Rarita–Schwinger theory
Let us now apply the first-order symplectic formalism to the massless Rarita–Schwinger fields minimally coupled to an external electromagnetic field. For this purpose, let us note that the Lagrangian of the theory in Eq. (55) can be recast in a more symmetric form as follows:
Similarly, by splitting the Lagrangian in Eq. (61) into its space and time components, one gets
where the symplectic coefficients are
and the related symplectic potential is
Note that although the gauge fields are non-dynamical variables, due to being external potentials, one cannot vary and then impose these variations to be vanished. Otherwise, as in the Quantum Electromagnetic Dynamics with external potential, the gauge-field current would be enforced to be zero which is not a desired situation. Hence, as in the free theories, here \(\psi _0\) and \( \bar{\psi }_0\) are the only zero modes of the theory. Therefore, variations with respect to \( \psi _0 \) and \(\bar{\psi }_0\), respectively, give the following constraint equations:
As was done in the free theories, by decomposing the fields into the local transverse and \(\gamma \)-traceless parts as in Eq. (23)Footnote 3 and using the constraints in Eq. (65) as well as by assuming the Darboux transformation Eq. (48), with an additional assumption of
the Lagrangian Eq. (62) turns into a completely transverse one,
where the transverse symplectic coefficients and potential read
Note that the symplectic potential also contains gauge-field parts. Furthermore, as is given in Eq. (117), the remaining variables (i.e., the longitudinal components) are called the Lagrange multipliers,
such that
which cannot be dropped via elimination of constraints anymore; so, according to [12, 13], they are the true constraints of the system. Thus, by setting \(\phi ^k(\psi ^T_k, \bar{\psi }^T_k) \) and \(\bar{\phi }^i(\psi ^T_k, \bar{\psi }^T_k) \) to zero, one arrives at a completely transverse Lagrangian,
Finally, with the definition of the symplectic dynamical variables \( (\xi _1, \xi _2)=(\psi ^T_k,\, \bar{\psi }^T_k) \), one obtains the non-vanishing equal-time FJ basic bracket for the gauged massless Rarita–Schwinger theory as follows:
which is consistent with the Pauli-spin-part of the fundamental bracket obtained in [10, 11] in which Adler studies the Dirac quantization of the non-Abelian gauged Rarita–Schwinger theory via the left-chiral component of the fermionic field. One should notice that such a difference is expected because in [10, 11], the corresponding gauge fields are non-Abelian variables; however, here the gauge fields are Abelian vector fields.
5 Gauged massive Rarita–Schwinger
In this section, we study the massive Rarita–Schwinger theory minimally coupled to an external electromagnetic field which is described by the Lagrangian
where the gauge-covariant derivative is \( \mathcal{D}_\nu =\partial _\nu +g A_\nu \). Accordingly, the field equations for the independent anti-commuting fermionic fields are
which with the help of the identity in Eq. (5) turns into

Moreover, contraction of the equation in Eq. (75) with \(\gamma _\lambda \) gives

And contraction of the field equation in Eq. (74) with \(\mathcal{D}_\lambda \) becomes

which, with the additional redefinition
turns into

Combining Eqs. (76) and (79), one gets the secondary constraint that determines the equation of motion of \(\psi ^0\) component as follows:
Observe that using Eq. (80) in Eq. (79) gives the relation

Finally, by plugging Eqs. (80) and (81) into the field equation in Eq. (75), one obtains

which is the equation that is used by Velo and Zwanziger in deducing the acausal wave propagation of the solution by finding the future-directed normals to the surfaces at each point [3].
5.1 Symplectic reduction for gauged massive Rarita–Schwinger theory
Finally, let us apply FJ symplectic Hamiltonian reduction to the massive Rarita–Schwinger field minimally coupled to an external electromagnetic field. In order to do so, let us rewrite the Lagrangian in Eq. (73) in a more symmetric form:
Subsequently, by splitting the Lagrangian in Eq. (83) into its space and time components, one gets
where the symplectic coefficients are
and the relevant Hamiltonian \( \mathcal{H}(\psi _0, \bar{\psi }_0, \psi _k, \bar{\psi }_k, A_0, A_k) \) is
Note that as is emphasized in the massless gauged part, since the gauge fields are external potentials, one is not allowed to set their variation to zero. Hence, here \(\psi _0, \, \, \bar{\psi }_0\) are the only Lagrange multipliers that induce constraints on the system. Therefore, eliminations of constraints yield
Like the free massive theory, by decomposing the dynamical components into the local transverse and traceless parts as in Eq. (23)Footnote 4 as well as using constraints in Eq. (87) and the Darboux transformation Eq. (48), with the additional assumption of
the Lagrangian, up to a boundary term, turns into
Here the transverse symplectic coefficients and potential are
Notice that, different from the free cases, the symplectic potential involves mass and gauge potentials. Here in Eq. (90), as in the previous sections, the Lagrange multipliers are the longitudinal parts of the vector–spinor field and the corresponding constraints read
which are the same as Eq. (70). Similarly, by setting Eq. (92) to zero [12, 13], one arrives at a completely transverse Lagrangian,
whose symplectic part is the same as the ones found so far. Thus, with the definition of the dynamical variables \( (\xi _1, \xi _2)=(\psi ^T_k,\,\bar{\psi }^T_k) \), the non-vanishing equal-time bracket for the gauged massive Rarita–Schwinger theory becomes
which is identical to the one found in [21].
6 Conclusions
In this work, we studied \(3+1\)-dimensional free and Abelian gauged Grassmannian Rarita–Schwinger theories for their massless and massive extensions in the context of Faddeev–Jackiw first-order symplectic formalism. We have obtained the fundamental brackets of theories which are consistent with some results that we found in the literature but obtained in a more simple way. The brackets are independent of whether the theories contain a mass or gauge field or not, and thus the structures of constraints and symplectic potentials determine the characteristic behaviors of the theories. It will be particularly interesting to find proper transformations that will relate the constraints obtained via the Faddeev–Jackiw symplectic method with the ones that are obtained via the Dirac method. But since the constraints obtained in both methods are rather complicated, in this paper, we restrict ourselves only to the Faddeev–Jackiw analysis of Rarita–Schwinger theories and leave this as a future work. With the comparison with the literature, we concluded that the Faddeev–Jackiw symplectic approach provides a more economical way in deriving the fundamental brackets for the Rarita–Schwinger theories. In addition to these, we notice that, in contrast to the massive theory, the Dirac field equations for free massless Rarita–Schwinger theory cannot be covariantly deduced.
Notes
Notice that, in this case, the longitudinal part becomes
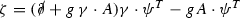 .
.In this case, from the constraint equation, one finds

References
W. Rarita, J. Schwinger, On a theory of particles with half integral spin. Phys. Rev. 60, 61 (1941)
K. Johnson, E.C.G. Sudarshan, Inconsistency of the local field theory of charged spin 3/2 particles. Ann. Phys. 13, 126 (1961)
G. Velo, D. Zwanziger, Propagation and quantization of Rarita-Schwinger waves in an external electromagnetic potential. Phys. Rev. 186, 1337 (1969)
D.Z. Freedman, P. van Nieuwenhuizen, S. Ferrara, Progress Toward a Theory of Supergravity. Phys. Rev. D 13, 3214 (1976)
M.T. Grisaru, H.N. Pendleton, P. van Nieuwenhuizen, Supergravity and the S Matrix. Phys. Rev. D 15, 996 (1977)
M.T. Grisaru, H.N. Pendleton, Soft Spin 3/2 Fermions Require Gravity and Supersymmetry. Phys. Lett. B 67, 323 (1977)
A.K. Das, D.Z. Freedman, Gauge Quantization for Spin 3/2 Fields. Nucl. Phys. B 114, 271 (1976)
N. Marcus, Composite anomalies in supergravity. Phys. Lett. B 157, 383 (1985)
S.L. Adler, SU(8) family unification with boson-fermion balance. Int. J. Mod. Phys. A 29, 1450130 (2014)
S.L. Adler, Quantized gauged massless Rarita-Schwinger fields. Phys. Rev. D 92(8), 085023 (2015)
S.L. Adler, Classical gauged massless Rarita-Schwinger fields. Phys. Rev. D 92(8), 085022 (2015)
L.D. Faddeev, R. Jackiw, Hamiltonian Reduction of Unconstrained and Constrained Systems. Phys. Rev. Lett. 60, 1692 (1988)
R. Jackiw, Diverse topics in theoretical and mathematical physics (World Scientific, Singapore, Singapore, 1995)
P.A.M. Dirac, Generalized Hamiltonian dynamics. Proc. R. Soc. Lond. A 246, 326 (1958)
E.S. Fradkin, T.E. Fradkina, Quantization of relativistic systems with Boson and Fermion first and second class constraints. Phys. Lett. B 72, 343 (1978)
I.A. Batalin, G.A. Vilkovisky, Relativistic S matrix of dynamical systems with Boson and Fermion constraints. Phys. Lett. B 69, 309 (1977)
M. Henneaux, C. Teitelboim, Quantization of gauge systems (Princeton University Press, Princeton, 1992)
D.Z. Freedman, A. Van Proeyen, Supergravity (Cambridge University Press, Cambridge, 2012)
M. Okawa, Covariant canonical quantization of massless Rarita-schwinger field. Prog. Theor. Phys. 62, 305 (1979)
V. Pascalutsa, Quantization of an interacting spin - 3 / 2 field and the Delta isobar. Phys. Rev. D 58, 096002 (1998)
K. Inoue, M. Omote, M. Kobayashi, Quantization of a spin 3/2 field interacting with the electromagnetic field. Prog. Theor. Phys. 63, 1413 (1980)
R. Casalbuoni, On the quantization of systems with anticommutating variables. Nuovo Cim. A 33, 115 (1976)
Acknowledgments
We would like to thank Roman Jackiw for suggesting the problem and several useful discussions. We would also like to thank Bayram Tekin for useful suggestions and Markus Schulze, Gilly Elor and Ibrahim Burak Ilhan for critical readings of the paper. S.D. is supported by the TUBITAK 2219 Scholarship.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Transverse and traceless decomposition of fields
In this section, let us give the derivations of Eq. (26) and Eq. (27). To solve the constraint equations, one can decompose the independent fields into its local transverse and \(\gamma \)-traceless parts as
where “T” and “\({}^\wedge \)” stand for the transverse and traceless parts, respectively. Here the \(\gamma \)-traceless parts are
Therefore, we have
To find how the constraint equations in Eq. (22) decompose under Eq. (95), let us focus on the following constraint equation:
Note that with the identity \(\epsilon ^{ijk} \gamma _5 \gamma _k=-\gamma ^0 \sigma ^{ij} \) and Eq. (95), Eq. (98) turns into
Furthermore, by using the relation
and the transverse and traceless properties of the fields in Eq. (97), one gets
Notice that after contraction with \( i \gamma _0 \) and relabeling of the dummy indices, it becomes
which yields
This structure is also valid for the other theories. The only difference arises in the definition of \(\zeta \), which we give in explicit form in each section. Finally, by substituting this result into the constraint in Eq. (98), it turns into
Because of the symmetric and anti-symmetric contraction in the j, k indices, the second term drops, and we are left with the transverse constraint equation
Appendix B: Faddeev–Jackiw Hamiltonian reduction for constrained and unconstrained systems
In this section, we review the Faddeev–Jackiw symplectic first-order formalism which was introduced particularly to quantize the constrained systems [12, 13]. The method works on the first-order Lagrangian and does not require any classification of constraints. To better understand how the method works, let us consider
With the definition of 2n-component phase-space coordinates,
Eq. (106) can be rewritten as a Lagrangian one-form
Here the symplectic \(2n \times 2n\) matrix is
where \(\text{ I }\) is the identity matrix; \(A_0 \equiv \frac{1}{2} \xi ^\alpha f^0_{\alpha \beta } \mathrm{d}\xi ^\beta \) is the canonical one-form; \(f^0 \equiv d A_0 \equiv \frac{1}{2} f^0_{\alpha \beta } \mathrm{d}\xi ^\alpha \mathrm{d}\xi ^\beta \) is the symplectic two-form. Note that \(f^0\) is constant [12, 13]. But, in general, the symplectic two-form does not have to be constant. Therefore, let us now consider the following generic Lagrangian:
where \(A_\alpha \) is an arbitrary one-form. The variation of Eq. (109) with respect to \(\xi \) yields
In the case when the symplectic matrix is non-singular, Eq. (110) becomes
Thus, by using Eq. (111) and the Poisson brackets for the bosonic variables, one obtains the FJ fundamental brackets as follows:
Note that, in the case of the Grassmannian variables, using the anti-commutation property of the variables as well as the Poisson brackets for the Grassmannian variables [22], one has
and the corresponding fundamental brackets become
On the other side, when there are constraints in the system which are induced by the existence of the zero modes, then the symplectic matrix cannot be inverted. In that case, according to the Darboux theorem, which states that, for any given one-form \(A=A_\alpha \mathrm{d} \xi ^\alpha \) where \( \alpha =1, \ldots , N \), one can always make the following changes in the variables:
so that A turns into \(A=A_\alpha dq^\alpha \). As is seen above, when there is no constraint, Eq. (115) diagonalizes \(f_{\alpha \beta }.\) However, when there are constraints, only a \( 2n \times 2n \) sub-block of \( f_{\alpha \beta } \) is diagonalized and the remaining \(N-2n\) degrees of freedom (corresponding to the zero modes \(z^\rho \)) will not be in the symplectic form [12, 13]; yet they occur in the rest of the Lagrangian:
The equations \(\frac{\partial \Phi }{\partial z^\alpha }=0\) can be used to eliminate the zero modes of z’s only if \(\frac{\partial ^2 \Phi }{\partial z^\rho \partial z^\beta }\) is non-singular. In the generic case, after diagonalization and elimination of as many z as possible, one ultimately arrives at
where the remaining z are denoted by \( \lambda _\rho \) (namely, Lagrange multipliers) and the \(\phi ^\rho \) are the only true constraints in the system
1.1 Symplectic reduction for Dirac theory of spin-\(\frac{1}{2}\) fields
In this section, to see how the method works, we provide a FJ Hamiltonian reduction for the Dirac theory for the spin-\(\frac{1}{2}\) theory as an example. For this purpose, let us note that the Lagrangian can be written

As mentioned above, we assume that the independent dynamical variables are anti-commuting Grassmann variables. In order to pass to the symplectic analysis of the system, one needs to separate the dynamical components from the non-physical ones by splitting the Lagrangian Eq. (119) into its time and space components. In doing so, one arrives at
whose variation, up to a boundary term, yields
from which one gets the Dirac field equations as follows:
As is seen from Eqs. (121) and (122), the symplectic matrix for the Dirac theory and its inverse are
One should observe that, in contrast to the bosonic case, the symplectic matrix for the Grassmannian variables is symmetric and the fundamental brackets are defined as follows:
from which one gets the basic bracket for the Dirac theory
This is also valid for the massless theory. Note that, since the theory does not have any gauge redundancy, one does not need to assume any gauge fixing.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Dengiz, S. Faddeev–Jackiw Hamiltonian reduction for free and gauged Rarita–Schwinger theories. Eur. Phys. J. C 76, 566 (2016). https://doi.org/10.1140/epjc/s10052-016-4411-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4411-3




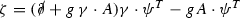 .
.