Abstract
In this paper we study a model of the two-dimensional quantum harmonic oscillator in a three-dimensional anti-de Sitter background. We use a generalized Schrödinger picture in which the analogs of the Schrödinger operators of the particle are independent of both the time and the space coordinates in different representations. The spacetime independent operators of the particle induce the Lie algebra of Killing vector fields of the \(AdS_3\) spacetime. In this picture, we have a metamorphosis of the Heisenberg uncertainty relations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In [1] it was proposed to classify the states of a relativistic particle by means of the invariant operators (\(\mathbf{p}\) = momentum, \(p_0=\sqrt{m^2c^4+c^2\mathbf{p}^2}\), m = mass,)
characterizing the infinite-dimensional unitary representations of the Lorentz group, and to carry out the expansion of the wave function in the momentum space representation over the functions (\(0\le \alpha <\infty \), \(\mathbf{n}^{2}({\theta },{\varphi })=1\))
The functions \({\xi }^{(0)} (\mathbf{p},{\alpha },\mathbf{n})\) are the eigenfunctions of the operator \(C_1(\mathbf{p})\), (\(C_1(\mathbf{p}){\Longrightarrow }{1+{\alpha }}^2\)). The boost and rotation generators of the Lorentz group have the form (\(\mathrm{spin}=0\))
The operator \(C_{2}(\mathbf{p})\) vanishes for a spinless particle.
The expansion proposed in [1] does not include any dependence on the time t and space coordinates \(\mathbf{x}\), i.e. it is ”spacetime independent”. In [2], in the framework of a two-particle equation of the quasipotential type, the expansion over the functions \(\xi ^{*}(\mathbf{p},{\alpha },\mathbf{n})\) was used to introduce the “relativistic configurational” representation (in following the \(\rho \mathbf{n}\)-representation, \(\rho =\alpha \hbar /mc\)). In this approach the variable \(\rho \) was interpreted as the relativistic generalization of a relative coordinate. It was shown that the corresponding operators of the Hamiltonian \(H(\rho ,\mathbf{n})\) and the 3-momentum \(\mathbf{P}(\rho ,\mathbf{n})\), defined on the functions \(\xi ^{*}(\mathbf{p},{\rho },\mathbf{n})\), has a form of the differential-difference operators.
In Refs. [3, 4] it has been shown that the \(\rho \mathbf{n}\)-representation may also be used in a so-called generalized Schrödinger picture in which the analogs of the Schrödinger operators of a particle are independent of both the time and the space coordinates in different representations. It was found that the operators \(H(\rho ,\mathbf{n})\), \(\mathbf{P}(\rho ,\mathbf{n})\), \(\mathbf{L}(\mathbf{n})\), and \(\mathbf{N}(\rho ,\mathbf{n})={\rho }\mathbf{n}+(\mathbf{n}\times \mathbf{L}-\mathbf{L}\times \mathbf{n})/2mc\) satisfy the commutations relations of the Poincaré algebra in the \(\rho \mathbf{n}\)-representation. We have two spacetime independent representations of the Poincaré algebra; the \(\mathbf{p}\) and the \(\rho \mathbf{n}\)-representation. In the GS-picture the \(\rho \mathbf{n}\)-representation may be used to describe extended objects like strings.
In the case of the one-dimensional momentum space representation (p = momentum, m = mass, \({p^2_0-c^2p^2}=m^2c^4)\) the eigenfunctions of the boost generator \(N(p)=ip_0{\partial }_{cp}\), (\(N{\Longrightarrow }{\frac{mc}{\hbar }\rho }\)) may be written in the form
The expansion
leads to the functions \(\psi ({\rho })\) in the \(\rho \)-representation. In the \(\rho \)-representation the Hamilton operator H and the momentum operator P of the particle have the form (\({\tilde{\lambda }}=\frac{\hbar }{mc}\))
and they satisfy the commutation relations of the Poincaré algebra
For a free particle in the Minkowski spacetime of two dimensions (\(d=2\)), the coordinates t, x may be introduced in the states with the help of the transformation
We obtain
where \(\psi (p,t,x)=\psi (p)\mathrm{exp}[-i(tp_0-xp)/\hbar ]\).
In the case of a point particle (\(\rho =0\)) we have the Fourier transform in relativistic quantum mechanics,
In (9), the spacetime coordinates appear in the states in the \(\rho \)- and in the p-representation. We have a metamorphosis of the Heisenberg uncertainty relation, \({\Delta }x{\cdot }{\Delta }p\ge {\hbar }/2\). From \([{\rho },P]=i{\hbar }H/mc^2\) in (7) it follows that instead of \({\Delta }x{\cdot }{\Delta }p\ge {\hbar }/2\), we have
The GS-picture may be used in a quantum theory of gravity in which objects need a sharply defined frame. In Ref. [4], this picture was used to describe the motion of a relativistic particle in anti-de Sitter spacetime (\(d=2\), \(d=4\)). It was found that the spacetime independent operators of the particle in an external field (like in the case of a harmonic oscillator) induce the Lie algebra of Killing vector fields of the \(AdS_4\) spacetime \((d=4;a=1,2,\ldots ,10;\) \(\lbrace {x^{i}\rbrace }\), \(i=1,2,3.)\)
Here \(\widetilde{\Phi }\) denotes the wave function of the particle. The operators of the Killing vector field \({K}_a(t,x^{i})\) satisfy the same commutation rules as the spacetime independent operators \(B _a({\rho },\mathbf{n})\), except for the minus signs on the right-hand sides. Equations (12) are valid for any d. In the present paper we use these equations to describe the motion of a particle in \(AdS_3\) spacetime. In the case of \(d=3\) we need six spacetime independent operators of the particle. In Sect. 2 we will now show that the operators of a relativistic model of the two-dimensional quantum harmonic oscillator in the \({\rho }\mathbf{n}\)-representation can be used in Eq. (12). This will allow us to obtain an exact expression for the energy levels of the particle and an expression for the spectrum of the \(AdS_3\) radius.
2 One particle quantum equation in \(AdS_3\) spacetime
In the two-dimensional momentum space representation, the first Casimir operator of the Lorentz group \(C_1(\mathbf{p})\) has the eigenfuctions (\(p^2_0-c^2p^2_1-c^2p^2_2=m^2c^4\))
where \((n_1={\cos \varphi }, n_2={\sin \varphi })\).
The Hamilton operator and the momentum operators of the particle defined on the functions \({\xi ^{*}}_2(\mathbf p,\rho ,\mathbf n)\) have the form [5]
The operators H, \(\mathbf{P}\), and the three operators of the Lorentz algebra in the \(\rho \mathbf{n}\)-representation
satisfy the commutation relations of the Poincaré algebra.
For the particle in an external field like the two-dimensional harmonic oscillator potential we use the following operators:
where \((\omega = \mathrm{frequency}, i=1,2)\)
In the nonrelativistic limit the operator \(\hat{P_0}(\rho )-mc^2\) assumes the form
The operators
and L, \({N}_i(\rho ,\mathbf{n})\) satisfy the commutations rules of the Lie algebra so(2, 2)
For the Casimir operator
we have
The explicit forms of the six operators \({K}_a(t,x^{i})\) depend on the realization in terms of the spacetime coordinates. We have the problem of determining observables in the GS-picture. In order to interpret the operator \(\hat{P_0}\) as a Hamilton operator, we choose the following realization (t, \(x_1\), \(x_2\) (\(x_1=r\cos \widetilde{\varphi }\), \(x_2=r\sin \widetilde{\varphi }\), \(i=1,2\))):
The set of the operators \(\lbrace {K_{03},K_{i3},K_{i0},K_{ij}}\rbrace \) determine the same Lie algebra as the operators \(\lbrace \hat{P_0},\hat{P}_i,N_i,L\rbrace \) except for the minus signs on the right-hand sides,
The operators \(\lbrace {K_{03},K_{i3},K_{i0},K_{ij}}\rbrace \) form a basis for the SO(2, 2) group generators and are related to the Killing vectors of the \(AdS_3\) spacetime with metric
Here, the constant \(\omega /c\) is related to the radius \(\kappa \) of the \(AdS_3\) spacetime (\(\kappa =c/{\omega }\)).
We can introduce the equation
which defines the operator \(\hat{P_0}(\rho ,\mathbf{n})\) as the Hamilton operator of the particle.
A general solution of \(\Phi (\rho ,\mathbf{n};t,x_1,x_2)\) can be written as a sum of separated solutions or the eigenfunctions of the operators \(\hat{P_0}(\rho ,\mathbf{n})\) and the Casimir operator \((\tau ={\omega }t\), \(\tan \sigma ={\omega }r/c)\),
The eigenfunctions of \(C(\tau ,\sigma ,\widetilde{\varphi })\) are \((n=0,1,2,..., {\vert \widetilde{m}\vert }=0,1,2,..., M=2,3,4,..., \lambda =2n+{\vert \widetilde{m}\vert }+M)\)
where \(N^{M}_{n{\vert \widetilde{m}\vert \widetilde{m}}}\) are the normalization constants and
are the hypergeometric functions. Thus we find
For the spectrum of \(i\hbar \frac{\partial }{\partial {t}}\) we have
The eigensolutions of the Hamilton operator \(\hat{P_0}(\rho ,\mathbf{n})\)
are \((\widetilde{\rho }=\frac{mc\rho }{\hbar }, M=1+\sqrt{1/4+(\frac{mc^2}{\hbar \omega }})^2, {l}= \vert {m}\vert =0,1,2,...,)\)
where \(c^{M}_{nl}\) are normalization constants and \(S_{n}(\widetilde{\rho })\) are the Hahn polynomials,
For the function \(\Phi (\rho ,\mathbf{n};t,x_1,x_2)\), we have (\(m=\widetilde{m}\), \(l={\vert \widetilde{m}\vert }\))
From
it follows that the oscillator frequency is discrete and for higher M decreases according to
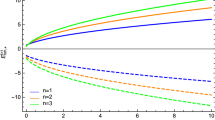
The energy spectrum of the particle can be written as
For the \(AdS_3\) radius \(\kappa =c/{\omega }\), we have \({\kappa }_M=\sqrt{(M^2-2M+3/4)}\) \(\hbar /mc\).
3 Conclusion
In this paper we have shown that a generalized Schrödinger picture may be used to describe a relativistic particle in a three-dimensional anti-de Sitter spacetime. A specific feature of this picture is that the frame itself becomes dynamical. It was found that in this picture we have a metamorphosis of the Heisenberg uncertainty relations. We have shown that the energy of the particle and the anti-de Sitter radius are discrete.
References
I.S. Shapiro, Expansion of a wave function in irreducible representations of the Lorentz group. Sov. Phys. Doklady. 1, 91–93 (1956)
V.G. Kadyshevsky, R.M. Mir-Kasimov, N.B. Skachkov, Quasipotential approach and the expansion in relativistic spherical functions. Nuovo Cimento. 55, 233–257 (1968)
R.A. Frick, On a Heisenberg picture and Fourier transform on the Lorentz group. Sov. J. Nucl. Phys. 38, 481–483 (1983)
R.A. Frick, Model of a relativistic oscillator in a generalized Schrödinger picture. Ann. Phys. (Berlin) 523(11), 871–882 (2011)
S.M. Nagiyev, E.I. Jafarov, M.Y. Efendiyev, The relativistic two-dimensional harmonic oscillator. Il Nuovo Cimento. 124B, 395–403 (2009)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Frick, R. A model of the two-dimensional quantum harmonic oscillator in an \(AdS_3\) background. Eur. Phys. J. C 76, 551 (2016). https://doi.org/10.1140/epjc/s10052-016-4381-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4381-5