Isospin violating decays of positive parity $B_s$ mesons in HM$\chi$PT

Abstract

Recent lattice QCD results suggest that the masses of the first two positive parity $B_s$ mesons lie below the BK threshold, similar to the case of $D^*_{s0}(2317)^+$ and $D_{s1}(2460)^+$ mesons. The mass spectrum of $B_s$ mesons seems to follow the pattern of a $D_s$ mass spectrum. As in the case of charmed mesons, the structure of positive parity $B_s$ mesons is very intriguing. To shed more light on this issue, we investigate the strong isospin violating decays $B_{s0}^{*0} \rightarrow B_s^0 \pi ^0$, $B_{s1}^{0} \rightarrow B_s^{*0} \pi ^0$, and $B_{s1}^{0} \rightarrow B_s^0 \pi \pi$ within heavy meson chiral perturbation theory. The two-body decay amplitude arises at tree level and we show that the loop corrections give significant contributions. On the other hand, in the case of three-body decay $B_{s1}^{0} \rightarrow B_s^0 \pi \pi$ the amplitude occurs only at loop level. We find that the decay widths for these decays are $\Gamma (B_{s1}^{0} \rightarrow B_s^0 \pi \pi )\sim 10^{-3}\,$ keV, and $\Gamma (B_{s0}^{*0} \rightarrow B_s^0 \pi ^0) \le 55\,$ keV, $\Gamma (B_{s1}^{0} \rightarrow B_s^{*0} \pi ^0) \le 50\,$ keV. More precise knowledge of the coupling constant describing the interaction of positive and negative parity heavy mesons with light pseudo-scalar mesons would help to increase the accuracy of our calculation.

1 Introduction

Two positive parity mesons $B_s$ states: the $J^P=1^+$ state $B_{s1}(5830)^0$ and the $J^P=2^+$ state $B^*_{s2}(5840)^0$ were observed by the CDF and LHCb collaborations [1–4]. Recent lattice results [5, 6], as well as other work [7–15], have indicated that the observed states are most likely members of the ($1^+,2^+$) doublet. However, the positive parity doublet of the $B_s$ states ($0^+,1^+$) is still unobserved. The above-mentioned studies also suggest that the ($0^+,1^+$) doublet of $B_s$ states might have masses below the BK and $B^*K$ thresholds. However, some relativistic quark models analysis [16–18] suggested that masses of the ($0^+,1^+$) doublet $B_s$ states should be above the BK and $B^*K$ thresholds. This reminds one strongly of the “history” of establishing the charm meson spectrum in which detection of positive parity states below DK threshold was not predicted by the quark models. After the observation of $D_{s 0}^*(2317)$ and $D_{s 1}(2460)$ charmed mesons, we faced a long-lasting dilemma on the structure of $D_s$ ($0^+,1^+$). The issue is whether $D_{s 0}^*(2317)$ and $D_{s 1}(2460)$ are $\bar{q}q$ states or more exotic compounds [14, 15, 19]. One of the first explanations of the low mass of $D_{s 0}^*(2317)$ was offered by the authors of [13], based on the unitarized model of DK mesons scattering. Similarly, the work of [14] based on the scattering of Goldstone bosons off heavy-light pseudo-scalar and vector mesons with the use of the approximate crossing symmetry of the unitarized scattering amplitude, predicted the existence of positive parity B meson states. The masses of positive parity heavy mesons were studied within the heavy meson chiral Lagrangians approach by the authors of [15, 20]. The dilemmas on the structure of positive parity charm meson states are nicely summarized in the work of [19].

It was already suggested by the authors of [19] that a study of the strong and radiative decay modes of positive parity $D_s$ states might help in differentiating between these scenarios. Since both systems of positive parity states $D_s$ and $B_s$ are rather similar, the systematic analyses of strong and radiative decay dynamics of $B_s$ mesons would help in clarifying their structure. In our study we rely on the results of lattice calculations presented in Ref. [5]. These authors determined the spectrum of $B_s$ 1P states and they found that the masses of $B_{s1}(5830)^0$ and $B^*_{s2}(5840)^0$ agree very well with the experimental results [1–4]. They predicted also the existence of the spin zero positive parity state ($J^P= 0^+$) with the mass $m_{B_{s0}} =5.711(13)(19)$ GeV and the state $J^P= 1^+$ with the mass $m_{B_{s0}} =5.750(17)(19)$ GeV. Both states have masses below the BK and $B^*K$ threshold. This immediately indicates that both states can decay strongly if isospin is violated. Motivated by the result of lattice calculation and relying on our findings in the appropriate charm sector [21], we determine the partial decay widths of both meson states to the final state containing one or two pions: $B_{s0}^{*0} \rightarrow B_s^0 \pi ^0$, $B_{s1}^{0} \rightarrow B_s^{*0} \pi ^0$, and $B_{s1}^{0} \rightarrow B_s^0 \pi \pi$.

Studies of these decays were performed already by [10–12, 22–24]. The authors of [23] assumed that the positive parity $0^+$ and $1^+$ $B_s$ states have a structure of BK molecules, accounting for the similarity with $D_s$, and they suggest that they are rather narrow states with partial decay widths about 50–$60\,$ keV. On the other hand, authors of [10–12, 22] used different approach based on the assumption that the decays proceed through the channels $B_{s0}^{*0} \rightarrow B_s^0 \eta \rightarrow B_s^0 \pi ^0$ and $B_{s1}^{0} \rightarrow B_s^{*0} \eta \rightarrow B_s^{*0} \pi ^0$ with the help of $\eta$–$\pi$ mixing and predicted the partial decay widths in the range of 10–40 GeV. As already discussed in [20, 21, 25, 26] chiral loop corrections play an important role in strong decays of $D_s$ positive parity states and their contribution to the strong decay modes can be as large as the effect of $\eta$–$\pi$ mixing. Since $\pi$ and $\pi \pi$ in the final state of these decays are having very small momenta, both decay modes are ideal to use heavy meson chiral perturbation theory (HM$\chi$PT).

In this paper, we determine the isospin violating decay amplitudes of positive parity $B_s$ mesons, members of the ($0^+,1^+$) doublet, using HM$\chi$PT. For two-body decays, there is a tree-level contribution to decay amplitude arising from the $\eta$–$\pi$ mixing and loop contribution which is the divergent. The divergent loop contribution requires the regularization by the counter-terms. On the other hand, in the isospin violating two-body decays of $D_{s0}^*(2317)$ and $D_{s1}(2460)$ mesons, chiral loops contribute significantly [21]. This was indicated already in Ref. [27] within a different framework in which only part of the loop contributions are included in the decay amplitudes of $D_{s0}^*(2317)$ and $D_{s1}(2460)$. As we pointed out in [21], the isospin violating three-body decay amplitude can arise at loop level only within HM$\chi$PT. These loop contributions are then finite. In the case of charm decays, the ratio of the decay widths for $D_{s1}(2460)^+\rightarrow D_s^{*+}\pi ^0$ and $D_{s1}(2460)^+\rightarrow D_s^+ \pi ^+ \pi ^-$ is known experimentally. From this ratio we were able to constrain the finite size of the counter-terms necessary to regularize the two-body decay amplitude $D_{s1}(2460)^+ \rightarrow D_s^{*+} \pi ^0$. The heavy quark symmetry implies the same size of counter-term contributions for the $B_s$ system as in the case of charm mesons. Therefore, by adopting the result of the lattice calculation showing that $B_s$ mesons, part of the ($0^+,1^+$) doublet, have masses below BK and $BK^*$, we are able to predict their partial decay widths.

The basic HM$\chi$PT formalism is introduced in Sect. 2. In Sect. Theampl we calculate the decay widths of the two-body strong decays of positive parity $B_s$ doublet ($0^+$, $1^+$). In Sect. 4, the calculation of the three-body decay width $B_{s1}^{0} \rightarrow B_s^0 \pi \pi$ decay mode will be presented, while a short conclusion will be given in Sect. 5.

2 Framework

In our analysis we rely on HM$\chi$PT (see e.g. [28, 29]). This approach combines the heavy quark effective theory with the chiral perturbation theory and can be used to describe the decays of mesons that are composed of one light and one heavy quark. The chiral perturbation theory works very well in the case where the pseudo-scalar mesons have low momenta. In the heavy meson limit, heavy mesons, pseudo-scalar and vector, as well as scalar and axial, become degenerate. The negative parity states are described by the field H, while the positive parity states are entering in the field S:

$$\begin{aligned} H= & {} \frac{1}{2}(1+v \cdot \gamma )[P^*_\mu \gamma ^\mu -P\gamma _5], \nonumber \\ S= & {} \frac{1}{2}(1+v \cdot \gamma )[P^*_{1\mu } \gamma ^\mu \gamma _5-P_0], \end{aligned}$$

(1)

where $P^*_\mu$ and P annihilate the vector and pseudo-scalar mesons, respectively, while $P^*_{1\mu }$ and $P_0$ annihilate the axial-vector and scalar mesons, respectively. Within chiral perturbation theory, the light pseudo-scalar mesons are accommodated into the octet $\Sigma =\xi ^2=e^{(2i\Pi /f)}$ with

$$\begin{aligned} \Pi = \left( \begin{array}{l@{\quad }l@{\quad }l} \pi ^0/\sqrt{2}+\eta _8/\sqrt{6} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\pi ^0/\sqrt{2}+\eta _8/\sqrt{6} &{} K^0 \\ K^- &{} \bar{K}^0 &{} -2\eta _8/\sqrt{6} \end{array} \right) \nonumber \\ \end{aligned}$$

(2)

and $f\sim 120\,$MeV at one-loop level [30]. The leading order of the HM$\chi$PT Lagrangian, which describes the interaction of heavy and light mesons, can be written as

$$\begin{aligned}&\mathcal{L}=- Tr[\bar{H}_a (iv\cdot \mathcal{D}_{ab}-\delta _{ab}\Delta _H)H_b]+gTr[\bar{H}_bH_a\gamma \cdot \mathcal{A}_{ab}\gamma _5]\nonumber \\&\quad +Tr[\bar{S}_a (iv\cdot \mathcal{D}_{ab})-\delta _{ab}\Delta _S)S_b]+\tilde{g} Tr[\bar{S}_b S_a\gamma \cdot \mathcal{A}_{ab}\gamma _5]\nonumber \\&\quad +hTr[\bar{H}_bS_a\gamma \cdot \mathcal{A}_{ab}\gamma _5], \end{aligned}$$

(3)

where $\mathcal{D}_{ab}^\mu =\delta _{ab}\partial ^\mu -\mathcal{V}_{ab}^\mu$ is a heavy meson covariant derivative, $\mathcal{V}_\mu =1/2(\xi ^\dagger \partial _\mu \xi +\xi \partial _\mu \xi ^\dagger )$ is the light meson vector current and $\mathcal{A}_\mu =i/2(\xi ^\dagger \partial _\mu \xi -\xi \partial _\mu \xi ^\dagger )$ is the light meson axial current. A trace is taken over the spin matrices and repeated light quark flavor indices. All terms in (3) are of the order $\mathcal{O}(p)$ in the chiral power counting (see e.g. [26]). Following the notation of [5], $\Delta _{SH} = \Delta _S -\Delta _H=375\, \mathrm{GeV}$, and in order to maintain a well-behaved chiral expansion, we consider that this difference is of the order of the pion momentum, $\Delta _{SH}\sim \mathcal{O}(p)$ as in [26].

Light mesons are described by the Lagrangian [28, 29], which is of the order $\mathcal{O}(p^2)$ in the chiral expansion,

$$\begin{aligned} \mathcal{L}_0=\frac{f^2}{8}Tr[\partial _\mu \Sigma \partial ^\mu \Sigma ^\dagger ]+\frac{f^2\lambda _0}{4}Tr[m_q \Sigma +\Sigma ^\dagger m_q], \end{aligned}$$

(4)

where $\lambda _0={m_\pi ^2}/{(m_u+m_d)}={(m^2_{K^+}-m^2_{K_0})}/{(m_u+m_d)}={(m^2_K-m^2_\pi /2)}/{m_s}\,$ and $m_q$ is a diagonal quark matrix. From the second term in (4), we can derive the $\eta$–$\pi$ mixing Lagrangian [31, 32]:

$$\begin{aligned} \mathcal{L}_{\eta -\pi _0}=\frac{m_\pi ^2 (m_u-m_d)}{\sqrt{3}(m_u+m_d)}\pi _0\eta \,. \end{aligned}$$

(5)

The scalar (pseudo-scalar) and vector (axial-vector) heavy meson propagators can be written in the form:

$$\begin{aligned} \frac{i}{2(k\cdot v-\Delta _i)} \qquad \mathrm{and} \qquad \frac{-i(g^{\mu \nu }-v^\mu v^\nu )}{2(k\cdot v-\Delta _i)}, \end{aligned}$$

(6)

respectively, where $\Delta _i$ in the propagator represents the residual mass of the corresponding field. The residual masses are responsible for mass splitting of the heavy meson states. The difference $\Delta _{SH}$ splits the masses of positive and negative parity states. In addition, we also have a mass splitting between $B_s$ and B states as well as a mass splitting between vector (axial-vector) and pseudo-scalar (scalar) fields. According to [33], the mass splitting between $B_s$ and B states is $87\,$MeV, while the splitting between vector and pseudo-scalar states is $45\,$MeV. Since these splittings are much smaller than $\Delta _{SH}$, they can be safely neglected.

The coupling constants g, h, and $\tilde{g}$ were already discussed by several authors and determined by several methods [34–51]. We will use recent results of the lattice QCD: $g=0.54(3)(^{+2}_{-4})$ [39], $\tilde{g}=-0.122(8)(6)$, and $h=0.84(3)(2)$ [45]. The lattice study for h coupling is derived from the non-strange scalar/axial states and then SU(3) symmetry has been used to relate non-strange/strange systems. However, based on the experimental and phenomenological studies of the B meson positive parity states, it was found that these systems with and without strangeness are rather different. That indicates the possibility that the nature of the positive parity $B_s$ system is not necessarily the same as in the case of positive parity B states, which can cause a difference in a value of the coupling constant h for these two systems. Furthermore, existing phenomenological determinations of the coupling constant h, based on light-cone sum rules [34, 38, 49] or HM$\chi$PT approach [26], are also performed on the non-strange systems and predict smaller values of $h \in (0.5$–0.6). Due to luck of lattice studies of the coupling constant h in the strange systems, we vary h in the range (0.5–0.95) in order to investigate its influence on decay widths.

Lattice results will also be used for the $B_{s0}^*$ and $B_{s1}$ masses, as well as $\Delta _{SH}$ [5]: $m_{B_{s0}}=5,711(13)(19)\,$GeV, $m_{B_{s1}}=5.75(17)(19)\,$GeV, and $\Delta _{SH}=375(13)(19)\,$MeV.

In order to absorb divergences coming from loop integrals, one needs to include counter-terms. Following [25, 26] the counter-term Lagrangian can be written as

$$\begin{aligned}&\mathcal{L}_{ct}= \lambda _1[\bar{H}_b\bar{H}_a(m_q^\xi )_{ba}]+\lambda ^\prime _1[\bar{H}_a\bar{H}_a(m_q^\xi )_{bb}] -\tilde{\lambda _1}[\bar{S}_b\bar{S}_a(m_q^\xi )_{ba}]\nonumber \\&\quad -\tilde{\lambda ^\prime _1}[\bar{S}_a\bar{S}_a(m_q^\xi )_{bb}]\nonumber \\&\quad +\frac{h \kappa _1^\prime \lambda _0}{(4\pi f)^2}Tr[(\bar{H} S \gamma _\mu \mathcal{A}^\mu \gamma _5)_{ab}(m_q^\xi )_{ba}]\nonumber \\&\quad +\frac{h \kappa _3^\prime \lambda _0}{(4\pi f)^2}Tr[(\bar{H} S \gamma _\mu \mathcal{A}^\mu \gamma _5)_{aa}(m_q^\xi )_{bb}]\nonumber \\&\quad +\frac{h\kappa _5^\prime \lambda _0}{(4\pi f)^2}Tr[\bar{H}_a S_a \gamma _\mu \mathcal{A}^\mu _{bc} \gamma _5(m_q^\xi )_{cb}]\nonumber \\&\quad + \frac{h\kappa _9^\prime \lambda _0}{(4\pi f)^2}Tr[\bar{H}_c S_a \gamma _\mu \mathcal{A}^\mu _{bc} \gamma _5(m_q^\xi )_{ab}]\nonumber \\&\quad +\frac{\delta _2^\prime }{(4\pi f)^2}Tr[\bar{H}_a S_b i v\cdot \mathcal{D}_{bc}\gamma _\mu \mathcal{A}^\mu _{ca} \gamma _5]\nonumber \\&\quad + \frac{\delta _3^\prime }{(4\pi f)^2}Tr[\bar{H}_a S_b i \gamma _\mu \cdot \mathcal{D}_{bc}^\mu v \cdot \mathcal{A}^\mu _{ca} \gamma _5]+h.c.+\cdots , \end{aligned}$$

(7)

where $m^\xi =(\xi m_q \xi -\xi ^\dagger m_q \xi ^\dagger )/2$ and $D^\alpha _{bc}A^\beta _{ca}=\partial ^\alpha A^\beta _{ba}+[v^\alpha A^\beta ]_{ba}$. At the given scale, the finite part of $\kappa ^\prime _3$ can be absorbed into the definition of h. Parameters $\lambda ^\prime _1$ and $\tilde{\lambda ^\prime _1}$ can be absorbed into the definition of heavy meson masses by a phase redefinition of H and S, while $\lambda _1$ and $\tilde{\lambda _1}$ split the masses of SU(3) flavor triplets of $H_a$ and $S_a$ [25, 26]. Therefore, only contributions proportional to $\kappa ^\prime _1$, $\kappa ^\prime _9$, $\kappa ^\prime _5$, $\delta ^\prime _2$, and $\delta ^\prime _3$ will be explicitly included in the amplitudes.

Fig. 1

Tree-level contribution to $B^{*0}_{s0} \rightarrow B_s \pi ^0$ and $B^{0}_{s1} \rightarrow B^*_s \pi ^0$ decay modes

Fig. 2

Chiral corrections to the B mesons wave functions

3 The amplitudes and the decay widths of two-body decay modes

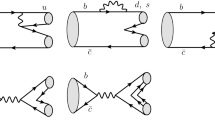
At the tree level, the $B^{*0}_{s0} \rightarrow B_s \pi ^0$ and $B^{0}_{s1} \rightarrow B^*_s \pi ^0$ decays occur through $\eta$–$\pi$ mixing as shown in Fig. 1. The decay widths can be written as

$$\begin{aligned} \Gamma =\frac{h^2}{2\pi f^2}|k_\pi |E_\pi ^2 \delta ^2_\mathrm{mix}, \end{aligned}$$

(8)

where $E_{\pi }$ and $k_{\pi }$ are the energy and momenta of the outgoing pion and $\delta _\mathrm{mix}$ is the $\eta$–$\pi$ mixing angle [25],

$$\begin{aligned} \delta _\mathrm{mix}=\frac{1}{2\sqrt{2}}\frac{m_u-m_d}{m_s-(m_u+m_d)/2}=\frac{-1}{87\sqrt{2}}\,. \end{aligned}$$

(9)

This yields

$$\begin{aligned} \Gamma (B^{0}_{s1} \rightarrow B^*_s \pi ^0)= 16\,\mathrm{keV}, \quad \Gamma (B^{*0}_{s0} \rightarrow B_s \pi ^0)=18\,\mathrm{keV}.\nonumber \\ \end{aligned}$$

(10)

By including chiral loop corrections, the decay width can be rewritten as

$$\begin{aligned} \Gamma =\frac{h^2}{2\pi f^2}|k_\pi |E_\pi ^2 \delta ^2_\mathrm{mix}\left| \frac{\sqrt{Z_{w,f} Z_{w,i}}}{Z_v}\right| ^2, \end{aligned}$$

(11)

where $Z_{w,f}$ and $Z_{w,i}$ denote the wave-function renormalization of the initial and final heavy meson states and $Z_v$ represents the vertex corrections.

Fig. 3

Chiral corrections to the $B^{0}_{s1} \rightarrow B^*_s \pi ^0$ decay mode

Fig. 4

Chiral corrections to the $B^{*0}_{s0} \rightarrow B_s \pi ^0$ decay mode

The wave-function renormalization factor is defined as

$$\begin{aligned} Z_{w,j}=1-\frac{1}{2}\frac{\partial \Pi _{j} (v \cdot p)}{\partial v \cdot p} \Big |_\mathrm{on\;mass\; shell}, \end{aligned}$$

(12)

where $\Pi _j(v \cdot p)$ is the meson self-energy calculated from the sunrise type diagrams in Fig. 2. For $Z_{w,j}$ we derive

$$\begin{aligned} Z_{w,j}=1-\mathcal{W}_j(m_{K^+})-\mathcal{W}_j(m_{K^0})-\frac{2}{3}\mathcal{W}_{j}(m_\eta ), \end{aligned}$$

(13)

with

$$\begin{aligned} \mathcal{W}_j(m_i)= & {} \frac{1}{16\pi ^2f^2}\nonumber \\&\times \left( 3\tilde{g}^2\bar{B}^\prime _{00}(0,m_i) -h^2\bar{B}^\prime _2(-\Delta _{SH},-\Delta _{SH},m_i)\right) ,\nonumber \\ \end{aligned}$$

(14)

for the positive parity mesons and

$$\begin{aligned} \mathcal{W}_j(m_i)= & {} \frac{1}{16\pi ^2f^2} \nonumber \\&\times \left( 3 g^2 \bar{B}^\prime _{00}(0,m_i) -h^2\bar{B}^\prime _2(\Delta _{SH},\Delta _{SH},m_i)\right) , \end{aligned}$$

(15)

for the negative parity mesons. Here, $\bar{B}^\prime _{00}$, $\bar{B}^\prime _2$ are the Veltman–Pasarino loop integrals defined in Appendix A.

The vertex correction is defined as

$$\begin{aligned} Z_v=1-\frac{\hat{\Gamma }(v\cdot p_i,v\cdot p_f,k^2)}{\hat{\Gamma }_{0}(v\cdot p_i,v\cdot p_f,k^2)} \Big |_\mathrm{on\;mass\; shell}. \end{aligned}$$

(16)

Here $\hat{\Gamma }$ is the vertex amplitude calculated from the Feynman diagrams presented in Figs. 3 and 4, while $\hat{\Gamma }_0$ is the vertex amplitude resulting from the tree-level Feynman diagram (see Fig. 1):

$$\begin{aligned}&Z_{v}=1-\Big (\delta ^\prime _\mathrm{mix}+\frac{2}{3}\mathcal{V}^\prime (m_\eta )-\frac{1}{2}\big (\mathcal{V}(m_{K^+})+\mathcal{V}(m_{K^0})\big )\nonumber \\&\quad +\frac{1}{\sqrt{2}\delta _\mathrm{mix}}\big (\mathcal{V}(m_{K^+})-\mathcal{V}(m_{K^0})\big )+\mathcal{V}_{ct}\Big ), \end{aligned}$$

(17)

where $\delta ^\prime _\mathrm{mix}=0.11$ includes corrections to the $\eta$–$\pi$ mixing angle beyond tree level [25, 30], while $\mathcal{V}$ and $\mathcal{V}^\prime$ are

$$\begin{aligned}&\mathcal{V}(m_i)=\frac{1}{16\pi ^2f^2}\left( (\bar{B}_{00}(-\Delta _{SH},m_i)-\bar{B}_{00}(\Delta _{SH},m_i)\right. \nonumber \\&\quad \left. +\bar{B}_{11}(-\Delta _{SH},m_i)-\bar{B}_{11}(\Delta _{SH},m_i)\right. \nonumber \\&\quad \left. -\Delta _{SH}\bar{B}_{1}(-\Delta _{SH},m_i)-\Delta _{SH}\bar{B}_{1}(\Delta _{SH},m_i))/2\right. \nonumber \\&\quad \left. -h^2\left( \bar{B}^\prime _{00}(-\Delta _{SH},\Delta _{SH},m_i)+\bar{B}^\prime _{11}(-\Delta _{SH},\Delta _{SH},m_i)\right) \right. \nonumber \\&\quad \left. +3g\tilde{g}\bar{B}^\prime _{00}(0,0,m_i)\right) , \end{aligned}$$

(18)

$$\begin{aligned}&\mathcal{V}^\prime (m_i)=\frac{1}{16\pi ^2f^2}\left( -h^2\left( \bar{B}^\prime _{00}(-\Delta _{SH},\Delta _{SH},m_i)\right. \right. \nonumber \\&\quad \left. \left. +\bar{B}^\prime _{11}(-\Delta _{SH},\Delta _{SH},m_i)\right) +3g\tilde{g}\bar{B}^\prime _{00}(0,0,m_i)\right) . \end{aligned}$$

(19)

Note that the isospin violating nature of both decay amplitudes manifests itself either by the proportionality of amplitude to the mixing parameter $\delta _\mathrm{mix}$, or by the mass difference $m_{K^0}-m_{K^+}$. Obviously in the isospin limit, the amplitudes vanish for $\delta _\mathrm{mix} \rightarrow 0$ and $m_{K^0}=m_{K^+}$.

The finite parts of the counter-terms are collected in the term $\mathcal{V}_{ct}$:

$$\begin{aligned}&\mathcal{V}_{ct}=\frac{1}{32\pi ^2f^2}\left( \left( m_K^2-\frac{m_\pi ^2}{2}\right) (\kappa ^\prime _1+\kappa ^\prime _9)\right. \nonumber \\&\quad +\left. \left( m_K^2-m_\pi ^2\!+\!\frac{\sqrt{2}(m^2_{K^+}-m^2_{K^0})}{\delta _\mathrm{mix}}\right) \kappa ^\prime _5\!+\!\frac{E_\pi }{2\lambda _0}(\delta _2^\prime \!+\!\delta _3^\prime )\right) .\nonumber \\ \end{aligned}$$

(20)

Neglecting the terms that are multiplied by $m_\pi ^2$ and $\frac{E_\pi }{2\lambda _0}$ and by taking $m^2_{K^+}=m^2_{K^0}$, all counter-terms can be replaced with the linear combination $\kappa ^\prime =\kappa ^\prime _1+\kappa ^\prime _9+\kappa ^\prime _5,$ yielding

$$\begin{aligned} \mathcal{V}_{ct}=\frac{m_K^2}{32\pi ^2f^2} \kappa ^\prime \,. \end{aligned}$$

(21)

Due to heavy meson symmetry, the same counter-term appears also in the case of $D_s$ positive parity meson decays. In [21] we were able to constrain the size of this counter-term using the experimentally known ratio of the decay widths of the $D_{s1}(2460) \rightarrow D_s^*\pi$ and $D_{s1}(2460) \rightarrow D_s \pi \pi$ decay modes. The decay widths are also rather sensitive to the value of the coupling constant h as already noticed in [21], for the charm meson decays. The wave-function renormalization factor is responsible for this behavior.

Fig. 5

Dependence of $\Gamma (B^0_{s1} \rightarrow B_s^{*0} \pi ^0)$ (right) and $\Gamma (B^{*0}_{s0} \rightarrow B_s \pi ^0)$ (left) on the coupling constant h

The dependence of the decay widths on the coupling constant h in the range (0.5–0.95) is shown in Fig. 5. As seen from Fig. 5, the decay widths are in the range of (0.1–55) keV for the range of coupling constant $h=0.84(3)(2)$ as found by lattice calculation [45]. This value of h has been obtained in the non-strange system and one might expect that the value is not necessarily the same for positive parity mesons containing a strange quark. As can be seen from Fig. 5, if one would measure larger decay widths than the above stated ones, this would indicate lower values of the coupling constant h and possibly a more complicated structure of the positive parity $B_s$ mesons. Nevertheless, due to the uncertainties in the values of the counter-terms, the allowed region for the decay widths grows rapidly if we lower the h. Note that we use the range of values for the counter-term (0.1–1.2) as found in [21]. Hopefully, measurements of the decay widths for positive parity $D_s$ mesons, planned in the near future, would enable us to determine counter-terms more precisely and consequently to help in achieving a better precision of our predictions. For the central value $h=0.84$, the range is 1 keV $\le \Gamma (B^{0}_{s1} \rightarrow B^*_s \pi ^0) \le 30\,$keV. The decay rates for $B^{0}_{s1} \rightarrow B^*_s \pi ^0$ and $B^{*0}_{s0} \rightarrow B_s \pi ^0$ are almost equal, with the small difference due to the different masses of the final and initial $B_s$ states.

Finally, we have checked the sensitivity of our results on the choice of the $B_{s0}^*$ and $B_{s1}$ masses as well as $\Delta _{SH}$. If we use the lattice results for the masses from Ref. [6] instead of [5], our results are modified by about 10 %.

4 The three-body decays: amplitudes and decay widths

In the case of $B^{0}_{s1}$, a three-body decay $B^{0}_{s1} \rightarrow B^0_s \pi \pi$ is also possible. The $B^{0}_{s1} \rightarrow B^0_s \pi \pi$ decay width, averaged over the $B^{0}_{s1}$ polarizations, can be written as

$$\begin{aligned} \mathrm{d}\Gamma =\frac{1}{(2\pi )^3}\frac{1}{32 M_i^3}|\mathcal{M}|^2 \mathrm{d}m^2_{12}\mathrm{d}m^2_{23}, \end{aligned}$$

(22)

where $M_i$ denotes the mass of $B^{0}_{s1}$. If $p_-$ and $p_+$ are the momenta of $\pi ^+$ and $\pi ^-$, respectively, and q is the momentum of $B_s^+$, then $\mathrm{d}m^2_{12}=(p_++p_-)^2$ and $\mathrm{d}m^2_{23}=(p_-+q)^2$. In the heavy quark limit $P^\mu =M_i v^\mu$, $q^\mu =M_fv^\mu$, and $\epsilon \cdot v=0$, the amplitude is simplified to the following form:

$$\begin{aligned} \mathcal{M}=\mathcal{A}\, \epsilon \cdot (p_+-p_-)=\mathcal{A}\, \epsilon \cdot \Delta p\,. \end{aligned}$$

Fig. 6

Non-vanishing contributions to $B_{s1}^0 \rightarrow B_s^0 \pi ^+ \pi ^-$ decay amplitude

The non-vanishing Feynman diagrams that contribute to the amplitude $\mathcal{A}$ are presented in Fig. 6. Note that all diagrams with $\eta$ meson in the loop give a vanishing contribution, as already discussed in [21]. The amplitude $\mathcal{A}$ can then be written as

$$\begin{aligned} \mathcal{A}=\frac{h\sqrt{M_iM_f}}{16\pi ^2 f^4}\left( a_1+a_2+b_1+b_2+c_1+c_2\right) , \end{aligned}$$

(23)

where parts of the amplitudes can be written as a linear combination of the Veltman–Pasarino functions:

$$\begin{aligned} a_1= & {} \frac{g}{2}\left( \bar{B}_1(-\Delta _{SH}, m_{K^0})-\bar{B}_1(-\Delta _{SH}, m_{K^+})\right) , \end{aligned}$$

(24)

$$\begin{aligned} a_2= & {} \frac{\tilde{g}}{2}\left( \bar{B}_1(\Delta _{SH}, m_{K^0})-\bar{B}_1(\Delta _{SH}, m_{K^+})\right) , \end{aligned}$$

(25)

$$\begin{aligned} b_1= & {} 2g\left( \left( \bar{B}_2^\prime (-\Delta _{SH},-\Delta _{SH}/2, m_{K^0})\right. \right. \nonumber \\&\left. \left. -\Delta /2\cdot \bar{B}_1^\prime (-\Delta _{SH},-\Delta _{SH}/2, m_{K^0})\right) \right. \nonumber \\&\left. -\left( \bar{B}_2^\prime (-\Delta _{SH},-\Delta _{SH}/2, m_{K^+})\right. \right. \nonumber \\&\left. \left. -\Delta /2\cdot \bar{B}_1^\prime (-\Delta _{SH},-\Delta _{SH}/2, m_{K^+})\right) \right) , \end{aligned}$$

(26)

$$\begin{aligned} b_2= & {} 2\tilde{g}\left( \left( \bar{B}_2^\prime (\Delta _{SH}/2,\Delta _{SH}, m_{K^0})\right. \right. \nonumber \\&\left. \left. +\Delta /2\cdot \bar{B}_1^\prime (\Delta _{SH}/2,\Delta _{SH}, m_{K^0})\right) \right. \nonumber \\&-\left. \left( \bar{B}_2^\prime (\Delta _{SH}/2,\Delta _{SH}, m_{K^+})\right. \right. \nonumber \\&\left. \left. +\Delta /2\cdot \bar{B}_1^\prime (\Delta _{SH}/2,\Delta _{SH}, m_{K^+}) \right) \right) , \end{aligned}$$

(27)

$$\begin{aligned} c_1= & {} -2g\left( \left( B_{00}(m_{K^0})-\Delta _{SH}\bar{C}_{00}(-\Delta _{SH},m_{K^0})\right) \right. \nonumber \\&-\left. \left. (B_{00}(m_{K^+})-\Delta _{SH}\bar{C}_{00}(-\Delta _{SH},m_{K^+})\right) \right) \nonumber \\ c_2= & {} -2\tilde{g}\left( B_{00}(m_{K^0})-B_{00}(m_{K^+})\right) \,. \end{aligned}$$

(28)

Here, $\bar{B}_1$, $\bar{B}_2$, $B_{00}$, and $\bar{C}_{00}$ are the Veltman–Passarino loop integrals defined in Appendix A. As the $B_{s1}^0 \rightarrow B_s^0 \pi ^+ \pi ^-$ decay mode does not have any tree level contributions from the heavy meson Lagrangian, the amplitude is expected to be finite. Although some of the above integrals are divergent, these divergences cancel out as expected, when we take the sum of all contributions. We can also notice that the amplitude vanishes in the case of $m_{K^+}=m_{K^0}$, showing the nature of the isospin violating decay mode. The obtained decay widths are

$$\begin{aligned}&\Gamma (B_{s1}^0 \rightarrow B_s^0 \pi ^+ \pi ^-)=(1\pm 0.3)\times 10^{-3}\,\mathrm{keV}, \qquad \qquad \nonumber \\&\Gamma (B_{s1}^0 \rightarrow B_s^0 \pi ^0 \pi ^0)=(0.7 \pm 0.2) \times 10^{-3}\,\mathrm{keV}. \end{aligned}$$

In the case of $B_{s1}^0 \rightarrow B_s^0 \pi ^0 \pi ^0$ a factor 1/2 was taken into account due to the two identical mesons in the final state.

5 Comments and discussion

Systematically using HM$\chi$PT, we determine the decay widths of the isospin violating decay modes of positive parity $B_s$ mesons: $B_{s0}^{*0} \rightarrow B_s^0 \pi ^0$, $B_{s1}^{0} \rightarrow B_s^{*0} \pi ^0$, and $B_{s1}^{0} \rightarrow B_s^0 \pi \pi$. The masses of the decaying particles and the values of the coupling constants are taken from the lattice studies.

We find that the decay width $\Gamma (B_{s1}^{0} \rightarrow B_s^0 \pi \pi ) \sim 10^{-3}\,$keV. This process occurs only at loop level and the decay amplitudes are proportional to the mass difference of $K^+$ and $K^0$. The small available phase space additionally suppresses the decay width. This decay might also be approached by the exchange of the $f_0$ resonances $B_{s1}^{0} \rightarrow B_s^0 f_0 \rightarrow B_s^0 \pi \pi$ [12]. However, in the HM$\chi$PT this is a higher order contribution and therefore is not considered in our analysis. The approach of Ref. [12] (see Table 1) uses the exchange of $\sigma$ resonance in which there is a significant $\bar{s}s$ component. However, a recent lattice calculation of [52] disfavors such a content of $\sigma$.

Table 1 Predictions of the $B^{*0}_{s0} \rightarrow B_s \pi ^0$ and $B^{0}_{s1} \rightarrow B^*_s \pi ^0$ decay widths

The two-body decays of $B_{s0}^{*0}$ and $B_{s1}^{0}$ occur at three level through $\eta$–$\pi$ mixing. We find that the chiral loop corrections can significantly enhance or suppress the decay amplitudes being almost of the same order of magnitude as the tree-level contribution. We can only give a range of values for the decay widths. Namely, the decay widths are very sensitive to the value of the coupling constant h and change significantly if the coupling constant h is varied within the error bars determined by the lattice studies [45]. Also, the counter-terms are known only within a range of values in [21]. Let us note that the experimental measurement of the decay widths of the positive parity mesons $D^*_{s0}(2317)^\pm$ and $D_{s1}(2460)^\pm$, planned in the near future by various experiments, can lead to a more precise determination of the counter-terms [21]. Together with a detection and a measurement of the decay widths and the branching ratios of the strong decays of the positive parity $(0^+,1^+)$ $B_s$ meson doublet, it will in principle allow one to extract the value of the coupling constant h exclusively from the $D_s$ and $B_s$ positive parity $(0^+,1^+)$ doublet system. If this value would then deviate significantly from what is found by assuming the validity of SU(3) symmetry or quark model considerations, it would point at an unusual nature of these states.

In Table 1, we give the results of other existing studies. The authors of [23] find higher values of the decay widths in the molecular picture of positive parity $B_s$ states. In their approach, however, wave-function renormalization, which in our case tends to lower the decay widths significantly, is not taken into consideration. Note also that the contributions of $K^*$ loops, present in [23], are a higher order correction in the HM$\chi$PT approach and therefore are not included in our analysis.

It will be interesting if current experimental searches at LHCb and planned studies at Belle II would lead to the discovery of both states $B_{s0}^{*0}$ and $B_{s1}^{0}$. We hope that our study might shed more light on this issue.

Appendix A: Loop integrals

By employing dimensional regularization, in the renormalization scheme with $\delta =\frac{2}{4-D}-\gamma _E+\ln 4\pi +1=0$, we have

$$\begin{aligned}&A_0(m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{\mathrm{d}^Dk}{(k^2-m^2+i\epsilon )}= m^2\left( \delta -\ln \frac{m^2}{\mu ^2}\right) +\mathcal{O}(D-4), \\&B_0(p,m,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\qquad \times \int \frac{\mathrm{d}^Dk}{(k^2-m^2+i\epsilon )((k+p)^2-m^2+i\epsilon )} \\&\quad =\delta -\int _0^1 \ln \frac{x^2p^2-xp^2+m^2}{\mu ^2}dx+\mathcal{O}(D-4), \\&B_{00}(p,m,m)=\frac{1}{2(D-1)}[A_0(m)+(2m^2-p^2/2)B_0(p,m,m)], \end{aligned}$$

which in the $D \rightarrow 4$ limit gives

$$\begin{aligned}&B_{00}(p,m,m)=\frac{1}{6}[A_0(m)+(2m^2-p^2/2)B_0(p,m,m)\\&\quad +2m^2-p^2/3], \end{aligned}$$

$$\begin{aligned} B_{00}(m)=B_{00}(\Delta _M v,m,m)\,. \end{aligned}$$

The loop integrals with one heavy meson propagator are

$$\begin{aligned}&\bar{B}_0(\Delta ,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{\mathrm{d}^Dk}{(k^2-m^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =-2\Delta \left[ \delta -\ln \frac{m^2}{\mu ^2}-2F\left( \frac{m}{\Delta }\right) +1\right] +\mathcal{O}(D-4), \end{aligned}$$

with

$$\begin{aligned}&F(1/x)=\Bigg \{ \begin{array}{ll} \frac{1}{x}\sqrt{x^2-1}\ln (x+\sqrt{x^2-1}+i\epsilon )\,; &{} |x|>1, \\ \frac{-1}{x}\sqrt{1-x^2}\left( \frac{\pi }{2}-\tan ^{-1}\left( \frac{x}{\sqrt{1-x^2}}\right) \right) \,; &{} |x|\le 1, \end{array} \\&\bar{B}^\mu (\Delta ,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k^\mu \, \mathrm{d}^Dk}{(k^2-m^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =\bar{B}_1(\Delta ,m) v^\mu , \\&\bar{B}_1(\Delta ,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k \cdot v\, \mathrm{d}^Dk }{(k^2-m^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =A_0(m)+\Delta \bar{B}_0(\Delta ,m), \\&\bar{B}^{\mu \nu }(\Delta ,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times v\int \frac{k^\mu k^\nu \, \mathrm{d}^Dk}{(k^2-m^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =\bar{B}_{00}(\Delta ,m) g^{\mu \nu }+\bar{B}_{11}(\Delta ,m) v^\mu v^\nu , \\&\bar{B}_{00}(\Delta ,m)=\frac{1}{D-1}[(m^2-\Delta ^2)\bar{B}_0(\Delta ,m)-\Delta A_0(m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned} \bar{B}_{00}(\Delta ,m)= & {} \frac{1}{3}[(m^2-\Delta ^2)\bar{B}_0(\Delta ,m)\\&-\Delta A_0(m)+2\Delta /3(3m^2-2\Delta ^2)], \end{aligned}$$

$$\begin{aligned} \bar{B}_{11}(\Delta ,m)=\frac{1}{D-1}[(D\Delta ^2-m^2)\bar{B}_0(\Delta ,m)+D\Delta A_0(m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned} \bar{B}_{11}(\Delta ,m)= & {} \frac{1}{3}[(4\Delta ^2-m^2)\bar{B}_0(\Delta ,m)\\&+4\Delta A_0(m)-2\Delta /3(3m^2-2\Delta ^2)], \end{aligned}$$

$$\begin{aligned} \bar{B}_{2}(\Delta ,m)=\bar{B}_{00}(\Delta ,m)+\bar{B}_{11}(\Delta ,m), \end{aligned}$$

$$\begin{aligned}&\bar{B}_0^\prime (\Delta _1,\Delta _2,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{\mathrm{d}^Dk}{(k^2-m^2)(v\cdot k-\Delta _1)(v\cdot k-\Delta _2)}\\&\quad =\frac{1}{\Delta _1-\Delta _2}[\bar{B}_0(\Delta _1,m)-\bar{B}_0(\Delta _2,m)], \end{aligned}$$

$$\begin{aligned}&\bar{B}^{\mu \prime }(\Delta _1,\Delta _2,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k^\mu \, \mathrm{d}^Dk}{(k^2-m^2)(v\cdot k-\Delta _1)(v\cdot k-\Delta _2)}\\&\quad =\bar{B}_1^\prime (\Delta _1,\Delta _2,m) v^\mu , \end{aligned}$$

$$\begin{aligned}&\bar{B}_1^\prime (\Delta _1,\Delta _2,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k\cdot v\, \mathrm{d}^Dk}{(k^2-m^2)(v\cdot k-\Delta _1)(v\cdot k-\Delta _2)}\\&\quad =\bar{B}_0(\Delta _2,m)+\Delta _1 \bar{B}_0^\prime (\Delta _1,\Delta _2,m), \end{aligned}$$

$$\begin{aligned}&\bar{B}_2^\prime (\Delta _1,\Delta _2,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{(k\cdot v)^2\, \mathrm{d}^Dk}{(k^2-m^2)(v\cdot k-\Delta _1)(v\cdot k-\Delta _2)}\\&\quad =A_0(m)+(\Delta _1+\Delta _2)\bar{B}_0(\Delta _2,m)+\Delta _1^2 \bar{B}_0^\prime (\Delta _1,\Delta _2,m), \end{aligned}$$

$$\begin{aligned}&\bar{B}^{\mu \nu \prime }(\Delta _1,\Delta _2,m)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k^\mu k^\nu \, \mathrm{d}^Dk}{(k^2-m^2)(v\cdot k-\Delta _1)(v\cdot k-\Delta _2)}\\&\quad =\bar{B}_{00}^\prime (\Delta _1,\Delta _2,m) g^{\mu \nu }+\bar{B}_{11}^\prime (\Delta _1,\Delta _2,m) v^\mu v^\nu , \end{aligned}$$

$$\begin{aligned}&\bar{B}_{00}^\prime (\Delta _1,\Delta _2,m)=\frac{1}{D-1}[m^2\bar{B}_{0}^\prime (\Delta _1,\Delta _2,m)\\&\quad -\Delta _1\bar{B}_{1}^\prime (\Delta _1,\Delta _2,m)-\bar{B}_{1}(\Delta _2,m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned}&\frac{1}{3}[m^2\bar{B}_{0}^\prime (\Delta _1,\Delta _2,m)-\Delta _1\bar{B}_{1}^\prime (\Delta _1,\Delta _2,m)\\&\quad -\bar{B}_{1}(\Delta _2,m)+2/3(3m^ 2-2(\Delta _1^2+\Delta _2^2+\Delta _1\Delta _2))], \end{aligned}$$

$$\begin{aligned}&\bar{B}_{11}^\prime (\Delta _1,\Delta _2,m)=\frac{1}{D-1}[-m^2\bar{B}_{0}^\prime (\Delta _1,\Delta _2,m)\\&\quad +D\Delta _1 \bar{B}_{1}^\prime (\Delta _1,\Delta _2,m)+D\bar{B}_{1}(\Delta _2,m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned}&\frac{1}{3}[-m^2\bar{B}_{0}^\prime (\Delta _1,\Delta _2,m)+4\Delta _1 \bar{B}_{1}^\prime (\Delta _1,\Delta _2,m)\\&\quad +4\bar{B}_{1}(\Delta _2,m)-2/3(3m^ 2-2(\Delta _1^2+\Delta _2^2+\Delta _1\Delta _2))] \end{aligned}$$

The loop integrals with two heavy meson propagator are

$$\begin{aligned}&{\bar{C}}^\mu (p,\Delta ,m_1,m_2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k^\mu \, \mathrm{d}^Dk}{(k^2-m_1^2+i\epsilon )((k-p)^2-m_2^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =\bar{C}_1(p,\Delta ,m_1,m_2) v^\mu , \end{aligned}$$

$$\begin{aligned}&{\bar{C}}_1(p,\Delta ,m_1,m_2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k\cdot v\, \mathrm{d}^Dk}{(k^2-m_1^2+i\epsilon )((k-p)^2-m_2^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =B_0(p,m_1,m_2)+\Delta \bar{C}_0(p,\Delta ,m_1,m_2), \end{aligned}$$

$$\begin{aligned}&{\bar{C}}^{\mu \nu }(p,\Delta ,m_1,m_2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{k^\mu k^\nu \, \mathrm{d}^Dk}{(k^2-m_1^2+i\epsilon )((k-p)^2-m_2^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\\&\quad =\bar{C}_{00}(p,\Delta ,m_1,m_2)g^{\mu \nu }+ \bar{C}_{11}(p,\Delta ,m_1,m_2)v^\mu v^\nu , \end{aligned}$$

$$\begin{aligned}&\bar{C}_{00}(\Delta ,m)=\bar{C}_{00}(-\Delta _M v,\Delta ,m,m)\\&\quad =\frac{1}{D-1}[\bar{B}_0(-\Delta _M+\Delta ,m)-(\Delta _M/2+\Delta ) B_0(\Delta _m v,m,m)\\&\qquad +(m^2-\Delta ^2)\bar{C}_0(\Delta _M v,\Delta ,m,m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned}&\bar{C}_{00}(\Delta ,m)=\bar{C}_{00}(-\Delta _M v,\Delta ,m,m)\\&\quad =\frac{1}{3}[\bar{B}_0(-\Delta _M+\Delta ,m)-(\Delta _M/2+\Delta ) B_0(\Delta _m v,m,m)\\&\qquad +(m^2-\Delta ^2)\bar{C}_0(\Delta _M v,\Delta ,m,m)-2/3(3/2\Delta _M-\Delta )], \\&\bar{C}_{11}(\Delta ,m)=\bar{C}_{11}(-\Delta _M v,\Delta ,m,m)\\&\quad =\frac{1}{D-1}[-\bar{B}_0(-\Delta _M+\Delta ,m)+D(\Delta _M/2+\Delta ) B_0(\Delta _m v,m,m)\\&\qquad -(m^2-D\Delta ^2)\bar{C}_0(\Delta _M v,\Delta ,m,m)], \end{aligned}$$

which in $D\rightarrow 4$ gives

$$\begin{aligned}&\bar{C}_{11}(\Delta ,m)=\bar{C}_{11}(-\Delta _M v,\Delta ,m,m)\\&\quad =\frac{1}{3}[-\bar{B}_0(-\Delta _M\!+\!\Delta ,m)\!+\!4(\Delta _M/2+\Delta ) B_0(\Delta _m v,m,m)\\&\quad -(m^2-4\Delta ^2)\bar{C}_0(\Delta _M v,\Delta ,m,m)+2/3(3/2\Delta _M-\Delta )]. \end{aligned}$$

The calculation of the integral leaves us with

$$\begin{aligned}&\bar{C}_0(p,\Delta ,m_1,m_2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\\&\times \int \frac{\mathrm{d}^Dk}{(k^2-m_1^2+i\epsilon )((k-p)^2-m_2^2+i\epsilon )(v\cdot k-\Delta +i\epsilon )}\,; \end{aligned}$$

it is done in [53]. For some calculations, we used the program FeynCalc [54].