R-matrix calculations for few-quark bound states

Abstract

The R-matrix method is implemented to study the heavy charm and bottom diquark, triquark, tetraquark, and pentaquarks in configuration space, as the bound states of quark–antiquark, diquark–quark, diquark–antidiquark, and diquark–antitriquark systems, respectively. The mass spectrum and the size of these systems are calculated for different partial wave channels. The calculated masses are compared with recent theoretical results obtained by other methods in momentum and configuration spaces and also by available experimental data.

1 Introduction

The original idea of the R-matrix theory was introduced by Kapur and Peierls [1], to remove unsatisfactory reliance on perturbation theory in nuclear reactions. It was a few years later that Wigner simplified the idea to the formulation of R-matrix theory in which all expressions are energy dependent [2–4]. Although the R-matrix theory was originally developed for treatment of nuclear resonances [4, 5], it can also be used to describe all types of reaction phenomena and can be considered as an elegant method to solve the Schrödinger equation. These extensions especially became possible after the work of Bloch [6], by introducing a singular operator between internal and external regions.

The solution of the Schrödinger equation for the bound states of few-quarks in momentum space is numerically difficult to handle, because the confining part of the potential leads to singularity at small momenta. To overcome this problem we have successfully used a regularized form of the quark–antiquark [7] and recently diquark–antidiquark ($D\bar{D}$) [8, 9] interactions to solve the Lippmann–Schwinger (LS) equation in momentum space and calculate the mass spectrum of heavy quarkonia and tetraquarks. To this aim one can keep the divergent part of the potential fixed after exceeding a certain distance, called the regularization cutoff. This procedure creates an artificial barrier and the influence of tunneling barrier is manifested by significant changes in the energy eigenvalues at small distances.

Recently we have shown that the homogeneous LS equation can be formulated in configuration space to study the heavy tetraquarks as a bound state of $D\bar{D}$ system [10]. The variational methods are also used to study the few-quark bound states [11–17]. In order to obtain the variational energy, one must minimize the lowest eigenvalue with respect to the variational parameters after diagonalizing the Hamiltonian matrix. The variational energy can be obtained by differentiating the lowest eigenvalue with respect to the variational parameters. The successful application of the R-matrix theory to describe the resonance and scattering states resulting from the interaction of particles or systems of particles, which can be nucleons, nuclei, electrons, atoms, and molecules [18, 19], motivated us to implement it to the few-quark bound states. In the present paper we show that R-matrix theory is an effective and efficient method to study the bound states of few-quarks by solving the Schrödinger equation in different partial wave channels. The successful implementation of the R-matrix method to heavy few-quark systems paves the way to accurately predict the masses of few-quark bound states composed of light quarks.

2 R-matrix method for few-quark bound states in configuration space

In our study for diquark, triquark, tetraquark, and pentaquark systems, we have used a two-body picture by considering them as the bound states of quark–antiquark ($q\bar{q}$), diquark–quark (Dq), diquark–antidiquark ($D\bar{D}$) and diquark–antitriquark ($D\bar{T}$) systems, respectively. The nonrelativistic bound state of any of these two-body systems with the pair relative distance ${\mathbf r}$ in a partial wave representation can be described by the Schrödinger equation. For simplicity of the notation we use AB for representation of these systems, where A and B stand for any of the subsystems. Since the AB interaction V(r) is a central force, thus the wave function of few-quark bound states consists of some type of radial function times a spherical harmonic function, i.e. $\Psi _{nlm}({\mathbf r}) = R_{nl}(r) Y_{lm}(\theta ,\phi )$. The radial function can be obtained by solution of the differential equation

$$\begin{aligned}&\left( H_{l}-E \right) R_{nl}(r) \nonumber \\&\quad =\left[ -\dfrac{\hbar ^2}{2\mu } \Biggl (\dfrac{\mathrm{d}^2}{\mathrm{d}r^2}+\dfrac{2}{r}\dfrac{\mathrm{d}}{\mathrm{d}r}-\dfrac{l(l+1)}{r^2} \Biggr )+V(r)-E\right] R_{nl}(r)\nonumber \\&\quad =0, \end{aligned}$$

(1)

where $E=m_{AB}-m_A - m_{B}$ is the AB binding energy ($m_{AB}$ is the mass of AB system composed of two subsystems A and B with masses $m_A$ and $m_B$). $\mu = \dfrac{m_{A} m_{B}}{m_A +m_{B}}$ is the reduced mass and l is the orbital angular momentum of relative motion of AB system. In R-matrix calculations, the radial wave function is considered in two internal ($r<r_c$) and external ($r>r_c$) regions as $R_{\mathrm{int}}$ and $R_{\mathrm{ext}}$, respectively. The parameter a is large enough to ensure that the mass spectrum is independent of it.

The internal wave function $R_{\mathrm{int}}$ is defined as combination of the basis functions $u_i(r)$,

$$\begin{aligned} R_{\mathrm{int}}=\sum _{i=1}^{N} c_i \, u_i(r), \end{aligned}$$

(2)

where

$$\begin{aligned} u_i(r)=r^l \, e^{\left( -\dfrac{r^2}{2\rho _i^2} \right) }. \end{aligned}$$

(3)

In our study, the basis states parameters $\rho _i$ are

$$\begin{aligned} \rho _i=\rho _0\lambda ^{i-1}, \quad ~\rho _0=1.2\dfrac{r_c}{\lambda ^{N-1}},\quad \lambda =1.3,\quad N=30. \end{aligned}$$

(4)

Since in the external region the interaction between diquark and antidiquark is fixed, the external wave function can be considered as a modified spherical Bessel function of the second kind,

$$\begin{aligned} R_{\mathrm{ext}}=C_l \, k_l(\kappa r), \end{aligned}$$

(5)

where $C_l$ is a constant parameter and $\kappa =\sqrt{2 \mu \, (-E+V_0)}$. Continuity of the internal and external wave functions and derivatives implies that

$$\begin{aligned} R_{\mathrm{int}}(r_c)= & {} R_{\mathrm{ext}}(r_c), \nonumber \\ R'_{\mathrm{int}}(r_c)= & {} R'_{\mathrm{ext}}(r_c). \end{aligned}$$

(6)

The Hamiltonian $H_{l}$ is not Hermitian in the internal region. To avoid this the Bloch operator is defined as

$$\begin{aligned} L(b)=\dfrac{\hbar ^2}{2\mu } \, \delta \left( r-r_c \right) \, \left( \dfrac{\mathrm{d}}{\mathrm{d}r}-\dfrac{b}{r} \right) . \end{aligned}$$

(7)

The dimensionless parameter b is an arbitrary real constant. The delta function indicates that the Bloch operator is a surface operator acting only on $r = r_c$. The operator $H_{l} + L(b)$ is Hermitian, and therefore has a discrete spectrum in the finite region. Using Eq. (6), the Schrödinger equation in the internal region can be approximated by

$$\begin{aligned} \biggl ( H_{l}+L(b)-E \biggr ) \, R_{\mathrm{int}}(r)=L(b) \, R_{\mathrm{ext}}(r). \end{aligned}$$

(8)

It means the logarithmic derivative of the wave function is continuous at $r=r_c$. By multiplying Eq. (8) with $u_{i'}$ and integrating in the internal region, we obtain the following equation to determine the unknown coefficients $c_i$:

$$\begin{aligned} \sum _{i=1}^N \, C_{i'i}(E,b) \, c_i= & {} \langle u_{i'}|L(b)|R_{\mathrm{ext}}\rangle \nonumber \\= & {} \dfrac{\hbar ^2 r_c}{2\mu } \, u_{i'}(r_c) \, \biggl ( aR'_{\mathrm{ext}}(r_c)-bR_{\mathrm{ext}}(r_c) \biggr ),\nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned} C_{i'i}(E,b)=\left\langle u_{i'} \left| H_{l}+L(b)-E \right| u_i \right\rangle . \end{aligned}$$

(10)

Solving Eq. (9) for $c_i$ and substituting them into Eq. (6), i.e., $R_{\mathrm{int}}(r_c)=\sum _{i=1}^N c_i\, u_i(r_c) = R_{\mathrm{ext}}(r_c)$, leads to

$$\begin{aligned} R_{\mathrm{int}}(r_c)=R(E,b) \, \biggl ( a\,R'_{\mathrm{ext}}(r_c)-b\,R_{\mathrm{ext}}(r_c) \biggr ), \end{aligned}$$

(11)

where R(E, b) is the R-matrix given by

$$\begin{aligned} R(E,b)=\dfrac{\hbar ^2 r_c}{2\mu } \sum _{i,i'=1}^N u_{i}(r_c) \, C^{-1}_{ii'}(E,b) \, u_{i'}(r_c). \end{aligned}$$

(12)

The wave function in the internal region is then given by

$$\begin{aligned} R_{\mathrm{int}}(r)=\dfrac{\hbar ^2 r_c}{2\mu \, R(E,b)} \, R_{\mathrm{ext}}(r_c) \sum _{i,i'=1}^N u_{i}(r) \, C^{-1}_{ii'}(E,b) \, u_{i'}(r_c). \end{aligned}$$

(13)

By choosing $b = \dfrac{a \, R'_{\mathrm{ext}}(r_c)}{R_{\mathrm{ext}}(r_c)} = \dfrac{\kappa r_c \, k'_l(\kappa r_c)}{k_l(k r_c)}$, where $k'_l(\kappa r_c) = \dfrac{\mathrm{d}k_l}{\mathrm{d}(\kappa r_c)}$, the right hand side of Eq. (9) will be zero and consequently leads to the following Schrödinger–Bloch equation:

$$\begin{aligned} \sum _{i=1}^{N} \left\langle u_{i'} \left| H_{l}+L \biggl (b(E) \biggr )-E \right| u_i \right\rangle c_i=0. \end{aligned}$$

(14)

Since b depends on $\kappa$ or the AB binding energy E, which we want to calculate, we have written $b \equiv b(E)$. Equation (14) can be written schematically as the eigenvalue equation

$$\begin{aligned} \mathcal{A}\, c = \lambda \, \mathcal{B} \, c \end{aligned}$$

(15)

where the matrix elements of the $\mathcal{A}$ and $\mathcal{B}$ matrices can be obtained:

$$\begin{aligned} \mathcal{A}_{ij}= & {} \left\langle u_{i} \left| H_{l}+L \biggl (b(E) \biggr ) \right| u_j \right\rangle , \nonumber \\ \mathcal{B}_{ij}= & {} \left\langle u_{i} \left| \right. u_i \right\rangle . \end{aligned}$$

(16)

Since the $\mathcal{A}$ matrix is energy dependent, the solution of the eigenvalue equation (15) can be started by an initial guess for the energy E and the search in the binding energy can be stopped when $\left| \dfrac{\lambda - E}{E} \right| \le 10^{-10}$. In order to solve Eq. (14), we have discretized the continuous variable r with Gauss–Legendre points using a hyperbolic–linear mapping [8]. To this aim we have transferred the $[0,\infty )$ domain to $[0,1]\cup [1,2]\cup [2,15]\, \text {GeV}^{-1}$ using 75, 75, and 50 nodes in each subinterval, respectively. It indicates that the parameter $r_c$, which divides the configuration space into internal and external regions, is chosen to be $r_c=15\, \text {GeV}^{-1}$ and we have numerically verified that the calculated masses of the tetraquarks are independent of the regularization cutoff a.

By having the AB binding energy and eigenvector c from the solution of eigenvalue Eq. (15), we can calculate the AB internal wave function by Eqs. (10), (12), and (13). Of course, one can calculate the internal wave function directly using Eq. (2). Using AB wave function, we can evaluate the expectation value $\langle {r}\rangle$ for AB pair distance as

$$\begin{aligned} \langle {r}\rangle= & {} \int _0^{\infty } \mathrm{d}r\, r^3 R^2(r) \nonumber \\= & {} \int _0^{r_c} \mathrm{d}r\, r^3 R_{\mathrm{int}}^2(r) + \int _{r_c}^{\infty } \mathrm{d}r\, r^3 R_{\mathrm{ext}}^2(r), \end{aligned}$$

(17)

where the AB radial wave function is normalized to 1, i.e. $\int _0^{\infty } \mathrm{d}r\, r^2 R^2(r) = 1$.

3 Results and discussion

For numerical solution of the integral equation (1) for $q \bar{q}$, Dq, and $D \bar{D}$ we have used the spin-independent interaction

$$\begin{aligned} V (r) = V_{\mathrm{Coul}} (r) + V_{\mathrm{conf}} (r), \end{aligned}$$

(18)

with the linear confining

$$\begin{aligned} V_{\mathrm{conf}} (r) = a \,r+b, \end{aligned}$$

(19)

and the Coulomb-like one-gluon exchange potential

$$\begin{aligned} V_{\mathrm{Coul}} (r) = \gamma \, \dfrac{F_{A} (r) F_{B} (r)}{r}, \quad \gamma = \dfrac{-4}{3} \alpha _s. \end{aligned}$$

(20)

$F_A$ and $F_{B}$ are the form factors of the subsystems A and B, respectively, and have the following functional form:

$$\begin{aligned} F (r)= 1-e^{\alpha r -\beta r^2}. \end{aligned}$$

(21)

The parameters of this model are fixed from the analysis of heavy quarkonia masses and radiative decays [20–22].

3.1 Heavy quarkonia

For this first test of application of the R-matrix method, we have solved the integral equation (1) to calculate the mass spectra of heavy quarkonia, mesons consisting heavy quark and antiquark. We have used the linear confining plus Coulomb potential of Eq. (18) with form factor $F(r)=1$. The parameters of potentials are $a=0.18$ GeV$^2$, $b=-0.29$ GeV with $\alpha _s=0.47$ for charmonium ($m_c=1.56$ GeV) and $\alpha _s=0.39$ for bottomonium ($m_b=4.93$ GeV). As we show in Table 1, our numerical results for masses of charmonium and bottomonium, obtained by the R-matrix method, are in excellent agreement with the solution of the Lippmann–Schwinger integral equation in momentum space [7] and configuration space [23], and also with the experimental data [24].

Table 1 The mass spectra of charmonium $\psi (c\bar{c})$ and bottomonium $\Upsilon (b \bar{b})$ for the linear confining plus Coulomb potential of Eq. (18) with form factor $F(r)=1$. The masses are given in GeV. The numbers in parentheses are the expectation value of the relative distance between quark–antiquark pair $\langle {r}\rangle$ in units of fm

3.2 Heavy baryons

In the next step we have calculated the masses of the ground state heavy baryons consisting of two light (u; d; s) and one heavy (c; b) quarks in the heavy quark–light diquark approximation. The used diquark mass and form factor parameters are given in Table 2. As we show in Table 3, our numerical results for different heavy baryons, calculated by nonrelativistic R-matrix method, are in good agreement with relativistic and spin-dependent results of EFG [25] and also with MLW results [26] of lattice nonrelativistic QCD. The relative difference between our and Ebert, Faustov, and Galkin (EFG) group results is less than $1.2~ (4.8) \, \%$ for bottom (charm) baryons. Clearly the difference comes from the relativistic effects and also spin terms of the potential that we have ignored in our calculations.

Table 2 The mass m and form factor parameters $\alpha$ and $\beta$ of light–light and heavy–light diquarks. q stands for up and down quarks, and S and A denote the scalar and axial vector diquarks

Table 3 Masses of the ground states of heavy charm and bottom baryons in units of GeV, calculated by nonrelativistic R-matrix method compared to results of EFG (from solution of relativistic LS equation), to MLW results (obtained from lattice nonrelativistic QCD) and also to the experimental date. The numbers in parentheses are the expectation value of the relative distance between light diquark and heavy quark pair $\langle {r}\rangle$ in units of fm. The symbols [] and $\{\}$ denote the scalar and axial vector diquarks

Table 4 Masses of charm diquark–antidiquark states in units of GeV, calculated by nonrelativistic R-matrix method compared to nonrelativistic Lippmann–Schwinger (LS) calculations and relativistic EFG results. The numbers in parentheses are the expectation value of the relative distance between $D\bar{D}$ pair $\langle {r}\rangle$ in units of fm

Table 5 The same as Table 4, but for bottom tetraquarks

3.3 Heavy tetraquarks

In our calculations for heavy tetraquarks we have used the masses of diquark (antidiquark) and form factor parameters of Ref. [28] which are given in Table 2.

Our numerical results for the masses of charm ($cq\bar{c}\bar{q}$ and $cs\bar{c}\bar{s}$) and bottom ($bq\bar{b}\bar{q}$ and $bs\bar{b}\bar{s}$) tetraquarks for the s-, p-, and d-wave channels with total spin $\mathcal{S}=0$ are listed in Tables 4 and 5. The tetraquark masses are calculated for scalar $S\bar{S}$ and axial-vector $A\bar{A}$ diquark–antidiquark contents. We have also calculated the expectation value of the relative distance between $D\bar{D}$ pair which can provide an estimate of the size of the tetraquarks.

We have compared our results for tetraquark masses with recent results obtained in momentum and configuration spaces by solution of the nonrelativistic Lippmann–Schwinger integral equation [8, 10] and also with those of previous relativistic studies by EFG reported in Refs. [28–30].

It indicates that the calculated masses for the ground state of charm tetraquarks (i.e. $cq\bar{c}\bar{q}$ and $cs\bar{c}\bar{s}$) with corresponding results from LS (in configuration space) [10] show that they are in excellent agreement. Our results are also in good agreement with those of LS (in momentum space) and EFG with a relative percentage difference estimated to be at most 2.5 and $4\,\%$, respectively. While our R-matrix calculations and LS results are both done in a nonrelativistic spin-independent scheme, there is some difference between the results obtained in momentum and configuration spaces. Clearly, the difference between our R-matrix results in configuration space and EFG results in momentum space is larger, and it comes from the relativistic effects and also from the spin contribution in the $D\bar{D}$ interaction, which appears in spin–orbit, spin–spin, and tensor spin–space terms [29]. As we have shown in Ref. [8] the relativistic effect leads to a small reduction in the mass of heavy tetraquarks and decreases the masses of charm and bottom tetraquarks by less than 2 and $0.2\,\%$, respectively, whereas the spin contribution may lead to small decrease or increase in the masses of the tetraquarks.

Fig. 1

The x–z cross section of the s-, p-, and d-wave probability densities $|\Psi _{nlm}({\mathbf r})|^2$ for $bq\bar{b}\bar{q}$ tetraquark in $S\bar{S}$ state for $m=0$

In Fig. 1 we have shown few examples of the probability density $|\Psi _{nlm}({\mathbf r})|^2$ of $bq\bar{b}\bar{q}$ tetraquark in $S\bar{S}$ state for the s-, p-, and d-wave channels. As we can see the tetraquark probability functions for higher states have been expanded to larger distances which leads to larger expectation value for the relative distance between $D \bar{D}$ pair. As we can see in Tables 4 and 5, the expectation value of the relative distance between $D \bar{D}$ pair is almost the same for scalar $S\bar{S}$ and axial-vector $A\bar{A}$ diquark–antidiquark contents. It is larger for higher states and its size changes roughly with a factor of 3 from 1s to 3p state. In Table 6 we compare our results for the masses of charm and bottom tetraquarks with the possible experimental candidates. They are in good agreement with a relative difference below $3.4\,\%$.

Table 6 Comparison of our numerical results for the masses of charm and bottom diquark–antidiquark states, calculated by the R-matrix method and possible experimental candidates. The expectation value $\langle {r}\rangle$ for the diquark–antidiquark pair distance is also calculated

3.4 Pentaquarks

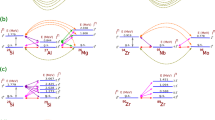
After successful application of the R-matrix method for diquark, triquarks, and tetraquarks we have also implemented it to study the pentaquarks as bound states of diquark–antitriquark systems (see Fig. 2).

In this study we have used two models of the $D\bar{T}$ interaction. In the following sections we present the models and our numerical results.

3.4.1 One-pion exchange potential

One-pion exchange potential (OPEP) acting between a nucleon and a heavy meson (D or B) given as [41]

$$\begin{aligned} V_{\pi } (r) =\left\{ \begin{array}{ll} V_0 , &{}\quad r< r_0 ,\\ 2 \mathbf{I}_N \cdot \mathbf{I}_H \biggl ( S_{12} V_T(r) + 2 \mathbf{S}_N \cdot \mathbf{S}_l V_c(r) \biggr ) , &{}\quad r > r_0, \end{array} \right. \nonumber \\ \end{aligned}$$

(22)

where

$$\begin{aligned} V_0= & {} -62.79 \quad \text {or} \quad -276 \, \text {MeV} , \nonumber \\ V_T(r)= & {} \dfrac{g_A g_H m_{\pi }^2 }{2 \pi f_{\pi }^2} \dfrac{e^{-m_{\pi }r}}{6r} \left( \dfrac{3}{m_{\pi }^2 r^2} + \dfrac{3}{m_{\pi }r} +1 \right) , \nonumber \\ V_c(r)= & {} \dfrac{g_A g_H m_{\pi }^2 }{2 \pi f_{\pi }^2} \dfrac{e^{-m_{\pi }r}}{3r} , \end{aligned}$$

(23)

and the labels are: nucleon isospin $I_N$, heavy meson isospin $I_H$ (total isospin $\mathbf{I} = \mathbf{I}_N + \mathbf{I}_H$), tensor force $S_{12}$, tensor potential $V_T (r)$, nucleon spin $S_N$, light quark in heavy meson spin $S_l$ (sum of nucleon spin and light quark spin $\mathbf{K} = \mathbf{S}_N + \mathbf{S}_l$) and central potential $V_c(r)$.

The parameters of the OPEP potential are given in Table 7.

Fig. 2

Pentaquark system as a diquark–antitriquark bound state

Table 7 The parameters of the OPEP potential used in the heavy pentaquark calculations

Our results for the masses of the pentaquarks composed of a nucleon and a meson (B and D mesons) for the $l=0$, $S=\frac{3}{2}$, and $J^P=\frac{3}{2}^+$ channel are given in Table 8. As we can see our results with R-matrix method are in excellent agreement with results of Cohen et al. [41].

Table 8 The masses of pentaquarks composed of a nucleon and a meson for the $l=0$, $S=\frac{3}{2}$, and $J^P=\frac{3}{2}^+$ channel. Upper panel: nucleon + B meson, lower panel: nucleon plus D meson. All masses are in GeV. Column A: constant potential, $V_0=-276$ MeV, and $r_0 = 1$ fm; B: constant potential, $V_0=-62.79$ MeV, and $r_0 = 1.5$ fm

Table 9 The parameters of the Cornell potential used in heavy pentaquark calculations

Table 10 Masses of charmoniumlike pentaquark $P_c^+$ in a diquark–antitriquark picture in units of MeV, calculated by nonrelativistic R-matrix method compared to Lebed’s results. The diquark–antitriquark separation $\langle {r}\rangle$ is also calculated in units of fm

3.4.2 Cornell potential

For the second test of pentaquark calculations, the nonrelativistic linear-plus-Coulomb Cornell potential is used. It has the following form [42]:

$$\begin{aligned} V(r) = V_c(r) + V_{\mathrm{spin-spin}}+ V_{\mathrm{spin-orbit}} + V_{\mathrm{tensor}} \end{aligned}$$

(24)

where

$$\begin{aligned} V_c(r)= & {} -\dfrac{4}{3} \dfrac{\alpha _s}{r} + br \nonumber \\ V_{\mathrm{spin-spin}}= & {} \dfrac{32 \pi \alpha _s}{9 m_D m_T} \left( \dfrac{\sigma }{\sqrt{\pi }} \right) ^3 e^{-\sigma ^2 r^2} \mathbf{S}_D \cdot \mathbf{S}_{\bar{T}} \nonumber \\ V_{\mathrm{spin-orbit}}= & {} \dfrac{1}{m_D m_T} \left( \dfrac{2\alpha _s}{r^3} - \dfrac{b}{2r} \right) \mathbf{L} \cdot \mathbf{S} \nonumber \\ V_{\mathrm{tensor}}= & {} \dfrac{1}{m_D m_T} \dfrac{4\alpha _s}{r^3} T, \end{aligned}$$

(25)

and the spin–spin, spin–orbit, and tensor operators can be calculated as

$$\begin{aligned}&{} \mathbf{S}_D \cdot \mathbf{S}_{\bar{T}} = \dfrac{1}{2} \left( \mathbf{S}^2 - \mathbf{S}_D^2 - \mathbf{S}_{\bar{T}}^2 \right) , \nonumber \\&{} \mathbf{L} \cdot \mathbf{S} = \dfrac{1}{2} \left( \mathbf{J}^2 - \mathbf{L}^2 - \mathbf{S}^2 \right) , \nonumber \\&\langle ^3L_J | T | ^3L_J \rangle = \left\{ \begin{array}{ll} \dfrac{-L}{6(2L+3)}, &{}\quad J=L+1 \\ \dfrac{1}{6}, &{}\quad J=L \\ -\dfrac{L+1}{6(2L-1)}, &{}\quad J=L-1. \end{array} \right. \end{aligned}$$

(26)

In Table 9, the parameters of the Cornell potential used in pentaquark calculations are given.

Our results for the masses of charmoniumlike pentaquark $P_c^+$ in the s- and p-wave channels are given in Table 10. In our calculations we have ignored tensor force and we have considered the central, spin–spin, and spin–orbit terms of the diquark–antitriquark interaction of Eq. (24).

Beside the small difference between our results for the masses of s- and p-wave charmoniumlike pentaquarks and Lebed’s results [43], which is about 5 % and comes from the tensor force being ignored, the diquark–antitriquark separation $\langle {r}\rangle$ for the s-wave channel with value of 0.306 fm is almost half of the separation obtained by Lebed with a value of 0.64 fm. For the p-wave channel, ignoring the tensor force leads to a relative difference of 14 % in the calculated separations.

In conclusion, we have implemented the R-matrix method to calculate the mass spectra of heavy quarkonia, baryons, tetraquarks, and pentaquarks in the two-body picture. Our numerical results for the masses of heavy charm and bottom few-quarks, even ignoring the relativistic effects, are in good agreement with other theoretical predictions and also with available experimental data.