1 Introduction

Recently, Banãdos, Silk, and West (BSW) [1] demonstrated that a Kerr black hole can act as a particle accelerator, i.e., when two particles collide arbitrarily close to the horizon of an extremal Kerr black hole, the center-of-mass energy (\(E_{\mathrm{CM}}\)) can grow infinitely in the limiting case of maximal rotation. The \(E_{\mathrm{CM}}\) becomes higher for an extremal black hole when one of the colliding particles has a critical angular momentum. This aroused much attention [1–23] in a series of subsequent papers by generalizing the BSW mechanism to different spacetimes, also opening a window into new physics with astrophysical applications, e.g., to understand the phenomenon like gamma ray bursts and AGNs in the Galaxy. Jacabson and Sotiriou [2] elucidated the BSW mechanism to discuss some practical limitations for the Kerr black hole to act as a particle accelerator. It was pointed out that infinite \(E_{\mathrm{CM}}\) for the colliding particles can only be attained when the black hole is exactly extremal and only in infinite time and on the horizon of the black hole. On the other hand, Lake [3] studied the BSW mechanism near the Cauchy horizon to show that \(E_{\mathrm{CM}}\) of the colliding particles is infinite. With the BSW mechanism extended to the Kerr–Newman black hole case [4], an unlimited \(E_{\mathrm{CM}}\) requires an additional restriction on the value of the spin parameter a. Zaslavskii [5] argued that a similar effect exists for a nonrotating but charged black hole even for the simplest case of radial motion of particles in a Reissner–Nordström background and also demonstrated that the BSW mechanism is a universal property of the rotating black holes [6, 7]. The BSW mechanism has been extended to an Einstein–Maxwell–Dilaton black hole [8], rotating stringy black hole [9], a Kerr–(anti-) de Sitter black hole [10], BTZ [11], a rotating black hole in Horava–Lifshitz gravity [12] and around the four-dimensional Kaluza–Klein extremal black hole in [8], and there resulted an infinitely large \(E_{\mathrm{CM}}\) near the horizon.

Later, Gao and Zhong showed that the BSW mechanism is possible for the nonextremal black holes, showing that for a critical angular momentum, the \(E_{\mathrm{CM}}\) diverges at the inner horizon. The interesting work of Grib and Pavlov [13–15] shows that the scattering energy of the particles in the center-of-mass frame can be arbitrarily large, not only for extremal black holes but also for nonextremal ones, when we take into account the multiple scattering. It turns out that the divergence of the \(E_{\mathrm{CM}}\) of the colliding particles is a phenomenon not only associated with black holes but also with naked singularities [16–19]. The BSW mechanism was further extended to the case of two different massive colliding particles near the Kerr black hole [20] and also in the case of Kerr–Newman black hole [21], and for the Kerr–Taub–NUT spacetime [22], suggesting that \(E_{\mathrm{CM}}\) depends not only on the rotation parameter a but also on the NUT charge n. These works on two different massive colliding particles are generalizations of previous studies (see also Harada and Kimura 2014 for a review of the BSW mechanism [23]).

While we are far away from any robust quantum theory of gravity that tell us how the singularities of classical black holes are solved, there are some models of black hole solutions without the central singularity. These are regular black holes first proposed by Bardeen metric [24], which is a solution of Einsteins gravity coupled to a nonlinear electrodynamics field [25]. Another interesting model is the Hayward’s black hole metric [26] and Ayón-Beato–García [25]. The rotating or Kerr-like solutions of the Bardeen and the Hayward’s metrics have also been obtained [27]. These rotating black holes violate even the weak energy condition is violated, but such a violation can be made very small [27]. Astrophysical black holes are more interested in the study of rotating regular black hole, but the actual nature of these objects has still to be tested [28, 29]. These regular black holes have an additional deviation parameter (say g) apart from the mass (M) and angular momentum (a), which provides a deviation from the Kerr black hole. It turns out that for these black holes, for each nonzero g, there exists a critical \(a_{E}\), which corresponds to a regular extremal black hole with degenerate horizons [30]. The BSW mechanism for these rotating regular black holes has also been analyzed in [31–33], suggesting that a rotating regular black hole can also act as a particle accelerator, which in turn provides a suitable framework for Planck-scale physics.

In the current paper, we want to discuss the collision of two different massive particles falling from rest at infinity in the background of rotating regular Hayward’s black holes.

Fig. 1
figure 1

Plot showing the behavior of the ergoregion in the xz-plane of a rotating regular Hayward’s black hole for \(g=0\) with different values of a. The blue and red lines correspond to the static limit surface and horizons, respectively

Full size image
Fig. 2
figure 2

Plot showing the behavior of the ergoregion in the xz-plane of a rotating regular Hayward’s black hole for different values of g. Here we take \(M=1\), \(\theta =\pi /2\). The blue and red lines correspond to the static limit surface and horizons, respectively

Full size image

2 Rotating regular Hayward’s black holes

The spherically symmetric Hayward’s metric [26] is given by

$$\begin{aligned} \mathrm{d}s^2 = -f(r)\mathrm{d}t^2+\frac{1}{f(r)}\mathrm{d}r^2 +r^2 \mathrm{d}\Omega ^2, \end{aligned}$$
(1)

with

$$\begin{aligned} f(r) = 1-\frac{2mr^2}{r^3+2l^2m} \quad \text { and } \quad \mathrm{d}\Omega ^2 = \mathrm{d}\theta ^2 +\sin ^2 \theta \mathrm{d}\phi ^2, \end{aligned}$$

where m is the mass and l is a constant. The metric (1) asymptotically behaves as

$$\begin{aligned} f(r) \sim 1-\frac{2m}{r} \quad \text { as } \; r \rightarrow \infty , \end{aligned}$$

where near the center

$$\begin{aligned} f(r) \sim 1-\frac{r^2}{l^2} \quad \text { as } \; r \rightarrow 0. \end{aligned}$$

The solution (1), for \(l=0\), reduces to the well-known Schwarzschild black hole and is flat for \(m=0\). The metric function and the curvature invariants are well behaved everywhere, including at the origin. The analysis of \(f(r)=0\) implies a critical mass \(m^* = 3\sqrt{3}l/4\) and a critical radius \(r^* = \sqrt{3}l\), such that a regular extremal black hole has degenerate horizons at \(r=r^*\) when \(m=m^*\). When \(m<m^*\), we have a regular nonextremal black hole horizon with both Cauchy and event horizon, corresponding to two roots of \(f(r)=0\), and no black hole when \(m>m^*\).

Next, the rotating spacetime corresponding to (1) is also obtained [27], which looks similar to the Kerr black hole except that M is replaced by m(r). In this section, we shall discuss the horizon structure and the ergoregion of a rotating regular Hayward’s black hole metric. The rotating regular Hayward’s black hole in Boyer–Lindquist coordinates reads [27]

$$\begin{aligned} \mathrm{d}s^2= & {} -\left[ 1-\frac{2m(r)r}{\Sigma }\right] \mathrm{d}t^2-\frac{4am(r)r \sin ^{2} \theta }{\Sigma }\mathrm{d}t \mathrm{d}\phi +\frac{\Sigma }{\Delta }\mathrm{d}r^2 \nonumber \\&+ \; \Sigma \mathrm{d} \theta ^2 +\left[ r^2+a^2+\frac{2 a^2 m(r)r \sin ^2 \theta }{\Sigma }\right] \sin ^2 \theta \mathrm{d} \phi ^2,\nonumber \\ \end{aligned}$$
(2)

where \(\Sigma \) and \(\Delta \), respectively, are given by

$$\begin{aligned} \Sigma= & {} r^2 + a^{2}\cos ^{2} \theta , \nonumber \\ \Delta= & {} r^2 + a^2 - 2 m(r) r. \end{aligned}$$
(3)

Here a is a rotation parameter, and m(r) is a function related to mass of the black hole via

$$\begin{aligned} m(r)=M \frac{r^{3+\alpha } \Sigma ^{-\alpha /2}}{r^{3+\alpha } \Sigma ^{-\alpha /2}+g^3 r^{\beta } \Sigma ^{-\beta /2}}, \end{aligned}$$
(4)

where M represents the black hole mass, g is the magnetic charge which provides a deviation from the standard Kerr black hole, and \(\alpha \), \(\beta \) are two real numbers. In the equatorial plane (\(\theta = \pi /2\)), the mass function (4) takes the form

$$\begin{aligned} m(r)=M \frac{r^3}{r^3+g^3}, \end{aligned}$$
(5)

which is independent of the parameters \(\alpha \), \(\beta \), and \(\theta \). The metric (2) represents a rotating regular Hayward’s black hole [27], which is a generalization of the Kerr spacetime because when \(g=0\), then it reduces to the standard Kerr black hole [34] and for both \(a=g=0\), the metric reduces to the Schwarzschild black hole [35]. A regular Hayward’s black hole satisfies the weak energy condition only for the nonrotating case (\(a=0\)) and violates the weak energy condition for the rotating case [27]. The metric is regular everywhere, including at \(r=0\), \(\theta =\pi /2\), as the Ricci scalar (\(R_{ab}R^{ab}\)) and the Kretschmann scalar (\(R_{abcd}R^{abcd}\)) are well behaved [31].

Table 1 Table for different values of a and g for a rotating regular Hayward’s black hole. \(\delta \) is the region between the static limit surface and event horizon (\(\delta ^{a}=r^{+}_{\mathrm{sls}}-r^{+}_{H}\))
Full size table

2.1 Ergoregion of rotating regular Hayward’s black hole

Recently, the horizon structure of the rotating regular Hayward’s black hole has been analyzed [31]. Here, we are going to discuss the ergoregion of the rotating regular Hayward’s black hole. The metric (2) becomes singular at \(\Delta =0\), which is a coordinate singularity. The event horizon of the rotating regular Hayward’s black hole is given by the zeros of \(\Delta =0\),

$$\begin{aligned} r^2 + a^2 -2 m(r) r=0. \end{aligned}$$
(6)

It is shown that Eq. (6) admits two roots, which correspond to, respectively, the event horizon and the Cauchy horizon. Definitely, the event horizon depends on \(\theta \), and hence it is different from the Kerr black hole. If the two horizons coincide, then we get an extremal black hole; otherwise it is known as a nonextremal black hole. Thus, the rotating regular Hayward’s black hole has an extremal black hole for each nonzero value of the deviation parameter g. There is another important surface of a black hole, particularly known as a static limit surface. The main property of the static limit surface is that the nature of particle geodesics changes after crossing the static limit surface, i.e., a timelike geodesic becomes spacelike and vice versa. The static limit surface satisfies \(g_{tt}=0\), i.e.,

$$\begin{aligned} r^2+ a^2 \cos ^{2} \theta - 2 m(r) r =0. \end{aligned}$$
(7)

From Eqs. (6) and (7), it is clear that the horizons and the static limit surface depend on the constants \(\alpha \), \(\beta \), g, and \(\theta \). It turns out that for each g, there exist critical \(a_E\) and \(r_H^E\), which corresponds to a regular extremal black hole with degenerate horizons, and \(a_E\) decreases whereas \(r^E_H\) increases with increase in g. The region between the event horizon and static limit surface is known as the ergoregion; from this region energy can be extracted via the Penrose process [36]. We show that as we increase the value of g for corresponding a, then the region between the event horizon and the static limit surface increases. In Figs. 1 and 2, we plot the contours of the horizon surfaces in the xz-plane of the rotating regular Hayward’s black hole to show the ergoregion for various values of g. The ergoregion for the rotating regular Hayward’s black hole is shown in Fig. 2, whereas the ergoregion of the Kerr black hole is shown in Fig. 1. The ergoregion has two boundaries: the event horizon and the outer static limit surface. The observer in the ergoregion cannot remain static. The ergoregion is sensitive to the deviation parameter g, and its area increases with g. This can be seen by the event horizon \(r_{H}^{+}\) and the static limit surface (\(r^+_{\mathrm{sls}}\)), which are depicted in Table 1, for various values of a and g. Interestingly, \(\delta ^a=r^+_{\mathrm{sls}}-r^+_H\) increases with g as well as a, thereby suggesting that the ergoregion is enlarged. Further, we find that for each value of rotation parameter a, there exists a critical value of \(g=g^*\), such that for \(g<g^*\), we have two horizons suggesting a nonextremal Hayward’s black hole, whereas for \(g=g^*\), one gets an extremal black hole where the two horizons coincide (cf. Fig. 2); for \(g>g^*\), we obtain no horizons or no black hole.

3 Equations of motion of the particle

Next, we calculate the equations of motion of a particle which will be necessary to determine the \(E_{\mathrm{CM}}\) of the two colliding particles for the rotating regular Hayward’s black hole (2). Indeed, we are interested in a study of the radial motion of the particle falling from rest at infinity in the background of a rotating regular Hayward’s black hole. Henceforth, we will restrict our discussion to the equatorial plane (\(\theta = \pi /2\)). The motion of the particle is determined by the Lagrangian

$$\begin{aligned} \mathcal {L}=\frac{1}{2} g_{\mu \nu } \frac{\mathrm{d} x^{\mu }}{\mathrm{d} \tau }\frac{\mathrm{d} x^{\nu }}{\mathrm{d} \tau }, \end{aligned}$$
(8)

where \(\tau \) is an affine parameter along the geodesic. Also, we know that the metric (2) has two Killing vectors, i.e., \(\xi ^a=\left( \frac{\partial }{\partial t}\right) ^a\) and \(\chi ^a=\left( \frac{\partial }{\partial \phi }\right) ^a\), which are, respectively, associated with two conserved quantities, the energy E and the angular momentum L. Furthermore, we can write the geodesic equations for a particle in terms of these conserved quantities

$$\begin{aligned} g_{ab} \xi ^a u^b= & {} -E, \\ g_{ab} \chi ^a u^b= & {} L, \end{aligned}$$

where \(u^a=\mathrm{d} x^a/\mathrm{d} \tau \), represents a 4-velocity. The above equations can be written as

$$\begin{aligned} g_{tt}u^{t}+g_{t \phi }u^{\phi }= & {} -E, \end{aligned}$$
(9)
$$\begin{aligned} g_{t \phi }u^{t}+g_{\phi \phi }u^{\phi }= & {} L. \end{aligned}$$
(10)

The 4-momentum of the particle having mass m is given by

$$\begin{aligned} p^ \mu = m u^{\mu }, \end{aligned}$$
(11)

where \(u^{\mu }\) is the 4-velocity of the particle. With the help of normalization of the 4-velocity \(u_{\mu }u^{\mu }=-1\), we can easily obtain the following relation:

$$\begin{aligned} p_{\mu }p^{\mu }=-m^2. \end{aligned}$$
(12)

This quantity is Lorentz invariant, i.e., it remains the same in all inertial frames under the Lorentz transformations and it also shows the conservation of momentum. Now, solving Eqs. (9) and (10) simultaneously, and using the condition (12), we obtain the geodesic equations [31, 32, 37, 38]

$$\begin{aligned} u^{t}= & {} \frac{1}{r^2 \Delta } \Big [-a (aE - L)\Delta + \left( r^2 + a^2\right) \mathcal {P} \Big ], \end{aligned}$$
(13)
$$\begin{aligned} u^{\phi }= & {} \frac{1}{r^2 \Delta } \Big [-(aE - L ) \Delta +a \mathcal {P} \Big ], \end{aligned}$$
(14)
$$\begin{aligned} u^{r}= & {} \pm \frac{1}{r^2} \sqrt{\mathcal {P}^2 -\Delta \left[ m^2 r^2 + (L-a E)^2 \right] }, \end{aligned}$$
(15)

where m corresponds to the mass of a particle, and

$$\begin{aligned} \mathcal {P} = (r^2 + a^2)E -L a. \end{aligned}$$

Equations (13)–(15) represent the motion of the particle around the rotating Hayward’s black hole. One can easily check that if we set \(g=0\), then Eqs. (13), (14), and (15) reduce to the geodesic equations of the Kerr black hole. Thus Eqs. (13), (14), and (15) are corrected by the deviation parameter g, and in the limit \(g \rightarrow 0\), we set the corresponding equations for the Kerr black hole [1]. The radial equation for the timelike particles moving along the geodesics is described by

$$\begin{aligned} \frac{1}{2} (u^r)^2 + V_{\mathrm{eff}} = 0, \end{aligned}$$
(16)

where \(V_{\mathrm{eff}}\) is the effective potential given by

$$\begin{aligned} V_{\mathrm{eff}} = -\frac{1}{2 r^4} \Big [[(r^2 + a^2)E -La]^2 -\Delta [m^2 r^2 + (L-a E)^2]\Big ], \end{aligned}$$
(17)

as the deviation parameter \( g \rightarrow 0\), \(V_{\mathrm{eff}}\) reduces to

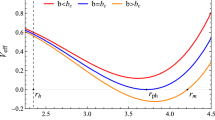
$$\begin{aligned} V_{\mathrm{eff}}= & {} -\frac{1}{2 r^4}\Big [[(r^2 + a^2)E -La]^2 \nonumber \\&-(r^2+a^2-2Mr) [m^2 r^2 + (L-a E)^2]\Big ], \end{aligned}$$
(18)

which is equivalent to the expression of a standard Kerr black hole [2]. We need to study \(V_{\mathrm{eff}}\) to get the range for the angular momentum with which the particle can approach the black hole. One can have an idea about the allowed and prohibited regions of the particle around the black hole, i.e., \(V_{\mathrm{eff}} \le 0\) and \(V_{\mathrm{eff}}>0\). We can obtain the possible values of angular momentum of the test particle by using the circular orbits conditions, i.e.,

$$\begin{aligned} V_{\mathrm{eff}}=0 \quad \text { and } \quad \frac{dV_{\mathrm{eff}}}{\mathrm{d}r}=0. \end{aligned}$$
(19)

Here, we are interested in calculating the range of the critical angular momentum with which particle can reach the horizon of the black hole, which can be calculated from the effective potential using Eq. (19). Since geodesics are timelike, i.e., \(\mathrm{d}t/\mathrm{d} \tau \ge 0\), Eq. (13) leads to

$$\begin{aligned} \frac{1}{r^2}\left[ -a(aE-L)+(r^2+a^2)\frac{\mathcal {P}}{\Delta }\right] \ge 0, \end{aligned}$$
(20)

and the above condition at the horizon reduces to

$$\begin{aligned}&E-\Omega _H L \ge 0, \nonumber \\&\Omega _H=\frac{a}{(r_H^E)^2+a^2}. \end{aligned}$$
(21)

The critical angular momentum of the particle is defined by \(L_C=E/\Omega _H\), where \(\Omega _H\) is the angular velocity of the black hole at the horizon. This has been calculated numerically for the rotating regular Hayward’s black hole in Ref. [31] for both extremal and nonextremal black holes. If \(L > L_C\), then the particle will never reach to the horizon of the black hole, where \(L_C\) is the critical angular momentum of the particle. Instead, if \(L < L_C\), then the particle will always fall into the black hole, and if \(L=L_C\), then the particle hits exactly at the event horizon of the black hole.

4 Center-of-mass energy of the colliding particles in Hayward’s black hole

We know the range of the angular momentum for which the particle can reach the horizon and a collision takes place at the horizon of the black hole. Here, we shall study the \(E_{\mathrm{CM}}\) for the collision of two particles with rest masses \(m_{1}\) and \( m_{2}\) (\(m_{1}\ne m_{2}\)), which are initially at rest at infinity, moving toward the rotating regular Hayward’s black hole and colliding in the vicinity of the event horizon. Let us consider the case that the particles are coming with energies \(E_1\), \(E_2\) and angular momentum \(L_{1}\), \(L_{2}\). The 4-momentum of the ith particle is \(p^{\mu }_{i} = m_{i} u^{\mu }_{i}\), where \(m_{i}\) and \( u^{\mu }_{i}\) correspond, respectively, to the mass and the 4-velocity of the ith particle (\(i=1,2\)), and the total 4-momenta of the particles is given by

$$\begin{aligned} p^{\mu }_{t} = p^{\mu }_{(1)} + p^{\mu }_{(2)} = m_{1} u^{\mu }_{(1)} + m_{2} u^{\mu }_{(2)}. \end{aligned}$$
(22)

Then \(E_{\mathrm{CM}}\) of the two particles is given by

$$\begin{aligned} E_{\mathrm{CM}}^2 = - p^{\mu }_{t} p_{t \mu } = m_{1}^2 + m_{2}^2 - 2 g_{\mu \nu } p^{\mu }_{(1)} p^{\nu }_{(2)}; \end{aligned}$$
(23)

by substituting Eq. (22) into Eq. (23), we have

$$\begin{aligned} E_{\mathrm{CM}}^2= & {} m_{1}^2+m_{2}^2-2m_{1}m_{2}g_{\mu \nu }u^{\mu }_{(1)}u^{\nu }_{(2)}, \end{aligned}$$
(24)

which, due to \(u^a u_a=-1\), can be rewritten in the following form:

$$\begin{aligned} E_{\mathrm{CM}}= & {} \sqrt{2 m_1 m_2} \sqrt{1+\frac{(m_{1}-m_{2})^2}{2m_{1}m_{2}}-g_{\mu \nu }u^{\mu }_{(1)}u^{\nu }_{(2)}}, \end{aligned}$$
(25)

when \(m_1=m_2=m_0\), Eq. (25) reduces to

$$\begin{aligned} E_{\mathrm{CM}}= & {} m_0\sqrt{2} \sqrt{1-g_{\mu \nu }u^{\mu }_{(1)}u^{\nu }_{(2)}}. \end{aligned}$$
(26)

Equation (25) is valid for the massive particles. Inserting the values of \(g_{\mu \nu }\), \(u^{\mu }_{(1)}\), and \(u^{\nu }_{(2)}\) from Eqs. (2), (13), (14), and (15) into Eq. (25), we can obtain \(E_{\mathrm{CM}}\) of the two particles for the rotating regular Hayward’s black hole,

$$\begin{aligned} \frac{E_{\mathrm{CM}}^2}{2 m_1 m_2}= & {} \frac{(m_{1}-m_{2})^{2}}{2 m_1 m_2} + \frac{1}{r(r^2-2 m(r) r+a^2)} \left[ \phantom {\sqrt{r(r^2+a^2)(E^2_{2}-m_2^2) +2 m(r)(a E_{2}-L_{2})^2 - L_{2}^{2}r + 2 m(r) r^2 m_2^2}}a^2[(2 m(r)+r)E_1 E_2+r] \right. \nonumber \\&-\;2a m(r)(L_{1} E_{2}+L_{2} E_{1}) -L_{1}L_{2} (-2m(r)+r)+[-2 m(r)+r(1+E_1 E_2)]r^2 \nonumber \\&-\;\sqrt{r(r^2+a^2)(E^2_{1}-m_1^2) +2 m(r)(a E_{1}-L_{1})^2 - L_{1}^{2}r + 2 m(r) r^2 m_1^2 } \nonumber \\&\left. \times \;\sqrt{r(r^2+a^2)(E^2_{2}-m_2^2) +2 m(r)(a E_{2}-L_{2})^2 - L_{2}^{2}r + 2 m(r) r^2 m_2^2}\right] , \end{aligned}$$
(27)

where the mass m(r) is given by Eq. (5). Obviously, the result Eq. (27) confirms that the parameter g has influence on \(E_{\mathrm{CM}}\). Thus, \(E_{\mathrm{CM}}\) depends on the parameters g and a. When \(g \rightarrow 0\), in Eq. (27), we obtain the \(E_{\mathrm{CM}}\) of two different mass particles of the Kerr black hole [20],

$$\begin{aligned} \frac{E_{\mathrm{CM}}^2}{2 m_{1} m_{2}}(g \rightarrow 0)= & {} \frac{(m_{1}-m_{2})^{2}}{2 m_1 m_2} +\frac{1}{r(r^2-2 M r+a^2)} \left[ \phantom {\sqrt{r(r^2+a^2)(E^2_{2}-m_2^2)+2M(a E_{2}-L_{2})^2 - L_{2}^2r + 2 M r^2 m_2^2}}a^2[(2 M+r)E_1 E_2+r] \right. \nonumber \\&-\;2a M(L_{1} E_{2}+L_{2} E_{1}) -L_{1}L_{2} (-2M + r)+[-2 M +r(1+E_1 E_2)]r^2 \nonumber \\&-\;\sqrt{r(r^2+a^2)(E^2_{1}-m_1^2)+2M(a E_{1}-L_{1})^2 - L_{1}^2 r + 2M r^2 m_1^2} \nonumber \\&\left. \times \;\sqrt{r(r^2+a^2)(E^2_{2}-m_2^2)+2M(a E_{2}-L_{2})^2 - L_{2}^2r + 2 M r^2 m_2^2}\right] . \end{aligned}$$
(28)

Furthermore, if we choose \(m_{1}=m_{2}=m_{0}\), and \(E_{1}=E_{2}=E=1\), then Eq. (27) reduces to

$$\begin{aligned} \frac{E_{\mathrm{CM}}^2}{2 m_0^2}= & {} \frac{ 1}{r(r^2-2 m(r) r +a^2)}\left[ \phantom {\sqrt{2 m(r) (a-L_{2})^2 - L_{2}^{2} r+2 m(r) r^2}}2 a^2 (m(r) +r) -2am(r)(L_{1}+L_{2})- L_{1}L_{2} (-2m(r) +r) \right. \nonumber \\&\left. +\;2(-m(r) +r)r^2 -\sqrt{2 m(r) (a-L_{1})^2 - L_{1}^{2} r +2 m(r)r^2} \sqrt{2 m(r) (a-L_{2})^2 - L_{2}^{2} r+2 m(r) r^2}\right] , \end{aligned}$$
(29)

which represents the \(E_{\mathrm{CM}}\) of two equal mass particles as shown in [31]. Again, if we consider the case when \(g \rightarrow 0\), \(M=1\), \(m_{1}=m_{2}=m_{0}\), and \(E_{1}=E_{2}=E=1\), then Eq. (27) reduces to

$$\begin{aligned} \frac{E_{\mathrm{CM}}^2}{2 m_0^2}(g \rightarrow 0)= & {} \frac{1}{r(r^2-2 r +a^2)}\left[ \phantom {\sqrt{2 (a-L_{1})^2 - L_{1}^{2} r + 2 r^2 }}2 a^2 (1+r) -2 a(L_{1}+L_{2})-L_{1}L_{2}(-2+r) \right. \nonumber \\&\left. +\;2(-1+r)r^2 - \sqrt{2 (a-L_{2})^2 - L_{2}^{2} r + 2 r^2 } \sqrt{2 (a-L_{1})^2 - L_{1}^{2} r + 2 r^2 } \right] , \end{aligned}$$
(30)

which is exactly the same expression as obtained in [1]. Thus, we have obtained \(E_{\mathrm{CM}}\) of the rotating regular Hayward’s black hole for two different mass particles which is a generalization of the Kerr black hole. One can easily check that Eq. (27) has the 0 / 0-form at the event horizon of the black hole; therefore we apply the l’Hôpital’s rule to find the limits of \(E_{\mathrm{CM}}\) at the event horizon of both extremal and nonextremal black holes one by one.

Fig. 3
figure 3

Plots showing the behavior of \(E_{\mathrm{CM}}\) vs. r for extremal rotating regular Hayward’s black hole with mass of the colliding particles \(m_{1}=1, m_{2}=2\) and different values of the angular momentum \(L_{1}\) and \(L_{2}\). The vertical line corresponds to the location of the event horizon

Full size image

4.1 Near horizon collision in near-extremal Hayward’s black hole

Now, we can study the properties of \(E_{\mathrm{CM}}\) (27) as \(r \rightarrow r_H^E\) of the extremal rotating regular Hayward’s black hole. We note that in the limit \(r \rightarrow r_H^E\), Eq. (27) has the 0 / 0-form. Hence, we apply the l’Hôpital’s rule twice and get the following form:

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_{1}m_{2}}(r \rightarrow r^{E}_{H})\nonumber \\&\quad = \frac{(m_{1}-m_{2})^2}{2m_{1}m_{2}} + \frac{1}{(E_1-\Omega _H L_1) (E_2-\Omega _H L_2)} \nonumber \\&\qquad \times \; \Big [0.60991 L_1 L_2 + 1.67177\big [(E_1-\Omega _H L_1)^2 m_{2}^2 \nonumber \\&\qquad +\;(E_2-\Omega _H L_2)^2 m_{1}^2\big ] -1.42804(L_1 E_2+L_2 E_1) \nonumber \\&\qquad +\;0.49184(L_{1}^2 E_{2}^2 +L_{2}^2 E_{1}^2) \nonumber \\&\qquad +\;(3.34356+0.98368 L_1 L_2)E_1 E_2\Big ], \end{aligned}$$
(31)

where \(a = a^E_H= 0.896105795790474\), \(M=1\), \(g=0.5\), \(r^E\_H=1.13802\). The critical values of the angular momentum can be calculated by \(E_i-\Omega _{H}L_{i}=0\) or \(L_{C_i}=E_i/\Omega _{H}\) \((i=1,2)\), where \(L_{C_i}\) represents the critical value of angular momentum of the ith particle and \(\Omega _{H}=a/(r_H^2+a^2)\) is the angular velocity at the event horizon of the black hole. It is clear from Eq. (31) that if either \(L_{C_1}=L_1\) or \(L_{C_2}=L_2\), then the \(E_{\mathrm{CM}}\) becomes infinite, i.e., the necessary condition for getting \(E_{\mathrm{CM}}\) infinite is \(L=L_C\) or \(\Omega _H L =E\), for each particle. One can also see the behavior of \(E_{\mathrm{CM}}\) vs. r for an extremal rotating regular Hayward’s black hole from Fig. 3; it can be seen that \(E_{\mathrm{CM}}\) is infinite for the critical values of angular momentum \(L_1=2.0, 2.0305, 2.34136, 2.52987\), corresponding to \(g=0, 0.2, 0.5, 0.6\), and it remains finite for other values.

Next we consider the limits \(E_ 1 = E_2 = E\), and \(m_1=m_2=m_0\); in this case Eq. (31) reduces to

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_0^2}(r \rightarrow r^{E}_{H})\nonumber \\&\quad = \frac{1}{(E-\Omega _H L_1) (E-\Omega _H L_2)} \nonumber \\&\qquad \times \;[0.60991 L_1 L_2 +1.67177[(E-\Omega _H L_1)^2 \nonumber \\&\qquad +\;(E-\Omega _H L_2)^2]m_{0}^2 -1.42804(L_1+L_2) E \nonumber \\&\qquad +\;0.49184(L_{1}^2+L_{2}^2)E^2+(3.34356+0.98368 L_1 L_2)E^2].\nonumber \\ \end{aligned}$$
(32)

Here the critical angular momentum in this case can be calculated by using \(L_{C}=E/\Omega _{H}\). One can observe from Eq. (32) that if either \(L_C=L_1\) or \(L_C=L_2\), i.e., if one of the particles is coming with a critical angular momentum, then we should get an infinite amount of \(E_{\mathrm{CM}}\) and the angular momentum of one of the particles is not equal to \(L_C\) or greater than \(L_C\); then the amount of \(E_{\mathrm{CM}}\) is finite. One can obtain the limit of \(E_{\mathrm{CM}}\) (27) for \(g \rightarrow 0\) at \(r \rightarrow r_H^E\), and \(a=a_E\), which will take the following form:

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_{1}m_{2}}(r \rightarrow r^{+}_{H})\nonumber \\&\quad = \frac{(m_{1}-m_{2})^2}{2m_{1}m_{2}}+\frac{1}{4 (E_1-\Omega _H L_1) (E_2-\Omega _H L_2)} \nonumber \\&\qquad \times \; \left[ 4 (E_1 -\Omega _H L_1)^2 m_2^2 + 8 E_2 (E_1-\Omega _H L_1)\right. \nonumber \\&\qquad -4 (E_1-\Omega _H L_1) L_2 +E_1^2 L_2^2 +E_2^2 L_1^2 -2 E_1 E_2 L_1 L_2 \nonumber \\&\qquad \left. +\;4 E_2^2 m_1^2 -4 E_2 L_2 m_1^2 + L_2^2 m_1^2 \right] ; \end{aligned}$$
(33)

it represents the Kerr black hole case of two different massive colliding particles.

Fig. 4
figure 4

Plots showing the behavior of \(E_{\mathrm{CM}}\) vs. r for a nonextremal rotating regular Hayward’s black hole with mass of the colliding particles \(m_{1}=1, m_{2}=2\), and for different values of \(L_1\), \(L_2\), and g. The vertical line corresponds to the location of event horizon

Full size image

4.2 Particle collision for nonextremal black hole

If the two horizons of (2) do not coincide, we have a nonextremal rotating regular Hayward’s black hole. As mentioned above, both the numerator and the denominator of Eq. (27) vanish at \(r \rightarrow r^{+}_H\). Hence, applying the l’Hôpital’s rule and calculating \(E_{\mathrm{CM}}\) at \(r \rightarrow r^{+}_H\), after a tedious calculation, we obtain

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_{1}m_{2}}(r \rightarrow r^{+}_{H})\nonumber \\&\quad = \frac{(m_{1}-m_{2})^2}{2m_{1}m_{2}} +\frac{0.5 (E_2-\Omega _H L_2)}{(E_1-\Omega _H L_1)} \nonumber \\&\qquad \times \; [0.872182 L_1^2 +3.41504 E_1 L_1 -16.8792 E_1^2 \nonumber \\&\qquad +\;1.97103 m_1^2\Big ]+\frac{0.5 (E_1-\Omega _H L_1)}{(E_2-\Omega _H L_2)} \Big [0.872182 L_2^2 \nonumber \\&\qquad +\;3.41504 E_2 L_2-16.8792 E_2^2 + 1.97103 m_2^2\Big ] \nonumber \\&\qquad +\;2.13440 (0.8 E_1-L_1) (0.8 E_2-L_2) \nonumber \\&\qquad -\;3.00658 L_1 L_2+1.97103 +15.51320 E_1 E_2, \end{aligned}$$
(34)

where \(a=0.8\), \(g=0.5\), and \( r^{+}_{H}=1.50328\). The expression \(E_i-\Omega _{H}L_{i}=0\) \((i=1,2)\) gives the critical angular momentum of a particle for the nonextremal black hole case, which is \(L'_{C_i}=E_i/\Omega _{H}\). It seems from Eq. (34) that either \(L_{C_1}^{'}=L_1\) or \(L_{C_2}^{'}=L_2\); then \(E_{\mathrm{CM}}\) diverges, but in this case it is not possible because \(L_{C_1}^{'}\) and \(L_{C_2}^{'}\) does not lie in the range of the angular momentum. Hence, one can say that \(E_{\mathrm{CM}}\) never becomes infinite; it will remain finite. Furthermore, for \(E_1 = E_2 =E\), and \(m_1=m_2=m_0\), Eq. (34) takes the form

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_0^{2}}(r \rightarrow r^{+}_{H})\nonumber \\&\quad = \frac{0.5 (E-\Omega _H L_2)}{(E-\Omega _H L_1)} \left( 0.872182 L_1^2 +3.41504 E L_1 \right. \nonumber \\&\qquad \left. -\;16.8792 E^2 + 1.97103 m_0^2\right) \nonumber \\&\qquad +\;\frac{0.5 (E-\Omega _H L_1)}{(E-\Omega _H L_2)}\left( 0.872182 L_2^2 +3.41504 E L_2 \right. \nonumber \\&\qquad \left. -\;16.8792 E^2 + 1.97103 m_0^2\right) \nonumber \\&\qquad +\;2.13440 (0.8 E-L_1) (0.8 E-L_2) -3.00658 L_1 L_2 \nonumber \\&\qquad +\;1.97103 +15.51320 E^2. \end{aligned}$$
(35)

Figure 4 shows the behavior of \(E_{\mathrm{CM}}\) with radius r for a nonextremal black hole, which indicates that \(E_{\mathrm{CM}}\) remains finite for each value of \(L_{1}\) and \(L_{2}\). Furthermore, the effect of g can also be seen from Fig. 4, which indicates that \(E_{\mathrm{CM}}\) increases with g. The limit of nonextremal \(E_{\mathrm{CM}}\) for two different mass particles, in the case of \(g \rightarrow 0\), has the following form:

$$\begin{aligned}&\frac{E_{\mathrm{CM}}^2}{2m_{0}^2}(r \rightarrow r^{+}_{H})\nonumber \\&\quad = \frac{(m_{1}-m_{2})^2}{2m_{1}m_{2}} -\frac{0.5 (E_2-\Omega _H L_2)}{E_1-\Omega _H L_1} \nonumber \\&\qquad \times \; \left( 19.712 E_1^2-3.2 E_1 L_1-1.2 L_1^2-3.072 m_1^2\right) \nonumber \\&\qquad +\; 2 (0.8 E_1-L_1) (0.8 E_2-L_2)+ 0.6 L_2^2 - 3.2 L_1 L_2 \nonumber \\&\qquad +\;1.6 E_2 L_2 + 18.432 E_1 E_2 -9.856 E_2^2\nonumber \\&\qquad +\;1.536 m_2^2+3.072, \end{aligned}$$
(36)

where \(a=0.8\), and \( r^{+}_{H}=1.6\). From Eq. (36), it is clear that \(E_{\mathrm{CM}}\) becomes infinite if one of the angular momenta gets a critical value.

5 Conclusion

The singularity theorems under fairly general conditions imply that a sufficiently massive collapsing object will undergo continual gravitational collapse, resulting in the formation of a singularity. However, it is widely believed that singularities do not exist in Nature, but that they are an artifact of general relativity. Hence, especially in the absence of well-defined quantum gravity, the regular models without singularities received much attention. Also, the astrophysical black holes may be different from the Kerr black holes predicted in general relativity [28], but the actual nature of these objects has still to be verified. The rotating regular Hayward’s black hole can be seen as one of the non-Kerr black hole metrics, which in Boyer–Lindquist coordinates is the same as the Kerr black hole with M replaced by a mass function m(r) , which has an additional parameter due to the magnetic charge g; Hayward’s black hole reduces to the Kerr black hole in the absence of charge (\(g=0\)). Interestingly, for each nonzero value of g, the Hayward’s black hole is extremal with critical spin parameter \(a^*\) with degenerate horizons [31]. In this paper, we have performed a detailed analysis of the ergoregion in the rotating regular Hayward’s black hole [27], and we discuss the effect of the deviation parameter g on the ergoregion. Our analysis reveals (cf. Fig. 2) that for each a there exists a critical \(g=g^*\) such that for \(g >g^*\), the rotating regular Hayward’s black hole has a disconnected horizon, and the horizons coincide when \(g=g^*\), and we have two horizons when \(g<g^*\). When the ergoregion of a rotating regular Hayward’s black hole is compared with the Kerr black hole (cf. Fig. 1), we find that the ergoregion is sensitive to the deviation parameter g, and the ergoregion enlarges as the value of the deviation parameter increases.

We have also studied the collision of two particles with different rest masses moving in the equatorial plane of the rotating regular Hayward’s black hole, and we calculated the \(E_{\mathrm{CM}}\) for these colliding particles. We obtain a general expression of \(E_{\mathrm{CM}}\) for the rotating regular Hayward’s black hole, the \(E_{\mathrm{CM}}\) is calculated when the collision takes place near the horizon for both extremal and nonextremal black holes. It is demonstrated that \(E_{\mathrm{CM}}\) not only depends on the rotation parameter a of the rotating regular Hayward’s black hole, but also on the deviation parameter g. Further, for an extremal black hole, we address the case of arbitrarily high \(E_{\mathrm{CM}}\) when the collision occurs near the horizon and one of the particles has critical angular momentum. We also calculate \(E_{\mathrm{CM}}\) for the nonextremal rotating regular Hayward’s black hole, and we found that \(E_{\mathrm{CM}}\) is finite with an upper bound which increases with an increase in the parameter g.