Could the observation of X(5568) be a result of the near threshold rescattering effects?

Abstract

We investigate the invariant mass distributions of $B_s\pi$ via different rescattering processes. The triangle singularity which appears in the rescattering amplitude may simulate the resonance-like bump around 5568 MeV. However, because the scattering $B_s^*\pi \rightarrow B_s\pi$ is supposed to be weak, if the pertinent background is much larger, it would be hard to ascribe the observation of X(5568) to rescattering effects.

1 Introduction

The study of exotic hadron spectroscopy is experiencing a renaissance in the last decade. More and more charmonium-like and bottomonium-like states (called XYZ) have been announced by experiments in various processes (see Refs. [1–4] for a review). Several charged structures with a hidden $\bar{b}b$ or $\bar{c}c$, such as the$Z_c^\pm (4430)$ [5, 6], $Z_b^\pm (10610,10650)$ [7], $Z_c^\pm (3900)$ [8, 9], and $Z_c^\pm (4020)$ [10] were observed by experiments, which would be exotic state candidates. Very recently, the D0 collaboration observed a narrow structure X(5568) in the $B_s^0\pi ^\pm$ invariant mass spectrum with $5.1\sigma$ significance [11]. The mass and width are measured to be $M_X=5567.8\pm 2.9^{+2.9}_{-1.9}$ MeV and $\Gamma _X=21.9\pm 6.4^{+5.0}_{-2.5}$ MeV, respectively. The quark components of the decaying final state $B_s^0 \pi ^\pm$ are $su\bar{b} \bar{d}$ (or $sd\bar{b} \bar{u}$), which requires X(5568) should be a structure with four different valence quarks.

After the discovery of X(5568), several theoretical investigations were carried out in order to understand its underlying structure. In Refs. [12–15], the X(5568) was thought to be a scalar or axial-vector tetraquark state, and the corresponding mass was calculated by constructing the diquark–antidiquark interpolating current in the framework of QCD sum rules. The tetraquark masses calculated with QCD sum rules are found to be consistent with the mass of X(5568). The tetraquark spectroscopy was also calculated by using the effective Hamiltonian approach in Ref. [16]. The lowest-lying scalar tetraquark is found to be about 150 MeV higher than the X(5568) in Ref. [16], but the authors argued that it is still likely to identify the X(5568) as the scalar tetraquark when the systematic errors in the model are considered. In Ref. [17], the authors estimated the partial decay width $X(5568) \rightarrow B_s^0 \pi ^+$ with the X(5568) being an S-wave $B\bar{K}$ molecular state.

Some non-resonance explanations have been proposed to connect resonance-like peaks with kinematic singularities induced by the rescattering effects [18–30]. It is shown that sometimes it is not necessary to introduce a genuine resonance to describe a resonance-like structure, because some kinematic singularities of the rescattering amplitudes will behave themselves as bumps in the invariant mass distributions. Before claiming that X(5568) is a genuine particle, such as a tetraquark or molecular state, it is also necessary to confirm or exclude the possibilities of those non-resonance explanations.

This work is organized as follows: in Sect. 2, the so-called triangle singularity (TS) mechanism is briefly introduced; In Sect. 3, we discuss several rescattering processes where the TS can be present; a brief summary and some discussion are given in Sect. 4.

2 TS mechanism

The possible manifestation of the TS was first noticed in the 1960s. It is found that the TSs of rescattering amplitudes can mimic resonance structures in the corresponding invariant mass distributions [31–41]. This offers a non-resonance explanation about the resonance-like peaks observed in experiments. Unfortunately, most of the proposed cases in 1960s were lack of experimental support. The TS mechanism was rediscovered in recent years and used to interpret some exotic phenomena, such as the largely isospin-violation processes, the production of some exotic states and so on [23–30, 42–47].

For the triangle diagram in Fig. 1, all of the three internal lines can be on-shell simultaneously in some special kinematic configurations. This case corresponds to the leading Landau singularity of the triangle diagram, and this leading Landau singularity is usually called the TS. The physical picture concerning the TS mechanism can be understood like this: The initial particles $k_a$ and $k_b$ first scatter into particles $q_2$ and $q_3$, then the particle $q_1$ emitted from $q_2$ catches up with $q_3$, and finally $q_2$ and $q_3$ will rescatter into particles $p_b$ and $p_c$. This implies that the rescattering diagram can be interpreted as a classical process in space-time in the presence of TS, and the TS will be located on the physical boundary of the rescattering amplitude [37].

Fig. 1

Triangle rescattering diagram under discussion. The internal mass which corresponds to the internal momentum $q_i$ is $m_i$ (i $=$1, 2, 3). The momentum symbols also represent the corresponding particles

The TS mechanism is very sensitive to the kinematic configurations of rescattering diagrams. It is therefore necessary to determine in which kinematic region the TS can be present. In Fig. 1, we define the invariants $s_1=(k_a+k_b)^2$, $s_2=(p_b+p_c)^2$ and $s_3=p_a^2$. The locations of TS can be determined by solving the so-called Landau equations [48–50]. For the diagram in Fig. 1, if we fix the internal masses $m_i$, the external invariants $s_2$ and $s_3$, we can obtain the solutions of TS in $s_1$, i.e.,

(1)

with $\lambda (x,y,z)= (x-y-z)^2- 4yz$. Likewise, by fixing $m_i$, $s_1$, and $s_3$ we can obtain similar solutions to TS in $s_2$, i.e.,

(2)

By means of the single dispersion representation of the 3-point function, we learn that within the physical boundary only the solution $s_1^-$ or $s_2^-$ will correspond to the TS of the rescattering amplitude, and $\sqrt{s_1^-}$ and $\sqrt{s_2^-}$ are usually defined as the anomalous thresholds [46, 49, 50]. For convenience, we further define the normal threshold $\sqrt{s_{1N}}$ ($\sqrt{s_{2N}}$) and the critical value $\sqrt{s_{1C}}$ ($\sqrt{s_{2C}}$) for $s_1$ ($s_2$) as follows [46]:

$$\begin{aligned} \begin{aligned} s_{1N}&=(m_2+m_3)^2, \\ s_{1C}&=(m_2+m_3)^2 +\frac{m_3}{m_1}[(m_2-m_1)^2-s_3], \\ s_{2N}&=(m_1+m_3)^2,\\ s_{2C}&=(m_1+m_3)^2 +\frac{m_3}{m_2}[(m_2-m_1)^2-s_3]. \end{aligned} \end{aligned}$$

(3)

If we fix $s_3$ and the internal masses $m_{1,2,3}$, when $s_1$ increases from $s_{1N}$ to $s_{1C}$, $s_2^-$ will move from $s_{2C}$ to $s_{2N}$. Likewise, when $s_2$ increases from $s_{2N}$ to $s_{2C}$, $s_1^-$ will move from $s_{1C}$ to $s_{1N}$. This is the kinematic region where the TS can be present. The discrepancies between normal and anomalous thresholds can also be used to represent the TS kinematic region. The maximum values of these discrepancies take the form

$$\begin{aligned} \begin{aligned} \Delta _{s_1}^{\max }&=\sqrt{s_{1C}} - \sqrt{s_{1N}}\\&\approx \frac{m_3}{2m_1(m_2+m_3)}[(m_2-m_1)^2-s_3], \\ \Delta _{s_2}^{\max }&=\sqrt{s_{2C}} - \sqrt{s_{2N}}\\&\approx \frac{m_3}{2m_2(m_1+m_3)}[(m_2-m_1)^2-s_3]. \end{aligned} \end{aligned}$$

(4)

In Ref. [41], it was argued that for the single channel rescattering process, when the corresponding resonance-production tree diagram is added coherently to the triangle rescattering diagram, the effect of the triangle diagram is nothing more than a multiplication of the singularity from the tree diagram by a phase factor. Therefore the singularities of triangle diagram cannot produce obvious peaks in the Dalitz plot projections. This is the so-called Schmid theorem. But for the coupled-channel cases, the situation will be quite different from the single channel case discussed in Ref. [41]. For the rescattering diagrams which will be studied in this paper, the intermediate and final states are different, therefore the singularities induced by the rescattering processes are still expected to be visible in the Dalitz plot projections. The reader is referred to Refs. [35, 51] for some comments about the Schmid theorem, and to Refs. [52, 53] for some discussions about the coupled-channel case. We will focus on the coupled-channel cases in this work.

3 Production of $B_s\pi$ via rescattering processes

3.1 Triangle diagram

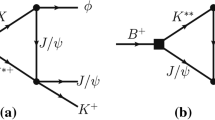
The mass of X(5568) is very close to the $B_s^*\pi ^\pm$-threshold, which is about 5555 MeV [2]. One may wonder whether there are some connections between X(5568) and the coupled-channel scattering $B_s^*\pi \rightarrow B_s\pi$ near threshold. In the high energy collisions, the production of $B_s\pi$ may receive contributions from rescattering diagrams illustrated in Fig. 2. The intriguing characteristic of this kind of diagrams is that the TSs are expected to be present in the rescattering amplitudes, which may result in some resonance-like bumps in $B_s\pi$ distributions around the $B_s^*\pi$-threshold accordingly.

The momentum and invariant conventions of Fig. 2 are the same as those of Fig. 1. According to Eqs. (3) and (4), the kinematic region where the TS can be present is displayed in Table 1.

Fig. 2

Production of $B_s\pi$ via the triangle rescattering diagrams a $[B_s^*\rho \pi ]$-loop and b $[B_s^* K^*\pi ]$-loop. The symbol A represents the incident state

Table 1 TS kinematic region corresponding to the rescattering diagrams in Fig. 2, in units of GeV

It can be seen that the kinematic region of TS in $s_1$ is very large for both of the diagrams in Fig. 2. $\Delta _{s_1}^{\max }$ is nearly 1 GeV for each of the diagrams. First, this is because the quantity $[(m_2-m_1)^2-s_3]$ in Eq. (4) is large. Physically, this quantity corresponds to the phase-space factor for $\rho \rightarrow \pi \pi$ ($K^*\rightarrow K\pi$), which is sizable. Second, the ratio $m_3/m_1$ is equal to $M_{B_s^*}/M_\pi$, which is also quite large. This means that the kinematic conditions of the presence of TS can be fulfilled in a very broad energy region of incident states. Then the kinematic requirement on the incident state would be largely relaxed, which is an advantage to observe the effects resulted by the TS mechanism. On the other hand, the kinematic region of TS in $s_2$ is relatively smaller. $\Delta _{s_2}^{\max }$ is about 0.2 GeV for each of the diagrams, which implies that the TS peaks in $B_s\pi$ distributions may not stay far away from the $B_s^*\pi$-threshold (normal threshold $\sqrt{s_{2N}}$).

Fig. 3

$M_{B_s\pi }$-dependence of the rescattering amplitude squared $|T|^2$ (after the appropriate sum and average over polarizations). Plots a and b correspond to Fig. 2a, b, respectively. W is the invariant mass $\sqrt{s_1}$ of incident state A. The vertical dashed line indicates the position of X(5568)

We will naively construct some effective Lagrangians to estimate the behavior of the rescattering amplitudes. Taking into account the conservation of angular momentum and parity, the quantum numbers of the incident state A are set to be $J^P=1^+$. Some of the Lagrangians read

$$\begin{aligned}&\mathcal {L}_{AB_s^* V}= g_{A} \epsilon ^{\mu \nu \alpha \beta } \partial _\mu A_\nu V_\alpha {B^*_s}_\beta , \end{aligned}$$

(5)

$$\begin{aligned}&\mathcal {L}_{VPP}= i g_{VPP} V^\mu (P \partial _\mu P^\prime - \partial _\mu P P^\prime ), \end{aligned}$$

(6)

where V and $P^{(\prime )}$ represent the light vector and pesudoscalar mesons, respectively. The process $B_s^*\pi \rightarrow B_s\pi$ can be P-wave scattering, and the corresponding Lagrangian takes the form

$$\begin{aligned} \mathcal {L}_{B_s^*B_s\pi \pi }= & {} g_{CT} \epsilon ^{\mu \nu \alpha \beta } {B^*_s}_\mu \partial _\nu B_s \partial _\alpha \pi \partial _\beta \pi . \end{aligned}$$

(7)

The P-wave scattering implies that the quantum numbers of $B_s^*\pi$ and $B_s\pi$ systems would be $J^P=1^-$. It should be mentioned that the processes $A\rightarrow B_s^* V$ in Fig. 2 can also happen through weak interactions in high energy collisions, therefore the parity does not have to be conserved for this vertex.

When the kinematic conditions of the TS are fulfilled, it implies that the particle $q_2$ in Fig. 1 is unstable. We then introduce a Breit–Wigner-type propagator $[q_2^2-m_2^2+i m_2 \Gamma _2]^{-1}$ to account for the width effect when calculating the triangle loop integrals. The complex mass of the intermediate state will remove the TS from physical boundary by a distance [36]. If the width $\Gamma _2$ is not very large, the TS will lie close to the physical boundary, and the scattering amplitude can still feel the influence of the singularity.

The numerical results for $B_s\pi$ invariant mass distributions corresponding to the rescattering processes in Fig. 2 are displayed in Fig. 3. We ignore the explicit couplings but just focus on the line shapes here. The distributions are calculated at several incident energy points. From Fig. 3, it can be seen that some bumps arise around the position of X(5568). Since the TS in $\sqrt{s_2}$ ($B_s\pi$ invariant mass) can be present for a very broad range of incident energy $\sqrt{s_1}$, the bumps around 5568 MeV would be enhanced to some extent due to the accumulative effects of the rescattering amplitudes at different incident energies.

The bumps in Fig. 3a are broader compared with those in Fig. 3b. This is because the decay width of the $\rho$-meson ($\sim$149 MeV) is larger than that of the $K^*$-meson ($\sim$50 MeV) [2]. The larger decay width will remove the corresponding TS in the complex-plane further away from the physical boundary. Furthermore, the P-wave scattering $B_s^*\pi \rightarrow B_s\pi$ will also smooth the TS peaks to some extent.

3.2 Long-range interaction and box diagram

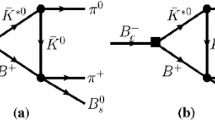
The scattering process $B_s^*\pi \rightarrow B_s\pi$ would be OZI suppressed. In the effective Lagrangian of Eq. (7), we assume we have a contact term, which may account for the short-range part of the corresponding interaction. If we take into account the t-channel contributions, because the momentum transfer in this process will be very small, some long-range interactions, such as the electromagnetic (EM) interaction, may become important. To judge whether the EM interaction may play a role in $B_s^*\pi \rightarrow B_s\pi$, we compare the contributions of t-channel processes illustrated in Fig. 4.

Fig. 4

The t-channel contributions for $B_s^*\pi \rightarrow B_s\pi$. a Photon exchange; b $\phi$-exchange

In Fig. 4a, b, we use the photon- and $\phi$-exchange diagrams to partly account for the EM and strong interactions, respectively. Some effective Lagrangians are constructed as follows

$$\begin{aligned}&\mathcal {L}_{B_s^*B_s\gamma }= i g_{B_s^* B_s\gamma } \epsilon ^{\mu \nu \alpha \beta } \partial _\mu {B^*_s}_\nu \partial _\alpha \mathcal {A}_\beta B_s , \end{aligned}$$

(8)

$$\begin{aligned}&\mathcal {L}_{B_s^*B_s\phi }= i g_{B_s^* B_s\phi } \epsilon ^{\mu \nu \alpha \beta } \partial _\mu {B^*_s}_\nu \partial _\alpha \phi _\beta B_s , \end{aligned}$$

(9)

$$\begin{aligned}&\mathcal {L}_{\gamma \pi \pi }= -i e \mathcal {A}^\mu (\partial _\mu \pi ^+ \pi ^- - \pi ^+ \partial _\mu \pi ^-). \end{aligned}$$

(10)

We first of all compare the coupling constants of these two diagrams. On adopting the vector meson dominance model [54–57], the ratio $R_{\gamma /\phi }\equiv e g_{B_s^* B_s\gamma }/ g_{\phi \pi \pi } g_{B_s^* B_s\phi }$ would be equal to $\sqrt{4\pi \alpha _e}g_{\gamma \phi } / g_{\phi \pi \pi }$, where the couplings $g_{\gamma \phi }$ and $g_{\phi \pi \pi }$ are estimated to be 0.0226 and 0.0072 according to the decay widths of $\phi \rightarrow e^+e^-$ and $\phi \rightarrow \pi \pi$, respectively. The ratio $R_{\gamma /\phi }$ is then obtained to be about 0.9 . According to this naive estimation, we can see that the EM couplings may not be very smaller compared with the OZI suppressed strong couplings. Without introducing any form factors to account for the off-shell effects, we further integrate over the momentum transfer t and obtain the cross section ratios $\sigma _{\gamma }/\sigma _{\phi }$ for different scattering energies, which is displayed in Fig. 5. It is shown that the cross section corresponding to Fig. 4a is larger than that corresponding to Fig. 4b by about three orders of magnitude. This is mainly because the quantity 1 / t is much larger than $1/(t-m_\phi ^2)$. As a result we could make a quantitative judgment that the contribution of EM interaction may be comparable with that of strong interaction.

Fig. 5

Total cross section ratio $\frac{\sigma _\gamma }{\sigma _\phi }$ corresponding to the t-channel scatterings in Fig. 4. $\sqrt{s}$ represents the scattering energy

Fig. 6

Production of $B_s\pi$ via the box rescattering diagrams a $[B_s^*\rho \pi \gamma ]$-loop and b $[B_s^* K^*\pi \gamma ]$-loop

Fig. 7

$M_{B_s\pi }$-dependence of the rescattering amplitude squared $|T|^2$ (after the appropriate sum and average over polarizations). Plots a, b correspond to Fig. 6a, b, respectively. W is the invariant mass $\sqrt{s_1}$ of incident state A. The vertical dashed line indicates the position of X(5568)

Taking into account the above arguments, the triangle diagram in Fig. 2 can be changed into the box diagram in Fig. 6 accordingly, and the numerical results for the $B_s\pi$ invariant mass distributions are displayed in Fig. 7. Because the masses of $B_s$ and $B_s^*$ are different, it can be judged that there is no infrared divergence in these box diagrams [58]. Compared with the resonance-like bumps in Fig. 3, the bumps in Fig. 7 are much narrower and more like resonance peaks. This implies that the interaction details of the scattering $B_s^*\pi \rightarrow B_s\pi$ may affect the TS mechanism to some extent.

If the long-range EM interactions play a dominant role in $B_s^*\pi \rightarrow B_s\pi$, one cannot expect there will be TS peaks arising in the $B_s\pi ^0$ invariant mass distributions, because there is no $\gamma \pi ^0\pi ^0$ vertex. We can further conclude that if the observation of X(5568) is due to the rescattering effects and the long-range EM interaction dominates the scattering $B_s^*\pi \rightarrow B_s\pi$, there will be no charge neutral partner of X(5568).

It should be mentioned that we did not take into account the contribution of any possible background in the numerical calculations, but the background could be essential for the rescattering processes discussed in this paper. Because the reaction $B_s^*\pi \rightarrow B_s\pi$ could be weak, if the background is very large, it is possible that the peaks resulted by the rescattering effects will be smoothed to some extent. However, the quantitative discussion on this uncertainty is beyond the scope of this paper, and it will be left for future work.

3.3 Weak interaction process

As stated before, the process $A\rightarrow B_s^* V$ can also happen via the weak interactions, such as $B_c^{(**)}\rightarrow B_s^* V$. Interestingly, according to the quark model calculation in Ref. [59], it can be noticed that there are many charm-beauty mesons $B_c^{(**)}$, of which the masses just fall into the region $6.2{-}7.5$ GeV. This energy region has a large overlap with the TS kinematic region displayed in Table 1. This is another support that the TS mechanism may play a role in the observation of X(5568).

4 Summary

In this paper, we investigated the invariant mass distributions of $B_s\pi$ via different rescattering processes. For a very broad incident energy region, one can expect that the TS bumps could be present around 5568 MeV in $B_s\pi$ distributions, which may simulate the resonance-like structure X(5568). However, to conserve the parity and angular momentum, the process $B_s^*\pi \rightarrow B_s\pi$ should be a P-wave scattering, of which the amplitude is suppressed by the low momentum of scattering particles. Furthermore, this process is also suppressed by the OZI rule. Therefore the scattering amplitude of $B_s^*\pi \rightarrow B_s\pi$ is supposed to be weak, which will weaken the possibility of ascribing the observation of X(5568) to rescattering effects. Some similar discussions can be found in Refs. [60, 61]. The rescattering processes induced by the EM interactions can make the TS bumps narrower, and even the amplitude strength can be comparable with that of strong interaction. But if the EM interactions play a dominant role in the rescattering effects, it can also be expected that the pertinent background would be much larger. Although the rescattering amplitudes could be enhanced to some extent by the TS mechanism, it is still hard to describe the X(5568) with rescattering effects. In a preliminary result of the LHCb collaboration [62], the existence of X(5568) is not confirmed based on their pp collision data, which makes the production mechanism and the underlying structure of X(5568) more puzzling. Further extensive experiments may help us to clarify the ambiguities and check different mechanisms.