Abstract
We consider the impact of several flavour-changing observables in the B- and the Kaon sectors on the parameter space of the NMSSM, in a minimal flavour violating version of this model. Our purpose consists in updating our previous results in [4] and designing an up-to-date flavour test for the public package NMSSMTools. We provide details concerning our implementation of the constraints in a series of brief reviews of the current status of the considered channels. Finally, we present a few consequences of these flavour constraints for the NMSSM, turning to two specific scenarios: one is characteristic of the MSSM-limit and illustrates the workings of charged-Higgs and genuinely supersymmetric contributions to flavour-changing processes; the second focus is a region where a light CP-odd Higgs is present. Strong limits are found whenever an enhancement factor – large \(\tan \beta \), light \(H^{\pm }\), resonant pseudoscalar – comes into play.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flavour-changing rare decays and oscillation parameters are known as uncircumventable tests of the Standard Model (SM) and its new-physics extensions. In the quark sector of the SM, flavour-violation is induced by the non-alignment of the Yukawa matrices, resulting in a Cabbibbo–Kobayashi–Maskawa (CKM) mixing matrix, and conveyed only by charged currents at tree-level. While tensions are occasionally reported – see e.g. [1] and references therein for a recent example – this minimal picture seems globally consistent with the current experimental status of flavour observables [2], such that new sources or new mediators of flavour violation are relevantly constrained by these measurements. Yet, a proper confrontation of a new-physics model to such experimental results does not depend exclusively on the accuracy of the measurements or of the theoretical predictions in the SM, but also on the magnitude of the effects induced beyond the SM (BSM).
In this paper, we will consider the well-motivated supersymmetric (SUSY) extension of the SM known as the Next-to-Minimal Supersymmetric Standard Model (NMSSM) – see [3] for a review – in a minimal flavour-violating version: we will assume that the squark sector is aligned with the mass-states in the quark sector, so that, at tree-level, only charged particles convey flavour-violating effects, which are always proportional to the CKM matrix. Our aims consist in updating our previous work in [4] to the current status of flavour observables and accordingly designing a tool for a test in the flavour-sector which will be attached to the public package NMSSMTools [5–8]. Beyond ours, several projects for the study of flavour observables in the NMSSM, or more generally in SUSY extensions of the SM, have been presented in the literature: see e.g. [9–16].
Our original work dealing with B-physics in the NMSSM [4] discussed the processes \(BR(\bar{B}\rightarrow X_s\gamma )\), \(BR(B^0_s\rightarrow \mu ^+\mu ^-)\), \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\) as well as the oscillation parameters \(\Delta M_{d,s}\). These processes had been implemented in the Fortran code bsg.f at (grossly) leading order (LO) in terms of the BSM contributions, using the NLO formalism for the SM and locally correcting it to account for NNLO effects in an ad-hoc fashion: in other words, this analysis essentially compiled results of the late 90’/early 2000’s [17–25]. In doing so, it ignored existing NLO results in the MSSM [26–28], focussed instead, at the loop level, on \(\tan \beta \)-enhanced Higgs-penguin contributions [22, 25] and only caught the early developments of the NNLO calculation in the SM [29, 30].
The SM analysis of \(BR(\bar{B}\rightarrow X_s\gamma )\) at NNLO has been recently updated in [31, 32]: the corresponding results account for significant progress since [29] and shift the SM expectation \(\sim \)1\(\sigma \) upwards, very close to the experimental measurement. Similarly, \(BR(B^0_s\rightarrow \mu ^+\mu ^-)\) has been considered up to three-loop order in the SM [33–35], shifting the result upwards with respect to the LO. Moreover, LHCb and CMS now provide an actual measurement of this process [36], which tightens the associated constraint significantly with respect to the previous upper limits. The SM status of \(\bar{B}\rightarrow X_sl^+l^-\) has also received some attention lately [37]. Finally, several other channels – e.g. \(B^+\rightarrow D^{(*)}\tau ^+\nu _{\tau }\), the \(b\rightarrow s\nu \bar{\nu }\) or the \(s\rightarrow d\nu \bar{\nu }\) transitions – have been suggested as complementary probes of new physics.
In addition to these recent developments concerning the SM and experimental status of flavour processes, we note that, as the NLO contributions in supersymmetric extensions of the SM can be extracted from e.g. [26–28], it is scientifically sound to include them into our implementation of the observables, so as to reduce the associated uncertainty in the test. This is particularly true in the case of \(BR(B^0_s\rightarrow \mu ^+\mu ^-)\), since this process is now measured and no longer simply bounded two orders of magnitude from above. The substantial shift in the SM estimate for \(BR(\bar{B}\rightarrow X_s\gamma )\) also tightens the constraint on BSM effects, so that enhanced precision is relevant.
Our purpose in this paper consists in describing the new status of flavour observables within the package NMSSMTools. In this implementation, we update the SM estimates and experimental measurements to current values. We also aim at an inclusion at NLOFootnote 1 of the SUSY contributions (whenever these results are accessible in the literature). We stress, however, that our study is restricted to a specific pattern of flavour violation – determined by the simplifying assumption in NMSSMTools of a squark sector strictly aligned with the quarks – where flavour-changing effects are only mediated by charged particles (i.e. not by gluinos and neutralinos) and in proportion to the CKM matrix. This ‘minimal’ version of flavour violation in a SUSY model appears as a phenomenologically justified assumption, since no compelling flavour-violating effects beyond the SM have been reported. We note however that this formulation is not stable under radiative corrections and that higher orders would restore neutral flavour-changing mediators. Moreover, as gluino vertices involve the strong coupling constant (though at high-energy), gluino corrections to LO diagrams – intervening e.g. at two-loop in the \(b\rightarrow s\gamma \) transition – can be viewed as NLO. We still neglect such effects under the assumption that they are suppressed by the large mass of the gluinos (again a phenomenologically justified approximation). Moreover, we will generally assume that the two first generations of sfermions are degenerate. Another situation which escapes our implementation of flavour-transitions (and more generally the partonic description of quarks employed in NMSSMTools) appears in the presence of very light Higgs states with mass below \(\sim \)1 GeV, where the interplay between the Higgs state and the strongly-interacting sector is non-trivial. Finally, sources of CP-violation beyond the SM are not considered here, i.e. the NMSSM parameters are assumed real (except for the CKM matrix). Concerning the observables, we retrieve and extend the list of [4], including rare B-decays – \(BR(\bar{B}\rightarrow X_{d,s}\gamma )\), \(BR(B^0_{d,s}\rightarrow \mu ^+\mu ^-)\), \(BR(\bar{B}\rightarrow X_sl^+l^-)\), \(BR(B\rightarrow X_s/K^{(*)}\bar{\nu }\nu )\), \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\), \(BR(B^+\rightarrow D^{(*)}\tau ^+\nu _{\tau })/BR(B^+\rightarrow D^{(*)}l^+\nu _{l})\) – a few rare Kaon decays – \(K\rightarrow \pi \bar{\nu }\nu \) – and oscillation parameters – \(\Delta M_{d,s}\), \(\Delta M_K\). On the other hand, we omit the exclusive channels \(B\rightarrow K^{(*)}l^+l^-\), which have grown popular since the LHC Run-I due to possible hints of tensions with the SM interpretation [1]. A first reason is that a clearer understanding of the reported anomalies may be in order, a second, that the SUSY framework may not be suited to resolving them (see e.g. [38] for a discussion in the MSSM). Other transitions – e.g. \(K\rightarrow \mu \nu \) – or observables could also be considered and we have no claim to exhaustivity, though we believe to have included most of the classical flavour tests for BSM physics.
In the following sections, we will first remind succinctly of the formalism employed to account for modified Higgs couplings at large \(\tan \beta \). We will then review briefly each observable and refer explicitly to the literature that we use in their implementation: in a first step, we shall focus on processes in the B sector before turning to Kaon physics. Finally, we will illustrate the workings of the new flavour constraints on the parameter space of the NMSSM, comparing the results of our new implementation with the former ones in a few scenarios, and discussing the relevance of the new observables that have been included. We also include a brief comparison with SuperIso [11–13].
2 \(\tan \beta \)-Enhanced corrections to the Higgs-quark couplings
The Higgs sector of the NMSSM consists of two doublets \(H_u=(H_u^+,H_u^0)^T\) and \(H_d=(H_d^0,H_d^-)^T\), as well as a singlet S. As in the MSSM, the tree-level couplings to quarks involve \(H_u\) and \(H_d\) in a Type-II 2-Higgs-Doublet-Model (2HDM) fashion:
where the diagonal Yukawa parameters can be written in terms of the tree level quark masses and the Higgs vacuum expectation values (v.e.v.’s) – defined as \(v_u=\left<H_u^0\right>=v\sin \beta \), \(v_d=\left<H_d^0\right>=v\cos \beta \), with \(v\equiv \left( 2\sqrt{2}G_F\right) ^{-1/2}\) – \(Y_u^f=m_u^f/v_u\), \(Y_d^f=m_d^f/v_d\) and \(V^{\text{ CKM }}\) represents the CKM matrix. f, \(f'\) refer to the generation index.
Yet, radiative corrections, particularly those driven by the SUSY sector, spoil this Type-II picture and generate effective terms such as – in the \(SU(2)\times U(1)\)-conserving approximation:
While in principle a higher-order concern, such terms may be enhanced for large values of \(\tan \beta \), so that a resummation becomes necessary for a consistent evaluation.
Here, as in our original work, Buras et al. [25] remains our main guide. This paper shows that the corrections to the Higgs-quark couplings driven by supersymmetric loops are well approximated in an effective \(SU(2)\times U(1)\)-conserving theory. Corrections to the down-Yukawa couplings and the associated Higgs-quark vertices are dominated by the loop-induced and \(\tan \beta \)-enhanced contributions to the \(H_u^{\dag } q_L d_R^c\) operator, which, in turn, can be encoded as the corrections to the down-type quark mass-matrix \(\Delta m_d^{ff'}\simeq Y_d^f\delta Y_d^{ff'}v_u\). Corrections to the up-Yukawa are somewhat more subtle, as \(\tan \beta \)-enhanced terms do not appear at the level of the quark masses, but only at that of some – e.g. charged – Higgs couplings. There, Buras et al. [25] shows that the parametrisation of [22], complemented by additional corrections, gives competitive numerical results. We will be working within these approximations.
In this framework, all the \(\tan \beta \)-enhanced Higgs-quark vertices can be encoded in terms of the ‘apparent’ quark masses \(\bar{m}_q^f\) and CKM matrix elements \(V^{eff}_{ff'}\), as well as a bunch of ‘\(\varepsilon \)-parameters’ which parametrise:
-
corrections to the down-type masses: \(\tilde{\varepsilon }_d(f)\tan \beta \equiv \text{ Re }[\Delta m_d^{ff}/m_d^f]\). Such diagonal contributions are mediated by gluino-sdownFootnote 2/neutralino-sdown or chargino-sup loops and can be extracted from Eqs. (2.5) and (A.2) in [25]. Note that, here as below, it is quite straightforward to infer the relevant NMSSM expressions from their couterparts in the MSSM, since the NMSSM only differs in the presence of singlet/singlino states, which are sterile in the couplings to SM fermions.
-
off-diagonal corrections to the down-type mass matrix: \(\varepsilon _Y^{ff'}\tan \beta \equiv \Delta m_d^{ff'}/m_d^fY_t^2V_{tf}V_{tf'}^*\) . These, in our minimal flavour violation approximation, are exclusively mediated by chargino-sup loops. Eqs. (2.5) and (A.2) of [25] again provide explicit expressions in terms of the supersymmetric spectrum.
-
for the up-type couplings, \(\varepsilon '_u(d)\) is defined as the effective correction to the \(H_d^+u_R^cd_L\) vertex (see [22]): \(\mathcal{L}\ni u_R^cY_uV_{ud}[H_u^+-\varepsilon '_u(d)H_d^+]d_L\). It is computed according to Eqs. (5.6)–(5.8) of [25], i.e. including relevant electroweak-gauge effects.
-
corrections to the CKM matrix elements can be encoded in terms of \(\tilde{\varepsilon }_0(f)\equiv \tilde{\varepsilon }_d(b)-Y_t^2\varepsilon _Y^{bf}\) so that:
$$\begin{aligned}&V_{ff}=V_{ff}^{eff}; V_{bf}=V_{bf}^{eff}\frac{1+\tilde{\varepsilon }_d(f)\tan \beta }{1+\tilde{\varepsilon }_0(f)\tan \beta }; \\&\quad V_{fb}=V_{fb}^{eff}\frac{1+\tilde{\varepsilon }_d(f)\tan \beta }{1+\tilde{\varepsilon }_0^*(f)\tan \beta },(f<b) \end{aligned}$$
The relevant flavour-changing Higgs-quark couplings are then given in Eqs. (3.55)–(3.61) and (5.8) of [25].
We note that, in this approach, the couplings of the Goldstone bosons expressed in terms of the effective quark masses and CKM elements are formally identical to the tree-level vertices expressed in terms of the tree-level masses and CKM matrix, so that the Goldstone bosons do not convey explicit \(\tan \beta \)-enhanced terms.
Another remark addresses the explicit calculation of the \(\varepsilon \)-parameters: we neglect the Yukawa couplings of the two first generations and assume degeneracy of the corresponding sfermions. Consequently, the unitarity of the CKM matrix can be invoked in order to include the contributions of both generations at once as, e.g., \(V_{cs}^*V_{cb}+V_{us}^*V_{ub}=-V_{ts}^*V_{tb}\).
3 Observables in the B-sector
In this section, we intend to present which B-physics observables are included within the new NMSSMTools flavour subroutines, and how. Let us first observe that a substantial part of the literature that we refer to below considers the MSSM, not the NMSSM: yet, as we mentioned in the previous section, generalising these results to the NMSSM offers no particular difficulty. Indeed, at the formal level, the contributions in the NMSSM differ from their analogues in the MSSM only by the inclusion of the singlet and singlino components – not directly coupled to SM fermions and gauge bosons – in the Higgs and neutralino sectors. The NMSSM thus generates no new topology in flavour-transitions (at least at NLO order) and it consequently proves sufficient to extend the sums over one CP-odd Higgs, two CP-even Higgs or four neutralino components of the MSSM to the two CP-odd Higgs, three CP-even Higgs or five neutralino mass-states of the NMSSM, whenever these particles intervene. In this sense, the impact of the NMSSM on flavour-observables with respect to the MSSM is essentially ‘kinematical’ in nature, meaning that in this extended model, the MSSM contributions are split and projected on various mass-states, with possibly unconventional characteristics from the point of view of the MSSM (e.g. light singlet-dominated Higgs states). Additionally, the couplings involving the Higgs and neutralino states should be replaced by the correct Feynman rules in the NMSSM (see e.g. appendix A.2 of [3] for the Higgs couplings), which typically consists in promoting trigonometric functions of the MSSM mixing angles \(\alpha \) and \(\beta \) to elements of the NMSSM rotation matrices in the CP-even and CP-odd Higgs sectors, S and P. We will not detail this straightforward procedure any further in the following and we will thus direct the reader to the MSSM literature without further comments. Then, we also wish to remind the reader that we work under the strict assumption that the squark sector is aligned with the quarks at the SUSY scale (defined by the squark masses), so that flavour-changing gluino or neutralino vertices vanish. This hypothesis is dictated by consistency with the general processing of squarks within NMSSMTools, which neglects any mixing of the generations at all scales. We note that the minimal flavour violation condition can be formulated in a much milder way, so that the Renormalisation Group Equations (RGE) would result in a non-alignment of quarks and squarks at the SUSY scale: such effects are necessarily beyond the scope of this work, or indeed the program it aims at completing.
3.1 \(B\rightarrow X_{s(d)}\gamma \)
As mentioned earlier, the status of \(B\rightarrow X_s\gamma \) in the SM has substantially evolved since the analyses of [29, 30]. The new NNLO SM estimate for \(E_0=1.6\) GeV [31, 32] (where \(E_0\) is the cut on the photon energy), shifted \(\sim \)1\(\sigma \) upwards with respect to the older estimate, is indeed very close to the experimental measurement [39] (combining results from CLEO, Belle and BABAR):
Trying to account for this result by tuning the c-quark mass in the NLO formalism, as we did in [4], potentially opens new sources of uncertainty. On the other hand, employing the full NNLO formalism is an effort-consuming task of limited interest (in our position), considering that BSM effects will be included at NLO only (see below). We therefore settled for a ‘middle-way’, using the NNLO formalism but encoding the pure SM NNLO effects within free parameters which are numerically evaluated by comparison with the numbers provided in [31, 32].
In the NNLO formalism, one can write [40]:
where:
-
C accounts for the normalisation using semi-leptonic decays: a current estimate can be extracted from Eqs. (D.1)–(D.3) of [32].
-
\(P(E_0)\) encodes the perturbative contribution in the \(\Delta B=1\) OPE in terms of the Wilson coefficients \(C_i^{\text{ eff }}\) at the low-energy scale \(\mu _b\simeq \)2 GeV. From Eqs. (2.10)–(3.11) in [40]:
-
Beyond the Wilson coefficients at LO \(C_i^{(0)\text{ eff }}\), QCD NLO \(C_i^{(1)\text{ eff }}\), QCD NNLO \(C_i^{(2)\text{ eff }}\) and QED NLO \(C_i^{(em)\text{ eff }}\), the NLO coefficients \(K_{ij}^{(1)}\) play a central role in this expression (for simplicity of notations, we factor out 2 in the case of \(K_{ii}^{(1)}\)). They can be extracted from Eqs. (3.2)–(3.13) of [40] as well as Eqs. (3.1) and (6.3) of [41] and convey the NLO corrections to the partonic process \(b\rightarrow s\gamma \) as well as the associated Bremsstrahlung contributions. All the \(\Phi _{ij}(\delta ,z)\) functions entering \(K_{ij}^{(1)}\) are fitted numerically. The only real difficulty lies in incorporating the third line of Eq. 5, which contains the NNLO Wilson coefficient \(C_7^{(2)\text{ eff }}(\mu _b)\) and the NNLO coefficients \(K_{ij}^{(2)}\). However, if we confine to the NLO for BSM contributions, we see that these missing quantities originate purely from the SM and may be parametrised as: \(P_2^{(2)}(SM)+Q_7^{(2)}(SM)\,C_7^{(0)\text{ BSM }}(\mu _0)+Q_8^{(2)}(SM)\,C_8^{(0)\text{ BSM }}(\mu _0)\), where \(\mu _0\simeq \)160 GeV is the matching scale and \(C_{7,8}^{(0)\text{ BSM }}\) only include the BSM effects. Using the numerical input from [31] – see Eqs. (6) and (10) – it will be possible to identify the coefficients \(P_2^{(2)}(SM)\) and \(Q_{7,8}^{(2)}(SM)\). Several other (numerically small) effects are actually absorbed within this parametrisation, though not formally NNLO. However, we include the contributions from 4-body final states (\(b\rightarrow sq\bar{q}\gamma \)) at NLO explicitly,Footnote 3 following [42, 43].
-
\(N(E_0)\) stands for non-perturbative corrections. From Eqs. (3.9) and (3.14) of [44]:
$$\begin{aligned}&N(E_0)\simeq \sum _{1\le i\le j\le 8}\tilde{N}_{ij}\ C_i^{(0)\text{ eff }\,*}(\mu _b)C_j^{(0)\text{ eff }}(\mu _b)\nonumber \\&\quad {\left\{ \begin{array}{ll} -6\tilde{N}_{17}=\tilde{N}_{27}\simeq -\frac{1}{9m_c^2}\left[ \lambda _2+\frac{1}{m_b}(\frac{\rho _1}{3}-\frac{13}{4}\rho _2)\right] \\ \tilde{N}_{77}=\frac{1}{2m_b^2}\left[ \lambda _1-9\lambda _2-\frac{11\rho _1-27\rho _2}{3m_b}\right] \end{array}\right. }\nonumber \\ \end{aligned}$$(6)where one can use the input from Appendix D – Eq. (D.1) – of [32], with the dictionary: \(\lambda _1=-\mu _{\pi }^2\); \(\lambda _2=\mu _G^2/3\); \(\rho _1=\rho _D^2\); \(\rho _2=\rho _{LS}^3/3\). This procedure is aimed at parametrising phenomenologically the non-perturbative effects, the parameters being determined in a fit of the semi-leptonic B decays. [31, 32] then invoke [46] to estimate the irreducible uncertainties.
-
We come to the Wilson coefficients at the low scale. These are connected to the Wilson coefficients at the high scale via the RGE. For the LO coefficients, the solution to the RGE’s – provided \(C_i^{(0)\text{ eff }}(\mu _0)=\delta _{i2}\), for \(i=1,\cdots ,6\) – can be found in Appendix E of [23]. Alternatively, one may directly use [47], which allows to derive the NLO coefficients as well:
$$\begin{aligned} {\left\{ \begin{array}{ll} C_k^{(0)\text{ eff }}(\mu _b)=\sum _{i=1}^8m_{kl,i}^{(00)}\eta ^{a_i}\,C_l^{(0)\text{ eff }}(\mu _0)\\ C_k^{(1)\text{ eff }}(\mu _b)=\sum _{i=1}^8\eta ^{a_i}\left\{ m_{kl,i}^{(00)}\,C_l^{(1)\text{ eff }}(\mu _0)\right. \\ \quad \left. +\left[ m_{kl,i}^{(10)}\eta +m_{kl,i}^{(11)}\right] C_l^{(0)\text{ eff }}(\mu _0)\right\} \end{array}\right. } \end{aligned}$$(7)with the ‘magic numbers’ \(a_i\), \(m_{kl,i}^{(00)}\), \(m_{kl,i}^{(10)}\) and \(m_{kl,i}^{(11)}\) of Tables 1, 3, 4 in the cited reference. Finally, the QED coefficient can be obtained from Eqs. (27), (85) and (86) of [24] – multiplied with a factor \(\left( \frac{\alpha _{em}}{4\pi }\right) ^{-1}\) – and proceeds originally from the study in Ref. [48].
Having sketchily described the general formalism in the previous lines, we are left with the sole remaining task of defining the Wilson coefficients at the matching scale. From the discussion above, it should be clear that, at the considered order, we need only the \(C_k^{(0)\text{ eff }}(\mu _0)\) and \(C_k^{(1)\text{ eff }}(\mu _0)\). Still, this improves on the treatment in [4] where only 2HDM effects were included at NLO.
-
The SM LO and NLO coefficients are borrowed from [18, 19], Eqs. (11) and (13), where care must be taken, however, to restore the \(\mu _0\ne M_W\) dependence. One may also consider Eqs. (28)–(31) and (35)–(40) of [20].
-
The additional 2HDM contributions are provided by Eqs. (52)–(64) of [20].
-
LO contributions from chargino/stop loops were given in [21] – Eqs. (4)–(7) – but the NLO effects in Eqs. (9)–(27) (of the same reference) are not straightforward. Instead, we prefer to use [26, 28]. In order to avoid the explicit \(\ln \frac{\mu _0}{m_{\tilde{T}}}\) in the NLO coefficient, we take care of defining the LO coefficients at the stop (or scharm/sup) scale directly, then running it down to \(\mu _0\) via the RGE’s – and taking into account the flavour-dependence in the running, i.e. the anomalous dimensions \(\frac{14}{23}\) and \(\frac{16}{23}\) for five flavours become \(\frac{14}{21}\) and \(\frac{16}{21}\) for six flavours.
-
Finally, for \(\tan \beta \)-enhanced two-loop effects at the level of the Higgs-quark couplings, we no longer follow [22], Eqs. (18)–(19) – which are phrased in terms of the tree-level, and not of the apparent, parameters – but Eqs. (6.51) and (6.53) of [25], the former amounting to 0 for the \(G^{\pm }\) contribution in the \(SU(2)\times U(1)\)-conserving limit. As before, effective neutral Higgs/bottom quark flavour-changing loops are included – see Eq. (6.61) in [25] and the correction for \(C_8\) in Eq. (79) of [49].
We note that, at two-loop order, diagrams involving one gluino propagator formally contribute at NLO: such effects were considered in e.g. [50]. We shall not include such contributions under the assumption that they are suppressed in the heavy-gluino limit.
At this point, the implementation at SM NNLO + BSM NLO is almost complete. The only remaining task consists in identifying the NNLO coefficients \(P_2^{(2)}(SM)\) and \(Q_{7,8}^{(2)}(SM)\) numerically. For this, we take good care of employing the input parameters described in Appendix D of [32] and turning off the BSM contributions. To recover the branching ratio in [31] – see Eq. (6) of this reference – we determine a correction \(P_2^{(2)}(SM)\) of the order of \(5\,\%\) of the total \(P(E_0)\). Then, linearising Eq. 5 in terms of LO BSM coefficients at the matching scale, we find that our implementation should be supplemented with coefficients \(Q_{7,8}^{(2)}(SM)\) at the permil level in order to recover the numbers appearing in Eq. (10) of [31]. These numbers are of the expected order of magnitude.
Let us finally comment on the error estimate. The SM + CKM + non-perturbative uncertainties have been combined in quadrature in Eq. (6) of [31] and we simply double the resulting number 0.23 in order to obtain \(2\sigma \) bounds. On top of this SM + CKM + non-perturbative error, we add linearly a higher-order uncertainty of \(10\,\%\) on the LO and \(30\,\%\) on the NLO new-physics contributions, each type – namely 2HDM, SUSY, neutral Higgs – being added separately in absolute value. To incorporate this uncertainty, we simply use the linearisation that has been employed to determine the NNLO parameters just before.
Now let us turn to \(BR[\bar{B}\rightarrow X_d\gamma ]\). \(BR[\bar{B}\rightarrow X_d\gamma ]\) was originally considered in [24] at NLO and then, in view of the BABAR measurement [51], by [52]. Finally, [31] extended the analysis to NNLO. Beyond the trivial substitution \(s\mapsto d\) in CKM matrix elements, the chief difference with \(BR[\bar{B}\rightarrow X_s\gamma ]\) originates in sizable contributions from the partonic process \(b\rightarrow d\bar{u}u\gamma \) – since the CKM ratio \(\frac{V_{ud}^*V_{ub}}{V_{td}^*V_{tb}}\) is not negligible. The latter can be sampled in several ways – see e.g. [53] – which provides some handle on the associated error estimate. We will be content with the evaluation using constituent quark masses given in Eq. (3.1) of [53], setting the ratio \(\frac{m}{m_b}\) – with m standing for the mass of the light quarks – in such a way as to recover, in the SM limit, the central value of [31], Eq. (8):
We can then check the consistency with Eq. (10) of [31] for the new physics contributions.
As before, the SM + CKM + non-perturbative uncertainties are taken over from [31], Eq. (8) – again we double the error bands to test the observable at the \(2\sigma \) level – and we add linearly the new physics uncertainties. On the experimental side, the BABAR measurement [51] has to be extrapolated to the test region, leading to the estimate [52]:
3.2 \(BR[B^0_{s(d)}\rightarrow \mu ^+\mu ^-]\)
\(BR[B^0_s\rightarrow \mu ^+\mu ^-]\) is the observable where the evolution since [4] has been the most critical. The experimental status has seen the upper bound \(\left. BR[B^0_s\rightarrow \mu ^+\mu ^-]\right| ^{\text{ exp. }} <5.8\cdot 10^{-8}\) (\(95\,\%\) CL) replaced by an actual measurement at LHCb and CMS [36, 39]:
The corresponding value agrees well with the recent SM calculation [33]:
It is thus no longer sufficient to consider effects driven by \(\tan \beta \)-enhanced Higgs penguins only, and we therefore design a more complete test at NLO in the new version of bsg.f.
The general formalism remains unchanged and the master formula can be recovered e.g. using Eqs. (5.15)–(5.16) of [27]:
As before, we shall neglect effects from the ‘mirror operators’ – which are suppressed as \(m_s/m_b\) – and focus on the leading coefficients \(c_A\) (pseudovector), \(c_S\) (scalar) and \(c_P\) (pseudoscalar) of the \((\bar{b}s)(\bar{\mu }\mu )\) system. The analysis is simplified by the fact that – provided the corresponding operators have been suitably normalised – these semi-leptonic coefficients have a trivial running.
-
The SM contribution to \(BR[B^0_s\rightarrow \mu ^+\mu ^-]\) is known up to three-loop QCD [34] and leading QED order [35]. It projects on the pseudovector operator exclusively. We shall use the numerical parametrisation of [33], Eq. (4), to account for it.
-
Additional 2HDM contributions appear in the form of Z-penguins, boxes and neutral-Higgs penguins. [27] provides the corresponding input in Eqs. (3.12), (3.13), (3.32), (3.36)–(3.39), (3.48) and (3.49).
-
The genuine supersymmetric contributions take the same form and can be found in Eqs. (3.14), (3.16), (3.32), (3.40), (3.42), (3.44), (3.46) of [27]. Instead of using Eqs. (3.50)–(3.58) of that same reference for the neutral-Higgs penguins, we resort to [25], Eqs. (6.35) and (6.36). As in [4] – see also [54] – we replace the squared Higgs mass in the denominator by a Breit–Wigner function, so as to account for potentially light Higgs states.
The prefactor induces an uncertainty related to CKM, lattice (hadronic form factor) and B-width measurement. These are combined in quadrature at the \(2\sigma \) level. In practice, we use: \(m_{B_s}=5.36677\) [55], \(\tau _{B_s}=(1.607\pm 0.010)\) ps [39], \(f_{B_s}=(226\pm 6)\) MeV – which is an ad-hoc combination of the various results presented in [56] – and \(|V_{tb}V_{ts}^*|= (41.3\pm 1.4)\cdot 10^{-3}\) [57]. Then, a higher-order uncertainty of \(2.2\,\%\) for the SM [33] and \(10\,\%\) for new physics contributions of each type are added linearly. We note that, together with the parametric (CKM, form factor) uncertainty, our error estimate in the SM limit is somewhat more conservative than that quoted in Eq. 11 and would amount to \(\sim \)8.5 % (at \(1\,\sigma \)).
A similar analysis can be conducted for \(BR[B^0_d\rightarrow \mu ^+\mu ^-]\). The experimental measurement [39]:
combines the LHCb and CMS limits. The formalism is the same as for the \(B^0_s\) decay up to the trivial replacement \(s\mapsto d\). In practice, we use the quantities \(m_{B_d}=5.27958\) [55], \(\tau _{B_d}=(1.520\,{\pm }\,0.004)\) ps [39], \(f_{B_d}=(188.5\,{\pm }\,5.25)\) MeV – again an ad-hoc combination of the various results presented in [56] – and \(|V_{tb}V_{td}^*|= (8.6\pm 2.8)\cdot 10^{-3}\) [57]. With this choice, we obtain a total (CKM-dominated) uncertainty of \(\sim \)35 % (at \(1\,\sigma \)) in the SM limit. Due to larger uncertainties, one expects milder limits than in the \(B^0_s\) case.
3.3 The \(b\rightarrow sl^+l^-\) transition
The process \(\bar{B}\rightarrow X_sl^+l^-\) was not considered in [4] but had been added in bsg.f later, including only the scalar contributions from \(\tan \beta \)-enhanced Higgs penguins. Here we aim at a more complete analysis.
The study in [37] provides a recent overview of the observables that can be extracted from \(\bar{B}\rightarrow X_sl^+l^-\). We will confine to the branching fractions in the low – [1, 6] GeV\(^2\) – and high – \(\ge 14.4\) GeV\(^2\) – \(m^2_{l^+l^-}\) ranges. Eqs. (B.33) and (B.36)–(B.38) of the considered paper provide the dependence of these rates on new-physics contributions to the (chromo-)magnetic operators as well as the semi-leptonic operators of the vector type. The sole SM evaluation can be extracted from Eqs. (5.13)–(5.15) of [37], while the prefactor in Eq. (4.6) of [37] can be evaluated separately to allow for a different choice of the central values of CKM/non-perturbative contributions: we choose to take the latter from [32] since the normalisation coincides with that of \(BR[\bar{B}\rightarrow X_s\gamma ]\).
The computation of the Wilson coefficients for the (chromo)-magnetic operators – \(C_7^{\text{ eff }}\), \(C_8^{\text{ eff }}\) – has already been described in connection with \(\bar{B}\rightarrow X_s\gamma \): we simply run these coefficients down to the matching scale of [37], \(\mu _0'=120\) GeV. Moreover, \(C_{10}\) coincides with \(c_A\) – discussed in the context of \(B_s^0\rightarrow \mu ^+\mu ^-\) – up to a normalisation factor. Only \(C_9\) is thus missing: it can be obtained in [28] – see Eq. (3.6) and Appendix A of this reference. Although the lepton flavour has very little impact on \(C_{9,10}\) – it intervenes only via the lepton Yukawa couplings in subleading terms – we still distinguish among \(C^e_{9,10}\) and \(C^{\mu }_{9,10}\).
While this is ignored by [37], \(\bar{B}\rightarrow X_sl^+l^-\) could also be mediated by scalar operators as shown in Eq. (2.5) of [58] – note that the coefficients \(C_{Q_{1,2}}\) there coincide, up to a normalisation factor, with \(c_{S,P}\) introduced before. Therefore, we add these contributions accordingly, estimating the integrals over \(m^2_{l^+l^-}\) numerically. To account for possibly light Higgs states, the Higgs-penguin contributions from SUSY loops are isolated in \(c_{S,P}\) and receive denominators of the form \(m^2_{l^+l^-}-m_{h_i^0}^2+\imath m_{h_i^0}\Gamma _{h_i^0}\), which are then integrated. Note that the scalar coefficients \(c_{S,P}\) depend linearly on the lepton mass, so that they matter only in the case of the muonic final state.
Finally, we come to the error estimate: the SM uncertainties (including e.g. CKM effects) are extracted from Eqs. (5.13)–(5.15) of [37]. Linearising Eqs. (B.33) and (B.36)–(B.38) (of that same reference) in terms of \(C^{\text{ BSM }}_{7,\,\ldots ,10}\), we associate a \(10\,\%\) uncertainty to these new-physics contributions and add it linearly. As the contributions from scalar operators is added ‘by hand’, we use a larger uncertainty of \(30\,\%\). The experimental values relevant for the \(\bar{B}\rightarrow X_sl^+l^-\) transition are extracted from Eqs. (1.1) and (1.2) in [37].
The normalised FB asymmetry \(\bar{A}_{FB}[\bar{B}\rightarrow X_sl^+l^-]\) could also be implemented using the results in [37]:
with the quantities \(\mathcal{H}_A\), \(\mathcal{H}_T\) and \(\mathcal{H}_L\) explicited in Appendix B of [37]. Note that the contributions from scalar operators are suppressed as \(\left( \frac{m_l}{m_b}\right) ^2\) [58] and may thus be neglected. However, the only experimental source (Belle) [59] chose a different binning, so that the results cannot be compared.
Beyond the inclusive decay rates, much effort has been mobilised in the study of the \(B\rightarrow K^{(*)}l^+l^-\) exclusive modes in the last few years. The full angular analysis of these modes provide two dozen independent observables [60]. Tensions with the SM estimates have been reported in some of these channels, however, leading to a substantial literature (see e.g. [1, 61, 62]). In this context, we choose to disregard these exclusive modes for the time being, waiting for a clearer understanding of the reported anomalies (we refer the reader to [38] for a discussion within the MSSM).
3.4 The \(b\rightarrow s\nu \bar{\nu }\) transition
The \(b\rightarrow s\nu \bar{\nu }\) transition is known to provide theoretically clean channels. While ignored in our original work, we decide to include the three following observables in the new version of the code: \(BR[B\rightarrow X_s\nu \bar{\nu }]\), \(BR[B\rightarrow K\nu \bar{\nu }]\) and \(BR[B\rightarrow K^*\nu \bar{\nu }]\).
We follow the analysis of [63] (Section 5.9), updated in [64]. The Wilson coefficients are provided at NLO in Section 3.2 of [27]. Under our assumption of minimal flavour violation, with no flavour-changing gluinos or neutralinos, and neglecting the masses of the light quarks, only the coefficient \(C_L\) (or \(X_L\) in the notations of [63]) receives contributions in the model. The relation between the branching ratios in the NMSSM and that in the SM thus becomes particularly simple: see Eqs. (229–232) of [63]. We employ the updated SM evaluations in Eqs. (10), (11) and (23) of [64]:
We also note that the ratio of the \(B^+\)/\(B^0\) lifetimes controls that of the \(B^+\rightarrow K^{(*)+}\)/\(B^0\rightarrow K^{(*)0}\) transitions.
The experimental upper bound on the inclusive branching ratio \(BR[B\rightarrow X_s\nu \bar{\nu }]\) originates from ALEPH [65]; those on the exclusive modes \(BR[B\rightarrow K\nu \bar{\nu }]\) and \(BR[B\rightarrow K^*\nu \bar{\nu }]\) are controlled by BABAR [66] and BELLE [67] respectively (see also the compilation in [39]). At \(90\,\%\) CL:
Generalising to the \(b\rightarrow d\nu \bar{\nu }\) transition is trivial, though not competitive at the moment.
3.5 Flavour transitions via a charged current
The central observable in the \(b\rightarrow u\) transition is \(BR[B^+\rightarrow \tau ^+\nu _{\tau }]\). Here, we perform little modification of the original implementation in [4]. In other words, we follow [68], where the effects of the W and charged-Higgs exchanges at tree-level, corrected by \(\tan \beta \)-enhanced supersymmetric loops, appear in Eq. (5–7) of the quoted paper. The uncertainty is assumed dominated by \(V_{ub}\) [55] and the hadronic form factor [56].
The \(b\rightarrow c\) transition has attracted some attention in the last few years. We will consider the ratios \(R_D\equiv \frac{BR(B^+\rightarrow D\tau ^+\nu _{\tau })}{BR(B^+\rightarrow Dl^+\nu _{l})}\) and \(R_{D^*}\equiv \frac{BR(B^+\rightarrow D^*\tau ^+\nu _{\tau })}{BR(B^+\rightarrow D^*l^+\nu _{l})}\).
These quantities show a tension between the SM predictions from lattice/HQET \(R_D^{\text{ SM }}=0.297\pm 0.017\), \(R_{D^*}^{\text{ SM }}=0.252\pm 0.003\) [69–72] or, more recently, \(R_D^{\text{ SM }}=0.299\pm 0.011\) [73], \(R_D^{\text{ SM }}=0.300\pm 0.008\) [74] and the experimental averages \(R_D^{\text{ exp }}=0.391\pm 0.050\), \(R_{D^*}^{\text{ exp }}=0.322\pm 0.022\) [39] (HFAG website), which combine results from BABAR [71, 72], LHCb [75] and Belle [76]. Note that these tensions in the \(b\rightarrow c\) transition are independent from the CKM uncertainty on \(V_{cb}\), due to the normalisation.
We follow the analysis in [77] which presents the corrections to the observables in a 2HDM context, allowing to account for modified Higgs-quark vertices with respect to Type II, such as those induced by \(\tan \beta \)-enhanced supersymmetric loops: see Eqs. (7–15) in the reference under consideration.
These contributions are mediated by a charged Higgs and we can easily translate, for the charged-Higgs/quark couplings, the notations of [77] to ours (see Sect. 2). We find the following Wilson coefficients:
We assume a \(30\,\%\) uncertainty on these new-physics coefficients, which we add linearly to the SM uncertainty quoted above. Since these observables are only marginally compatible with the SM prediction, we do not devise an actual test for them, but simply propose an evaluation.
3.6 \(B_{d,s}^0\) oscillation parameters \(\Delta M_{d,s}\)
The old version of the code used the formalism of [25] to encode the SM – see Eq. (6.7) of that work – as well as the \(\tan \beta \)-enhanced double-penguin contributions – Eqs. (6.12)–(6.22) of [25] – while the one-loop BSM boxes – see Eq. (6.3) of [25] – were taken from Eqs. (94)–(98) of [78]. (For the latter, only the contributions involving charged particles are relevant under our assumption of minimal flavour violation, i.e. the box contributions mediated by gluinos or neutralinos and sdowns vanish.)
In the new version of the code, we upgrade the approach to \(\Delta M_{d,s}\) to the NLO formalism:
-
The box contributions from charged Higgs/tops and chargino/squarks are matched onto the relevant base of operators – see e.g. Eq. (2.1) in [79] – according to the formulae in Appendix A.4 of [25]. They are run down from the new-physics scale – \(m_{H^{\pm }}\) and the squark scale respectively – down to the matching scale of 166 GeV via RGE solutions for 6 flavours: see [79], Appendix C. As before, SM and double-penguin contributions are also included within this formalism.
-
We follow Section 3.1 of [79] to connect the matching scale to the low-energy matrix elements – 5-flavour running.
-
The low-energy physics is described by the so-called ‘Bag’ parameters – matrix elements of the operators. We rely essentially on the lattice calculations of [80], except for the operator \(Q^{VLL}\), which receives the SM contributions and has thus attracted more recent attention. In this later case, we use the current FLAG average [56] for \(\hat{B}_{B_{d,s}}\) – which coincides with the Bag parameter up to a rescaling.
These ingredients allow to derive a prediction for \(\Delta M_{d,s}\) using the master formula of [25], Eqs. (6.6)–(6.8). The hadronic form factors \(f_{B_{s,d}}\) are taken from [56], where we combine the various results. For the CKM elements, we continue to rely on the evaluation from tree-level processes proposed in [57]. Note that our central value for \(\Delta M_s\) in the SM limit is somewhat higher than the latest estimates [81, 82]. This is essentially due to the choice for the lattice input: [81, 82] have their own averaging, leading to a smaller form factor, while we follow [56].
We come to the error estimate. The uncertainty associated to the SM contributions to the operator \(Q^{VLL}\) is often neglected in the literature. Equation (11) of [81] shows however that there could be an error of at least a few permil. We therefore associate a \(1\,\%\) uncertainty to this contribution, which we add linearly to a \(30\,\%\) uncertainty on each type – charged Higgs Box/SUSY Box/double penguin – of new-physics contribution. Then, the uncertainties on the Bag parameters are taken from [56, 80] and combined in quadrature at the \(2\sigma \) level. Finally, we factor out the uncertainties on the CKM [57] and lattice form factor [56], adding them in quadrature at the \(2\sigma \) level. Note that the CKM uncertainty dominates the total error on \(\Delta M_{d}\) (at the level of \(60\,\%\)) and is actually of the order of magnitude of the central value, so that it is important not to linearise the associated error. In the SM limit, we obtain an uncertainty (at the \(1\,\sigma \) level) of \(\sim \)11 % for \(\Delta M_s\) and \(\sim \)40 % for \(\Delta M_d\).
These results are then confronted to the experimental measurements [39]:
4 Observables in the Kaon-sector
4.1 The \(s\rightarrow d\nu \bar{\nu }\) transition
The physics of Kaons also provides limits on new physics, one example being the \(s\rightarrow d \nu \bar{\nu }\) transition. We again follow [63] (Section 5.8), together with the updated SM results of [83].
The Wilson coefficients mediating the transition [84] are very similar to those intervening in the \(b\rightarrow s \nu \bar{\nu }\) transition, except that the interplay of CKM matrix elements is formally different. The normalisation to \(V_{td}V_{ts}^*\), instead of \(V_{tb}V_{ts}^*\), gives more weight to the two first generations: for completion, we thus incorporate the effects proportional to the charm Yukawa coupling. Note that we continue to neglect the quark masses of the first generation and that tree-level neutralino and gluino couplings do not mediate flavour transitions (per assumption), so that only the \(X_L\) (in the notations of [63] and equivalent to the \(C_L\) of Sect. 3.4) coefficient is relevant.
The decay of a charged kaon to \(\pi ^+\nu \bar{\nu }\), as well as that of the neutral \(K_L\) to \(\pi ^0\nu \bar{\nu }\), can then be encoded in terms of this Wilson coefficient: see Eqs. (213–214) of [63], where, however, we substitute the more recent SM input of Eqs. (2.2), (2.9), (2.11) of [83].
On the experimental side, the process involving charged mesons is constrained by [85] to \(BR[K^+\rightarrow \pi ^+\nu \bar{\nu }]=(17.3_{-10.5}^{+11.5})\cdot 10^{11}\); for the neutral mesons, [86] provides the bound \(BR[K_L\rightarrow \pi ^0\nu \bar{\nu }]<2.6\cdot 10^{-8}\) (\(90\,\%\) CL).
4.2 \(K-\bar{K}\) mixing
As for the B mesons, one can consider the mixing of K and \(\bar{K}\) mesons. Associated quantities are very precisely measured experimentally [55]:
where \(\Delta M_K\) stands for the mass-difference between \(K_L\) and \(K_S\) and \(\varepsilon _K\) measures indirect CP-violation in the \(K-\bar{K}\) system.
However, the theoretical evaluations of these quantities of the \(K-\bar{K}\) system suffer from a substantial uncertainty associated to long-distance effects. Several estimates based on representations of large N QCD had been proposed in the \(80^{\text{ ies }}\) – see e.g. [87]. Lately, lattice collaborations have been emphasising the possibility to perform an evaluation in a realistic kinematical configuration in the near future: see e.g. [88]. We will follow [89] (see also discussion and literature therein) in estimating the long-distance contribution to \(\Delta M_K\) at \((20\pm 10)\,\%\) of the experimental value, while [90] provides some lattice input for \(\varepsilon _K\): we take over the quantity \(\xi _0\) from Eq. (74) and the error estimate on \(\xi _{LD}\), Eq. (75) (of that reference) – these values were originally computed in [91] and [92], and Eq. (67) of [90] explicits their impact on \(\varepsilon _K\).
We now turn to the short-distance contributions in the \(K-\bar{K}\) system. The discussion is very similar to the case of the \(B-\bar{B}\) mixing in Sect. 3.6. We follow [93] for the SM part: this paper performed a NNLO evaluation of the charm contribution – see Eq. (15) in that work – completing earlier results for the mixed charm-top [94] and top [95] contributions. Note that [89, 90] also propose recent evaluations of the quantity \(\eta _{cc}\), with slightly lower central value, but we choose to stick to the conservative estimate of [93]. The master formulae for \(\Delta M_K\) and \(\varepsilon _K\) are provided in Eqs. (18) and (16) of this reference, respectively – see also Eqs. (XVIII.6–9) of [17], as well as Eqs. (XII.3–5) for the expression of the functions \(S_0\). The kaon mass of 0.4976 GeV and the form factor \(f_K=0.1563\pm 0.0009\) GeV are taken from [55] and [56] respectively.
The inclusion of BSM contributions follows the general NLO formalism of [79]: see Eqs. (7.24–7.32). Eqs. (3.20–3.38) (of this reference) explicit the running between the matching- and the low-energy scales. However, we will be using more recent ‘Bag parameters’ for a low-energy scale of 3 GeV: Table XIII of [96] compiles several recent lattice calculations, which we put to use. As in the \(B-\bar{B}\) case, the Wilson coefficients account for Higgs/quark and chargino/squark box diagrams as well as Higgs double-penguin contributions and we follow appendix A of [25]. Yet, we also include effects associated to the charm Yukawa, as the interplay of CKM elements gives more weight to such terms than for the \(B-\bar{B}\) mixing. Finally, we use appendix C of [79] to run each new-physics contribution from the relevant BSM scale (charged-Higgs or squark mass) down to the matching scale of 166 GeV.
The SM uncertainty, where the uncertainty on the \(\eta _{cc}\) parameter and the long distance effects dominate, is added linearly to the uncertainty driven by the bag parameters and a \(30\,\%\) error on higher-order contributions to the BSM Wilson coefficients. Moving to the SM limit and considering the theoretical error at \(1\,\sigma \), we obtain a total uncertainty of about \(35\,\%\) for \(\Delta M_K\) and \(15\,\%\) for \(\varepsilon _K\).
Note that one can lead a similar analysis for the \(D-\bar{D}\) mixing, which we do not consider here, however.
5 Sampling the impact of the flavour constraints
Based on the discussion of the previous sections, we design two Fortran subroutines bsg.f and Kphys.f for the evaluation in the NMSSM of the considered observables in the B- and the Kaon-sectors (respectively), as well as a confrontation to experimental results. These subroutines are then attached to the public tool NMSSMTools [5–8].
5.1 Comparing the new and the old codes
In order to test the differences between the new and the former implementations of B-physics observables in bsg.f, we perform a scan over the plane defined by \(m_{H^{\pm }}\) – the charged Higgs mass – and \(\tan \beta \) and display the exclusion contours associated with flavour constraints in Figs. 1 and 2. The chosen region in the NMSSM parameter space corresponds to the MSSM-limit, with degenerate sfermions and hierarchical neutralinos. Note that we disregard the phenomenological limits from other sectors (e.g. Higgs physics, Dark matter, etc.), which are largely orthogonal to the flavour-constraints and would unnecessarily complicate the picture. We consider a large value of the trilinear stop coupling \(|A_t|=2.5\) TeV, which is known to enhance effects driven by supersymmetric loops, and study separately the two opposite signs – a negative value of \(A_t\), when \(\mu >0\), typically triggers destructive interferences among the SUSY and 2HDM contributions to \(\bar{B}\rightarrow X_s\gamma \).
Exclusion contours due to the flavour constraints in the plane \(\{m_{H^{\pm }},\tan \beta \}\) for \(\lambda =\kappa =2\cdot 10^{-4}\), \(\mu =2M_1=M_2=M_3/5=300\) GeV, \(m_{\tilde{F}}=1\) TeV, \(A_t=2.5\) TeV, \(A_{b,\tau }=-1.5\) TeV, \(A_{\kappa }=-500\) GeV. The plot on the first row has been obtained with the new code while the plot of the second row results from the old version. Points excluded by the various constraints are coloured in red (horizontal lines) – \(\bar{B}\rightarrow X_s\gamma \) – blue (vertical lines) – \(B_s^0\rightarrow \mu ^+\mu ^-\) – dark green (circles) – \(\bar{B}\rightarrow X_sl^+l^-\) – light green (oblique lines) – \(B^+\rightarrow \tau ^+\nu _{\tau }\) – yellow (diamonds) – \(\Delta M_s\) – and orange (triangles) – \(\Delta M_d\) – while remaining gray points satisfy all these limits
Similar plots and scan as in Fig. 1, but with \(A_t=-2.5\) TeV
The general appearance of the exclusion contours in Figs. 1 and 2 remains qualitatively similar, when comparing the results obtained with the new (plots on the top) and old (plots on the bottom) versions of the code.Footnote 4 Yet, quantitatively, one witnesses a few deviations:
-
The limits from \(\bar{B}\rightarrow X_s\gamma \) are more severe in the new version, which is mostly apparent in Fig. 1 (\(A_t>0\)): this is not unexpected since the larger SM central value – closer to the experimental measurement – correspondingly disfavours new physics effects that interfere constructively with the SM contribution (2HDM effects or supersymmetric loops for \(\mu ,\,A_t>0\)). Consequently, the areas with a light charged Higgs or large \(\tan \beta \) receive excessive BSM contributions in view of the experimental measurement and are thus disfavoured. Moreover, note that the NLO implementation reduces somewhat the error bar associated to higher-order new-physics contributions, which also results in tighter bounds for the more recent code. For \(A_t<0\), one observes two separate exclusion regions: for low values of \(\tan \beta \) and \(m_{H^{\pm }}\), the 2HDM contribution is large (excessive) while the negative SUSY effect is too small to balance it; on the contrary, with large \(\tan \beta \) and heavy \(H^{\pm }\), the SUSY contribution dominates and is responsible for the mismatch with the experimental measurement. In between, the destructive interplay between the SM and 2HDM effects on one side and the SUSY loops on the other succeeds in keeping \(BR[\bar{B}\rightarrow X_s\gamma ]\) within phenomenologically acceptable values.
-
Limits from \(B_s^0\rightarrow \mu ^+\mu ^-\) used to be little sensitive to the sign of \(A_t\) in the older implementation. This is no longer true, the reason being that the scalar coefficients \(c_{S,P}\) receive new contributions, namely 2HDM- and SUSY-mediated Z-penguins and boxes, which (had been neglected in the previous version of the code and) may interfere constructively or destructively with the Higgs-penguin effects. This channel appears as the most sensitive one, together with \(\bar{B}\rightarrow X_s\gamma \), in the considered scenario. Given the shape of the exclusion regions driven by \(\bar{B}\rightarrow X_s\gamma \), however, \(B_s^0\rightarrow \mu ^+\mu ^-\) seems most relevant for \(A_t<0\) (Fig. 2). Expectedly, the limits are tighter for large \(\tan \beta \), where SUSY contributions are enhanced.
-
Limits from \(\bar{B}\rightarrow X_sl^+l^-\) differ more significantly between the two implementations – although they remain subleading. In particular, an excluded region appears at low \(\tan \beta \): it is largely driven by the 2HDM contributions to the semi-leptonic vector coefficients \(C_{9,10}\) – which indeed involve terms in \(\tan ^{-1}\beta \). On the other hands, the exclusion region at low \(m_{H^{\pm }}\) is largely unchanged: it is associated with the enhancement of the Higgs-penguin contributions for a light Higgs sector.
-
Despite the corrections to the \(\tan \beta \)-enhanced Higgs/quark vertices, the constraints from \(B^+\rightarrow \tau ^+\nu _{\tau }\), \(\Delta M_s\) and \(\Delta M_d\) are little affected by the modernisation of the code and remain subleading.
We observe that \(\bar{B}\rightarrow X_s\gamma \) and \(B_s^0\rightarrow \mu ^+\mu ^-\) intervene as the determining limits from the flavour sector in the considered scenario: they exclude all the region beyond  (for our specific choice of parameters in Figs. 1, 2). The low \(m_{H^{\pm }}\)-region is in tension with most of the observables in the B-sector (unsurprisingly), though \(\bar{B}\rightarrow X_s\gamma \) and \(B_s^0\rightarrow \mu ^+\mu ^-\) again appear as the limiting factors at low-to-moderate \(\tan \beta \). Interestingly, \(\bar{B}\rightarrow X_sl^+l^-\) seems to offer a competitive test for
(for our specific choice of parameters in Figs. 1, 2). The low \(m_{H^{\pm }}\)-region is in tension with most of the observables in the B-sector (unsurprisingly), though \(\bar{B}\rightarrow X_s\gamma \) and \(B_s^0\rightarrow \mu ^+\mu ^-\) again appear as the limiting factors at low-to-moderate \(\tan \beta \). Interestingly, \(\bar{B}\rightarrow X_sl^+l^-\) seems to offer a competitive test for  .
.
We perform a second test in a region involving a light CP-odd Higgs state with mass below 15 GeV – still presuming nothing of the limits from other sectors: note that this is a phenomenologically viable scenario in the NMSSM, although the limits on unconventional decays of the SM-like Higgs state at \(\sim \)125 GeV place severe constraints on the properties of the light pseudoscalar. The results are displayed in Fig. 3 – in terms of the mass of the pseudoscalar \(m_{A_1}\) and \(\tan \beta \) – and confirm the trends that we signaled before:
Exclusion contours due to the flavour constraints in the plane \(\{\tan \beta ,m_{A_1}\}\) for \(\lambda =0.45\) \(\kappa =0.4\), \(\mu =2M_1=M_2=M_3/5=300\) GeV, \(m_{\tilde{F}}=1\) TeV, \(A_{b,\tau }=-1.5\) TeV, \(A_t=-2.5\) TeV, \(A_{\kappa }=-30\) GeV. The charged Higgs mass varies very little across the plot and is of order \(\sim \)350 GeV. Above, the results with the new code; below, the results of the old version. The colour code remains the same as before. The symbols are also unchanged, except for \(\bar{B}\rightarrow X_sl^+l^-\), with horizontal lines, and, \(\bar{B}\rightarrow X_s\gamma \), with circles (for reasons of visibility)
Top Exclusion contours due to the flavour constraints in the plane \(\{m_{H^{\pm }},\tan \beta \}\) for \(\lambda =\kappa =2\cdot 10^{-4}\), \(\mu =2M_1=M_2=M_3/3=500\) GeV, \(m_{\tilde{F}}=1\) TeV, \(A_t=0.5\) TeV, \(A_{b,\tau }=-1.5\) TeV, \(A_{\kappa }=-500\) GeV. Bottom Exclusion contours due to the flavour constraints in the plane \(\{\tan \beta ,m_{A_1}\}\) for \(\lambda =0.45\) \(\kappa =0.4\), \(\mu =2M_1=M_2=M_3/3=500\) GeV, \(m_{\tilde{F}}=1\) TeV, \(A_{b,\tau }=-1.5\) TeV, \(A_t=0.5\) TeV, \(A_{\kappa }=0\) GeV. Both plots are obtained with the new version of the code. The colour (symbol) code remains the same as before
-
Limits from \(\bar{B}\rightarrow X_s\gamma \) intervene here at low \(\tan \beta \) – where the supersymmetric contributions cannot balance the effect triggered by the charged-Higgs (note that \(A_t<0\)). A few points are also excluded for low \(m_{A_1}\) and large \(\tan \beta \): these result from the two-loop effect mediated by a neutral Higgs. They prove subleading in the considered region.
-
Limits from \(B_s^0\rightarrow \mu ^+\mu ^-\) appear somewhat tighter in the new implementation. In particular, a narrow corridor where the new physics effects reverse the SM contribution is visible in the plot on the bottom of Fig. 3 (which corresponds to the older implementation of the limits) – from \((m_{A_1}\sim 6,\tan \beta \sim 2)\) to \((m_{A_1}\sim 15,\tan \beta \sim 5)\); this region is no longer accessible with the more recent code (it is, in fact, shifted to lower values of \(\tan \beta \)). This channel is the main flavour limit in the considered region, due to the large contribution mediated by an almost on-shell Higgs penguin.
-
Limits from \(\bar{B}\rightarrow X_sl^+l^-\) intervene in two fashions. One is the exclusion driven by an almost-resonant pseudoscalar and the associated bounds are essentially unchanged with respect to the older implementation. Additionally, a new excluded area appears at low \(\tan \beta \).
-
Limits from \(\Delta M_{d,s}\) are qualitatively unchanged among the two versions, though the bounds associated with \(\Delta M_d\) seem somewhat more conservative in the new implementation. These constraints remain subleading however, in view of the more efficient \(BR(B_s^0\rightarrow \mu ^+\mu ^-)\), and confine to the resonant regime – note e.g. the allowed ‘corridor’ where new-physics contributions reverse the SM effect – or the very-low range
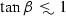 .
. -
Limits from \(B^+\rightarrow \tau ^+\nu _{\tau }\) do not intervene here.
\(B_s^0\rightarrow \mu ^+\mu ^-\) thus appears as the constraint that is most sensitive to the enhancement-effect related to a near-resonant pseudoscalar. The exclusion effects are most severe for larger \(\tan \beta \) as the Higgs-penguin is correspondingly enhanced. For  , \(\bar{B}\rightarrow X_sl^+l^-\) proves a sensitive probe in its new implementation.
, \(\bar{B}\rightarrow X_sl^+l^-\) proves a sensitive probe in its new implementation.
Note that, in the two scenarios that we discussed here, the precise limits on the \(\{m_{H^{\pm }},\tan \beta \}\) or \(\{\tan \beta ,m_{A_1}\}\) planes of course depend on the details of the parameters. In particular, the large value of \(|A_t|\) triggers enhanced SUSY effects, resulting in severe bounds on the considered planes. We thus warn the reader against over-interpreting the impression that only corners of the parameter space of the NMSSM are in a position to satisfy B-constraints at \(95\,\%\) CL, as Figs. 1, 2 and 3 might lead one to believe. To counteract this effect, we present in Fig. 4 the limits from flavour processes obtained with the new implementation, for \(A_t=500\) GeV and a somewhat heavier chargino/neutralino sector. The plot on the top again considers the plane \(\{m_{H^{\pm }},\tan \beta \}\) in the MSSM limit. SUSY contributions are suppressed by the choice of low \(A_t\). Correspondingly, limits from \(\bar{B}\rightarrow X_s\gamma \) only intervene in the region with low \(m_{H^{\pm }}<300\) GeV. The constraints driven by \(B_s^0\rightarrow \mu ^+\mu ^-\) eventually exclude the large  range but are obviously weaker than before. On the other hand, the exclusion contour associated with \(B^+\rightarrow \tau ^+\nu _{\tau }\) and \(\bar{B}\rightarrow X_sl^+l^-\) remain largely unaffected. The plot on the bottom part of Fig. 4 addresses the scenario with a light pseudoscalar: contrarily to the case of Fig. 3, CP-odd masses above \(m_{A_1}\sim \)6 GeV are left unconstrained by the flavour test, with exclusions intervening only at very-low \(\tan \beta \) or for \(m_{A_1}\) in the immediate vicinity of a resonant energy (for \(B_s^0\rightarrow \mu ^+\mu ^-\), \(\Delta M_s\) or \(\bar{B}\rightarrow X_sl^+l^-\)).
range but are obviously weaker than before. On the other hand, the exclusion contour associated with \(B^+\rightarrow \tau ^+\nu _{\tau }\) and \(\bar{B}\rightarrow X_sl^+l^-\) remain largely unaffected. The plot on the bottom part of Fig. 4 addresses the scenario with a light pseudoscalar: contrarily to the case of Fig. 3, CP-odd masses above \(m_{A_1}\sim \)6 GeV are left unconstrained by the flavour test, with exclusions intervening only at very-low \(\tan \beta \) or for \(m_{A_1}\) in the immediate vicinity of a resonant energy (for \(B_s^0\rightarrow \mu ^+\mu ^-\), \(\Delta M_s\) or \(\bar{B}\rightarrow X_sl^+l^-\)).
5.2 Impact of the new flavour tests
Beyond the observables that had been considered in [4], we have extended our analysis to several new channels. We now wish to discuss their impact on the NMSSM parameter space.
Exclusion contours driven by \(\bar{B}\rightarrow X_d\gamma \) (red, horizontal lines), \(B_d^0\rightarrow \mu ^+\mu ^-\) (light green, vertical lines), \(B\rightarrow X_s/K\bar{\nu }\nu \) (dark green, circles), the \(K-\bar{K}\) mixing (yellow, diamonds) and \(K\rightarrow \pi \bar{\nu }\nu \) (orange, triangle) in the plane \(\{m_{H^{\pm }},\tan \beta \}\) for the scenario of Fig. 1. The limits obtained with the observables considered in Fig. 1 are shown on the background in black (crosses). The case of \(A_t>0\) is depicted on the top, while \(A_t<0\) is on the bottom
In Fig. 5, we consider the scenario of Fig. 1 once more and present the exclusion limits driven by the newly implemented channels. Note that the constraints considered in the previous section form the black exclusion zone on the background. The limits from the various channels shown in this plane seem to be essentially subleading in view of these previous constraints of Fig. 1.
-
Limits from \(\bar{B}\rightarrow X_d\gamma \) intervene essentially for \(A_t>0\) (i.e. for constructive SUSY contributions), large \(\tan \beta \) (driving large SUSY contributions) and light \(H^{\pm }\) (driving large 2HDM contributions). Yet the corresponding bounds are superseded by \(\bar{B}\rightarrow X_s\gamma \).
-
\(B_d^0\rightarrow \mu ^+\mu ^-\) intervenes in the large \(\tan \beta \)/low \(m_{H^{\pm }}\) corner as well, e.g. for \(A_t<0\), but seems less sensitive than \(B_s^0\rightarrow \mu ^+\mu ^-\), except in the low
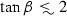 region.
region. -
The processes of the \(b\rightarrow s\bar{\nu }\nu \) and \(s\rightarrow d\bar{\nu }\nu \) transitions are found to be well under the current experimental upper bounds.
-
The \(K-\bar{K}\) mixing excludes a few points (driven by \(\varepsilon _K\) where the SM is slightly off, with respect to the experimental results) but is not competitive in view of the, admittedly conservative, uncertainties.
Note that the limits induced by the \(b\rightarrow c\tau \nu _{\tau }\) channels have been omitted in Fig. 5. Given the current data, this transition would exclude the whole \(\{m_{H^{\pm }},\tan \beta \}\) plane, with the exception of the large \(\tan \beta \)/low \(m_{H^{\pm }}\) corner – which is excluded by most of the other flavour constraints: the significant discrepancy of the SM estimate with the experimental measurement, especially for \(B\rightarrow D^*\tau \nu _{\tau }\), explains this broad exclusion range. SUSY 2HDM effects cannot reduce the gap much, except in already excluded regions of the parameter space.
Exclusion contours driven by \(\bar{B}\rightarrow X_d\gamma \), \(B_d^0\rightarrow \mu ^+\mu ^-\), \(B\rightarrow X_s/K\bar{\nu }\nu \), the \(K-\bar{K}\) mixing and \(K\rightarrow \pi \bar{\nu }\nu \) in the plane \(\{\tan \beta ,m_{A_1}\}\) for the scenario of Fig. 3. The limits obtained with the observables considered in Fig. 3 are shown on the background in black. We employ the same colour/symbol code as for Fig. 5
Then, we return to the light pseudoscalar scenario of Fig. 3 and display the constraints associated with the new channels in Fig. 6. Again, these limits are found to be weaker than those shown in the previous section. Limits from \(B_d^0\rightarrow \mu ^+\mu ^-\) prove the most constraining of the new channels in this regime: this again results from the enhancement of the Higgs-penguin mediated by a resonant \(A_1\). Subleading constraints from the \(K-\bar{K}\) mixing also intervene at low  and for very light CP-odd Higgs with
and for very light CP-odd Higgs with  GeV. Again, the discrepancy among SM predictions and experimental measurements for the \(b\rightarrow c\tau \nu _{\tau }\) transition cannot be interpreted in this scenario, so that applying a \(95\,\%\) CL test for the ratios \(R_{D^{(*)}}\) would lead to the exclusion of the whole portion of parameter space displayed in Fig. 6.
GeV. Again, the discrepancy among SM predictions and experimental measurements for the \(b\rightarrow c\tau \nu _{\tau }\) transition cannot be interpreted in this scenario, so that applying a \(95\,\%\) CL test for the ratios \(R_{D^{(*)}}\) would lead to the exclusion of the whole portion of parameter space displayed in Fig. 6.
Finally, we complete this discussion by considering the parameter sets of Fig. 4, where the flavour limits discussed in the previous section were found weaker. The impact of the new channels can be read in Fig. 7. The corresponding exclusion regions in the considered regime with \(A_t=500\) GeV again prove narrower than those considered in Fig. 4. (Note again that we have omitted the \(b\rightarrow c\tau \nu _{\tau }\) channels, however.)
Exclusion contours driven by \(\bar{B}\rightarrow X_d\gamma \), \(B_d^0\rightarrow \mu ^+\mu ^-\), \(B\rightarrow X_s/K\bar{\nu }\nu \), the \(K-\bar{K}\) mixing and \(K\rightarrow \pi \bar{\nu }\nu \) for the scenarii of Fig. 4. The limits obtained with the observables considered in Fig. 4 are shown on the background. The colour/symbol code is left unchanged
Therefore, we find that the new channels tested in bsg.f and Kphys.f are typically less constraining than the older ones, which we discussed before. Limits from \(\bar{B}\rightarrow X_d\gamma \) and \(B_d^0\rightarrow \mu ^+\mu ^-\) are found to be significant, however, and an evolution of the experimental limits or an improvement in understanding the SM uncertainties may provide them with more relevance in the future. The \(b\rightarrow c\tau \nu _{\tau }\) transition stands apart as the tension between SM and experiment resists an NMSSM interpretation, at least in the scenarios that we have been considering here.
As a final remark, let us mention that the flavour routines that we discussed are not designed to address very light CP-odd states, below the threshold for decays to pions or even muons, as e.g. [97] considered – note that the decay widths computed within NMSSMTools are not reliable for masses below \(\sim \)1 GeV and that the interplay of the light Higgs with the hadronic sector is non-trivial. In such cases, the light pseudoscalar could be long-lived and decay outside of the detectors, hence behave like an invisible final state. Moreover large branching fractions for the decay \(A_1\rightarrow e^+e^-\) appear at low mass and could induce sizable contributions to the \(b\rightarrow s e^+e^-\) and \(s\rightarrow d e^+e^-\) transitions: this will not be properly tested.
5.3 A short comparison with SuperIso
SuperIso [11–13] is a public tool devoted to the calculation of flavour observables in a number of models, among which the NMSSM. The list of channels that are considered there differs somewhat from ours, including e.g. observables in the \(B\rightarrow K^{*}\mu ^+\mu ^-\) transition. Six processes – \(BR(\bar{B}\rightarrow X_{s}\gamma )\), \(BR(B^0_{s}\rightarrow \mu ^+\mu ^-)\), \(\left. BR(\bar{B}\rightarrow X_s\mu ^+\mu ^-)\right| _{1~\mathrm{GeV}^2<m^2_{l^+l^-}<6~\mathrm{GeV}^2}\), \(\left. BR(\bar{B}\rightarrow X_s\right. \left. \mu ^+\mu ^-)\right| _{m^2_{l^+l^-}>14.4~\mathrm{GeV}^2}\), \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\) and \(BR(B^+\rightarrow D\tau ^+\nu _{\tau })/BR(B^+\rightarrow Dl^+\nu _{l})\) – coincide with those considered in the present work, so that we may attempt a brief (and necessarily limited) comparison. For this, we will employ the current version of SuperIso – i.e. 3.5 – and feed it the slha output of NMSSMTools as input for several points (to ensure that we perform the comparison for exactly the same spectra).
Comparison with SuperIso for several points in the scenario of Fig. 1, with \(M_A=800\) GeV. Our results appears as a black dot (central value) with error bars corresponding to the \(2\sigma \) theoretical uncertainties. The output of SuperIso is plotted as red diamonds. The experimental measurement with \(2\sigma \) error bars is also shown in the background, as green lines
In Fig. 8, we consider the MSSM-like scenario of Fig. 1, where we fix \(M_A=800\) GeV and restrict to eight values of \(\tan \beta \). The six common observables of bsg.f and SuperIso are displayed, with our estimate appearing as a black dot accompanied by its \(2\sigma \) theoretical uncertainty; the central value delivered by SuperIso (to our knowledge, SuperIso does not provide an error estimate) is shown as red diamonds and the experimental measurements is plotted in green in the background (for reference). Let us first emphasize that the theoretical estimates roughly agree, in the sense that the central value computed by SuperIso generally falls within the uncertainty range of our prediction. Furthermore, the variations of the central values share a common trend (i.e. the estimates of both codes rise or go down simultaneously) for all observables and the results coincide almost exactly in the case of \(\left. BR(\bar{B}\rightarrow X_sl^+l^-)\right| _{1~\mathrm{GeV}^2<m^2_{l^+l^-}<6~\mathrm{GeV}^2}\), \(\left. BR(\bar{B}\rightarrow X_sl^+l^-)\right. \left. \right| _{m^2_{l^+l^-}>14.4~\mathrm{GeV}^2}\) and \(BR(B^+\rightarrow D\tau ^+\nu _{\tau })/BR(B^+\rightarrow Dl^+\nu _{l})\).
Looking more closely, however, we observe some discrepancies. Their origins are potentially multiple – use of distinct experimental (e.g. CKM) or lattice input, inclusion of the contributions at different orders, diverging treatment of SUSY corrections to the Higgs/down quark system, etc. Actually, given the large parametric uncertainties of the input, the results may differ without any inconsistency. Characterizing these discrepancies with accuracy goes beyond the scope of this paper or indeed the skills of its author, since a detailed comparison would require access to intermediate quantities in SuperIso. Here we will merely state what differences appear and propose an interpretation based on what superficial means stay at our disposal.
Let us first consider \(BR(\bar{B}\rightarrow X_{s}\gamma )\), where the two predictions coincide at low \(\tan \beta \) but tend to diverge apart at large \(\tan \beta \), resulting in only a marginal agreement at \(\tan \beta =40\). This effect develops far from the phenomenologically relevant regime – the predicted \(BR(\bar{B}\rightarrow X_{s}\gamma )\) cannot be reconciled with its experimental value then – and the question of concordance between the two codes may thus appear of limited importance. Still, we notice in the documentation of SuperIso that large-\(\tan \beta \) corrections to the SM contributions for the Wilson coefficients \(C_{7,8}\) – corresponding to the re-definition of the Goldstone boson couplings to down-type quarks, subsequent to the inclusion of radiative corrections – are included in this tool, according to Eq. (18) of [22] or Eq. (B.72) of [9]. We checked that a naive implementation of this contribution would account numerically for the difference between our results and those of SuperIso in Fig. 8 – although this could also be a mere coincidence. Including this contribution would be inappropriate, at least in our case. Indeed, as was shown in [25] and as we reminded in Sect. 2, such contributions are only consistent with an uncorrected description, at LO, of the Higgs/down-quark system – the b-mass and CKM elements would then be pure lagrangian parameters which do not coincide with the measured b mass or CKM elements.
For \(BR(B^0_{s}\rightarrow \mu ^+\mu ^-)\), the small deviations between the predictions of SuperIso and bsg.f are more difficult to trace. At low \(\tan \beta \), they simply result from distinct choices for the estimate of the SM contribution – see Eq. 11. Then another likely contributor is the divergent treatment of Higgs-penguin contributions: SuperIso employs the NLO expansion of [27] while we rely exclusively on the effective lagrangian (at LO) describing the Higgs / down-type couplings in terms of the physical quark masses (see Sect. 2). Finally, for \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\), the central values are almost parallel and it is easy to identify the source of the discrepancy as the choice of distinct values of \(V_{ub}\): as such, this difference is accounted for in the parametric uncertainty that we implemented.
Comparison with SuperIso for several points in the scenario of Fig. 3, with \(\tan \beta =6\). Same symbol/colour code as in Fig. 8. The results for \(BR(\bar{B}\rightarrow X_sl^+l^-)\) in the low \(m^2_{l^+l^-}\) range (\(1~\mathrm{GeV}^2<m^2_{l^+l^-}<6~\mathrm{GeV}^2\)) at \(m_{A_1}=2\) GeV and in the high \(m^2_{l^+l^-}>14.4~\mathrm{GeV}^2\) range at \(m_{A_1}=4\) GeV are of order 0.1 (beyond the plotted region)
In Fig. 9, we turn to the low-\(m_{A_1}\) scenario of Fig. 3, setting \(\tan \beta =6\) and choosing five values of \(m_{A_1}\). The results for \(BR(\bar{B}\rightarrow X_{s}\gamma )\) and \(BR(B^+\rightarrow D\tau ^+\nu _{\tau })/BR(B^+\rightarrow Dl^+\nu _{l})\) look very compatible between the two codes. Again, the deviation for \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\) – within theoretical uncertainties – can be interpreted in terms of the choice of \(V_{ub}\). On the other hand, for \(BR(B^0_{s}\rightarrow \mu ^+\mu ^-)\), the two codes only agree as far as concluding that the points give a branching fraction far beyond the experimentally acceptable range. The two estimates actually differ by orders of magnitude. First, we note that, so far from the physical region (where BSM effects should remain small), the question of explaining this difference could appear as largely academical. Then, a fair guess would assign this discrepancy to the divergent descriptions of the Higgs penguin contributions. More precisely, SuperIso employs the formalism of [98] in the presence of a light pseudoscalar. Instead of characterising the pseudoscalar – and in particular its couplings – strictly in terms of the associated rotation matrix, the latter reference directly injects lagrangian parameters (using tree-level relations; e.g. via the quantity \(\delta _-\)) into the expressions of the Wilson coefficients. While receivable in a description of the NMSSM Higgs sector at tree-level, these formulae will not properly account for a radiatively-corrected Higgs sector (as e.g. delivered by NMSSMTools): the properties of a light state may vary sizably in this fashion. Additionally, the conventions of [98] differ somewhat from those usually employed in the NMSSM – particularly a factor \(\sqrt{2}\) for the singlet v.e.v. We checked that a naive use of the expressions in [98] could easily account for a factor O(10) at the level of the Wilson coefficients, hence might be the source of the disparity of the estimates performed by SuperIso and bsg.f for \(BR(B^0_{s}\rightarrow \mu ^+\mu ^-)\) in Fig. 9. If so, we believe that our description of the Higgs penguins is better suited, as it properly implements the properties of the loop-corrected Higgs sector. The predictions for \(BR(\bar{B}\rightarrow X_sl^+l^-)\) in the low and high \(m^2_{l^+l^-}\) ranges should be considered under the same light: our estimates only depart from the experimentally allowed region when the pseudoscalar falls under the tested range in \(m^2_{l^+l^-}\) – i.e. for \(m_{A_1}=2\) GeV in the low range and \(m_{A_1}=4\) GeV in the high range – which seems physically intuitive and is consistent with our relatively mild excess in \(B^0_{s}\rightarrow \mu ^+\mu ^-\) (the effective \(A_1-b-s\) coupling is not extremely large in our approach). On the other hand, considering the predictions of SuperIso, the presence of a pole in the integral over \(m^2_{l^+l^-}\) does not appear to make much of a difference and the \(BR(\bar{B}\rightarrow X_sl^+l^-)\) are invariably excessive (the effective \(A_1-b-s\) coupling computed by SuperIso is much larger than the one in bsg.f as could already be inferred from \(B^0_{s}\rightarrow \mu ^+\mu ^-\)). Another difference is that our result is averaged over \(l=e\) and \(l=\mu \) final states, while SuperIso only considers \(l=\mu \): this is relevant in view of the Higgs couplings being related to \(m_l\).
We shall close the comparison with SuperIso here. We found a qualitative agreement between the estimates of this code and ours in most cases. As for the discrepancies, we can understand them most of the time, either in terms of different choices of the parameters – for \(BR(B^+\rightarrow \tau ^+\nu _{\tau })\) – or divergent processing of the effective Higgs/down quark couplings – for \(BR(\bar{B}\rightarrow X_{s}\gamma )\) or \(BR(B^0_{s}\rightarrow \mu ^+\mu ^-)\). In the latter case, we believe that we have employed a consistent formalism. We also stress that these effects appear for large new-physics contributions, i.e. far from the phenomenologically relevant regime. Yet a full understanding of these differences would require a much more detailed analysis and goes beyond our ambitions for this paper.
6 Conclusions
We have considered a set of flavour observables in the NMSSM, updating and extending our former analysis in [4]. These channels have been implemented in a pair of Fortran subroutines, which allow for both the evaluation of the observables in the NMSSM and confrontation with the current experimental results. We have taken into account the recent upgrades of the SM status of e.g. \(BR[\bar{B}\rightarrow X_s\gamma ]\) or \(BR[B_s^0\rightarrow \mu ^+\mu ^-]\) and included BSM effects at NLO. The tools thus designed will be/have been partially made public within the package NMSSMTools [5–8].
We observe that the bounds on the NMSSM parameter space driven by \(BR[\bar{B}\rightarrow X_s\gamma ]\) or \(BR[B_s^0\rightarrow \mu ^+\mu ^-]\) have become more efficient, which should be considered in the light of the recent evolution of the SM status and/or the experimental measurement for both these channels. In particular, the large \(\tan \beta \) region is rapidly subject to constraints originating from the flavour sector. Similarly, the light pseudoscalar scenario is tightly corseted due to the efficiency of Higgs-penguins in the presence of such a light mediator.
Among the new channels that we have included, we note the specific status of the \(b\rightarrow c\tau \nu _{\tau }\) transition, where the discrepancy between SM and experiment seems difficult to address in a SUSY context.
Other channels of the flavour-changing sector may prove interesting to include in the future. Note e.g. the current evolution in the \(B\rightarrow K^{(*)}l^+l^-\) observables.
Notes
We note that the label ‘NLO’ covers different realities depending on the observables: while it generally stands for ‘LO + full QCD corrections’, it is sometimes employed simply for ‘LO + QCD running’, as in the case of \(\Delta M_{d,s}\). We align our terminology on that of our sources.
Here as later on, we employ ‘sup’ and ‘sdown’ in the sense of ‘up-type sfermions’ and ‘down-type sfermions’ without referring to the first generation exclusively.
We thank J. Virto for his suggestion and assistance.
Note that the old version of the code had been updated to include recent experimental values, so that the differences with the new implementation are fully controlled by the theoretical treatment of the observables.
References
S. Descotes-Genon, L. Hofer, J. Matias, J. Virto, arXiv:1510.04239 [hep-ph]
T. Hurth, F. Mahmoudi, Rev. Mod. Phys. 85, 795 (2013). arXiv:1211.6453 [hep-ph]
U. Ellwanger, C. Hugonie, A.M. Teixeira, Phys. Rept. 496, 1 (2010). arXiv:0910.1785 [hep-ph]
F. Domingo, U. Ellwanger, JHEP 0712, 090 (2007). arXiv:0710.3714 [hep-ph]
U. Ellwanger, J.F. Gunion, C. Hugonie, JHEP 0502, 066 (2005). arXiv:hep-ph/0406215
U. Ellwanger, C. Hugonie, Comput. Phys. Commun. 175, 290 (2006). arXiv:hep-ph/0508022
U. Ellwanger, J.F. Gunion, C. Hugonie, JHEP 0502, 066 (2005). arXiv:hep-ph/0406215
U. Ellwanger, C. Hugonie, Comput. Phys. Commun. 175, 290 (2006). arXiv:hep-ph/0508022. http://www.th.u-psud.fr/NMHDECAY/nmssmtools.html
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 174, 577 (2006). arXiv:hep-ph/0405253
G. Degrassi, P. Gambino, P. Slavich, Comput. Phys. Commun. 179, 759 (2008). arXiv:0712.3265 [hep-ph]
F. Mahmoudi, Comput. Phys. Commun. 178, 745 (2008). arXiv:0710.2067 [hep-ph]
F. Mahmoudi, Comput. Phys. Commun. 180, 1579 (2009). arXiv:0808.3144 [hep-ph]
F. Mahmoudi, Comput. Phys. Commun. 180, 1718 (2009). http://superiso.in2p3.fr/
J. Rosiek, P. Chankowski, A. Dedes, S. Jager, P. Tanedo, Comput. Phys. Commun. 181, 2180 (2010). arXiv:1003.4260 [hep-ph]
A. Crivellin, J. Rosiek, P.H. Chankowski, A. Dedes, S. Jaeger, P. Tanedo, Comput. Phys. Commun. 184, 1004 (2013). arXiv:1203.5023 [hep-ph]. http://www.fuw.edu.pl/susy_flavor/
W. Porod, F. Staub, A. Vicente, Eur. Phys. J. C 74(8), 2992 (2014). arXiv:1405.1434 [hep-ph]. http://sarah.hepforge.org/FlavorKit.html
G. Buchalla, A.J. Buras, M.E. Lautenbacher, Rev. Mod. Phys. 68, 1125 (1996). arXiv:hep-ph/9512380
K.G. Chetyrkin, M. Misiak, M. Munz, Phys. Lett. B 400, 206 (1997)
K.G. Chetyrkin, M. Misiak, M. Munz, Phys. Lett. B 425, 414 (1998). arXiv:hep-ph/9612313
M. Ciuchini, G. Degrassi, P. Gambino, G.F. Giudice, Nucl. Phys. B 527, 21 (1998). arXiv:hep-ph/9710335
M. Ciuchini, G. Degrassi, P. Gambino, G.F. Giudice, Nucl. Phys. B 534, 3 (1998). arXiv:hep-ph/9806308
G. Degrassi, P. Gambino, G.F. Giudice, JHEP 0012, 009 (2000). arXiv:hep-ph/0009337
P. Gambino, M. Misiak, Nucl. Phys. B 611, 338 (2001). arXiv:hep-ph/0104034
T. Hurth, E. Lunghi, W. Porod, Nucl. Phys. B 704, 56 (2005). arXiv:hep-ph/0312260
A.J. Buras, P.H. Chankowski, J. Rosiek, L. Slawianowska, Nucl. Phys. B 659, 3 (2003). arXiv:hep-ph/0210145
C. Bobeth, M. Misiak, J. Urban, Nucl. Phys. B 567, 153 (2000). arXiv:hep-ph/9904413
C. Bobeth, A.J. Buras, F. Kruger, J. Urban, Nucl. Phys. B 630, 87 (2002). arXiv:hep-ph/0112305
C. Bobeth, A.J. Buras, T. Ewerth, Nucl. Phys. B 713, 522 (2005). arXiv:hep-ph/0409293
M. Misiak et al., Phys. Rev. Lett. 98, 022002 (2007). arXiv:hep-ph/0609232
T. Becher, M. Neubert, Phys. Rev. Lett. 98, 022003 (2007). arXiv:hep-ph/0610067
M. Misiak et al., Phys. Rev. Lett. 114(22), 221801 (2015). arXiv:1503.01789 [hep-ph]
M. Czakon, P. Fiedler, T. Huber, M. Misiak, T. Schutzmeier, M. Steinhauser, JHEP 1504, 168 (2015). arXiv:1503.01791 [hep-ph]
C. Bobeth, M. Gorbahn, T. Hermann, M. Misiak, E. Stamou, M. Steinhauser, Phys. Rev. Lett. 112, 101801 (2014). arXiv:1311.0903 [hep-ph]
T. Hermann, M. Misiak, M. Steinhauser, JHEP 1312, 097 (2013). arXiv:1311.1347 [hep-ph]
C. Bobeth, M. Gorbahn, E. Stamou, Phys. Rev. D 89(3), 034023 (2014). arXiv:1311.1348 [hep-ph]
V. Khachatryan et al., CMS and LHCb Collaborations, Nature 522, 68 (2015). arXiv:1411.4413 [hep-ex]
T. Huber, T. Hurth, E. Lunghi, JHEP 1506, 176 (2015). arXiv:1503.04849 [hep-ph]
F. Mahmoudi, S. Neshatpour, J. Virto, Eur. Phys. J. C 74(6), 2927 (2014). arXiv:1401.2145 [hep-ph]
Y. Amhis et al. [Heavy Flavor Averaging Group (HFAG) Collaboration], arXiv:1412.7515 [hep-ex]. http://www.slac.stanford.edu/xorg/hfag/
M. Misiak, M. Steinhauser, Nucl. Phys. B 764, 62 (2007). arXiv:hep-ph/0609241
A.J. Buras, A. Czarnecki, M. Misiak, J. Urban, Nucl. Phys. B 631, 219 (2002). arXiv:hep-ph/0203135
M. Kaminski, M. Misiak, M. Poradzinski, Phys. Rev. D 86, 094004 (2012). arXiv:1209.0965 [hep-ph]
T. Huber, M. Poradzinski, J. Virto, JHEP 1501, 115 (2015). arXiv:1411.7677 [hep-ph]
C.W. Bauer, Phys. Rev. D 57, 5611 (1998)
C.W. Bauer, Phys. Rev. D 60, 099907 (1999). arXiv:hep-ph/9710513
M. Benzke, S.J. Lee, M. Neubert, G. Paz, JHEP 1008, 099 (2010). arXiv:1003.5012 [hep-ph]
M. Czakon, U. Haisch, M. Misiak, JHEP 0703, 008 (2007). arXiv:hep-ph/0612329
P. Gambino, U. Haisch, JHEP 0110, 020 (2001). arXiv:hep-ph/0109058
L. Hofer, U. Nierste, D. Scherer, JHEP 0910, 081 (2009). arXiv:0907.5408 [hep-ph]
T.F. Feng, Phys. Rev. D 70, 096012 (2004). arXiv:hep-ph/0405192
P. del Amo Sanchez et al., [BaBar Collaboration], Phys. Rev. D 82, 051101 (2010). arXiv:1005.4087 [hep-ex]
A. Crivellin, L. Mercolli, Phys. Rev. D 84, 114005 (2011). arXiv:1106.5499 [hep-ph]
H.M. Asatrian, C. Greub, Phys. Rev. D 88(7), 074014 (2013). arXiv:1305.6464 [hep-ph]
G. Hiller, Phys. Rev. D 70, 034018 (2004). arXiv:hep-ph/0404220
K.A. Olive et al. [Particle Data Group Collaboration], Chin. Phys. C 38, 090001 (2014). http://pdg.lbl.gov/
S. Aoki et al., Eur. Phys. J. C 74, 2890 (2014). arXiv:1310.8555 [hep-lat]. http://itpwiki.unibe.ch/flag/
P. Ball, R. Fleischer, Eur. Phys. J. C 48, 413 (2006). arXiv:hep-ph/0604249
A.S. Cornell, N. Gaur, JHEP 0309, 030 (2003). arXiv:hep-ph/0308132
Y. Sato et al. [Belle Collaboration], arXiv:1402.7134 [hep-ex]
W. Altmannshofer, P. Ball, A. Bharucha, A.J. Buras, D.M. Straub, M. Wick, JHEP 0901, 019 (2009). arXiv:0811.1214 [hep-ph]
W. Altmannshofer, D.M. Straub, Eur. Phys. J. C 73, 2646 (2013). arXiv:1308.1501 [hep-ph]
S. Descotes-Genon, J. Matias, J. Virto, Phys. Rev. D 88, 074002 (2013). arXiv:1307.5683 [hep-ph]
A.J. Buras, J. Girrbach, Rept. Prog. Phys. 77, 086201 (2014). arXiv:1306.3775 [hep-ph]
A.J. Buras, J. Girrbach-Noe, C. Niehoff, D.M. Straub, JHEP 1502, 184 (2015). arXiv:1409.4557 [hep-ph]
R. Barate et al. [ALEPH Collaboration], Eur. Phys. J. C 19, 213 (2001). arXiv:hep-ex/0010022
J.P. Lees et al. [BaBar Collaboration], Phys. Rev. D 87(11), 112005 (2013). arXiv:1303.7465 [hep-ex]
O. Lutz et al. [Belle Collaboration], Phys. Rev. D 87(11), 111103 (2013). arXiv:1303.3719 [hep-ex]
A.G. Akeroyd, S. Recksiegel, J. Phys. G 29, 2311 (2003). arXiv:hep-ph/0306037
J.F. Kamenik, F. Mescia, Phys. Rev. D 78, 014003 (2008). arXiv:0802.3790 [hep-ph]
S. Fajfer, J.F. Kamenik, I. Nisandzic, Phys. Rev. D 85, 094025 (2012). arXiv:1203.2654 [hep-ph]
J.P. Lees et al., [BaBar Collaboration], Phys. Rev. Lett. 109, 101802 (2012). arXiv:1205.5442 [hep-ex]
J.P. Lees et al. [BaBar Collaboration], Phys. Rev. D 88(7), 072012 (2013). arXiv:1303.0571 [hep-ex]
J.A. Bailey et al. [MILC s Collaboration], Phys. Rev. D 92(3), 034506 (2015). arXiv:1503.07237 [hep-lat]
H. Na et al. [HPQCD Collaboration], Phys. Rev. D 92(5), 054510 (2015). arXiv:1505.03925 [hep-lat]
R. Aaij et al. [LHCb Collaboration], arXiv:1506.08614 [hep-ex]
M. Huschle et al. [Belle Collaboration], arXiv:1507.03233 [hep-ex]
A. Crivellin, C. Greub, A. Kokulu, Phys. Rev. D 86, 054014 (2012). arXiv:1206.2634 [hep-ph]
S. Bertolini, F. Borzumati, A. Masiero, G. Ridolfi, Nucl. Phys. B 353, 591 (1991)
A.J. Buras, S. Jager, J. Urban, Nucl. Phys. B 605, 600 (2001). arXiv:hep-ph/0102316
D. Becirevic, V. Gimenez, G. Martinelli, M. Papinutto, J. Reyes, JHEP 0204, 025 (2002). arXiv:hep-lat/0110091
A. Lenz et al., Phys. Rev. D 83, 036004 (2011). arXiv:1008.1593 [hep-ph]
A. Lenz, U. Nierste, arXiv:1102.4274 [hep-ph]
A.J. Buras, D. Buttazzo, J. Girrbach-Noe, R. Knegjens, arXiv:1503.02693 [hep-ph]
A.J. Buras, T. Ewerth, S. Jager, J. Rosiek, Nucl. Phys. B 714, 103 (2005). arXiv:hep-ph/0408142
A.V. Artamonov et al., [E949 Collaboration], Phys. Rev. Lett. 101, 191802 (2008). arXiv:0808.2459 [hep-ex]
J.K. Ahn et al., [E391a Collaboration], Phys. Rev. D 81, 072004 (2010). arXiv:0911.4789 [hep-ex]
J. Bijnens, J.M. Gerard, G. Klein, Phys. Lett. B 257, 191 (1991)
Z. Bai, N.H. Christ, T. Izubuchi, C.T. Sachrajda, A. Soni, J. Yu, Phys. Rev. Lett. 113, 112003 (2014). arXiv:1406.0916 [hep-lat]
A.J. Buras, J. Girrbach, Eur. Phys. J. C 73(9), 2560 (2013). arXiv:1304.6835 [hep-ph]
J.A. Bailey et al. [SWME Collaboration], Phys. Rev. D 92(3), 034510 (2015). arXiv:1503.05388 [hep-lat]
T. Blum et al., Phys. Rev. Lett. 108, 141601 (2012). arXiv:1111.1699 [hep-lat]
N.H. Christ et al., [RBC and UKQCD Collaborations], Phys. Rev. D 88, 014508 (2013). arXiv:1212.5931 [hep-lat]
J. Brod, M. Gorbahn, Phys. Rev. Lett. 108, 121801 (2012). arXiv:1108.2036 [hep-ph]
J. Brod, M. Gorbahn, Phys. Rev. D 82, 094026 (2010). arXiv:1007.0684 [hep-ph]
A.J. Buras, M. Jamin, P.H. Weisz, Nucl. Phys. B 347, 491 (1990)
Y.C. Jang et al. [SWME Collaboration], arXiv:1509.00592 [hep-lat]
S. Andreas, O. Lebedev, S. Ramos-Sanchez, A. Ringwald, JHEP 1008, 003 (2010). arXiv:1005.3978 [hep-ph]
Z. Heng, R.J. Oakes, W. Wang, Z. Xiong, J.M. Yang, Phys. Rev. D 77, 095012 (2008). arXiv:0801.1169 [hep-ph]
Acknowledgments
F. Domingo is grateful to U. Ellwanger for useful comments and thanks D. Barducci for spotting a numerical instability in the pre-released version of bsg.f. This work is supported by CICYT (Grant FPA 2013-40715-P).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Domingo, F. Update of the flavour-physics constraints in the NMSSM. Eur. Phys. J. C 76, 452 (2016). https://doi.org/10.1140/epjc/s10052-016-4298-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4298-z







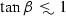 .
.
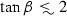 region.
region.


