1 Introduction

The Unruh effect [1–4] predicts that the Minkowski vacuum as seen by an observer accelerating uniformly will appear as a warm gas emitting black-body radiation at the Unruh temperature. The Unruh effect produces a decoherence-like effect [5]. It degrades the quantum information shared between an inertial observer and an accelerated observer, as seen in the latter’s frame, in the case of bosonic or Dirac field modes [6, 7]. The studies on Unruh effect form a part of the endeavour to understand relativistic aspects of quantum information [8–12]; see for example the review [13].

The Unruh channel, from the perspective of quantum information, is special in the sense that it is conjugate degradable [14]. This feature enables the computation of the channel capacity, both classical and quantum, as well as a trade-off between them for a number of scenarios [15, 16].

An important step towards the experimental realisation in the domain of relativistic quantum information could be achieved from circuit quantum electrodynamics (cQED), making use of superconducting quantum interferometric devices (SQUIDs) [17]. Also, the concept of geometric phase has been used to propose a possible detection of Unruh temperature at accelerations small enough to be experimentally feasible [18]. Further, there have been attempts to understand the quantum metrology aspects of the Unruh effect [19, 20].

Here we take up the problem of studying Fisher [21] and its variant skew information [22, 23] for the Unruh effect on a Dirac field mode in the context of open quantum systems [24]. These help in revealing the intrinsic sensitivity of the system of interest with respect to change of state parameters, such as the ambient temperature. Both the quantum Fisher and the skew information are two different aspects of the classical Fisher information in the quantum regime [25], with the skew and Fisher information being related to the Hellinger and Bures distance, respectively [26–28].

The Fisher information provides a lower bound on the error of an estimation [29]. The estimation of the initial state parameters has been of interest for quite some time and in recent years this approach has been turned towards state estimation in the context of open quantum systems [30, 31].

In this work, we develop a Bloch vector representation characterising the Unruh channel acting on a qubit, providing a uniform platform for understanding quantum Fisher and skew information, both with and without external noises. With this we are in a position to study the intrinsic sensitivity of the Unruh channel for the Dirac qubit to variation of the parameters characterising both the pure Unruh channel and the channel in an external environment.

For the external noises, we take the experimentally relevant [32–34] purely dephasing QND (quantum non-demolition) [35, 36] as well as the squeezed generalised amplitude damping (SGAD) noise [37, 38]. The QND channel is a purely quantum effect incorporating decoherence without dissipation, while the SGAD channel is a very general noisy channel in that it incorporates both the effects of finite temperature and bath squeezing. We observe the non-trivial interplay between temperature and bath squeezing on the Fisher and skew information. In particular, it is observed that in some regimes squeezing can play a constructive role in enhancing the information against the deteriorating influence of temperature.

Plan of the work is as follows. In Sect. 2 we briefly discuss the importance of quantum Fisher information in the context of estimation theory and motivate the use of the Bloch vector formalism for the study of Unruh effect with(out) external noises. We then develop the Bloch vector formalism characterising the Unruh channel. In the next section quantum Fisher information for the Unruh channel without any external noise is studied. In Sect. 5 we extend the above by incorporating the effect of external noises, both the purely dephasing phase damping and the SGAD channels. Since the skew information is another variant of the quantum Fisher information, we probe skew information both for the pure Unruh channel and for the cases where the channel is affected by external noises, QND as well as SGAD. Finally we draw our conclusions.

2 Quantum Fisher information in the Bloch vector formalism

With the advent of experimental progress, estimation theory has become a powerful tool for activities such as state reconstruction, tomography and metrology [39]. Quantum Fisher information plays a prominent role in these activities where a question of central importance is the determination of an unknown parameter characterising the system and to reduce the error in these estimations. Their roots are related to the famous Cramer–Rao bound, which is related to the fundamental founds on the efficiency of the estimation problem. Quantum Fisher information is the quantum counterpart of these bounds.

It is well known that the Unruh process is an inherently noisy one. Thus it is of interest to have an understanding of this process from the prospective of the estimation problem and hence the motivation for a study of the Unruh effect using Fisher information. Efforts have been made along these directions, for example, in [30] where a systematic study was made of the problem of Fisher information in the presence of a number of well-known noisy channels such as the phase damping, which is essentially a QND channel and generalised amplitude damping (GAD) channel, which is a subset of the SGAD channel. A similar study was also made in [31] where the problem of estimation of probe states with the feature of best resistance to noise was studied. In both of these works, the geometric visualisation offered by the Bloch vector formalism was made use of in estimating the Fisher information.

In [20] these studies were applied to the problem of pure Unruh effect both for the scalar and the Dirac field mode. Here, using the Kraus operators characterising the pure Unruh channel, we develop a Bloch vector treatment of the quantum Fisher information of the Unruh effect of a Dirac field mode. Further, we study the effect of external noises, both QND and SGAD, on the Fisher estimation. This enables us to study the interplay between the external temperature and reservoir squeezing, a quantum correlation, on the Fisher information. Our constructions are analytic in nature.

Any two level system can be represented in the Bloch vector formalism as

$$\begin{aligned} \rho = \frac{1}{2} \left(\mathbb {I}+ \mathbf {\zeta } \cdot \sigma \right), \end{aligned}$$
(1)

where \(\sigma \) are the standard Pauli matrices and \(\mathbf {\zeta }\) is the Bloch vector. Quantum Fisher information in terms of the Bloch vector \(\mathbf {\zeta }(\alpha )\) is given by [30, 31]

$$\begin{aligned} F_q(\alpha ) = \frac{\left[\mathbf {\zeta }(\alpha ) \cdot \partial _{\alpha }\mathbf {\zeta }(\alpha )\right]^2}{1-|\mathbf {\zeta } (\alpha )|^2} + \left[\partial _{\alpha }\mathbf {\zeta }(\alpha )\right]^2, \end{aligned}$$
(2)

where q denotes quantum and \(\alpha \) is the parameter to be estimated, for example, the polar and azimuthal angles \(\theta \) and \(\phi \), respectively, of a qubit. From now on we will abbreviate \(F_q(\alpha )\) by \(F_{\alpha }\). We will make use of this in our work.

3 Bloch vector formalism for Unruh channel

Here we provide a sketch of the tools required to obtain a Bloch vector representation of the Unruh channel. The basic ingredient that goes into this endeavour is the Choi theorem [40, 41] which is applied here by considering the maximally entangled two Dirac field modes state \(\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle )\) in which the second mode is Unruh accelerated. This results in [5]

$$\begin{aligned} \rho _U=\frac{1}{2}\left( \begin{array}{llll} \cos ^2r&{}0&{}0&{}\cos r\\ 0&{}\sin ^2r&{}0&{}0\\ 0&{}0&{}0&{}0\\ \cos r&{}0&{}0&{}1 \end{array} \right) , \end{aligned}$$
(3)

where r is the Unruh parameter given by \(\cos r=\frac{1}{\sqrt{e^{-\frac{2\pi \omega c}{a_u}}+1}}\). Here \(a_u\) is the uniform Unruh acceleration and \(\omega \) is the Dirac particle frequency. As \(a_u\) ranges from \(\infty \) to 0, \(\cos r \in [\frac{1}{\sqrt{2}},1]\). The spectral decomposition of the above state gives

$$\begin{aligned} \rho _U=\sum _{j=0}^3|\xi _j\rangle \langle \xi _j|, \end{aligned}$$
(4)

where \(|\xi _j\rangle \) are the eigenvectors normalised to the value of the eigenvalue. Choi’s theorem [40, 41], by making use of channel-state duality, then provides a root to obtaining the Kraus operators relevant to the channel generating the state in Eq. 3. Essentially, each \(|\xi _j\rangle \) yields a Kraus operator obtained by folding the \(d^2\) elements of the eigenvector into a \(d\times d\) matrix, by taking each sequential d-element segment of \(|\xi _j\rangle \), writing it as a column, and then juxtaposing these columns to form the matrix [40, 41]. Here \(d=2\).

Spectral decomposition of \(\rho _U\), Eq. 4, yields the following eigenvectors, corresponding to two non-vanishing eigenvalues:

$$\begin{aligned} |\xi _0\rangle= & {} (\cos r,0,0,1),\nonumber \\ |\xi _1\rangle= & {} (0,\sin r,0,0). \end{aligned}$$
(5)

A straightforward application of Choi’s theorem now yields the following Kraus operators for the Unruh channel \(\mathscr {E}_U\):

$$\begin{aligned} \mathscr {K}^U_1=\left( \begin{array}{cclr} \cos r&{}0\\ 0&{}1 \end{array}\right) ;\quad {\mathscr {K}}^U_2=\left( \begin{array}{cclr} 0&{}0\\ \sin r&{}0 \end{array}\right) , \end{aligned}$$
(6)

whereby

$$\begin{aligned} \mathscr {E}_U(\rho ) = \sum _{j=1,2} {\mathscr {K}}^U_j \rho \left( {\mathscr {K}}^U_j\right) ^\dag , \end{aligned}$$
(7)

with the completeness condition

$$\begin{aligned} \sum _{j=1,2} \left( {\mathscr {K}}^U_j\right) ^\dag {\mathscr {K}}^U_j = \mathbb {I}. \end{aligned}$$
(8)

From the above Kraus representation, it would appear that the Unruh channel is formally similar to an AD channel, which models the effect of a zero temperature bath [35–37]. This is surprising as the Unruh effect corresponds to a finite temperature and would naively be expected to correspond to finite temperature channels such as the GAD or SGAD channels.

For the initial state \(\rho = |0\rangle \langle 0|\cos ^2\frac{\theta }{2} + |0\rangle \langle 1|e^{i\phi }\cos \frac{\theta }{2}\sin \frac{\theta }{2} +|1\rangle \langle 0|e^{-i\phi }\cos \frac{\theta }{2}\sin \frac{\theta }{2} +|1\rangle \langle 1|\sin ^2\frac{\theta }{2},\) the Bloch vector can be seen to be \(\zeta _0 = \left(\cos \phi \sin \theta ,\, -\sin \phi \sin \theta ,\, \cos \theta \right)\). Evolving this state under the Unruh channel, characterised by the above Kraus operators leads to a state, which could be called the Unruh–Dirac (UD) qubit state, whose Bloch vector is

$$\begin{aligned} \mathbf {\zeta }= \left( \begin{array}{lll} \cos r \cos \phi \sin \theta \\ - \cos r \sin \phi \sin \theta \\ \cos ^2r \cos \theta - \sin ^2r \end{array} \right) =A \mathbf {\zeta _0}+C. \end{aligned}$$
(9)

From this A and C can be found to be

$$\begin{aligned} A= \left( \begin{array}{clclclr} \cos r &{} 0 &{} 0\\ 0 &{} \cos r &{} 0 \\ 0 &{} 0 &{} \cos ^2 r \end{array} \right) , \quad C= \left( \begin{array}{clr} 0 \\ 0\\ -\sin ^2 r \end{array}\right) . \end{aligned}$$
(10)

This, we believe, is a new result with the A and C matrices completely characterising the Unruh channel and will be used in the investigations below.

4 Quantum Fisher information for Unruh channel without external noise

That the Unruh channel is an inherently noisy channel is made explicit by its Kraus representation, Eqs. (6) and (7). Here we will estimate the UD qubit state using quantum Fisher information. For this purpose we will make use of A and C from Eq. (10) and \(\mathbf {\zeta }\) from Eq. (9) as inputs in Eq. (2).

When no external noise is acting, i.e., for the case of the pure Unruh channel, it can be seen that

$$\begin{aligned} F_\theta= & {} \cos ^2r,\nonumber \\ F_\phi= & {} \cos ^2r\sin ^2\theta . \end{aligned}$$
(11)

The Fisher information with respect to the parameter \(\theta \), \(F_\theta \), is independent of the state parameter \(\theta \) while the Fisher information with respect to the parameter \(\phi \), \(F_\phi \) is state dependent and depends upon \(\theta \). It should be noted that both these expressions of Fisher information have no \(\phi \) dependence. Also it can be observed from the above expressions that the Fisher information cannot be increased by increasing the Unruh acceleration. This is consistent with the fact that the Unruh acceleration produces a thermal like effect and quantum estimation would be expected not to increase with increase in temperature.

Fig. 1
figure 1

a Plot of \(F_\theta \) with respect to Unruh parameter for acceleration r; b plot of \(F_\phi \) with respect to r and \(\theta \)

Full size image

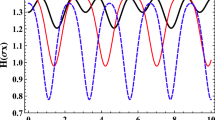
This is also evident from Fig. 1, where \(F_{\theta }\) is plotted as a function of the Unruh parameter r whereas \(F_{\phi }\), is plotted with respect to r and \(\theta \). As r goes from \(\pi /4\) to 0, i.e., \(\cos r\) goes from \(1/\sqrt{2}\) to 1, which implies the Unruh acceleration a decreasing from infinity to zero, \(F_{\theta }\) increases to 1. Since the Unruh acceleration is directly proportional to temperature, as acceleration decreases, temperature also decreases and quantum Fisher information increases. This is also seen for \(F_\phi \), albeit only for \(\theta =\pi \).

Further, it can be seen from above that \(F_\theta \) depends upon the Unruh parameter r. It should be noted that this result is obtained for an Unruh channel, by accelerating one partner of the maximally entangled state, as indicated in the previous section. It is interesting to observe here that for an analogous study of Unruh effect on a different state, not necessarily maximally entangled, \(F_\theta \) was shown to be independent of r [20]. This suggests that Fisher information which is an important tool in state estimation could also be used as a witness for quantum correlations.

5 Quantum Fisher information for Unruh channel with external noise

Now we will analyse the effect of external noise on the Unruh channel using the Bloch vector formalism of quantum Fisher information. For this purpose, we consider two general external noisy channels: (a) phase damping channel, which is of the QND kind and involves pure dephasing, and (b) the SGAD channel, which includes the effects of decoherence along with dissipation and accounts for finite bath temperature as well as squeezing. We adopt the following procedure. Starting from the UD qubit state, Eq. (9), application of the external noise channel results in

$$\begin{aligned} \rho _\mathrm{in} \xrightarrow {\mathscr {E}\mathrm{(phase/SGAD)}} \rho _\mathrm{new}. \end{aligned}$$
(12)

From \(\rho _\mathrm{new}\), we get the new Bloch vector \(\mathbf {\zeta }_\mathrm{new}\), which is related to the original state Bloch vector as

$$\begin{aligned} \mathbf {\zeta }_\mathrm{new}= & {} A' \mathbf {\zeta } +C' = A'(A\mathbf {\zeta _0}+C)+C'\nonumber \\= & {} AA'\mathbf {\zeta _0} + (A'C+C')\equiv A_\mathrm{new}\mathbf {\zeta _0}+C_\mathrm{new}. \end{aligned}$$
(13)

Here \(\mathbf {\zeta }\) and \(\mathbf {\zeta _0}\) are as in Eq. (9). From the above equation, it can be seen that the effect of the external noise channel on the Unruh channel is encoded in \(A_\mathrm{new}=A'A\) and \(C_\mathrm{new} = (A'C + C')\). Thus we need to find \(A'\) and \(C'\) for the desired channels using the Kraus operator formalism.

5.1 Phase damping channel

In the context of open quantum systems, one is interested in the dynamics of the system of interest, for example, the UD qubit in this case, by taking into account the effect of the ambient environment on its evolution. Let the total Hamiltonian H be \(H=H_S + H_R + H_{SR}\), where \(H_S\), \(H_R\) are the system and reservoir Hamiltonians, respectively, and \(H_{SR}\) is the interaction between the two. If \([H_S, H_{SR}]=0\), then it implies decoherence without dissipation, that is, pure dephasing. This is a purely quantum mechanical effect and such an interaction is called a QND interaction. The phase damping channel is a well-known noisy channel incorporating QND interaction.

The Kraus operators corresponding to the phase damping channel, modelling the QND interaction of a qubit, with the two levels having a separation of \(\hbar \omega _0\), interacting with a squeezed thermal bath are [35, 36]

$$\begin{aligned} K_1= & {} \sqrt{\frac{1+e^{-(\hbar \omega _0)^2\gamma (t)}}{2}}\left( \begin{array}{cc} e^{-i\hbar \omega _0 t}&{}0\\ 0&{}1 \end{array}\right) ;\nonumber \\ K_2= & {} \sqrt{\frac{1-e^{-(\hbar \omega _0)^2\gamma (t)}}{2}}\left( \begin{array}{cc} -e^{-i\hbar \omega _0 t}&{}0\\ 0&{}1 \end{array}\right) . \end{aligned}$$
(14)

Assuming an Ohmic bath spectral density with an upper cut-off frequency \(\omega _c\), the expression of \(\gamma (t)\), characterising the bath, can be obtained from [35, 36]. It depends on the reservoir temperature T as well as on the bath squeezing parameters a and s. For the Unruh channel in the presence of phase damping noise the modified Bloch vector for the UD qubit, Eq. (13), is

$$\begin{aligned} \zeta _{\text {new}}= \begin{pmatrix} \cos r\sin \theta \cos (\phi +\omega _0 t)e^{-(\hbar \omega _0)^2\gamma (t)/4}\\ -\cos r\sin \theta \sin (\phi +\omega _0 t)e^{-(\hbar \omega _0)^2\gamma (t)/4}\\ \cos ^2r \cos \theta - \sin ^2r \end{pmatrix}. \end{aligned}$$
(15)
Fig. 2
figure 2

a Variation of \(F_\theta \) (Fisher information with respect to the parameter \(\theta \)) and b \(F_\phi \) (Fisher information with respect to parameter \(\phi \)) for QND interaction with the bath for a time (t) and the Unruh parameter (r). The parameter settings are \(\theta =\pi /4\), \(\phi =\pi /4\), \(a=0\), \(T=0.5\), \(s=0.5\), \(\omega _0=1\), \(\omega _c=100\), \(\gamma _0=0.1\)

Full size image

The analytical expressions for the quantum Fisher information with respect to parameters \(\theta \) and \(\phi \) are

$$\begin{aligned} F_\theta= & {} \frac{\cos ^2 r \left( 2(1+\cos 2r) + \cos (2 r-\theta ) + 4 e^{\frac{\gamma (t) (\hbar \omega _0) ^2}{2}}(\cos \theta -1)-6\cos \theta + \cos (2r+\theta ) \right) }{4(1-\cos \theta ) + 2e^{\frac{\gamma (t) (\hbar \omega _0) ^2}{2}}(\cos 2r -3 + 2\cos ^2r\cos \theta )},\nonumber \\ F_\phi= & {} e^{-\frac{\gamma (t) (\hbar \omega _0) ^2}{2}} \cos ^2r \sin ^2\theta , \end{aligned}$$
(16)

respectively. The above expressions of the Fisher information reduce, for \(\gamma (t)=0\), to their pure Unruh counterparts in Eq. (11). Also, both \(F_{\theta }\) and \(F_{\phi }\) are independent of the azimuthal angle \(\phi \), as in the pure Unruh case.

From Fig. 2 it can be seen that both \(F_\theta \) and \(F_\phi \) decrease with time with increase in Unruh acceleration parametrised by r. However, for \(r<0.2\), \(F_\theta \) is stable with the evolution of time. The Fisher information can also be shown to decrease with increasing T. Further, squeezing is seen to have a depleting effect on the Fisher information.

5.2 SGAD channel

Usually, \([H_S, H_{SR}]\ne 0\), implying decoherence along with dissipation. Linbladian evolution [24] is a general class of evolutions which incorporates the effects of decoherence and dissipation. The SGAD channel is a very general Linbladian noisy channel incorporating the effects of bath squeezing, dissipation and decoherence. The Kraus operators for this channel are [37, 38]

$$\begin{aligned} K_{1}\equiv & {} \sqrt{p_1}\left[ \begin{array}{ll} \sqrt{1-\alpha } &{} 0 \\ 0 &{} 1 \end{array} \right] , \nonumber \\ K_{2}\equiv & {} \sqrt{p_1}\left[ \begin{array}{ll} 0 &{} 0 \\ \sqrt{\alpha } &{} 0 \end{array} \right] , \nonumber \\ K_{3}\equiv & {} \sqrt{p_2}\left[ \begin{array}{ll} \sqrt{1-\mu } &{} 0 \\ 0 &{} \sqrt{1-\nu } \end{array}\right] , \nonumber \\ K_{4}\equiv & {} \sqrt{p_2}\left[ \begin{array}{ll} 0 &{} \sqrt{\nu } \\ \sqrt{\mu }e^{-i\phi _s} &{} 0 \end{array} \right] , \end{aligned}$$
(17)

where \(p_1+p_2=1\) [37]. The expression for \(p_2\), \(\nu \), \(\mu \) and \(\alpha \) can be obtained from [37]. These expressions depend upon N and a where \( N = N_\mathrm{th}[\cosh ^2(s) + \sinh ^2(s)] + \sinh ^2(s)\) and \(a=\sinh (2s)( 2N_\mathrm{th}+1)\). Here \(N_\mathrm{th}= 1/(e^{\hbar \omega _0/k_B T} - 1)\) is the Planck distribution giving the number of thermal photons at the frequency \(\omega _0\) while s and \(\phi _s\) are bath squeezing parameters.

Fig. 3
figure 3

a Variation of \(F_\theta \) (Fisher information with respect to the parameter \(\theta \)) and b \(F_\phi \) (Fisher information with respect to parameter \(\phi \)) for SGAD interaction with bath interaction time (t) and the Unruh parameter (r). The parameter settings are \(T=0.5\), \(s=0.5\), \(\theta =\pi /4\), \(\phi =\pi /4\), \(\phi _s=0\), \(\omega _0=0.1\), \(\gamma _0=0.1\)

Full size image

Under the action of the SGAD channel, the effective Bloch vector Eq. (13) becomes

$$\begin{aligned} \zeta _{\text {new}}= \begin{pmatrix} \cos r\sin \theta \left( \left( p_1\sqrt{1-\alpha }+p_2\sqrt{(1-\mu )(1-\nu )}\right) \cos \phi +p_2\sqrt{\mu \nu }\cos (\phi -\phi _s)\right) \\ -\cos r\sin \theta \left( \left( p_1\sqrt{1-\alpha }+p_2\sqrt{(1-\mu ) (1-\nu )}\right) \sin \phi -p_2\sqrt{\mu \nu }\sin (\phi -\phi _s)\right) \\ \left( 1-2p_1\alpha -2p_2\mu \right) \cos ^2r\cos ^2\frac{\theta }{2} -\left( 1-2p_2\nu \right) \left( \sin ^2r\cos ^2\frac{\theta }{2}+\sin ^2 \frac{\theta }{2}\right) \\ \end{pmatrix}. \end{aligned}$$
(18)

As a result, the Fisher information with respect to the Unruh qubit parameters \(\theta \) and \(\phi \), i.e., \(F_\theta \) and \(F_\phi \), respectively, can be shown to be

$$\begin{aligned} F_\theta \!= & {} \!\frac{\cos ^2\theta (\mathscr {A}_+^2\!+\!\mathscr {B}_+^2)\!+\!\sin ^2\theta ~ \mathscr {C}^2 \!+\!\left( \mathscr {C}\mathscr {D}\!+\! (\mathscr {A}_+ \!+\! \mathscr {B}_+)\cos \theta \right) ^2\sin ^2\theta }{1- (\mathscr {F} - \mathscr {C}\cos ^2\frac{\theta }{2})^2-(\mathscr {A}_+^2\!+\!\mathscr {B}_+^2) \sin ^2\theta },\nonumber \\ F_\phi= & {} \frac{\sin ^2\theta (\mathscr {A}_-^2+\mathscr {B}_-^2)+(\mathscr {A}_+ \mathscr {B}_-+\mathscr {A}_-\mathscr {B}_+)^2\sin ^4\theta }{1- (\mathscr {F} - \mathscr {C}\cos ^2\frac{\theta }{2})^2 -(\mathscr {A}_+^2+\mathscr {B}_+^2)\sin ^2\theta }. \end{aligned}$$
(19)

The terms appearing in these expressions can be found in Appendix A. In the absence of external noise, \(F_\theta \) and \(F_\phi \), Eq. (19), reduce to Eq. (11), corresponding to the pure Unruh channel.

Fig. 4
figure 4

a Variation of \(F_\theta \) (Fisher information with respect to parameter \(\theta \)) for SGAD interaction with bath temperature (T) and squeezing (s); b variation of \(F_\phi \) (Fisher information with respect to parameter \(\phi \)) for SGAD interaction with bath temperature (T) and squeezing (s). The parameter settings are \(r=\pi /8\), \(\theta =\pi /4\), \(\phi =\pi /4\), \(\phi _s=0\), \(\omega _0=0.1\), \(\gamma _0=0.1\), \(t=2\)

Full size image

From Fig. 3, it is evident that both \(F_\theta \) and \(F_\phi \) decrease with time for all values of r. This is in contrast with the corresponding behaviour of \(F_\theta \) in the presence of a phase damping channel. The fall in \(F_\phi \) here is more dramatic as compared to its phase damping counterpart.

The variation of \(F_\theta \) and \(F_\phi \) with respect to temperature and squeezing are shown in Fig. 4. Fisher information shows an interesting behaviour with respect to squeezing. For a given \(T>0.5\), as s becomes nonzero, both \(F_\theta \) and \(F_\phi \) show a general trend of increasing and stabilising after \(|s|=1\). To summarise, here squeezing turns out to be a useful quantum resource in that it quantifies the resilience of the quantum system to the effects of the external noisy channel.

Another feature that is observed is that as the temperature due to the external noise channel increases, the pattern of \(F_\phi \) with respect to the Unruh parameter r and state parameter \(\theta \), as seen in Fig. 1b, remains unchanged although the magnitude of \(F_\phi \) decreases, with the depletion being more dramatic for the case of the SGAD channel as compared to the QND channel.

6 Skew information

Another variant of Fisher information which accounts for the amount of information in the quantum state with respect to its non commutation with a conserved quantity is the skew information [25, 30]. This can be shown to have a metrical structure given by the quantum Hellinger distance [25], which in turn is related to the quantum affinity and is intrinsically connected to the quantum Chernoff distance [42]. In this sense skew and Fisher information are variants of the same fundamental quantity with Fisher deriving its metrical origin from the Bures distance [27, 28]. Recently there has been a lot of activity concerning the connection between the skew information and quantum coherence [23]. We thus find it instructive to compute the skew information for the present problem of the Unruh channel with and without the influence of external noisy channels.

The skew information in terms of Bloch vector \(\mathbf {\zeta }(\alpha )\) is given by

$$\begin{aligned} S_q(\alpha )= & {} \frac{2|\partial _{\alpha }\mathbf {\zeta }(\alpha )|^2}{1+\sqrt{1-|\mathbf {\zeta }(\alpha )|^2}} +\left[ \mathbf {\zeta }(\alpha )\cdot \partial _{\alpha }\mathbf {\zeta }(\alpha )\right] ^2 \nonumber \\&\times \left( \frac{1}{1-|\mathbf {\zeta }(\alpha )|^2}-\frac{1}{1+\sqrt{1-|\mathbf {\zeta } (\alpha )|^2}} \right) , \end{aligned}$$
(20)

where q denotes quantum and \(\alpha \) is the parameter to be estimated, for example, the polar and azimuthal angles \(\theta \) and \(\phi \), respectively, of the UD qubit. From now on we will abbreviate \(S_q(\alpha )\) by \(S_{\alpha }\).

Fig. 5
figure 5

For the pure Unruh channel: a variation of \(S_\theta \) (skew information with respect to the parameter \(\theta \)); b variation of \(S_\phi \) (skew information with respect to the parameter \(\theta \))

Full size image

Using the Bloch vector \(\mathbf {\zeta }(\alpha )\), Eq. (9), the skew information for the pure Unruh channel with respect to the parameters \(\theta \) and \(\phi \), i.e., \(S_\theta \) and \(S_\phi \), respectively, can be shown to be

$$\begin{aligned} S_\theta= & {} \frac{ \cos ^2r \left( 7+2 \cos 2 \theta + 8 \cos ^2\frac{\theta }{2}\sin 2r +2\cos 2r \sin ^2 \theta \right) }{4\left( 1+ \cos ^2\frac{\theta }{2}\sin 2r\right) ^2},\nonumber \\ S_\phi= & {} \frac{2 \cos ^2r \sin ^2\theta }{1+\cos ^2\frac{\theta }{2} \sin 2r}. \end{aligned}$$
(21)

Unlike the analogous case of Fisher information \(F_\theta \) for the pure Unruh channel, Eq. (11), we see that \(S_\theta \) depends both on r and \(\theta \).

From Fig. 5, it is seen that the skew information, for the pure Unruh channel, with respect to the parameter \(\theta \), decreases with increase in the Unruh parameter r, a behaviour which is consistent with that of its Fisher counterpart. However, in contrast to the Fisher information, for a given r, there is a general trend of increase in \(S_{\theta }\) as \(\theta \) goes from 0 to \(2\pi \). This increase is more dramatic for higher values of Unruh acceleration. The behaviour of \(S_\phi \) is similar to that of its Fisher counterpart \(F_{\phi }\), Fig. 1b. However, for higher values of r (>0.5), \(S_\phi \) has a steeper fall as compared to its corresponding \(F_\phi \), Fig. 1.

6.1 Phase damping

The skew information with respect to parameters \(\theta \) and \(\phi \), \(S_{\theta }\) and \(S_{\phi }\), due to the influence of the phase damping (QND) noise channel on the UD quibit are given by

$$\begin{aligned} S_\theta= & {} \frac{2\cos ^2r \left( e^{-\frac{1}{2}\gamma (\hbar \omega _0) ^2}\cos ^2\theta + \cos ^2r\sin ^2\theta \right) }{1+\sqrt{1-\mathscr {H}}}\nonumber \\&\,+\mathscr {G}^2\sin ^2\theta \left( \frac{1}{1-\mathscr {H}}- \frac{1}{1+\sqrt{1-\mathscr {H}}}\right) ,\nonumber \\ S_\phi= & {} \frac{2 e^{-\frac{\gamma (\hbar \omega _0) ^2}{2}} \cos ^2 r\sin ^2\theta }{1+\sqrt{1-\mathscr {H}}}. \end{aligned}$$
(22)

Here \(\mathscr {G}\) and \(\mathscr {H}\) are

$$\begin{aligned} \mathcal {G}\!= & {} \!e^{-\gamma (\hbar \omega _0) ^2}\cos ^4r \left( \cos \theta + e^{\frac{1}{2}\gamma (\hbar \omega _0) ^2}(\sin ^2r-\cos ^2r\cos \theta )\right) ,\nonumber \\ \mathcal {H}= & {} (\sin ^2 r-\cos ^2 r \cos \theta )^2-e^{-\frac{\gamma (\hbar \omega _0) ^2}{2}} \cos ^2 r \sin ^2\theta . \end{aligned}$$
(23)

In the absence of external noise, \(S_\theta \) and \(S_\phi \) reduces to their pure Unruh counterparts in Eq. (21). The variation of skew information \(S_\theta \) and \(S_\phi \) with respect to time of evolution t, Unruh parameter r, temperature (T) and squeezing (s) can be shown to be similar to their Fisher counterparts.

6.2 SGAD channel

As a result of the action of the SGAD channel on the UD qubit, the skew information with respect to parameters \(\theta \) and \(\phi \) are, respectively, given by

$$\begin{aligned} S_\theta= & {} \frac{2\left( \cos ^2\theta (\mathscr {A}_+^2+\mathscr {B}_+^2) +\mathscr {C}^2\sin ^2\theta \right) }{1+\sqrt{1- (\mathscr {F} - \mathcal {C}\cos ^2\frac{\theta }{2})^2-(\mathcal {A}_+^2+\mathscr {B}_+^2) \sin ^2\theta }}\nonumber \\&\,+\left( \mathscr {C}\mathscr {D}\sin \theta +(\mathscr {A}_+^2+\mathscr {B}_+^2)\sin \theta \cos \theta \right) ^2\times \mathscr {J},\nonumber \\ S_\phi= & {} \frac{2\left( \mathscr {A}_-^2+\mathscr {B}_-^2\right) \sin ^2\theta }{1+\sqrt{1- (\mathscr {F} - \mathscr {C}\cos ^2\frac{\theta }{2})^2 -(\mathscr {A}_+^2+\mathscr {B}_+^2)\sin ^2\theta }}\nonumber \\&\,+ \left( \mathscr {A}_+\mathscr {B}_- + \mathscr {A}_-\mathscr {B}_+ \right) ^2\sin ^4\theta \times \mathcal {J}, \end{aligned}$$
(24)

where \(\mathscr {A}_{\pm },~\mathscr {B}_{\pm },~\mathscr {C},~ \mathscr {D},~\mathscr {F}\) are as in Eq. (A1) and \(\mathscr {J}\) is defined in Eq. (A2). The above equation reduces to Eq. (21), in the absence of external noise.

Like its Fisher counterpart, it can be shown that both \(S_\theta \) and \(S_\phi \) decrease with time for all values of r. The behaviour of these two skew information types with respect to the parameters T and s are qualitatively similar to their Fisher counterparts. Hence the rich structure exhibited by \(F_\theta \) and \(F_\phi \) are also seen here for their skew counterparts. From the behaviour of the skew information, as observed in this section, we see that it is, barring a few differences, quite similar to the corresponding Fisher information. This is consistent with the notion that the Fisher and skew information are variants of the same information content.

7 Conclusions

Quantum Fisher information plays a prominent role in state estimation and reconstruction, tomography and metrology. Its variant, skew information, is gaining prominence in studies probing the nature of quantum coherence. In this work, we provide a detailed exposition of both the Fisher and the skew information, for an Unruh–Dirac qubit. This helps in revealing the intrinsic sensitivity of the system of interest with respect to the change of state parameters, such as the ambient temperature and squeezing.

An important feature of this work is that by using the Bloch vector formalism, a clear and unified treatment of the Unruh effect both in its pure form and in the presence of experimentally relevant external noise channels is provided. The use of a Bloch vector representation, developed here for the Unruh effect, enables us to provide analytical expressions for quantum Fisher and skew information, both with and without external noises.

We study the evolution of Fisher and skew information with time and also the impact of external environmental parameters such as temperature and squeezing on their evolution. The external noises are modelled by both purely dephasing phase damping and the squeezed generalised amplitude damping (SGAD) noise channels. An interesting interplay between the external reservoir temperature and squeezing on the Fisher and skew information is observed, in particular, for the action of the SGAD channel. It is seen that for some regimes, squeezing can enhance the quantum information against the debilitating influence of the noise channels. Similar features are also observed for the analogous study of skew information, highlighting a similar origin of the Fisher and skew information. These studies, we hope, are a contribution in the direction of efforts towards understanding and implementing relativistic quantum information.