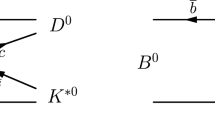Study of $\Lambda _b\rightarrow \Lambda (\phi ,\eta ^{(\prime )})$ and $\Lambda _b\rightarrow \Lambda K^+K^-$ decays

Abstract

We study the charmless two-body $\Lambda _b\rightarrow \Lambda (\phi ,\eta ^{(\prime )})$ and three-body $\Lambda _b\rightarrow \Lambda K^+K^-$ decays. We obtain $\mathcal{B}(\Lambda _b\rightarrow \Lambda \phi )=(3.53\pm 0.24)\times 10^{-6}$ to agree with the recent LHCb measurement. However, we find that $\mathcal{B}(\Lambda _b\rightarrow \Lambda (\phi \rightarrow )K^+ K^-)=(1.71\pm 0.12)\times 10^{-6}$ is unable to explain the LHCb observation of $\mathcal{B}(\Lambda _b\rightarrow \Lambda K^+ K^-)=(15.9\pm 1.2\pm 1.2\pm 2.0)\times 10^{-6}$, which implies the possibility for other contributions, such as that from the resonant $\Lambda _b\rightarrow K^- N^*,\,N^*\rightarrow \Lambda K^+$ decay with $N^*$ as a higher-wave baryon state. For $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$, we show that $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ,\,\Lambda \eta ^\prime )= (1.47\pm 0.35,1.83\pm 0.58)\times 10^{-6}$, which are consistent with the current data of $(9.3^{+7.3}_{-5.3},<3.1)\times 10^{-6}$, respectively. Our results also support the relation of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ) \simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^\prime )$, given by the previous study.

1 Introduction

The charmless two-body $\Lambda _b$ decays of $\Lambda _b\rightarrow p K^-$ and $\Lambda _b\rightarrow p\pi ^-$ have been observed by the CDF Collaboration [1] with the branching ratios of ${ O}(10^{-6})$, which are in accordance with the recent measurements on $\Lambda _b\rightarrow \Lambda \phi$ and $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ by the LHCb Collaboration, given by [2, 3]

$$\begin{aligned} \mathcal{B}(\Lambda _b\rightarrow \Lambda \phi )= & {} (5.18\pm 1.04\pm 0.35^{+0.67}_{-0.62})\times 10^{-6}\,,\nonumber \\ \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta )= & {} (9.3^{+7.3}_{-5.3})\times 10^{-6}\,,\nonumber \\ \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^{\prime })< & {} 3.1\times 10^{-6}\,,\;(\text {90}~{\%}~\text {C.L.}) \end{aligned}$$

(1)

where the evidence is seen for the $\eta$ mode at the level of 3$\sigma$-significance.

Theoretically, $\Lambda _b\rightarrow p (K^{*-},\pi ^-,\rho ^-)$ decays via $b\rightarrow u\bar{u} (d,s)$ at the quark level have been studied in the literature [4–10]. In particular, it is interesting to point out that the direct CP violating asymmetry in $\Lambda _b\rightarrow p K^{*-}$ is predicted to be as large as 20 %, which is promising as regards observation in the future measurements. On the other hand, the decay of $\Lambda _b\rightarrow \Lambda \phi$ via $b\rightarrow s\bar{s} s$ has not been well explored even though both the decay branching ratio and the T-odd triple-product asymmetries [11–13] have been examined by the experiment at LHCb [2]. According to the newly measured three-body $\Lambda _b\rightarrow \Lambda K^+ K^-$ decay by the LHCb Collaboration, given by [14]

$$\begin{aligned} \mathcal{B}(\Lambda _b\rightarrow \Lambda K^+ K^-)=(15.9\pm 1.2\pm 1.2\pm 2.0)\times 10^{-6},\nonumber \\ \end{aligned}$$

(2)

it implies a resonant $\Lambda _b\rightarrow \Lambda \phi ,\,\phi \rightarrow K^+ K^-$ contribution with the signal seen at the low range of $m^2(K^+ K^-)$ from the Dalitz plot. However, to estimate this resonant contribution, one has to understand $\mathcal{B}(\Lambda _b\rightarrow \Lambda \phi )$ in Eq. (1) first. Such a study is also important for further examinations of the triple-product asymmetries [15–18]. For $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$, the relation of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta )\simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^{\prime })$ found in Ref. [19] seems to be inconsistent with the data in Eq. (1). Moreover, the first work on $\Lambda _b\rightarrow \Lambda \eta ^{\prime }$ with the branching ratios predicted to be $O(10^{-6}-10^{-5})$ in comparison with the data in Eq. (1) was done before the observations of $\Lambda _b\rightarrow p(K^-,\,\pi ^-)$, which can be used to extract the $\Lambda _b\rightarrow \mathbf{B}_n$ transition form factors from QCD models [8, 9, 20]. For a reconciliation, we would like to reanalyze $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$.

In this work, we will use the factorization approach for the theoretical calculations of $\Lambda _b\rightarrow \Lambda \phi$ and $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ as those in the $\Lambda _b\rightarrow p (K^{*-},\pi ^-,\rho ^-)$ decays [8, 9].

Fig. 1

Feynman diagrams a, b and c–e from $\Lambda _b^0\rightarrow \Lambda \phi$ and $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ decays, respectively

2 Formalism

In terms of the effective Hamiltonian for the charmless $b\rightarrow s s\bar{s}$ transition at the quark level shown in Fig. 1, the amplitude of $\Lambda _b\rightarrow \Lambda \phi$ based on the factorization approach can be derived as [21]

$$\begin{aligned}&\mathcal{A}(\Lambda _b\rightarrow \Lambda \phi )=\frac{G_F}{\sqrt{2}} \alpha _3\langle \phi |\bar{s}\gamma _\mu s|0\rangle \langle \Lambda |\bar{s}\gamma _\mu (1-\gamma _5)b|\Lambda _b\rangle ,\nonumber \\ \end{aligned}$$

(3)

with $G_F$ the Fermi constant, $V_{q_1q_2}$ the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, and $\alpha _3=-V_{tb}V_{ts}^*(a_3+a_4+a_5-a_9/2)$, where $a_i\equiv c^{\mathrm{eff}}_i+c^{\mathrm{eff}}_{i\pm 1}/N_c$ for $i=$odd (even) are composed of the effective Wilson coefficients $c_i^{\mathrm{eff}}$ defined in Ref. [21] with the color number $N_c$. As depicted in Fig. 1, the amplitudes of $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ are given by

$$\begin{aligned}&\mathcal{A}(\Lambda _b\rightarrow \Lambda \eta ^{(\prime )})\nonumber \\&\quad = \frac{G_F}{\sqrt{2}}\bigg \{ \bigg [\beta _2\langle \eta ^{(\prime )}|\bar{q}\gamma _\mu \gamma _5 q|0\rangle + \beta _3\langle \eta ^{(\prime )}|\bar{s} \gamma _\mu \gamma _5 s|0\rangle \bigg ] \nonumber \\&\qquad \times \langle \Lambda |\bar{s} \gamma _\mu (1-\gamma _5) b|\Lambda _b\rangle \nonumber \\&\qquad +\beta _6 \langle \eta ^{(\prime )}|\bar{s}\gamma _5 s|0\rangle \langle \Lambda |\bar{s}(1-\gamma _5) b|\Lambda _b\rangle \bigg \}, \end{aligned}$$

(4)

with $q=u$ or d, where $\beta _2=-V_{ub}V_{us}^*\,a_2+V_{tb}V_{ts}^*(2a_3-2a_5+a_9/2)$, $\beta _3=V_{tb}V_{ts}^*(a_3+a_4-a_5-a_9/2)$, and $\beta _6=V_{tb}V_{ts}^*\,2a_6$. The matrix elements of the $\Lambda _b\rightarrow \Lambda$ baryon transition in Eqs. (3) and (4) have been parameterized as [22, 23]

$$\begin{aligned} \langle \Lambda |\bar{s}\gamma _\mu (1-\gamma _5)b|\Lambda _b\rangle= & {} \bar{u}_{\Lambda }(f_1\gamma _\mu -g_1\gamma _\mu \gamma _5)u_{\Lambda _b},\nonumber \\ \langle \Lambda |\bar{s}(1-\gamma _5)b|\Lambda _b\rangle= & {} \bar{u}_{\Lambda }(f_S\gamma _\mu -g_P\gamma _\mu \gamma _5)u_{\Lambda _b}, \end{aligned}$$

(5)

where $f_1$, $g_1$, $f_S$, and $g_P$ are the form factors, with $f_S=[(m_{\Lambda _b}-m_{\Lambda })/(m_b-m_s)] f_1$ and $g_P=[(m_{\Lambda _b}+m_{\Lambda })/(m_b+m_s)] g_1$ by virtue of equations of motion. Note that, in Eq. (5), we have neglected the form factors related to $\bar{u}_{\Lambda }\sigma _{\mu \nu }q^\nu (\gamma _5)u_{\Lambda _b}$ and $\bar{u}_{\Lambda }q_\mu (\gamma _5) u_{\Lambda _b}$ that flip the helicity [24]. With the double-pole momentum dependences, $f_1$ and $g_1$ can be written as [8, 9]

$$\begin{aligned} f_1(q^2)=\frac{f_1(0)}{(1-q^2/m_{\Lambda _b}^2)^2},\quad g_1(q^2)=\frac{g_1(0)}{(1-q^2/m_{\Lambda _b}^2)^2},\nonumber \\ \end{aligned}$$

(6)

where we have taken $C_F(\Lambda _b\rightarrow \Lambda )\equiv f_1(0)=g_1(0)$ as the leading approximation based on the SU(3) flavor and SU(2) spin symmetries [25, 26]. We remark that the perturbative corrections to the $\Lambda _b\rightarrow \Lambda$ transition form factors from QCD sum rules have been recently computed in Ref. [27]. Clearly, for more precise evaluations of the form factors, these corrections should be included.

Table 1 $\alpha _i\,(\beta _i)$ with $N_c=2,\,3$, and $\infty$

The matrix elements in Eqs. (3) and (4) for the meson productions read [28]

$$\begin{aligned}&\langle \phi |\bar{s}\gamma _\mu s|0\rangle =m_\phi f_\phi \varepsilon _\mu ^*,\quad \langle \eta ^{(\prime )}|\bar{q}\gamma _\mu \gamma _5 q|0\rangle = -\frac{i}{\sqrt{2}}f^q_{\eta ^{(\prime )}} q_\mu ,\nonumber \\&\langle \eta ^{(\prime )}|\bar{s}\gamma _\mu \gamma _5 s|0\rangle =-if^s_{\eta ^{(\prime )}} q_\mu ,\quad 2m_s \langle \eta ^{(\prime )}|\bar{s}\gamma _5 s|0\rangle =-ih^s_{\eta ^{(\prime )}},\nonumber \\ \end{aligned}$$

(7)

with the polarization $\varepsilon _\mu ^*$ and four-momentum $q_\mu$ vectors for $\phi$ and $\eta ^{(\prime )}$, respectively, where $f_\phi$, $f^q_{\eta ^{(\prime )}}$, and $h^s_{\eta ^{(\prime )}}$ are decay constants. Unlike the usual decay constants, $f^q_{\eta ^{(\prime )}}$ and $f^s_{\eta ^{(\prime )}}$ are the consequences of the $\eta$–$\eta ^\prime$ mixing, in which the Feldmann, Kroll and Stech (FKS) scheme is adopted as [29, 30]

$$\begin{aligned} \left( \begin{array}{c} \eta \\ \eta ' \end{array}\right) = \left( \begin{array}{cc} \cos \phi &{}-\sin \phi \\ \sin \phi &{}\cos \phi \end{array}\right) \left( \begin{array}{c} \eta _q\\ \eta _s \end{array}\right) , \end{aligned}$$

(8)

with $|\eta _q\rangle =(|u\bar{u}+d\bar{d}\rangle )/\sqrt{2}$ and $|\eta _s\rangle =|s\bar{s}\rangle$, where the mixing angle is extracted as $\phi =(39.3\pm 1.0)^\circ$. As a result, $f^q_{\eta ^{(\prime )}}$ and $f^s_{\eta ^{(\prime )}}$ actually mix with the decay constants $f_q$ and $f_s$ for $\eta _q$ and $\eta _s$, respectively. Note that $h^s_{\eta ^{(\prime )}}$ in Eq. (7) contains the contribution from the QCD anomaly, given by

$$\begin{aligned} 2m_s\langle \eta ^{(\prime )}|\bar{s} i\gamma _5 s|0\rangle = \partial ^\mu \langle \eta ^{(\prime )}|\bar{s} \gamma _\mu \gamma _5 s|0\rangle + \left\langle \eta ^{(\prime )}|\frac{\alpha _s}{4\pi }G\tilde{G}|0\right\rangle ,\nonumber \\ \end{aligned}$$

(9)

where $\alpha _s$ is the strong coupling constant, $G(\tilde{G})$ is the (dual) gluon field tensor, $\partial ^\mu \langle \eta ^{(\prime )}|\bar{s} \gamma _\mu \gamma _5 s|0\rangle =f_{\eta ^{(\prime )}}m_{\eta ^{(\prime )}}^2$, and $\langle \eta ^{(\prime )}|\alpha _s G\tilde{G}|0\rangle \equiv 4\pi a_{\eta ^{(\prime )}}$. Explicitly, one has [28]

$$\begin{aligned} h^s_{\eta ^{(\prime )}}=a_{\eta ^{(\prime )}}+f^s_{\eta ^{(\prime )}} m_{\eta ^{(\prime )}}^2, \end{aligned}$$

(10)

which will be used in the numerical analysis.

3 Numerical results and discussions

For our numerical analysis, the CKM matrix elements in the Wolfenstein parameterization are given by [31]

$$\begin{aligned} (V_{ub},\,V_{us},\,V_{tb},\,V_{ts})=(A\lambda ^3(\rho -i\eta ),\lambda ,1,-A\lambda ^2)\,, \end{aligned}$$

(11)

with $(\lambda ,\,A,\,\rho ,\,\eta )=(0.225,\,0.814,\,0.120\,\pm \,0.022,\,0.362\pm \, 0.013)$.

In Table 1, we fix $N_c=3$ for $a_i$ but shift it from 2 to $\infty$ in the generalized version of the factorization approach to take into account the non-factorizable effects as the uncertainty. For the form factors, we use $C_F(\Lambda _b\rightarrow \Lambda )=-\sqrt{2/3}\,C_F(\Lambda _b\rightarrow p)$ [26] with $C_F(\Lambda _b\rightarrow p)=0.136\pm 0.009$ [8, 9]. Apart from $f_\phi =0.231$ GeV [32], we adopt the decay constants for $\eta$ and $\eta ^{\prime }$ from Ref. [28], given by

$$\begin{aligned} (f^q_{\eta },f^q_{\eta ^\prime },f^s_{\eta },f^s_{\eta ^\prime })= & {} (0.108,\,0.089\,,-0.111,\,0.136)\,\text {GeV},\nonumber \\ (h^s_{\eta },h^s_{\eta ^\prime })= & {} (-0.055,\,0.068)\,\text {GeV}^3, \end{aligned}$$

(12)

respectively. Subsequently, we obtain the branching ratios, given in Table 2.

Table 2 Numerical results for the branching ratios with the first and second errors from the non-factorizable effects and the form factors, respectively, in comparison with the experimental data [2, 3] and the study in Ref. [19]. Note that, in column 3, the two values without and with the parentheses correspond to the form factors in the approach of QCD sum rules and the pole model, respectively

As seen in Table 1, $\alpha _3$ for $\Lambda _b\rightarrow \Lambda \phi$ is sensitive to the non-factorizable effects. In comparison with the data in Table 2 and Eq. (1), the $\Lambda _b\rightarrow \Lambda \phi$ decay is judged to receive the non-factorizable effects with $N_c=2$, such that $\mathcal{B}(\Lambda _b\rightarrow \Lambda \phi )=(3.53\pm 0.24)\times 10^{-6}$. With $\mathcal{B}(\phi \rightarrow K^+ K^-)=(48.5\pm 0.5)~\%$ [31], we get $\mathcal{B}(\Lambda _b\rightarrow \Lambda (\phi \rightarrow ) K^+ K^-)=(1.71\pm 0.12)\times 10^{-6}$, which is much lower than the data of $(15.9\pm 4.4)\times 10^{-6}$ in Eq. (2), leaving some room for other contributions, such as the resonant $\Lambda _b\rightarrow K^- N^*,\,N^*\rightarrow \Lambda K^+$ decay with $N^*$ denoted as the higher-wave baryon state. Here, we would suggest a more accurate experimental examination on the $\Lambda K$ invariant mass spectrum, which depends on the peak around the threshold of $m_{\Lambda K}\simeq m_\Lambda +m_K$, while the Dalitz plot might possibly reveal the signal [14]. The result of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta )=(1.47\pm 0.35)\times 10^{-6}$ in Table 2 shows a consistent result with the data due to its large uncertainty. On the other hand, $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^\prime )=(1.83\pm 0.58)\times 10^{-6}$ agrees with the experimental upper bound. The $\eta$ and $\eta ^\prime$ modes with $\mathcal{B}\simeq 10^{-6}$ are mainly resulted from the form factor $C_F(\Lambda _b\rightarrow \Lambda )\sim 0.14$ extracted in Refs. [8, 9] in agreement with the calculation in QCD models [6, 22–24], which explains why $\mathcal{B}(\Lambda _b\rightarrow p K^-,\,p \pi ^-)$ are also around $10^{-6}$ [31]. As seen in Table 2, our results for the $\eta ^{(')}$ modes are smaller than those in Ref. [19]. In addition, we note that the result of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^\prime )=11.33(3.24)\times 10^{-6}$ in the QCD sum rule (pole) model [19], apparently exceeds the data. However, the predictions for $\Lambda _b\rightarrow \Lambda \eta$ in Ref. [19] are still consistent with the current data.

We also point out that the relation of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ) \simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^\prime )$ still holds as in Ref. [19].

It is well known that the gluon content of $\eta ^{(\prime )}$ can contribute to the flavor-singlet $B\rightarrow K\eta ^{(\prime )}$ decays in three ways [28]: (i) the $b\rightarrow sgg$ amplitude related to the effective charm decay constant, (ii) the spectator scattering involving two gluons, and (iii) the singlet weak annihilation. It is interesting to ask if these three production mechanisms are also relevant to the corresponding $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ decays. For (i), its contribution to $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ has been demonstrated to be small [19] since, by effectively relating $b\rightarrow sgg$ to $b\rightarrow s c\bar{c}$, the $c\bar{c}$ vacuum annihilation of $\eta ^{(\prime )}$ is suppressed due to the decay constants $(f^c_{\eta },f^c_{\eta ^{\prime }})\simeq (-1,-3)$ MeV [28] being much smaller than $f^q_{\eta ^{(\prime )}}$ in Eq. (12). For (ii), since one of the gluons from the spectator quark connects to the recoiled $\eta ^{(\prime )}$, the contribution belongs to the non-factorizable effect, which has been inserted into the effective number of $N_c$ (from 2 to $\infty$) in our generalized factorization approach. For (iii), it is the sub-leading power contribution which does not contribute to $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$.

Finally, we remark that, in the b-hadron decays, such as those of B and $\Lambda _b$, the generalized factorization with the floating $N_c=2 \rightarrow \infty$ [21] can empirically estimate the non-factorizable effects, such that it can be used to explain the data as well as make predictions. On the other hand, the QCD factorization [28] could in general calculate the non-factorizable effects in some specific processes. Although the current existing studies on $\Lambda _b\rightarrow \Lambda (\phi ,\eta ^{(\prime )})$ are based on the generalized factorization, it is useful to calculate these decay modes in the QCD factorization. In particular, since the decay of $\Lambda _b\rightarrow \Lambda \phi$ with $N_c=2$ has shown to be sensitive to the non-factorizable effects, its study in the QCD factorization is clearly interesting.

4 Conclusions

In sum, we have studied the charmless two-body $\Lambda _b\rightarrow \Lambda \phi$ and $\Lambda _b\rightarrow \Lambda \eta ^{(\prime )}$ and three-body $\Lambda _b\rightarrow \Lambda K^+ K^-$ decays. By predicting $\mathcal{B}(\Lambda _b\rightarrow \Lambda \phi )=(3.53\pm 0.24)\times 10^{-6}$ to agree with the observation, we have found that $\mathcal{B}(\Lambda _b\rightarrow \Lambda (\phi \rightarrow )K^+ K^-)=(1.71\pm 0.12)\times 10^{-6}$ cannot explain the observed $\mathcal{B}(\Lambda _b\rightarrow \Lambda K^+ K^-)=(15.9\pm 4.4)\times 10^{-6}$, which leaves much room for the contribution from the resonant $\Lambda _b\rightarrow K^- N^*,\,N^*\rightarrow \Lambda K^+$ decay. We have obtained $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ,\,\Lambda \eta ^\prime )= (1.47\pm 0.35,1.83\pm 0.58)\times 10^{-6}$ in comparison with the data of $(9.3^{+7.3}_{-5.3},<3.1)\times 10^{-6}$, respectively. In addition, our results still support the relation of $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ) \simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ^\prime )$. It is clear that future more precise experimental measurements on the present $\Lambda _b$ decays are important to test the QCD models, in particular the generalized factorization one.