The Dirac form factor predicts the Pauli form factor in the Endpoint Model

Abstract

We compute the momentum-transfer dependence of the proton Pauli form factor $F_{2}$ in the Endpoint overlap Model. We find the model correctly reproduces the scaling of the ratio of $F_{2}$ with the Dirac form factor $F_{1}$ observed at the Jefferson Laboratory. The calculation uses the leading-power, leading-twist Dirac structure of the quark light-cone wave function and the same endpoint dependence previously determined from the Dirac form factor $F_{1}$. There are no parameters and no adjustable functions in the Endpoint Model’s prediction for the scaling behavior of $F_{2}$. The model’s predicted momentum dependence of the ratio $F_{2}(Q^{2})/F_{1}(Q^{2})$ is quite insensitive to the endpoint wave function, which explains why the observed ratio scales like 1 / Q down to rather low momentum transfers. We also fit the magnitude of this ratio by adjusting the parameters of the wave function. The Endpoint Model appears to be the only comprehensive model consistent with all form factor information as well as reproducing fixed-angle proton–proton scattering at large momentum transfer. Any one of the processes is capable of predicting the others.

1 Introduction

The electromagnetic form factors, $F_{1}$ and $F_{2}$, are an important probe of the internal structure of nucleons. A popular theoretical model assumes that at high momentum transfer these quantities can be factorized into a hard scattering contribution and a so-called distribution amplitude. The distribution amplitude has no information as regards the proton wave function except the parton momentum fraction Feynman-x dependence and some spin factors of a short-distance expansion. The focus of the short-distance (SD) model [1–7] is a perturbatively calculable hard scattering kernel. The model generates an order by order expansion in powers of the inverse momentum transfer-squared, $1/Q^2$. The expansion has often been claimed to be the unique prediction of QCD. However, the task of comparing the model to the larger theory of QCD was never completed, and it obviously cannot be explored within the SD model itself.

Yet model predictions can be compared to experimental data. The SD model predicts that $F_{2}(Q^{2})/F_{1}(Q^{2}) \rightarrow 1/Q^2$ for large Q [1, 8]. The experimental results obtained at the Jefferson lab [9–13], however, showed that the ratio $F_{2}(Q^{2})/F_{1}(Q^{2}) \sim 1/Q$ in the energy range $2\ \mathrm{GeV}^{2}<Q^{2}<8.5\ \mathrm{GeV}^{2}$. This contradicted the prediction of the SD model that some thought had been established. The results played an important role in dramatizing the failure of the SD model, which had also been anticipated earlier [14, 15]. It is now clear that the SD model might apply only at very large energies, which are inaccessible experimentally. Even at asymptotic energies there is no proof the model dominates. Since the SD model fails it is imperative to explore alternatives.

Work by Miller et al., Lin et al., and Cloet et al. [16–18] has reproduced the experimentally observed momentum dependence of $F_2$. These calculations emphasize the importance of the quark wave functions, i.e. the role of hadron structure, as opposed to the role of perturbation theory.

Kivel and Vanderhaeghen [19] used Soft Collinear Effective Theory (SCET) to analyze soft spectator contributions which represent a class of diagrams which also give the SD scaling of $Q^2 F_{2}/F_{1} \sim \mathrm{const}$ for large $Q^{2}$. It is possible that at smaller $Q^2$ of order few GeV$^2$, the soft spectator contributions might lead to the observed experimental behavior. However, it is not clear how to extract these contributions systematically. In an earlier analysis, Belitsky et al. [20] obtained the dependence $F_{2}(Q^{2})/F_{1}(Q^{2}) \rightarrow (1/Q^2)\,\log (Q^{2}/\Lambda _\mathrm{QCD}^{2})$, which matches with the observed data, by introducing higher twist light-cone wave functions. The logarithmic term is a result of an integration over the soft endpoint region, where the assumptions of the SD model no longer hold. Hence we find that some studies in the past [19, 20] have attributed the observed experimental behavior of $F_2/F_1$ to the contributions arising from the soft spectator quarks in the endpoint region.

Diehl et al. [21] parametrized the generalized parton distributions (GPD) both in the small and large t regions. In the small t and small x (momentum fraction) region they used Regge phenomenology assuming dominance of the leading meson trajectories. At large t they assumed that the soft Feynman mechanism dominates the form factors and controls the nature of the GPD. The parametrized forms agree with the pdf’s (parton distribution functions) at $t=0$ and with the elastic form factors for large t. These parametrizations give expressions for $F_{1}$ and $F_{2}$ which provide a good fit to both the proton and the neutron form factors. Work by Guidal et al. [22] presents an alternative Regge parametrization and also shows a consistent fit for both proton form factors. Both these parametrizations agree well with the current data on $F_2/F_1$.

In a series of papers [23–25] the nucleon form factors have been calculated within the framework of light-cone sum rules. The authors use perturbative QCD including up to twist four corrections to the leading-order distribution amplitudes. The soft contributions arising from the endpoint region are also included in the calculation. An interesting feature of the calculation is that the soft contributions involve the same distribution amplitude which arise in the hard scattering calculation. Furthermore the final form of the distribution amplitude does not differ too much from the leading-order form. Although the results of these papers are very interesting, it is generally believed that nucleon form factors cannot currently be calculated from first principles. In particular this calculation also relies on modeling of the soft endpoint region. Furthermore a detailed calculational scheme should provide some understanding of the basic features of the data. In the case of exclusive processes the most striking feature is their scaling behavior. Since the soft contributions give substantial contributions to these processes, it is important to understand how they can lead to the observed momentum dependence.

1.1 Significance of the endpoint region

The significance of the endpoint region for the calculation of the ratio $F_2/F_1$ is rather interesting in view of the recent claim [26] that an Endpoint Model (EP model) can comprehensively explain the scaling behavior of many exclusive processes [1, 27, 28]. The model relates the observed scaling to the behavior of the quark wave function as Feynman-$x\rightarrow 1$. In this limit one of the quarks carries most of the proton longitudinal momentum. The relationship of this model with the structure functions in the limit $x\rightarrow 1$ has also been explored in [30]. The model appeared several times in the literature [29–31], yet it was dismissed prematurely, often for reasons that its premises contradicted the assumptions of the SD model. For that reason the EP region was long regarded as a nuisance. Many efforts were made to attempt to show the EP model’s contribution would be suppressed, but the efforts made were unsuccessful. Indeed persistent “spin puzzles” of inclusive observables have brought the endpoint region and polarization effects from quark mass insertions back into consideration [32–34].

Once given fair consideration, the EP model appears to provide the simplest explanation of several experimental observations. In [26], we applied the EP model to compute the pion form factor, the proton Dirac form factor $F_{1}(Q^{2})$, and the proton–proton elastic scattering cross section at high momentum transfer. We found that one consistent wave function for the endpoint region could be extracted by fitting the experimental form factor data. The same wave function then predicts the scaling behavior observed in proton–proton fixed-angle scattering. It was also shown that the valence quark wave function gives dominant contribution to the cross section [26]. This is because each additional parton leads to a suppression factor of 1 / Q due to the phase space integration in the endpoint region. We extend this study here in order to determine the proton Pauli form factor $F_{2}$. We find that the formalism predicts the scaling behavior $F_{2}(Q^{2})$ without introducing any new parameters.

1.2 Physical picture

Let us briefly explain the physics. It is well known that quark mass insertions produce a quark helicity flip, which can ultimately produce the proton helicity (more specifically, chirality) flip characterizing $F_2$. Quark mass terms are negligible in the high energy limit of the SD model. This is because they compete with terms scaling like the large momentum Q. The role of a quark mass is qualitatively different in the EP model. The soft quarks with momentum fractions $x\sim 0$ already have very small momenta. Their momenta are of the order of the QCD chiral symmetry breaking scale $\Lambda \sim \Lambda _\mathrm{QCD}$. The phenomenon of dynamical chiral symmetry breaking, see for example [35–38], is expected to lead to an effective mass of the soft quarks of the order of $\Lambda$. Hence for the soft quarks the contribution from a quark mass is not a relatively small effect, and cannot be neglected. Let us repeat that the attempt to banish small momentum regions from QCD never worked out. An unexpected consequence of small momenta appearing at leading-power order is that mass effects can appear at the same order.

Another effect makes this even more interesting. Under a Lorentz transformation with rapidity y in the z direction, the big light cone + component transforms by $\mathrm{e}^y$ and the small component like $\mathrm{e}^{-y}$. All previous calculations known to us at leading-power order integrate quark wave functions over the small momentum in the first step. This appears to be much more safe than integrating over the transverse momentum components, which scale like 1 compared to $\mathrm{e}^{-y}$. Yet we have discovered a limit-interchange error occurs. Integrating away the small components is the first step of the SD model producing a visible factorization into separated hadronic parts. The assumption, actually a hope, that some factorization dominates is what demands that step. Yet that step instantly causes $F_2$ to scale no larger than $1/Q^6$. When the small momenta components are retained in the scattering process we find a contribution to $F_2$ scaling like $1/Q^5$. The integrals cannot be represented by effective, pre-integrated quantities that depend only on Feynman-x. This phenomenon contradicts the tenets of factorization. In the EP model, the leading-power contribution to $F_2$ comes from an inseparable union of initial and final state proton states.

Finally all of this occurs with one simple wave function, which happens to be the most often cited, leading-twist example. There is no particular reason to favor leading twist coming from a short distance expansion. There is every reason to use a wave function of leading power in the large momentum P. It is seldom noticed that the leading-power, leading-twist wave function has both chirally even and chirally odd components. A single wave function can both maintain the proton’s chirality in $F_{1}$ and flip the chirality in $F_{2}$.

We emphasize that the primary motivation of the present paper is to explain the scaling behavior of $F_2$. Although soft mechanism has been invoked earlier to fit the form factor data, an understanding of why it leads to scaling for $F_2$ is missing so far in the literature. The fact that both $F_1$ and $F_2$ besides other exclusive processes show scaling behavior at $Q^2$ larger than a few GeV$^2$ is an indication of a simple underlying mechanism. Our claim is that this is the soft endpoint mechanism. A detailed modeling of the soft amplitudes, in particular the two soft quark propagators, is required for an explicit calculation. This particular soft amplitude is also identified as an important non-perturbative input required for the calculation of form factors in SCET [19]. Here we use a simple model of this amplitude. In this model the two soft quarks behave as dressed quarks with effective masses generated by dynamical chiral symmetry breaking. These masses are scale dependent and cannot simply be set equal to the constituent quark masses. The actual value depends on the momentum scale of the calculation and we treat this value as a parameter.

In Sect. 2, we show that by respecting the necessary integration region, while using the endpoint dependence of the proton wave function obtained in [26], we obtain the experimentally observed scaling behavior for $F_2/F_1$. This is a remarkable prediction of the model: If attention had been given 30 years ago, it would have predicted $F_2$ in advance of the data. Reversing the argument, the observed scaling dependence of $F_2/F_1$ predicts $F_1$ and pp scattering at high momentum transfer. None of these facts requires appealing to an unusually large logarithmic correction, or an unusually large dimensionful scale. As far as we know it is the first time that one model is actually consistent with the known data on exclusive processes.

Quark orbital angular momentum is a topic of great interest. No orbital angular momentum (OAM) enters the SD model, because a theoretical preference for factorization demands integrating over quark transverse momenta before the actual reaction has even been set up. Information about transverse size is lost by that step. When OAM is re-cast into a twist expansion [20] the sequence of operations dictated by the SD model produces a $1/Q^6$ dependence for $F_2$. References [39, 40] showed that avoiding the SD assumptions and performing the transverse momentum integrations to compute $F_2$ led to power law dependence for $F_2$ intermediate between $1/Q^4$ and $1/Q^6$. That is, the integration region assumed to dominate asymptotically was not the actually dominant region, whether or not an endpoint issue was considered. While the asymmetry of the endpoint integration regions produces a rather obvious role for OAM, which is not the focus of this paper. This paper is about using the same leading-twist Dirac and endpoint structure found in the $F_{1}$ calculation to calculate $F_{2}$. The calculation is relatively simple, and agrees remarkably with data. Even more remarkably, the ratio $F_{2}(Q^{2})/F_{1}(Q^{2})$ is quite insensitive to the endpoint wave function, explaining why the observed ratio goes like 1 / Q down to rather small momentum transfer.

2 Endpoint (EP) calculation

Here we describe the calculation of $F_2$ through the quark mass contribution. One quark is struck by the virtual photon. The remaining quarks will be in a small momentum region, such that their incoming and outgoing momenta are entirely determined by their wave functions. No interactions are computed for those particles, because perturbative interactions would double-count what is already included in the wave functions. We will use the same wave functions to compute $F_2$ as previously determined [26] from $F_1$, found to be consistent with pp scattering.

2.1 Coordinates

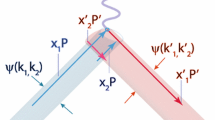
The basic diagram for proton electromagnetic form factor is given by Fig. 1. The initial and final proton 4-momenta are P and $P'$, with $q=P'-P$. Initial quark momenta $k_j$ (masses $m_j$) are unprimed, while final momenta use the same label with a prime. In Fig. 1 $k_{3}$ denotes the struck quark, and $k_1$, $k_2$ denote the spectators. Our coordinates are $(\mathrm{energy}, p_{x}, p_y, p_z).$ We use a Lorentz frame where the incoming and outgoing protons momenta are

$$\begin{aligned} P^{\mu }= & {} \left( \sqrt{{Q^{2}\over 2} + m_{P}^2},-{Q \over 2},0 ,{Q \over 2} \right) , \nonumber \\ P'^{\mu }= & {} \left( \sqrt{{Q^{2}\over 2} + m_{P}^2},{Q \over 2},0 ,{Q \over 2}\right) , \nonumber \\ q^{\mu }= & {} (0,Q,0,0)\,. \end{aligned}$$

(1)

Here $m_{P}$ is the mass of the proton.

We introduce a basis for transverse momenta:

$$\begin{aligned} y^{\mu }= & {} (0, 0, 1, 0) = y'; \quad \hat{P}\cdot y=\hat{P}'\cdot y'=0; \\ n^{\mu }= & {} \frac{1}{\sqrt{2}} (0, -1, 0, -1), \quad \hat{P}\cdot n= 0; \\ n'^{\mu }= & {} \frac{1}{\sqrt{2}} (0, 1, 0, -1), \quad \hat{P}'\cdot n'=0. \end{aligned}$$

Here $\hat{P} = (0,-\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}})$ and $\hat{P}' = (0,\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}})$ are the unit vectors along the direction of propagation of the incoming and outgoing protons, respectively. The components of the quark 3-momenta are expressed as

$$\begin{aligned} \vec {k}_{i}= & {} x_{i}\frac{Q}{\sqrt{2}}\hat{P}+ k_{in}\vec n +k_{iy} \vec y\nonumber \\= & {} (-x_{i}Q/2, \, 0, \, x_{i}Q/2) + (-k_{in}/\sqrt{2}, \, k_{iy}, \, -k_{in}/\sqrt{2}); \nonumber \\ \vec {k}^{\,'}_{i}= & {} x'_{i}\frac{Q}{\sqrt{2}}\hat{P}^{'}+ k'_{in} \vec n'+ k'_{iy} \vec y\nonumber \\= & {} (x'_{i}Q/2, \, 0, \, x'_{i}Q/2 ) + (k'_{in}/\sqrt{2}, \, k'_{iy}, \, -k'_{in}/\sqrt{2}). \end{aligned}$$

(2)

The four momenta of the quarks are then given by

$$\begin{aligned} k_{i}^{\mu }= & {} \left( k_{i}^{0},-x_{i}\frac{Q}{2}-\frac{k_{in}}{\sqrt{2}},k_{iy},x_{i}\frac{Q}{2}-\frac{k_{in}}{\sqrt{2}}\right) \nonumber \\ k_{i}^{'\mu }= & {} \left( k_{i}^{'0},x'_{i}\frac{Q}{2}+\frac{k'_{in}}{\sqrt{2}},k'_{iy},x'_{i}\frac{Q}{2}-\frac{k'_{in}}{\sqrt{2}}\right) . \end{aligned}$$

(3)

Fig. 1

The basic kinematics of the endpoint contribution to the proton form factor. The photon with momentum q scatters with one of the quarks which carries the dominant fraction of the proton momentum

2.2 The matrix element

The nucleon form factors are defined by the equation

$$\begin{aligned} \langle p^\prime s^\prime |J^{\mu }|ps\rangle= & {} -{i}e \left[ F_{1}(Q^{2})(\overline{N}^{\prime }\gamma ^{\mu }N)\right. \nonumber \\&\left. + \frac{ F_{2}(Q^{2})}{2 m_{P}} (\overline{N}^{\,\prime } {i}\sigma ^{\mu \nu }q_{\nu }N) \right] \, \end{aligned}$$

(4)

where $J^{\mu }$ is the electromagnetic current operator and N denotes the Dirac spinors. Let $\Psi _{\alpha \beta \gamma }$ be the Bethe–Salpeter 3-quark proton wave function with spinor indices $\alpha ,\beta ,\gamma$. These indices correspond to the u, u, d quarks which carry momenta $k_{1},k_{2},k_{3}$, respectively. Let the symbol $\mathcal {M}^{\mu }$ stand for the quark–photon vertex, propagator factors, and momentum conservation factors, displayed in a moment. The model for the reaction is

$$\begin{aligned}&\left\langle {p^\prime s^\prime |{J^\mu }|ps} \right\rangle = \int {\mathop \prod \limits _i } \frac{{{\mathrm{d}^4}{k_i}}}{{{{(2\pi )}^4}}}\frac{{{\mathrm{d}^4}k{^\prime _i}}}{{{{(2\pi )}^4}}}{(2\pi )^4}\nonumber \\&\quad {\delta ^4} \left( {{k_1} + {k_2} + {k_3} - P} \right) {(2\pi )^4}{\delta ^4}\left( {k_{1}^\prime + k_{2}^\prime + k_{3}^\prime - P^\prime } \right) \nonumber \\&\quad \times \left[ {{{\bar{\Psi }'}_{\alpha ^\prime \beta ^\prime \gamma ^\prime }}(k_{i}^\prime ) \times \mathcal{M}_{\alpha ^\prime \beta ^\prime \gamma ^\prime \alpha \beta \gamma }^\mu \times {\Psi _{\alpha \beta \gamma }}({k_i})} \right] . \end{aligned}$$

(5)

Here $\mathcal {M}^{\mu }$ is

(6)

The three terms correspond to the photon striking the u, u, d quarks, respectively. Note the delta functions $\delta ^{4}(k_{1}-k_{1}^{'}),\delta ^{4}(k_{2}-k'_{2}),\delta ^{4}(k_{3}-k'_{3})$ which explicitly enforce momentum conservation of spectator quarks. As mentioned above, the spectators have been modelled simply as two noninteracting quarks, which is what introduces the inverse propagators. Here we keep only the three valence quark wave function since, as shown in [26], this gives dominant contribution.

The initial light-cone coordinates are defined as

$$\begin{aligned} k^{+}_{i}= & {} k^{0}_{i}+\frac{x_{i}Q}{\sqrt{2}}; \quad k^{-}_{i}=k^{0}_{i}-\frac{x_{i}Q}{\sqrt{2}} . \end{aligned}$$

Final state symbols have a prime. In the literature, it is standard to use the coordinates $\kappa ^{-} = k^{-}p^{+}$; $\kappa ^{+} = k^{+}/p^{+}$; $\kappa ^{'-}= k^{'-}p^{'+};\kappa ^{'+}= k^{'+}/p^{'+}$ which is just parameterizing the light-cone coordinates with the momenta $p^{+}= P^{0} + Q/\sqrt{2}$, $p^{'+}=P^{'0}+ Q/ \sqrt{2}$.

2.3 Integration

It is generally assumed that wave functions $\overline{\Psi ^{\prime }}(k'_{i})$, $\Psi (k_{i})$ which are functions of the 4-momenta $k_i'$ and $k_i$ are peaked near the on-shell region. In that region, the actual wave function can be replaced by its integral over the small momentum component $\kappa _{i}^{-}, \kappa _{i}^{'-}$, producing the usual light-cone wave function $\overline{Y^{\prime }}(x'_{i},\vec {k}'_{\perp i}), Y(x_{i},\vec {k}_{\perp i})$ [41]. The above expression for scattering kernel $\mathcal {M}^\mu$ has an important dependence on $\kappa _i^-$ and $\kappa _i^{\prime -}$ of the spectator quarks, which cannot be overlooked. Hence the rest of the calculation cannot use the same approximation and the process is indivisibly linked together by the integrations. This is the point where our calculation begins to differ from previous ones.

The basic problem is that for the soft spectator quarks it is not reasonable to assume that their four momentum square, $k^2$, is approximately zero. We expect $k^2$ to be of the order of $\Lambda ^2$. In a constituent quark model, these quarks are assumed to be approximately on-mass-shell with masses of the order of few hundred MeV for the up and down quarks. In general the behavior of the quark propagator is expected to be more complicated and one can model its form by solving a truncated Schwinger–Dyson equation [35–38]. In particular the propagator is not expected to display a pole due to quark confinement and furthermore the effective mass should display a dependence on the momentum scale $k^2$. For very large $k^2$, the mass function (or running mass) of u and d should approach the perturbative value of a few MeV and at $k^2\sim \Lambda ^2$, it is expected to take a value close to the constituent quark mass [38]. For our purpose, it is adequate and self-consistent to assume that $\mathcal {M}^{\mu }$ is dominated by the on-shell region with an effective fixed mass $m_i$ and to replace $\kappa _i^{-},\kappa _i^{'-}$ dependence of the spectator by the on-shell expression,

$$\begin{aligned} \kappa _i^{-} = \frac{m_{i}^{2}+\vec {k}_{\perp i}^{2}}{\kappa _i^{+}}. \end{aligned}$$

(7)

A more general treatment using a model mass function is postponed to future research. On the other hand, the struck quark is a perturbative object. Treating it consistently uses a mass of order of a few MeV. We ignore the tiny and power-suppressed helicity-flip contributions from the struck quark. Using this approximation we obtain

Fig. 2

Chirality flow in the calculation of $F_{2}$, indicated by arrows. Chirally even vertices conserve helicity and chirally odd ones flip helicity. The standard leading-twist wave function contains both types, shown across the top. A typical combination of diagrams flipping the final state proton chirality is shown at the bottom. This diagram needs one (1) internal flip of low momentum spectator quark chirality, which appears as the closed loop with a mass insertion indicated by “X”

$$\begin{aligned}&\langle p^\prime s^\prime |J^{\mu }|ps \rangle =\int \prod _{i}\frac{\mathrm{d}\kappa ^{+}_{i}\mathrm{d}\vec {k}_{\perp i}}{(2\pi )^{4}}\frac{\mathrm{d}\kappa ^{'+}_{i}\mathrm{d}\vec {k}'_{\perp i}}{(2\pi )^{4}} (2\pi )^4(2\pi )^4\nonumber \\&\quad \times \delta (\kappa ^{+}_{1}+\kappa ^{+}_{2}+\kappa ^{+}_{3}-1) \delta ^{2}(k_{\perp 1}+k_{\perp 2}+k_{\perp 3})\nonumber \\&\quad \times \delta (\kappa ^{'+}_{1}+\kappa ^{'+}_{2}+\kappa ^{'+}_{3}-1) \delta ^{2}(k'_{\perp 1}+k'_{\perp 2}+k'_{\perp 3})\nonumber \\&\quad \times \left( \int \prod _{j}\mathrm{d}\kappa ^{\prime -}_{j}\delta (\kappa ^{\prime -}_{1}+\kappa ^{\prime -}_{2}+\kappa ^{\prime -}_{3}-m^{2}_{p}) \overline{\Psi ^{\prime }}_{\alpha ^{'}\beta ^{'}\gamma ^{'}}(k^{'\mu }_{i})\right) \nonumber \\&\quad \times \mathcal {M}^{\mu }(k_{i},k^{\prime }_{i}) \left( \int \prod _{l} \mathrm{d}\kappa ^{-}_{l}\delta (\kappa ^{-}_{1}+\kappa ^{-}_{2}+\kappa ^{-}_{3}-m^{2}_{p})\right. \nonumber \\&\quad \times \left. \phantom {\left( \int \prod _{l} \mathrm{d}\kappa ^{-}_{l}\delta (\kappa ^{-}_{1}+\kappa ^{-}_{2}+\kappa ^{-}_{3}-m^{2}_{p})\right. }\Psi _{\alpha \beta \gamma }(k^{\mu }_{i})\right) . \end{aligned}$$

(8)

We next make a change of variables which gives the standard form with

$$\begin{aligned} \langle p^\prime s^\prime |J^{\mu }|ps \rangle= & {} \int \prod _{i} \mathrm{d}x_{i}\mathrm{d}\vec {k}_{\perp i} \mathrm{d}x^{'}_{i}\mathrm{d}\vec {k}'_{\perp i}\nonumber \\&\times \delta (x_{1}+x_{2}+x_{3}-1)\nonumber \\&\times \delta ^{2}(k_{\perp 1}+k_{\perp 2}+k_{\perp 3})\delta (x'_{1}+x'_{2}+x'_{3}-1)\nonumber \\&\times \delta ^{2}(k'_{\perp 1}+k'_{\perp 2}+k'_{\perp 3})\nonumber \\&\times \left( \overline{Y^{\prime }}_{\alpha ^{'}\beta ^{'}\gamma ^{'}}(x'_{i},\vec {k}'_{\perp i}) \mathcal {M}^{\mu } Y_{\alpha \beta \gamma }(x_{i},\vec {k}_{\perp i}) \right) .\nonumber \\ \end{aligned}$$

(9)

For simplicity, we will concentrate on the diagram in which the external photon strikes the d quark. A complete calculation with all terms will be presented in Sect. 2.6.

The delta functions of Eqs. (6) and (9) lead to the following conditions:

$$\begin{aligned} x_{1}= & {} 1 - x_{2} - x_{3}; \quad x'_{1} = 1 - x'_{2} - x'_{3};\nonumber \\ k_{1n}= & {} -k_{2n} - k_{3n}; \quad k_{1y} = -k_{2y} - k_{3y} ; \nonumber \\ k'_{1n}= & {} -k'_{2n} - k'_{3n}; \quad k'_{1y} = -k'_{2y} - k'_{3y} ;\nonumber \\ k_{2y}= & {} k'_{2y}; k_{3y} = k'_{3y} ; \quad x'_{2}= x_{2}; x'_{3}= x_{3};\nonumber \\ k_{3n}= & {} \frac{Q}{\sqrt{2}}(1-x'_{3}) ; \quad k'_{3n}=\frac{Q}{\sqrt{2}}(1-x_{3}); \nonumber \\ k_{2n}= & {} \frac{Q}{\sqrt{2}}(-x'_{2}) ; \quad k'_{2n}=\frac{Q}{\sqrt{2}}(-x_{2}). \end{aligned}$$

(10)

The light-cone wave function Y of leading twist and leading power of large P is [42, 43],

(11)

Here $\mathcal {V,A,T}$ are scalar functions of the quark momenta, N is the proton spinor, $N_{c}$ the number of colors, C the charge conjugation operator, $\sigma _{\mu \nu }= \frac{{i}}{2}[\gamma _{\mu },\gamma _{\nu }]$, and $f_{N}$ is a normalization. This wave function was previously used to compute $F_{1}$, and is now being applied to compute $F_2$.

It may come as a surprise that the same chirality structure creating $F_{1}$ can predict $F_{2}$. Figure 2 shows a cartoon of the chirality flow. Each term in the $Y_{\alpha \beta \gamma }$ collection has been classified as chirally even or chirally odd depending on whether it conserves helicity (even, anti-commuting with $\gamma _{5}$) or flips helicity (odd, commuting with $\gamma _{5})$. Since momentum conservation is trivial it is not shown. The chirality flow of the $\mathcal {V, A, T}$ terms are shown at the top. A typical combination of diagrams flipping the final state proton chirality is shown at the bottom. This diagram needs one (1) internal flip of low momentum spectator quark chirality, which appears as the closed loop with a mass insertion indicated by “X”. The cartoon shows how the Dirac algebra works without needing to do the algebra.

Returning to Eq. (9), inserting the wave function Eq. (11), and extracting the terms which lead to $F_{2}$ yields

The $1/Q^{2}$ factor after the integration measure comes from the Q dependence of $\delta (k_{i}^{0}-k^{'0}_{i}) = \delta ((k_{i}^{-}+x_{i}Q/\sqrt{2})-(k_{i}^{'-}+x'_{i}Q/\sqrt{2}))$ and $\mathcal {C}$ is a constant that includes normalization of the wavefunctions and other constants that are common to both $F_{1}$ and $F_{2}$.

Isolating the $F_{2}$ contribution gives

$$\begin{aligned} \overline{N}^{\prime }\frac{{i}}{2}\sigma ^{\mu \nu }q_{\nu }N \, F_{2}\sim & {} \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^2}\, \left[ \overline{N}'\frac{{i}}{2m_{P}}\sigma ^{\mu \nu }q_{\nu }N\right] \,\\&\times 8m_{P}[(P\cdot k_{1})m_{2}+(P\cdot k_{2})m_{1}]\,\ \mathcal {T}^{*}\mathcal {V} \end{aligned}$$

along with other terms which yield similar $Q^2$ dependence.

2.4 The EP wave function and $F_{2}$

The leading-power wave functions of Ref. [26] were determined in the EP region:

$$\begin{aligned} \mathcal {V,A,T} \propto (1-x_{3})\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}}, \end{aligned}$$

(12)

where $k_T^2 = k_{\perp 1}^2 + k_{\perp 2}^2 + k_{\perp 3}^2$. The exponential dependence on the transverse momentum is a generic form that restricts the range of $x_3\in (1-\frac{\Lambda }{Q},1)$ and $x_2\in (0,\frac{\Lambda }{Q})$. The dot products are

$$\begin{aligned}&P\cdot k_{i} = k^{0}_{i}\sqrt{\frac{Q^2}{2}+m^{2}_{P}}-x_{i}\frac{Q^{2}}{2}\,. \end{aligned}$$

In terms of the light-cone variables, this gives

$$\begin{aligned} P\cdot k_{i}= & {} \left( k_{i}^{-}+x_{i}\frac{Q}{\sqrt{2}}\right) \sqrt{\frac{Q^2}{2}+m^{2}_{P}}-x_{i}\frac{Q^{2}}{2} \\&\sim \left( \frac{m^{2}_{i}+k_{\perp i}^{2}}{x_{i}Q}+x_{i}\frac{Q}{\sqrt{2}}\right) \frac{Q}{\sqrt{2}}-x_{i}\frac{Q^{2}}{2}\sim \Lambda Q. \end{aligned}$$

It follows that

$$\begin{aligned} F_{2}\propto & {} \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^2} \nonumber \\&\times 8m_{P} [(\Lambda Q) m_{2}+(\Lambda Q)m_{1}]\,\nonumber \\&\times (1-x_{3})\mathrm {e}^{-\frac{ k_{T}^{2}}{\Lambda ^{2}}}\,(1-x'_{3})\mathrm {e}^{-\frac{k_{T}^{'2}}{\Lambda ^{2}}} \nonumber \\\sim & {} \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^2} Q (1-x_{3})(1-x_{3})\mathrm {e}^{-\frac{ k_{T}^{2}}{\Lambda ^{2}}}\mathrm {e}^{-\frac{k_{T}^{'2}}{\Lambda ^{2}}} \nonumber \\= & {} \frac{1}{Q^2} Q \frac{1}{Q^3}\frac{1}{Q} = \frac{1}{Q^{5}}. \end{aligned}$$

(13)

Hence we obtain the observed $1/Q^5$ behavior of the Pauli form factor [9–13].

2.5 The ratio of form factors

In our estimate of the form factor $F_2$ we used the wave function given in Eq. (12), whose x dependence was determined by fitting the Dirac form factor, $F_1$. However, it is easy to see that the ratio $F_2/F_1$ is independent of the precise form of the wave function within the Endpoint Model.

Consider a rather arbitrary wave function

$$\begin{aligned} \mathcal {V,A,T} \propto f(x_3)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}}. \end{aligned}$$

(14)

This leads to the Dirac form factor [26],

$$\begin{aligned} F_{1}\propto & {} \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^2} [ 8 Q^2 m_{1}m_{2}]\,\nonumber \\&\times f(x_3)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}}\,\ f(x'_3) \mathrm {e}^{- k_{T}^{'2}/\Lambda ^{2}} \end{aligned}$$

(15)

using Eq. (10), $x_2'=x_2$, and $x_3'=x_3$. Similarly the form factor $F_2$ becomes

$$\begin{aligned} F_{2}\propto & {} \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^2} 8m_{P} \left[ (\Lambda Q) m_{2}\right. \nonumber \\&\left. +(\Lambda Q)m_{1}\right] \, f(x_3)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}}\,f(x'_3)\mathrm{e}^{- k_{T}^{'2}/\Lambda ^{2}}. \end{aligned}$$

(16)

Taking the ratio gives

$$\begin{aligned} \frac{F_{2}}{F_{1}}\propto \frac{\frac{1}{Q^2} 8m_{P} [(\Lambda Q)m_{2}+(\Lambda Q)m_{1}]}{\frac{1}{Q^2}[8 Q^2 m_{1}m_{2}]}\propto \frac{1}{Q}. \end{aligned}$$

(17)

Thus the ratio of form factors in the EP model is independent of the precise form of the wave function.

The JLAB data [10] shows $QF_{2}/F_{1} \sim$ constant starting from $Q^2$ as low as 2 GeV$^2$. At such low values $F_1$ differs significantly from its high-$Q^2$scaling behavior, which is observed to set in for $Q^2 > 5\ \mathrm{GeV}^2$ [44]. In the low $Q^2$ regime a more complicated wave function is needed to fit the data. However, Eq. (17) follows quite generally since the dependence on the wave function cancels out while taking the ratio.

2.6 Complete calculation of $F_2/F_1$ within the EP model

The above analysis shows that the EP model leads to the correct scaling for $F_2/F_1$. If we consider that the complete contribution for the form factors comes from the EP model, the data for the ratio $F_2/F_1$ is a good starting point to study the allowed range of parameters in the model. The free parameters available to us in the EP model are the wave function coefficients v, a, t as shown below and the effective masses in the spectator quark propagators .

$$\begin{aligned} \mathcal {V}= & {} v (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}};\nonumber \\ \mathcal {A}= & {} a (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}};\nonumber \\ \mathcal {T}= & {} t (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}} \end{aligned}$$

(18)

where $x_i$ is the momentum fraction of the struck quark.

Our analysis above was restricted to the diagram involving the interaction of the photon with the d quark. A complete calculation using all the terms in Eq. (6) involves two additional diagrams which correspond to the interaction of the photon with the u quarks. This calculation was done with the help of FEYNCALC [45]. The resulting expression leads to the following terms for $F_1$ at leading order in $1/Q^2$:

$$\begin{aligned} F_{1}= & {} -\mathcal {C}\left[ \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^{2}}\right. \\&\left. -\frac{1}{3}\left( [4 (k_1\cdot P^{\prime } )(k_2\cdot P) + 4(k_1\cdot P)(k_2\cdot P^{\prime } )\right. \right. \\&\left. \left. - 4(k_1\cdot k_2)(P\cdot P^{\prime } )\right. -4m_1 m_2 (P\cdot P^{\prime } )]\mathcal {V}^{*}\mathcal {V} \right. \\&\left. - [4 (k_1\cdot P^{\prime } )(k_2\cdot P) + 4(k_1\cdot P)(k_2\cdot P^{\prime } )\right. \\&\left. - 4(k_1\cdot k_2)(P\cdot P^{\prime } ) -4m_1 m_2 (P\cdot P^{\prime } )]\mathcal {A}^{*}\mathcal {A}\right. \\&\left. \left. +[-8(k_2\cdot P^{\prime } )(k_1\cdot P)-8(k_1\cdot P^{\prime } )(k_2\cdot P)\right. \right. \\&\left. \left. +8 (k_1\cdot k_2)(P\cdot P^{\prime } )] \mathcal {T}^{*}\mathcal {T}\right) \right. \\&\left. +\int \mathrm{d}k_{1y}\mathrm{d}k_{2y} \mathrm{d}x_{1}\mathrm{d}x_{2}\frac{1}{Q^{2}} \frac{2}{3}\left( 4 m_2 m_3 (P\cdot P^{\prime } )\mathcal {V}^{*}\mathcal {T}\right. \right. \\&\left. +4 m_2 m_3 (P\cdot P^{\prime } ) \mathcal {T}^{*}\mathcal {V} \right. \\&\left. + \left[ - 8(k_2 \cdot k_3)(P\cdot P^{\prime } ) + 8(k_3\cdot P^{\prime } )(k_2\cdot P ) \right. \right. \\&\left. \left. + 8(k_2\cdot P ^{\prime } )(k_3\cdot P)\right] \mathcal {T}^{*}\mathcal {T}\right) \\&\left. +\int \mathrm{d}k_{2y}\mathrm{d}k_{3y} \mathrm{d}x_{1}\mathrm{d}x_{2}\frac{1}{Q^{2}} \frac{2}{3}\left( 4 m_1 m_3 (P\cdot P^{\prime } )\mathcal {V}^{*}\mathcal {T}\right. \right. \\&\left. +4 m_1 m_3 (P\cdot P^{\prime } ) \mathcal {T}^{*}\mathcal {V} \right. \\&\left. \left. + [ - 8(k_1 \cdot k_3)(P\cdot P^{\prime } ) + 8(k_3\cdot P^{\prime } )(k_1\cdot P )\right. \right. \\&\left. \left. + 8(k_1\cdot P^{\prime } )(k_3\cdot P)]\mathcal {T}^{*}\mathcal {T}\right) \right] . \end{aligned}$$

The three integrals represent the contributions coming from photon striking the d quark and the two u quarks, respectively and hence the struck quark has momentum fraction $x_{3},x_{1},x_{2}\rightarrow 1$, respectively. The corresponding expression for the Pauli form factor is given by

$$\begin{aligned} F_{2}= & {} -\mathcal {C}\left[ \int \mathrm{d}k_{2y}\mathrm{d}k_{3y}\mathrm{d}x_{2}\mathrm{d}x_{3}\frac{1}{Q^{2}} \frac{-1}{3} [8 m_P m_2 (k_1\cdot P)\right. \\&\left. + 8 m_P m_1 (k_2\cdot P)](\mathcal {V}^{*}\mathcal {T}+\mathcal {T}^{*}\mathcal {V}) \right. \\&\left. +\int \mathrm{d}k_{1y}\mathrm{d}k_{2y} \mathrm{d}x_{1}\mathrm{d}x_{2}\frac{1}{Q^{2}}\frac{2}{3} \left( -8 m_P m_3 (k_2\cdot P) \mathcal {V}^{*}\mathcal {V}\right. \right. \\&\left. - 8 m_P m_3 (k_2\cdot P) \mathcal {A}^{*}\mathcal {A} \right. \\&\left. \left. + 8 m_P m_2 (k_3\cdot P)\mathcal {V}^{*}\mathcal {T}+ 8 m_P m_2 (k_3\cdot P)\mathcal {T}^* \mathcal {V}\right) \right. \\&\left. +\int \mathrm{d}k_{1y}\mathrm{d}k_{2y} \mathrm{d}x_{1}\mathrm{d}x_{2}\frac{1}{Q^{2}}\frac{2}{3} \left( -8 m_P m_3 (k_1\cdot P) \mathcal {V}^{*}\mathcal {V}\right. \right. \\&\left. - 8 m_P m_3 (k_1\cdot P) \mathcal {A}^{*}\mathcal {A} \right. \\&\left. \left. + 8 m_P m_1 (k_3\cdot P)\mathcal {V}^{*}\mathcal {T}+8 m_P m_1 (k_3\cdot P)\mathcal {T}^* \mathcal {V}\right) \right] . \end{aligned}$$

After carrying out the above integrations for a fixed mass of the soft quarks, we obtain $F_2/F_1$ as a function of v, a, t. In dealing with the ratio, we can ignore the normalizations common to both form factors. We also simplify our analysis by assuming that the coefficients v, a, t are real. The experimental data suggests that $Q F_{2}/F_{1}\sim 1.2$ [13] at large Q. For different values of the soft quark masses, we have obtained a range of values for a / v, t / v which lead to the correct ratio. The resulting parameters are plotted in Fig. 3 for two different values of the soft quark mass. We find that the experimental ratio could be obtained only for soft quark masses $m_q \lesssim 100\text { MeV}$. As expected this is much larger than the perturbative values of the u and d quark masses. However, it is somewhat smaller than the constituent quark mass values which are expected to be of order 350 MeV. From a model calculation of the momentum scale dependence of the quark masses [38], we find that the value 350 MeV is obtained in the infrared regime corresponding to invariant momentum square $k^2$ of order $\Lambda ^2$. Hence we deduce that the effective momentum scale of the spectator quark is somewhat larger than $\Lambda ^2$ but much smaller than the perturbative scale. From Fig. 3 we see that we can obtain a good fit to data even if we set the parameter $a=0$. This is equivalent to assuming that the wave function $\mathcal {A}$ is subdominant.

Fig. 3

Allowed values of the wave function parameters a / v , t / v for two different values of the effective spectator quark mass $m_q$

3 Soft gluon exchange

It can be verified that addition of low momentum gluons in the interaction will not change the scaling behavior of the Pauli form factor $F_{2}$. Consider the simple case of 2 gluon exchange illustrated in Fig. 4.

The matrix element for this diagram is

where

$$\begin{aligned}{}[\mathrm{d}k_{i}]= & {} \prod _{i}\mathrm{d}x_{i}\mathrm{d}k_{i\perp } \delta (x_{1}+x_{2}+x_{3}-1)\\&\times \delta ^{2}(\vec {k}_{1\perp }+\vec {k}_{2\perp }+\vec {k}_{3\perp }). \end{aligned}$$

Evaluating the traces and extracting the coefficient of $\overline{N}'{i}\sigma ^{\mu \nu } q_{\nu }N$ we find

$$\begin{aligned} \overline{N}'{i}\sigma ^{\mu \nu } q_{\nu }N \,F_{2}\sim & {} \int [\mathrm{d}k_{i}][\mathrm{d}k'_{i}]g_{s}^{4}\\&\times \left( - \frac{1}{3}\right) \frac{8{i}m_{2}(p_{f_{2}}\cdot P)(\overline{N}'{i}\sigma ^{\mu \nu } q_{\nu }N)\mathcal {T}^{*}\mathcal {V}}{(p_{f_{1}}^{2}-m_{2}^{2})(p_{f_{2}}^{2}-m_{3}^{2})p_{g_{1}}^{2}p_{g_{2}}^{2}} \end{aligned}$$

Keeping only leading-power term for the limit $Q\gg \Lambda$, dropping transverse momentum integrals of order the hadronic scale and substituting $\mathcal {V},\mathcal {T}$ from Eq. (12) gives

$$\begin{aligned} F_{2}\sim & {} \int \mathrm{d}x_{2}\mathrm{d}x_{3}\mathrm{d}x'_{2}\mathrm{d}x'_{3} \, \frac{8m_{2}g_{s}^{4}\frac{Q^{2}}{2}}{\Lambda ^{2}(-(1-x_{3})Q^{2})\Lambda ^{2}\Lambda ^{2}} \\&\times (1-x_{3})(1-x'_{3}) \end{aligned}$$

Fig. 4

A 2 gluon exchange contribution to the proton form factor

Each integral $dx_2 dx'_2$ over an interval of length $\Lambda /Q$ contributes a power of 1 / Q. The integration of $1-x_3$ over $1-\Lambda /Q< x_3<1$ contributes a power of 1 / Q and similarly for $x'_{3}$ we have a contribution of $1/Q^2$. It follows that

$$\begin{aligned} F_{2} \propto \int \mathrm{d}x_{2}\mathrm{d}x'_{2}\mathrm{d}x_{3} \mathrm{d}x'_{3} (1-x'_{3})\propto \frac{1}{Q\times Q \times \cdots Q} \sim \frac{1}{Q^{5}}. \end{aligned}$$

Thus the gluon exchanges do not change the leading-power behavior.

4 Conclusions

As mentioned in the Introduction, if the EP model had been given adequate attention 30 years ago, a fit to the known $1/Q^{4}$ dependence of $F_{1}$ would have then predicted $F_{2}/F_{1} \sim 1/Q$ at large Q, just as eventually observed. The calculation was never done, despite the model’s visibility after initial development by Drell, Yan, Feynman, and others [29–31].

Between then and now came a period attempting to dispense with hadron structure in form factors, and replacing protons with perturbation theory, which revealed very little about hadron structure. We find that one simple pattern of an EP wave function, previously determined in Ref. [26] and going like $1-x$, explains many independent experiments. The EP region produces the original and earliest quark-counting model [30]. For each spectator integration $\mathrm{d}x$ restricted to $x \lesssim \Lambda /Q$ an integral goes like $\Lambda /Q$. For each hard struck quark with $1-\Lambda /Q \lesssim x \le 1$ an integral goes like $\Lambda /Q$. Thus three quarks leads to $F_{1}\sim 1/Q^{4}$. The leading-twist Dirac structure, which has no room for orbital angular momentum, still allows a reversal of the proton’s chirality characterizing $F_{2}$, and $F_{2}\sim 1/Q^{5}$. These are not asymptotic limits, but generic results of power-counting that apply in the region $Q>> \Lambda$, namely $Q \gtrsim$ GeV.

The fact that $QF_{2}(Q^{2})/F_{1}(Q^{2})$ is nearly constant with Q down to relatively low values of momentum transfer is now understood. At small $Q^2\sim 2$ GeV$^2$ the EP wave function may deviate from the simple form we have assumed in Eq. (12). However, the integrations for $F_{2}$ are so nearly like those for $F_{1}$ that the details of the wave function cancel in the ratio $F_{2}/F_{1}$. The rule that $F_{2}/F_{1}\sim 1/Q$ for $Q>>$GeV naturally extends itself into the region of $Q\sim$ few GeV. When future experiments probe higher momentum transfers we are confident that $QF_{2}(Q^{2})/F_{1}(Q^{2})$ will remain constant, regardless of what might occur with the numerator and denominator.

Using our simple model for the soft spectator quark propagators we have also computed the value of the ratio $QF_2(Q^2)/F_1(Q^2)$. We find that we can fit the experimental value of this ratio for a wide range of parameters of the wave function with the effective mass of the soft spectator quarks, $m_q\lesssim 100$ MeV. We expect that the up and down running quark masses are of the order of a few MeV at very high momentum. As expected, the extracted value of the spectator quark mass is much larger than the perturbative value. At very low momentum, model calculations [38] suggest that the running quark masses take values of the order of a few hundred MeV. Hence in our case the masses take values intermediate between these two regimes.