Improved measurement of the absolute branching fraction of $D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }$

Abstract

By analyzing 2.93 fb$^{-1}$ of data collected at $\sqrt{s}=3.773$ GeV with the BESIII detector, we measure the absolute branching fraction ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })=(8.72 \pm 0.07_\mathrm{stat.} \pm 0.18_\mathrm{sys.})\%$, which is consistent with previous measurements within uncertainties but with significantly improved precision. Combining the Particle Data Group values of ${\mathcal B}(D^0\rightarrow K^-\mu ^+\nu _\mu )$, ${\mathcal B}(D^{+}\rightarrow \bar{K}^0 e^{+}\nu _{e})$, and the lifetimes of the $D^0$ and $D^+$ mesons with the value of ${\mathcal B}(D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu })$ measured in this work, we determine the following ratios of partial widths: $\Gamma (D^0\rightarrow K^-\mu ^+\nu _\mu )/\Gamma (D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })=0.963\pm 0.044$ and $\Gamma (D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu })/\Gamma (D^{+}\rightarrow \bar{K}^0 e^{+}\nu _{e})=0.988\pm 0.033$.

1 Introduction

Experimental studies of D semileptonic decays provide helpful information to understand D decay mechanisms. Their decay branching fractions (${\mathcal B}$) can serve to test isospin conservation and leptonic universality in D semileptonic decays. Isospin conservation implies that the partial widths ($\Gamma$) of $D^{0}\rightarrow K^{-}\mu ^{+}\nu _{\mu }$ and $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ should be equal. Furthermore, Ref. [1] predicts that $\Gamma (D\rightarrow \bar{K}\mu ^{+}\nu _{\mu })$ is less than $\Gamma (D\rightarrow \bar{K}e^{+}\nu _{e})$ by about 3 % due to different form factors and phase space. Using the branching fractions and the lifetimes of the $D^0$ and $D^+$ mesons ($\tau _{D^0}$, $\tau _{D^+}$), taken from the Particle Data Group (PDG) [2], we obtain $\Gamma (D^0\rightarrow K^-\mu ^+\nu _\mu )/\Gamma (D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })=0.91\pm 0.07$ and $\Gamma (D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })/\Gamma (D^{+}\rightarrow \bar{K}^0e^{+}\nu _{e})=1.04\pm 0.07,$ where the uncertainties are dominated by ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })$ [2]. Thus, an improved measurement of ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })$ will be helpful to understand D decay mechanisms with better accuracy. In addition, the improved ${\mathcal B}(D^+\rightarrow \bar{K}^0 \mu ^{+}\nu _\mu )$ can also be used to precisely determine the form factor $f^K_+(0)$ and the quark mixing matrix element $|V_{cs}|$ from D semileptonic decays [3].

Previous measurements of ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })$ come from MARKIII [4], FOCUS [5] and BESII [6]. In this paper, by analyzing 2.93 fb$^{-1}$ of data  [7, 8] collected at the center-of-mass energy of $\sqrt{s}=3.773$ GeV by the BESIII detector  [9], we determine the absolute branching fraction of $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$. Throughout the paper, charge conjugation is implied.

2 BESIII detector and Monte Carlo

The BESIII detector is a cylindrical detector with a solid-angle coverage of 93 % of $4\pi$ that operates at the BEPCII collider. It consists of several main components. A 43-layer main drift chamber (MDC) surrounding the beam pipe performs precise determinations of charged particle trajectories and provides a measurement of the specific ionization energy loss (dE / dx) that is used for charged particle identification (PID). An array of time-of-flight counters (TOF) is located radially outside the MDC and provides additional PID information. A CsI(Tl) electromagnetic calorimeter (EMC) surrounds the TOF and is used to measure the energies of photons and electrons. A solenoidal superconducting magnet located outside the EMC provides a 1 T magnetic field in the central tracking region of the detector. The iron flux return of the magnet is instrumented with about 1272 m$^2$ of resistive plate muon counters (MUC) arranged in nine layers in the barrel and eight layers in the endcaps that are used to identify muons with momentum greater than 0.5 GeV/c. More details about the BESIII detector are described in Ref. [9].

A GEANT4-based [10] Monte Carlo (MC) simulation software package, which includes the geometric description of the detector and its response, is used to determine the detection efficiency and to estimate the potential backgrounds. An inclusive MC sample, which includes the $D^0\bar{D}^0$, $D^+D^-$, and non-$D\bar{D}$ decays of $\psi (3770)$, the initial state radiation (ISR) production of $\psi (3686)$ and $J/\psi$, the $q\bar{q}$ ($q=u$, d, s) continuum process, the Bhabha scattering events, and the di-muon and di-tau events, is produced at $\sqrt{s}=3.773$ GeV. The $\psi (3770)$ decays are generated by the MC generator KKMC [11, 12], in which ISR effects [13, 14] and final state radiation (FSR) effects [15] are simulated. The known decay modes of the charmonium states are generated using EvtGen [16, 17] with the branching fractions set to PDG values [18], and others are generated using LundCharm [19]. The $D^+ \rightarrow \bar{K}^0 \mu ^+\nu _\mu$ signal is simulated with the modified pole model [20].

3 Method

In $e^{+}e^{-}$ collisions at $\sqrt{s}=3.773$ GeV, the $\psi$(3770) resonance decays predominately into a $D^0\bar{D}^0$ or a $D^+D^-$ pair. In an event where a $D^{-}$ meson (called the single tag (ST) $D^{-}$ meson) is fully reconstructed, the presence of a $D^{+}$ meson is guaranteed. In the systems recoiling against the ST $D^-$ mesons, we can select the semileptonic decays of $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ (called the double tag (DT) events). For a special ST mode i, the ST and DT yields observed in data are given by

$$\begin{aligned} N^{i}_\mathrm{ST} = 2 N_{D^+D^-} {\mathcal B}^i_\mathrm{ST} \epsilon ^i_\mathrm{ST}, \end{aligned}$$

(1)

and

$$\begin{aligned} N^{i}_\mathrm{DT} = 2 N_{D^+D^-} {\mathcal B}^i_\mathrm{ST} {\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }) \epsilon ^i_{\mathrm{ST},D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }}, \end{aligned}$$

(2)

where $N_{D^+D^-}$ is the number of $D^+D^-$ pairs produced in data, ${\mathcal B}^i_\mathrm{ST}$ and ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })$ are the branching fractions for the ST mode i and the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ decay, $\epsilon ^i_\mathrm{ST}$ is the efficiency of reconstructing the ST mode i (called the ST efficiency), and $\epsilon ^i_{\mathrm{ST},D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }}$ is the efficiency of simultaneously finding the ST mode i and the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ decay (called the DT efficiency). Based on these two equations, the absolute branching fraction for $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ can be determined by

$$\begin{aligned} {\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }) = \frac{N^\mathrm{tot}_\mathrm{DT}}{N^\mathrm{tot}_\mathrm{ST}\bar{\epsilon }_{D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }}}, \end{aligned}$$

(3)

where $\bar{\epsilon }_{D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }} = \sum _i (N^i_\mathrm{ST} \epsilon ^i_{\mathrm{ST},D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }}/\epsilon ^i_\mathrm{ST})/N^\mathrm{tot}_\mathrm{ST}$ is the averaged efficiency of reconstructing the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ decay by the ST yields in data.

4 ST $D^{-}$ mesons

The ST $D^{-}$ mesons are reconstructed using six hadronic decay modes: $K^{+}\pi ^{-}\pi ^{-}$, $K^0_{S}\pi ^{-}$, $K^{+}\pi ^{-}\pi ^{-}\pi ^{0}$, $K^0_{S}\pi ^{-}\pi ^{0}$, $K^0_{S}\pi ^{+}\pi ^{-}\pi ^{-}$ and $K^{+}K^{-}\pi ^{-}$. The decays of $K^0_{S}$ and $\pi ^0$ mesons are identified in $K^0_{S}\rightarrow \pi ^{+}\pi ^{-}$ and $\pi ^0\rightarrow \gamma \gamma$, respectively.

All charged tracks used in this analysis are required to be within a polar-angle ($\theta$) range of $|\mathrm {cos~\theta }|<0.93$. Except for those from $K^0_{S}$ decays, all tracks are required to originate from an interaction region defined by $V_{xy}<$ 1.0 cm and $|V_{z}|<$ 10.0 cm, where $V_{xy}$ and $|V_{z}|$ refer to the distances of closest approach of the reconstructed track to the Interaction Point (IP) in the xy plane and the z direction (along the beam), respectively.

The charged kaons and pions are identified by the dE / dx and TOF information. The combined Confidence Levels for pion and kaon hypotheses ($CL_{\pi }$ and $CL_{K}$) are calculated, respectively. A charged track is identified as a kaon (pion) if the confidence levels satisfy $CL_{K}>CL_{\pi }$ ($CL_{\pi }>CL_{K}$).

The charged tracks from $K^0_{S}$ decays are required to satisfy $|V_{z}|<$ 20.0 cm. The two oppositely charged tracks are assigned as $\pi ^+\pi ^-$ without PID. The $\pi ^+\pi ^-$ pair is constrained to originate from a common vertex and is required to have an invariant mass within $|M_{\pi ^{+}\pi ^{-}} - M_{K_{S}^{0}}|<$ 12 MeV$/c^{2}$, where $M_{K_{S}^{0}}$ is the $K^0_{S}$ nominal mass [2]. The $K^0_S$ candidate is required to have a decay length larger than 2 standard deviations of the vertex resolution away from the IP.

Photon candidates are selected using the information from the EMC. It is required that the shower time be within 700 ns of the event start time, the shower energy be greater than 25 (50) MeV if the crystal with the maximum deposited energy in that cluster is in the barrel (endcap) region [9], and the opening angle between the candidate shower and any charged tracks be greater than $10^{\circ }$. To reconstruct $\pi ^0$, the invariant mass of the accepted $\gamma \gamma$ pair is required to be within (0.115, 0.150) GeV$/c^{2}$. To improve resolution, a kinematic fit is performed to constrain the $\gamma \gamma$ invariant mass to the $\pi ^{0}$ nominal mass [2].

To identify the ST $D^{-}$ mesons, we define two variables, the energy difference $\Delta E=E_{mKn\pi } - E_\mathrm{beam}$ and the beam energy constrained mass $M_\mathrm{BC} = \sqrt{E^{2}_\mathrm{beam}-|\vec {p}_{mKn\pi }|^{2}}$ of the $mKn\pi$ ($m=1, 2$; $n=1, 2, 3$) final states, where $E_\mathrm{beam}$ is the beam energy, $\vec {p}_{mKn\pi }$ and $E_{mKn\pi }$ are the measured momentum and energy of the $mKn\pi$ final state in the $e^+e^-$ center-of-mass frame. For each ST mode, if there is more than one combination surviving, only the one with the minimum $|\Delta E|$ is kept. To suppress combinatorial backgrounds, $\Delta E$ is required to be within $(-25, +25)$ MeV for the $K^{+}\pi ^{-}\pi ^{-}$, $K^0_{S}\pi ^{-}$, $K^0_{S}\pi ^{+}\pi ^{-}\pi ^{-}$ and $K^{+}K^{-}\pi ^{-}$ final states, and be within $(-55, +40)$ MeV for the $K^{+}\pi ^{-}\pi ^{-}\pi ^{0}$ and $K^0_{S}\pi ^{-}\pi ^{0}$ final states.

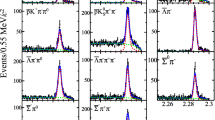
To obtain the ST yield, we apply a fit to the $M_\mathrm{BC}$ distributions of the accepted $mKn\pi$ final states for data. In the fits, the $D^{-}$ signal is modeled by a MC-determined shape of the $M_\mathrm{BC}$ distribution convoluted with a double Gaussian function and the combinatorial background shape is described by the ARGUS function [21]. The fit results are shown in Fig. 1. The candidates with $M_\mathrm{BC}$ in the range (1.863, 1.877) GeV/$c^2$ (signal region) are kept for further analysis. The ST yields and the ST efficiencies estimated from the inclusive MC sample are summarized in Table 1. The total ST yield is $N^\mathrm{tot}_\mathrm{ST}= 1522474 \pm 2215$.

Fig. 1

(color online) Fits to the $M_\mathrm{BC}$ distributions of a $K^{+}\pi ^{-}\pi ^{-}$, b $K^0_{S}\pi ^{-}$, c $K^{+}\pi ^{-}\pi ^{-}\pi ^{0}$, d $K^0_{S}\pi ^{-}\pi ^{0}$, e $K^0_{S}\pi ^{+}\pi ^{-}\pi ^{-}$ and (f) $K^{+}K^{-}\pi ^{-}$ combinations. The dots with error bars are data, the blue solid curves are the fit results, the red dashed curves are the fitted backgrounds and the pair of red arrows in each sub-figure denote the ST $D^-$ signal region

Table 1 Summary of the ST yields ($N^i_\mathrm{ST}$), the ST and DT efficiencies ($\epsilon ^i_\mathrm{ST}$ and $\epsilon ^i_\mathrm{DT}$), and the efficiencies of detecting $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ ($\epsilon ^i_{D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }}$). The efficiencies (in percent) do not include ${\mathcal B}(\pi ^0\rightarrow \gamma \gamma )$ and ${\mathcal B}(\bar{K}^0\rightarrow \pi \pi )$. ${+-}$ and 00 denote the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ signals, which are reconstructed via $\bar{K}^0\rightarrow \pi ^+\pi ^-$ and $\bar{K}^0\rightarrow \pi ^0\pi ^0$, respectively. The DT efficiencies have been corrected according to the differences of the efficiencies of the $\mu ^+$ tracking, the $\mu ^+$ PID, the $\pi ^0$ reconstruction of the signal side and the $E^{\mathrm{extra}~\gamma }_\mathrm{max}$ (see text) requirement between data and MC. The i represents the ith ST mode. The uncertainties are statistical only

5 DT events

From the surviving charged tracks and photons in the systems against the ST $D^-$ mesons, the $D^+\rightarrow \bar{K}^0\mu ^+\nu _\mu$ candidates are selected with the following, optimized criteria. The $\bar{K}^0$ is reconstructed using the decays $\bar{K}^0\rightarrow \pi ^{+}\pi ^{-}$ and $\bar{K}^0\rightarrow \pi ^{0}\pi ^{0}$. To select $\bar{K}^0(\pi ^{0}\pi ^{0})$, the $\pi ^{0}\pi ^{0}$ invariant mass is required to be within (0.45, 0.51) GeV/$c^{2}$. If more than one combination survives, the one with the minimum $\chi ^2_1(\pi ^0\rightarrow \gamma \gamma )+\chi ^2_2(\pi ^0\rightarrow \gamma \gamma )$ is kept, where $\chi ^2_1$ and $\chi ^2_2$ are the chi-squares of the mass-constrained fits on $\pi ^0\rightarrow \gamma \gamma$. The good charged tracks, photons, $\pi ^0$, and $\bar{K}^0(\pi ^+\pi ^-)$ candidates are selected with the same criteria as those used in the ST selection.

We require that there be only one good additional charged track with charge opposite to that of the ST $D^-$ meson. For muon identification, we combine the dE / dx, TOF and EMC information to calculate the Confidence Levels for electron, pion, kaon and muon hypotheses ($CL_{e}$, $CL_{\pi }$, $CL_{K}$, $CL_{\mu }$), respectively. The charged track is assigned as a muon candidate if the confidence levels satisfy $CL_{\mu }>CL_{K}$, $CL_{\mu }>CL_{e}$ and $CL_{\mu }>$ 0.001. To decrease the rate of mis-identifying pions as muons, we require that the energies deposited in the EMC by muons be within (0.1, 0.3) GeV.

Since the neutrino is undetectable, we define a kinematic quantity

$$\begin{aligned} U_\mathrm{miss} \equiv E_\mathrm{miss} - |\vec {p}_\mathrm{miss}|, \end{aligned}$$

where $E_\mathrm{miss}$ and $|\vec {p}_\mathrm{miss}|$ are the energy and momentum of the missing particle in the DT event, respectively. $E_\mathrm{miss}$ is calculated by

$$\begin{aligned} E_\mathrm{miss} = E_\mathrm{beam} - E_{\bar{K}^0} - E_{\mu ^+}, \end{aligned}$$

where $E_{\bar{K}^0}$ and $E_{\mu ^+}$ are the measured energies of $\bar{K}^0$ and $\mu ^{+}$, respectively. $\vec {p}_\mathrm{miss}$ is defined as

$$\begin{aligned} \vec {p}_\mathrm{miss} = |\vec {p}_{D^{+}} - \vec {p}_{\bar{K}^0} - \vec {p}_{\mu ^+}|, \end{aligned}$$

where $\vec {p}_{\bar{K}^0}$ and $\vec {p}_{\mu ^+}$ are the measured momenta of $\bar{K}^0$ and $\mu ^+$, $\vec {p}_{D^{+}}$ is the constrained momentum of $D^+$ meson

$$\begin{aligned} \vec {p}_{D^{+}} = (-\hat{p}_{D_\mathrm{ST}^{-}}) \sqrt{E_\mathrm{beam}^{2}-m_{D^{+}}^{2}}, \end{aligned}$$

where $\hat{p}_{D_\mathrm{ST}^{-}}$ is the momentum direction of the ST $D^{-}$ meson and $m_{D^{+}}$ is the $D^{+}$ nominal mass [2].

Figures  and show the distributions of the $\bar{K}^0\mu ^+$ invariant masses ($M_{\bar{K}^0\mu ^+}$) and the maximum energies ($E^{\mathrm{extra}~\gamma }_\mathrm{max}$) of any of the extra photons which have not been used in the DT event selection from data and the inclusive MC sample, respectively, in which the backgrounds are dominated by $D^+ \rightarrow \bar{K}^0 \pi ^+(\pi ^0)$. To suppress these backgrounds, we require that the $D^+\rightarrow \bar{K}^0\mu ^+\nu _\mu$ candidates have $M_{\bar{K}^0\mu ^+}<1.6$ GeV/$c^2$ and $E^{\mathrm{extra}~\gamma }_\mathrm{max}<0.15$ GeV.

Fig. 2

The $M_{\bar{K}^0\mu ^+}$ distributions of the a $D^{+}\rightarrow \bar{K}^0(\pi ^+\pi ^-)\mu ^{+}\nu _{\mu }$ and b $D^{+}\rightarrow \bar{K}^0(\pi ^0\pi ^0)\mu ^{+}\nu _{\mu }$ candidates of data (points with error bars) and the inclusive MC sample (histograms). The perpendicular black arrow shows the requirement $M_{\bar{K}^0\mu ^+}<1.6$ GeV/$c^2$. Other backgrounds are dominated by $D^+ \rightarrow \bar{K}^0\pi ^+\pi ^0$. For this figure, $U_\mathrm{miss}$ is required to be within $(-0.06, +0.06)$ GeV

Fig. 3

The $E^{\mathrm{extra}~\gamma }_\mathrm{max}$ distributions of the a $D^{+}\rightarrow \bar{K}^0(\pi ^+\pi ^-)\mu ^{+}\nu _{\mu }$ and b $D^{+}\rightarrow \bar{K}^0(\pi ^0\pi ^0)\mu ^{+}\nu _{\mu }$ candidates of data (points with error bars) and the inclusive MC sample (histograms). The perpendicular black arrow shows the requirement $E^{\mathrm{extra}~\gamma }_\mathrm{max}<0.15$ GeV. For this figure, $U_\mathrm{miss}$ is required to be within $(-0.06, +0.06)$ GeV

The DT efficiency is determined by analyzing signal MC events. Dividing $\epsilon _\mathrm{DT}$ by $\epsilon _\mathrm{ST}$, we obtain the efficiency of detecting $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ ($\epsilon ^{+-}_{D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }}$) for each ST mode. They are summarized in Table 1. The averaged efficiencies of detecting $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ are determined to be

$$\begin{aligned} \bar{\epsilon }^{+-}_{D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }} = \frac{\sum _i (N^{i}_\mathrm{ST} \epsilon ^{i,+-}_{D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }} )}{N^\mathrm{tot}_\mathrm{ST}} = (35.97\pm 0.11)\,\% \end{aligned}$$

and

$$\begin{aligned} \bar{\epsilon }^{00}_{D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }} = \frac{\sum _i (N^{i}_\mathrm{ST} \epsilon ^{i,00}_{D^{+}\rightarrow \bar{K}^0 \mu ^{+}\nu _{\mu }})}{N^\mathrm{tot}_\mathrm{ST}} =(21.10\pm 0.10)\,\%, \end{aligned}$$

where the i denotes the sum over the six ST modes and ${+-}$ and 00 denote the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ signals, which are reconstructed via $\bar{K}^0\rightarrow \pi ^+\pi ^-$ and $\bar{K}^0\rightarrow \pi ^0\pi ^0$, respectively.

To determine the signal yield, we perform simultaneous fits to the two $U_\mathrm{miss}$ distributions of the DT candidates, in which $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ is reconstructed via $\bar{K}^0\rightarrow \pi ^+\pi ^-$ and $\bar{K}^0\rightarrow \pi ^0\pi ^0$. In the fits, we constrain the numbers of the efficiency and branching fraction corrected DT events and $D^+\rightarrow \bar{K}^0\pi ^+\pi ^0$ peaking backgrounds, respectively, under the assumption that $K^0_S$ contributes to half of the neutral kaon decays. We use MC-determined shapes convoluted with Gaussian functions to describe the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ signal and the $D^{+}\rightarrow \bar{K}^0\pi ^{+}\pi ^{0}$ peaking background, and MC-based shape is also employed to represent the rest of the background and their overall normalizations are free parameters in the fits. The fit results are shown in Fig. 4. From the constrained fits, we determine the efficiency and branching fraction corrected DT production yield in data to be

$$\begin{aligned} N^\mathrm{prd}_\mathrm{DT} = 132712 \pm 1041, \end{aligned}$$

corresponding to the observed DT yields $N^{+-,\mathrm obs}_\mathrm{DT} = 16516 \pm 130$ and $N^{00,\mathrm obs}_\mathrm{DT} = 4198 \pm 33$ for the $+-$ and 00 modes, respectively.

Fig. 4

(color online) Fits to the $U_\mathrm{miss}$ distributions of the a $D^{+}\rightarrow \bar{K}^0(\pi ^+\pi ^-)\mu ^{+}\nu _{\mu }$ and b $D^{+}\rightarrow \bar{K}^0(\pi ^0\pi ^0)\mu ^{+}\nu _{\mu }$ candidates, where the histograms are the inclusive MC sample, the dots with error bars are data, the blue solid curves are the fit results, the blue dashed curves are the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ signals, the red dotted curves are the $D^{+}\rightarrow \bar{K}^0\pi ^{+}\pi ^0$ peaking backgrounds and the black dot-dashed curves are from other backgrounds

We compare the $\cos \theta$ and momentum distributions of $\bar{K}^0$ and $\mu ^+$ as well as the $\pi \pi$ invariant mass distrubtions from the $D^{+}\rightarrow \bar{K}^0(\pi ^{+}\pi ^{-})\mu ^{+}\nu _{\mu }$ and $D^{+}\rightarrow \bar{K}^0(\pi ^{0}\pi ^{0})\mu ^{+}\nu _{\mu }$ candidates between data and MC, as shown in Figs. 5, 6 and 7, respectively. Here, $U_\mathrm{miss}$ is required to be within $(-0.06, +0.06)$ GeV, which includes about 98 % of $D^{+}\rightarrow \bar{K}^0(\pi ^{+}\pi ^{-})\mu ^{+}\nu _{\mu }$ and 86 % of $D^{+}\rightarrow \bar{K}^0(\pi ^{0}\pi ^{0})\mu ^{+}\nu _{\mu }$ signals. In these figures, we can see good agreement between data and MC.

Fig. 5

(color online) Comparisons of the $\cos \theta$ and momentum distributions of a, b $\bar{K}^0$ and c, d $\mu ^+$ from the $D^{+}\rightarrow \bar{K}^0(\pi ^+\pi ^-)\mu ^{+}\nu _{\mu }$ candidates, where the dots with error bars are data, the red histograms are the inclusive MC sample, and the hatched histograms are the MC simulated backgrounds

Fig. 6

(color online) Comparisons of the $\cos \theta$ and momentum distributions of a, b $\bar{K}^0$ and c, d $\mu ^+$ from the $D^{+}\rightarrow \bar{K}^0(\pi ^0\pi ^0)\mu ^{+}\nu _{\mu }$ candidates, where the dots with error bars are data, the red histograms are the inclusive MC sample, and the hatched histograms are the MC simulated backgrounds

Fig. 7

(color online) Comparisons of the a $\pi ^+\pi ^-$ and b $\pi ^0\pi ^0$ distributions of the $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ candidates, where the dots with error bars are data, the red histograms are the inclusive MC sample and the arrow pairs denote the $K^0$ mass windows

6 Systematic uncertainty

The common systematic uncertainty in ${\mathcal B}(D^+\rightarrow \bar{K}^0\mu ^+\nu _\mu )$ measured with $\bar{K}^0\rightarrow \pi ^{+}\pi ^{-}$ and $\bar{K}^0\rightarrow \pi ^{0}\pi ^{0}$ arises from the uncertainties in the fits to the $M_\mathrm{BC}$ distributions, the $\Delta E$ and $M_\mathrm{BC}$ requirements, the $\mu ^+$ tracking, the $\mu ^+$ PID, the $E^\mathrm{extra~\gamma }_\mathrm{max}$ requirement, the $M_{\bar{K}^0\mu ^{+}}$ requirement and the $U_\mathrm{miss}$ fit. The uncertainty in the fits to the $M_\mathrm{BC}$ distributions is estimated to be 0.5 % by examining the relative change of the yields of data and MC via varying the fit range, the combinatorial background shape or the endpoint of the ARGUS function. To estimate the uncertainties in the $\Delta E$ and $M_\mathrm{BC}$ requirements, we examine the branching fractions by enlarging the $\Delta E$ windows by 5 or 10 MeV and varying the $M_\mathrm{BC}$ windows by $\pm 1$ MeV$/c^2$, respectively. The maximum changes of the branching fractions, which are 0.3 and 0.3 % for $\Delta E$ and $M_\mathrm{BC}$ requirements, are assigned as the uncertainties, respectively. The uncertainties in the tracking and PID for $\mu ^+$ are estimated by analyzing $e^+e^-\rightarrow \gamma \mu ^+\mu ^-$ events. The differences of the two-dimensional (momentum and $\cos \theta$) weighted tracking efficiencies of data and MC are determined to be $(+0.2\pm 0.5)\,\%$ and $(-1.5\pm 0.5)\,\%$, respectively. We assign 0.5 and 0.5 % as the systematic uncertainties in the tracking and PID for $\mu ^+$ after correcting for these differences, respectively. Due to different topologies, there may be difference between the weighted efficiencies for the muons in $D^+\rightarrow \bar{K}^0\mu ^+\nu _\mu$ and $e^+e^-\rightarrow \gamma \mu ^+\mu ^-$. This difference, which is estimated to be 0.5 % by analyzing the two kinds of signal MC events, is considered as a systematic uncertainty. By examining the doubly tagged hadronic $D\bar{D}$ decays, we find that the difference of the acceptance efficiencies with $E_\mathrm{max}^\mathrm{extra~\gamma }<0.15$ GeV of data and MC is $(+3.6\pm 0.1)\,\%$. So, we assign 0.1 % as the uncertainty in the $E_\mathrm{max}^\mathrm{extra~\gamma }$ requirement after correcting the MC efficiency to data. The uncertainty in the $M_{\bar{K}^0\mu ^{+}}$ requirement is estimated to be 0.8 % by comparing the branching fractions measured with alternative requirements of $M_{\bar{K}^0\mu ^{+}}<$ 1.55 and 1.65 GeV$/c^{2}$ with the nominal value. The uncertainty in the $U_\mathrm{miss}$ fit is estimated to be 0.8 % by comparing the branching fractions measured using different signal shape, background shape and fit range with the nominal value. Here, to examine the uncertainty in the background shape, we vary the relative strengths of each of the components in the inclusive MC sample and shift the estimated numbers of other peaking backgrounds by $1\sigma$. In our previous work, the uncertainty in the signal MC generator is estimated to be 0.1 %, which is obtained by comparing the DT efficiencies before and after re-weighting the $q^2 = (p_D-p_K)^2$ distribution of the signal MC events of $D^0\rightarrow K^-e^+\nu _e$ to data [23], where the $p_D$ and $p_K$ are the momenta of D and K mesons. Adding these in quadrature, we obtain the total common systematic uncertainty $\delta _\mathrm{sys}^\mathrm{com}$ to be 1.6 %.

For the measurement with $\bar{K}^0\rightarrow \pi ^{+}\pi ^{-}$, the independent systematic uncertainty arises from the uncertainties in the $\bar{K}^0 \rightarrow \pi ^{+}\pi ^{-}$ reconstruction, the MC statistics (0.4 %), and ${\mathcal B}(\bar{K}^0\rightarrow \pi ^+\pi ^-)$ (0.1 %) [2]. The uncertainty in the $\bar{K}^0 \rightarrow \pi ^{+}\pi ^{-}$ reconstruction is estimated to be 1.5 % by studying $J/\psi \rightarrow K^{*\mp }K^{\pm }$ and $J/\psi \rightarrow \phi \bar{K}^0 K^{\pm }\pi ^{\mp }+c.c.$ events [22]. Adding these uncertainties in quadrature, we obtain the total independent systematic uncertainty ($\delta _\mathrm{sys}^\mathrm{ind}$) for $\bar{K}^0\rightarrow \pi ^{+}\pi ^{-}$ mode to be 1.6 %.

For the measurement with $\bar{K}^0\rightarrow \pi ^{0}\pi ^{0}$, the independent systematic uncertainty arises from the uncertainties in the $\pi ^{0}$ selection, the $\bar{K}^0$ mass window, the MC statistics (0.5 %), ${\mathcal B}(\bar{K}^0\rightarrow \pi ^0\pi ^0)$ (0.2 %) [2] and the $\chi ^2_1+\chi ^2_2$ selection method. The $\pi ^0$ reconstruction efficiency is verified by analyzing the hadronic decays $D^0\rightarrow K^-\pi ^+$ and $K^-\pi ^+\pi ^+\pi ^-$ versus $\bar{D^0}\rightarrow K^-\pi ^+\pi ^0$ and $K_{S}^{0}(\pi ^+\pi ^-)\pi ^0$. The difference of the $\pi ^0$ reconstruction efficiencies of data and MC is found to be $(-1.1\pm 1.0)\,\%$ per $\pi ^0$. After correcting the detection efficiency of the signal side for this difference, the systematic uncertainty in $\pi ^0$ reconstruction is taken as $1.0\,\%$ per $\pi ^0$. Here, the photons from the $\bar{K}^0\rightarrow K^0_S(\pi ^0\pi ^0)$ decays are reconstructed under an assumption that the $K^0_S$ meson decayed at the IP. We investigate the DT efficiencies of two kinds of signal MC events, in which the lifetimes of $K^0_S$ meson from the signal side are set at the nominal value and 0, respectively. Their difference is less than 0.2 %, which is considered as the systematic uncertainty of the $K^0_S(\pi ^0\pi ^0)$ reconstruction. To avoid the effect of the $D^+ \rightarrow \bar{K}^0\pi ^+\pi ^0$ peaking backgrounds, the uncertainty in the $\bar{K}^0(\pi ^0\pi ^0)$ mass window is estimated by examining the ${\mathcal B}(D^+ \rightarrow \bar{K}^0e^+\nu _e)$ using the same $\bar{K}^0(\pi ^0\pi ^0)$ selection criteria. We compare the branching fractions measured using alternative $\bar{K}^0(\pi ^0\pi ^0)$ mass windows (0.460, 0.505), (0.470, 0.500), (0.480, 0.500) GeV/$c^2$ with the nominal value. The maximum change of the re-measured branching fractions 0.9 % is taken as the systematic uncertainty. The uncertainty in the $\chi ^2_1+\chi ^2_2$ selection method is estimated to be 0.3 %, which is the difference of the $\pi ^0\pi ^0$ acceptance efficiencies of the hadronic decays of $D^0\rightarrow K^-\pi ^+\pi ^0$ versus $\bar{D}^0\rightarrow K^+\pi ^-\pi ^0$ between data and MC. Adding these in quadrature, we obtain the total independent systematic uncertainty ($\delta _\mathrm{sys}^\mathrm{com}$) for $\bar{K}^0\rightarrow \pi ^{0}\pi ^{0}$ mode to be 2.3 %.

Table 2 Systematic uncertainties (%) in the measurement of ${\mathcal B}(D^{+}\rightarrow \bar{K}^{0} \mu ^{+}\nu _{\mu })$. $\delta _\mathrm{sys}^\mathrm{com}$ and $\delta _\mathrm{sys}^\mathrm{ind}$ denote the common and independent systematic uncertainties for $+-$ and 00 modes

Table 2 summarizes the systematic uncertainties in the measurement of ${\mathcal B}(D^{+}\rightarrow \bar{K}^{0} \mu ^{+}\nu _{\mu })$. Quadratically combining the independent uncertainties for $+-$ and 00 modes after considering their observed DT yields as weights, we obtain the independent uncertainty to be 1.4 %. Adding the common and independent uncertainties in quadrature yields the total systematic uncertainty 2.1 %.

7 Branching fraction

The branching fraction of $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ is determined by

$$\begin{aligned} {\mathcal B}(D^+\rightarrow \bar{K}^0\mu ^+\nu _\mu ) = \frac{N^\mathrm{prd}_\mathrm{DT}}{N^\mathrm{tot}_\mathrm{ST}}, \end{aligned}$$

(4)

where $N^\mathrm{prd}_\mathrm{DT}$ is the DT production yield corrected for detection efficiency and daughter decay branching fractions, which has been constrained to be the same for $+-$ and 00 modes in the simultaneous fits, and $N^\mathrm{tot}_\mathrm{ST}$ is the total ST yield.

Inserting the numbers of $N^\mathrm{prd}_\mathrm{DT}$ and $N^\mathrm{tot}_\mathrm{ST}$ in Eq. (4), we obtain

$$\begin{aligned} {\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }) = (8.72 \pm 0.07 \pm 0.18)\,\%, \end{aligned}$$

(5)

where the first uncertainty is statistical and the second systematic.

Furthermore, we examine the measured branching fractions for $D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }$ by separately using each of the ST modes, which are shown Fig. 8. We can see that they are consistent with the nominal result within uncertainties very well. Here, the uncertainties are statistical only. The average branching fraction over the six ST modes, weighted by their statistical uncertainties, is $(8.70\pm 0.07)\,\%$ and is consistent with our nominal result.

Fig. 8

Comparison of the branching fractions. Dots with error bars are results measured using different ST modes, and shadow band is the nominal result. Only statistical uncertainties are shown

8 Summary and discussion

In summary, by analyzing 2.93 fb$^{-1}$ of data collected at $\sqrt{s}=$ 3.773 GeV with the BESIII detector, we measure the absolute branching fraction ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu }) = (8.72 \pm 0.07_\mathrm{stat.} \pm 0.18_\mathrm{sys.})\,\%$, which is consistent with previous measurements within uncertainties but with significantly improved precision. Combining the ${\mathcal B}(D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })$ measured in this work with the $\tau _{D^0}$, $\tau _{D^+}$, ${\mathcal B}(D^0\rightarrow K^-\mu ^+\nu _\mu )$ and ${\mathcal B}(D^{+}\rightarrow \bar{K}^0e^{+}\nu _{e})$ taken from the world average [2], we determine the ratios of the partial widths $\Gamma (D^0\rightarrow K^-\mu ^+\nu _\mu )/\Gamma (D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })=0.963\pm 0.044,$ which supports isospin conservation holding in the exclusive semi-muonic decays of $D^{+}$ and $D^{0}$ mesons, and $\Gamma (D^{+}\rightarrow \bar{K}^0\mu ^{+}\nu _{\mu })/\Gamma (D^{+}\rightarrow \bar{K}^0e^{+}\nu _{e})=0.988\pm 0.033,$ which is consistent with the predicted value in Ref. [1] within uncertainties.