The coherent cross section of vector mesons in ultraperipheral PbPb collisions at the LHC

Abstract

The coherent cross section of $J/\psi$, $\rho$, and $\phi$ are computed in the dipole model in the ultraperipheral PbPb collisions. The IP-Sat and IIM model are applied in the calculation of the differential cross section of the dipole scattering off the nucleon, and three kinds of forward vector meson wave functions are used in the overlap. The prediction of $J/\psi$ and $\rho$ is compared with the experimental data of the ALICE collaboration, and the prediction of $\phi$ is also given in this paper.

1 Introduction

The production of vector mesons through virtual photon–hadron scattering had been studied in deep inelastic scattering at HERA [1]. The ultraperipheral collisions at the LHC offer an interesting way to study the photoproduction of vector mesons through a real photon scattering off a hadron in the high energy limit [2, 3]. Recently, the ALICE collaboration have measured vector meson production in PbPb ultraperipheral collisions [4–8]. On the theoretical front, the photon production of vector mesons has been studied through various approaches, including perturbative quantum chromodynamics (pQCD), $k_T$-factorization, and the color dipole model (CDM) [9–13, 15, 15–19, 21, 21–23]. In this work, we use the dipole model to predict the vector meson production in PbPb ultraperipheral collisions at $\sqrt{s_\mathrm{NN}}=2.76\,\,\mathrm{TeV}$. The goal of this work is to update the prediction of vector mesons with a new fit of the IP-Sat model and several wave function models.

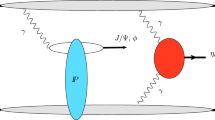
According to the dipole model, the process of the photon–hadron scattering can be viewed as a sequence of three steps. At the first step, the virtual or real photon splits into a dipole with quark and antiquark. At the second step, the dipole scatters off the hadrons. At the last step, the dipole becomes a vector meson. The amplitude of the photon–hadron scattering contains three portions, the light-cone wave function of the photon splitting into a dipole, the cross section of the dipole scattering off the proton, and the forward wave function for the vector mesons. The calculation of the cross section of the dipole scattering off a proton is relative to the gluon distribution in the small-x region. In the literature, various parameterization models have successfully been implemented to calculate the cross section of the dipole scattering off a proton, such as the GBW model [24, 25], the IP-Sat model [26–29], and the IIM model [30–33]. The light-cone wave function of the photon splitting into the dipole can be calculated in QED, but the forward wave function of the vector meson cannot be calculated analytically. The forward wave functions of vector meson almost are modeled as the light-cone wave function of the photon, and the models of the vector mesons include the Gauss-LC [28], the DGKP [34, 35], the boosted Gaussian [36, 37], and so on.

This paper is organized as follows: a brief review of the dipole model and the wave function will be presented in Sect. 2, the numerical results and some discussion will be presented in Sect. 3.

2 The coherent vector meson cross section

2.1 Formulas in the ultraperipheral collision

In this work, we consider the coherent cross section of the vector meson in the PbPb ultraperipheral collisions. In hadronic collisions, when the impact parameter is larger, the two hadrons almost do not touch each other, but the real photon can be emitted from the hadrons in the high energy limits. Therefore the real photon can scatter off the hadrons, and in this process, the rapidity distribution can be factorized into the equivalent photon flux and the cross section of the photon–hadron scattering. The formula is

$$\begin{aligned} \frac{\mathrm{d}\sigma ^{h_1h_2}}{\mathrm{d}y}=\bigg [n^{h_1}(\omega )\sigma ^{\gamma h_2}(\omega )\bigg ]_{\omega _\mathrm{left}}+\bigg [n^{h_2}(\omega )\sigma ^{\gamma h_1}(\omega )\bigg ]_{\omega _\mathrm{right}},\nonumber \\ \end{aligned}$$

(1)

where y is the rapidity of the vector meson, $\sigma ^{\gamma A}(\omega )$ is the cross section of the photon–hadron scattering, $n(\omega )$ is the equivalent photon flux in the hadrons, with $\omega _\mathrm{left}=\frac{M_\mathrm{v}}{2}\exp (-y)$ and $\omega _\mathrm{right}=\frac{M_\mathrm{v}}{2}\exp (y)$, where $M_\mathrm{v}$ is the mass the vector meson. In proton–proton scattering, the equivalent photon flux is [39]

$$\begin{aligned} n(\omega )= & {} \frac{\alpha _{em}}{2\pi }\bigg [1+\bigg (1-\frac{2\omega }{ \sqrt{s_\mathrm{NN}}}\bigg ) \bigg ]\nonumber \\&\times \bigg [\ln D-\frac{11}{6}+\frac{3}{D}-\frac{3}{2D^2}+\frac{1}{3D^3} \bigg ], \end{aligned}$$

(2)

where $\sqrt{s_\mathrm{NN}}$ is the nucleon–nucleon center energy, $D=1+\frac{0.71\mathrm {GeV}^2}{Q^2_\mathrm{min}}$, with $Q^2_\mathrm{min}=\omega ^2/\gamma _\mathrm{L}^2$, $\gamma _\mathrm{L}$ is the Lorentz factor, with $\gamma _\mathrm{L}=\sqrt{s_\mathrm{NN}}/2m_p$. In nucleus–nucleus scattering, the equivalent photon flux is [9–11]

$$\begin{aligned} n(\omega )=\frac{2 Z^2\alpha _{em}}{\pi }\left[ \xi K_1(\xi ) K_0(\xi )-\frac{\xi ^2}{2}[K_1^2(\xi )-K_0^2(\xi )]\right] ,\nonumber \\ \end{aligned}$$

(3)

where $\xi =2\omega R_A/\gamma _\mathrm{L}$, with $R_A$ is the radius of the nucleus, $K_0(x)$ and $K_1(x)$ are of Bessel functions of the second kind.

$\sigma (\omega )$ is the cross section of the photon–hadron scattering. It can be integrated from the differential cross section. The coherent differential cross section of the photon-proton scattering is calculated as [27, 28]

$$\begin{aligned} \frac{\mathrm{d}\sigma ^{\gamma p\rightarrow Vp}}{\mathrm{d}t}=\frac{R_g^2(1+\beta ^2)}{16\pi } \left| \mathcal {A}^{\gamma p\rightarrow Vp}(x_p, Q^2,\Delta )\right| ^2, \end{aligned}$$

(4)

where the amplitude is computed as

$$\begin{aligned}&\mathcal {A}^{\gamma p\rightarrow Vp}(x_A, Q^2,\Delta )= i\int \mathrm{d}^2r\int _0^1\frac{\mathrm{d}z}{4\pi }\nonumber \\&\quad \times \int \mathrm{d}^2b(\Psi _V^*\Psi _{\gamma })_{T}(z,r,Q^2) \times e^{-i(b-(1-z)r)\cdot \Delta }\frac{\mathrm{d}\sigma _{q\bar{q}}}{\mathrm{d}^2b}. \nonumber \\ \end{aligned}$$

(5)

Here $t=-\Delta ^2$, the relationship between $x_p$ and y is $x_p=M_\mathrm{v}\exp (-y)/\sqrt{s_\mathrm{NN}}$, and T denotes the transverse overlap of the wave functions of the photon and the vector meson. Finally, $\mathcal {N}(x,r,b)$ is the amplitude of the dipole scattering off the nucleon, which will be considered in the next subsection. The factor $\beta$ is the ratio of the real part to the imaginary part of the amplitude, and it is computed to be

$$\begin{aligned} \beta =\tan \left( \frac{\pi }{2}\delta \right) , \end{aligned}$$

(6)

where $\delta$ is calculated as

$$\begin{aligned} \delta =\frac{\partial \ln (\mathrm {Im}\mathcal {A}(x))}{\partial \ln 1/x}. \end{aligned}$$

(7)

The factor $R_g^2$ reflects the skewedness [40],

$$\begin{aligned} R_g=\frac{2^{2\delta +3}}{\sqrt{\pi }}\frac{\Gamma (\delta +5/2)}{\Gamma (\delta +4)}. \end{aligned}$$

(8)

The differential cross section of $\gamma A\rightarrow VA$ is written as

$$\begin{aligned} \frac{\mathrm{d}\sigma ^{\gamma A\rightarrow VA}}{\mathrm{d}t}=\frac{R_g^2(1+\beta ^2)}{16\pi } \left| \langle \mathcal {A}^{\gamma A\rightarrow VA}(x_p, Q^2,\Delta )\rangle _N\right| ^2,\nonumber \\ \end{aligned}$$

(9)

where the average amplitude is calculated as [41–43]

$$\begin{aligned}&\langle \mathcal {A}^{\gamma A\rightarrow VA}(x_p, Q^2,\Delta )\rangle _N \nonumber \\&= i\int \mathrm{d}^2r\int _0^1\frac{\mathrm{d}z}{4\pi } \int \mathrm{d}^2b(\Psi _V^*\Psi _{\gamma })_{T} \nonumber \\&\quad \times (z,r,Q^2)e^{-i(b-(1-z)r)\cdot \Delta }\nonumber \\&\quad \times 2(1-\exp (-2\pi B_pAT_A(b)\mathcal {N}(x_p,r)). \end{aligned}$$

(10)

The shape function is defined as

$$\begin{aligned} T_A(b)=\int _{-\infty }^{\infty }\mathrm{d}z\rho _A(\sqrt{b^2+z^2}), \end{aligned}$$

(11)

with the Wood–Saxon distribution

$$\begin{aligned} \rho _A(r)=\frac{N}{\exp (\frac{r-R_A}{\delta _0})+1}, \end{aligned}$$

(12)

where $\delta _0=0.54$ fm, $R_A=(1.12\mathrm \,\mathrm{fm})A^{1/3}-(0.86 \mathrm \,\mathrm{fm})A^{-1/3}$, A is the number of nuclei.

2.2 The IP-Sat and IIM model

There are various approaches to calculate the cross section of dipole scattering off the proton. The GBW model was proposed by Golec-Biernat and Wüsthoff [24, 25], but the GBW model has a shortcoming in that it does not match the DGLAP evolution equation at large $Q^2$. Then the Impact Parameter saturation (IP-Sat) model was proposed according to the DGLAP evolution equation. The amplitude of the IP-Sat model reads [41–43]

$$\begin{aligned} \frac{\mathrm{d}\sigma _{q\bar{q}}}{\mathrm{d}^2b}=2\left[ 1-\exp \left( -\frac{1}{2\pi B_p}\frac{\pi ^2}{2N_c}r^2\alpha _s(\mu ^2)xg(x, \mu ^2)T_p(b)\right) \right] , \end{aligned}$$

(13)

Table 1 The parameters of the IP-Sat model [29]

Table 2 The parameters of the IIM model [31]

where $T_p(b)$ is defined by

$$\begin{aligned} T_p(b)=\exp \left( -\frac{b^2}{2B_p}\right) . \end{aligned}$$

(14)

The scale $\mu ^2$ has a relationship with the dipole size r,

$$\begin{aligned} \mu ^2=\mu ^2_0+\frac{C}{r^2}, \end{aligned}$$

(15)

with $C=4$, where $xg(x,\mu ^2)$ is the gluon distribution in the proton. The initial gluon distribution is

$$\begin{aligned} xg(x, \mu ^2_0)=A_gx^{-\lambda _g}(1-x)^{5.6}. \end{aligned}$$

(16)

The parameters $A_g$, $\mu ^2_0$, $\lambda _g$, $B_p$ are determined from a fit to the experimental data of reduce cross section. We take the values of parameters according to Ref. [29]. There are two sets of the parameters, which are different from Refs. [27, 28], especially for the mass of the light quarks. In the fit of Kowalski et al., the mass of the light quark is $m_\mathrm{q}=0.14$ GeV, in the fit of Rezaeian et al., the mass of the light quarks is $m_\mathrm{q}\approx 0 \mathrm{GeV}$ (Table 1).

In Refs. [26, 43], the authors used a factorized impact parameter saturation model, reading

$$\begin{aligned} \frac{\mathrm{d}\sigma _{q\bar{q}}}{\mathrm{d}^2b}\approx & {} 2T_p(b)\mathcal {N}(x,r)\nonumber \\= & {} 2T_p(b)\left[ 1-\exp \bigg (-\frac{1}{2\pi B_p}\frac{\pi ^2}{2N_c}r^2\alpha _s(\mu ^2)xg(x, \mu ^2)\bigg )\right] .\nonumber \\ \end{aligned}$$

(17)

We use the fIP-Sat model to calculate the vector meson cross section in photon–nucleus scattering.

On the other hand, Iancu, Itakura and Munier proposed a saturation model based on the solution to the BK evolution equation [30], while we use the impact parameter dependent saturation model. We take the same form as Refs. [31, 43],

$$\begin{aligned} \frac{\mathrm{d}\sigma _{q\bar{q}}}{\mathrm{d}^2b}=2T_b(b)\mathcal {N}(x,r), \end{aligned}$$

(18)

and the amplitude is written as

$$\begin{aligned} \mathcal {N}(x,r)={\left\{ \begin{array}{ll} \mathcal {N}_0(\frac{rQ_{s}}{2})^{2(\gamma _s+(1/\kappa \lambda Y)\ln (2/rQ_s))},\quad rQ_s\le 2, \\ 1-\exp \big (-a\ln ^2(b rQs)\big ),\quad \quad \quad \!\!\! rQ_s>2, \end{array}\right. }\nonumber \\ \end{aligned}$$

(19)

with $Y=\ln (1/x)$ and $\kappa =9.9$, where $Qs(x,b)=(x_0/x)^{\lambda /2}$ GeV, a and b are

$$\begin{aligned} a= & {} -\frac{\mathcal {N}^2_0\gamma _s^2}{(1-\mathcal {N}_0)^2\ln (1-\mathcal {N}_0)},\nonumber \\ b= & {} \frac{1}{2}(1-\mathcal {N}_0)^{-(1-\mathcal {N}_0)/(2\mathcal {N}_0\gamma _s)}. \end{aligned}$$

(20)

The parameters $B_p, \mathcal {N}_0, \gamma _c, \lambda , x_0$ need to be determined from the fit to the experimental data $F_2$. We take the parameter the same as Ref. [31], and they are presented in Table 2.

Table 3 The parameter of the wave functions, columns 6, 7 are the parameters of Gauss-LC, columns 8, 9 are the parameters of the boosted Gaussian model, columns 10, 11 are the parameters of the DGKP model

2.3 The forward vector meson wave functions

$(\Psi _V^*\Psi _{\gamma })_{T}(r,z)$ is the transverse overlap of the functions of vector meson and the photon. There are various models for the forward vector meson wave function in the literature. In this work, we take the three kinds of model for the vector meson wave functions. First, we consider the boosted Gaussian and Gauss-LC model, the overlap takes the following form in the boosted Gaussian and Gauss-LC model [28]:

(21)

where $e=\sqrt{4\pi \alpha _{em}}$, $m_f$ is the mass of quarks, $e_f$ is the electric charge of the quarks, $\epsilon =\sqrt{z(1-z)Q^2+m_f^2}$, $N_c$ is the number of colors. The scalar function $\phi _T(r,z)$ of Gauss-LC model [28] reads

$$\begin{aligned} \phi _T(r,z)=N_T(z(1-z))^2\exp \left( -\frac{r^2}{2R_T^2}\right) . \end{aligned}$$

(22)

The boosted Gaussian model is simplified from NNPZ model [36, 37], and the scalar function of the boosted Gaussian reads

$$\begin{aligned}&\phi _T(z,r)=N_Tz(1-z) \nonumber \\&\quad \quad \times \exp \left( -\frac{m_f^2\mathcal {R}^2}{8z(1-z)}- \frac{2z(1-z)r^2}{\mathcal {R}^2}+\frac{m_f^2\mathcal {R}^2}{2}\right) . \end{aligned}$$

(23)

The DGKP model is another famous model for the forward vector meson wave function [34–36]. In this work, we also consider the contribution of the DGKP model. The overlap is different from the above models. In the DGKP model, the overlap reads [36]

$$\begin{aligned}&(\Psi _V^*\Psi _{\gamma })_T(r,z)=\frac{e f_v}{M_\mathrm{v}}f_T(z)\nonumber \\&\quad \times \exp \left( -\frac{\omega _T^2r^2}{2} \right) \{(\omega _T^2\epsilon r[(z^2+(1-z)^2)]K_1(\epsilon r)+m_f^2K_0(\epsilon r)\},\nonumber \\ \end{aligned}$$

(24)

where $f_v$ is the decay constant of the vector meson, and f(z) reads

$$\begin{aligned} f_T(z)=N_T\sqrt{z(1-z)}\exp \left( -\frac{M_\mathrm{v}^2(z-1/2)^2}{2\omega ^2_T}\right) . \end{aligned}$$

(25)

The parameters of the vector meson functions are determined by the normalization condition and the decay constants. We present the parameters in Table 3. Some parameters are taken from Refs. [28, 33].

3 Results and discussion

Fig. 1

The coherent $J/\psi$ rapidity distribution in PbPb collisions at $\sqrt{s_{\mathrm{NN}}}= 2.76\,\,\mathrm{TeV}$ computed using the fIP-Sat model and compared to the experimental data of ALICE [4, 5], the black thick lines use the parameters of the fIP-Sat model parameter set 2 in Table 1; the green thin curves are the results from Ref. [22]

In this section, we shall give our prediction using the fIP-Sat and IIM model with different kinds of wave functions, and we compare the prediction to the experimental data. In the calculation using the IIM model, we take the mass of the charm quark as $m_c=1.4~\mathrm{GeV}$, and the mass of the light quarks as $m_\mathrm{q}=0.14~\mathrm{GeV}$. In the calculation using the fIP-Sat model, we take the mass of the quarks as two parameters sets, in parameter set 1, the quark mass is $m_c = 1.27~\mathrm{GeV}$ and $m_\mathrm{q}=0.01~\mathrm{GeV}$, in parameter set 2, the quark mass is $m_c = 1.4~\mathrm{GeV}$ and $m_\mathrm{q}=0.01~\mathrm{GeV}$ [38]. The parameters of the wave functions are taken according to the quark mass in the fIP-Sat or the IIM model, which are presented in Table 3, $Q^2=$0 $\mathrm {GeV}^2$ in all calculations in this work because the photon is real.

In Fig. 1, we present the prediction of the rapidity distribution of $J/\psi$ in PbPb at $\sqrt{s_{\mathrm{NN}}}= 2.76~\mathrm{TeV}$. The prediction was also calculated using the parameters in Ref. [28]. We can see that the result of this work is lower than the result of Ref. [22]. As we use the newer fit of IP-Sat model [29] in this paper.

Fig. 2

The coherent $J/\psi$ rapidity distribution in PbPb collisions at $\sqrt{s_{\mathrm{NN}}}=2.76\,\,\mathrm{TeV}$ computed using the IIM and fIP-Sat model with the Gauss-LC (solid), the boosted Gaussian (dashed), the DGKP (dot-dashed) and then compared to the experimental data of ALICE [4, 5]

Fig. 3

The coherent $\rho$ meson rapidity distribution in PbPb collisions at $\sqrt{s_{\mathrm{NN}}}=2.76~\mathrm{TeV}$ computed using the IIM and the fIP-Sat model with the Gauss-LC (solid), the boosted Gaussian (dashed), the DGKP (dot-dashed) and then compared to the experimental data of ALICE [8]

Fig. 4

The coherent $\phi$ rapidity distribution in PbPb collisions at $\sqrt{s_{\mathrm{NN}}}=$2.76 TeV computed using the IIM and the fIP-Sat model with the Gauss-LC (solid), the boosted Gaussian (dashed), and the DGKP (dot-dashed)

The prediction using the IIM model is also calculated in this work, which is compared with two sets of parameters of the fIP-Sat models. The results are presented in Fig. 2. We can see that the result of parameter set 2 is closer to the experimental data than the result of the IIM model and parameter set 1. The result of the Gauss-LC wave function is closer than the boosted Gaussian and the DGKP model.

The rapidity distribution of the $\rho$ meson was also measured at ALICE [8]. The prediction had been presented in Ref. [44]. We also compute the prediction of the $\rho$ meson, which is showed in Fig. 3. We compute the result of the $\rho$ meson using the IIM and the fIP-Sat model with two sets of parameters. We take the light quarks mass $m_\mathrm{q}= 0.14~\mathrm{GeV}$ in the IIM model and take the light quark mass $m_\mathrm{q}= 0.01~\mathrm{GeV}$ in the fIP-Sat model.

We also give the prediction of the rapidity distribution of the $\phi$ meson in PbPb collisions at $\sqrt{s_{\mathrm{NN}}}=2.76~\mathrm{TeV}$ in Fig. 4. There is no experimental data for the $\phi$ meson. We expect the experimental data of the $\phi$ meson at the LHC in the future.

In summary, we calculate the coherent cross section of vector mesons in PbPb ultraperipheral collisions with the fIP-Sat and the IIM model. The parameters of this work are determined in a fit of HERA data. We find that the newer fit of the IP-Sat model is more accurate than the older fit in the calculation of $J/\psi$ production. The IIM model is a little higher than the fIP-Sat model in $J/\psi$ and $\rho$ calculations. The production of $\phi$ is also calculated in this work and we hope that in the future the production will be measured at the LHC.