Horizon structure of rotating Einstein–Born–Infeld black holes and shadow

Abstract

We investigate the horizon structure of the rotating Einstein–Born–Infeld solution which goes over to the Einstein–Maxwell’s Kerr–Newman solution as the Born–Infeld parameter goes to infinity ($\beta \rightarrow \infty$). We find that for a given $\beta$, mass M, and charge Q, there exist a critical spinning parameter $a_{E}$ and $r_{H}^{E}$, which corresponds to an extremal Einstein–Born–Infeld black hole with degenerate horizons, and $a_{E}$ decreases and $r_{H}^{E}$ increases with increase of the Born–Infeld parameter $\beta$, while $a<a_{E}$ describes a non-extremal Einstein–Born–Infeld black hole with outer and inner horizons. Similarly, the effect of $\beta$ on the infinite redshift surface and in turn on the ergo-region is also included. It is well known that a black hole can cast a shadow as an optical appearance due to its strong gravitational field. We also investigate the shadow cast by the both static and rotating Einstein–Born–Infeld black hole and demonstrate that the null geodesic equations can be integrated, which allows us to investigate the shadow cast by a black hole which is found to be a dark zone covered by a circle. Interestingly, the shadow of an Einstein–Born–Infeld black hole is slightly smaller than for the Reissner–Nordstrom black hole, which consists of concentric circles, for different values of the Born–Infeld parameter $\beta$, whose radius decreases with increase of the value of the parameter $\beta$. Finally, we have studied observable distortion parameter for shadow of the rotating Einstein–Born–Infeld black hole.

1 Introduction

In Maxwell’s electromagnetic field theory, the field of a point-like charge is singular at the charge position and hence it has infinite self-energy. To overcome this problem in classical electrodynamics, the nonlinear electromagnetic field has been proposed by Born and Infeld [1], with main motivation, to resolve self-energy problem by imposing a maximum strength of the electromagnetic field. In this theory the electric field of a point charge is regular at the origin and this nonlinear theory for the electromagnetic field was able to tone down the infinite self-energy of the point-like charged particle. Later, Hoffmann [2] coupled general relativity with Born–Infeld electrodynamics to obtain a spherically symmetric solution for the gravitational field of an electrically charged object. Remarkably, after a long dormancy period, the Born–Infeld theory made a come back to the stage in the context of more modern developments, which is mainly due to the interest in nonlinear electrodynamics in the context of low energy string theory, in which Born–Infeld type actions appeared [3–5]. Indeed, the low energy effective action in an open superstring in loop calculations lead to Born–Infeld type actions [3]. These important features of the Born–Infeld theory, together with its corrective properties concerning singularities, further motivate to search for gravitational analogs of this theory in the past [6–11], and also interesting measures have been taken to get the spherically symmetric solutions [12–14]. The thermodynamic properties and causal structure of the Einstein–Born–Infeld black holes drastically differ from those of the classical Reissner–Nordstrom black holes. Indeed, it turns out that the Einstein–Born–Infeld black hole singularity is weaker than that of the Reissner–Nordstrom black hole. Further properties of these black holes, including the motion of the test particles has also been addressed [15]. It is worthwhile to mention that Kerr [16] and Kerr–Newman metrics [17] are undoubtedly the most significant exact solutions in the general relativity, which represent rotating black holes that can arise as the final fate of gravitational collapse. The generalization of the spherically symmetric Einstein–Born–Infeld black hole in the rotating case, the Kerr–Newman like solution, was studied by Lombardo [18]. In particular, it was demonstrated [1] that the rotating Einstein–Born–Infeld solutions can be derived starting from the corresponding exact spherically symmetric solutions [2] by the complex coordinate transformation previously developed by Newman and Janis [17]. The rotating Einstein–Born–Infeld black hole metrics are axisymmetric, asymptotically flat, and dependent on the mass, charge, and spin of the black hole as well as on a Born–Infeld parameter ($\beta$) that measures potential deviations from the Kerr metric Kerr–Newman metrics. The rotating Einstein–Born–Infeld metric includes the Kerr–Newman metric as a special case if this deviation parameter diverges ($\beta \rightarrow \infty$) as well as the Kerr metric when this parameter vanishes ($\beta =0$). In this paper, we carry out a detailed analysis of the horizon structure of rotating Einstein–Born–Infeld black hole and we explicitly make manifest the effect $\beta$ has. Recently, the horizon structure has been studied for various space-time geometries, see, e.g., [19–22]. We also investigate the apparent shape of the non-rotating Einstein–Born–Infeld black hole to visualize the shape of the shadow and compare the results with the images for the corresponding Reissner–Nordstrom black hole. In spite of the fact that a black hole is invisible, its shadow can be observed if it is in front of a bright background [23] as a result of the gravitational lensing effect, see, e.g., [24–30]. The photons that cross the event horizon, due to strong gravity, are removed from the observable universe which lead to a shadow (silhouette) imprinted by a black hole on the bright emission that exists in its vicinity. So far the shadows of the compact gravitational objects in the different cases have been extensively studied, see, e.g., [31–48]. Furthermore a new general formalism to describe the shadow of black hole as an arbitrary polar curve expressed in terms of a Legendre expansion was developed in a recent paper [49]. The organization of the paper is as follows: in Sect. 2, we study the structure and location of an event horizon and the infinite redshift surface of the rotating Einstein–Born–Infeld black holes. We also discuss the particle motion around the rotating Born–Infeld black hole in Sect. 2, which helps us to investigate the shadow of the black hole in Sect. 3. In Sect. 4 the emission energy is analyzed of rotating Einstein–Born–Infeld black holes. Finally, in Sect. 5, we conclude by summarizing the main results. We use units which fix the speed of light and the gravitational constant via $G = c = 1$, and we use the metric signature ($-,\;+,\;+,\;+$).

2 Rotating Einstein–Born–Infeld black hole

The action for the gravitational field coupled to a nonlinear Born–Infeld electrodynamics (or an Einstein–Born–Infeld action) in $(3+1)$ dimensions reads [1, 2]

$$\begin{aligned} S= \int \mathrm{d}^{4}x\sqrt{-g}\left[ \frac{R}{16\pi G}+\mathcal {L}(\mathcal {F})\right] , \end{aligned}$$

(1)

where R is scalar curvature, $g \equiv \det |g_{\mu \nu }|$, and $\mathcal {L}(\mathcal {F})$ is given by

$$\begin{aligned} \mathcal {L}(\mathcal {F})=\frac{\beta ^{2}}{4\pi G}\left( 1-\sqrt{1+\frac{2\mathcal {F}}{\beta ^{2}}}\right) , \end{aligned}$$

(2)

with $\mathcal {F}=\frac{1}{4} F_{\mu \nu }F^{\mu \nu }$; $F_{\mu \nu }$ denotes the electromagnetic field tensor. Here $\beta ^2$ is the Born–Infeld parameter, equal to the maximum value of electromagnetic field intensity, and it has the dimension of [length]$^{-2}$. Equation (1) leads to the Einstein field equations,

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R= \kappa T_{\mu \nu } , \end{aligned}$$

(3)

and the electromagnetic field equation

$$\begin{aligned} \nabla _{\mu }(F^{\mu \nu } \mathcal {L,_F})=0 . \end{aligned}$$

(4)

The energy-momentum tensor is

$$\begin{aligned} T_{\mu \nu }=\mathcal {L}g_{\mu \nu }-F_{\mu \sigma }F_{\nu }^{\sigma } , \end{aligned}$$

(5)

where $\mathcal {L,_F}$ denotes the partial derivative of $\mathcal {L}$ with respect to F.

The gravitational field of a static and spherically symmetric compact object with mass M and a nonlinear electromagnetic source in the Einstein–Born–Infeld theory has first been investigated by Hoffmann [2] and the space-time metric is [2, 50–53]

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left[ 1-\frac{2GM}{r}+\frac{Q^{2}\left( r\right) }{r^{2}}\right] \mathrm{d}t^{2} \nonumber \\&+\left[ 1-\frac{2GM}{r}+\frac{Q^{2}\left( r\right) }{r^{2}}\right] ^{-1}\mathrm{d}r^{2}\nonumber \\&+\,r^{2}\left( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \ \mathrm{d}\varphi ^{2}\right) , \end{aligned}$$

(6)

with the square of the electric charge

$$\begin{aligned} Q^2(r)= & {} \frac{2\beta ^{2}r^{4}}{3}\left( 1-\sqrt{1+\zeta ^2(r)}\right) \nonumber \\&+\frac{4Q^{2}}{3} F\left( \frac{1}{4},\frac{1}{2},\frac{5}{4},-\zeta ^2(r)\right) , \end{aligned}$$

(7)

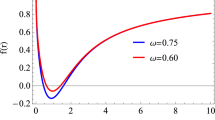
where F is the Gauss hypergeometric function [54] and the new notation $\zeta ^2(r)=Q^2/(\beta ^2 r^4)$ is introduced. From the radial dependence of $Q^2(r)$ plotted in Fig. 1 one can see its strong dependence on the $\beta$ parameter close to the center of the black hole. The rotating counterpart of the Einstein–Born–Infeld black hole has been obtained in [18]. The gravitational field of a rotating Einstein–Born–Infeld black hole space-time is described by the metric which in the Boyer–Lindquist coordinates is given by [18]

$$\begin{aligned} \mathrm{d}s^2= & {} \frac{\Delta - a^2 \sin ^2 \theta }{\rho ^2} \mathrm{d}t^2 - \frac{\rho ^2}{\Delta } \, \mathrm{d}r^2 \nonumber \\&+ \, 2 a \sin ^2 \theta \left( 1 - \frac{\Delta - a^2 \sin ^2 \theta }{\rho ^2} \right) \mathrm{d}t \, \mathrm{d} \phi - \rho ^2 \, \mathrm{d} \theta ^2 \nonumber \\&- \, \sin ^2 \theta \left[ \rho ^2 + a^2 \sin ^2 \theta \left( 2 - \frac{\Delta - a^2 \sin ^2\theta }{\rho ^2}\right) \right] \mathrm{d} \phi ^2 , \nonumber \\ \end{aligned}$$

(8)

with

$$\begin{aligned} \Delta= & {} r^{2}-2GMr+Q^{2}\left( r\right) +a^{2}, \quad \text{ and }\nonumber \\ \rho ^2= & {} r^2+a^2\cos ^2\theta . \end{aligned}$$

(9)

Fig. 1

Plots showing the dependence of the square of the electric charge $Q^2(r)$ on the radial coordinate r for different values of the Born–Infeld parameter $\beta$. The left panel is for $Q=0.5$ and the right panel is for $Q=0.9$ in asymptotics

The parameters a, M, Q, and $\beta$, respectively, correspond to rotation, mass, the electric charge, and the Born–Infeld parameter. We let the parameters Q and $\beta$ be positive. In the limit $\beta \rightarrow \infty$ (or $Q(r)=Q$) and $Q\ne 0$, one obtains the corresponding solution for the Kerr–Newman black hole, while one has a Kerr black hole [16] when $\beta \rightarrow 0$. The metric (8) is a rotating charged black hole which generalizes the standard Kerr–Newman black hole and we call it the rotating Einstein–Born–Infeld black hole. The non-rotating case, $a=0$, corresponds to the metric of the static Einstein–Born–Infeld black hole obtained by Hoffmann in [2]. The metric (8) has a curvature singularity at the set of points where $\rho =0$ and $M=Q\ne 0$. For $a\ne 0$, it corresponds to a ring with radius a, in the equatorial plane $\theta =\pi /2$ and hence is termed a ring singularity. The properties of the rotating Einstein–Born–Infeld metric (8) are similar to that of the general relativity counterpart Kerr–Newman black hole. We first show that it is possible to get a certain range of values of a, M, and Q where the metric (8) is a black hole. The metric (8), like the Kerr–Newman one, is singular at $\Delta =0$, and it admits two horizons like surfaces, viz., the static limit surface and the event horizon. Here, we shall look for these two surfaces for the rotating Einstein–Born–Infeld metric (8) and discuss the effect of the nonlinear parameter $\beta$. The horizons of the Einstein–Born–Infeld black hole (8) are dependent on the parameters M, a, Q, and $\beta$, and they are calculated by equating the $g^{rr}$ component of the metric (8) to zero, i.e.,

$$\begin{aligned} \Delta = r^{2}-2GMr+Q^{2}\left( r\right) +a^{2}=0, \end{aligned}$$

(10)

which depends on Q(r), a function of r, and is different from the Kerr–Newman black hole, where Q is just a constant. The solution Eq. (10) can have either no roots (naked singularity), or two roots (horizons) depending on the values of these parameters. It is difficult to solve Eq. (10) analytically and hence we seek numerical solutions. It is seen that Eq. (10) admits two horizons $r_{EH}^{-}$ and $r_{EH}^{+}$ for a suitable choice of parameters, which corresponds to two positive roots of Eq. (10), with $r_{EH}^{+}$ determining the event horizons and $r_{EH}^{-}$ the Cauchy horizon. Further, it is worthwhile to mention that one can set the parameters so that $r_{EH}^{-}$ and $r_{EH}^{+}$ are equal and we have an extremal black hole. We have plotted the event horizons in Figs. 2 and 3 for different values of mass M, charge Q, parameter $\beta$, and spinning parameter a. Like, the Kerr–Newman black hole, the rotating space-time (8) has two horizons, viz., the Cauchy horizon and the event horizon. The figures reveal that there exist a set of values of parameters for which we have two horizons, i.e., a black hole with both inner and outer horizons. One can also find values of parameters for which one gets an extremal black hole where the two horizons coincide. The region between the static limit surface and the event horizon is termed the quantum ergosphere, where it is possible to enter and leave again, and the object moves in the direction of the spin of the black hole.

Fig. 2

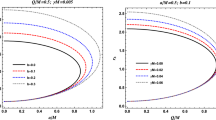
The rotation parameter a dependence of the radial coordinate r for the different values of the electric charge Q and Born–Infeld parameter $\beta$. The lines separate the region of black holes with naked singularity ones. The left panel is for the Born–Infeld parameter $\beta =0.5$ and the right panel is for the Born–Infeld parameter $\beta =0.05$

Fig. 3

The rotation parameter a dependence of the radial coordinate r for the different values of the electric charge Q and Born–Infeld parameter $\beta$. The lines separate the region of black holes with naked singularity ones. The left panel is for the electric charge $Q=0.5$ and the right panel is for the electric charge $Q=0.7$

We have numerically studied the horizon properties for nonzero values of $a,\;\beta$, and Q (cf. Fig. 4) by solving Eq. (10). It turns out that the Born–Infeld parameter $\beta$ has a profound influence on the horizon structure when compared with the Kerr black hole. We find that for given values of the parameters $\beta ,Q$, there exist extremal values of $a=a_{E}$ and $r=r^{E}_{H}$ such that for $a<a_{E}$, Eq. (10) admits two positive roots, which corresponds to, respectively, a black hole with two horizons or a black hole with both Cauchy and event horizons. We found no root at $a>a_{E}$, the case of a ‘naked singularity’, ‘see Fig. 4, i.e., the existence of a naked singularity. Further, one can find values of parameters for which these two horizons coincide and we get extremal black holes. Similarly, we have shown that for given values of the parameters $a,\beta$, we get an extremal value of $Q=Q_E$, for which two horizons coincide and we get extremal black holes as shown in Fig. 4. Interestingly, the value of $Q_E$ decreases with increase in $\beta$.

Fig. 4

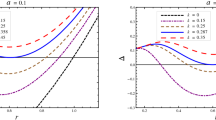
Plots showing the radial dependence of $\Delta$ for the different values of the Born–Infeld parameter $\beta$, electric charge Q, and rotation parameter a (with $M=1$). Top, the left panel is for $a=0.87$ and $\beta =0.05$. Top, the right panel is for $a=0.87$ and $\beta =0.5$. Bottom, the left panel is for $Q=0.5$ and $\beta =0.05$. Bottom, the right panel is for $Q=0.5$ and $\beta =0.5$

Infinite redshift surface or static limit surface While in the case of a rotating black hole, in general, the horizon is also the surface where $g_{tt}$ changes sign, in the rotating Einstein–Born–Infeld case, like the Kerr–Newman case, these surfaces do not coincide. The location of an infinite redshift surface or static limit surface requires the coefficient of $\mathrm{d}{t}^2$ to vanish, i.e., it must satisfy

$$\begin{aligned} r^{2}-2GMr+Q^{2}\left( r\right) +a^{2} \cos ^2(\theta ) = 0. \end{aligned}$$

(11)

Equation (11) is solved numerically for the behavior of the static limit surface, which is shown in Figs. 5 and 6. The Einstein–Born–Infeld metric (8) admits two static limit surfaces $r_{SLS}^{-}$ and $r_{SLS}^{+}$, corresponding to two positive roots of Eq. (11) when the parameters M, Q, a,  and $\beta$ are chosen suitably (cf. Figs. 5, 6). Interestingly the radius of the static limit surface decreases with increase in the value of the parameter $\beta$. The static limit surface shows a similar extremal behavior, which is depicted in Figs. 5 and 6. Like any other rotating black hole, there is a region outside the outer horizon where $g_{tt} > 0$. The region, i.e. $r_{SLS}^{+}< r < r_{EH}^{+}$ is called the ergo-region, and its outer boundary $r = r_{SLS}^{+}$ is called the quantum ergosphere.

Fig. 5

Plots showing the radial dependence of $g_{tt}$ component of metric tensor for the different values of Born–Infeld parameter $\beta$ and electric charge Q (with $M=1$). Top, the left panel is for $\beta =0.05$, $a=0.45$, and $\alpha =\pi /6$. Top, the right panel is for $\beta =0.5$, $a=0.45$, and $\alpha =\pi /6$. Bottom, the left panel is for $\beta =0.05$, $a=0.45$, and $\alpha =\pi /3$. Bottom, right panel is for $\beta =0.5$, $a=0.45$, and $\alpha =\pi /3$

Fig. 6

Plots showing the radial dependence of $g_{tt}$ component of metric tensor for the different values of parameter $\beta$ and rotation parameter a (with $M=1$). Top, the left panel is for $\beta =0.05$, $Q=0.6$, and $\alpha =\pi /6$. Top, right panel is for $\beta =0.5$, $Q=0.6$, and $\alpha =\pi /6$. Bottom, the left panel is for $\beta =0.05$, $Q=0.6$, and $\alpha =\pi /3$. Bottom, the right panel is for $\beta =0.5$, $Q=0.6$ and $\alpha =\pi /3$

Null geodesics in Einstein–Born–Infeld black hole space-time Next, we turn our attention to the study of the geodesic of a photon around Einstein–Born–Infeld black hole. We need to study the separability of the Hamilton–Jacobi equation using the approach due to Carter [55]. First, for generality we consider the motion for a particle with mass $m_{0}$ falling in the background of a rotating Einstein–Born–Infeld black hole. The geodesic motion for this black hole is determined by the following Hamilton–Jacobi equations:

$$\begin{aligned} \frac{\partial S}{\partial \tau } = -\frac{1}{2} g^{\mu \nu } \frac{\partial S}{\partial x^{\mu }} \frac{\partial S}{\partial x^{\nu }}, \end{aligned}$$

(12)

where $\tau$ is an affine parameter along the geodesics, and S is the Jacobi action. For this black hole background the Jacobi action S can be separated as

$$\begin{aligned} S = \frac{1}{2} m_0^2 \tau -Et + L \phi + S_{r}(r) + S_{\theta }(\theta ), \end{aligned}$$

(13)

where $S_{r}$ and $S_{\theta }$ are, respectively, functions of radial coordinate r and angle $\theta$. Like the Kerr space-time, the rotating Born–Infeld black hole also has two Killing vector fields due to the assumption of stationarity and axisymmetry of the space-time, which in turn guarantees the existence of two conserved quantities for a geodesic motion, viz. the energy E and the axial component of the angular momentum L. Thus, the constants $m_0$, E , and L correspond to rest mass, conserved energy, and rotation parameter related through $m_{0}^2= -p_{\mu }p^{\mu }$, $E=-p_{t}$, and $L=p_{\phi }$. Obviously for a photon null geodesic, we have $m_{0}=0$, and from (12) we obtain the null geodesics in the form of the first-order differential equations

$$\begin{aligned} \rho ^2\frac{\mathrm{d}t}{\mathrm{d}\tau }= & {} \frac{r^2+a^2}{\Delta }\left[ (r^2+a^2){E} -a {L} \right] \nonumber \\&+\, a({L} -a{E} \sin ^2 \theta ),\end{aligned}$$

(14)

$$\begin{aligned} \rho ^2\frac{\mathrm{d}\phi }{\mathrm{d}\tau }= & {} \frac{a}{\Delta }\left[ (r^2+a^2){E} -a {L} \right] \nonumber \\&+\,\left( \frac{L}{\sin ^2 \theta } -a {E}\right) , \end{aligned}$$

(15)

$$\begin{aligned} \rho ^2\frac{\mathrm{d}r}{\mathrm{d}\tau }= & {} \sqrt{\mathcal {R}}, \end{aligned}$$

(16)

$$\begin{aligned} \rho ^2\frac{\mathrm{d}\theta }{\mathrm{d}\tau }= & {} \sqrt{\Theta }, \end{aligned}$$

(17)

where the functions $\mathcal {R}(r)$ and $\Theta (\theta )$ are defined as

$$\begin{aligned} \mathcal {R}= & {} \left[ (r^2+a^2){E} -a {L} \right] ^2-\Delta \left( \mathcal {K}+({L} - a {E})^2 \right) , \ \nonumber \\ \Theta= & {} \mathcal {K}+\cos ^2\theta \left( a^2 {E}^2 -\frac{{L} ^{2}}{\sin ^2\theta }\right) . \end{aligned}$$

(18)

Thus, we find that Hamilton–Jacobi equation (12), using (13), is separable due to the existence of $\mathcal {K}$, namely the Carter constant of separation. The above equations govern the propagation of light in the Einstein–Born–Infeld black hole background. In fact, for $Q = 0$, they are just the null geodesic equations for the Kerr black hole. The constant $K=0$ is the necessary and sufficient condition for motion of the particles initially in the equatorial plane to remain there. Any particle which crosses the equatorial plane has $K>0$.

Effective potential The discussion of effective potential is a useful tool for describing the motion of test particles around Einstein–Born–Infeld black hole. Further, we have to study the radial motion of a photon for determining the black hole shadow boundary. The radial equation for timelike particles moving along the geodesic in the equatorial plane ($\theta =\pi /2$) is described by

$$\begin{aligned} \frac{1}{2} \dot{r}^2 + V_\mathrm{eff} = 0, \end{aligned}$$

(19)

with the effective potential

$$\begin{aligned} V_\mathrm{eff} = -\frac{[E (r^2 + a^2) -La]^2 -\Delta (L-a E)^2}{2 r^4}\ . \end{aligned}$$

(20)

From the last expression (20) one easily get the plots presented in Figs. 7 and 8. There we have considered motion of the photon around an Einstein–Born–Infeld black hole for the different values of the electric charge Q and Born–Infeld parameter $\beta$. It is shown that with increasing electric charge Q or rotating parameter a the particle is getting closer to the central object.

Fig. 7

The radial dependence of effective potential $V_\mathrm{eff}$ for the photon for the different values of electric charge Q. The left panel is for $\beta =0.05$ and $a=0.5$; the right one is for $\beta =0.5$ and $a=0.5$

Fig. 8

The radial dependence of effective potential $V_\mathrm{eff}$ for the photon for the different values of rotation parameter a. The left panel is for $\beta =0.05$ and $Q=0.6$; the right one is for $\beta =0.5$ and $Q=0.6$

3 Shadow of Einstein–Born–Infeld black hole

Now, it is a general belief that a black hole, if it is in front of a bright background produced by a far-away radiating object, will cast a shadow. The apparent shape of a black hole silhouette is defined by the boundary of the black and it was first studied by Bardeen [56]. The ability of very long baseline interferometry (VLBI) observation has been improved significantly at short wavelengths, which led to the strong expectation that within a few years it may be possible to observe by a direct image with a high resolution the accretion flow around a black hole corresponding to a black hole event horizon [57, 58]. This may allow us to test gravity in the strong field regime and investigate the properties of black hole candidates. The VLBI experiments also look for the shadow of a black hole, i.e. a dark area in front of a luminous background [56, 59]. Hence, their is a significant effort to study black hole shadows and this has become a quite active research field [31–48] (for a review, see [60]). For the Schwarzschild black hole the shadow of the black hole is a perfect circle [60], and it is enlarged in the case of a Reissner–Nordstr$\ddot{o}$m black hole [61]. Here, we plan to discuss the shadow of the Einstein–Born–Infeld black hole, and we shall confine our discussion to the both static and rotating cases. It is possible to study equatorial orbits of a photon around a Einstein–Born–Infeld black hole via the effective potential. It is generally known that the photon orbits are of three types: scattering, falling, and unstable [62, 63]. The falling orbits are due to the photons arriving from infinity that cross the horizon and fall down into the black hole, they have more energy than the barrier of the effective potential. The photons arriving from infinity move along the scattering orbits and come back to infinity, and with energy less than the barrier of the effective potential. Finally, the maximum value of the effective potential separates the captured and the scattering orbits and defines unstable orbits of constant radius (it is a circle located at $r=3M$ for the Schwarzschild black hole) which is responsible for the apparent silhouette of a black hole. A distant observer will be able to see only the photons scattered away from the black hole, while those captured by the black hole will form a dark region. If the black hole appears between a light source and a distant observer, the photons with small impact parameters fall into the black hole and form a dark zone in the sky which is usually termed a black hole shadow. We consider the following series expansion:

$$\begin{aligned} \frac{4Q^{2}}{3} F\left( \frac{1}{4},\frac{1}{2},\frac{5}{4},-\zeta ^2(r) \right)\approx & {} \frac{4Q^2}{3} \left( 1- \frac{\zeta ^2(r)}{10}\right) \nonumber \\&+\, \mathcal {O}\left( \frac{1}{\beta ^4}\right) . \end{aligned}$$

(21)

Also, all the higher order terms from now onwards are dropped from the series expansion of $F\left( \frac{1}{4},\frac{1}{2},\frac{5}{4},-\zeta ^2(r)\right)$, which yields

$$\begin{aligned} Q^2(r)\approx & {} \frac{2\beta ^{2}r^{4}}{3}\left( 1-\sqrt{1+\zeta ^2(r)}\right) + \frac{4Q^2}{3} \left( 1- \frac{\zeta ^2(r)}{10}\right) \nonumber \\&+ \,\mathcal {O}\left( \frac{1}{\beta ^4}\right) , \end{aligned}$$

(22)

and accordingly $\Delta$ is also modified and we denote the new $\Delta$ as $\Delta '$:

$$\begin{aligned} \Delta ^{\prime }= & {} -2+\frac{8Q^2 \zeta ^2(r)}{15 r}+\frac{4Q^2}{3r \sqrt{1+\zeta ^2(r)}} \nonumber \\&+\,2r-\frac{8\beta ^2 r^3}{3}\left( -1+\sqrt{1+\zeta ^2(r)}\right) . \end{aligned}$$

(23)

Henceforth, all our calculations are valid up to $\mathcal {O}(\frac{1}{\beta ^4})$ only. The effective potential for the photon attains a maximum, goes to negative infinity beneath the horizon, and asymptotically goes to zero at $r \rightarrow \infty$. In the standard Schwarzschild black hole, the maximum of the effective potential occurs at $r=3M$, which is also the location of the unstable orbit, having no minimum. The behavior of the effective potential as a function of the radial coordinate r for different values of the parameter $\beta$, rotation parameter a, and Q are depicted in Figs. 7 and 8. It is observed that the potential has a minimum, which implies the presence of stable circular orbits. The apparent shape of the black hole is obtained by observing the closed orbits around the black hole governed by three impact parameters, which are functions of E, $L_{\phi }$, and $L_{\psi }$ and the constant of separability $\mathcal{K}$. The equations determining the unstable photon orbits, to be used in order to obtain the boundary of shadow of the black holes, are Eq. (18) or

$$\begin{aligned} R(r)=0=\partial R(r)/\partial r, \end{aligned}$$

which are fulfilled by the values of the impact parameters

$$\begin{aligned} \xi = \frac{(r^2+a^2) \Delta ^{\prime }-4 r \Delta }{\Delta ^{\prime } a} \end{aligned}$$

(24)

and

$$\begin{aligned} \eta = \frac{16\Delta r^2 a^2-\left( (r^2+a^2) \Delta ^{\prime }-4 r \Delta -a \Delta ^{\prime }\right) }{(\Delta ^{\prime } a)^2}, \end{aligned}$$

(25)

which determine the contour of the shadow, whereas the parameters $\xi$ and $\eta$ satisfy

$$\begin{aligned}&\xi ^2+\eta \nonumber \\&\quad =\frac{4 A \Big (\frac{8Q^2 r_{0} \zeta ^2(r_{0})}{15}-\frac{8Q^2 r_{0}}{3}+\frac{2Q^2 r_{0}}{3 \sqrt{1+\zeta ^2(r_{0})}}+3r_{0}^2-r_{0}^3\Big )}{-1+\frac{4 Q^2 \zeta ^2(r_{0})}{15r_{0}}+\frac{2Q^2}{3r_{0} \sqrt{1+\zeta ^2(r_{0})}}+r_{0}-\frac{4}{3} \beta ^2 r_{0}^3\left( -1+\sqrt{1+\zeta ^2(r_{0})}\right) } \nonumber \\&\qquad + \frac{60 \beta ^2 r_{0}^4 B}{C} +O(a^2) \end{aligned}$$

(26)

with

$$\begin{aligned} A= & {} -1+\frac{4Q^2 \zeta ^2(r_{0})}{15 r_{0}}+\frac{2Q^2}{3r_{0} \sqrt{1+\zeta ^2(r_{0})}} \nonumber \\&-\,r_{0}-\frac{4}{3} \beta ^2 r_{0}^3\left( -1+\sqrt{1+\zeta ^2(r_{0})}\right) , \end{aligned}$$

(27)

$$\begin{aligned} B= & {} 6 Q^6 -14 \beta ^2 Q^4 r_{0}^4+15 \beta ^2 Q^2 r_{0}^5 - 10 \beta ^4 Q^2 r_{0}^{8}\nonumber \\&+15 \beta ^4 r_{0}^{9} +10 \beta ^6 r_{0}^{12}-10 \beta ^6 r_{0}^{12} \sqrt{1+\zeta ^2(r_{0})}, \end{aligned}$$

(28)

$$\begin{aligned} C= & {} 4 \beta Q^4\sqrt{1+\zeta ^2(r_{0})}+ 20 \beta ^5 r_{0}^8\left( -1+\sqrt{1+\zeta ^2(r_{0})}\right) \nonumber \\&-\,5\beta ^3 r_{0}^4 \Big (2Q^2-3r_{0}(r_{0}-1) \sqrt{1+\zeta ^2(r_{0})}\Big )^2. \end{aligned}$$

(29)

The shadow of the Einstein–Born–Infeld black holes may be determined by virtue of the above equation. In order to study the shadow of the Einstein–Born–Infeld black hole, it is necessary to introduce the celestial coordinates according to [64]:

$$\begin{aligned}&\lambda =\lim _{r_{0}\rightarrow \infty }\left( -r_{0}^{2}\sin \theta _{0}\frac{\mathrm{d}\phi }{\mathrm{d}r}\right) ,\end{aligned}$$

(30)

$$\begin{aligned}&\mu =\lim _{r_{0}\rightarrow \infty }r_{0}^{2}\frac{\mathrm{d}\theta }{\mathrm{d}r} . \end{aligned}$$

(31)

The celestial coordinates can be rewritten as

$$\begin{aligned} \lambda =-\xi \csc \theta _{0} \end{aligned}$$

(32)

and

$$\begin{aligned} \mu =\pm \sqrt{\eta + a^2 \cos ^{2}\theta _{0}-\xi \cot ^{2}\theta _{0}}, \end{aligned}$$

(33)

and they formally coincide with the case of tte Kerr black hole. However, in reality $\xi$ and $\eta$ are different for the Einstein–Born–Infeld black hole. The celestial coordinate in the equatorial plane ($\theta _0=\pi /2$), where the observer is located, becomes

$$\begin{aligned} \lambda =-\xi \end{aligned}$$

(34)

and

$$\begin{aligned} \mu =\pm \sqrt{\eta } . \end{aligned}$$

(35)

The apparent shape of the Einstein–Born–Infeld black hole shadow can be obtained by plotting $\lambda$ vs. $\mu$ as

$$\begin{aligned} \lambda ^2+\mu ^2=\xi ^2+\eta , \end{aligned}$$

(36)

which suggests that the shadow of Einstein–Born–Infeld black holes in the ($\lambda ,\mu$) space is a circle with radius of the quantity defined by the right hand side of Eq. (26). Thus, the shadow of the black hole depends both on the electric charge Q and the Born–Infeld parameter $\beta$. Figures 9 and 10 are for the different values of these parameters.

Fig. 9

Shadow of the black hole for the different values of the electric charge Q. Top, the left panel is for the Born–Infeld parameter $\beta =0.01$. Top, the right panel is for the Born–Infeld parameter $\beta =0.1$. Bottom, the left panel is for the Born–Infeld parameter $\beta =1$. Bottom, the right panel is for the Born–Infeld parameter $\beta =10$ (with $M=1$ and $a=0$)

Fig. 10

Shadow of the black hole for the different values of the Born–Infeld parameter $\beta$. Top, the left panel is for electric charge $Q=0.3$. Top, the right panel is for the electric charge $Q=0.5$. Bottom, the left panel is for the electric charge $Q=0.7$. Bottom, the right panel is for the electric charge $Q=0.9$ (with $M=1$ and $a=0$)

In the limit, $\beta \rightarrow \infty$, the above expression reduces to

$$\begin{aligned} \xi ^2+\eta= & {} \lambda ^2+\mu ^2= \frac{2 r_{0}^2 (r_{0}^{2}-3)+4 r_{0} Q^2}{(r_{0}-1)^2}, \end{aligned}$$

(37)

which is the same as that for the Reissner–Nordstrom black hole. In addition, if we switch off the electric charge $Q=0$, one gets the expression for the Schwarzschild case, which reads

$$\begin{aligned} \xi ^2+\eta= & {} \lambda ^2+\mu ^2=\frac{2 r_{0}^2 (r_{0}^{2}-3)}{(r_{0}-1)^2} . \end{aligned}$$

(38)

In order to extract more detailed information from the shadow of the Einstein–Born–Infeld black holes, we must address the observables. In general, there are two observable parameters: the radius of the shadow, $R_{s}$, and the distortion parameter, $\delta _{s}$ [65]. For a non-rotating black hole there is only single parameter, $R_{s}$, which corresponds to the radius of the reference circle. From Figs. 9 and 10 one can get a numerical value for the radius of black hole shadow which is clearly shown in Fig. 11. As is shown from the Figs. 12 and 13, the shadow of the rotating Einstein–Born–Infeld black hole has been considered for various values of electric charge Q and Born–Infeld parameter $\beta$. The influence of the rotating parameter a on the shadow of black hole is distorted, while with increasing electric charge of the black hole the shadow becomes a circle. One of the observable parameters is the distortion parameter of the black hole’s shadow. The observable distortion parameter is shown for different values of the rotating parameter, electric charge, and Born–Infeld parameter in Fig. 14.

Fig. 11

The dependence of observable radius of black hole shadow $R_{s}$ from the electric charge Q and Born–Infeld parameter $\beta$. The left panel shows graphs for the different values of the Born–Infeld parameter $\beta$. The right panel shows graphs for the different values of the electric charge Q

Fig. 12

Shadow of rotating black hole for the different values of the Born–Infeld parameter $\beta$, rotating parameters a, and electric charge Q. Solid line is $Q=0$ and dashed line is $Q=0.5$ (with $M=1$)

Fig. 13

Shadow of rotating black hole for the different values of the Born–Infeld parameter $\beta$, rotating parameters a, and electric charge Q. Solid line is $Q=0$ and dashed line is $Q=0.5$ (with $M=1$)

Fig. 14

The dependence of observable distortion parameter of black hole shadow $\delta _{s}$ from the electric charge Q, Born–Infeld parameter $\beta$, and rotation parameter $a=0.9$. The right panel shows graphs for the different values of Born–Infeld parameter $\beta$ and the left panel shows graphs for the different values of the electric charge Q

At high energies the absorption cross section of a black hole shows a variation around a limiting constant value and for the distant observer placed at infinity the black hole shadow is responsible to its high energy absorption cross section. For a black hole having a photon sphere, the limiting constant value coincides with the geometrical cross section of the photon sphere [66].

4 Emission energy of rotating Einstein–Born–Infeld black holes

For completeness, here we investigate the rate of energy emission from the Einstein–Born–Infeld black hole with the help of

$$\begin{aligned} \frac{\mathrm{d}^2E(\omega )}{\mathrm{d}\omega \mathrm{d}t}= \frac{2 \pi ^2 \sigma _\mathrm{lim}}{\exp {\omega /T}-1}\omega ^3 , \end{aligned}$$

(39)

where $T=\kappa /2\pi$ is the Hawking temperature, and $\kappa$ is the surface gravity. At the outer horizon the temperature T is equal to

$$\begin{aligned} T= & {} \frac{2Q^4\sqrt{1+\zeta ^2(r_{+})} -2 \beta ^2 Q^2 r_{+}^4\left( 1+2 \sqrt{1+\zeta ^2(r_{+})}\right) }{12\beta ^2 \pi r_{+}^5(a^2+r_{+}^2)\sqrt{1+\zeta ^2(r_{+})} }\nonumber \\&+ \,\frac{3r_{+}^4 \beta ^2 D}{12\beta ^2 \pi r_{+}^5(a^2+r_{+}^2)\sqrt{1+\zeta ^2(r_{+})} } , \end{aligned}$$

(40)

where

$$\begin{aligned} D= & {} -a^2 \sqrt{1+\zeta ^2(r_{+})} \nonumber \\&+\,r_{+}^2\left( \sqrt{1+\zeta ^2(r_{+})}+2\beta ^2 r_{+}^2\big (\sqrt{1+\zeta ^2(r_{+})}-1\big )\right) .\nonumber \\ \end{aligned}$$

(41)

The limiting constant $\sigma _\mathrm{lim}$ defines the value of the absorption cross section vibration for a spherically symmetric black hole:

$$\begin{aligned} \sigma _\mathrm{lim} \approx \pi R_s^2 . \end{aligned}$$

(42)

Consequently according to [67] we have

$$\begin{aligned} \frac{\mathrm{d}^2E(\omega )}{\mathrm{d}\omega \mathrm{d}t}=\frac{2\pi ^3 R_s^2}{e^{\omega /T}-1}\omega ^3 . \end{aligned}$$

The dependence of energy emission rate from frequency for the different values of electric charge Q and parameter $\beta$ is shown in Fig. 15. One can see that with increasing electric charge Q or parameter $\beta$ the maximum value of the energy emission rate decreases, caused by a decrease of the area of the horizon.

Fig. 15

Energy emission of black hole in Einstein–Born–Infeld gravity. The left panel is for the electric charge $Q=0.5$ and the right panel is for the Born–Infeld parameter $\beta =0.05$

5 Conclusion

In recent years the Born–Infeld action has received significant attention due to the development of superstring theory, where it has been demonstrated to naturally arise in string-generated corrections when one considers an open superstring. This leads to interest in extending the Reissner–Nordstrom black hole solutions in Einstein–Maxwell theory to the charged black hole solution in Einstein–Born–Infeld theory [6]. In view of this, we have investigated the horizon structure of the charged rotating black hole solution in Einstein–Born–Infeld theory, and explicitly we discuss the effect of the Born–Infeld parameter $\beta$ on the event horizon and the optical properties of black hole as well. Further, this rotating Einstein–Born–Infeld black hole solution generalizes both the Reissner–Nordstrom ($\beta \rightarrow \infty$ and $a=0$) and the Kerr–Newman solutions ($\beta \rightarrow \infty$). Interestingly, it turns out that for given values of parameters {$M,Q, \beta$}, there exists $a=a_E$ for which the solution (8) might be an extremal black hole, which decreases with increase of the parameter $\beta$. Further, we have also analyzed infinite redshift surfaces, ergo-regions, energy emission, and Hawking temperature of the rotating Einstein–Born–Infeld black hole. The Einstein–Born–Infeld black hole’s horizon structure has been studied for different values of the electric charge Q and the Born–Infeld parameter $\beta$, which explicitly demonstrates that the outer (inner) horizon radius decreases (increases) with the increase with the electric charge Q and Born–Infeld parameter $\beta$. We have done our calculations numerically as it is difficult to solve the analytical solution and found that the obtained results are different from the Kerr–Newman case due to the nonzero Born–Infeld parameter $\beta$.

It is well known that a black hole can cast a shadow as an optical appearance due to its strong gravitational field. Using the gravitational lensing effect, we have also investigated the shadow cast by the non-rotating ($a=0$) and rotating ($a\ne 0$) Einstein–Born–Infeld black hole and demonstrated that the null geodesic equations can be integrated, which allows us to investigate the shadow cast by a black hole which is found to be a dark zone covered by a circle. The shadow is slightly smaller and less deformed than that for its Reissner–Nordstrom counterpart. In addition, the Born–Infeld parameter $\beta$ also changes the shape of the black hole’s shadow. In the case of the non-rotating black hole considered only the radius of the shadow is an observable parameter; it is obtained by numerical calculation. On the other hand, the influence of the rotating parameter a on the shadow’s shape of the black hole is distorted, while with increasing electric charge of the black hole the shadow becomes a circle. The observable distortion parameter is a most important feature for comparing with observations. From our results, with increasing electric charge distortion parameter the black hole’s shadow circle becomes a pure circle, and on the other hand with increasing Born–Infeld parameter the circle of the shadow will be more distorted.

The effective potential for geodesic motion of the photon around the rotating Einstein–Born–Infeld black hole has been studied for different values of the electric charge and spin parameter of the black hole. With increasing either the rotation parameter or the electric charge of the black hole, a particle is moving closer to the central object. Hence, the circular orbit of the photon becomes closer to the center of the rotating Einstein–Born–Infeld black hole.

It will be of interest to discuss energy extraction from the rotating Einstein–Born–Infeld black hole, as the ergo-region is influenced by the Born–Infeld parameter and hence it may enhance the efficiency of the Penrose process. This and related work are the subjects of forthcoming papers. Finally, in particular our results in the limit $\beta \rightarrow \infty$ reduced exactly to the Kerr–Newman black hole, and to the Kerr black hole when $Q(r)=0$.