1 Introduction

It is well known that inflation presents most compelling solution of many problems of big bang model, namely the horizon, the flatness, the homogeneity, and the monopole problems [1, 2]. The most fascinating feature of the inflationary universe model is that it interprets the origin of the observed anisotropy in the cosmic microwave background radiations, and also the distribution of large scale structures [3]. But some questions arise in the theory of inflation, one of them being how to end this inflationary epoch and enter in the big bang phase. Warm inflation provides a possible solution to this problem. Standard inflation, known as cold inflation, has two regimes: slow roll and reheating. In the slow-roll limits, the universe expands as potential energy dominates the kinetic energy and the interaction of inflation (scalar field) with other fields become negligible. In the reheating epoch, kinetic energy is comparable to potential energy and inflation oscillates around the minimum of its potential, while losing its energy to massless particles. After reheating, the universe is filled with radiation.

Warm inflation provides a mechanism in which reheating is avoided. During the warm inflationary period, dissipative effects are important, so that radiation production takes place at the same time as inflationary expansion. The strong regime in warm inflation is that in which damping effects on inflation dynamics of the radiation field are strong, these dissipating effects originates from a friction term which describe the physical process of decay of inflation field into a thermal bath due to its interaction with other field. Decay of remaining inflationary field or dominant radiation create the mater component of universe. Warm inflation comes to an end when the universe heats up to become radiation dominated and gets connected with the big bang scenario [4, 5]. In standard inflation density perturbations are generated due to quantum fluctuations associated to the inflation scalar field, which are necessary for the large scale structure formation at the late time in the evolution of the universe [6]. However, in warm inflation, thermal fluctuations instead of quantum fluctuations become a source of density perturbations [7, 8].

Monerat et al. [9] studied the cosmology of the early universe and the initial condition for inflation in a model with radiation and Chaplygin gas (CG). Antonella et al. [10] discussed warm inflation on the brane. Del campo and Herrera [11] considered a warm inflationary model with the generalized Chaplygin gas (GCG), and they used a standard scalar field and dissipation coefficient of the form \(\Gamma \propto \phi ^{n}\) and then developed a model with a chaotic potential. Setare and Kamali investigated warm tachyon inflation by assuming intermediate [12] and a logamediate scenario [13]. Bastero-Gill et al. obtained the expressions for the dissipation coefficient in supersymmetric (SUSY) models in [14]. This result provides possibilities for the realization of warm inflation in SUSY field theories.

Herrera et al. [15] studied intermediate inflation in the context of GCG using standard and tachyon scalar fields. The same authors dealt with the dissipation coefficient \(\Gamma =c\frac{T^{m}}{\phi ^{m-1}}\) in the context of warm intermediate and logamediate inflationary models [16]. They also studied warm inflation in loop quantum cosmology with the same dissipative coefficient [17]. Bastero-Gill et al. in [18] have also explored inflation by assuming the quartic potential. Sharif and Saleem [19] studied inflationary models with a generalized cosmic Chaplygin gas (GCCG). Setare and Kamali analyzed warm viscous inflation on the brane in [5]. They have also considered a generalized de Sitter scale factor including a single scalar field and studied q-inflation in the context of warm inflation with two forms of damping term [20]. Panotopoulos and Videla [21] investigated the quartic potential model in the framework of warm inflation by using a decay rate proportional to the temperature and showed that it is compatible with the latest observational data. We extend this work with the inclusion of Chaplygin gas (CG) models.

The goal of the present work is to investigate the realization of a warm quartic inflationary model in the context of CG models. This paper is organized as follows: the next section deals with the basic background equations of a warm inflationary scenario. In Sect. 3, we construct models with GCG, MCG, and GCCG by using a quartic potential. In the last section, we summarize our results.

2 Basic inflationary scenario

We start by using the Friedmann–Robertson–Walker (FRW) metric and consider a spatially flat universe which contains a self interacting inflation field \(\phi \) and radiation field, where \(V(\phi )\) is the scalar potential, \(\rho _{\phi }\) and \(\rho _{\gamma }\) are the energy densities of inflation field and radiation field, respectively; then we write down a modified Friedmann equation of the form

(1)

where \(M_{p}=\frac{1}{\sqrt{8\pi G}}\) is the reduced Planck mass, and \(\rho _{\phi }=\frac{\dot{\phi }^{2}}{2}+V(\phi )\) and \(P_{\phi }=\frac{\dot{\phi }^{2}}{2}-V(\phi )\) are the energy densities and potential of the scalar field, respectively. Energy-momentum conservation leads to the following equations [4, 5]:

$$\begin{aligned} \dot{\rho _{\phi }}+3H(\rho _{\phi }+P_{\phi })= - \Gamma \dot{\phi }^{2},\quad \dot{\rho _{\gamma }}+4H(\rho _{\gamma })= \Gamma \dot{\phi }^{2}.\nonumber \\ \end{aligned}$$
(2)

The dynamics of warm inflation is described by adding a friction term in the equation of motion given by

$$\begin{aligned} \ddot{\phi }+(3H+\Gamma )\dot{\phi }+V'=0, \end{aligned}$$
(3)

\(\Gamma \) is the dissipation coefficient. During the inflation era, \(\Gamma \) is responsible for the decay of the scalar field into radiation, this decay rate can be a function of the scalar field or temperature or depends on both \(\Gamma (T,\phi )\) or simply is a constant. During warm inflation the production of radiation is quasi-stable, i.e. \(\dot{\rho _{\gamma }}\ll 4H\rho _{\gamma }\) and \(\dot{\rho _{\gamma }}\ll \Gamma \dot{\phi }^{2}\) [4, 5, 7, 22–24], the energy density associated with scalar field dominates over the energy density of radiation field, i.e. \(\rho _{\phi }\gg \rho _{\gamma }\). Assuming the set of slow-roll conditions, i.e. \( \dot{\phi }^{2}\ll V(\phi )\) and \(\ddot{\phi }\ll (3H+\Gamma )\dot{\phi }\) [4, 5], then the equations of motion reduces to

$$\begin{aligned} 3H(1+R)\dot{\phi }\simeq -V',\quad 4H\rho _{\gamma }\simeq \Gamma \dot{\phi }^{2}, \end{aligned}$$
(4)

here a dot means derivative with respect to time and \( V'=\frac{\partial V}{\partial \phi } \). The dissipation coefficient is a basic quantity, which has been calculated from first principles in the context of supersymmetry. In these models, there is a scalar field with multiplets of heavy and light fields that makes it possible to obtain several expression for the dissipation coefficient. The general form for \(\Gamma \) can be written as [25, 26]

$$\begin{aligned} \Gamma =b\frac{T^{m}}{\phi ^{m-1}}, \end{aligned}$$

where b is associated to dissipative microscopic dynamics and exponent m is integer. In the literature different cases have been studied for the different values of m, in the special case \(m=1\), i.e. \(\Gamma \propto T\) represents the high temperature SUSY case, for the value \(m=0\) i.e. \(\Gamma \propto \phi \) corresponds to an exponentially decaying propagator in the high temperature SUSY model; for \(m=-1\) i.e. \(\Gamma \propto \frac{\phi ^{2}}{T}\), we have agreement with the non-SUSY case [27, 28]. We introduce the parameter \(R = \frac{\Gamma }{3H}\), which is the relative strength of thermal damping compared to the expansion damping. In warm inflation, we can assume two possible scenarios; one is the weak dissipative regime defined as \(R \ll 1\), in which Hubble damping is still the dominant term, and the other one is the strong dissipative regime defined as \(R \gg 1\), and \(\Gamma \) controls the damped evolution of the inflation field in it.

Moreover, the thermalization energy density of the radiation field can be written as \(\rho _{\gamma }=CT^{4}\), where we have the constant \(C=\pi ^{2}g_{*}/30\), and \(g_{*}\) denotes the number of relativistic degrees of freedom; in a Minimal Supersymmetric Standard Model (MSSM), \(g_{*}=228.75\) and \(C\simeq 70\) [7]. Using Eq. (4) and \(\rho _{\gamma }\propto T^{4}\) the temperature becomes

$$\begin{aligned} T=\bigg [\frac{\Gamma V'^{2}}{6^{2}CH^{3}(1+R)^{2}}\bigg ]^{\frac{1}{4}}. \end{aligned}$$
(5)

The slow-roll parameters of warm inflation are given by [7]

$$\begin{aligned} \epsilon = \frac{-\dot{H}}{H^{2}},\quad \eta =\frac{-\ddot{H}}{H\dot{H}},\quad \beta =-\frac{1}{H}\frac{\mathrm{d}}{\mathrm{d}t}(ln\Gamma ). \end{aligned}$$

In warm inflation, the slow-roll conditions are expressed as \(\epsilon \ll 1+R\), \(\eta \ll 1+R\), \(\beta \ll 1+R\). On the other hand, the number of e-folds is calculated by using the standard formula

$$\begin{aligned} N=\int _{t_{*}}^{t_\mathrm{end}}H \mathrm{d}t. \end{aligned}$$
(6)

Here, \(t_{*}\) and \(t_\mathrm{end}\) denote the time when inflation starts and comes to an end, respectively.

Next, we discuss the perturbation parameters for the current scenario by assuming CG models. The perturbation parameters of the warm inflation are obtained in [7]. The amplitude of the power spectrum of the curvature perturbation is given by

$$\begin{aligned} P_{R}=\bigg (\frac{\pi }{4}\bigg )^{\frac{1}{2}}\frac{H^{\frac{5}{2}}\Gamma ^{\frac{1}{2}}T}{\dot{\phi }^{2}}, \end{aligned}$$
(7)

and we can calculate the scalar spectral index \(n_{s}\) by using \(n_{s} = 1+\frac{dP_{R}}{dlnk}\), which is equivalent to

$$\begin{aligned} n_{s}=1-\frac{9\epsilon }{4}+\frac{3\eta }{2}-\frac{9\beta }{4}. \end{aligned}$$
(8)

However, the tensor-to-scalar ratio turns out to be [20]

$$\begin{aligned} r=\frac{32G\dot{\phi }^{2}}{\Gamma ^{\frac{1}{2}}\pi ^{\frac{3}{2}}TH^{\frac{1}{2}}}. \end{aligned}$$
(9)

In the following, we take a standard scalar field and \(\Gamma \propto T\) to study how these conditions affect the inflationary dynamics for a quartic potential.

3 Chaplygin inflationary models with quartic potential

We consider a quartic potential, \(V(\phi )=\frac{\lambda _{*}\phi ^{4}}{4}\), which is a simple Higgs potential as developed in particle physics theories [29]. In the following work, we assume an inflation decay rate \(\Gamma =bT\) and a quartic potential in warm inflation models with a Chaplygin gas.

3.1 Generalized Chaplygin gas

The CG is considered to be an alternative description of accelerating expansion and it has a connection with string theory. CG emerges as an effective fluid of generalized D-branes in a \((d+1,1)\) space time where the action can be written as a generalized Born–Infield action [30]. Kammshchick [31] considered the FRW universe composed of CG and showed that the universe is in agreement with current observations of cosmic acceleration. Its extended form is GCG, whose equation of state (EoS) is as follows:

$$\begin{aligned} P_{gcg}= - \frac{A}{\rho _{gcg}^{\lambda }} , \end{aligned}$$

where \(P_{gcg}\) and \(\rho _{gcg}\) denote the pressure and energy density, respectively, and \(0<\lambda \le 1\), and A is the positive constant. The energy density of GCG can be obtained by using equation of continuity and given by

$$\begin{aligned} \rho _{gcg}=\bigg (A+\frac{B}{a^{3(1+\lambda )}}\bigg )^{\frac{1}{1+\lambda }} , \end{aligned}$$
(10)

where B is a positive integration constant and a is a scale factor. We start with the modified Friedmann equation of the form

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}}\bigg (\bigg (A+\rho _{\phi }^{1+\lambda }\bigg )^{\frac{1}{1+\lambda }}+\rho _{\gamma }\bigg ). \end{aligned}$$
(11)

This modification is possible due to an extrapolation of Eq. (10) so that

$$\begin{aligned} \rho _{gcg}=\bigg (A+\rho _{m}^{1+\lambda }\bigg )^{\frac{1}{1+\lambda }} \rightarrow \bigg (A+\rho _{\phi }^{1+\lambda }\bigg )^{\frac{1}{1+\lambda }}, \end{aligned}$$
(12)

where \(\rho _{m}\) denotes the matter energy density. During the inflation era, the energy density of the scalar field dominates the energy density of the radiation field, i.e., \( \rho _{\phi }\gg \rho _{\gamma }\), and it is of the order of the potential i.e. \(\rho _{\phi }\sim V\). For simplicity, we take \(\lambda =1\), for which the Friedmann equation takes the form

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}}\sqrt{A+\rho _{\phi }^{2}} \sim \frac{1}{3M_{p}^{2}}\sqrt{A+V^{2}}. \end{aligned}$$
(13)

3.1.1 Weak dissipative regime

Here, we consider the weak dissipative regime where \(R \ll 1\); the Friedmann and Klein–Gordon equations take the standard form in the slow-roll approximation. By taking \(\Gamma =bT\), the temperature of the radiation field becomes

$$\begin{aligned} T=\bigg (\frac{bV'^{2}}{6^{2}CH^{3}}\bigg )^{\frac{1}{3}}. \end{aligned}$$

For a weak dissipative regime, the slow-roll parameters are as follows:

$$\begin{aligned}&\epsilon =\frac{M_{p}^{2}VV'^{2}}{2(A+V^{2})^{\frac{3}{2}}},\quad \\&\eta =\frac{M_{p}^{2}}{(A+V^{2})^{\frac{1}{2}}}\bigg (V''+\frac{V'^{2}}{V} -\frac{3VV'^{2}}{2(A+V^{2})}\bigg ) ,\\&\beta =M_{p}^{2}\bigg (\frac{4V''(A+V^{2})-3V'^{2}V}{6(A+V^{2})^{\frac{3}{2}}}\bigg ). \end{aligned}$$

By using Eq. (6), the number of e-folds becomes

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{\sqrt{A+V^{2}}}{V'}d\phi . \end{aligned}$$

The amplitude of the power spectrum given in Eq. (7) takes the form

$$\begin{aligned} P_{R}= & {} \bigg (\frac{81\pi b^{2}}{12^{2}CV'^{2}}\bigg )^{\frac{1}{2}} \bigg (\frac{\sqrt{A+V^{2}}}{3M_{p}^{2}}\bigg )^{\frac{3}{2}} . \end{aligned}$$
(14)

By inserting the values in Eq. (8), the scalar spectral index turns out to be

$$\begin{aligned} n_{s}-1= & {} \frac{3M_{p}^{2}}{2(A+V^{2})^{\frac{1}{2}}}\bigg (\frac{-9VV'^{2}}{4(A+V^{2})}\nonumber \\&-\frac{3}{2}\bigg (\frac{4V''(A+V^{2})-3V'^{2}V}{6(A+V^{2})}\bigg )+V''+\frac{V'^{2}}{V} \bigg ).\nonumber \\ \end{aligned}$$
(15)

The tensor-to-scalar ratio given in Eq. (9) becomes

$$\begin{aligned} r=\frac{192G\sqrt{3CM_{p}^{2}}V'}{9b\pi ^{\frac{3}{2}}(A+V^{2})^{\frac{1}{4}}}. \end{aligned}$$
(16)

We use \(V=\frac{\lambda _{*}\phi ^{4}}{4}\) and \(V'=\lambda _{*}\phi ^{3}\) to express r and \(n_{s}\) as a function of \(\phi \),

$$\begin{aligned} n_{s}-1= & {} \frac{12M_{p}^{2}}{2(16A+\lambda ^{2}_{*}\phi ^{8})^{\frac{1}{2}}} \bigg (\frac{-6\lambda ^{3}_{*}\phi ^{10}}{16A+\lambda ^{2}_{*}\phi ^{8}} +4\lambda _{*}\phi ^{2} \bigg ),\quad \\ r= & {} \frac{384G\sqrt{3CM_{p}^{2}}\lambda _{*} \phi ^{3}}{9b\pi ^{\frac{3}{2}}(16A+\lambda ^{2}_{*}\phi ^{8})^{\frac{1}{4}}}. \end{aligned}$$
Fig. 1
figure 1

Plot of the tensor–scalar ratio r versus scalar spectral index \(n_{s}\) for the GCG model in the weak dissipative regime (left panel) and the strong dissipative regime (right panel)

Full size image

3.1.2 Strong dissipative regime

Now we consider a strong dissipative regime where \(R \gg 1\), in the slow-roll approximation; the temperature is given as

$$\begin{aligned} T=\bigg (\frac{V'^{2}}{4bCH}\bigg )^{\frac{1}{5}}. \end{aligned}$$

For the strong regime, the slow-roll parameters lead to

$$\begin{aligned} \epsilon= & {} \frac{M_{p}^{2}VV'^{2}}{2R(A+V^{2})^{\frac{3}{2}}} \\ \eta= & {} \frac{M_{p}^{2}}{R(A+V^{2})^{\frac{1}{2}}}\bigg (V''+\frac{V'^{2}}{V}-\frac{3VV'^{2}}{2(A+V^{2})}\bigg ) ,\\ \beta= & {} \frac{1}{R}M_{p}^{2}\bigg (\frac{2V''(A+V^{2})-V'^{2}V}{5(A+V^{2})^{\frac{3}{2}}}\bigg ). \end{aligned}$$

The expression of the number of e-folds takes the following form:

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{\sqrt{A+V^{2}}}{V'}R\mathrm{d}\phi . \end{aligned}$$

In a similar way we can obtain the amplitude of the power spectrum, the scalar spectral index, and the tensor-to-scalar ratio as follows:

$$\begin{aligned} P_{R}=\bigg (\frac{\pi }{4}\bigg )^{\frac{1}{2}}\frac{b^{\frac{9}{5}}}{V'^{\frac{3}{5}}(4C)^{\frac{7}{10}}} \bigg (\frac{\sqrt{A+V^{2}}}{3M_{p}^{2}}\bigg )^{\frac{9}{10}}, \end{aligned}$$
(17)
$$\begin{aligned} n_{s}-1= & {} \bigg (\frac{3(4C)^{\frac{1}{5}}}{b^{\frac{4}{5}}V'^{\frac{2}{5}}}\bigg ) \frac{(3M_{p}^{2})^{\frac{2}{5}}}{2(A+V^{2})^{\frac{1}{5}}}\nonumber \\&\times \bigg (V''+\frac{V'^{2}}{V} -\frac{9VV'^{2}}{4(A+V^{2})}\nonumber \\&-\frac{3}{2}\bigg (\frac{2V''(A+V^{2})-V'^{2}V}{5(A+V^{2})}\bigg )\bigg ), \end{aligned}$$
(18)
$$\begin{aligned} r=\frac{32G(4C)^{\frac{7}{10}}V'^{\frac{3}{5}}}{b^{\frac{9}{5}}\pi ^{\frac{3}{2}}}\bigg (\frac{\sqrt{A+V^{2}}}{3M_{p}^{2}}\bigg )^{\frac{1}{10}}. \end{aligned}$$
(19)

In terms of the scalar field, r and \(n_{s}\) turn out to be

$$\begin{aligned} n_{s}-1= & {} \bigg (\frac{3(4C)^{\frac{1}{5}}}{b^{\frac{4}{5}}(\lambda _{*}\phi ^{3})^{\frac{2}{5}}}\bigg ) \frac{(3M_{p}^{2})^{\frac{2}{5}}}{10(16A+\lambda ^{2}_{*}\phi ^{8})^{\frac{1}{5}}}\nonumber \\&\times \bigg (\frac{-39\lambda ^{3}_{*}\phi ^{10}}{16A+\lambda ^{2}_{*}\phi ^{8}} +26\lambda _{*}\phi ^{2} \bigg ), \end{aligned}$$
(20)
$$\begin{aligned} r= & {} \frac{32G(4C)^{\frac{7}{10}}(\lambda _{*}\phi ^{3})^{\frac{3}{5}}}{b^{\frac{9}{5}} \pi ^{\frac{3}{2}}}\bigg (\frac{\sqrt{16A+\lambda _{*}^{2}\phi ^{8}}}{12M_{p}^{2}}\bigg )^{\frac{1}{10}}. \end{aligned}$$
(21)

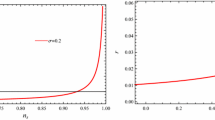
We plot r versus \(n_{s}\) for the GCG models in Fig. 1 for weak (left panel) and strong dissipative regimes (right panel), respectively. However, the parameters appearing in the model have the values \(M_{p}=1\), \(\lambda _{*}=10^{-10}\), \(A=10^{-45}\), \(b=0.3\). The trajectories in Fig. 1 show the increasing behavior of r with respect to \(n_{s}\). It can be noted that in the weak dissipative regime (left panel of Fig. 1) the range of the tensor-to-scalar ratio becomes \(r<0.006\) for \(0.4<n_{s}<1\). However, it is \(r=0.05\) corresponding to \(n_{s}=0.96\) for the strong dissipative regime (left panel of Fig. 1). It is observed that WMAP9 [32] provides the value of tensor scalar ratio as \(r<0.13\) and the spectral index is measured to be \(n_{s}=0.972\pm 0.013\). According to the Planck data, \(r<0.11\) and \(n_{s}=0.968\pm 0.006\) [33]. In view of these observations, our results for the GCG model are compatible with observational data [32, 33].

3.2 Modified Chaplygin gas

The MCG has an equation of state as follows [34]:

$$\begin{aligned} P_\mathrm{mcg}=\mu \rho _\mathrm{mcg} - \frac{\nu }{\rho _\mathrm{mcg}^{\lambda }} , \end{aligned}$$

where \(P_\mathrm{mcg}\) and \(\rho _\mathrm{mcg}\) denote the pressure and energy density, respectively, and \(0\le \lambda \le 1\), \(\mu \), \(\nu \) are positive constants. We use the energy conservation equation and express the density of MCG in this form:

$$\begin{aligned} \rho _\mathrm{mcg}=\bigg (A+\frac{c}{a^{3(1+\lambda )(1+\mu )}}\bigg )^ {\frac{1}{1+\lambda }} , \end{aligned}$$
(22)

where c is a constant of integration and \( A = \frac{\nu }{1+\mu }\). We start with the modified Friedmann equation of the form

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}}\bigg (\bigg (A+\rho _{\phi }^{(1+\lambda )(1+\mu )}\bigg )^ {\frac{1}{1+\lambda }}+\rho _{\gamma }\bigg ), \end{aligned}$$
(23)

this modification is possible only due to an extrapolation of Eq. (22), so that

$$\begin{aligned} \rho _\mathrm{mcg}=\bigg (A+\rho _{m}^{(1+\lambda )(1+\mu )}\bigg )^{\frac{1}{1+\lambda }} \rightarrow \bigg (A+\rho _{\phi }^{(1+\lambda )(1+\mu )}\bigg )^{\frac{1}{1+\lambda }},\nonumber \\ \end{aligned}$$
(24)

where \(\rho _{m}\) denotes the matter energy density, and hence the Friedmann equation takes the form

$$\begin{aligned} H^{2}= & {} \frac{1}{3M_{p}^{2}}(A+\rho _{\phi }^{(1+\lambda )(1+\mu )})^ {\frac{1}{1+\lambda }}\nonumber \\\sim & {} \frac{1}{3M_{p}^{2}}(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}. \end{aligned}$$
(25)

3.2.1 Weak dissipative regime

For the weak dissipative regime the temperature remains the same as given in the GCG case. However, the slow-roll parameters take the following form:

$$\begin{aligned} \epsilon= & {} \frac{M_{p}^{2}(1+\mu )V^{(1+\lambda )(1+\mu )-1}V'^{2}}{2(A +V^{(1+\lambda )(1+\mu )})^{\frac{2+\lambda }{1+\lambda }}} ,\\ \eta= & {} \frac{M_{p}^{2}}{(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1 +\lambda }}}\nonumber \\&\times \bigg (2V''+\frac{V'^{2}((1+\lambda )(1+\mu )-1)}{V} \\&-\frac{V^{(1+\lambda )(1+\mu )-1}V'^{2}(1+\lambda )(1+\mu )}{(A+V^{(1+\lambda )(1+\mu )})}\bigg ),\\ \beta= & {} M_{p}^{2}\bigg (\frac{4(A+V^{(1+\lambda )(1+\mu )})V''-3(1+\mu ) V'^{2}V^{(1+\lambda )(1+\mu )-1}}{6(A+V^{(1+\lambda )(1+\mu )})^ {\frac{2+\lambda }{1+\lambda }}}\bigg ). \end{aligned}$$

The number of e-folds is obtained:

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{(A+V^{(1+\lambda ) (1+\mu )})^{\frac{1}{1+\lambda }}}{V'}\mathrm{d}\phi . \end{aligned}$$

Other perturbed parameters turn out to be

$$\begin{aligned} P_{R}=\bigg (\frac{81\pi b^{2}}{12^{2}CV'^{2}}\bigg )^{\frac{1}{2}}\bigg (\frac{(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\bigg )^{\frac{3}{2}}, \end{aligned}$$
(26)
$$\begin{aligned} n_{s}-1= & {} \frac{3M_{p}^{2}}{2(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}\bigg (\frac{V'^{2}((1+\lambda )(1+\mu )-1)}{V} \nonumber \\&-\frac{V^{(1+\lambda )(1+\mu )-1}V'^{2}}{(A+V^{(1+\lambda )(1+\mu )})}\bigg (\frac{3}{4}(1+\mu )+(1+\lambda )(1+\mu )\bigg )+2V''\nonumber \\&-\frac{3}{2}\bigg (\frac{4(A+V^{(1+\lambda )(1+\mu )})V''-3(1+\mu )V'^{2}V^{(1+\lambda )(1+\mu )-1}}{6(A+V^{(1+\lambda )(1+\mu )})}\bigg )\bigg ),\nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned} r=\frac{192G\sqrt{3CM_{p}^{2}}V'}{9b\pi ^{\frac{3}{2}}(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{2(1+\lambda )}}}. \end{aligned}$$
(28)

By using a quartic potential r and \(n_{s}\) are expressed as function of \(\phi \),

$$\begin{aligned} n_{s}-1= & {} \frac{3M_{p}^{2}}{2(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}\nonumber \\&\times \bigg (\lambda _{*}\phi ^{2}((1+\lambda )(1+\mu )-1)\nonumber \\&-\frac{(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )-1}\lambda _{*}^{2}\phi ^{6}}{(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})}\nonumber \\&\times \bigg (\frac{3}{4}(1+\mu )+(1+\lambda )(1+\mu )\bigg )+6\lambda _{*}\phi ^{2}\nonumber \\&-\frac{3}{12(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})}\nonumber \\&\times \bigg (4(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})\lambda _{*}\phi ^{2}\nonumber \\&-3(1+\mu )\lambda _{*}^{2}\phi ^{6}(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )-1}\bigg )\bigg ), \end{aligned}$$
(29)
$$\begin{aligned} r=\frac{192G\sqrt{3CM_{p}^{2}}\lambda _{*}\phi ^{3}}{9b\pi ^{\frac{3}{2}}(A +(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})^{\frac{1}{2(1+\lambda )}}}. \end{aligned}$$
(30)
Fig. 2
figure 2

Plot of the tensor–scalar ratio r versus scalar spectral index \(n_{s}\) for the MCG model in the weak dissipative regime (left panel) and the strong dissipative regime (right panel)

Full size image

3.2.2 Strong dissipative regime

Here, we mention that the temperature remains the same as obtained in the GCG case for the strong regime. However, the slow-roll parameters take the form

$$\begin{aligned} \epsilon= & {} \frac{M_{p}^{2}(1+\mu )V^{(1+\lambda )(1+\mu )-1}V'^{2}}{2R(A+V^{(1+\lambda )(1+\mu )})^{\frac{2+\lambda }{1+\lambda }}},\\ \eta= & {} \frac{M_{p}^{2}}{R(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}\\&\times \bigg (2V'' +\frac{V'^{2}((1+\lambda )(1+\mu )-1)}{V}\\&-\frac{V^{(1+\lambda )(1+\mu )-1}V'^{2}(1+\lambda )(1+\mu )}{(A+V^{(1+\lambda )(1+\mu )})}\bigg ), \end{aligned}$$
$$\begin{aligned} \beta= & {} \frac{1}{R}M_{p}^{2}\bigg (\frac{4(A+V^{(1+\lambda )(1+\mu )})V''-(1+\mu )V'^{2} V^{(1+\lambda )(1+\mu )-1}}{10(A+V^{(1+\lambda )(1+\mu )})^{\frac{2+\lambda }{1+\lambda }}}\bigg ). \end{aligned}$$

The number of e-folds is given by

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}{V'}R\mathrm{d}\phi . \end{aligned}$$

Other perturbed quantities lead to

$$\begin{aligned} P_{R}=\bigg (\frac{\pi }{4}\bigg )^{\frac{1}{2}}\frac{b^{\frac{9}{5}}}{V'^{\frac{3}{5}}(4C)^{\frac{7}{10}}}\bigg (\frac{(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\bigg )^{\frac{9}{10}}, \end{aligned}$$
(31)
$$\begin{aligned} n_{s}-1= & {} \frac{3(4C)^{\frac{1}{5}}}{2b^{\frac{4}{5}}V'^{\frac{2}{5}}}\frac{(3M_{p}^{2})^{\frac{2}{5}}}{(A+V^{(1+\lambda )(1+\mu )})^{\frac{2}{5(1+\lambda )}}}\nonumber \\&\times \bigg (\frac{V'^{2}((1+\lambda )(1+\mu )-1)}{V} -\frac{V^{(1+\lambda )(1+\mu )-1}V'^{2}}{(A+V^{(1+\lambda )(1+\mu )})}\nonumber \\&\times \bigg (\frac{3}{4}(1+\mu )+(1+\lambda )(1+\mu )\bigg )+2V''\nonumber \\&-\frac{3}{2}\bigg (\frac{4(A+V^{(1+\lambda )(1+\mu )}V''-(1+\mu )V'^{2}V^{(1+\lambda )(1+\mu )-1})}{10(A+V^{(1+\lambda )(1+\mu )})}\bigg )\bigg ), \nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned} r= & {} \frac{32G(4C)^{\frac{7}{10}}V'^{\frac{3}{5}}}{b^{\frac{9}{5}}\pi ^{\frac{3}{2}}} \bigg (\frac{(A+V^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\bigg )^{\frac{1}{10}}. \end{aligned}$$
(33)

By putting in the value of V and \(V'\), we get r and \(n_{s}\) in terms of \(\phi \),

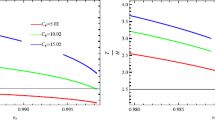
$$\begin{aligned} n_{s}\!-\!1= & {} \frac{3(4C)^{\frac{1}{5}}}{2b^{\frac{4}{5}}(\lambda _{*}\phi ^{3})^{\frac{2}{5}}} \frac{(3M_{p}^{2})^{\frac{2}{5}}}{(A+(0.25\lambda _{*}\phi ^{4})^{(1 \!+\!\lambda )(1+\mu )})^{\frac{2}{5(1+\lambda )}}}\nonumber \\&\times \bigg ( \lambda _{*}\phi ^{2}((1+\lambda )(1+\mu )-1)\\&-\frac{(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )-1}\lambda _{*}^{2}\phi ^{6}}{(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})}\nonumber \\&\times \bigg (\frac{3}{4}(1+\mu )+(1+\lambda )(1+\mu )\bigg )\\&-\frac{3}{20(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})}\nonumber \\&\times \bigg (4(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})\lambda _{*}\phi ^{2}\\&-(1\!+\!\mu )\lambda _{*}^{2}\phi ^{6}(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )-1}\!\bigg ) \!+\!6\lambda _{*}\phi ^{2}\!\bigg ),\\ r= & {} \frac{32G(4C)^{\frac{7}{10}}(\lambda _{*}\phi ^{3})^{\frac{3}{5}}}{b^{\frac{9}{5}}\pi ^{\frac{3}{2}}}\nonumber \\&\times \bigg (\frac{(A+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda ) (1+\mu )})^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\bigg )^{\frac{1}{10}}. \end{aligned}$$

It can be noted from Fig. 2 that we have plots of r in terms of \(n_{s}\) for the MCG models in the weak and the strong regimes where r and \(n_{s}\) are expressed as a function of \(\phi \). The parameters appearing in the model have the values \(\lambda =1\), \(\mu =0.5\), \(\lambda _{*}=10^{-3}\), \(A=10^{-25}\), \(b=25\). The range of the tensor–scalar ratio is \(r<0.045\), when the spectral index is \(0.6<n_{s}<1\), in the weak regime (left panel). However, we get \(r<0.15\) for \(0.7<n_{s}<1\) with \(b=60\) for the strong dissipative regime (right panel). The observed range of r and \(n_{s}\) is compatible with the data provided by WMAP9 [32] and Planck [33].

3.3 Generalized cosmic Chaplygin gas

Gozalez Diaz [35] introduced the GCCG model; its equation of state is given by

$$\begin{aligned} P_\mathrm{gccg}=- \rho ^{-\lambda }[A+(\rho _\mathrm{gccg}^{1+\lambda } - A)^{-\omega }] , \end{aligned}$$

where \(A=\frac{D}{1+\omega }-1\) and D can take a positive or a negative value. \(\lambda \) is a positive constant and \(-l<\omega <0\), \(l>1\). If we take \(\omega \rightarrow 0\) then this equation of state reduces to the GCG model. We obtain the energy density of GCCG by integrating the energy conservation equation,

$$\begin{aligned} \rho _\mathrm{gccg} = \bigg [A +\bigg (1+\frac{B}{a^{3(1+\lambda )(1+\omega )}}\bigg )^{\frac{1}{1+\omega }}\bigg ]^{\frac{1}{1+\lambda }}. \end{aligned}$$
(34)

The modified Friedmann equation in view of GCCG becomes

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}}\bigg (\bigg (A+\bigg (1+\rho _{\phi }^{(1+\lambda )(1 +\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )\bigg )^{\frac{1}{1+\lambda }}+\rho _{\gamma }\bigg ). \end{aligned}$$
(35)

This modification is possible only due to an extrapolation of Eq. (34) so that

$$\begin{aligned} \rho _\mathrm{gccg}=\bigg (A+(1+\rho _{m}^{(1+\lambda )(1+\omega )})^{\frac{1}{1 +\omega }}\bigg )^{\frac{1}{1+\lambda }}\nonumber \\ \rightarrow \bigg (A+\bigg (1+\rho _{\phi }^{(1 +\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}. \end{aligned}$$
(36)

For this case, the Friedmann equation takes the form

$$\begin{aligned} H^{2}= & {} \frac{1}{3M_{p}^{2}}\bigg (A+\bigg (1+\rho _{\phi }^{(1+\lambda ) (1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }},\nonumber \\\sim & {} \frac{1}{3M_{p}^{2}}\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}. \end{aligned}$$
(37)

3.3.1 Weak dissipative regime

In this regime, the slow-roll parameters become

$$\begin{aligned} \epsilon= & {} \frac{M_{p}^{2}V^{(1+\lambda )(1+\omega )-1}\bigg (1+V^{(1+\lambda ) (1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}V'^{2}}{2\bigg (A+\bigg (1+V^{(1+\lambda ) (1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{2+\lambda }{1+\lambda }}},\\ \eta= & {} \frac{M_{p}^{2}}{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}\\&\times \bigg (2V''+\frac{V'^{2}((1+\lambda )(1+\omega )-1)}{V}\\&-\frac{\omega (1+\lambda )V^{(1+\lambda )(1+\omega )-1}V'^{2}}{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )}\\&-\frac{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}}{\bigg (A+\bigg (1+V^{(1+\lambda ) (1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}V'^{2}\\&\times (1+\lambda )V^{(1+\lambda )(1+\omega )-1}\bigg ), \end{aligned}$$
$$\begin{aligned} \beta= & {} \left( \frac{4\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )V''-3V'^{2}V^{(1+\lambda ) (1+\omega )-1}\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}}{6\bigg (A+\bigg (1+V^{(1+\lambda ) (1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{2+\lambda }{1+\lambda }}}\right) \\&\times M_{p}^{2}. \end{aligned}$$

By using Eq. (6), the number of e-folds is given as

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{\bigg (A+\bigg (1+V^{(1+\lambda )(1 +\mu )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}{V'}\mathrm{d}\phi . \end{aligned}$$

The perturbed parameters take the form

$$\begin{aligned}&P_{R}=\bigg (\frac{81\pi b^{2}}{12^{2}CV'^{2}}\bigg )^{\frac{1}{2}}\nonumber \\&\quad \times \left( \frac{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\right) ^{\frac{3}{2}},\end{aligned}$$
(38)
$$\begin{aligned}&n_{s}-1=\frac{3M_{p}^{2}}{2\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}\nonumber \\&\quad \times \bigg (\frac{V'^{2}((1+\lambda )(1+\omega )-1)}{V}\nonumber \\&\quad -\frac{3}{12\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}\nonumber \\&\quad \times \bigg (4V''\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )\nonumber \\&\quad -3V'^{2}V^{(1+\lambda )(1+\omega )-1}\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}\bigg )+2V''\nonumber \\&\quad -\frac{\omega (1+\lambda )V^{(1+\lambda )(1+\omega )-1}V'^{2}}{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )}\nonumber \\&\quad -\frac{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}}{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}V'^{2}\nonumber \\&\quad \times (1+\lambda )V^{(1+\lambda )(1+\omega )-1}\bigg (\frac{3}{4}+(1+\lambda )\bigg )\bigg ), \end{aligned}$$
(39)
$$\begin{aligned}&r=\frac{192G\sqrt{3CM_{p}^{2}}V'}{9b\pi ^{\frac{3}{2}}\bigg (A+\bigg (1+V^{(1+\lambda )(1+\mu )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{2(1+\lambda )}}}. \end{aligned}$$
(40)

We can write r and \(n_{s}\) in terms of \(\phi \) as follows:

$$\begin{aligned} n_{s}-1= & {} \frac{3M_{p}^{2}}{2(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1 +\omega }})^{\frac{1}{1+\lambda }}}\\&\times \bigg (4((1+\lambda )(1+\omega )-1)\lambda _{*}\phi ^{2}+6\lambda _{*}\phi ^{2}\\&-\frac{3}{12(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})}\\&\times \bigg (12\lambda _{*}\phi ^{2}(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})\\&-3\lambda _{*}^{2}\phi ^{6}(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}\\&\times (1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{-\omega }{1+\omega }}\bigg )\\&-\frac{(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}\lambda _{*}^{2}\phi ^{6}}{(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})}\omega (1+\lambda )\\&-\frac{(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{-\omega }{1+\omega }}}{(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})}\\&\times \bigg (\frac{3}{4}+(1+\lambda )\bigg )\\&\times \lambda _{*}^{2}\phi ^{6}(1+\lambda )(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}\bigg ), \\ r= & {} \frac{192G\sqrt{3CM_{p}^{2}}\lambda _{*}\phi ^{3}}{9b\pi ^{\frac{3}{2}}(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\mu )})^{\frac{1}{1+\omega }})^{\frac{1}{2(1+\lambda )}}}. \end{aligned}$$

3.3.2 Strong dissipative regime

For the strong regime, the slow-roll parameters take the form

$$\begin{aligned} \epsilon= & {} \frac{M_{p}^{2}V^{(1+\lambda )(1+\omega )-1}\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}V'^{2}}{2R\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{2+\lambda }{1+\lambda }}},\\ \eta= & {} \frac{M_{p}^{2}}{R\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}\\&\times \bigg (2V''+\frac{V'^{2}((1+\lambda )(1+\omega )-1)}{V}\\&-\frac{\omega (1+\lambda )V^{(1+\lambda )(1+\omega )-1}V'^{2}}{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )}\\&-\frac{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}}{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}V'^{2}\\&\times (1+\lambda )V^{(1+\lambda )(1+\omega )-1}\bigg ),\\ \end{aligned}$$
$$\begin{aligned} \beta= & {} \left( \frac{4\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg ) -V'^{2}V^{(1+\lambda )(1+\omega )-1}\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1 +\omega }}}{10\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{2 +\lambda }{1+\lambda }}}\right) \frac{1}{R}M_{p}^{2}. \end{aligned}$$
Fig. 3
figure 3

Plot of the tensor–scalar ratio r versus scalar spectral index \(n_{s}\) for the GCCG model in the weak dissipative regime (left panel) and the strong dissipative regime (right panel)

Full size image

The number of e-folds leads to

$$\begin{aligned} N=\frac{1}{M_{p}^{2}}\int _{\phi _\mathrm{end}}^{\phi _{*}}\frac{\bigg (A +\bigg (1+V^{(1+\lambda )(1+\mu )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}{V'}R\mathrm{d}\phi . \end{aligned}$$

The corresponding perturbed quantities become

$$\begin{aligned} P_{R}= & {} \bigg (\frac{\pi }{4}\bigg )^{\frac{1}{2}}\frac{b^{\frac{9}{5}}}{V'^{\frac{3}{5}}(4C)^{\frac{7}{10}}}\nonumber \\&\times \left( \frac{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\right) ^{\frac{9}{10}}, \end{aligned}$$
(41)
$$\begin{aligned} n_{s}-1= & {} \frac{3(4C)^{\frac{1}{5}}}{2b^{\frac{4}{5}}V'^{\frac{2}{5}}}\frac{(3M_{p}^{2})^{\frac{2}{5}}}{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{2}{5(1+\lambda )}}}\nonumber \\&\times \bigg (\frac{V'^{2}((1+\lambda )(1+\omega )-1)}{V}\nonumber \\&-\frac{3}{20\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}\nonumber \\&\times \bigg (4V''\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )\nonumber \\&-V'^{2}V^{(1\!+\!\lambda )(1\!+\!\omega )-1}\bigg (1\!+\!V^{(1\!+\!\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}\bigg )+2V''\nonumber \\&-\frac{\omega (1+\lambda )V^{(1+\lambda )(1+\omega )-1}V'^{2}}{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )}\nonumber \\&-\frac{\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{-\omega }{1+\omega }}}{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )}V'^{2}\nonumber \\&\times (1+\lambda )V^{(1+\lambda )(1+\omega )-1}\bigg (\frac{3}{4}+(1+\lambda )\bigg )\bigg ), \end{aligned}$$
(42)
$$\begin{aligned} r= & {} \frac{32G(4C)^{\frac{7}{10}}V'^{\frac{3}{5}}}{b^{\frac{9}{5}}\pi ^{\frac{3}{2}}}\nonumber \\&\times \left( \frac{\bigg (A+\bigg (1+V^{(1+\lambda )(1+\omega )}\bigg )^{\frac{1}{1+\omega }}\bigg )^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\right) ^{\frac{1}{10}}. \end{aligned}$$
(43)

However, r and \(n_{s}\) as a function of \(\phi \) are

$$\begin{aligned}&n_{s}-1=\frac{3(4C)^{\frac{1}{5}}}{2b^{\frac{4}{5}}(\lambda _{*}\phi ^{3})^{\frac{2}{5}}}\\&\quad \times \frac{(3M_{p}^{2})^{\frac{2}{5}}}{(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})^{\frac{2}{5(1+\lambda )}}}\\&\quad \times \bigg (4\lambda _{*}\phi ^{2}((1+\lambda )(1+\omega )-1)\\&\quad -\frac{3}{20(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})}\\&\quad \times \bigg (12\lambda _{*}\phi ^{2}(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})\\&\quad -(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}\lambda _{*}^{2}\phi ^{6}\\&\quad \times (1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{-\omega }{1+\omega }}\bigg )\\&\quad -\frac{(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}\lambda _{*}^{2}\phi ^{6}}{(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})}\\&\quad \times \omega (1+\lambda )\\&\quad -\frac{(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{-\omega }{1+\omega }}}{(A+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})} \bigg (\frac{3}{4}+(1+\lambda )\bigg )\\&\quad \times \lambda _{*}^{2}\phi ^{6}(1+\lambda )(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )-1}+6\lambda _{*}\phi ^{2}\bigg ),\\&r=\frac{32G(4C)^{\frac{7}{10}}(\lambda _{*}\phi ^{3})^{\frac{3}{5}}}{b^{\frac{9}{5}}\pi ^{\frac{3}{2}}}\nonumber \\&\quad \times \bigg (\frac{(A+(1+(1+(0.25\lambda _{*}\phi ^{4})^{(1+\lambda )(1+\omega )})^{\frac{1}{1+\omega }})^{\frac{1}{1+\lambda }}}{3M_{p}^{2}}\bigg )^{\frac{1}{10}}. \end{aligned}$$

The plots of r versus \(n_{s}\) for the GCCG models in the weak and the strong regimes are shown in Fig. 3. The constant parameters are \(\lambda =1\), \(\omega =-0.5\), \(M_{p}=1\), \(\lambda _{*}=10^{-2}\), \(A=10^{-5}\), \(b=30\). In the weak regime (left panel), the tensor–scalar ratio is confined to \(r<0.12\) when the spectral index is \(n_{s}<1\). In the strong regime, we get \(r<0.08\) for \(b=80,~0.2<n_{s}<1\). These values show that the GCCG model is compatible with the data provided by WMAP9 and Planck [32, 33].

4 Conclusions

Warm inflation presents a compelling solution for the main problem of the inflationary theory, namely how this inflationary period will come to an end. In this type of models, radiations are produced during inflation, and a dissipative coefficient is introduced. This is the reason why we have investigated the warm inflationary scenario inspired with quartic form of potential \(V=\frac{\lambda _{*}\phi ^{4}}{4}\) and the well-known form of the dissipative coefficient \(\Gamma \propto T\). In order to find the consistency of the results, we have assumed various well-known Chaplygin gas models such as GCG, MCG, and GCCG. Also, we have considered this universe to be filled with radiation and a standard scalar field and accordingly the Friedmann equations are modified. In the slow-roll approximation, we have investigated inflationary parameters such as the number of e-folds, the scalar spectrum, the scalar spectral index, and the tensor-to-scalar ratio both in the weak and the strong dissipative regimes.

To analyze our results, we have plotted the graphs between the tensor-to-scalar ratio r and scalar spectral index \(n_{s}\) for each model in the weak (where \(\Gamma \ll 3H\)) and the strong (where \(\Gamma \gg 3H\)) dissipative regimes. For the GCG model, it is found that in the weak dissipative regime with \(0.4<n_{s}<1\), we have \(r<0.006\), and in the strong dissipative regime, \(r=0.05\) at \(n_{s}=0.96\) (referred to in Fig. 1). In the MCG model, the spectral index lies between \(0.6<n_{s}<1\), the range of the tensor–scalar ratio is \(r<0.045\) in the weak regime. However, in the strong regime, we have obtained the range \(r<0.15\) for \(0.7<n_{s}<1\). In the GCCG model, for the weak regime when the spectral index is \(n_{s}<1\), the tensor–scalar ratio is confined to \(r<0.12\). But in the strong regime for \(b=80\), \(0.2<n_{s}<1\), we get \(r<0.08\).

In addition, WMAP9 provides the value of the tensor–scalar ratio \(r<0.13\) and the spectral index is measured to be \(n_{s}=0.972\pm 0.013\), according to the Planck data \(r<0.11\) and \(n_{s}=0.968\pm 0.006\). We have concluded remarking that the obtained range/values of r corresponding to the well-settled \(n_{s}\) are well supported to WMAP9 [32] and Planck data [33] in all models of CG models.