1 Introduction

According to the highly redshift observation of the Supernova Ia [1, 2], galaxy clusters [3, 4], and cosmic microwave background radiation [5], the current universe is expanding in an accelerating way. Then our current universe may be described by the de Sitter space-time. Moreover, the recently observational data by BICEP2 [6] may confirm that the early universe in a good approximation is also the de Sitter universe. Therefore, the construction of the quantum field theory in de Sitter space is very important for better understanding of the evolution of the early and current universe. The rigorous mathematical construction of quantum field theory in de Sitter space-time, based on the unitary irreducible representations of the de Sitter group and the analyticity of the complexified de Sitter space-time, was previously presented in [7]. The unitary irreducible representations of the de Sitter group are extracted completely by Takahashi [8] and the analyticity of the complexified de Sitter space-time is investigated by Bros et al. [9–12].

In this paper, the massless spin-\(\frac{3}{2}\) field or vector-spinor gauge field is considered. The massless means that they propagate on the de Sitter light-cone. First by using the group de Sitter algebra, the gauge-invariant field equation is presented [7, 13, 14]. For similarity to other gauge theories, such as Yang–Mills gauge theory, the gauge-covariant derivative and the gauge-invariant Lagrangian density can be envisaged along the lines proposed in [7]. The variation of this Lagrangian density would give us an equation of motion which is obtained by the group de Sitter algebra.

In the gauge-covariant derivative, the gauge potential is a vector-spinor field. Consequently the corresponding gauge group must have spinorial generator to justify a set of well-defined gauge-covariant derivatives. Therefore, a set of anti-commutative generators satisfy a superalgebra. The all possible closed de Sitter superalgebra for even N (N is the number of fermionic generators) had been obtained [15, 16]. In the de Sitter ambient space notation, a closed \(N=1\) de Sitter supersymmetry algebra can be defined [17]. So, here we just consider one spinorial generator and, in accordance with it, one vector-spinor field. The quanta of this field is named gravitino which is supposed to be the fermionic partner of graviton (spin-2 quanta of gravitational field!).

In the gauge quantum field theory, it has been shown that if we want to conserve casuality and covariance, an indefinite metric must be used [18]. In other words, there are states with negative or null norm that establish a general Fock quantization with field operators that are not essentially self-adjoint [19], so, one has to adopt the well-known Gupta–Bleuler quantization. The Gupta–Bleuler formalism is an alternative way that is used by Gupta and Bleuler to quantize the electromagnetic field [20, 21]. But it seems to be universal, and it has been extensively applied to the quantization of gauge-invariant theories. Binegar et al. [22] have shown a complete Gupta–Bleuler quantization procedure of QED that is manifestly conformally invariant. In a curved static space-time, the Gupta–Bleuler quantization of the electromagnetic gauge fields is explained by Furlani [23] as well as for globally hyperbolic space-times in [24]. The Gupta–Bleuler structure has been applied to the massless minimally coupled scalar field [25, 26], massless vector field [27] and massless spin-2 field [28] in de Sitter space. Here, we study this structure for a massless vector-spinor or spin-\(\frac{3}{2}\) fields.

In Sect. 2, first, the notation and terminology of the de Sitter ambient space formalism are recalled. Using de Sitter group algebra, the gauge-invariant field equation is presented. The gauge-covariant derivative is defined. Also we look closely at an action in which its associated equation of motion, is exactly consistent with the group algebra result [7]. Section 3 is devoted to the construction of Gupta–Bleuler triplet for vector-spinor field and its corresponding indecomposable representation. The solution of the gauge-fixing field equation is obtained in Sect. 4. The field solution can be written in terms of a polarization vector-spinor state and a conformally coupled massless scalar field. The pure gauge state, spinor state, physical state, divergence part, and general solution are presented. In Sect. 5, the vector-spinor quantum field operators and their covariant two-point function are defined. Finally, a brief conclusion and an outlook are given in Sect. 6.

2 Field equations

2.1 de Sitter ambient space formalism

The de Sitter space-time is the vacuum solution of Einstein’s equation with a positive cosmological constant. It can be considered as a hyperboloid embedded in five-dimensional Minkowski space:

$$\begin{aligned} M_H= & {} \{x \in \mathbbm {R}^5| \; \; x \cdot x=\eta _{\alpha \beta } x^\alpha x^\beta =-H^{-2}\},\\&\quad \alpha ,\beta =0,1,2,3,4, \end{aligned}$$

where \(\eta _{\alpha \beta }=\text {diag}(1,-1,-1,-1,-1)\). The de Sitter metric is

$$\begin{aligned} ds^2= & {} \eta _{\alpha \beta }\mathrm{d}x^{\alpha }\mathrm{d}x^{\beta }|_{x^2=-H^{-2}}= g_{\mu \nu }^{\mathrm{d}S}\mathrm{d}X^{\mu }\mathrm{d}X^{\nu },\nonumber \\&\mu =0,1,2,3. \end{aligned}$$

\(X^\mu \) is for the de Sitter intrinsic coordinates and \(x^\alpha \) is for the five-dimensional de Sitter ambient space formalism. For simplicity, the Hubble parameter is taken to be equal to unity, \(H=1\). The isometry group of the de Sitter space-time is the ten-parameter group \(SO_0(1,4)\). The de Sitter group has two Casimir operators:

$$\begin{aligned} Q^{(1)}=-\frac{1}{2}L_{\alpha \beta }L^{\alpha \beta }, \;\;\; \text{ and } \;\;\; Q^{(2)}=-W_\alpha W^\alpha , \end{aligned}$$

where \( W_\alpha =\frac{1}{8}\epsilon _{\alpha \beta \gamma \delta \eta } L^{\beta \gamma }L^{\delta \eta }. \) \(\epsilon _{\alpha \beta \gamma \delta \eta }\) is the antisymmetrical Levi-Civita tensor and \(L_{\alpha \beta }=M_{\alpha \beta }+S_{\alpha \beta }\) are ten infinitesimal generators of the de Sitter group. The orbital part \(M_{\alpha \beta }\) is defined by

$$\begin{aligned} M_{\alpha \beta }=-i(x_\alpha \partial _\beta -x_\beta \partial _\alpha )=-i\left( x_\alpha \partial ^\top _\beta -x_\beta \partial ^\top _\alpha \right) , \end{aligned}$$

where \(\partial ^\top _\beta =\theta _\beta {}^{\alpha }\partial _\alpha \) is the transverse derivative (\(x.\partial ^\top =0\)) and \(\theta _{\alpha \beta }=\eta _{\alpha \beta }+x_\alpha x_\beta \) known as the projection tensor. The spinorial part \(S_{\alpha \beta }\) with half-integer spin, \(s=l+\frac{1}{2}\), reads

$$\begin{aligned} S_{\alpha \beta }^{(s)}=S_{\alpha \beta }^{(l)}+S_{\alpha \beta }^{(\frac{1}{2})}, \end{aligned}$$

in which the first term acts on a tensor index as

$$\begin{aligned}&S_{\alpha \beta }^{(l)}\Psi _{\gamma _1\ldots \gamma _l}\\&\quad =-i\sum \limits _{i=1}^l\left( \eta _{\alpha {\gamma _i}} \Psi _{\gamma _1\ldots (\gamma _i\rightarrow \beta )\ldots \gamma _l}-\eta _{\beta {\gamma _i}} \Psi _{\gamma _1\ldots (\gamma _i\rightarrow \alpha )\ldots \gamma _l}\right) . \end{aligned}$$

The second term is

$$\begin{aligned} S_{\alpha \beta }^{(\frac{1}{2})}=-\frac{i}{4}[\gamma _{\alpha },\gamma _{\beta }], \end{aligned}$$

where the \(\gamma \)-matrices satisfy the basic Clifford algebra

$$\begin{aligned} \{\gamma ^{\alpha },\gamma ^{\beta }\}=2\eta ^{\alpha \beta }\mathbb {I}_{4\times 4}. \end{aligned}$$

The best \(\gamma \)-matrices representation for our discussion is [12, 32]:

$$\begin{aligned} \gamma ^0=\left( \begin{array}{clcr} \mathbb {I}_{2\times 2} &{} \;\; 0 \\ 0 &{}-\mathbb {I}_{2\times 2} \\ \end{array}\right) ,\,\,\gamma ^4=\left( \begin{array}{clcr} 0 &{} \mathbb {I}_{2\times 2} \\ -\mathbb {I}_{2\times 2} &{}0 \\ \end{array}\right) , \end{aligned}$$
$$\begin{aligned}&\gamma ^1=\left( \begin{array}{clcr} 0 &{} i\sigma ^1 \\ i\sigma ^1 &{}0 \\ \end{array} \right) ,\quad \gamma ^2=\left( \begin{array}{clcr} 0 &{} -i\sigma ^2 \\ -i\sigma ^2 &{}0 \\ \end{array} \right) ,\\&\gamma ^3=\left( \begin{array}{clcr} 0 &{} i\sigma ^3 \\ i\sigma ^3 &{}0 \\ \end{array} \right) , \end{aligned}$$

where \(\mathbb {I}_{2\times 2}\) and \(\sigma ^i\)’s are the unit \(2\times 2\) matrix and the Pauli matrices, respectively.

2.2 Gauge-invariant equation

The field equation can be written by using the second-order Casimir operator of the de Sitter group [7]:

$$\begin{aligned} \left( Q_{j,p}^{(1)}-\left<Q_{j,p}^{(1)}\right>\right) \Psi (x)=0, \end{aligned}$$
(2.1)

where the eigenvalues of the Casimir operator, which classify the unitary irreducible representations of the de Sitter group, are

$$\begin{aligned} \left<Q_{j,p}^{(1)}\right>=\left( -j(j+1)-(p+1)(p-2)\right) . \end{aligned}$$

j and p are parameters which take values corresponding to different types of representations, namely: the principal \((U^{(j,p)})\), the complementary \((V^{(j,p)})\), and the discrete series \((\Pi ^\pm _{j,p})\). A la Wigner, the quantum field operator transforms by the unitary irreducible representations of the de Sitter group.

In the following, we will concentrate on the spin-\(\frac{3}{2}\) massless vector-spinor field corresponding to the values \(j=p=\frac{3}{2}\) in the discrete series with \(\left<Q_{\frac{3}{2},\frac{3}{2}}^{(1)}\right>=-\frac{5}{2}\). Therefore, (2.1) becomes

$$\begin{aligned} \left( Q_{\frac{3}{2}}^{(1)}+\frac{5}{2}\right) \Psi _\alpha =0, \end{aligned}$$
(2.2)

where \(Q_{j,p}^{(1)}\equiv Q_{j}^{(1)}\) and [12]

The “scalar” Casimir operator \(Q_0^{(1)}\) is

$$\begin{aligned} Q_0^{(1)}=-\frac{1}{2}M^{\alpha \beta }M_{\alpha \beta }=-\partial _\alpha ^\top \partial ^{\alpha \top }. \end{aligned}$$

The vector-spinor solution of the field equation (2.2) with the condition \(\partial ^\top .\Psi =0\) is singular [29]. This condition is necessary for the transformation of the field operator by an unitary irreducible representation of the de Sitter group. One can solve the problem of the singularity by release of the divergencelessness condition, i.e. \(\partial ^\top .\Psi \ne 0\). Then the quantum field operator transforms by an indecomposable representation of the de Sitter group and the field equation must be gauge invariant [7]. The massless vector-spinor gauge invariant field equation is [7, 13, 14]

$$\begin{aligned} \left( Q_{\frac{3}{2}}^{(1)}+\frac{5}{2}\right) \Psi _\alpha + \nabla _{\alpha }^\top \partial ^\top \cdot \Psi =0. \end{aligned}$$
(2.3)

\(\nabla _{\alpha }^\top \) is a transverse-covariant derivative which maps a tensor-spinor field of rank l to a tensor-spinor field of rank \(l+1\) on the de Sitter ambient space formalism [7]:

where and \(\gamma ^\top _\alpha =\theta _{\alpha }^{\beta }\gamma _\beta \). It is clear that if someone eliminates from the above definition, the transverse-covariant derivative will be transverse again. But the de Sitter algebra and the definition of the Casimir operator persuade us to add this term [7]. Then one can prove the following identities:

$$\begin{aligned} Q^{(1)}_{\frac{3}{2}}\nabla _{\alpha }^\top =\nabla _{\alpha }^\top Q^{(1)}_{\frac{1}{2}}\,\,\,,\,\,\,\partial ^\top \cdot \nabla ^\top \psi =-\left( Q^{(1)}_{\frac{1}{2}}+ \frac{5}{2}\right) \psi . \end{aligned}$$
(2.4)

By using these identities, one can show that the field equation (2.3) is invariant under the following gauge transformation:

$$\begin{aligned} \Psi _\alpha \longrightarrow \Psi ^g_\alpha =\Psi _\alpha +\nabla _{\alpha }^\top \psi . \end{aligned}$$

\(\psi \) is an arbitrary spinor field and

2.3 Gauge-covariant derivative

The local or gauge symmetries are fundamental in the nature to explain the electromagnetic, weak and strong nuclear interactions by the gauge vector fields. To construct a gauge-invariant Lagrangian, the gauge-covariant derivative is defined such that any gauge fields are associated with the generators of the local symmetry group.

Here, the gauge field is a vector-spinor field (\(\Psi _\alpha \)) which satisfies an anti-commuting algebra, then the associated generator must be a spinor and satisfy the anti-commutation relations. In this case, the super-gauge-covariant derivative is defined by [7]

$$\begin{aligned} D^\Psi _\beta \equiv \nabla _{\beta }^\top +i \left( \Psi _{\beta }\right) ^\dag \gamma ^0 \mathcal{Q}=\nabla _{\beta }^\top +i\left( -\bar{\Psi }_{\beta }\gamma ^4\right) ^{i} \mathcal{Q}_i, \end{aligned}$$

where \(\mathcal Q\) is a fermionic generator which transforms as a spinor under the de Sitter group [17]. \(\bar{\Psi }_{\beta }=\Psi _{\beta }^\dag \gamma ^0\gamma ^4\) and \(i=1,\ldots ,4\) is the spinorial index. By this fermionic generator, one cannot define a closed algebra. It was proved that this spinor generator, \(\mathcal Q\), with the de Sitter group algebra satisfies the following \(N=1\) supersymmetric de Sitter algebra in the ambient space formalism [17]:

$$\begin{aligned} \{\mathcal{Q}_i,\mathcal{Q}_j\}=\left( S^{(\frac{1}{2})}_{\alpha \beta }\gamma ^4 \gamma ^2\right) _{ij}L^{\alpha \beta }, \end{aligned}$$
$$\begin{aligned}{}[\mathcal{Q}_i,L_{\alpha \beta }]=\left( S^{(\frac{1}{2})}_{\alpha \beta }\mathcal{Q} \right) _i, \;\; [\widehat{\mathcal{Q}}_i,L_{\alpha \beta }]=-\left( \widehat{\mathcal{Q}} S^{(\frac{1}{2})}_{\alpha \beta }\right) _i, \end{aligned}$$
$$\begin{aligned}{}[L_{\alpha \beta }, L_{\gamma \delta }] = -i(\eta _{\alpha \gamma }L_{\beta \delta }+\eta _{\beta \delta } L_{\alpha \gamma }-\eta _{\alpha \delta }L_{\beta \gamma }-\eta _{\beta \gamma } L_{\alpha \delta }), \end{aligned}$$
(2.5)

where \(\widehat{\mathcal{Q}}_i\equiv \left( \mathcal{Q}^t \gamma ^4 C\right) _i\). \(\mathcal{Q}^t\) is the transpose of \(\mathcal Q\) and C is the charge conjugation [30]. One can prove that \(\widehat{\mathcal{Q}}\gamma ^4\mathcal Q \) is a scalar field under de Sitter group transformations [30].

Therefore, naturally the vector-spinor gauge field \(\Psi _{\beta }\) (associated to the fermionic generator \(\mathcal{Q}\)) must be coupled with a tensor gauge field \(\mathcal{K}_{\beta }{}^{\gamma \delta }\) (associated to the generator \(L_{\gamma \delta }\)) [7]. \(\mathcal{K}_{\beta }{}^{\gamma \delta }\) is a massless spin-2 rank-3 mixed-symmetric tensor field [7]. In this case, the general gauge-covariant derivative, with \(\mathcal{H}_\alpha {}^{A}\equiv \left( \mathcal{K}_{\beta }{}^{\gamma \delta }, \Psi _{\beta }^i\right) \) as gauge fields, can be defined by

$$\begin{aligned} D^\mathcal{H}_\beta =\nabla ^\top _\beta +i \mathcal{H}_{\beta }{}^{A} T_A, \end{aligned}$$

where \( T_A \equiv \left( L_{\alpha \beta }, \mathcal{Q}_i\right) \) are the generators of \(N=1\) super-de Sitter algebra (2.5). For simplicity, they can be written in the following compact form:

$$\begin{aligned}{}[T_A,T_B\}=\mathcal{C}_{BA}{^{C}}T_C. \end{aligned}$$

The symbol of [ \(\}\) is an anti-commutation if and only if the two T’s are fermionic; otherwise, it is a commutation symbol. The general form of a local infinitesimal gauge transformation acting on the gauge field can be written as

$$\begin{aligned} \delta _\epsilon \mathcal{H}_\beta {}^{A}=D^\mathcal{H}_\beta \epsilon ^A =\nabla ^\top _\beta \epsilon ^A + \mathcal{C}_{BC}{}{^{A}}\mathcal{H}_\beta {^{C}} \epsilon ^B. \end{aligned}$$

According to the general framework, one can obtain

$$\begin{aligned}{}[D^\mathcal{H}_\alpha ,D^\mathcal{H}_\beta \ \}=R_{\alpha \beta }{}^{A}T_A, \end{aligned}$$

where R is the “curvature” and is defined as

$$\begin{aligned}&R_{\alpha \beta }{}^{A}=\nabla ^\top _\alpha \mathcal{H}_\beta {}^{A}-\nabla ^\top _\beta \mathcal{H}_\alpha {}^{A}+\mathcal{H}_\beta {}^{B}\mathcal{H}_\alpha {}^{C}\mathcal{C}_{BC}{}^{A},\nonumber \\&x^\alpha R_{\alpha \beta }{}^{A}=0= x^\beta R_{\alpha \beta }{}^{A}. \end{aligned}$$

Here we only consider the vector-spinor field part, then the curvature for this part is

$$\begin{aligned} R_{\alpha \beta }{}^{i}=\nabla ^\top _\alpha \Psi _\beta {}^{i}-\nabla ^\top _\beta \Psi _\alpha {}^{i} +\mathcal{H}_\beta {}^{B}\mathcal{H}_\alpha {}^{C}\mathcal{C}_{BC}{}^{i}, \end{aligned}$$

where the transverse-covariant derivative acts on \(\Psi _\beta \) in the following form:

2.4 Gauge invariant Lagrangian density

The super-gauge-invariant action or the supergravity Lagrangian in the de Sitter ambient space formalism is [7, 31]

$$\begin{aligned} S_g=\int \mathrm{d}\mu (x) R_{\alpha \beta }{}^{A}g_{AB} R^{\alpha \beta B}, \end{aligned}$$

where \(g_{AB}\) is numerical constant matrix and \(d\mu (x)\) is the de Sitter invariant volume element [10]. For the vector-spinor field part, the action is given by

$$\begin{aligned} S_g[\Psi ,\mathcal{K}]=\int \mathrm{d}\mu (x) \left( \tilde{R}^i\right) _{\alpha \beta }\left( R^i\right) ^{\alpha \beta }, \end{aligned}$$

where

$$\begin{aligned} \tilde{R}^i_{\alpha \beta }=\tilde{ \nabla }^\top _\alpha \tilde{\Psi }_\beta {}^{i} -\tilde{\nabla }^\top _\beta \tilde{\Psi }_\alpha {}^{i} +\mathcal{H}_\beta {}^{\mathcal{B}}\mathcal{H}_\alpha {}^{\mathcal{C}}\mathcal{C}_{\mathcal{B}\mathcal{C}}{}^{i}. \end{aligned}$$

The conjugate spinor is defined as \(\tilde{\Psi }_{\alpha }\equiv \Psi ^\dag _{\alpha }\gamma ^0\) and its transverse covariant derivative must be defined by [7]

$$\begin{aligned} \tilde{ \nabla }^\top _\beta \tilde{\Psi }_{\alpha }\equiv \partial ^\top _\beta \tilde{\Psi }_{\alpha }-x_{\alpha }\tilde{\Psi }_{\beta }, \;\;\; \tilde{\nabla }_\alpha ^\top \tilde{\psi }=\partial _\alpha ^\top \tilde{\psi }. \end{aligned}$$
(2.6)

In the approximation of the linear field equation, the action is

$$\begin{aligned} S[\Psi , \tilde{\Psi }]\simeq & {} \int \mathrm{d}\mu (x)\left[ \left( \tilde{\nabla }^\top _\alpha \tilde{ \Psi }_\beta -\tilde{\nabla }^\top _\beta \tilde{ \Psi }_\alpha \right) \right. \nonumber \\&\left. \times \left( \nabla ^{\top \alpha } \Psi ^\beta -\nabla ^{\top \beta } \Psi ^\alpha \right) \right] . \end{aligned}$$
(2.7)

Using the Euler–Lagrange equation, the field equations for two dynamical variables, \(\Psi \) and \(\tilde{\Psi }\), can be obtained [Appendix A]:

$$\begin{aligned} (x_\alpha -\partial ^{\top }_{\alpha }) \left( \nabla ^{\top \alpha } \Psi ^{\beta }-\nabla ^{\top \beta } \Psi ^{\alpha } \right) =0, \end{aligned}$$
(2.8)
(2.9)

The above equations of motion in terms of the Casimir operator can be rewritten in the following forms:

$$\begin{aligned} \left( Q_{\frac{3}{2}}^{(1)}+\frac{5}{2}\right) \Psi _\alpha + \nabla _{\alpha }^\top \partial ^\top \cdot \Psi =0, \end{aligned}$$
(2.10)
(2.11)

It is also shown that (2.10) is completely consistent with Eq. (2.3) that is calculated on the basis of the group theory approach. The vector-spinor Lagrangian density is then invariant under the following gauge transformations [Appendix B]:

$$\begin{aligned} \Psi _\alpha \longrightarrow \Psi ^g_\alpha =\Psi _\alpha +\nabla _{\alpha }^\top \psi , \end{aligned}$$
$$\begin{aligned} \tilde{\Psi }_\alpha \longrightarrow \tilde{\Psi }^g_\alpha =\tilde{\Psi }_\alpha +\partial _{\alpha }^\top \tilde{\psi }. \end{aligned}$$

We would like to introduce a gauge-fixing parameter c:

$$\begin{aligned} \left( Q_{\frac{3}{2}}^{(1)}+\frac{5}{2}\right) \Psi _\alpha + c\nabla _{\alpha }^\top \partial ^\top \cdot \Psi =0. \end{aligned}$$
(2.12)

Equation (2.3), which is a gauge-invariant equation, is a special case of the above equation. When \(c\ne 1\), we have a field equation which is not gauge invariant. The choice of the gauge-fixing parameter c determines the space of gauge solutions, which will be considered in the next section.

3 Gupta–Bleuler triplet

The appearance of the Gupta–Bleuler triplet is crucial for the covariant quantization of the gauge fields [18, 22, 27]. The ambient space formalism allows us to exhibit this triplet for the vector-spinor gauge field in exactly the same manner as it occurs for the Minkowskian counterpart. We start with the gauge-fixing field equation (2.12). The de Sitter invariant bilinear form (or inner product) on the space of solutions is defined for two modes of the field equation (2.12). Let us now define the structure of the space of solutions as the Gupta–Bleuler triplet \(V_g \subset V \subset V_c\).

The indefinite inner product space \(V_c\) includes all the solutions of the field equation (2.12). In other words, the elements of this space are physical and unphysical states with all possible norms such as negative, null, and positive. The subspace V is defined as the space of solutions with the divergencelessness condition, \(\partial ^\top \cdot \Psi =0\). This subspace V is a semi-definite inner product space and an invariant subspace of \(V_c\) (but not invariantly complemented). According to (2.12), it is a manifestly c-independent subspace of solutions. Finally, the gauge subspace \(V_g \subset V\) is defined as \(\Psi _\alpha ^g=\nabla _\alpha ^\top \psi ^p\), where p stands for a pure gauge state. It establishes a subspace with the null norm, which is an invariant subspace of V (but not invariantly complemented). The elements of \(V_g\) are orthogonal to all states in V including themselves. The coset space \(V/V_g\) is the space of the physical states. In the following, we present these three spaces.

3.1 The pure gauge state

Putting the gauge solution \(\Psi _\alpha ^g =\nabla _{\alpha }^\top \psi ^p\) into (2.12) and by using (2.4), we obtain

(3.1)

where \(\psi ^p\) is a spinor field. We will make the following assumptions:

  • If \(c=1\), the spinor field \(\psi ^p\) is arbitrary and unlimited. The field equation is gauge invariant. The gauge vector-spinor space is constructed by a spinor field \(\psi ^p\).

  • If \(c\ne 1\), then \(\psi ^p\) obeys the following field equation:

    $$\begin{aligned} \nabla _{\alpha }^\top \left( Q_{\frac{1}{2}}^{(1)}+\frac{5}{2}\right) \psi ^p=0, \end{aligned}$$

    or, for simplicity, we can choose

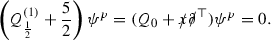    (3.2)

    In this case, the gauge is fixing and the field equation is not a gauge invariant.

This field can be associated to the de Sitter group representation \(\Pi _{\frac{1}{2},{-\frac{1}{2}}}\).

Table 1 The Gupta–Bleuler triplet states
Full size table

3.2 The divergence spinor state

The divergence vector-spinor state is defined as \(\partial ^\top \cdot \Psi ^d \ne 0\). If one takes the divergence of the field equation (2.12),

$$\begin{aligned} \partial ^{\top \alpha }\left[ \left( Q_\frac{3}{2}^{(1)}+\frac{5}{2}\right) \Psi ^\mathrm{d}_\alpha +c\nabla _{\alpha }^\top \partial ^\top \cdot \Psi ^\mathrm{d}\right] =0, \end{aligned}$$

then one obtains [Appendix C]

At this point, one must consider the two cases \(c=1\) and \(c\ne 1\):

  • If \(c=1\), \(\partial ^\top \cdot \Psi ^d\equiv \psi ^s\), where s stands for spinor state, \(\psi ^s\) is an arbitrary spinor field and we have a gauge invariant.

  • If \(c\ne 1\), then \(\psi ^s\) satisfies the following field equation:

    $$\begin{aligned} \left( Q_{\frac{1}{2}}^{(1)}+\frac{5}{2}\right) \psi ^s=0, \end{aligned}$$
    (3.3)

    and the gauge is fixed.

The quotient space \(V_c/V\) is the space of spinor states \(\psi ^s\). This field, similar to the pure gauge state, can be associated with the representation \(\Pi _{\frac{1}{2},{-\frac{1}{2}}}\).

3.3 The physical state

The quotient space \(V/V_g\) is the space of the physical states. These states are the solutions of the field equation (2.2) with the conditions: \(\partial ^\top \cdot \Psi ^\mathrm{phy}=0\), \(\gamma \cdot \Psi ^\mathrm{phy}=0\), and \(\Psi _\alpha ^\mathrm{phy}\ne \nabla _{\alpha }^\top \psi \). These fields are transformed by the discrete series representation \(\Pi ^\pm _{\frac{3}{2},{\frac{3}{2}}}\).

In this way, we obtain approximately what is known as the indecomposable group representation structure for the massless vector-spinor field,

$$\begin{aligned}&\underbrace{\Pi _{\frac{1}{2},-\frac{1}{2}}}_{\mathrm{spinor \; representation}}\;\longrightarrow \underbrace{\Pi _{\frac{3}{2},\frac{3}{2}}^{+} \oplus \Pi _{\frac{3}{2},\frac{3}{2}}^{-}}_{\mathrm{physical \; representation}}\\&\quad \longrightarrow \underbrace{\Pi _{\frac{1}{2},-\frac{1}{2}}}_{\mathrm{pure \; gauge \; representation}} \end{aligned}$$

where the arrows indicate the state leak under the group action. The spin-\(\frac{3}{2}\) unitary irreducible representations of the de Sitter group with the helicity \(\pm \frac{3}{2}\) get involved in the central part \(\Pi ^\pm _{\frac{3}{2},{\frac{3}{2}}}\) and one can see that they contract to the Poincaré massless spin-\(\frac{3}{2}\) representations when the curvature tends to zero [7]. As we can see, the spinor and pure gauge states are associated with the representation \(\Pi _{\frac{1}{2},-\frac{1}{2}}\).

4 Field solution

For simplicity, the vector-spinor field solution is divided into three parts:

$$\begin{aligned} \Psi _\alpha (x)=\Psi _\alpha ^g+\Psi _\alpha ^\mathrm{d}+\Psi _\alpha ^\mathrm{phy}, \end{aligned}$$

where \(\Psi _\alpha ^g\) is the pure gauge solution, \(\Psi _\alpha ^\mathrm{d}\) is the divergence part solution and \(\Psi _\alpha ^\mathrm{phy}\) is the physical solution. We have defined \(\Psi _\alpha ^g=\nabla _\alpha ^\top \psi ^p\), so, if one takes the divergence of it, one obtains

The gauge solution satisfies the divergencelessness condition \(\partial ^\top \cdot \Psi ^g=0\). Then the spinor field equation is (3.2). Also, one cannot impose the condition for spinor and gauge state due to the homogeneous degree of spinor field states (see Eq. (4.4)). From the unitary irreducible representations of the de Sitter group, we know that the physical solution must satisfy the conditions \(\partial ^\top \cdot \Psi ^\mathrm{phy}=0\) and . Therefore, the only divergence part is \(\partial ^\top \cdot \Psi ^d \ne 0\). For a classification, see Table 1.

4.1 The pure gauge and divergence spinor solution

The pure gauge field \(\psi ^{p}\) and the spinor state \(\psi ^{s}\) satisfy similar field equations, see Eqs. (3.2) and (3.3):

(4.1)

By using the identity

(4.2)

there exist two possibilities for the first-order field equation. The first one is

(4.3)

with the degree of homogeneity \(-3\) and 0 [7]. The other field equation reads

(4.4)

with the degree of homogeneity \(-4\) and 1. For the second case, due to the positive homogeneous degree 1, one cannot construct a covariant quantum field operator [7].

The solution of the field equation (4.3) can be written in the following form:

(4.5)

where \(\phi _m\) is a massless minimally scalar field (\(Q_0^{(1)}\phi _m=0\)). \(\mathcal{U}\) is an arbitrary constant spinor which can be fixed by imposing the condition that it becomes the spinor field in the null curvature limit [12, 32]. The solution of the massless minimally coupled scalar field can be written in terms of the de Sitter plane wave: \((x\cdot \xi )^\sigma \) [7, 10], where \(\xi \) is a five-vector in the positive cone \(\mathcal{C}^+\):

$$\begin{aligned} \xi \in \mathcal{C}^+= & {} \{ \xi \in R^5;\;\; \eta _{\alpha \beta }\xi ^\alpha \xi ^\beta =(\xi ^0)^2-\vec \xi \cdot \vec \xi -(\xi ^4)^2\nonumber \\= & {} 0,\; \xi ^0>0 \}. \end{aligned}$$
(4.6)

For the massless minimally coupled scalar field, the degree of homogeneity is \(\sigma =0,-3\). The constant solution poses the famous zero mode problem for this field. By using the following relation between the minimally coupled and the conformally coupled scalar fields \(((Q_0-2)\phi _c=0)\) in the de Sitter ambient space formalism [7]:

$$\begin{aligned} \phi _m=\left[ Z\cdot \partial ^\top +2Z\cdot x\right] \phi _c, \end{aligned}$$
(4.7)

this problem can be surmounted [34]. \(Z_\alpha \) is a constant five-vector. The solution of the massless conformally coupled scalar field can be written in terms of the de Sitter plane wave: \((x\cdot \xi )^\sigma \), \(\sigma =-1,-2\) [7, 10]. Then the spinor field (4.5) can be written in terms of the massless conformally coupled scalar field as

(4.8)

There appear an arbitrary constant spinor \(\mathcal{U}\) and an arbitrary constant five-vector \(Z^\alpha \), which will be fixed in the null curvature limit.

4.2 The physical state solution

The physical part, which is defined by the conditions \(\partial ^\top \cdot \Psi _{\alpha }^{phy}=0\) and , satisfies the following field equation:

There are two possibilities for the relevant first-order field equation:

and

The latter is conformal invariant [14], and in the following, only this solution will be considered. The physical vector-spinor field solution can be written in terms of a polarization vector-spinor \(\mathbf D ^\mathrm{phy}_\alpha \) and a spinor field \(\psi _1\) [14]:

$$\begin{aligned} \Psi _\alpha ^\mathrm{phy}=\mathbf D ^\mathrm{phy}_\alpha (x,\partial ^\top ,Z)\psi _1, \end{aligned}$$

where

The spinor field \(\psi _1\) satisfies

Its solution can be written in terms of a massless conformally coupled scalar field \(\phi _c\) as [14]:

(4.9)

This spinor field and its related two-point functions can in fact be extracted from a massive spinor field in the principal series representation by setting \(\nu =-i\) [32].

4.3 \(\Psi _{\alpha }^{\mathrm{d}}\) solution with \(c=\frac{2}{3}\)

The divergence part is defined as \(\partial ^\top \cdot \Psi _{\alpha }=\partial ^\top \cdot \Psi _{\alpha }^\mathrm{d}\ne 0\) and . It satisfies the field equation:

$$\begin{aligned} \left( Q^{(1)}_{\frac{3}{2}}+\frac{5}{2}\right) \Psi _{\alpha }^\mathrm{d}+c\nabla _\alpha ^\top \partial ^\top \cdot \Psi ^\mathrm{d}=0. \end{aligned}$$
(4.10)

This vector-spinor field \(\Psi _{\alpha }^\mathrm{d}\) can be expressed by three spinor fields \(\zeta _1,\zeta _2\), and \(\zeta _3\) as follows [14]:

$$\begin{aligned} \Psi _\alpha ^{d}=Z_{\alpha }^\top \zeta _1+\nabla _\alpha ^\top \zeta _2+\gamma _\alpha ^\top \zeta _3. \end{aligned}$$
(4.11)

By replacing (4.11) in the field equation (4.10), one obtains

(4.12)
(4.13)
(4.14)

Equation (4.12) can be rewritten as

(4.15)

so, there are two possibilities for the first-order field equations: (1) the conformally coupled spinor field

(4.16)

and (2) the minimally coupled spinor field

(4.17)

Their corresponding solutions are

If \(\zeta _1\) is a minimally coupled spinor field and \(c=\frac{2}{3}\), Eqs. (4.13) and (4.14) have a solution and the spinor fields \(\zeta _2\) and \(\zeta _3\) can be written in terms of \(\zeta _{1m}\) as [Appendix D]:

(4.18)

and

(4.19)

where w is a constant arbitrary parameter.

4.4 The general solution

In this subsection, we want to find a general solution without any conditions. This solution can be written as

$$\begin{aligned} \Psi _\alpha =Z_{\alpha }^\top \psi _1+\nabla _\alpha ^\top \psi _2+\gamma _\alpha ^\top \psi _3. \end{aligned}$$
(4.20)

Similar to the previous subsection, by replacing (4.20) in the field equation (2.12), one obtains

(4.21)
(4.22)
(4.23)

The field equation (4.21) is similar to the field equation of the spinor field \(\zeta _1\) and there are two first-order field equations for \(\psi _1\) as Eq. (4.15). By using the identities (D.4), (D.5), and (D.6) [Appendix D], the spinor fields \(\psi _2\) and \(\psi _3\) can be written in terms of the spinor field \(\psi _1\) as

(4.24)
(4.25)

where \(n_1,\ldots , m_3\) are the constant arbitrary parameters.

Replacing these solutions in Eqs. (4.22) and (4.23) and using the spinor field equation (4.17) for \(\psi _1\), we obtain a solution only for the value \(c=\frac{2}{3}\):

$$\begin{aligned} n_1=\frac{3}{4}+3t, \;\; n_2=\frac{1}{12}+t, \;\;\;n_3=-\frac{1}{2}-4t, \end{aligned}$$
$$\begin{aligned} m_1=-\frac{5}{4}-6t, \;\; m_2=t, \;\;\;m_3=-\frac{3}{4}-3t, \end{aligned}$$

where t is a constant arbitrary parameter. In this case, the general solution becomes

(4.26)

where the spinor field \(\psi _{1m}\) is

For this solution, there are a constant parameter t, a constant spinor \(\mathcal{U}\), and two constant five-vectors \(Z^\alpha \) and \(Z'^\alpha \). One of the problems of this solution is that these constant parameters cannot be fixed in the null curvature limit. Another problem is that c is fixed with value \(\frac{2}{3}\), then the solution is not a general solution and should be ignored.

Similar to the above procedure and using the spinor field equation (4.16) for \(\psi _1\), the general solution becomes

(4.27)

where

$$\begin{aligned}&n_1=\frac{c(4c-1)-1}{2(1-c)}, \;\; n_2=\frac{3c-2}{4(1-c)}, \;\;\;n_3=-\frac{c(4c-3)}{4(1-c)},\\&m_1=-\frac{c^2(2c+3)+2(1-3c)}{c(1-c)}, \\&m_2=-\frac{c(16c-23)+8}{4(1-c)}, \\&m_3=\frac{4c(1-c)-1}{4(1-c)}. \end{aligned}$$

The spinor field \(\psi _{1c}\) is

In this case, there are a constant spinor \(\mathcal{U}\) and a constant five-vector \(Z_\alpha \), which can be fixed in the null curvature limit and specify the indecomposable representation of the de Sitter group. There exists a five-dimensional trivial representation with respect to \(Z_\alpha ^{(\lambda )}\) [35]. For a thorough investigation regarding the five existing polarization states \(\lambda = 0,1, 2, 3, 4\), the reader may refer to [35]. The solution (4.27) is also a general solution since c is arbitrary. In the next section, the quantum field operator and its corresponding two-point function are constructed by this solution.

5 Quantum field operator and two-point function

In the previous section, it is proved that the ambient space formalism permits us to write the vector-spinor field in terms of a vector-spinor polarization state and a massless conformally coupled scalar field (4.27):

$$\begin{aligned} \Psi _\alpha \equiv \mathcal{D}_\alpha (x,\partial ,Z)\mathcal{U}\phi _c, \end{aligned}$$
(5.28)

where

First, we recall the construction of the quantum field operator and the two-point function for the massless conformally coupled scalar field \(\phi _c\), then it is simply generalized to the massless vector-spinor field.

5.1 Massless conformally coupled scalar field

In the ambient space formalism the massless conformally coupled scalar field solution can be written in terms of the de Sitter plane wave \((x\cdot \xi )^{\sigma }\) with \(\sigma =-1,-2\) [9]. This plane-wave solution cannot be defined globally in de Sitter space, but it can be defined globally in complex de Sitter space-time [9–11]:

$$\begin{aligned}&M_H^{(c)}=\left\{ z=x+iy\in \mathbbm {C}^5;\;\;\right. \nonumber \\&\quad \eta _{\alpha \beta }z^\alpha z^\beta =(z^0)^2-\vec z\cdot \vec z-(z^4)^2=\left. -H^{-2}\right\} \nonumber \\&\quad =\left\{ (x,y)\in \mathbbm {R}^5\times \mathbbm {R}^5; x^2-y^2=-H^{-2},\; x\cdot y=0\right\} .\nonumber \\ \end{aligned}$$
(5.29)

Let \(T^\pm = \mathbbm {R}^5+iV^\pm \) to be the forward and backward tubes in \( \mathbbm {C}^5\). The domain \(V^+\)(resp. \(V^-)\) stems from the causal structure on \(M_H\):

$$\begin{aligned} V^\pm =\left\{ x\in \mathbbm {R}^5;\;\; x^0\mathop {<}\limits ^{>} \sqrt{\parallel \vec x\parallel ^2+(x^4)^2}\right\} . \end{aligned}$$
(5.30)

Then we introduce their respective intersections with \(M_H^{(c)}\)

$$\begin{aligned} \mathcal{T}^\pm =T^\pm \cap M_H^{(c)}, \end{aligned}$$
(5.31)

which are called the forward and backward tubes of the complex de Sitter space \(M_H^{(c)}\). Finally, the “tuboid” on \(M_H^{(c)}\times M_H^{(c)}\) is defined by

$$\begin{aligned} \mathcal{T}_{12}=\left\{ (z,z');\;\; z\in \mathcal{T}^+,z' \in \mathcal{T}^- \right\} . \end{aligned}$$
(5.32)

If z varies in \(\mathcal{T}^+\) (or \(\mathcal{T}^-\)) and \(\xi \) lies in the positive cone \(\mathcal{C}^+\) (4.6):

$$\begin{aligned} \xi \in \mathcal{C}^+=\left\{ \xi \in \mathcal{C}; \; \xi ^0>0 \right\} , \end{aligned}$$

the plane-wave solutions are globally defined since the imaginary part of \((z.\xi )\) has a fixed sign (for more details, see [10]). In terms of the de Sitter complex plane wave, the field operator can be written in the following form [7, 34]:

$$\begin{aligned} \phi _c(z)=\sqrt{ c_0 }\int _{S^3} \mathrm{d}\mu (\mathbf{\xi }) \left\{ \; a({\tilde{\xi }})(z\cdot \xi )^{-2} +a^\dag (\mathbf{\xi })(z\cdot \xi )^{-1} \right\} , \end{aligned}$$
(5.33)

where \(\xi ^\alpha =(1, \vec \xi , \xi ^4)\), \(\tilde{\xi }^\alpha =(1, -\vec \xi , \xi ^4)\), and the vacuum state is defined as [7]:

$$\begin{aligned}&a(\mathbf{\xi })|\Omega >=0,\;\; a^\dag (\mathbf{\xi })|\Omega >=|\xi >, \;\;< \xi ' |\xi >=\delta _{S^3}(\xi -\xi '), \\&\int _{S^3} d\mu (\mathbf{\xi })\delta _{S^3}(\xi -\xi ') =1. \end{aligned}$$

The notations are defined explicitly in [7].

The analytic two-point function is defined in terms of the complex de Sitter plane waves by [9, 10]

$$\begin{aligned} W_c(z_1,z_2)= & {} \left<\Omega |\phi (z_1)\phi (z_2)|\Omega \right>\nonumber \\= & {} c_0\int _{S^3}d\mu (\xi ) (z_1\cdot \xi )^{-2}(z_2.\cdot \xi )^{-1}, \end{aligned}$$
(5.34)

and \(c_0\) is obtained by using the local Hadamard condition. The vacuum state \(|\Omega >\) in this case is exactly equivalent to the Bunch–Davies vacuum state [7]. One can easily calculate (5.34) in terms of the generalized Legendre function [10]:

$$\begin{aligned} W_c(z_1,z_2)= & {} \frac{-iH^2}{2^4\pi ^2} P_{-1}^{(5)}(H^2 z_1\cdot z_2)= \frac{H^2}{8\pi ^2}\frac{-1}{1-\mathcal{Z}(z_1,z_2)}\nonumber \\= & {} \frac{H^2}{4\pi ^2}(z_1-z_2)^{-2}, \end{aligned}$$
(5.35)

where \(\mathcal{Z}(z_1,z_2)=-H^2 z_1\cdot z_2\). The Wightman two-point function \(\mathcal{W}_c(x_1,x_2)\) is the boundary value (in the sense of its interpretation as a distribution function, according to Theorem A.2 in [10]) of the function \(W_c(z_1, z_2)\) which is analytic in the domain \(\mathcal{T}_{12}\) of \(M_H^{(c)}\times M_H^{(c)}\) [10]. The boundary value is defined for \(z_1 =x_1+iy_1\in \mathcal{T}^-\) and \(z_2=x_2+iy_2\in \mathcal{T}^+\) as

$$\begin{aligned} \mathcal{Z}(z_1,z_2)=\mathcal{Z}(x_1,x_2)-i\tau \epsilon (x_1^0,x_2^0), \end{aligned}$$

where \(y_1=(-\tau ,0,0,0,0)\in V^-\), \(y_2=(\tau ,0,0,0,0)\in V^+\), and \(\tau \rightarrow 0\). Then one obtains [10, 12, 33]

$$\begin{aligned}&\mathcal{W}_c(x_1,x_2)=\frac{-H^2}{8\pi ^2}\lim _{\tau \rightarrow 0}\frac{1}{1-\mathcal{Z}(x_1,x_2)+i\tau \epsilon (x_1^0,x_2^0)}\nonumber \\&\quad =\frac{-H^2}{8\pi ^2}\left[ P\frac{1}{1-\mathcal{Z}(x_1,x_2)} -i\pi \epsilon (x_1^0,x_2^0)\delta (1-\mathcal{Z}(x_1,x_2))\right] ,\nonumber \\ \end{aligned}$$
(5.36)

where the symbol P is the principal part and \(\mathcal{Z}(x_1,x_2)\) is the geodesic distance between the two points \(x_1\) and \(x_2\) on the de Sitter hyperboloid:

$$\begin{aligned} \mathcal{Z}(x_1,x_2)=-H^2 x_1\cdot x_2=1+\frac{H^2}{2} (x_1-x_2)^2, \end{aligned}$$

and

$$\begin{aligned} \epsilon (x_1^0-x_2^0)=\left\{ \begin{array}{l@{\quad }l} 1&{}\,x_1^0>x_2^0 \\ 0&{}\,x_1^0=x_2^0\\ -1&{}\,x_1^0<x_2^0\\ \end{array} \right. . \end{aligned}$$
(5.37)

5.2 Massless Vector-spinor field

Using Eqs. (5.28) and (5.33), in the complex de Sitter space, the vector-spinor field operator is then defined by [7]

$$\begin{aligned} \Psi _\alpha (z)\equiv & {} \sqrt{ c_0 } \int _{S^3} d\mu (\xi )\sum _{\lambda =0}^4\sum _{r=1,2}\mathcal{D}_\alpha (z,\partial ,Z^\lambda ) \mathcal{U}^r(\xi ) \nonumber \\&\times \left\{ \; a(\tilde{\xi })(z\cdot \xi )^{-2} +a^\dag (\xi )(z\cdot \xi )^{-1} \right\} , \end{aligned}$$
(5.38)

where the explicit form of \(\mathcal{U}^r\) is defined in [12, 32]. The explicit form of the polarization five-vector \(Z^\lambda \) depends on the indecomposable representation of the de Sitter group [35]. As a simple case, one can choose [7, 34]:

$$\begin{aligned} \sum _{\lambda =0}^4 \sum _{\lambda '=0}^4 Z^{(\lambda )}_\alpha Z^{(\lambda ')}_\beta =\eta _{\alpha \beta },\;\;\; Z^{(\lambda )}\cdot Z^{(\lambda ')}=\eta ^{\lambda \lambda '}. \end{aligned}$$
(5.39)

The analytic function \(S_{\alpha \beta }(z,z')\) is defined as [32]

$$\begin{aligned} S_{\alpha \beta }(z,z')=\langle \Omega |\Psi _\alpha (z)\bar{\Psi }_\beta (z')|\Omega \rangle , \end{aligned}$$

where \(z,z'\in M_H^c\) and \(|\Omega \rangle \) is the vacuum state. By using the identity [12]

the two-point function can be written in the following compact form:

$$\begin{aligned} S_{\alpha \beta }(z,z')=\sum _{\lambda ,\lambda '}\mathcal{D}_\alpha (z,\partial ,Z^\lambda ) S_c(z,z'){\bar{\mathcal{D}}_\beta }(z',\overleftarrow{\partial }',Z^{\lambda '}), \end{aligned}$$
(5.40)

where \(\bar{\mathcal{D}}=\gamma ^0\gamma ^4\mathcal{D}^\dag \gamma ^0\gamma ^4\) and \(S_{c}\) is the two-point function of massless conformally spinor field [12]:

(5.41)

The two-point functions of the massless conformally coupled scalar field (\(W_c)\) and the massless spinor field (\(S_c\)) are constructed on Bunch–Davis vacuum states and preserve the Hadamard structure [9, 10, 32]. Then our two-point function (5.40), which is constructed from a massless conformally coupled scalar field and a polarization tensor-spinor, preserves the correct Hadamard structure. The polarization tensor-spinor takes the derivative of the \(W_c\) and the derivative cannot break the Hadamard structure. It is important to note that in our construction the negative norm states do not appear for the scalar field (5.33) and the Bunch–Davis vacuum state is used.

6 Conclusions

In this paper, the massless vector-spinor or super-gauge field \(\Psi _\alpha \) is studied in the de Sitter ambient space formalism. The super-gauge-invariant Lagrangian density is presented by using the super-gauge-covariant derivative. The Gupta–Bleuler triplet is discussed. It is shown that the field solutions are built up from a conformally coupled scalar field and a vector-spinor polarization state. Finally, the quantum field operator and its corresponding two-point function are calculated. The two-point function is analytic in this construction. Since the quantum field theory in our formalism is unitary and analytic, a unitary supergravity in the de Sitter ambient space formalism seems quite plausible.

In this paper the free field quantization is considered, using the interaction Lagrangian which is defined in ambient space notation by the gauge principle [7] one can perform the one-loop correction for various fields that (may) couple to the gravitino. By coupling this vector-spinor gauge field with the massless spin-2 gauge field in the de Sitter ambient space formalism, a unitary supergravity may be obtained, which will be studied in a forthcoming paper.