Probing flavor models with $^{\text {76}}$Ge-based experiments on neutrinoless double-$\beta$ decay

Abstract

The physics impact of a staged approach for double-$\beta$ decay experiments based on $^{\text {76}}$Ge is studied. The scenario considered relies on realistic time schedules envisioned by the Gerda and the Majorana collaborations, which are jointly working towards the realization of a future larger scale $^{\text {76}}$Ge experiment. Intermediate stages of the experiments are conceived to perform quasi background-free measurements, and different data sets can be reliably combined to maximize the physics outcome. The sensitivity for such a global analysis is presented, with focus on how neutrino flavor models can be probed already with preliminary phases of the experiments. The synergy between theory and experiment yields strong benefits for both sides: the model predictions can be used to sensibly plan the experimental stages, and results from intermediate stages can be used to constrain whole groups of theoretical scenarios. This strategy clearly generates added value to the experimental efforts, while at the same time it allows to achieve valuable physics results as early as possible.

1 Introduction

Neutrino physics led to big discoveries in the past decades, the greatest being the observation of neutrino oscillations [1], which prove that neutrino masses (albeit tiny) must be non-zero and that neutrino flavors mix. In a nutshell, this means that an electron neutrino does not have a fixed mass but it is rather a quantum-mechanical superposition of several mass eigenstates. While nowadays most oscillation parameters are known [2] and a new era of precision neutrino physics has started, several fundamental questions are still unanswered. Probably the most important question is whether neutrinos have a Majorana nature, i.e., if they are identical to their antiparticles, which would signal a violation of lepton number and thus lead beyond the very successful standard model of particle physics. Such questions can be answered by the observation of neutrinoless double-$\beta$ decay ($0\nu \beta \beta$) [3], a nuclear transition in which two neutrons decay simultaneously into two protons by emitting two electrons but no neutrino, thus changing lepton number by two units and possibly signaling a Majorana neutrino mass [4, 5].

The experimental search for $0\nu \beta \beta$ is a very active field of particle and nuclear physics. Various isotopes for which $0\nu \beta \beta$ is energetically allowed and many detection techniques are pursued. Examples are: $^{\text {76}}$Ge with high purity Ge detectors [6–8], $^{\text {130}}$Te with TeO$_2$ bolometric detectors [9], $^{\text {136}}$Xe with liquid Xe time projection chambers [10], or Xe-loaded organic liquid scintillator detectors [11]. Historically, $^{\text {76}}$Ge-based experiments have been leading the field, and the resulting constraints on the half-life of the process are among the most stringent ones [12–14]. Two $^{\text {76}}$Ge-based experiments are currently active and will yield results in the near future: Gerda [6] and Majorana [7, 8]. These two collaborations conceive of eventually realizing a common large scale $^{\text {76}}$Ge (LSGe) experiment [15], capable of probing the theoretically allowed region for the inverted mass ordering (i.e., the experimentally favorable scenario corresponding to the upper yellow band in Fig. 1). For such a challenging experiment, a modular design and a staged approach implementation are needed, meaning that the target mass will be progressively increased.

This paper presents realistic projections of the sensitivity achievable by a global analysis of the data from current and future experiments searching for $0\nu \beta \beta$ in $^{\text {76}}$Ge. Among $0\nu \beta \beta$ experiments, the ones based on $^{\text {76}}$Ge stand out because they are designed to perform quasi background-free measurements. Their data can hence be combined without limiting assumptions on the background modeling. We also point out that the sensitivity of a global analysis should be considered when planning the mass-increasing strategy of a project, in order to maximize the benefit for both theory and experiment. Indeed, in case no signal will be observed, large classes of theoretical neutrino models can be excluded already by intermediate stages of an experiment.

2 $0\nu \beta \beta$ and neutrino mass sum rules

The physics observable accessible with $0\nu \beta \beta$ experiments is the effective Majorana neutrino mass $|m_{ee}|= |m_1 c_{12}^2 c_{13}^2 + m_2 s_{12}^2 c_{13}^2 e^{i\alpha _{21}} + m_3 s_{13}^2 e^{i(\alpha _{31} - 2\delta )}|$, which depends on sines (s) and cosines (c) of leptonic mixing angles $\theta _{ij}$, mass eigenvalues, and phases [16, 17]. It is related to the $0\nu \beta \beta$ half-life by [18]:

$$\begin{aligned} 1/ T_{1/2}^{0\nu }= G_{0\nu } |\mathcal {M}_{0\nu }|^2 |m_{ee}|^2, \end{aligned}$$

(1)

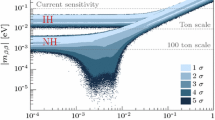
where $G_{0\nu } = 2.42 \times 10^{-26}\, {\mathrm{year}}^{-1}\mathrm{eV}^{-2}$ is a phase-space factor and $\mathcal {M}_{0\nu }$ is the dimensionless nuclear matrix element (NME) which parametrizes the nuclear physics. The allowed range for $|m_{ee}|$ as a function of the smallest neutrino mass m is constrained by the measurements of the neutrino mixing parameters, see Fig. 1.

Fig. 1

Allowed regions for the effective mass $|m_{ee}|$ calculated using global fit parameters [2], along with the median sensitivity of specific stages of $^{\text {76}}$Ge-based experiments considered in the text. The width of the sensitivity bands accounts for the nuclear physics uncertainties. The disfavored regions are the most optimistic bounds from $^{\text {136}}$Xe-based experiments [10, 11] and Planck [19], the latter converted to the smallest neutrino mass and averaged between both mass orderings

Nevertheless, information about the absolute neutrino mass that is inferred by combining all experiments is affected by systematic uncertainties of the analysis procedure [20], the NMEs [21–33], and the mixing parameters [16, 17]. Consequently, even pinning down the neutrino mass ordering – whether normal, $m_1 < m_2 < m_3$ (blue), or inverted, $m_3 < m_1 < m_2$ (yellow) – is challenging.

This situation could drastically change with additional input from neutrino physics. The smallness of neutrino masses can be theoretically explained by suppression mechanisms at tree- [34–43] or loop-level [44–50] and the large mixing angles by flavor models based on discrete symmetries [51–54], which motivate them by relating their values to finite symmetry groups. Certain models even predict correlations between observables. Prime examples are neutrino mass sum rules [55–58], such as $\tilde{m}_1 + \tilde{m}_2 = \tilde{m}_3$ or $1/\tilde{m}_1 + 1/\tilde{m}_3 = 2/\tilde{m}_2$, which correlate the complex neutrino mass eigenvalues $\tilde{m}_i$. These rules are complex equations and thus deliver a constraint on the mass scale m and a relation between the Majorana phases $\alpha _{21,31}$. Reference [58] investigated more than 50 flavor models divided into 12 classes, which – as Fig. 2 shows – can greatly decrease the allowed range for $|m_{ee}|$, thereby offering the possibilities of gaining valuable knowledge on the neutrino sector already by the intermediate steps in a staged approach towards detecting $0\nu \beta \beta$.

Fig. 2

Range of the effective mass allowed for different classes of neutrino flavor models that are characterized by specific sum rules. The median sensitivity for specific stages of $^{\text {76}}$Ge-based experiments considered in the text is also displayed, along with indications of how these regions would extend if further variations of the NMEs are taken into account (see discussion in Sect. 5)

3 $^{\text {76}}$Ge-based experiments

The advantages of using high purity Ge (HPGe) detectors for $0\nu \beta \beta$ searches have been recognized early [59]. HPGe detectors can be produced from germanium isotopically enriched in $^{\text {76}}$Ge ($^{\text {enr}}$Ge, typically 87 % enrichment). The experimental signature expected for $0\nu \beta \beta$ inside the detector is a peak in the energy spectrum at the Q value of the $^{\text {76}}$Ge decay, which is known to be $Q_{\beta \beta }=2039.061(7)$ keV [60]. Remarkable advantages of this detection technique are the intrinsic radio-purity of the detectors, the excellent spectroscopic performance ($\lesssim$0.1 % energy resolution at $Q_{\beta \beta }$), and the high detection efficiency. In addition, these detectors are a well consolidated technology widely used for $\gamma$-ray spectroscopy, which proved to be reliable and suitable for long-term experiments. The detector geometries considered for $0\nu \beta \beta$ experiments include three types: coaxial, Broad Energy Germanium (BEGe), and P-type Point Contact (PPC) [61–63]. Each geometry results in a specific electric field inside the detector, which affects the performance of event-reconstruction techniques based on the time evolution of the read-out electrical signals (i.e., pulse shape analysis). HPGe detectors must be operated at cryogenic temperatures and are commonly installed in vacuum cryostats. This approach was adopted by past $0\nu \beta \beta$ experiments [12, 13], which operated coaxial-type detectors in low background cryostats surrounded by massive lead and copper shieldings.

Nowadays, the Majorana collaboration is pursuing a design based on PPC-type detectors and multiple cryostat modules built from ultrapure electroformed copper. Two modules are currently being assembled (i.e., the Majorana Demonstrator [7, 8]) at the Sanford Underground Research Facility (USA). The first module hosts 16.8 kg of $^{\text {enr}}$Ge detectors and will be fully operational in the second half of 2015. The completion of the second cryostat containing further 12.6 kg of  $^{\text {enr}}$Ge  detectors is scheduled by the end of 2015. The experiment is designed to operate the detectors at a background level of $0.75 \times 10^{-3}$ $\text {cts}/(\text {keV}\,\text {kg}\,\text {year})$ at $Q_{\beta \beta }$.¹ The Gerda collaboration is exploring in parallel an alternative design in which an array of bare $^{\text {enr}}$Ge detectors is operated directly in ultra radio-pure liquid argon, which acts as coolant material, passive shielding against external radioactivity, and active veto-system when its scintillation light is detected. The setup is installed in the Gran Sasso underground laboratories of INFN in Italy. Gerda has completed its first phase of operation (Phase I), during which ${\sim }$15 kg of $^{\text {enr}}$Ge detectors (mostly coaxial type) have been operated with a background level of $10^{-2}$ $\text {cts}/(\text {keV}\,\text {kg}\,\text {year})$, yielding a limit of ${T_{1/2}^{0\nu }}\ge 2.1 \times 10^{25}$ year [14]. The apparatus is currently being upgraded to operate additional 17 kg of $^{\text {enr}}$Ge BEGe-type detectors and new sensors for the argon scintillation light. A second data taking phase (Phase II) is planned to start in the second half of 2015 with a background level of $10^{-3}$ $\text {cts}/(\text {keV}\,\text {kg}\,\text {year})$  at $Q_{\beta \beta }$ [64].

Both the Majorana Demonstrator and Gerda Phase II will start the exploration of $T_{1/2}^{0\nu }$ at the scale of $10^{26}$ year, i.e., ${|m_{ee}|}\,{\sim } 0.1$ eV. The results collected by these experiments during the first years of operation are essential to define the design of the LSGe experiment and down-select the best technologies to operate ${\gtrsim }1000$ kg of target mass at a background level of ${\lesssim }10^{-4}$ $\text {cts}/(\text {keV}\,\text {kg}\,\text {year})$ at $Q_{\beta \beta }$. With such parameters, the LSGe experiment will probe $T_{1/2}^{0\nu }$ at the level of $10^{27}$–$10^{28}$ year and hence explore an essential part of the parameter space for inverted mass ordering or – with a fortunate value of $\theta _{12}$ and better precision coming from experiments like JUNO [65] or RENO-50 [66] – even the whole parameter space.

4 Global sensitivity

The sensitivity achievable by a global analysis of Gerda Phase I and Phase II, the Majorana Demonstrator, and a future LSGe experiment has been studied by assuming the data sets in Table 1. Following the approach adopted by the Gerda collaboration, data from Gerda Phase I are divided into two data sets according to the two detector types.² The separation into two data sets is assumed also for Phase II. The experimental parameters like efficiency, background level, and data taking time are taken from Ref. [14]. The energy resolution is taken from recent R&D results [64, 67, 68]. BEGe-type detectors provide higher energy resolution and superior background reduction performance with respect to the coaxial type. Data from Majorana Demonstrator are also split between the two modules into two data sets. Efficiencies of PPC- and BEGe-type detectors are assumed equal. This assumption is fully consistent with the first results presented by the Majorana collaboration [63], from which the energy resolution is taken.

Table 1 Parameters assumed for each data set: detector mass, efficiency $\epsilon$, background level at $Q_{\beta \beta }$, energy resolution (full width at half maximum, FWHM) at $Q_{\beta \beta }$, start time, and duration of the data taking $\Delta t$. The start time of current (future) experiments is indicated with $t_0$ ($t_1$) and expected to be in the second half of 2015 (in the 2020s)

A staged approach is assumed for the LSGe experiments. Given realistic constraints on the production of $^{\text {enr}}$Ge material³ the total target mass of 1000 kg is assumed to be progressively increased by installing one new module with 200 kg of detectors per year. The detectors are considered to perform similarly to BEGe-type detectors.

The total number of $0\nu \beta \beta$ events in each data set as a function of $T_{1/2}^{0\nu }$ is:

$$\begin{aligned} N^{0\nu } = \ln 2 \cdot N_{A} \cdot \epsilon \cdot \eta /\left( m_{a} \cdot T_{1/2}^{0\nu }\right) , \end{aligned}$$

(2)

where $N_A$ is Avogadro’s number, $\epsilon$ the efficiency, $\eta$ the exposure, and $m_a$ the molar mass of $^{\text {enr}}$Ge. In this work, the exposure $\eta$ is defined as the product of total detector mass and data taking time. The efficiency $\epsilon$ is given by the product of: the fraction of $^{\text {76}}$Ge in the detector material (${\sim }$87 %), the fraction of active detector volume (87 % for coaxial, 92 % for BEGe/PPC detectors), the efficiency of the analysis cuts (90 %, dominated by pulse shape analysis), and the probability that $0\nu \beta \beta$ events in the detector active volume are correctly reconstructed at $Q_{\beta \beta }$ (92 % for coaxial, 90 % for BEGe/PPC detectors). These efficiencies are taken from Ref. [14]. A duty cycle of 95 % is assumed for all experiments, which accounts for calibration time and hardware maintenance.

A statistical approach is adopted to estimate the $T_{1/2}^{0\nu }$ lower limit achievable by a global analysis of the various data sets. More than $10^{6}$ time-stamps are randomly selected. Given a time-stamp, background events with a uniform energy distribution in the range $Q_{\beta \beta }\pm 0.1$ MeV are generated with Monte Carlo techniques. Events are generated independently for each data set according to its background level, exposure, and efficiency. A simultaneous fit of all data sets is performed, using a constant probability density for the background and a Gaussian for the $0\nu \beta \beta$ signal (centroid at $Q_{\beta \beta }$). The 90 % C.L. upper limit on number of $0\nu \beta \beta$ counts extracted from the fit is converted into a 90 % C.L. lower limit on $T_{1/2}^{0\nu }$ by using Eq. (2). The fit procedure is based on an unbinned profile likelihood analysis in which the number of $0\nu \beta \beta$ counts is bounded to positive values. The free parameters of the fit are the number of signal counts (the parameter of interest) and the background levels (nuisance parameters). Systematic uncertainties (energy scale, resolution, efficiency) have been studied by adding Gaussian pull terms to the likelihood function and found to worsen the limits by ${\lesssim }1\,\%$. The coverage of the method has been tested for a sample of time-stamps and found to provide a conservative overcoverage.

The results are shown in Fig. 3. The top panel illustrates the integrated exposure over time. The increase of exposure is driven by Gerda Phase I (between 2012 and mid 2013), Gerda Phase II and the Majorana Demonstrator (between $t_0$ and $t_0$+4 year) and the LSGe experiment (between $t_1$ and $t_1$+10 year). The middle panel shows the distribution of the 90 % C.L. lower limits on $T_{1/2}^{0\nu }$. The uppermost part of the distribution is populated by the data set realizations with no background events at $Q_{\beta \beta }$ (i.e., fully background-free). It grows linearly with the exposure and has a sharp cut-off due to the constraint $N^{0\nu }\ge 0$ imposed on the fit. The bottom panel shows the distribution of the 90 % upper limits on $|m_{ee}|$. This distribution is computed by converting each $T_{1/2}^{0\nu }$ limit through Eq. (1), which introduces an additional systematic uncertainty on each limit due to the uncertain NME calculations. The effect of this systematic uncertainty is maximally included in the plot assuming NME values in the range between 4.6 and 5.8 [58]. Thus, the median line becomes a band and the central intervals broaden. The median intervals obtained when intersecting the black band with the vertical red dashed lines (i.e., with our example exposure values) precisely correspond to the widths of the red bands in Figs. 1 and 2. The impact of the uncertainties on the NME calculation is further discussed in Sect. 5.

Fig. 3

Top panel Integrated exposure assumed for the calculation as a function of time before (solid line) and after (dashed line) efficiency correction. Middle (bottom) panel Distribution of the 90 % C.L. lower limits on $T_{1/2}^{0\nu }$ (upper limits on $|m_{ee}|$) derived by a global analysis of multiple realizations of the experiments. The vertical red lines corresponds to specific values of exposure/sensitivity discussed in the text. The time axis is broken and future dates are given with respect to the start of Gerda Phase II and the Majorana Demonstrator ($t_0$), and of the future LSGe experiment ($t_1$)

Our calculation shows how successive experiments can improve the median experimental sensitivity by an order of magnitude. Gerda Phase I reached a sensitivity of $T_{1/2}^{0\nu }> 2.6 \times 10^{25}$ year ($|m_{ee}|> 215$–272 meV) with an exposure of ${\sim }$20 kg year (leftmost red line in Fig. 3). Gerda Phase II and the Majorana Demonstrator will improve the sensitivity up to $T_{1/2}^{0\nu }> 4 \times 10^{26}$ year ($|m_{ee}|> 58$–74 meV) by collecting an exposure of $3 \times 10^{2}$ $\text {kg}\,\text {year}$ in 4 year. The LSGe experiment will rise the sensitivity up to $T_{1/2}^{0\nu }> 8 \times 10^{27}$ year ($|m_{ee}|> 13$–16 meV) in 10 year of data taking and a final exposure of $8 \times 10^{3}$ $\text {kg}\,\text {year}$. It is noteworthy that a sensitivity of $T_{1/2}^{0\nu }> 3 \times 10^{27}$ year ($|m_{ee}|> 19$–24 meV) can be reached with about $2 \times 10^{3}$  $\text {kg}\,\text {year}$ in 4 years of data taking with the LSGe experiment.

5 Uncertanties on the nuclear matrix element calculation

The range of NME values used in Fig. 3 to convert $T_{1/2}^{0\nu }$ into $|m_{ee}|$ covers all the calculations available in the literature except for the shell model. This type of model predicts an “outlier” value [58] for the NME down to 2.2 [31–33], and it is not included in our range (4.6–5.8) for two reasons. Firstly, to have a reasonable computation time, shell model calculations are performed with an incomplete set of basis states [70], which in particular results in missing/neglected spin-orbit partners and a violation of one consistency check (the Ikeda sum rule). If one of the “working” methods to compute the NMEs, namely the so-called quasi random phase approximation (QRPA) is restricted to the same reduced set of basis states, it does in fact reproduce the result of the shell model computation [23, 71]. Secondly, $^{\text {76}}$Ge is a nucleus with triaxial symmetry in the ground state [72] and thus very hard to describe in the shell model. Thus, we do in fact not consider the shell model to be a very good description of $^{\text {76}}$Ge. Nonetheless, to show the impact of an extended NME range that covers also the shell model (2.2–5.8), we added in Fig. 2 the horizontal black solid lines at the tips of the red bands. As visible, including the shell model would allow the two leftmost red bands to overlap.

A second additional source of uncertainties comes from the value of the axial vector coupling which was assumed to be $g_A=1.25$ in the previous discussion. The axial vector coupling could have a relatively strong dependence on the Q value of a decay, an effect called quenching [73–76]. In order to illustrate the effect of the quenching as well, we varied $g_A$ between 1.25 and 0.58, the latter value obtained from the phenomenological parametrization of $g_A$ put forward in Eq. (9) of the third Ref. [73–76]. We have done this exercise for all NME computations for which the references did actually give the decisive explicit information.⁴ In Fig. 2, two different NME ranges are indicated: 3.2–11.3 (including quenching but not including the shell model) marked by the horizontal black dashed lines and 0.5–11.3 (including both quenching and the shell model) marked by the horizontal black dotted lines. While the former option does not lead to strong qualitative changes compared to the case with the shell but without quenching (except for a small overlap of the two inner bands), including all uncertainties leads to such a considerable broadening that in fact no information at all can be drawn anymore.

This discussion makes it clear how important an increased understanding from the theoretical side is: if indeed it was clear that the shell model provided a bad description of $^{\text {76}}$Ge, even the full variation by the quenching would not completely destroy the possibility to distinguish different flavor models. If, on the contrary, quenching could be understood on a level of at least narrowing down the range for $g_A$, it may be possible to at least draw some conclusions and e.g. exclude models predicting the highest values of $|m_{ee}|$. However, if all errors persist in their full range, it will not be possible to make a decent statement.

6 Impact on flavor models

The ultimate question to answer is what can be learned about neutrinos from future $^{\text {76}}$Ge-based experiments. Starting with the red bands, Fig. 1 shows how challenging it is to fully probe the parameter space allowed for $|m_{ee}|$ in the most general situation, even considering the future LSGe experiment and inverted mass ordering. Intermediate sensitivity stages seem unable to provide remarkable physics results unless a signal is observed. However, we demonstrate in Fig. 2 that whole groups of neutrino flavor models, namely those predicting particular mass sum rules, can be excluded already by intermediate stages. For example, the rule $\tilde{m}_1^{-1} + \tilde{m}_2^{-1} = \tilde{m}_3^{-1}$ yields for inverted ordering a smallest neutrino mass of 51 meV (48 meV) for the best-fit (3$\sigma$) values of the neutrino mass squares. This region can be almost probed by Gerda Phase II and the Majorana Demonstrator, and fully probed (i.e., even considering NME uncertainties) by first stages of the LSGe experiment. Thus, by using sum rule predictions as orientation when planning the stages, one can exploit the synergies between theoretical models and experimental sensitivities to enhance the physics outcome even of the intermediate stages. This synergy goes so far that some groups of models could be distinguished despite the uncertainties, and our considerations would be strengthened by better knowledge on the NMEs, the mass ordering, and $\theta _{12}$ – especially because sum rules are quite stable to radiative corrections [77]. Additionally, we point out that a remarkable number of models could be already ruled out with ${\sim }2 \times 10^{3}$ $\text {kg}\,\text {year}$ of exposure. Such an exposure could be collected by a single module of the LSGe experiment or by upgrades of Gerda Phase II and the Majorana Demonstrator which are already under consideration within the experimental community (see material presented at the [15, 78]).

However, depending on how strong the uncertainties both due to the NME and due to quenching affect $0\nu \beta \beta$ in $^{\text {76}}$Ge, the conclusions to be drawn may be considerably weakened. In our example above, the sum rule $\tilde{m}_1^{-1} + \tilde{m}_2^{-1} = \tilde{m}_3^{-1}$ could only be excluded with an exposure of ${[{\sim }}2 \times 10^{3}$ kg year is at least one source of error is reduced. If we make no progress on both quenching and the NMEs, not even the scenario with the highest exposure (${{\sim }}8 \times 10^{3}$ kg year) would allow to rule out this (or any other) sum rule. We thus have to improve our theoretical understanding of the nuclear transition in order to realistically draw solid conclusion, as generally true for $0\nu \beta \beta$.

7 Conclusions

In conclusion, realistic sensitivity projections have been presented for current and future $^{\text {76}}$Ge-based experiments. A global analysis of different data sets is reliable and should be performed. The global sensitivity and its impact on flavor models should be carefully considered when designing the mass-increasing strategy of the future projects. Synergies between theory and experiment can push us to new frontiers in neutrino physics.