1 Introduction

The hadronic production of quarkonia, bound states of either a charm and anti-charm quark pair (e.g. \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\)) or a bottom and anti-bottom quark pair (e.g. \(\mathrm{\Upsilon }\)(1S), \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S)), is generally understood as the result of a hard scattering that produces the heavy-quark pair, followed by the evolution of this pair into a colorless bound state. There are mainly three approaches used to describe quarkonium production, which differ mostly in the way the produced heavy-quark pair evolves into the bound state: the Color Evaporation Model [1, 2], the Color Singlet Model [3] and Non-Relativistic QCD [4]. To date, none of these approaches is able to describe consistently all data available on quarkonium production [5, 6].

In this paper we present the production cross sections of \({\mathrm{J}/\psi }\), \({\psi (\mathrm{2S})}\), \(\mathrm{\Upsilon }\)(1S), \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S) at forward rapidity (\(2.5<y<4\)), measured in pp collisions at a center-of-mass energy \(\sqrt{s}=8\) TeV with the ALICE detector. All quarkonia are reconstructed in the dimuon-decay channel. The differential production cross sections are measured as a function of the transverse momentum \({p_\mathrm{T}}\) and rapidity y, over the \({p_\mathrm{T}}\) ranges \(0<{p_\mathrm{T}}<20\) GeV/c for \({\mathrm{J}/\psi }\), \(0<{p_\mathrm{T}}<12\) GeV/c for all other resonances, and for \(2.5<y<4\). Our measurement extends the transverse momentum reach of the \({\mathrm{J}/\psi }\) cross section from \({p_\mathrm{T}}=12\) GeV/c up to \({p_\mathrm{T}}= 20\) GeV/c with respect to results from LHCb [7]. The \({\psi (\mathrm{2S})}\) results are the first published at this energy. For \(\mathrm{\Upsilon }\) mesons, differential cross sections at forward rapidity and \(\sqrt{s}=8\) TeV have already been published by LHCb [8]. Our measurement provides a unique cross-check of these results. Moreover, it is the first time ALICE measures the \(\mathrm{\Upsilon }\)(3S) cross section. All cross sections reported here are inclusive and contain, on top of the direct production of the quarkonium, a contribution from the decay of higher-mass excited states. Charmonium (\({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\)) cross sections also contain a contribution from b-hadron decay.

The paper is organized as follows: the ALICE detector and the data sample used for this analysis are briefly described in Sect. 2, the analysis procedure is discussed in Sect. 3 and results are presented in Sect. 4.

2 Detector and data sample

The ALICE detector is described in [9] and its performance in [10]. The following subsystems are used for measuring the quarkonium production cross sections at forward rapidity: the Muon Spectrometer [11], the first two layers of the Inner Tracking System (ITS) [12], the V0 scintillator hodoscopes [13] and the T0 Cherenkov counters [14].

The Muon Spectrometer consists of five tracking stations (MCH) comprising two planes of Cathode Pad Chambers each, followed by two trigger stations (MTR) consisting of two planes of Resistive Plate Chambers each. It is used to detect muons produced in the pseudo-rapidity range \(-4<\eta <-2.5\) Footnote 1. The third tracking station is located inside a warm 3 T m dipole magnet, to allow for momentum measurements. This apparatus is completed by two absorbers that filter out hadrons and low \({p_\mathrm{T}}\) muons, positioned (i) between the Interaction Point (IP) and the first tracking station, and (ii) between the last tracking station and the first trigger station. A third absorber, surrounding the beam pipe, protects the detectors from secondary particles produced inside the beam pipe. The MTR system delivers single- or di-muon triggers, of either same or opposite sign, with a programmable threshold on the transverse momentum of each muon. The ITS consists of 6 layers of silicon detectors, placed at radii ranging from 3.9 to 43 cm from the beam axis. Its two innermost layers are equipped with Silicon Pixel Detectors (SPD) and cover the pseudo-rapidity ranges \(|\eta |<2\) and \(|\eta |<1.4\) for the inner and the outer layer, respectively. They are used for the reconstruction of the collision primary vertex. The V0 detectors are two scintillator arrays located on both sides of the IP and covering the pseudo-rapidity ranges \(-3.7<\eta <-1.7\) and \(2.8<\eta <5.1\). The T0 detectors are two arrays of quartz Cherenkov counters, also placed at forward rapidity on both sides of the IP and covering the pseudo-rapidity ranges \(-3.3<\eta <-3\) and \(4.6<\eta <4.9\). The coincidence of a signal in both sides of either the T0 or the V0 detectors is used as an interaction trigger and as input for the luminosity determination.

The data used for this analysis have been collected in 2012. About 1400 proton bunches were circulating in each LHC beam. Collisions were delivered in a so-called beam-satellite mode, for which the high-intensity bunches of one of the two beams were collided with nearly-empty satellite bunches from the other [10]. In this configuration, the average instantaneous luminosity delivered by the LHC to ALICE was about \(5\times 10^{30}\) cm\(^{-2}\) s\(^{-1}\). The number of interactions per bunch-satellite crossing was about 0.01 on average with a corresponding pile-up probability of about 0.5 %, reaching a maximum of \(\sim \)1 %.

Events are selected using a dimuon trigger which requires that two muons of opposite sign are detected in the MTR, with a threshold of 1 GeV/c applied online to the \({p_\mathrm{T}}\) of each muon, in coincidence with the crossing of two bunches at the IP. The data sample recorded with this trigger corresponds to an integrated luminosity \({L_\mathrm{int}}= 1.23\) pb\(^{-1}\). It is evaluated on a run-by-run basis by multiplying the dimuon trigger live-time with the delivered luminosity. The latter is estimated using the number of T0-based trigger counts and the corresponding cross section, \(\sigma _\mathrm{T0}\), measured using the van der Meer scan method [15]. The systematic uncertainty on this quantity includes contributions from (i) the measurement of \(\sigma _\mathrm{T0}\) itself and (ii) the difference between the luminosity measured with the T0 detectors and the one measured with the V0 detectors. The quadratic sum of these contributions amounts to about 5 % and is correlated between all measurements presented in this paper.

3 Analysis

The differential quarkonium production cross section in a given \({p_\mathrm{T}}\) and y interval is:

$$\begin{aligned} \frac{d^2\sigma }{d{p_\mathrm{T}}dy}=\frac{1}{\Delta {p_\mathrm{T}}\Delta y}\frac{1}{{L_\mathrm{int}}}\frac{N}{\mathrm{BR}_{\mu \mu }{A\epsilon }}, \end{aligned}$$
(1)

where \(\mathrm{BR}_{\mu \mu }\) is the branching ratio of the quarkonium state in two muons, \(\Delta {p_\mathrm{T}}\) and \(\Delta y\) are the widths of the \({p_\mathrm{T}}\) and y intervals under consideration, N is the measured number of quarkonia in these intervals and \({A\epsilon }\) is the product of the corresponding acceptance and efficiency corrections, which account for detector effects and analysis cuts. The branching ratio values and uncertainties have been taken from the Particle Data Group (PDG) [16]. The other ingredients, namely N and \({A\epsilon }\), have been evaluated using the analysis procedure described in [17].

The number of quarkonia measured in a given \({p_\mathrm{T}}\) and y interval is evaluated using fits to the invariant mass distribution of opposite-sign muon pairs \({\mu ^+\mu ^-}\). These pairs are formed by combining the tracks reconstructed in the muon spectrometer and selected using the same criteria as in [17]:

  • muon identification is performed by matching each track reconstructed in the MCH with a track in the MTR that fulfills the trigger condition;

  • tracks are selected in the pseudo-rapidity range \(-4<\eta <-2.5\), which corresponds to the muon spectrometer geometrical acceptance;

  • the transverse position of the tracks at the end of the front absorber, \(R_\mathrm{{abs}}\), is in the range \(17.6 < R_\mathrm{{abs}} < 89.5\) cm, in order to reject muons crossing the high-density section of the front absorber;

  • tracks must pass a cut on the product of their total momentum, p, and their distance to the primary vertex in the transverse plane, called DCA. The maximum value allowed is set to \(6\times \sigma _{p}\mathrm{DCA}\), where \(\sigma _{p}\mathrm{DCA}\) is the resolution on this quantity, which accounts for the total momentum and angular resolutions of the muon spectrometer as well as for the multiple scattering in the front absorber. This cut reduces the contamination of fake tracks and particles from beam-gas interactions.

The fit to the \({\mu ^+\mu ^-}\) invariant mass distribution is performed separately in the charmonium and bottomonium regions, and for each \({p_\mathrm{T}}\) and y interval under consideration. In all cases the fitting function consists of a background to which two (three) signal functions are added, one per charmonium (bottomonium) state under study.

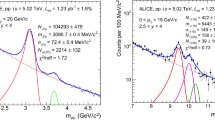
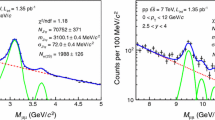
For charmonia, the fit is performed over the invariant mass range \(2<{M_{\mu \mu }}<5\) GeV/\(c^2\). For the background component, either a pseudo-Gaussian function whose width varies linearly with the invariant mass or the product of an exponential function and a fourth order polynomial function have been used, with all parameters left free in the fit. For the signal, the sum of either two extended Crystal Ball functions (one for each resonance) or two pseudo-Gaussian functions have been used [18]. Both functions (Crystal Ball or pseudo-Gaussian) consist of a Gaussian core, to which parametrized tails are added on both sides, which fall off slower than for a Gaussian function. Due to the poor signal-to-background (S/B) ratio in the tail regions, the values of the parameters that enter the definition of these tails have been evaluated using Monte Carlo (MC) simulations described later in this section, and kept fixed in the fit. The \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\) signals are fitted simultaneously. For the \({\mathrm{J}/\psi }\), the mass, width and normalization of the signal function are left free. For the \({\psi (\mathrm{2S})}\), only the normalization is free, whereas the mass and the width are calculated from the values obtained for the \({\mathrm{J}/\psi }\): the mass is computed so that the difference with respect to the \({\mathrm{J}/\psi }\) mass is the same as quoted by the PDG [16]; the width is derived from the \({\mathrm{J}/\psi }\) width using a scale factor of about 1.1, estimated in MC simulations and validated with fits to the \({p_\mathrm{T}}\)- and y-integrated invariant mass distributions from the data, with both widths left free. An example of fit to the \({p_\mathrm{T}}\)- and y-integrated dimuon invariant mass distribution in the \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\) mass region is shown in the left panel of Fig. 1. The result from this fit is used for the computation of the charmonium cross sections quoted at the beginning of Sect. 4.

For the \(\mathrm{\Upsilon }\) resonances, the fit is performed over the invariant mass range \(6<{M_{\mu \mu }}<14\) GeV/\(c^2\). The same signal functions as for the \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\) have been used for each of the three resonances, albeit with different values for the parameters of the tails. For the background component, either the sum of two exponential functions or the sum of two power law functions have been used, with all parameters left free. The masses and widths of the \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S) resonances have been fixed to the ones of the \(\mathrm{\Upsilon }\)(1S) in a similar way as for the \({\psi (\mathrm{2S})}\) and \({\mathrm{J}/\psi }\) case, and using a similar scale factor for the width. An example of fit to the \({p_\mathrm{T}}\)- and y-integrated dimuon invariant mass distribution in the \(\mathrm{\Upsilon }\) mass region is shown in the right panel of Fig. 1.

Fig. 1
figure 1

Dimuon invariant mass distributions in the region of charmonia (left) and bottomonia (right). Dashed lines correspond to the background. Solid lines correspond to either the signal functions, or the sum of all signal and background functions. In the charmonia region, the sum of two extended Crystal Ball functions is used for the signal and a pseudo-Gaussian function is used for the background. In the bottomonia region, the sum of three extended Crystal Ball functions is used for the signal and the sum of two exponential functions is used for the background

Full size image

The number of quarkonia is taken as the mean of the values obtained when (i) combining all possible signal and background functions described above; (ii) varying the parameters that have been fixed, such as those of the tails of the signal functions or the ratio between the \({\psi (\mathrm{2S})}\) and the \({\mathrm{J}/\psi }\) signal widths, and (iii) modifying the mass range used for the fit.

Approximately 82500 \({\mathrm{J}/\psi }\), 1850 \({\psi (\mathrm{2S})}\), 480 \(\mathrm{\Upsilon }\)(1S), 140 \(\mathrm{\Upsilon }\)(2S) and 50 \(\mathrm{\Upsilon }\)(3S) are measured. The corresponding S/B ratios, evaluated within three times the width of the signal function with respect to the quarkonium mass are 4.5 for \({\mathrm{J}/\psi }\), 0.2 for \({\psi (\mathrm{2S})}\), 1 for \(\mathrm{\Upsilon }\)(1S), 0.4 for \(\mathrm{\Upsilon }\)(2S) and 0.2 for \(\mathrm{\Upsilon }\)(3S). This statistics allows us to divide the data sample further as a function of either \({p_\mathrm{T}}\) or y for \({\mathrm{J}/\psi }\), \({\psi (\mathrm{2S})}\) and \(\mathrm{\Upsilon }\)(1S). For \(\mathrm{\Upsilon }\)(2S), only two bins in y are measured, whereas for \(\mathrm{\Upsilon }\)(3S), only the \({p_\mathrm{T}}\)- and y-integrated value is provided, due to limited statistics. For \({\mathrm{J}/\psi }\), the S/B ratio increases from 3 to 10 with increasing \({p_\mathrm{T}}\) and from 4 to 6 with increasing y. For \({\psi (\mathrm{2S})}\), it increases from 0.1 to 0.9 with increasing \({p_\mathrm{T}}\) and from 0.1 to 0.2 with increasing y. For \(\mathrm{\Upsilon }\)(1S), it increases from 0.8 to 1.4 with increasing \({p_\mathrm{T}}\) and shows no significant variation with respect to y. No significant variation with respect to y is observed for \(\mathrm{\Upsilon }\)(2S) either.

The systematic uncertainty on the signal extraction is estimated by taking the root mean square of the values from which the number of quarkonia is derived. For a given quarkonium state, this uncertainty is considered as uncorrelated as a function of both \({p_\mathrm{T}}\) and y. It is however partially correlated between \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\) as well as among the three resonances of the \(\mathrm{\Upsilon }\) family. For \({\mathrm{J}/\psi }\) this uncertainty increases from less than 1 to 14 % with increasing \({p_\mathrm{T}}\). It shows no significant variation with respect to y and amounts to about 1 %. Larger values are obtained for \({\psi (\mathrm{2S})}\) due to the smaller S/B ratio. For instance, the uncertainty reaches 18 % in the y interval \(2.5<y<2.75\). In the \(\mathrm{\Upsilon }\) sector, the systematic uncertainty is about 3, 6 and 10 % for \(\mathrm{\Upsilon }\)(1S), \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S), respectively, with little variation as a function of either \({p_\mathrm{T}}\) or y.

Acceptance and efficiency corrections, \({A\epsilon }\), are evaluated separately for each quarkonium state using MC simulations. Each state is generated randomly using realistic \({p_\mathrm{T}}\) and y probability distribution functions [11, 17]. It is decayed in two muons, properly accounting for the possible emission of an accompanying radiative photon [19, 20]. The muons are then tracked in a model of the apparatus obtained with GEANT 3.21 [21] which includes a realistic description of the detector performance during data taking as well as its variation with time. The same procedure and analysis cuts as for data are then applied to the MC simulations for track reconstruction and measurement of the quarkonium yields. All simulated quarkonia are assumed to be unpolarized, consistently with existing measurements [22–25].

The systematic uncertainty on \({A\epsilon }\) has several contributions: (i) the parametrization of the input \({p_\mathrm{T}}\) and y distributions; (ii) the track reconstruction efficiency and the accuracy with which the detector performance is reproduced in the MC simulations; (iii) the trigger efficiency and (iv) the matching between tracks reconstructed in the MCH and tracks reconstructed in the MTR. These contributions have been evaluated using the same procedures as in [17], for the first one by utilizing several alternative input \({p_\mathrm{T}}\) and y distributions, and for the other three by comparing data and MC at the single muon level and propagating the resulting differences to the dimuon case. The resulting systematic uncertainty is the quadratic sum of these contributions. It is partially correlated as a function of both \({p_\mathrm{T}}\) and y. For all quarkonium states, it amounts to about 8 % on average, increases from 7 to 9 % with increasing \({p_\mathrm{T}}\) and shows no visible dependence on y.

An additional correction is applied to the number of measured quarkonia, to account for the observation that a fraction of the opposite-sign muon pairs of a given quarkonium state is sometimes misidentified by the trigger system as a same-sign pair and thus missed. The magnitude of this effect could not be properly reproduced in the MC simulations and is therefore not accounted for in the \({A\epsilon }\) corrections. For \({\mathrm{J}/\psi }\) and \(\mathrm{\Upsilon }\)(1S), it is instead evaluated directly on data by means of a dedicated trigger configuration that selects both same- and opposite-sign muon pairs instead of opposite-sign pairs only. The statistical and systematic uncertainties on the extraction of the signal in each configuration are used to evaluate the systematic uncertainty on the resulting correction. For \({\mathrm{J}/\psi }\), the correction amounts to about 1 % on the \({p_\mathrm{T}}\)- and y-integrated yield. It increases from 0.6 % to 8 % with increasing \({p_\mathrm{T}}\) and shows little dependence on y. Slightly larger values are obtained for \(\mathrm{\Upsilon }\)(1S) albeit with larger uncertainties. For \({\psi (\mathrm{2S})}\), the same corrections as for \({\mathrm{J}/\psi }\) have been used, whereas for \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S) we used the same corrections as for \(\mathrm{\Upsilon }\)(1S).

Tables 1 and 2 provide a summary of the relative systematic uncertainties on the charmonia and bottomonia cross sections, respectively.

Table 1 Relative systematic uncertainties associated to the \({\mathrm{J}/\psi }\) and \({\psi (\mathrm{2S})}\) cross section measurements. Values in parenthesis correspond to minimum and maximum values as a function of \({p_\mathrm{T}}\) and y
Full size table
Table 2 Relative systematic uncertainties associated to the \(\mathrm{\Upsilon }\)(1S), \(\mathrm{\Upsilon }\)(2S) and \(\mathrm{\Upsilon }\)(3S) cross section measurements. Values in parenthesis correspond to minimum and maximum values as a function of \({p_\mathrm{T}}\) and y
Full size table

4 Results

The measured inclusive quarkonium production cross sections, integrated over \(0<{p_\mathrm{T}}<20\) GeV/c for \({\mathrm{J}/\psi }\), \(0<{p_\mathrm{T}}<12\) GeV/c for all other resonances, and \(2.5<y<4\), are:

\(\sigma _{{\mathrm{J}/\psi }} = 8.98\pm 0.04\mathrm{(stat)}\pm 0.82\mathrm{(syst)}\) \(\upmu \)b,

\(\sigma _{{\psi (\mathrm{2S})}} = 1.23\pm 0.08\mathrm{(stat)}\pm 0.22\mathrm{(syst)}\) \(\upmu \)b,

\(\sigma _{\mathrm{\Upsilon }\mathrm{(1S)}} = 71\pm 6\mathrm{(stat)}\pm 7\mathrm{(syst)}\) nb,

\(\sigma _{\mathrm{\Upsilon }\mathrm{(2S)}} = 26\pm 5\mathrm{(stat)}\pm 4\mathrm{(syst)}\) nb and

\(\sigma _{\mathrm{\Upsilon }\mathrm{(3S)}} = 9\pm 4\mathrm{(stat)}\pm 1\mathrm{(syst)}\) nb.

These values are in agreement, within at most \(1.4\sigma \), with measurements performed by LHCb at the same energy and in the same rapidity range [7, 8], assuming that all uncertainties but the one on the branching ratios are uncorrelated between the two experiments. For \({\mathrm{J}/\psi }\), our cross section value corresponds to an increase of \((29\pm 17)\) % with respect to the ALICE measurement at \(\sqrt{s}=7\) TeV [17]. A similar increase is obs