1 Introduction

For quite some time, physicists have considered Einstein’s general relativity (GR) to be an effective theory of gravity. Therefore, in order to find the happy marriage between quantum theory and gravity, we need to know the underlying fundamental theory of gravity. One recent proposal in this quest has been the Horava–Lifshitz (HL) theory [1], that is, a power-counting renormalizable theory with consistent ultraviolet (UV) behavior. Furthermore, the theory has one fixed point in the infrared (IR) limit, namely GR [1–4]. In terms of the above, black holes (BHs) are important solutions for field equations in any gravitational theory, including those of Einstein–Hilbert, Brans–Dicke, HL, f(R), string theories, and any generalization or modification of Einstein’s gravity. At the quantum level, BHs play the same role as hydrogen atom and we hope they give us some clues about the observables of any quantum theory of gravity. As such, it is important to study the physical properties of BH solutions, such as decay rate, gray-body factors, or their quasinormal modes. Quasinormal modes (QNMs), known as “ringing” in BHs, are very important in order to understand the classical and quantum aspects of BH physics. The QNMs give us hints about the stability of the BH under consideration, as in this paper, and can be used to compute the spectrum of the area operator using the semiclassical approach developed by Hod [5]. The determination of QNMs is based on the dynamics of matter fields and on the metric perturbations in the BH background. In this work indeed, we are interested in the stability of the \(1+1\)-dilatonic HL BH using a QNMs’ approach; QNMs associated with the perturbations of different fields have been considered in different works [6], including those involving dS and AdS space [7–14] and higher dimensional models, where the QNMs can be computed for a brane situated in the vicinity of a D-dimensional BH [15]. A similar situation occurs in \(2+1\) dimensions [16–18], and for acoustic BHs [19–21]. QNMs of dilatonic BHs in \(3+1\) dimensions can be found in Refs. [22–24]. Two-dimensional theories of gravity have recently attracted much attention [25–27] as simple toy models that possess many features of gravity in higher dimensions. They also have BH solutions which play important roles in revealing various aspects of spacetime geometry and quantization of gravity, and which are also related to string theory [28, 29]. The QNMs of \(1+1\) dilatonic BHs for scalar and fermionic perturbations were studied in [30–33].

The determination of QNMs for a specific geometry implies solving the field equations for different types of perturbations (scalar, fermionic, vectorial, etc.), with suitable boundary conditions that reflect the fact that this geometry describes a BH. The QNMs of a classical scalar perturbation of a BH are defined as the solutions of the Klein–Gordon equation characterized by purely ingoing waves at the horizon, \(\Phi \sim e^{-i\omega (t+r)}\), since, at least classically, an outgoing flux is not allowed at the horizon. In addition, one has to impose boundary conditions on the solutions in the asymptotic region (infinity), and for that reason it is crucial to use asymptotic geometry for the spacetime under study. In the case of an asymptotically flat spacetime, the condition we need to impose over the wave function is to have a purely outgoing wave function \(\Phi \sim e^{-i\omega (t-r)}\) at infinity [7]. In general, the QNMs are given by \(\omega _\mathrm{{QNM}}=\omega _{R}+i\omega _{I}\), where \(\omega _{R}\) and \(\omega _{I}\) are the real and imaginary parts of the frequency \(\omega _\mathrm{{QNM}}\), respectively. Therefore, the study of QNMs can be implemented as one possible simple alternative test for studying the stability of the system. In this sense, any imaginary frequency with the wrong sign would mean an exponentially growing mode, rather than a damping one.

The organization of this article is as follows: In Sect. 2, we describe briefly the HL theory and specify the \(1+1\)-dilatonic BH solutions. In Sect. 3, we compute the QNMs and explore the criteria for the stability of the two BH metrics under consideration. We finish with conclusions in Sect. 4.

2 Generalities of the Horava–Lifshitz gravity

In the following, we will describe the HL theory as developed in Ref. [4]. The HL theory provided a new approach to quantum gravity and its principal idea is based on the breaking of the Lorentz invariance by equipping the spacetime with additional geometric structure, a preferred foliation which defines the splitting of the coordinates into space and time; in this theory the Lorentz invariance is assumed to appear only at the low energies limit. One can decompose the spacetime as follows:

$$\begin{aligned} \mathrm{d}s^{2} = (N^{2}-N_{i}N^{i})\mathrm{d}t^{2}-2N_{i}\mathrm{d}x^{i}\mathrm{d}t-h_{ij}\mathrm{d}x^{i}\mathrm{d}x^{j}, \end{aligned}$$
(1)

where \(N, N^{i}\) are the lapse and shift functions, respectively, and \(h_{ij}\) is the three-dimensional metric. The action is given by

$$\begin{aligned} S = \frac{M^{2}_\mathrm{{Pl}}}{2}\int \mathrm{d}^{3}x\mathrm{d}t\sqrt{h}N\left( K_{ij}K^{ij}-\gamma K^{2}-\mathcal {V} \right) , \end{aligned}$$
(2)

where \(M_\mathrm{{Pl}}\) is the Planck mass, \(\gamma \) is a dimensionless constant, and \(K_{ij}\) is the well-known extrinsic curvature tensor, which is stated in the ADM formulation as

$$\begin{aligned} K_{ij}= \frac{1}{2N}\left( \dot{h}_{ij}-\nabla _{i}N_{j}-\nabla _{j}N_{i} \right) , \end{aligned}$$
(3)

K being its trace. The last term in (2), \(\mathcal {V}\), is invariant under three-dimensional diffeomorphisms and is known as the “potential” term. This term is a function of the three-dimensional metric and its derivatives. In explicit form we have

$$\begin{aligned} \mathcal {V}&= -\xi R + \frac{1}{M^{2}_{Pl}}\left( \pi _{1}\Delta R + \pi _{2}R_{ij}R^{ij} + \cdots \right) \nonumber \\&\quad +\frac{1}{M^{4}_{Pl}}\left( \sigma _{1}\Delta ^{2} R + \sigma _{2}R_{ij}R^{jk}R^{i}{}_{k} + \cdots \right) , \end{aligned}$$
(4)

where \(\xi , \pi _{n}, \sigma _{n}\) are coupling constants, \(R_{ij}\) and R are the Ricci tensor and the scalar curvature constructed with the spatial metric. We have \(\Delta := h^{ij}\nabla _{i}\nabla _{j}\). The introduction of the “potential” term in (2) improves the UV behavior of the graviton propagator and additionally leads to different scaling of space and time

$$\begin{aligned} \mathbf {x} \rightarrow \rho ^{-1}\mathbf {x}, \ t \rightarrow \rho ^{-3}t, \ \ N \rightarrow N, \ \ N^{i} \rightarrow \rho ^{2}N_{i}, \ \ h_{ij}\rightarrow h_{ij}. \end{aligned}$$
(5)

When the lapse function depends only on time, \(N=N(t)\), we say that we are dealing with the “projectable” version of the HL theory and the “non-projectable” version is given when the lapse function may depend on space and time. In Ref. [34] an extension of the non-projectable version of HL gravity was made by the introduction of an extra mode in the “potential” term, i.e., \(\mathcal {V}(h_{ij})\rightarrow \mathcal {V}(h_{ij},a_{i})\). It was shown that this extra mode can acquire a regular quadratic Lagrangian. The extra mode is given by

$$\begin{aligned} a_{i} := \frac{\partial _{i}N}{N}. \end{aligned}$$
(6)

Geometrically this vector represents the proper acceleration of the unit normals to the spatial slices. For the two-dimensional case there are only two terms that contribute to the quadratic Lagrangian: R and \(a_{i}a^{i}\).

2.1 Lowest dimensional Horava–Lifshitz black hole

The HL gravity has two-dimensional solutions that characterize dilatonic BHs and can be used to study the physical properties of BHs in general; furthermore, some features of this theory, due to the fact that it utilizes two dimensions, open the possibility of understanding physical consequences in higher dimensional theories. As a summary, let us start with the HL-dilaton gravity in two dimensions presented in Ref. [35],

$$\begin{aligned} S = S_\mathrm{{HL}}+S_{\phi }, \end{aligned}$$
(7)

where, as mentioned before, the quadratic Lagrangian for the HL theory in two dimensions comes from the contribution of the terms R and \(a_{i}a^{i}\); we have

$$\begin{aligned} S_\mathrm{{HL}} = \frac{M^{2}_\mathrm{{Pl}}}{2}\int \mathrm{d}t\mathrm{d}x\sqrt{g}\left( (1-\lambda )K^{2}+\eta g^{11}a_{1}a_{1} \right) \end{aligned}$$
(8)

and

$$\begin{aligned} S_{\phi }= & {} \int \mathrm{d}t\mathrm{d}xN\sqrt{g}\left[ \frac{1}{2N}\left( \partial _{t}\phi -N^{1}\nabla _{1}\right) ^{2}-\alpha (\nabla _{1}\phi )^{2}\right. \nonumber \\&\quad \left. -V(\phi ) -\beta \phi \nabla ^{1}a_{1}-\varsigma \phi a^{1}\nabla _{1}\phi \right] , \end{aligned}$$
(9)

where \(\alpha \), \(\beta , \eta \), and \(\varsigma \) are constants. Using the fact that \(K=0\) and admitting \(N_{1} = 0\) together with the relativistic limit \(\beta =\varsigma =0\), we are left with the action

$$\begin{aligned} S= \frac{M^2_\mathrm{{Pl}}}{2}\int \mathrm{d}t\mathrm{d}x \left( -\frac{1}{2}\eta N^2a^2_1+\alpha N^2\phi '^2-V(\phi )\right) . \end{aligned}$$
(10)

From now on, the prime denotes a derivative with respect the coordinate x. In two dimensions the extra mode \(a_{i}\) is simply \(a_1=\partial _{1}\ln N = \left( \ln N \right) '\). In Ref. [35], a new set of BH solutions in two-dimensional HL gravity was found for action (10). The solutions are described by

$$\begin{aligned} N(x)=\sqrt{\frac{A}{\eta }x^2-2C_1x+\frac{B}{\eta x}+\frac{C}{3 \eta x^2}+2C_2}\,\,\,\, \end{aligned}$$
(11)

and

$$\begin{aligned} \phi (x)=\ln \sqrt{\frac{A}{\eta }x^2-2C_1x+\frac{B}{\eta x}+\frac{C}{3 \eta x^2}+2C_2}\,; \end{aligned}$$
(12)

these solutions were obtained by using the quantity

$$\begin{aligned} V_{\phi }(x) = A + \frac{B}{x^{3}}+\frac{C}{x^{4}}, \end{aligned}$$
(13)

the derivative of the scalar potential given as a function of an implicit scalar field which in turns depends on the spatial coordinate. This was done because for generalized potentials it is not always possible to obtain analytical solutions. We would like to focus our attention on the following two cases:

  • First case: This is described by fixing the constants in the following way: \(A=B=C=0\), \(C_1= -M\), \(C_2=-1/2\), and \(\eta =1\). In this case \(V_{\phi }=0\). Therefore, the metric for this solution can be written as follows:

    $$\begin{aligned} \mathrm{d}s^{2} = -(2Mx -1)\mathrm{d}t^{2} + \frac{1}{2Mx - 1}\mathrm{d}x^{2}, \end{aligned}$$
    (14)

    where the parameter M is related to the lapse function N. This solution was found for the first time in [36].

  • Second Case: Here we fix the constants as \(A=\Lambda \), \(B=C=0\), \(C_1=-M\), and \(C_2=-\frac{\epsilon }{2}\); therefore, we have \(V_{\phi }=\Lambda \), and the solution is given by

    $$\begin{aligned} \mathrm{d}s^{2} = \left[ \left( \frac{\Lambda }{\eta }\right) x^{2} + 2Mx - \epsilon \right] \mathrm{d}t^{2} + \frac{1}{\left( \frac{\Lambda }{\eta }\right) x^{2} + 2Mx - \epsilon }\mathrm{d}x^{2}. \end{aligned}$$
    (15)

    The horizon of the black hole is located at

    $$\begin{aligned} x_{\pm } = -\frac{\eta M}{\Lambda } \pm \sqrt{\frac{\eta }{\Lambda }\left( \frac{\eta M^{2}}{\Lambda } + \epsilon \right) }. \end{aligned}$$
    (16)

    If we define the variables \(u = \sqrt{\Lambda / \eta }x + \sqrt{\eta / \Lambda }M\) and \(u_{+} = \sqrt{(\eta / \Lambda )M^{2} + \epsilon }\), we get

    $$\begin{aligned} \mathrm{d}s^{2} = -\left( u^{2} - u_{+}^{2} \right) \mathrm{d}t^{2} + \frac{l^{2}}{\left( u^{2} - u_{+}^{2}\right) }\mathrm{d}u^{2}, \end{aligned}$$
    (17)

    which is a suitable expression to study the quasinormal modes of this black hole, and we have defined \(l = (\Lambda /\eta )^{1/4}\). In this new coordinate system, the horizon of the black hole is located at \(u = u_{+}\). The spacetimes, described by (14) and (15), are conformally flat [37].

3 Quasinormal modes

In order to study the QNMs, we consider a scalar field minimally coupled to gravity propagating in the background of the two-dimensional HL BH. We consider the following action for the scalar field:

$$\begin{aligned} S[\varphi ] = \int \mathrm{d}^{2}x \sqrt{-g}\left( -\frac{1}{2}(\nabla \varphi )^{2} - \frac{1}{2}m^{2}\varphi ^{2} \right) , \end{aligned}$$
(18)

where m is the mass of the scalar field. From the variation of \(\delta \phi \) the field equation is given by

$$\begin{aligned} \Box \varphi - m^{2}\varphi = 0, \end{aligned}$$
(19)

where \(\Box \) is the D’Alambertian operator, in the following sections, we will solve the Klein–Gordon Eq. (19) for the spacetimes described in the previous section.

3.1 Spacetime metric \(\mathrm{d}s^{2} = -(2Mx -1)\mathrm{d}t^{2} + \frac{1}{2Mx - 1}\mathrm{d}x^{2}\)

3.1.1 Massive scalar field

The case of a massive scalar field perturbing the background described by the metric (14) was discussed for the first time in [36, 37]. If we use \(\varphi (t,x)=e^{-i\omega t}\varphi (x)\) the equation of motion (19) is represented by

$$\begin{aligned}&(2Mx-1)\frac{\mathrm{d}^{2}\varphi (x)}{\mathrm{d}x^{2}} + 2M \frac{\mathrm{d}\varphi (x)}{\mathrm{d}x} \nonumber \\&\quad +\frac{\omega ^{2}}{2Mx-1}\varphi (x)-m^2\varphi (x)= 0.\nonumber \\ \end{aligned}$$
(20)

For this metric and massive scalar field, the QNMs were computed in [38], where the authors claimed that the solution for the QNMs are completely different from the standard case where the QNMs have a discrete spectrum. They proposed a real and continuous spectrum for the QNMs of a scalar perturbation. In the next section, we look at this situation, but instead we use the confluent hypergeometric function \(_{0}F_1(a,b;x)\) place of the modified Bessel functions. Now, using the tortoise coordinate defined by \(x_{*}=\frac{1}{2M}\ln (2Mx-1)\) we can write Eq. (20) as a Schroedinger type equation with effective potential [38]

$$\begin{aligned} V_\mathrm{{eff}} =m^{2}e^{2Mx_{*}}; \end{aligned}$$
(21)

this potential diverges when \(x_{*}\rightarrow \infty \). If we consider the variable \(z=\frac{m}{M}e^{Mx_{*}}\) [36], after some straightforward algebra, the equation of motion (20) can be written as the Bessel equation,

$$\begin{aligned} z^2\frac{\mathrm{d}^2\varphi (z)}{\mathrm{d}z^2}+z\frac{\mathrm{d}\varphi (z)}{\mathrm{d}z}+\left( \nu ^2+z^2\right) \varphi (z)=0, \end{aligned}$$
(22)

where \(\nu =\frac{i\omega }{M}\); this equation can be transformed into the confluent hypergeometric equation using the change \(\varphi (z)=(2iz)^{\nu }e^{-2z}F(z)\) [39], and we find

$$\begin{aligned} z\frac{\mathrm{d}^2F(z)}{\mathrm{d}z^2} + (2\nu +1-2iz)\frac{\mathrm{d}F(z)}{\mathrm{d}z}+2i\left( \nu +\frac{1}{2}\right) F(z)=0, \end{aligned}$$
(23)

whose solution is given in terms of the confluent hypergeometric, or Kummer, functions

$$\begin{aligned} F(z)= & {} A\Phi \left( \nu +\frac{1}{2},2\nu +1;2iz\right) \nonumber \\&+B(2iz)^{-2\nu }\Phi \left( -\nu +\frac{1}{2},1-2\nu ;2iz\right) , \end{aligned}$$
(24)

where A, B are constants and the number \(\nu \) in general does not need to be an integer [39]. In the following we will consider two cases for the \(\nu \) parameter since we are interested in exploring all its possible values.

  • non-integer \(\nu \)

    In order to compute the QNMs, we need to impose adequate boundary conditions that represent a purely outgoing wave at infinity and purely ingoing wave near the horizon of the BH (a condition often used in flat spacetime). Another situation occurs when the asymptotic behavior of the spacetime is not flat, e.g. asymptotically AdS space; in these kinds of spaces, the potential diverges at infinity, and we can therefore impose \(\varphi =0\) (Dirichlet boundary condition) or \(\frac{\mathrm{d}\varphi }{\mathrm{d}x}=0\) (Neumann boundary condition) at infinity. As we can see from Eq. (21), in this case we have an asymptotically AdS space. Therefore, we need to apply boundary conditions to the QNMs over the general solution of Eq. (23), which is given by

    $$\begin{aligned} \varphi (z)&=Ae^{-2z}z^{\nu }\Phi \left( \nu +\frac{1}{2},2\nu +1;2iz\right) \nonumber \\&\quad +Be^{-2z}z^{-\nu }\Phi \left( -\nu +\frac{1}{2},1-2\nu ;2iz\right) ; \end{aligned}$$
    (25)

    to satisfy the boundary conditions properly, we set \(A=0\) in order to have only ingoing waves at the horizon (\(z=0\)). The asymptotic behavior of \(\Phi \) at infinity is given by [40]

    $$\begin{aligned} \Phi (p,q;z)\rightarrow \frac{\Gamma (q)}{\Gamma (p)}z^{p-q}e^z, \end{aligned}$$
    (26)

    and therefore our solution at infinity (\(z \rightarrow \infty \)) reads as follows:

    $$\begin{aligned} \varphi (z)\sim Bz^{-\frac{1}{2}}e^{2(i-1)z}\frac{\Gamma (1-2\nu )}{\Gamma (-\nu +1/2)}. \end{aligned}$$
    (27)

    We can see that the scalar field vanishes as \(z \rightarrow \infty \), and this confirms the absence of QNMs for this HL BH under scalar perturbation. A similar situation was found in Ref. [18] for the QNMs of the extremal BTZ BH. The conclusion of this case was discussed in [38], and it represents a continuous spectrum. Additionally, if we impose the Neumann boundary condition, we obtain a similar asymptotic vanishing behavior for the flux

    $$\begin{aligned} J_r(z)=\varphi ^*(z)\frac{\mathrm{d}\varphi (z)}{\mathrm{d}z}-\varphi (z)\frac{\mathrm{d}\varphi ^*(z)}{\mathrm{d}z}. \end{aligned}$$
    (28)

    In light of the meaning of QNMs, for any BH perturbation its geometry produces damped oscillations. This is the so-called ringing in BHs. It is well known that the frequencies of these oscillations and their damping periods are completely fixed by the BH properties, and, as such, are independent of the nature of the initial perturbation. In Ref. [38] it was shown that for scalar perturbations the oscillations have a continuous spectrum and are not discrete, as would be expected for a BH. This result is very strange and in our opinion, devoid of physical meaning; this is because it is well known that oscillations of QNMs are similar to normal modes of a closed system. In the next section, we consider the second solution of the confluent hypergeometric equation and show that QNM oscillations have a discrete spectrum.

  • \(\nu \) integer

Now we shall consider the case where \(\nu \) is an integer number. For \(\nu \) integer, the solution of Eq. (23) changes. In Eq. (25), the function \(\Phi (p,q;z)\) of the second term must be replaced by [41]

$$\begin{aligned}&W(\alpha ,\gamma ;z)=M(\alpha ,\gamma ;z)\left( \ln z+\psi (1-\alpha )-\psi (\gamma )+C\right) \nonumber \\&\quad +\sum _{n=1}^{\infty }\frac{\Gamma (n+\alpha )\Gamma (\gamma )B_nz^n}{\Gamma (\alpha )\Gamma (n+\gamma )n!} \\&\quad +(-1)^{\gamma }\sum _{n=1}^{\infty }\frac{\Gamma (\gamma )\Gamma {n+\alpha -\gamma +1}\Gamma (\gamma -n-1)(-1)^n}{\Gamma (\alpha )n!z^{\gamma -n-1}}\,, \end{aligned}$$

where

$$\begin{aligned} \psi (\alpha )=\frac{\Gamma '(\alpha )}{\Gamma (\alpha )} \end{aligned}$$
(29)

represents the digamma function, \(C=0.577216\ldots \) is the Euler constant, and

$$\begin{aligned} B_n&=\left( \frac{1}{\alpha }+\frac{1}{\alpha +1}+\cdots +\frac{1}{\alpha +n-1}\right) \nonumber \\&\quad -\left( \frac{1}{\gamma }+\frac{1}{\gamma +1}+\cdots +\frac{1}{\gamma +n-1}\right) . \end{aligned}$$
(30)

Then we have

$$\begin{aligned} \varphi (z)= & {} Ae^{-2z}z^{\nu }\Phi \left( \nu +\frac{1}{2},2\nu +1;2iz\right) \nonumber \\&+Be^{-2z}z^{-\nu }W(p,q;z). \end{aligned}$$
(31)

In order to have only ingoing waves at the horizon (\(z=0\)), we set \(A=0\). The asymptotic behavior of the W-function at infinity is given by

$$\begin{aligned} W(p,q;y)\rightarrow \pi \cot (\pi p)\frac{\Gamma (q)}{\Gamma (p)}y^{p-q}e^y. \end{aligned}$$
(32)

Therefore, the general solution at infinity reads as follows:

$$\begin{aligned} \varphi (z){\sim } B\pi \cot \left[ -\pi \left( \nu +\frac{1}{2}\right) \right] z^{-\left( 4\nu +\frac{3}{2}\right) }\frac{\Gamma (2\nu +1)}{\Gamma (-\nu -1/2)} e^{2(i-1)z}. \end{aligned}$$
(33)

If we consider that \(\nu + 1/2=\frac{2n+1}{2}\), where n is an integer number, we are able to fulfill the Dirichlet boundary condition at infinity. From this result we can obtain the frequency of the QNMs as

$$\begin{aligned} \omega =-inM, \end{aligned}$$
(34)

and using the Neumann condition for a vanishing flux at infinity, we obtain the same result for the QNMs as expressed in Eq. (34).

3.1.2 Massless case

For the metric (14), when \(m=0\), we use the standard definition for QNMs, the Klein–Gordon Eq. (19) which reads

$$\begin{aligned} (2Mx-1)\frac{\mathrm{d}^{2}\varphi (x)}{\mathrm{d}x^{2}} + 2M \frac{\mathrm{d}\varphi (x)}{\mathrm{d}x} + \frac{\omega ^{2}}{2Mx-1}\varphi (x) = 0,\nonumber \\ \end{aligned}$$
(35)

where we have assumed \(\phi (t,x) = \varphi (x)e^{-i\omega t}\). If we define the quantity \(x_{+} = 1/2M\) and the change of variable \(z = 1 - x_{+}/x\) we can write Eq. (35) as follows:

$$\begin{aligned} (1-z)^{2}\frac{\mathrm{d}^{2}\varphi }{\mathrm{d}z^{2}}-2(1-z)\frac{\mathrm{d}\varphi }{\mathrm{d}z}+\frac{(1-z)}{z}\frac{\mathrm{d}\varphi }{\mathrm{d}z}+\left( \frac{\tilde{\omega }}{z}\right) ^{2} \varphi = 0,\nonumber \\ \end{aligned}$$
(36)

where \(\tilde{\omega } = x_{+}\omega \). Note that in the new coordinate z, the horizon of the BH is located at \(z = 0\) and infinity at \(z=1\). With the change \(\varphi (z) = z^{\alpha }(1-z)^{\beta }F(z)\), the last equation reduces to the hypergeometric differential equation for the function F(z), that is,

$$\begin{aligned} z(1-z)F''(z) + (c-(a+b+1)z)F'(z)-abF(z)=0.\qquad \end{aligned}$$
(37)

In this case the coefficients a, b, and c are given by the relations

$$\begin{aligned} c= & {} 2\alpha +1, \end{aligned}$$
(38)
$$\begin{aligned} a+b= & {} 2\alpha + 2\beta + 1, \end{aligned}$$
(39)
$$\begin{aligned} ab= & {} \alpha (\alpha - 1) + \beta (\beta -1)+2\alpha + 2\beta + 2\alpha \beta , \end{aligned}$$
(40)

providing the expressions for the coefficients

$$\begin{aligned} a= & {} \alpha +\beta ,\end{aligned}$$
(41)
$$\begin{aligned} b= & {} 1+\alpha +\beta , \end{aligned}$$
(42)

and for the exponents we obtain

$$\begin{aligned} \alpha = \beta = -ix_{+}\omega . \end{aligned}$$
(43)

Without loss of generality, we have chosen the negative signs for the exponents. The solution of the radial equation reads

$$\begin{aligned} F(z)= & {} C_{1}F_{1}(a,b,c;z)\nonumber \\&+\,C_{2}z^{1-c}F_{1}(a-c+1,b-c+1,2-c;z), \end{aligned}$$
(44)

where \(C_{1}\) and \(C_{2}\) are arbitrary constants and \(F_{1}(a,b,c;z)\) is the hypergeometric function. The solution for \(\varphi (z)\) is given by

$$\begin{aligned} \varphi (z)= & {} C_{1}z^{-ix_{+}\omega }(1-z)^{-ix_{+}\omega }F_{1}(a,b,c;z) \nonumber \\&+\, C_{2}z^{ix_{+}\omega }(1-z)^{-ix_{+}\omega }F_{1}(a-c+1,b-c+1,2-c;z).\nonumber \\ \end{aligned}$$
(45)

In the neighborhood of the horizon \(z=0\), the function \(\varphi (z)\) behaves as

$$\begin{aligned} \varphi (z) = C_{1}e^{-ix_{+}\omega \ln z} + C_{2}e^{ix_{+}\omega \ln z}, \end{aligned}$$
(46)

for the scalar field \(\phi \) one gets

$$\begin{aligned} \phi \sim C_{1}e^{-i\omega \left( t + x_{+}\ln z\right) } + C_{2}e^{-i\omega \left( t - x_{+}\ln z\right) }. \end{aligned}$$
(47)

The first term in the last equation corresponds to an ingoing wave at the BH, while the second one represents an outgoing wave. In order to compute the QNMs, we must impose the requirement that there exist only ingoing waves at the horizon of the BH; then \(C_{2} = 0\). The radial solution at the horizon is given by

$$\begin{aligned} \varphi (z) = C_{1}z^{-ix_{+}\omega }(1-z)^{-ix_{+}\omega }F_{1}(a,b,c;z). \end{aligned}$$
(48)

In order to implement the boundary conditions at infinity, \(z=1\), we use the linear transformation \(z\rightarrow 1-z\), and then we apply Kummer’s formula [42] for the hypergeometric function,

$$\begin{aligned} \varphi (z)= & {} C_{1}z^{-ix_{+}\omega }(1-z)^{-ix_{+}\omega }\frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}\nonumber \\&\times F_{1}(a,b;a+b-c+1;1-z)\nonumber \\&+ C_{1}z^{-ix_{+}\omega }(1-z)^{ix_{+}\omega }\frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}\nonumber \\&\times F_{1}(c-a,c-b;c-a-b+1;1-z). \end{aligned}$$
(49)

This solution near infinity, \(z=1\), takes the form

$$\begin{aligned} \varphi (z)= & {} C_{1}(1-z)^{-ix_{+}\omega }\frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}\nonumber \\&+C_{1}(1-z)^{ix_{+}\omega }\frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}, \end{aligned}$$
(50)

and the scalar field solution near infinity behaves as

(51)

To compute the QNMs, we also need to impose the boundary conditions on the solution of the radial equation at infinity, meaning that only purely outgoing waves are allowed there. Therefore, the second term in the last equation must vanish; this is fulfilled, at the poles of \(\Gamma (a)\) or \(\Gamma (b)\), where the scalar field satisfies the considered boundary condition only when

$$\begin{aligned} a = -n \quad \text{ or }\quad b=-n, \end{aligned}$$
(52)

where \(n = 0, 1, 2,\ldots \). These conditions determine the form of the quasinormal modes,

$$\begin{aligned} \omega = -\frac{i}{2x_{+}}\left( n + 1\right) . \end{aligned}$$
(53)

3.2 Spacetime metric \(\mathrm{d}s^{2} = \left( \left( \frac{\Lambda }{\eta }\right) x^{2} + 2Mx - \epsilon \right) \mathrm{d}t^{2} + \frac{1}{\left( \frac{\Lambda }{\eta }\right) x^{2} + 2Mx - \epsilon }\mathrm{d}x^{2}\)

For the second metric given in Eq. (17), we have a spacetime that is not asymptotically flat; thus, as mentioned before, we use a definition for the QNMs different from the one used in an asymptotically flat spacetime. The formal treatment for this kind of spacetime is presented in [7], where one defined QNMs to be modes with only ingoing waves near the horizon and vanishing at infinity. Thus, the Klein–Gordon equation (19) can be written as

$$\begin{aligned} -\frac{1}{u^{2}-u_{+}^{2}}\partial _{t}\partial _{t}\phi + \frac{2}{l^{2}}u \partial _{u}\phi + \frac{1}{l^{2}}(u^{2}-u_{+}^{2})\partial _{u}\partial _{u}\phi - m^{2}\phi =0, \end{aligned}$$
(54)

now, we will consider a solution of type \(\phi (t,u) = \varphi (u)e^{-i\omega t}\) and the definition \(l = (\lambda /\eta )^{1/4}\), for which the radial equation can be written as follows:

$$\begin{aligned} \frac{1}{l^{2}}(u^{2}-u_{+}^{2})\varphi ''(u) + \frac{2}{l^{2}}u\varphi '(u) + \left( \frac{\omega ^{2}}{u^{2}-u_{+}^{2}} - m^{2} \right) \varphi (u) =0, \end{aligned}$$
(55)

where the prime denotes derivatives with respect the variable u. If we define the change of variable \(z=1-u_{+}^{2}/u^{2}\) [43] and follow the procedure stated for the massless case, the Eq. (55) transforms into the hypergeometric differential Eq. (37) for the function F(z), where the coefficients a, b, c are given by the following relations:

$$\begin{aligned}&a + b = 2\alpha + 2\beta + \frac{1}{2},\end{aligned}$$
(56)
$$\begin{aligned}&ab = \alpha (\alpha -1)+\beta (\beta -1)+2\alpha \beta + \frac{3}{2}\alpha + \frac{3}{2}\beta ,\end{aligned}$$
(57)
$$\begin{aligned}&c = 2\alpha + 1, \end{aligned}$$
(58)

which gives

$$\begin{aligned} a= & {} \alpha + \beta ,\end{aligned}$$
(59)
$$\begin{aligned} b= & {} \alpha + \beta + \frac{1}{2}, \end{aligned}$$
(60)

and for the exponents \(\alpha \) and \(\beta \)

$$\begin{aligned} \alpha= & {} -i\frac{l}{u_{+}}\omega ,\end{aligned}$$
(61)
$$\begin{aligned} \beta= & {} \frac{1}{4}\left( 1 - \sqrt{1+4m^{2}l^{2}} \right) , \end{aligned}$$
(62)

where, without loss of generality, we have chosen the negative signs. The solution of the radial equation reads

$$\begin{aligned} F(z)= & {} C_{1}F_{1}(a,b,c;z)\nonumber \\&+\,C_{2}z^{1-c}F_{1}(a-c+1,b-c+1,2-c;z), \end{aligned}$$
(63)

where \(C_{1}\) and \(C_{2}\) are arbitrary constants and \(F_{1}(a,b,c;z)\) is the hypergeometric function. Since \(\varphi (z) = z^{\alpha }(1-z)^{\beta }F(z)\), the behavior of the scalar field near the horizon (\(z=0\)) is given by

$$\begin{aligned} \phi \sim C_{1}e^{-i\omega \left( t + \frac{l}{u_{+}}\ln z\right) } + C_{2}e^{-i\omega \left( t - \frac{l}{u_{+}}\ln z\right) }. \end{aligned}$$
(64)

Then the scalar field \(\phi \) is purely ingoing at the horizon for \(C_{2} = 0\), and therefore the radial solution is

$$\begin{aligned} \varphi (z) = C_{1}z^{\alpha }(1-z)^{\beta }F_{1}(a,b,c;z). \end{aligned}$$
(65)

In order to implement boundary conditions at infinity (\(z=1\)), we use the linear transformation \(z \rightarrow 1-z\) for the hypergeometric function and we obtain

$$\begin{aligned} \varphi (z)= & {} C_{1}z^{\alpha }(1-z)^{\beta }\frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}\nonumber \\&\times F_{1}(a,b;a+b-c+1;1-z)\nonumber \\&+C_{1}z^{\alpha }(1-z)^{c-a-b+\beta }\frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}\nonumber \\&\times F_{1}(c-a,c-b;c-a-b+1;1-z). \end{aligned}$$
(66)

Using the condition of the flux

(67)

where

$$\begin{aligned} \Gamma _{1}= & {} \frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)},\end{aligned}$$
(68)
$$\begin{aligned} \Gamma _{2}= & {} \frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}, \end{aligned}$$
(69)

then the flux (67) has a leading term \((1-z)^{1-2\beta }\) and vanishes at infinity only if we impose the requirement that

$$\begin{aligned} a = -n \quad \text{ or }\quad b = -n, \end{aligned}$$
(70)

where \(n = 0, 1, 2, 3\ldots \). These conditions lead to the determination of the quasinormal modes as follows:

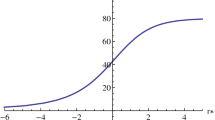
$$\begin{aligned} \omega = -i\frac{u_{+}}{4l}\left[ 4n+3-\sqrt{1+4m^{2}l^{2}}\right] . \end{aligned}$$
(71)

Our results are represented in Fig. 1, where it is one sees that, for a scalar field with large mass, the BH becomes unstable, while for lower values of the mass, or \(m=0\), this kind of black hole is stable.

Fig. 1
figure 1

In this plot we depict the behavior of the QNMs expressed in Eq. (71), with some parameter values, \(l=1\) and \(u_{+} = \sqrt{5}\). We can see that the BH becomes unstable for large values of the mass m

Full size image

4 Final remarks

This article was devoted to studying the response of two \(1+1\) BHs under scalar perturbations. We focused on the BH solutions found in Ref. [35] in the context of HL gravity. The BHs studied in the present paper also correspond to solutions arising from standard GR plus the dilaton field; therefore, the physical properties of these BHs can be used in different contexts. We noted that in studying the QNM oscillations of the metric (14) with massive scalar field perturbations it is necessary to look at the solution in terms of the confluent hypergeometric, or Kummer, functions, and, as a result, we found two different cases, in one case we have absent QNMs under scalar perturbations and in the second case we have a discrete spectrum. These results are different from those obtained in Ref. [38], where the QNMs are a continuous spectrum. Also, we computed the frequencies of the massless scalar field as sources of perturbations, and again we obtained a discrete spectrum. From these results, we conclude that this BH is stable under massive and massless scalar perturbations.

On the other hand, for spacetimes in which the cosmological constant does not vanish, we found, in addition to the exact quasinormal frequencies, that when the mass of the scalar field is large, the geometry becomes unstable. Finally, we would like to note that the frequencies found in this article are purely imaginary, and as such they represent pure damping behavior.