Quantifying jet transport properties via large $p_T$ hadron production

Abstract

Nuclear modification factor $R_{AA}$ for large $p_T$ single hadron is studied in a next-to-leading order perturbative QCD parton model with medium-modified fragmentation functions (mFFs) due to jet quenching in high-energy heavy-ion collisions. The energy loss of the hard partons in the quark–gluon plasma is incorporated in the mFFs which utilize two most important parameters to characterize the transport properties of the hard parton jets: the jet transport parameter $\hat{q}_{0}$ and the mean free path $\lambda _{0}$, both at the initial time $\tau _0$. A phenomenological study of the experimental data for $R_{AA}(p_{T})$ is performed to constrain the two parameters with simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits to Relativistic Heavy Ion Collider as well as Large Hadron Collider data. We obtain for energetic quarks $\hat{q}_{0}\approx 1.1 \pm 0.2$ GeV$^2$/fm and $\lambda _{0}\approx 0.4 \pm 0.03$ fm in central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV, while $\hat{q}_{0}\approx 1.7 \pm 0.3$ GeV$^2$/fm, and $\lambda _{0}\approx 0.5 \pm 0.05$ fm in central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV. Numerical analysis shows that the best fit favors a multiple scattering picture for the energetic jets propagating through the bulk medium, with a moderate averaged number of gluon emissions. Based on the best constraints for $\lambda _{0}$ and $\tau _0$, the estimated value for the mean-squared transverse momentum broadening is moderate which implies that the hard jets go through the medium with small reflection.

1 Introduction

A strongly coupled quark gluon plasma (sQGP) consisting of deconfined quarks and gluons may have been created in the central region of high-energy nuclear collisions at the BNL Relativistic Heavy Ion Collider (RHIC) and the CERN Large Hadron Collider (LHC). One important evidence for the formation of sQGP from the experiment results are the jet quenching phenomena [1, 2] that include the strong suppression of single hadron spectra [3–7], back-to-back dihadron [8, 9] and photon-triggered hadron [10, 11] as well as jet productions [12, 13] with large transverse momentum in central $A+A$ collisions as compared to $p+p$ collisions. These observed jet quenching patterns in heavy-ion collisions at RHIC/LHC can be described well by different theoretical models [14–25] that incorporate parton energy loss induced by multiple parton scattering and gluon bremsstrahlung as it propagates through the dense matter.

A widely used parameter controlling the parton energy loss is the jet transport parameter $\hat{q}$ [26], or the mean-squared transverse momentum broadening per unit length for a jet in a strong interacting medium, which is also related to the gluon distribution density of the medium [26, 27] and therefore characterizes the medium property as probed by an energetic jet. To estimate the jet transport parameter $\hat{q}$ intense theoretical studies have been made, such as with the weakly coupled QCD [28–30], the strong-coupled AdS/CFT [31, 32], and the lattice calculations [33, 34]. Recently, a phenomenological investigation had been carried out to extract the initial value of jet transport coefficient $\hat{q}_{0}$ at initial time $\tau _0$, which gives $\hat{q}_{0}\approx 1.2 \pm 0.3$ GeV$^2$/fm in $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV and $\hat{q}_{0}\approx 1.9 \pm 0.7$ GeV$^2$/fm in $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV for a given quark with initial energy of 10 GeV [35].

In this paper we will extract the initial jet transport parameter $\hat{q}_{0}$ and the initial mean free path $\lambda _{0}$ at initial time $\tau _0$ on the bulk medium evolution by comparing the experimental data at RHIC/LHC with numerical simulations of single hadron yields with large $p_T$ in a next-to-leading order (NLO) pQCD parton model, where the EPS09 parametrization set of NLO nuclear parton distribution functions (nPDFs) has been used to take into account of possible initial-state cold nuclear matter effects, and a phenomenological model [18, 20] for medium-modified fragmentation functions calculated in leading order (LO) at twist-4 in the high-twist approach of jet quenching [36–38] has been utilized to incorporate parton energy loss. The evolution of the bulk medium used in the study for parton propagation was given by a $(3 + 1)$-dimensional ideal hydrodynamic model [39, 40] which is constrained by experimental data on the hadron spectra. From calculations with the two independent inputs for the parameters and simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits to the RHIC and the LHC data, we obtain for energetic quarks $\hat{q}_{0}\approx 1.1 \pm 0.2$ GeV$^2$/fm and $\lambda _{0}\approx 0.4 \pm 0.03$ fm in central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV, while we have $\hat{q}_{0}\approx 1.7 \pm 0.3$ GeV$^2$/fm and $\lambda _{0}\approx 0.5 \pm 0.05$ fm in central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV. This simultaneous and separate constraint of the two initial values should give a precise and quantitative description for jet quenching to probe the medium properties. For a parton jet propagating through the bulk medium, the average transverse momentum broadening squared $\langle q_T^2 \rangle$ depends on the transport parameter as well as the mean free path, $\langle q_T^2 \rangle = \hat{q} \lambda$. Our numerical results show that the mean transverse momentum broadening squared of energetic partons for one scattering at initial time $\tau _0$ in the center of the fireball at LHC is about two times of that at RHIC.

The rest of the paper is organized as follows. We first give a brief overview of the NLO pQCD parton model for single inclusive hadron spectra and a phenomenological model for medium-modified fragmentation functions in Sect. 2. Then the numerical calculations for phenomenological studies of the experimental data on single hadron suppression and extraction of the jet transport parameter and the mean free path are carried out in Sect. 3. We present some discussions in Sect. 4 and finally summarize our study in Sect. 5.

2 NLO pQCD parton model and modified fragmentation functions

We will utilize the pQCD parton model at NLO for the initial jet production spectra which has been applied to large $p_T$ hadron production in high-energy hadron–hadron reactions with great successes [41, 42]. In the model the differential cross section of hadron yields has been expressed as a convolution of NLO parton–parton scattering cross sections, parton distribution functions (PDFs) in nucleons, and parton fragmentation functions (FFs),

$$\begin{aligned} \frac{\mathrm{d}\sigma _{pp}}{\mathrm{d}y\mathrm{d}^2p_T}= & {} \sum _{abcd}\int \mathrm{d}x_a\mathrm{d}x_b f_{a}(x_a,\mu ^2) f_{b}(x_b,\mu ^2) \nonumber \\&\times \frac{\mathrm{d}\sigma }{\mathrm{d}\hat{t}}(ab\rightarrow cd) \frac{D_{h/c}(z_{c},\mu ^2)}{\pi z_{c}} +\mathcal {O}(\alpha _s^3) , \end{aligned}$$

(1)

where $\mathrm{d}\sigma (ab\rightarrow cd)/\mathrm{d}\hat{t}$ denotes the leading-order (LO) elementary parton scattering cross sections at $\alpha _s^2$. The NLO contributions in $\mathcal {O}(\alpha _s^3)$ involve both $2\rightarrow 3$ tree level processes and one loop virtual corrections to $2\rightarrow 2$ tree processes. Processes at $2\rightarrow 3$ tree level include $qq \rightarrow qqg$, $q\bar{q} \rightarrow q\bar{q}g$, $q\bar{q} \rightarrow ggg$, $qg \rightarrow qgg$, $qg \rightarrow qq\bar{q}$, $gg \rightarrow q\bar{q}g$, $gg \rightarrow ggg$, etc, which include soft and collinear contributions. A standard $\overline{\mathrm{MS}}$ renormalization scheme is applied to control ultraviolet divergence in one loop virtual corrections to $2\rightarrow 2$ tree processes. More detailed discussions on calculations at NLO could be found in [43, 44]. In this paper the numerical calculations are carried out with a NLO Monte Carlo program [41, 42] where two cut-off parameters, $\delta _s$ and $\delta _c$, are employed to isolate the collinear and soft divergences in the squared matrix elements of the $2\rightarrow 3$ processes. The regions with the divergences are integrated over in n-dimensional phase space and the results are added with the squared matrix elements of the $2\rightarrow 2$ processes. This gives a set of two-body and three-body weights depending on $\delta _s$ and $\delta _c$. But the dependence will be eliminated after the weights are combined in the calculation of physical observables, and the final numerical results are insensitive to the cut-off parameters [41, 42].

We employ the same factorized form for the inclusive large $p_T$ particle production cross section in nucleus–nucleus collisions, which can be computed as a convolution of nuclear thickness functions, the nuclear parton distribution functions (nPDFs), elementary parton–parton scattering cross sections, and effective medium-modified parton fragmentation functions (mFFs) [18, 20],

$$\begin{aligned} \frac{\mathrm{d}N_{AB}}{\mathrm{d}y\mathrm{d}^2p_T}= & {} \sum _{abcd}\int \mathrm{d}^2r \mathrm{d}x_a\mathrm{d}x_b t_A(\mathbf{r})t_B(|\mathbf{r}-\mathbf{b}|) \nonumber \\&\times f_{a/A}(x_a,\mu ^2,\mathbf{r}) f_{b/B}(x_b,\mu ^2,|\mathbf{r}-\mathbf{b}|) \nonumber \\&\times \frac{\mathrm{d}\sigma }{\mathrm{d}\hat{t}}(ab\rightarrow cd)\nonumber \\&\times \frac{D_{h/c}(z_{c},\mu ^2,E, \mathbf{b}, \mathbf{r})}{\pi z_{c}} +\mathcal {O}(\alpha _s^3), \end{aligned}$$

(2)

at fixed impact parameter $\mathbf b$ in the transverse plane of the beam direction. In Eq. (2) the average over the azimuthal angle of the initial fast parton is implicitly implied. The nuclear thickness function $t(\mathbf{r})$ is calculated with the Woods–Saxon distribution function for nucleons in a nucleus and has been normalized by requiring $\int \mathrm{d}^{2}r t_{A}(\mathbf{r})=A$. The nuclear parton distributions per nucleon (nPDFs) $f_{a/A}(x_a,\mu ^2,\mathbf{r})$ can be parameterized as the production of the parton distributions inside free nucleons $f_{a/N}(x,\mu ^2)$ and the nuclear shadowing factor $S_{a/A}(x,\mu ^2,\mathbf{r})$,

$$\begin{aligned} f_{a/A}(x,\mu ^2,\mathbf {r})= & {} S_{a/A}(x,\mu ^2,\mathbf {r}) \left[ \frac{Z}{A}f_{a/p}(x,\mu ^2)\right. \nonumber \\&\left. +\left( 1-\frac{Z}{A}\right) f_{a/n}(x,\mu ^2) \right] , \end{aligned}$$

(3)

where Z denotes the charge and A is the mass number of the nucleus. In the numerical simulations we use the CTEQ6M parametrization [45] for the nucleon parton distributions $f_{a/N}(x,\mu ^2)$, and the EPS09 parametrization of nPDFs [46]. Since the parton–parton scattering cross sections are computed up to NLO, the CTEQ6M parametrization and the EPS09 parametrization are both used at NLO. For simplicity, we only use the central-fit set of EPS09 parametrization in following numerical calculations.

An energetic parton jet produced in the hard scattering may suffer multiple scattering with thermal partons in the QGP created in nucleus–nucleus collisions. The jet-medium scattering and medium-induced gluon radiation should give rise to new contributions to parton fragmentation functions (FFs) in vacuum and thus leads to medium-modified fragmentation functions, which may evolve with the scale Q [15, 18, 20, 49, 50], in a similar way to the DGLAP evolution in vacuum. If the parton jet travels a distance L inside the medium with the inelastic scattering mean free path $\lambda$, the probability for the jet scattering n times to the medium can be assumed to obey Poisson distribution [47, 48]. Therefore, the effect of parton energy loss in the dense QCD medium can be calculated in the high-twist approach of jet quenching and the effective medium-modified parton fragmentation functions (mFFs) are given by [15, 18, 20, 49]

$$\begin{aligned}&D_{h/c}(z_c,\mu ^2,\Delta E_c) = (1-e^{-\langle \frac{L}{\lambda }\rangle }) \left[ \frac{z_c^\prime }{z_c} D^0_{h/c}(z_c^\prime ,\mu ^2) \right. \nonumber \\&\quad +\left. \left\langle \frac{L}{\lambda }\right\rangle \frac{z_g^\prime }{z_c} D^0_{h/g}(z_g^\prime ,\mu ^2)\right] +e^{-\langle \frac{L}{\lambda }\rangle } D^0_{h/c}(z_c,\mu ^2), \end{aligned}$$

(4)

where $z_c^\prime =p_T/(p_{Tc}-\Delta E_c)$ is the rescaled momentum fraction of the hadron from the fragmentation of the quenched parton which has the initial transverse momentum $p_{Tc}$ and loses energy $\Delta E_c$ during its propagation inside the hot medium. Furthermore $z_g^\prime =\langle L/\lambda \rangle p_T/\Delta E_c$ is the rescaled momentum fraction of the hadron from the fragmentation of a radiated gluon with initial energy $\Delta E_c/{\langle \frac{L}{\lambda }\rangle }$ and $z_c=p_T/p_{Tc}$ is the momentum fraction for jet fragmentation in vacuum. ${\langle \frac{L}{\lambda }\rangle }$ times scattering will provide ${\langle \frac{L}{\lambda }\rangle }$ gluon emissions, so there is a factor ${\langle \frac{L}{\lambda }\rangle }$ in the fragmentation contribution of emitted gluon in the above equation. As shown in Ref. [47], the above mFFs satisfy the momentum sum rule by construction, $\Sigma _h\int zD_{h/c}(z_c,\mu ^2,\Delta E_c)=1$.

The weight factor $\mathrm{exp}({-\langle \frac{L}{\lambda }\rangle })$ is the probability for those partons escaping the medium without suffering any inelastic scattering, and the weight factor $1-\mathrm{exp}({-\langle \frac{L}{\lambda }\rangle })$ is the probability for partons encountering at least one inelastic scattering. The rescaled fraction in Eq. (4) is got by energy shifting due to energy loss $\Delta E_c$. For a given jet, the energy loss $\Delta E_c$ and the scattering number ${\langle \frac{L}{\lambda }\rangle }$ both depend on the local medium density in the jet trajectory and characterize the medium properties. This approximative approach for the medium-modified fragmentation function reproduces the main effect of the medium-induced radiation [15], and it is therefore similar to another approximative approach in Refs. [51, 52] where the modified fragmentation function is concluded as a convolution of the vacuum fragmentation function and the probability for a given jet to be quenched to a final jet inside the medium. We also note the difference between our approach and the ones used in Refs. [51, 52]. In the higher-twist formalism [36–38], one considers twist-4 processes of the splitting of a highly virtual parton ($\mu \gg \Lambda _{QCD}$) in QCD medium and evaluates the contribution of medium-induced gluon radiation, which gives rise to the effectively modified parton fragmentation functions and their corresponding (medium-modified) QCD evolution equations with respect to the hard scale $\mu$. This is different from that in Refs. [51, 52] where the medium contribution is computed at the medium scale. Also in Refs. [51, 52] a convolution with a Poisson probability for multiple emissions is used for the energy shift to take into account the fluctuation of energy loss.

In a high-twist approach the total energy loss $\Delta E = \Delta E_c(E,\mathbf{b}, \mathbf{r})$ is related to the jet transport parameter via,

$$\begin{aligned} \frac{\Delta E}{E}= & {} C_{A} \frac{\alpha _{s}}{2\pi } \int \mathrm{d}y^{-} \int _{0}^{Q^{2}} \frac{d l_T^2}{l_{T}^{4}} \int _\epsilon ^{1-\epsilon } \mathrm{d} z [1+(1-z)^2] \nonumber \\&\times \,\hat{q}_{F}(y) 4 \sin ^{2}(x_{L}p^{+}y^{-}/2), \end{aligned}$$

(5)

as shown in Ref. [53], in which one can refer for more details. $y^-$ denotes a jet place in its trajectory, and is the same as normal time $\tau$ used in the following calculations. In the above expression, the LPM effect for the induced gluon emission originates from the destructive interference of two kinds of processes, i.e. the soft-hard and hard-hard processes, which become identical to each other and lead to a cancellation of their contributions when the transverse momentum of the radiated gluon is small and the formation time of radiated gluon is rather large [36–38]. This is exactly the same as the LPM effect in the double scattering in the GLV opacity expansion formalism [54]. In the case of multiple soft scattering, as discussed in Refs. [26, 30, 55–59] the LPM effect is caused by similar interferences and plays a dominant role when the coherent emission of a single gluon in a multiple scattering process is considered and leads to a suppression of the energy loss as compared to the additive contribution of $n({=}\langle \frac{L}{\lambda }\rangle )$ independent scattering of one gluon radiation.

We emphasize that, in our model, the parton matrix elements are calculated at NLO, and EPS nuclear PDFs at NLO are utilized to include the initial-state cold nuclear matter effects, whereas the parton energy loss due to the final-state hot medium effect is given by a LO derivation of the parton energy loss resulting from effective medium-modified fragmentation functions in twist-4 at the high-twist expansion approach. Recently several theoretical attempts [28–30, 60, 61] have been made to calculate momentum broadening and parton energy loss due to multiple scattering in medium beyond leading order, which may be incorporated phenomenologically to a complete NLO calculations of particle or jet productions in high-energy nuclear collisions. It is also noticed that recently theoretical investigation of color decoherence has been developed for jets resolving and energy redistributing in the QCD medium [62–64].

The jet transport parameter for a gluon is 9 / 4 times of a quark, which is assumed to be proportional to the local parton density in a dynamical evolving medium and expressed as [21, 27, 65],

$$\begin{aligned} \hat{q} (\tau ,r)= \hat{q}_0\frac{\rho _{g}(\tau ,\mathbf{r}+\mathbf{n}\tau )}{\rho _{g}(\tau _{0},0)} \frac{p^\mu u_\mu }{p_0}\,, \end{aligned}$$

(6)

for a parton produced at a transverse position $\mathbf{r}$ at an initial time $\tau _0$ and traveling along the direction $\mathbf{n}$. $\hat{q}_{0}$ denotes the jet transport parameter at the center of the bulk medium at the initial time $\tau _{0}$. $\rho _{g}$ is the gluon density at a given temperature $T(\tau , r)$, and in numerical calculations we assume $\rho _g\propto (1-f)T^3$ for the medium as an ideal gas. As introduced in Refs. [39, 40, 65], the fraction $f(\tau , r)$ of the hadronic phase at any given time and local position is given by

$$\begin{aligned} f(\tau , r) = \left\{ \begin{array}{l} 0 \\ 0 \sim 1 \\ 1 \end{array} \;\; \;\; \begin{array}{l} \text {if }T>170 \text { MeV},\\ \text {if }T=170 \text { MeV},\\ \text {if }T<170 \text { MeV}, \end{array} \right. \end{aligned}$$

(7)

where we consider the mixed phase contribution and neglect the pure hadron phase contribution. During the mixed phase at $T = 170$ MeV the hadron phase fraction will be $f = 0 \sim 1$ while the QGP phase faction will be $1-f$. With the time evolution during the mixed phase the fraction value f will increase from 0 to 1. In the following numerical calculations the time-dependent fraction f is given by simulations of the hydrodynamic model [39, 40]. $p^\mu$ is the four momentum of the jet and $u^\mu$ is the four flow velocity in the collision frame. The average number of scatterings along the parton propagating path is given by

$$\begin{aligned} \langle L/\lambda \rangle =\frac{1}{\lambda _0}\int _{\tau _0}^{\infty } d\tau \frac{\rho _{g}(\tau ,\mathbf{r}+\mathbf{n}\tau )}{\rho _{g}(\tau _{0},0)}, \end{aligned}$$

(8)

where $\lambda _0$ is the mean free path at the initial time $\tau _{0}$, and for a quark jet it is 9 / 4 times of that for a gluon jet. The parameter $\lambda _0$ as well as $\hat{q}_{0}$ will be independently input in the following numerical calculations and simultaneously constrained by experiment data.

Fig. 1

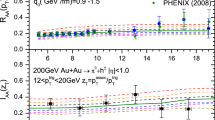
a The hadron cross sections at mid-rapidity in $p+p$ and central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV. b, c The corresponding nuclear modification factor with different values of the jet transport parameter $\hat{q}_{0}$ and the mean free path $\lambda _0$. The data are from [67–69]

Fig. 2

a The hadron cross sections at mid-rapidity in $p+p$ and central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV. b, c The corresponding nuclear modification factor with different values of the jet transport parameter $\hat{q}_{0}$ and the mean free path $\lambda _0$. The data are from [6, 7]

The fragmentation function in vacuum $D^0_{h/c}(z_c,\mu ^2)$ in Eqs. (1) and (4) is given by the AKK parametrization [66]. Here we use the NLO AKK FFs parametrization. For inclusive hadron production given by Eqs. (1) and (2), there are three independent scales: the renormalization scale $\mu _{\mathrm{ren}}$, the factorization scale $\mu _{\mathrm{fact}}$, and the fragmentation scale $\mu _{\mathrm{frag}}$. We choose $\mu _{\mathrm{ren}}=\mu _{\mathrm{fact}}=\mu _{\mathrm{frag}}=1.2p_T$ in our numerical analysis for both $p+p$ and $A+A$ collisions.

3 Extracting parameter values in simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits to $R_{AA}$ data

In the model for the effective medium-modified fragmentation functions (mFFs) discussed in Sect. 3, information on the space-time evolution of the local temperature and flow velocity in the bulk medium along the jet propagation path should be provided. In our simulation we will utilize a ($3+1$)-dimensional ideal hydrodynamic model [39, 40] to obtain the space-time evolution of the bulk matter created in central nucleus–nucleus collisions.

With a given space-time profile of the gluon density, one can then utilize the preceding effective mFFs to obtain the high $p_T$ hadron spectra. In actual calculations for the spectra or cross section at fixed values of the hadron transverse momentum $p_T$ in Eqs. (1) and (2), the factorization and renormalization scales are all chosen as $\mu _f=\mu _R$ = 1.2 $p_T$. Shown in Fig. 1a are the hadron cross sections in $p+p$ and 0–5 % $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV with given parameter values $\hat{q}_{0} = 1.1$ GeV$^2$/fm and $\lambda _0 = 0.4$ fm, as compared to PHENIX data [67–69]. The theoretical cross section for $A+A$ collisions is scaled as $(\mathrm{d}N_{AA}/\mathrm{d}y\mathrm{d}^2p_T)/{T_{AA}(b)}$ where $T_{AA}(b)=\int \mathrm{d}^{2}r t_{A}(\mathbf{r})t_{A}(\mathbf{r}-\mathbf{b})$. We choose $b = 2$ fm for 0–5 % $\mathrm{Au}+\mathrm{Au}$ and $b = 2.1$ fm for 0–5 % $\mathrm{Pb}+\mathrm{Pb}$ collisions. Shown in Fig. 2a are for 0–5 % $\mathrm{Pb}+\mathrm{Pb}$ collisions with given parameter values $\hat{q}_{0} = 1.7$ GeV$^2$/fm and $\lambda _0 = 0.5$ fm, as compared to CMS and ALICE data [6, 7]. It is observed that the theoretical results with chosen parameters of $\hat{q}_{0}$ and $\lambda _0$ could describe the experimental data at the RHIC and the LHC very well.

Shown in panels (b) and (c) of Figs. 1 and 2 are the suppression factor or nuclear modification factor,

$$\begin{aligned} R_{AA}=\frac{\mathrm{d}N_{AA}/\mathrm{d}y\mathrm{d}^2p_T}{T_{AA}(b) \mathrm{d}\sigma _{pp}/\mathrm{d}y\mathrm{d}^2p_T}. \end{aligned}$$

(9)

To compare theoretical results with the RHIC and LHC data, we may fix one parameter of $\hat{q}_{0}$ or $\lambda _0$, and then choose different values for another parameter. For given $\lambda _0$ the nuclear modification factor decreases with the increasing of $\hat{q}_0$, while for given $\hat{q}_0$ the nuclear modification factor increases with the increasing of $\lambda _0$.

For the two parameters $\hat{q}_0$ and $\lambda _{0}$ we fix one parameter and constrain another by $\chi ^2/\mathrm{d.o.f.}$ fitting to data for the nuclear suppression factor. The $\chi ^{2} /\mathrm{d.o.f.}$ is defined as follows:

$$\begin{aligned} \chi ^2/\mathrm{d.o.f.}=\sum _{i=1}^{N}\left[ \dfrac{(V_{\mathrm{th}}-V_{\mathrm{exp}})^2}{\sum _t \sigma _t^2}\right] _i \Big /N, \end{aligned}$$

(10)

where $V_{\mathrm{th}}$ stands for the theoretical value, $V_{\mathrm{exp}}$ denotes the experimental value, $\sum _t \sigma _t^2$ gives the quadratic sum over all types of errors that one chosen point has, and N the number of data points selected.

In numerical calculations the jet transport parameter $\hat{q}_0$ and the mean free path $\lambda _0$ are two independent inputs. We choose for a quark jet $\hat{q}_{0}$ $=$ 0.1–3.0 GeV$^2$/fm and $\lambda _0$ $=$ 0.1–1.0 fm, while for a gluon jet the values are, respectively, multiplied by 9/4 for $\hat{q}_{0}$ and 4/9 for $\lambda _{0}$ because of different color factors in the gluon–gluon and quark–gluon interacting vertex. From simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits to experimental data at RHIC and LHC shown in Fig. 3, one can extract values of the jet transport parameter $\hat{q}_0$ and the mean free path $\lambda _0$ at the center of the most central $A+A$ collisions with the given initial time $\tau _0=0.6$ fm. For an energetic quark jet, the best fits to the combined PHENIX data [67–69] give $\hat{q}_{0}=1.1 \pm 0.30$ GeV$^2$/fm and $\lambda _0 = 0.4 \pm 0.03$ fm in 0–5 % central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV, while the best fits to the combined ALICE [7] and CMS [6] data lead to $\hat{q}_{0}\approx 1.7 \pm 0.3$ GeV$^2$/fm, and $\lambda _{0}\approx 0.5 \pm 0.05$ fm in 0–5 % central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV.

Fig. 3

The $\chi ^2/\mathrm{d.o.f.}$ as a function of the initial quark jet transport parameter $\hat{q}_0$ and the initial mean free path $\lambda _{0}$. The upper panel is from fitting to the combined PHENIX data [67–69] on $R_{AA}(p_T)$ for $\pi ^0$ with $p_T$ $=$ 5–20 GeV at mid-rapidity in 0–5 % central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV. The lower panel is from fitting to the combined ALICE [7] and CMS [6] data on $R_{AA}(p_T)$ for charged hadrons with $p_T$ $=$ 10–100 GeV at mid-rapidity in 0–5 % central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV

4 Discussions

In general, the jet transport parameter should depend on the scale as shown by recent studies on the renormalization of the jet transport parameter [70–72]. In our numerical simulations for the initial values for $\hat{q}_0$ and $\lambda _0$ given by Eqs. (6) and (8), we assume they are constants for different jet transverse momentums as a reasonable approximation for phenomenological studies at the RHIC and the LHC. Note that the best fits shown in Fig. 3 are obtained for hadrons with $p_T$ $=$ 5–20 GeV at the RHIC, while we have $p_T$ $=$ 10–100 GeV at the LHC, so what we constrain for $\hat{q}_0$ and $\lambda _0$ may be understood as the averaged values for jets with different transverse momentum. Roughly speaking, what we constrain for $\hat{q}_0$ and $\lambda _0$ should depend on a much greater transverse momentum at the LHC than at the RHIC because of the much wider kinematical region of jet $p_T$ at the LHC.

In the formulation for the medium-modified fragmentation functions in Eq. (4), the final-state medium effect of jet quenching is controlled both by the total energy loss $\Delta E \propto \hat{q}_0$ in Eq. (5) and the multiple scattering number $\langle \frac{L}{\lambda }\rangle \propto \frac{1}{\lambda _0}$ in Eq. (8). Therefore the suppression factor $R_{AA}$ is quantified by the two independent parameters $\hat{q}_0$ and $\lambda _0$. The trend for the simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits in Fig. 3 shows that an increasing $\hat{q}_0$ must be associated with an increasing $\lambda _0$ to fit well the data at both the RHIC and the LHC. In fact, a larger $\lambda _0$ gives a smaller scattering number, and then a larger $\hat{q}_0$ is needed to release greater energy loss per scattering in order to describe the experimental data. This implicit relation between the two parameters is consistent with theoretical estimates for the jet transport parameter and the mean free path which are related to each other via the local temperature in a weakly coupled QCD medium [26, 73].

Of interest are the two different limits as demonstrated in Fig. 3, the single scattering limit with large $\lambda _0$, e.g. $\lambda _0 = 0.7$ fm at RHIC, and the infinite number scattering limit with very small $\lambda _0$, e.g. $\lambda _0 = 0.1$ fm at LHC. The numerical simulations for the simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits at both RHIC and LHC show that in the single scattering limit the suppression factor $R_{AA}$ is insensitive to $\hat{q}_0$ and sensitive to $\lambda _0$, whereas in the infinite number scattering limit $R_{AA}$ is sensitive to $\hat{q}_0$ and insensitive to $\lambda _0$. According to an assumption [47, 48] for parton scattering obeying a Poisson distribution, the probability for those partons escaping the system without suffering any inelastic scattering is $\mathrm{exp}({-\langle \frac{L}{\lambda }\rangle })$, while the probability for partons encountering at least one inelastic scattering gives $1-\mathrm{exp}({-\langle \frac{L}{\lambda }\rangle })$. One can see these two weight factors in the medium-modified fragmentation function in Eq. (4). In the infinite number scattering limit with small $\lambda _0$, $\mathrm{exp}({-\langle \frac{L}{\lambda }\rangle })$ is very small with large $\frac{L}{\lambda }$, the first term of Eq. (4) with dependence on $\hat{q}_0$ will dominate the total fragmentation contribution, so $R_{AA}$ is sensitive to $\hat{q}_0$ and less insensitive to $\lambda _0$. On the other hand, in single scattering limit with large $\lambda _0$, the second term of Eq. (4) gives the dominant contribution, thus $R_{AA}$ is insensitive to $\hat{q}_0$ and more sensitive to $\lambda _0$. We observe that our best fits for $\hat{q}_0$ and $\lambda _0$ are found in the region between the single scattering limit and the infinite number scattering limit due to a competition effect between the energy loss per scattering quantified by $\hat{q}_0$ and the scattering number quantified by $\lambda _0$, which implies that the data favor a regime of mean free paths that suggests multiple scattering in the medium.

From Fig. 3 we can extract the $\hat{q}_0$ range of values for energetic quarks as constrained by the measured suppression factors of single hadron spectra at RHIC and LHC as follows:

$$\begin{aligned} \hat{q}_0 \approx \left\{ \begin{array}{l} 1.1 \pm 0.2 \\ 1.7 \pm 0.3 \end{array} \, \mathrm{GeV}^2/\mathrm{fm} \quad \text {at} \; \begin{array}{l} {T=373 \,\mathrm{MeV}},\\ {T=473 \,\mathrm{MeV}}, \end{array} \right. \end{aligned}$$

at the highest temperatures reached in the most central $\mathrm{Au}+\mathrm{Au}$ collisions at RHIC and $\mathrm{Pb}+\mathrm{Pb}$ collisions at LHC. As shown in Fig. 4 for the scaled jet transport parameter $\hat{q}/T^3$, our result falls within the range of $\hat{q}_0/T^3_0$ for energetic quarks extracted from experimental data on $R_{AA}$ by the Jet Collaboration, though it is considerably smaller than that given by a strong-coupled AdS/CFT calculation [31, 32] as well as a lattice calculation [33, 34].

Fig. 4

The scaled jet transport parameter $\hat{q}/T^3$ for an initial quark jet at the center of the most central $A+A$ collisions at an initial time $\tau _0=0.6$ fm extracted by comparing the theoretical simulations with experimental data at both RHIC and LHC. The dashed boxes indicate the corresponding results of the Jet Collaboration [35]

In addition, from Fig. 3 one can extract the $\lambda _{0}$ range of values for energetic quarks as constrained by the measured suppression factors of single hadron spectra at RHIC and LHC as

$$\begin{aligned} \lambda _{0} \approx \left\{ \begin{array}{l} 0.4 \pm 0.03 \\ 0.5 \pm 0.05 \end{array} \, \mathrm{fm} \quad \text {at} \; \begin{array}{l} {T=373\, \mathrm{MeV}},\\ {T=473 \,\mathrm{MeV}}. \end{array} \right. \end{aligned}$$

In a theoretical estimate [73] for the mean free path, ${1}/{\lambda _{g}}=\rho \sigma =3\alpha _s(Q^2)T$ for which the elastic cross section $\sigma$ is used at leading order and the density $\rho$ is for an ideal gas. One can introduce the K factor to account for higher-order correction and the more realistic interaction among the medium particles [74, 75],

$$\begin{aligned} \frac{1}{\lambda _{g}}=3K\alpha _s(Q^2)T. \end{aligned}$$

(11)

Considering $\lambda _{q}=\frac{9}{4}\lambda _{g}$, and assuming the scale $Q^2=ET$ for a hard parton with energy E traversing a hot QCD medium with temperature T, we find that, with K $=$ 2.5–4.0, $\lambda _{q}$ given by the above equation is equal to our best fit for the mean free path at the highest temperatures in both RHIC and LHC. The K factor is bigger than what would be naturally expected, which might be caused by LO $\sigma$ as well as the ideal gas density $\rho$ in the theoretical evaluation of ${1}/{\lambda _{g}}=\rho \sigma$. A higher-order correction for the cross section may provide a factor of $\sim$2, while other effects such as corrections due to the difference between the real dynamics of the QGP and the simple picture of an ideal gas may account for the remaining enhancement to K. For instance, a strongly interacting QGP may give a larger cross section than a weakly coupled QGP. Thus the comparison of the model simulation with the data seems imply that the hot QCD medium at the RHIC and LHC is more likely a strongly interacting medium, which is surely model-dependent and further validations from other observables will be needed for a robust conclusion. It is noted that in numerical estimates we use parton energy E $=$ 8–25 GeV for $p_T$ $=$ 5–20 GeV hadron production at RHIC while E $=$ 15–120 GeV for $p_T$ $=$ 10–100 GeV hadron production at LHC, and therefore the running coupling $\alpha _s(Q^2)$ is appreciably smaller at LHC than at RHIC.

Fig. 5

The averaged number of gluon emissions from a propagating quark as a function of the vertex place of the hard scattering. The created quarks propagate along the $+x$ direction to escape off the fire ball

The phenomenological model given by Eq. (4) assumes that one scattering will induce one gluon emission from the propagating parton, so for a given propagating parton the total scattering number equals the total number of gluon emissions from this parton. Recent theoretical calculation gives the averaged number of gluon emissions $\langle N_g\rangle$ from a propagating parton in HT-BW approach within the high-twist framework of parton energy loss [35, 76]. In the HT-BW model, the medium-modified FFs are given by numerically solving a set of modified DGLAP evolution equations within the high-twist approach with an initial condition given by Poisson convolution of multiple gluon radiations, which has been shown [76] to give the best agreement with data for the nuclear modification factor $R_{AA}$ in high-energy heavy-ion collisions. Especially, the averaged number of gluon emissions $\langle N_g\rangle$ from a propagating parton is given [76] in the study for modified DGLAP evolution equations, which can be compared with our extracted number of medium-induced emissions $\langle \frac{L}{\lambda }\rangle$. Shown in Fig. 5 is the comparison for gluon emission number between our model (solid and dash curves) and the HT-BW approach (dot and dotted-dash curves denoted as “HT-BW”), where the initial quark jets are produced in the point $(x,y=0)$ of x axis and propagate along $+x$ direction in the transverse plane to escape off the fire ball. The quark transverse momentum is, for example, chosen as $p_T^\mathrm{jet}$ $=$ 10 GeV for RHIC and 30 GeV for LHC in central $A+A$ collisions. Our results for the averaged number of gluon emissions are consistent with the HT-BW method, and justify the validity of the model as shown in Refs. [18, 20].

Fig. 6

The temperature dependence of the average transverse momentum broadening squared for energetic quarks for one scattering at the initial time $\tau _0$ in the center of the fireball

According to the definitions for the jet transport parameter and the mean free path [26],

$$\begin{aligned} \hat{q}=\rho \int \mathrm{d}q_T^2 \frac{\mathrm{d}\sigma }{\mathrm{d}q_T^2} q_T^2, \end{aligned}$$

(12)

$$\begin{aligned} \frac{1}{\lambda }=\rho \int \mathrm{d}q_T^2 \frac{\mathrm{d}\sigma }{\mathrm{d}q_T^2}, \end{aligned}$$

(13)

one can estimate the average transverse momentum broadening squared,

$$\begin{aligned} \langle q_T^2\rangle =\hat{q} \lambda . \end{aligned}$$

(14)

Then our best fitting values for $\hat{q}_0$ and $\lambda _{0}$ give

$$\begin{aligned} \langle q_T^2\rangle =\hat{q} \lambda \approx \left\{ \begin{array}{l} 0.44 \pm 0.11 \\ 0.85 \pm 0.20 \end{array} \, \mathrm{GeV}^2 \quad \text {at} \; \begin{array}{l} {T=373 \,\mathrm{MeV}},\\ {T=473\, \mathrm{MeV}}, \end{array} \right. \end{aligned}$$

for energetic quarks with one scattering at the initial time $\tau _0$ in the center of the fireball, as shown in Fig. 6. Our numerical results show that, for energetic parton jets scattering inside the bulk medium at the highest temperature, the average transverse momentum broadening squared at LHC is about twice of that at RHIC. Compared to the initial parton jet energy, the broadening is moderate, which implies that the jet may traverse through the medium with small reflection and justifies the eikonal approximation usually used in jet quenching calculations.

As we stated before the AKK FFs in vacuum are used in our numerical simulations. It is noted that a recent theoretical study [77] has confronted seven sets of NLO FF parameterizations with inclusive charged-particle spectra in $p+p$ collisions at the LHC and identified that most of the theoretical predictions including AKK08 tend to overpredict the measured cross sections by up to a factor of two due to the too-hard gluon-to-hadron FFs. In this paper we focus on the medium properties demonstrated by the nuclear modification factor $R_{AA}$ which is a ratio of spectra between $A+A$ and $p+p$ collisions and therefore is expected not to be very sensitive to the choice of FFs parametrization as well as the scale. We have redone our simulations with a Kretzer parametrization of the FFs [78], which show the extracted ${\hat{q}}_0$ ($\lambda _0$) is less (larger) by about 10–20 % by using AKK08 FFs rather than by using Kretzer FFs.

5 Summary

We have used the NLO pQCD parton model with effective modified fragmentation functions due to radiative parton energy loss to study single hadron spectra in high-energy heavy-ion collisions at both RHIC and LHC. The energy loss of the hard partons is incorporated in the modified fragmentation functions which utilize two most important parameters to characterize the properties of the bulk medium: the jet transport parameter $\hat{q}_{0}$ and the mean free path $\lambda _{0}$, both at the initial time $\tau _0$. We perform the phenomenological study of the experimental data for $R_{AA}(p_{T})$ to constrain the two parameters with simultaneous $\chi ^2/\mathrm{d.o.f.}$ fits to RHIC as well as LHC data, and obtain for energetic quarks $\hat{q}_{0}\approx 1.1 \pm 0.2$ GeV$^2$/fm and $\lambda _{0}\approx 0.4 \pm 0.03$ fm in central $\mathrm{Au}+\mathrm{Au}$ collisions at $\sqrt{s_{NN}}=200$ GeV, while $\hat{q}_{0}\approx 1.7 \pm 0.3$ GeV$^2$/fm, and $\lambda _{0}\approx 0.5 \pm 0.05$ fm in central $\mathrm{Pb}+\mathrm{Pb}$ collisions at $\sqrt{s_{NN}}=2.76$ TeV. Numerical analysis shows that the best fit falls between the single scattering limit and multiple scattering limit for the energetic jets propagating through the bulk medium. These results indicate that the average transverse momentum broadening squared $\langle q_T^2 \rangle = \hat{q}\lambda$ of energetic partons for one scattering at initial time $\tau _0$ in the center of the fireball at LHC, $\langle q_T^2 \rangle _{\mathrm{LHC}} \approx 0.85$ GeV$^2$, which is twice that of $\langle q_T^2 \rangle _{\mathrm{RHIC}} \approx 0.44$ GeV$^2$ found at RHIC.