Warm intermediate inflationary Universe model in the presence of a generalized Chaplygin gas

Abstract

A warm intermediate inflationary model in the context of generalized Chaplygin gas is investigated. We study this model in the weak and strong dissipative regimes, considering a generalized form of the dissipative coefficient $\Gamma =\Gamma (T,\phi )$, and we describe the inflationary dynamics in the slow-roll approximation. We find constraints on the parameters in our model considering the Planck 2015 data, together with the condition for warm inflation $T>H$, and the conditions for the weak and strong dissipative regimes.

1 Introduction

It is well known that in modern cosmology in our understanding of the early Universe there has been introduced a new stage of the Universe, described by the inflationary scenario [1–6]. This early phase solves some of the problems of the standard big bang model, like the flatness, horizon, density of monopoles, etc. However, the most important feature of the inflationary scenario is that it provides a novel mechanism to account for the large-scale structure [7–12] and also it explains the origin of the observed anisotropy of the cosmic microwave background (CMB) radiation [13–15].

On the other hand, in the warm inflation scenario, the radiation production takes place at the same time that inflationary expansion [16, 17]. In this form, the presence of radiation during the inflationary expansion implies that inflation could smoothly end into the radiation domination epoch, without introduce a reheating phase. In this way, the warm inflation scenario avoids the graceful exit problem. In the warm inflation scenario, the dissipative effects are crucial during the inflationary expansion, and these effects arise from a friction term which drives the process of the scalar field dissipating into a thermal bath. Originally the idea of consider particle production in the inflationary scenario was developed in Ref. [18], from the introduction of an anomalous dissipation term in the equation of motion of the scalar field. However, the introduction of the $\Gamma \dot{\phi }^2$ friction term in the dynamics of the inflaton field $\phi$, as a source of radiation production, was introduced in Refs. [19, 20], where $\Gamma$ corresponds to the dissipative coefficient. In fact, if the radiation field is in an extremely excited state during the inflationary epoch, and if there is a strong damping effect on the inflaton dynamics, then a strong dissipative regime is obtained, and the other possibility is called the weak dissipative regime.

On the other hand, a fundamental condition for warm inflation to occur is that the temperature of the thermal bath must satisfy $T>H$, where H is the Hubble rate. Under this condition, the thermal fluctuations play a fundamental role in producing the primordial density fluctuations, indispensable for large-scale structure formation. In this sense, the thermal fluctuations of the inflaton field predominate over the quantum ones [21, 22]. For a review of warm inflation, see Refs. [23–25].

Also, it is well known that the generalized Chaplygin gas (GCG) is another model that explains the acceleration phase of the Universe. The GCG has an exotic equation of state $p=p(\rho )$, given by [26]

$$\begin{aligned} p_{Ch}=-\frac{A}{\rho _{Ch}^{\beta }}, \end{aligned}$$

(1)

where $\rho _{Ch}$ and $p_{Ch}$ correspond to the energy density and pressure of the GCG, respectively, and the quantities $\beta$ and A are constants. For the special case in which $\beta = 1$, this equation of state corresponds to the original Chaplygin gas [26], and the case of $\beta =0$ corresponds to the $\Lambda$ CDM model. From the perturbative analysis considering the fluid version of the GCG, negative values for $\beta$ are not allowed, since the square of the speed of sound $c_s^2=\beta \,A\rho ^{-(\beta +1)}$ becomes negative, and therefore this representation presents strong instabilities. However, in the representation of the GCG as a canonical self-interacting scalar field (where $c_s^2=1$) the perturbative analysis can be performed even for negative values of $\beta$ [27]. Moreover, from the Supernova SN Ia analysis, negative values for $\beta$ are favored when the GCG is considered as a fluid [28, 29]. In this form, different representations of the Chaplygin gas, namely as a fluid, tachyonic field, a self-interacting scalar field or a variant of gravity among others, modify the constraints on the cosmological parameters, in particular on the value of $\beta$. In the following, we will consider any value of $\beta$, except the value $\beta =-1$, since our physical quantities and solutions present divergences.

Considering the stress-energy conservation equation and Eq. (1), the energy density can be written as

$$\begin{aligned} \rho _{Ch}= & {} \left[ A+\frac{B}{a^{3(1+\beta )}}\right] ^{\frac{1}{1+\beta }} \nonumber \\ \!= & {} \!\rho _{Ch0}\left[ A_s+\frac{(1-A_s)}{a^{3(1+\beta )}}\right] ^ {\frac{1}{1+\beta }},\quad \text{ where } \ A_s\!=\!A/\rho _{Ch0}^{1+\beta }. \nonumber \\ \end{aligned}$$

(2)

Here, $a=a(t)$ is the scale factor and the quantity B is a positive integration constant. From the solution given by Eq. (2), the energy density of the GCG is characterized by two parameters, $A_s$ (or equivalently A) and $\beta$. The parameters $A_s$ and $\beta$ are constrained by the observational data. In particular, $A_s=0.73_{-0.06}^{+0.06}$ and $\beta =-0.09_{-0.12}^{+0.15}$ have been obtained in Refs. [30, 31], the values $0.81\lesssim A_s\lesssim 0.85$ and $0.2\lesssim \beta \lesssim 0.6$ have been obtained in Ref. [32], and the constraints $A_s=0.775_{-0.0161-0.0338}^{+0.0161+0.037}$ and $\beta =0.00126_{-0.00126-0.00126}^{+0.000970+0.00268}$ have been obtained from the Markov Chain Monte Carlo method [33]; see also Refs. [34–36].

In the construction of inflationary models inspired by the Chaplygin gas, Eq. (2) can be extrapolate in the Friedmann equation to study an inflationary scenario [37]. In this extrapolation, we identify the energy density of matter with the contribution of the energy density associated to the standard or tachyonic scalar field [32, 38–40]. Specifically this modification is realized from an extrapolation of Eq. (2), so that $\rho _{Ch}=\left[ A+\rho _m^{(1+\beta )}\right] ^{\frac{1}{1+\beta }}\rightarrow [A+\rho _\phi ^{(1+\beta )}]^{\frac{1}{(1+\beta )}}$, where $\rho _m$ corresponds to the matter energy density and $\rho _\phi$ corresponds to the scalar field energy density [37]. In this form, the effective Friedmann equation from the GCG may be viewed as a variant of gravity, which is of great interest in the study of the early Universe motivated by string/M-theory [41–44]. In this context, and in particular, if the effective Friedmann equation is different from the standard Friedmann equation, then we consider it to be a modified gravity. In general if the field equations are anything other than Einstein’s equations, or the action is different, then we view it as a modified theory of gravity. For a review of modified gravity theories and cosmology, see e.g., Ref. [45].

In the context of exact solutions, an expansion of the power-law type can be found from an exponential potential, where the scale factor evolves as $a(t)\sim t^{p}$, where $p>1$ [46]. de Sitter inflation is another exact solution to the background equations, which can be obtained from a constant effective potential [1]. However, another type of exact solution corresponds to intermediate inflation, where the expansion rate is slower than de Sitter inflation, but faster than power-law inflation. In this model, the scale factor a(t) evolves as

$$\begin{aligned} a(t)=\exp [\,\alpha \,t^{f}], \end{aligned}$$

(3)

where $\alpha$ and f are two constants; $\alpha >0$ and $0<f<1$ [47–50].

The model of intermediate inflation was in the beginning formulated as an exact solution to the background equations, nevertheless, this model may be studied under the slow-roll approximation together with the cosmological perturbations. In particular, under the slow-roll analysis, the effective potential is a power-law type, and the scalar spectral index becomes $n_s\sim 1$, and exactly $n_s=1$ (Harrizon–Zel’dovich spectrum) for the special value $f=2/3$ [51–57]. In the same way, the tensor-to-scalar ratio r becomes $r\ne 0$ [58–61]. Also, another motivation to study intermediate inflation comes from string/M-theory [62–64] (see also Refs. [65–72]). Here, it is possible to resolve the initial singularity and also to give an account of the present acceleration of the Universe, among others [73–81].

The main goal of the present work is to study the development of an intermediate-GCG model in the context of warm inflation. To achieve this, we will not view the solution given by Eq. (2) as a result of the adiabatic fluid from Eq. (1), and therefore as a fluid representation, but rather, recognize the energy density of matter as the contribution of the energy density associated with a standard scalar field. From this perspective we will obtain a modified Friedmann equation, and we will analyze the GCG as a representation of the variant of gravity [37]. From this modification itself, we will study the warm inflation scenario, and we will consider this model to present dissipative effects coming from an interaction between a standard scalar field and a radiation field. In relation to the friction term, we consider a generalized form of the dissipative coefficient $\Gamma =\Gamma (T,\phi )$, and we study how it influences the inflationary dynamics. In this form, we will study the background dynamics and the cosmological perturbations for our model in two regimes, namely the weak and strong dissipative regimes. Also, we find constraints on the parameters of our model considering the new data of Planck 2015 [15], together with the condition for warm inflation, given by $T>H$, and the conditions for weak ($\Gamma <3H$) and strong ($\Gamma >3H$) dissipative regimes.

The outline of the paper is as follows: the next section presents a short description of the warm intermediate inflationary model in the context of the GCG. In Sects. 3 and 4, we discuss the warm GCG model in the weak and strong dissipative regimes. In each section, we find explicit expressions for the dissipative coefficient, scalar potential, scalar power spectrum, and tensor-to-scalar ratio. Finally, Sect. 5 resumes our finding and exhibits our conclusions. We chose units so that $c=\hbar =1$.

2 The warm inflationary phase and the GCG

During warm inflation, the Universe is filled with a self-interacting scalar field with energy density $\rho _{\phi }$ together with a radiation field of energy density $\rho _{\gamma }$. In this way, the total energy density $\rho _\mathrm{total}$ corresponds to $\rho _\mathrm{total}=\rho _\phi +\rho _\gamma$. In the following, we will consider the energy density $\rho _{\phi }$ associated to the scalar field to be defined as $\rho _{\phi }=\dot{\phi }^{2}/2+V(\phi )$ and the pressure as $P_{\phi }=\dot{\phi }^{2}/2-V(\phi )$, where $V(\phi )$ corresponds to the effective scalar potential.

On the other hand, the GCG model can also be considered to achieve an inflationary scenario from the modified Friedmann equation, given by [32]

$$\begin{aligned} H^{2}={\kappa \over 3} \left( \left[ A+\rho _{\phi }^{1+\beta }\right] ^{1 \over 1+\beta }+\rho _{\gamma }\right) . \end{aligned}$$

(4)

Here H corresponds to the Hubble rate, defined as $H=\dot{a}/a$, and the constant $\kappa =8\pi G=8\pi /m_{p}^{2}$ ($m_{p}$ denotes the Planck mass). Dots mean derivatives with respect to cosmic time.

The modification in the Friedmann equation given by Eq. (4), is the so-called Chaplygin inflation [32]. In this form, the GCG inflationary model may be viewed as a modification of the gravity according to Eq. (4).

The dynamical equations for the energy densities $\rho _{\phi }$ and $\rho _{\gamma }$ in the warm inflation scenario are given by [16, 17]

$$\begin{aligned}&\dot{\rho _{\phi }}+3\,H\,(\rho _{\phi }+P_{\phi })=-\Gamma \dot{\phi }^{2},\nonumber \\&\text{ or } \text{ equivalenty } \quad \ddot{\phi }+3H\dot{\phi }+V'=-\Gamma \dot{\phi } , \end{aligned}$$

(5)

and

$$\begin{aligned} \dot{\rho }_{\gamma }+4H\rho _{\gamma }=\Gamma \dot{\phi }^{2}, \end{aligned}$$

(6)

where $V'=\partial V/\partial \phi$ and $\Gamma >0$ corresponds to the dissipative coefficient. It is well known that the coefficient $\Gamma$ is responsible of the decay of the scalar field into radiation. In general, this coefficient can be assumed to be a constant or a function of the temperature T of the thermal bath $\Gamma (T)$, or the scalar field $\phi$, i.e., $\Gamma (\phi )$, or both $\Gamma (T,\phi )$ [16, 17]. The general form for the dissipative coefficient $\Gamma (T,\phi )$ is given by [82, 83]

$$\begin{aligned} \Gamma (T,\phi )=C_{\phi }\,\frac{T^{m}}{\phi ^{m-1}}, \end{aligned}$$

(7)

where the constant $C_\phi$ is associated with the microscopic dissipative dynamics, and the value m is an integer. Depending of the different values of m, the dissipative coefficient given by Eq. (7) includes different cases [82, 83]. In particular, the value of $m=3$, or equivalently $\Gamma = C_\phi T^3\phi ^{-2}$, has been studied in Refs. [84–87]. For the cases $m=1$, $m=0$, and $m=-1$, the dissipative coefficient is related to the supersymmetry and non-supersymmetry cases [82, 83, 86].

Considering that during the scenario of warm inflation the energy density associated to the scalar field $\rho _{\phi }\gg \rho _{\gamma }$ [16–21, 88–90], i.e., the energy density of the scalar field predominates over the energy density of the radiation field, then Eq. (4) may be written as

$$\begin{aligned} H^{2}\!\approx \! {\kappa \over 3}\,\left( A+\rho _{\phi }^{1+\beta }\right) ^{ 1\over 1+\beta } \!=\!{\kappa \over 3}\,\left[ A\!+\!\left( {\dot{\phi }\over 2}\!+\! V(\phi )\right) ^{1+\beta }\right] ^{ 1\over 1+\beta }. \end{aligned}$$

(8)

Now, combining Eqs. (5) and (8), the quantity $\dot{\phi }^2$ becomes

$$\begin{aligned} \dot{\phi }^{2}= {\frac{2 }{\kappa }}\frac{(-\dot{H})}{(1+R)}\, \left[ 1-A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{- \beta \over 1+\beta } , \end{aligned}$$

(9)

where the parameter R corresponds to the ratio between $\Gamma$ and the Hubble rate, which is defined as

$$\begin{aligned} R=\frac{\Gamma }{3H}; \end{aligned}$$

(10)

we note that for the case of the weak dissipative regime, the parameter $R<1$ i.e., $\Gamma <3H$, and during the strong dissipation regime, we have $R>1$ or equivalently $\Gamma >3H$.

We also consider that the radiation production is quasi-stable, then $\dot{\rho }_{\gamma }\ll 4H\rho _{\gamma }$ and $\dot{\rho }_{\gamma }\ll \Gamma \dot{\phi }^{2}$; see Refs. [16–21, 88–90]. In this form, combining Eqs. (6) and (9), the energy density for the radiation field can be written as

$$\begin{aligned} \rho _{\gamma }= & {} \frac{\Gamma \dot{\phi }^{2}}{4H}=\frac{\Gamma (-\dot{H})}{2\kappa H(1+R)} \,\left[ 1-A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{- \beta \over 1+\beta } \nonumber \\= & {} C_{\gamma }\,T^{4}, \end{aligned}$$

(11)

where the quantity $C_{\gamma } =\pi ^{2}\,g_{*}/30$, in which $g_{*}$ denotes the number of relativistic degrees of freedom. In particular, for the Minimal Supersymmetric Standard Model (MSSM), $g_{*}= 228.75$ and $C_{\gamma } \simeq 70$ [21].

From Eq. (11), we see that the temperature of the thermal bath T is given by

$$\begin{aligned} T\!=\!\left[ \frac{\Gamma \,(-\dot{H})}{2\,\kappa \,\,C_{\gamma }H\,(1+R)}\right] ^{1/4} \,\left[ 1\!-\!A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{- \beta \over 4(1+\beta )}, \end{aligned}$$

(12)

and considering Eqs. (8), (9), and (11) the effective potential becomes

$$\begin{aligned} V&=\left[ \left( {3\,H^2 \over \kappa }\right) ^{1+\beta }-A\right] ^{1\over 1+\beta }\nonumber \\&\quad +\frac{\dot{H}(2+3R)}{2 \kappa (1+R)} \,\left[ 1-A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{- \beta \over 1+\beta }. \end{aligned}$$

(13)

Here, we note that this effective potential could be expressed in terms of the scalar field, in the case of the weak (or strong) dissipative regime.

Similarly, combining Eqs. (7) and (12) the dissipation coefficient $\Gamma$ may be written as

$$\begin{aligned} \Gamma ^{{\frac{4-m }{4}}}&= C_{\phi }\,\phi ^{1-m} \left[ \frac{-\dot{H}}{2\kappa \, C_{\gamma }H(1+R)}\right] ^{m/4}\,\nonumber \\&\quad \times \left[ 1-A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{-m\, \beta \over 4(1+\beta )}. \end{aligned}$$

(14)

Here, Eq. (14) determines the dissipative coefficient in the weak (or strong) dissipative regime in terms of the scalar field (or the cosmic time).

In the following, we will analyze our warm generalized Chaplygin gas model in the context of intermediate inflation. To achieve this, we will consider a general form of the dissipative coefficient $\Gamma$ given by Eq. (7), for the specific cases $m = 3, m = 1, m = 0$, and $m = -1$. Also, we will restrict ourselves to the weak and strong dissipative regimes.

3 The weak dissipative regime

We start by considering our model to evolve according to the weak dissipative regime, in which $\Gamma <3H$. In this way, the standard scalar field $\phi$ as a function of cosmic time, from Eqs. (3) and (9), is found to be

$$\begin{aligned} \phi (t)-\phi _{0}=\frac{B[t]}{K}, \end{aligned}$$

(15)

where $\phi (t=0)=\phi _0$ corresponds to an integration constant, and K is a constant given by

$$\begin{aligned} K\!=\!(1+\beta )\, \sqrt{6\,(1-f)}\,\left( {\kappa \over 3}\right) ^{\frac{2-f}{4(1-f)}}\, (\alpha \,f)^{\frac{-1}{2(1-f)}}\,A^{\frac{f}{4(1+\beta )(1-f)}}; \end{aligned}$$

B[t], denotes the incomplete Beta function [91], defined as

$$\begin{aligned} B[t]= & {} B\left[ A\,\left( {\kappa \over 3\alpha ^2f^2}\right) ^{1+\beta }\,t^{2(1+\beta )(1-f)};\right. \nonumber \\&\left. \frac{f}{4(1+\beta )(1-f)},\frac{2+\beta }{2(1+\beta )}\right] . \end{aligned}$$

In the following we will assume the integration constant $\phi _{0}=0$ (without loss of generality). From the solution of the scalar field given by Eq. (15), the Hubble rate H in terms of the scalar field becomes $H(\phi )=\alpha \,f\,\left( B^{-1}[K\,\phi ]\right) ^{-(1-f)}$, where $B^{-1}[K\,\phi ]$ represents the inverse of the function B[t].

Considering the slow-roll approximation in which $\dot{\phi }^2/2<V(\phi )$, then from Eq. (13) the scalar potential as a function of the scalar field, can be written as

$$\begin{aligned} V(\phi )\approx \left[ \left( {3\,\alpha ^2f^2\over \kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)}}\right) ^{1+\beta } -A\right] ^{1\over 1+\beta }. \end{aligned}$$

(16)

Assuming that the model evolves according to the weak dissipative regime, then the dissipative coefficient $\Gamma$ as a function of the scalar field, for the case of $m \ne 4$, as a result is

$$\begin{aligned} \Gamma (\phi )&= C_{\phi }^{{\frac{4}{4-m}}}\left[ \frac{1-f}{2\kappa \,C_{\gamma }\,B^{-1}[K\,\phi ]}\right] ^{\frac{m}{4-m}} \phi ^{{\frac{4(1-m) }{4-m}}} \nonumber \\&\quad \times \,\left[ 1-A\left( {\kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{- m\,\beta \over (4-m)(1+\beta )} , \end{aligned}$$

(17)

here, we have considered Eq. (14).

On the other hand, we see that the dimensionless slow-roll parameter $\varepsilon$, from Eq. (14) is given by $\varepsilon =-\frac{\dot{H}}{H^{2}}=\left( {\frac{1-f}{Af}}\right) {1\over (B^{-1}[K\,\phi ])^{f}}$. In this way, the condition $\varepsilon <$1 (condition for inflation to occur) is satisfied for values of the scalar field, such that $\phi >{1\over K}B\left[ \left( {\frac{1-f}{Af}}\right) ^{1/f}\right]$.

From the definition of the number of e-folds, N, between two different values of cosmic time, $t_{1}$ and $t_{2}$, or between two values of the scalar field, namely $\phi _{1}$ and $\phi _{2}$, we have

$$\begin{aligned} N&=\int _{t_{1}}^{t_{2}}\,H\,\mathrm{d}t\nonumber \\&=\alpha \,\left( t_{2}^{f}-t_{1}^{f}\right) =\alpha \,\left[ (B^{-1}[K\,\phi _{2}])^{f}-(B^{-1}[K\,\phi _{1}])^{f} \right] . \end{aligned}$$

(18)

Here, we have used Eq. (15).

The inflationary scenario begins at the earliest stage possible, for which $\varepsilon =1$; see Refs. [51–57]. In this form, from the definition of the parameter $\varepsilon$, the value of the scalar field $\phi _{1}$ as a result is

$$\begin{aligned} \phi _{1}={1\over K}B\left[ \left( {\frac{1-f}{Af}}\right) ^{1/f}\right] . \end{aligned}$$

(19)

In the following we will analyze the scalar and tensor perturbations during the weak dissipative regime ($R<1$) for our Chaplygin warm model. It is well known that the density perturbation may be written as ${\mathcal {P} _{\mathcal {R}}}^{1/2}=\frac{H}{\dot{\phi }}\,\delta \phi$ [16, 17]. However, during the warm inflation scenario, a thermalized radiation component is present, so the inflation fluctuations are principally thermal instead of quantum [16–21, 88–90]. In fact, for the weak dissipation regime, the inflaton fluctuation $\delta \phi ^{2}$ is found to be $\delta \phi ^{2}\simeq H\,T$ [21, 88–90, 92]. Therefore, the power spectrum of the scalar perturbation ${\mathcal {P}_{\mathcal {R}}}$, from Eqs. (9), (12), and (14), becomes

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}&= {\sqrt{3\pi }\kappa \over 4}\, \left( \frac{C_{\phi }}{2\kappa C_{\gamma }}\right) ^{{\frac{1}{4-m}}}\phi ^{{\frac{1-m}{4-m}}}H^{{\frac{11-3m}{4-m}}}(-\dot{H})^{-{\frac{3-m}{4-m}}}\nonumber \\&\quad \times \left[ 1-A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{ \beta (3-m)\over (1+\beta )(4-m)}, \end{aligned}$$

(20)

or equivalently the power spectrum of the scalar perturbation may be expressed in terms of the scalar field as

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}&= k_{1}\phi ^{\,\frac{1-m}{4-m}} \left( B^{-1}[K\,\phi ] \right) ^{\frac{2f(4-m)+m-5}{4-m}}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{ \beta (3-m)\over (1+\beta )(4-m)}, \end{aligned}$$

(21)

where the constant $k_{1}$ is defined as $k_{1}={\sqrt{3\pi }\kappa \over 4}\left( \frac{C_{\phi }}{2\kappa C_{\gamma }}\right) ^{{\frac{1}{4-m}}}(\alpha \,f)^{2} \,(1-f)^{{\frac{m-3}{4-m}}}$.

Also, the power spectrum may be written as a function of the number of e-folds N, leading to

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}(N)&= k_{2}(B[J(N)])^{\,\frac{1-m}{4-m}} \left( J[N] \right) ^{\frac{2f(4-m)+m-5}{4-m}}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{ \beta (3-m)\over (1+\beta )(4-m)}. \end{aligned}$$

(22)

Here, the quantity J(N) is defined as $J(N)=\left[ {1+f(N-1)\over Af} \right] ^{\frac{1}{f}}$, and $k_{2}$ is a constant given by $k_{2}=k_{1}K^{-\frac{1-m}{4-m}}.$

From the definition of the scalar spectral index $n_{s}$, given by $n_{s}-1=\frac{\text {d}\ln \,{\mathcal {P}_{R}}}{\text {d}\ln k}$, considering Eqs. (15) and (22), the scalar spectral index in the weak dissipative regime as a result is

$$\begin{aligned} n_{s}=1-{5-m-2f(4-m)\over Af(4-m)(B^{-1}[K\,\phi ])^f} +n_2 +n_3, \end{aligned}$$

(23)

where the quantities $n_2$ and $n_3$ are defined as

$$\begin{aligned} n_{2}= & {} {1-m \over 4-m}\sqrt{{2(1-f)\over \kappa Af}} {(B^{-1}[K\,\phi ])^{-f/2}\over \phi } \\&\times \left[ 1-A\left( {\kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-\beta \over 2(1+\beta )} \end{aligned}$$

and

$$\begin{aligned} n_{3}\!= & {} \! 2A\beta {(3-m) \over (4\!-\!m)}{ (1\!-\!f)\left( \kappa / 3\right) ^{1+\beta } \over (Af)^{3+2\beta }} (B^{-1}[K\,\phi ])^{2-3f+2\beta (1-f))} \\&\times \left[ 1-A\left( {\kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-1}, \end{aligned}$$

respectively.

In fact, the scalar spectral index also can be rewritten in terms of the number of e-folds N. From Eqs. (18) and (19) we have

$$\begin{aligned} n_{s}=1-\frac{5-m-2f(4-m)}{(4-m)[1+f(N-1)]}+n_2 +n_3, \end{aligned}$$

(24)

where the functions $n_2=n_2(N)$ and $n_3=n_3(N)$ now are defined as

$$\begin{aligned} n_{2}= & {} K{1-m \over 4-m}\sqrt{{2(1-f)\over \kappa Af}} {(J[N])^{-f/2}\over B[J(N)]} \\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-\beta \over 2(1+\beta )} \end{aligned}$$

and

$$\begin{aligned} n_{3}= & {} 2A\beta {(3-m) \over (4-m)}{ (1-f)\left( \kappa / 3\right) ^{1+\beta } \over (Af)^{3+2\beta }} (J[N])^{2-3f+2\beta (1-f))}\nonumber \\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-1}, \end{aligned}$$

respectively.

Fig. 1

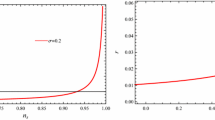
Left panel Ratio $\Gamma /3H$ versus the scalar spectral index $n_s$. Right panel Ratio T / H versus the scalar spectral index $n_s$. For both panels we have considered different values of the parameter $C_\phi$ for the special case $m=3$ i.e., $\Gamma \propto T^3/\phi ^2$, during the weak dissipative regime. In both panels, the dotted, dashed, and solid lines correspond to the pairs ($\alpha =0.009$, $f=0.583$), ($\alpha =0.005$, $f=0.583$), and ($\alpha =0.002$, $f=0.582$), respectively. In these plots we have used the values $C_\gamma =70$, $A=0.775$, $\beta =0.00126$ and $m_p=1$

On the other hand, tensor perturbations do not couple to the thermal background, so gravitational waves are only generated by quantum fluctuations, as in standard inflation [93]

$$\begin{aligned} {\mathcal {P}}_{g}=8\kappa \left( \frac{H}{2\pi }\right) ^{2}. \end{aligned}$$

(25)

From this spectrum, it is possible to construct a fundamental observational quantity, namely the tensor-to-scalar ratio $r={\mathcal {P}}_{g}/{\mathcal {P}_{\mathcal {R}}}$. In this way, from Eq. (22) and the expression of ${\mathcal {P}}_{g}$, the tensor-to-scalar ratio as a function of the scalar field yields

$$\begin{aligned} r(\phi )&= {2\,\kappa \,\alpha ^2 f^2 \over \pi ^2\,k_{1}} \,\phi ^{\,-\frac{1-m}{4-m}} \left( B^{-1}[K\,\phi ] \right) ^{-\frac{3-m}{4-m}}\nonumber \\&\quad \times \left[ 1- A\left( {\kappa \left( B^{-1}[K\,\phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{- \beta (3-m)\over (1+\beta )(4-m)} . \end{aligned}$$

(26)

In a similar way to the case of the scalar perturbations, the tensor-to-scalar ratio can be expressed in terms of the number of e-folds N, resulting in

$$\begin{aligned} r(N)&= {2\,\kappa \,\alpha ^2 f^2 \over \pi ^2\,k_{2}} (B[J(N)])^{-\frac{1-m}{4-m}} \left( J[N] \right) ^{-\frac{3-m}{4-m}}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{- \beta (3-m)\over (1+\beta )(4-m)} . \end{aligned}$$

(27)

Here, we have used Eqs. (18) and (26).

In the left and right panels of Fig. 1 we show the evolution of the ratio $\Gamma /3H$ versus the scalar spectral index and the evolution of the ratio T / H versus the scalar spectral index, during the weak dissipative regime for the special case $m=3$ i.e., $\Gamma (\phi ,T)=C_\phi \,T^3/\phi ^2$. In both panels, we have considered different values of the parameter $C_\phi$. In fact, the left panel shows the condition $\Gamma <3H$ for the weak dissipative regime. In the right panel we show the essential condition for warm inflation scenario to occur, given $T>H$.

In order to write down quantities that relate $\Gamma /3H$, T / H and the spectral index $n_s$, we consider Eqs. (3), (14), and (15), and we obtain numerically in the first place the ratio $\Gamma /3H$ as a function of the scalar spectral index $n_s$. Also, combining Eqs. (3) and (12), we find numerically the ratio between the temperature T and the Hubble rate H as a function of the spectral index $n_s$. In both panels, we use the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, see Ref. [33], and $m_p=1$. Here we find numerically, from Eqs. (22) and (24), that the values $\alpha =0.009$ and $f=0.583$ correspond to the parameter $C_\phi =10^{6}$. Here, we have used the values ${\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}$, $n_s=0.97$, and the number of e-folds $N=60$. In the same way, for the value of the parameter $C_\phi =10^{7}$, we find numerically the values $\alpha =0.005$ and $f=0.583$. On the other hand, for the parameter $C_\phi =10^{8}$, we find the values $\alpha =0.002$ and $f=0.582$. From the left panel, we obtain an upper bound for $C_\phi <10^8$, considering the condition for the weak dissipative regime $\Gamma <3H$. From the right panel we find a lower bound for the parameter $C_\phi >10^6$, from the essential condition for warm inflation to occur, given by $T>H$.

Fig. 2

Evolution of the tensor-to-scalar ratio r versus the scalar spectral index $n_s$ in the weak dissipative regime for the special case $\Gamma \propto T^3/\phi ^2$ i.e., $m=3$. Here, we have considered the two-dimensional marginalized constraints from the new data of Planck 2015 [15]. In this plot we have considered three different values of the parameter $C_\phi$. In this panel, the dotted, dashed, and solid lines correspond to the pairs ($\alpha =0.009$, $f=0.583$), ($\alpha =0.005$, $f=0.583$), and ($\alpha =0.002$, $f=0.582$), respectively. As before, we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$

Fig. 3

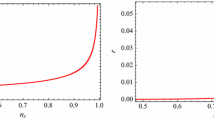
Evolution of the ratio $\Gamma /3H$ versus the scalar spectral index $n_s$ (left panel) and the evolution of the ratio T / H versus the scalar spectral index $n_s$ (right panel) in the weak dissipative regime for the specific value of $m=1$ ($\Gamma \propto T$), for three different values of the parameter $C_\phi$. In both panels, the dotted, dashed, and solid lines correspond to the pairs ($\alpha =0.377$, $f=0.296$), ($\alpha =0.674$, $f=0.294$), and ($\alpha =0.798$, $f=0.296$), respectively. Also, we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$

In Fig. 2 we show the consistency relation $r=r(n_s)$ for the specific case of $m=3$. Here, we observe that the tensor-to-scalar ratio becomes $r\sim 0$ for the range $10^6<C_\phi <10^8$, during the weak dissipative regime (see the figure). In this form, the range for the parameter $C_\phi$ is well corroborated from the Planck 2015 data [15]. However, we note that the consistency relation $r=r(n_s)$ does not impose a constraint on the parameter $C_\phi$ for the weak dissipative regime. In this way, for the specific case of $m=3$, the range of the parameter $C_\phi$ during the weak dissipative regime is given by $10^{6}< C_\phi < 10^{8}$.

In Fig. 3 we show the evolution of the ratio $\Gamma /3H$ versus the scalar spectral index (left panel) and the evolution of the ratio T / H versus the scalar spectral index (right panel), during the weak dissipative regime for the special case $m=1$, i.e., $\Gamma (\phi ,T)\propto \,T$. As before, we consider Eqs. (3), (12), (14), and (15), and we find numerically the ratio $\Gamma /3H$ and the ratio between the temperature T and the Hubble rate H in terms of the scalar spectral index $n_s$, for three different values of the parameter $C_\phi$. Again, in both panels, we use the values $C_\gamma =70$, $A=0.775$, $\beta =0.00126$, and $m_p=1$. As before, we find numerically, from Eqs. (22) and (24), that the values $\alpha =0.377$ and $f=0.296$ correspond to the value of the parameter $C_\phi =0.025$. Here, again we have used the values ${\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}$, $n_s=0.97$, and the number of e-folds $N=60$. As before, for the value $C_\phi =10^{-5}$, we find numerically the values $\alpha =0.674$ and $f=0.294$, and for $C_\phi =10^{-6}$, we obtain $\alpha =0.798$ and $f=0.296$. On the other hand, we study the consistency relation $r=r(n_s)$ for the specific case of $m=1$, and we observe that the parameter $C_\phi$ is well corroborated from the latest data of Planck (figure not shown). Again, we note that the ratio $\Gamma /3H<1$ gives an upper bound for $C_\phi$, while the condition for warm inflation, $T>H$, gives the lower bound for the parameter $C_\phi$. In this way, for the special case in which $m=1$, the range of the parameter $C_\phi$ during the weak dissipative regime is given by $10^{-6}< C_\phi < 0.025$.

Table 1 Results for the constraints on the parameters $\alpha$, f and $C_\phi$ during the weak dissipative regime

Fig. 4

Left panel Ratio $\Gamma /3H$ versus the scalar spectral index $n_s$. Right panel Ratio T / H versus the scalar spectral index $n_s$. For both panels we have considered different values of the parameter $C_\phi$ for the special case $m=3$ (or equivalently $\Gamma \propto T^3/\phi ^2$), during the weak dissipative regime. In both panels, the dotted, dashed, and solid lines correspond to the pairs ($A=5.5\times 10^{-4}$, $\beta =-0.56$), ($A=2.9\times 10^{-3}$, $\beta =-0.61$), and ($A=5\times 10^{-3}$, $\beta =-0.62$), respectively. Now in these plots we have used the values $C_\gamma =70$, $\alpha =10^{-3}$, $f=0.7$ and $m_p=1$

For the cases $m=0$ and $m=-1$, and considering the condition for the weak dissipative regime $\Gamma <3H$, we find an upper bound for the parameter $C_\phi$; for the case $m=0$, this bound is found to be $C_\phi <10^{-7}$. We find numerically the values $\alpha =0.633$ and $f=0.269$, corresponding to $C_\phi =10^{-7}$. For the case $m=-1$, this bound is given by $C_\phi <10^{-12}$, and for $C_\phi =10^{-12}$ we find the values $\alpha =0.817$ and $f=0.254$. Now, from the essential condition for warm inflation to occur, $T>H$, as before, we obtain a lower bound for $C_\phi$; for the specific value $m=0$ i.e., $\Gamma \propto \phi$ the lower bound is given by $C_\phi >10^{-12}$, numerically leading to the values $\alpha =1.152$, $f=0.270$ for $C_\phi >10^{-12}$. Finally, for the value $m=-1$ the bound is given by $C_\phi >10^{-18}$. In this case, for $C_\phi =10^{-18}$, we find the values $\alpha =1.443$, $f=0.255$. Moreover, we observe that these values for $C_\phi$ are well corroborated by the latest data of Planck, considering the consistency relation $r=r(n_s)$ for the cases $m=0$ and $m=-1$ (not shown). However, this consistency relation does not impose a constraint on $C_\phi$.

It is interesting to note that the range for the parameter $C_\phi$ for the weak dissipative regime is obtained only from the condition for the weak dissipative regime $\Gamma <3H$, which gives an upper bound, and the essential condition for warm inflation to occur, $T>H$, which gives a lower bound. We observe that the consistency relation $r=r(n_s)$ does not impose a constraint on $C_\phi$ for this regime.

Table 1 summarizes the constraints on the parameters $\alpha$, f and $C_\phi$, for the different values of the parameter m, considering a general form for the dissipative coefficient $\Gamma =\Gamma (T,\phi )$, in the weak dissipative regime. We note that these constraints on our parameters result as consequence of the conditions $\Gamma <3H$ (upper bound) and $T>H$ (lower bound). Here we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$.

For the sake of numerical evaluation let us consider different values for the parameters A, $\beta$, and $C_\phi$, but now the parameters $\alpha$, f, and m are fixed. In the following, we will find numerically the values of the parameter A and $\beta$ from Eqs. (22) and (24), considering the values ${\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}$, $n_s=0.97$, and the number of e-folds $N=60$.

In the left and right panels of Fig. 4 we show the plot of $\Gamma /3H$ as a function of the scalar spectral index $n_s$ and the plot of the ratio T / H as a function of the scalar spectral index, for the weak dissipative regime, for the special case $m=3$, considering the values $\alpha =10^{-3}$ and $f=0.7$. As before, in both panels, we have considered different values of the parameter $C_\phi$. Again, the left plot shows the condition $\Gamma <3H$ for the model evolves according to the weak dissipative regime, and in the right panel we show the essential condition for warm inflation scenario to occur, given $T>H$.

As before, for the quantities $\Gamma /3H$, T / H and the scalar spectral index $n_s$, we take Eqs. (3), (14), and (15), and we find numerically the ratio $\Gamma /3H$ as a function of the scalar spectral index. Also, from Eqs. (3) and (12), we obtain numerically the ratio T / H as a function of the spectral index $n_s$. Now we use the values $C_\gamma =70$, $\rho _{Ch0}=1$, $\alpha =10^{-3}$, and $f=0.7$. As before, we see numerically, from Eqs. (22) and (24), that the values $A=5.5\times 10^{-4}$ and $\beta =-0.56$ correspond to the parameter $C_\phi =10^{7}$. Here, we have used the observational constraints ${\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}$, $n_s=0.97$, and the number of e-folds $N=60$. On the other hand, for the value of the parameter $C_\phi =5\times 10^{7}$, we find numerically the values $A=2.9\times 10^{-3}$ and $\beta =-0.61$. Likewise, for the parameter $C_\phi =10^{8}$, we find the values $A=5\times 10^{-3}$ and $\beta =-0.62$. Here we note that from the left panel, we find an upper bound for the parameter $C_\phi$, given by $C_\phi <10^8$, taking the condition for the weak dissipative regime $\Gamma <3H$. Similarly, from the right panel, we find a lower bound for the parameter $C_{\phi }$, given by $C_\phi >10^7$, from the essential condition for warm inflation to occur, given by $T>H$. Also, we note that from the consistency relation $r=r(n_s)$, for the specific case of $m=3$, the tensor-to-scalar ratio becomes $r\sim 0$ for the range $10^7<C_\phi <10^8$, during this regime (not shown). In this way, the range for the parameter $C_\phi$ is in agreement with the Planck 2015 results [15]. As before, we observe that the consistency relation $r=r(n_s)$ does not impose any constraint on the parameter $C_\phi$ for the weak dissipative regime when the parameters $\alpha$ and f are fixed.

In this way, for the special case $m=3$, the ranges for the parameters $C_\phi$, A and $\beta$ during the weak dissipative regime are given by $10^7<C_\phi <10^8$, $5.5\times 10^{-4}<A<5\times 10^{-3}$ and $-0.62<\beta <-0.55$, respectively. We note that in the representation of the GCG as a variant of gravity, our analysis favors negative values for the parameter $\beta$.

For the case $m=1$, and considering our model to evolve according to the weak dissipative regime, i.e., $\Gamma <3H$, we find an upper bound for the parameter $C_\phi$. Analogously to the previous case, and when the parameters $\alpha$ and f are fixed to $\alpha =10^{-3}$ and $f=0.7$, respectively, we numerically find that the values $A=154.7$ and $\beta =-1.3$ correspond to $C_\phi =1.1\times 10^{-2}$. Now, from the essential condition for warm inflation to occur, $T>H$, we obtain a lower bound for $C_\phi$, given by $C_\phi >3.6\times 10^{-5}$, and numerically we find that the values $A=2995$, and $\beta =-1.4$ correspond to $C_\phi =3.6\times 10^{-5}$. We observe that these values for $C_\phi$ are well corroborated from the Planck 2015 results. Moreover, the tensor-to-scalar ratio becomes $r\sim 0$ (not shown), and as before the r–$n_s$ plane does not impose any constraint on $C_\phi$. In this way, for the special case $m=1$, the allowed ranges for the parameters $C_\phi$, A, and $\beta$ for the weak dissipative regime are given by $3.6\times 10^{-5}<C_\phi <1.1\times 10^{-2}$, $154.7<A<2995$, and $-1.4<\beta <-1.3$, respectively. We note that our analysis favors negative values for $\beta$.

For the cases in which $\Gamma \propto \phi$ (or equivalently $m=0$) and $\Gamma \propto \phi ^2/T$ (or equivalently $m=-1$), we find that these models do not work in the weak dissipative regime, since the scalar spectral index $n_s>1$, and then these cases are disproved from the observational data.

Table 2 Results for the constraints on the parameters A, $\beta$ and $C_\phi$ during the weak dissipative regime

Table 2 summarizes the constraints on the parameters A, $\beta$, and $C_\phi$, for the different values of the parameter m, considering a general form for the parameter $\Gamma =\Gamma (T,\phi )$, in the weak dissipative regime. As before, these constraints result as a consequence of the conditions $\Gamma <3H$ (upper bound) and $T>H$ (lower bound). Here, we have fixed the values $C_\gamma =70$, $\rho _{Ch0}=1$, $\alpha =10^{-3}$, $f=0.7$, and $m_p=1$.

4 The strong dissipative regime

In this section we analyze the inflationary dynamics of our Chaplygin warm model in the strong dissipative regime $\Gamma >3H$. By using Eqs. (9) and (14), we obtain the solution of the scalar field $\phi (t)$, in terms of the cosmic time. Here, we study the solution for the scalar field for two different values of the parameter m, namely the cases $m=3$ and $m\ne 3$. For the specific case $m=3$, the solution $\phi (t)$ is found to be

$$\begin{aligned} \phi (t)-\phi _0=\exp \left[ \frac{\tilde{B}[t]}{\tilde{K}}\right] , \end{aligned}$$

(28)

where $\phi (t=0)=\phi _{0}$ is an integration constant and the quantity $\tilde{K}$ is the constant defined as

$$\begin{aligned} \tilde{K}\!\equiv \! 2^{7\over 8}\,{(1+\beta )C_{\phi }^{1/2}\over (4C_{\gamma })^{3/8}} \, \,{\left( \kappa /3\right) ^{{1\over 8}+\frac{2+5f}{16(1-f)}}\over (\alpha \,f)^{{5\over 8}+\frac{2+5f}{16(1-f)}}} (1\!-\!f)^{7\over 8}\,A^{\frac{2+5f}{16(1+\beta )(1-f)}}. \end{aligned}$$

The function $\tilde{B}[t]$ is given by

$$\begin{aligned} \tilde{B}[t]&\equiv B\left[ A\,\left( {\kappa \over 3\alpha ^2f^2}\right) ^{1+\beta }\,t^{2(1+\beta )(1-f)};\right. \nonumber \\&\quad \left. \frac{2+5f}{16(1+\beta )(1-f)},\,\frac{8+7\beta }{8(1+\beta )}\right] , \end{aligned}$$

(29)

and this function corresponds to the incomplete beta function; see Ref. [91].

For the specific case in which $m\ne 3$, the solution for the scalar field is found to be

$$\begin{aligned} \varphi (t)-\varphi _0=\frac{\tilde{B}_{m}[t]}{\tilde{K}_{m}}, \end{aligned}$$

(30)

where the new scalar field $\varphi$ is defined as $\varphi (t)\!=\!\frac{2}{3-m}\phi (t)^{\frac{2}{3-m}}$. Again, $\varphi _0$ corresponds to an integration constant that can be assumed $\varphi _0=0$. Also, $\tilde{K}_m$ is a constant defined as $\tilde{K}_m\equiv 2^{4+m\over 8}\,{(1+\beta )C_{\phi }^{1/2}\over (4C_{\gamma })^{m/8}} \, \,{\left( \kappa /3\right) ^{{4-m\over 8}+\frac{m(2-f)-4(1-2f)}{16(1-f)}}\over (\alpha \,f)^{{8-m\over 8}+\frac{m(2-f)-4(1-2f)}{16(1-f)}}} (1-f)^{4+m\over 8}\,A^{\frac{m(2-f)-4(1-2f)}{16(1+\beta )(1-f)}}$. The function $\tilde{B}_m[t]$ in Eq. (30), for the specific case $m\ne 3$, also corresponds to the incomplete beta function, given by

$$\begin{aligned} \tilde{B}_m[t]&\equiv B\left[ A\,\left( {\kappa \over 3\alpha ^2f^2}\right) ^{1+\beta }\,t^{2(1+\beta )(1-f)};\right. \nonumber \\&\quad \left. \frac{m(2-f)-4(1-2f)}{16(1+\beta )(1-f)},\,\frac{8+\beta (4+m)}{8(1+\beta )}\right] . \end{aligned}$$

(31)

Considering Eqs. (3), (28), and (30), the Hubble rate as a function of the scalar field may be written as

$$\begin{aligned} H(\phi )=\frac{Af}{(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{1-f}},\quad \text {for } \ m=3, \end{aligned}$$

(32)

and

$$\begin{aligned} H(\varphi )=\frac{Af}{(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{1-f}},\quad \text {for } \ m\ne 3. \end{aligned}$$

(33)

From Eq. (13), we find that the effective scalar potential $V(\phi )$ (or equivalently $V(\varphi )$), under the slow-roll approximation, is

$$\begin{aligned} V(\phi )\simeq \left[ \left( {3\,\alpha ^2f^2\over \kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)}}\right) ^{1+\beta } -A\right] ^{1\over 1+\beta }, \end{aligned}$$

(34)

for the specific case $m=3$, and we obtain

$$\begin{aligned} V(\varphi )\simeq \left[ \left( {3\,\alpha ^2f^2\over \kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)}}\right) ^{1+\beta } -A\right] ^{1\over 1+\beta }, \end{aligned}$$

(35)

for the case $m\ne 3$.

Now combining Eqs. (14), (28), and (30), the dissipative coefficient $\Gamma$ as a function of the scalar field as a result is

$$\begin{aligned} \Gamma (\phi )&= \delta \phi ^{-2}(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-\frac{3(2-f)}{4}}\nonumber \\&\quad \times \left[ 1\!-\!A \left( {\kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-\frac{3\beta }{4(1+\beta )}}, \end{aligned}$$

(36)

for the case $m=3$. Here $\delta$ is a constant and is given by $\delta =C_{\phi }\left[ \frac{Af(1-f)}{2\kappa C_{\gamma }}\right] ^{3/4}$. For the special case in which $m\ne 3$ we find that the dissipative coefficient becomes

$$\begin{aligned} \Gamma (\phi )&= \delta _m \phi ^{1-m}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-\frac{m(2-f)}{4}}\nonumber \\&\quad \times \left[ 1\!-\!A\left( {\kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-\frac{\beta m}{4(1+\beta )}}, \end{aligned}$$

(37)

where $\delta _m=C_{\phi }\left[ \frac{Af(1-f)}{2\kappa C_{\gamma }}\right] ^{m/4}$ is a constant.

During the strong dissipative regime, the dimensionless slow-roll parameter $\varepsilon$ is defined as $\varepsilon =-\frac{\dot{H}}{H^{2}}=\frac{1-f}{Af(\tilde{B}^{-1}[\tilde{K}\ln \phi ]) ^f}$, for the specific case of $m=3$ and for the case $m\ne 3$, this parameter becomes $\varepsilon =\frac{1-f}{Af(\tilde{B}_m^{-1}[\tilde{K}_ m\varphi ])^f}$. Analogous to the case of the weak dissipative regime, if $\ddot{a}>0$, then the scalar field $\phi >\exp [\frac{1}{\tilde{K}}\tilde{B}[(\frac{1-f}{Af})^{1/f}]]$ for $m=3$, and for the case $m\ne 3$ the result is $\varphi >\frac{1}{\tilde{K}_m}\tilde{B}_m[(\frac{1-f}{Af})^{1/f}]$. As before, the value of the scalar field at the beginning of inflation is $\phi _1=\exp [\frac{1}{\tilde{K}}\tilde{B}[(\frac{1-f}{Af})^{1/f}]]$, for the specific value of $m=3$, and for the special case $m\ne 3$ we get $\varphi _1=\frac{1}{\tilde{K}_m}\tilde{B}_m[(\frac{1-f}{Af})^{1/f}]$.

In relation to the number of e-folds N in the strong regime, we find that combining Eqs. (3), (28), and (30) yields

$$\begin{aligned} N= & {} \int _{t_{1}}^{t_{2}}\,H\,\mathrm{d}t=\alpha [(\tilde{B}^{-1}[\tilde{K}\ln \phi _2])^f \nonumber \\&-(\tilde{B}^{-1}[\tilde{K}\ln \phi _1])^f], \quad \text{ for } \ m=3, \end{aligned}$$

(38)

and

$$\begin{aligned} N=\alpha [(\tilde{B}_m^{-1}[\tilde{K}_m\varphi _2])^f-(\tilde{B}_ m^{-1}[\tilde{K}_m\varphi _1])^f],\quad \text{ for } \ m\ne 3. \end{aligned}$$

(39)

Now we will study the cosmological perturbations in the strong regime $R=\Gamma /3H>1$. Following Refs. [16, 17], the fluctuation $\delta \phi ^2$ in the strong dissipative regime is found to be $\delta \phi ^{2}\simeq \frac{k_{F}T}{2\pi ^{2}}$, where the function $k_{F}$ corresponds to the freeze-out wave-number, defined as $k_{F}=\sqrt{\Gamma H}=H\sqrt{3R}>H$. In this form, the power spectrum of the scalar perturbation $P_{\mathcal {R}}$, considering Eqs. (3), (12), and (14) as a result is

$$\begin{aligned}&P_{\mathcal {R}}\simeq \frac{H^{\frac{5}{2}}\Gamma ^{\frac{1}{2}}T}{2\pi ^{2} \dot{\phi }^{2}}=\frac{\kappa }{12\pi ^2}C_{\phi }^{3/2}\left( \frac{3}{2\kappa C_{\gamma }} \right) ^{\frac{3m+2}{8}}\nonumber \\&\quad \times \phi ^{\frac{3(1-m)}{2}}H^{3/2}(-\dot{H})^{\frac{3m-6}{8}}\left[ 1- A\left( {3\,H^2 \over \kappa }\right) ^{-(1+\beta )}\right] ^{-\frac{\beta (3m-6)}{8(1+\beta )}}. \end{aligned}$$

(40)

Also, the power spectrum $\mathcal {P}_{\mathcal {R}}$ may be expressed in terms of the scalar field $\phi$. From Eqs. (3), (28), (30), and (40), we see that the scalar power spectrum becomes

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}&= k(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^ {\frac{3(5f-6)}{8}}\phi ^{-3}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-\frac{3\beta }{8(1+\beta )}}, \end{aligned}$$

(41)

for the special case of $m=3$. Here k is a constant and is defined as $k=\frac{\kappa }{12\pi ^2}C_{\phi }^{3/2} \left( \frac{3}{2\kappa C_{\gamma }}\right) ^{11/8}(Af)^{15/8}(1-f)^{3/8}$. For the case of $m\ne 3$, we find that the power spectrum becomes

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}&= k_m(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^ {\frac{3[f(m+2)-2m]}{8}}\phi ^{\frac{3}{2}(1-m)}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-\frac{\beta (3m-6)}{8(1+\beta )}}, \end{aligned}$$

(42)

where the constant $k_m$ is given by$k_m=\frac{\kappa }{12\pi ^2}C_{\phi }^{3/2}\left( \frac{3}{2\kappa C_{\gamma }}\right) ^{\frac{3m+2}{8}}(Af)^{\frac{3m+6}{8}}(1-f)^{\frac{3m-6}{8}}$.

In a similar way, the scalar power spectrum can be expressed in terms of the number of e-folds N. Combining Eqs. (38) and (39) in (41) and (42) we have

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}&= k(J[N])^{\frac{3(5f-6)}{8}}\exp \left( -\frac{3}{\tilde{K}}\tilde{B}[J[N]]\right) \nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-\frac{3\beta }{8(1+\beta )}}, \end{aligned}$$

(43)

for the particular case of $m=3$. For the specific case $m\ne 3$ we obtain

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}&= \tilde{\gamma }_m(J[N])^{\frac{3[f(2+m)-2m]}{8}} (\tilde{B}_m[J[N]])^{\frac{3(1-m)}{3-m}}\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-\frac{\beta (3m-6)}{8(1+\beta )}}, \end{aligned}$$

(44)

where the constant $\tilde{\gamma }_m$ is defined as $\tilde{\gamma }_m=k_m\left( \frac{2\tilde{K}_m}{3-m}\right) ^{-\frac{3(1-m)}{3-m}}$.

Now combining Eqs. (41) and (42), we find that the scalar spectral index $n_s$ is

$$\begin{aligned} n_s=1+\frac{3(5f-6)}{8Af}(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-f}+ n_1+n_2, \end{aligned}$$

(45)

for the value $m=3$. Here the quantities $n_1$ and $n_2$ are defined as

$$\begin{aligned} n_1= & {} -3\left( \frac{6}{\kappa }\right) ^{1/2}\frac{1}{C_{\phi }^{1/2}}\left( \frac{3}{2\kappa C_{\gamma }}\right) ^{-3/8}(Af)^{-3/8}\nonumber \\&\times (1-f)^{1/8}(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{\frac{1}{8}(2-3f)} \\&\times \left[ 1-A\left( {\kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-\frac{3\beta }{8(1+\beta )}} \end{aligned}$$

and

$$\begin{aligned} n_2= & {} \frac{3^{-\beta }}{4}\kappa ^{1+\beta }A \beta (1-f)(Af)^{-(3+2\beta )}\\&\times (\tilde{B}^{-1}[\tilde{K}\ln \phi ]) ^{-f(3+2\beta )+2(1+\beta )} \\&\times \left[ 1-A\left( {\kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-1}, \end{aligned}$$

respectively. For the case $m\ne 3$, we find that the scalar spectral index as a result is

$$\begin{aligned} n_s=1+\frac{3[f(m+2)-2m]}{8Af}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-f}+n_{1_{m}}+n_{2_{m}}, \end{aligned}$$

(46)

where the functions $n_{1_{m}}$ and $n_{2_{m}}$ are given by $n_{1_{m}}=\frac{3(1-m)}{2}\left( \frac{6}{\kappa }\right) ^{1/2}\left( \frac{3}{2\kappa C_{\gamma }}\right) ^{-m/8}$ $\times \frac{1}{C_{\phi }^{1/2}}(Af)^{-m/8}(1-f)^{\frac{4-m}{8}}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-\frac{[4+m(f-2)]}{8}}\phi ^{\frac{m-3}{2}}\left[ 1-A\left( {\kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{\beta (m-4)}{8(1+\beta )}},$ and $n_{2_{m}}=\frac{(3m-6)}{4}\left( \frac{\kappa }{3}\right) ^{1+\beta }A \beta (Af)^{-(3+2\beta )}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-f(3+2\beta )+2(1+\beta )} \left[ 1-A\left( {\kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-1}$.

Analogously as before, we may express the scalar spectral index $n_s$ in terms of the number of e-folds N. Considering Eqs. (38), (39), (45), and (46) we obtain

$$\begin{aligned} n_s=1+\frac{3(5f-6)}{8Af}(J[N])^{-f}+n_1+n_2, \end{aligned}$$

(47)

for the case of $m=3$. Here the functions $n_1$ and $n_2$ are given by

$$\begin{aligned} n_1(J[N])= & {} -3\left( \frac{6}{\kappa }\right) ^{1/2}\frac{1}{C_{\phi }^{1/2}}\left( \frac{3}{2\kappa C_{\gamma }}\right) ^{-3/8}\\&\times (Af)^{-3/8} (1-f)^{1/8}(J[N])^{\frac{1}{8}(2-3f)} \\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )} \right] ^{-\frac{3\beta }{8(1+\beta )}} \end{aligned}$$

and

$$\begin{aligned} n_2= & {} \frac{3^{-\beta }}{4}\kappa ^{1+\beta }A \beta (1-f)(Af)^{-(3+2\beta )}\\&\times (J[N]) ^{-f(3+2\beta )+2(1+\beta )} \\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-1}, \end{aligned}$$

respectively. For the case $m\ne 3$, the scalar spectral index in terms of N becomes

$$\begin{aligned} n_s=1+\frac{3[f(m+2)-2m]}{8Af}(J[N])^{-f}+n_{1_{m}}+n_{2_{m}}, \end{aligned}$$

(48)

where the quantities $n_{1_{m}}$ and $n_{2_{m}}$ are defined as

$$\begin{aligned}&n_{1_{m}}(J[N])=\frac{6(1-m)}{3-m}(1-f)(1+\beta )\\&\quad \times \left( \frac{\kappa A^{\frac{1}{1+\beta }}}{3}\right) ^{\frac{m(2-f)-4(1-2f)}{16(1-f)}} (Af)^{-\frac{1}{8}[4+m(2-f)]} \\&\quad \times (J[N])^{-\frac{1}{8}[4+m(2-f)]}(\tilde{B}_m[J[N]])^{-1}\\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{\beta (m-4)}{8(1+\beta )}} \end{aligned}$$

and

$$\begin{aligned} n_{2_{m}}= & {} \frac{(3m-6)}{4}\left( \frac{\kappa }{3}\right) ^{1+\beta }A \beta (Af)^{-(3+2\beta )} \\&\times (J[N])^{-f(3+2\beta )+2(1+\beta )}\\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{-1}. \end{aligned}$$

Also, we find that the tensor-to-scalar-ratio r in terms of the scalar field may be written as

$$\begin{aligned} r&=\frac{2\kappa }{\pi ^2 k}(Af)^2(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{\frac{(f+2)}{8}} \phi ^3\nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( \tilde{B}^{-1}[\tilde{K}\ln \phi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{3\beta }{8(1+\beta )}}, \end{aligned}$$

(49)

for the specific case $m=3$ and

$$\begin{aligned} r= & {} \frac{2\kappa }{\pi ^2 k_m}(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{ \frac{1}{8}[6m+f(10-3m)-16]}\phi ^{\frac{3}{2}(m-1)} \nonumber \\&\times \left[ 1-A\left( {\kappa \left( \tilde{B}_m^{-1}[\tilde{K}_m\varphi ]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{3\beta (m-2)}{8(1+\beta )}}, \end{aligned}$$

(50)

for the case of $m\ne 3$.

Finally, the tensor-to-scalar ratio r in terms of the number of e-folds N, from Eqs. (38) and (49), becomes

$$\begin{aligned} r&=\frac{2\kappa }{\pi ^2 k}(Af)^2(J[N])^{\frac{(f+2)}{8}}\exp \left[ 3\frac{\tilde{B}[J[N]]}{\tilde{K}}\right] \nonumber \\&\quad \times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{3\beta }{8(1+\beta )}}, \end{aligned}$$

(51)

for the special case $m=3$, and from Eqs. (39) and (50), the tensor-to-scalar ratio $r=r(N)$ becomes

$$\begin{aligned} r= & {} \frac{2\kappa }{\pi ^2 k_m}(Af)^2(J[N])^{\frac{1}{8}[6m+f(10-3m)-16]}\nonumber \\&\times \left( \frac{3-m}{2}\frac{\tilde{B}_m[J[N]]}{\tilde{K}_m}\right) ^{\frac{3(m-1)}{3-m}} \nonumber \\&\times \left[ 1-A\left( {\kappa \left( J[N]\right) ^{2(1-f)} \over 3\,\alpha ^2f^2}\right) ^{(1+\beta )}\right] ^{\frac{3\beta (m-2)}{8(1+\beta )}}, \end{aligned}$$

(52)

for the case of $m\ne 3$.

Fig. 5

Left panel Ratio $\Gamma /3H$ versus the scalar spectral index $n_s$. Right panel Ratio T / H versus the scalar spectral index $n_s$. For both panels we have used different values of the parameter $C_\phi$, for the special case $m=3$, i.e., $\Gamma \propto T^3/\phi ^2$ during the strong dissipative regime. Also, in both panels, the dotted, solid, and dashed lines correspond to the pairs ($\alpha =1.46\times 10^{-5}$, $f=0.703$), ($\alpha =6.91\times 10^{-6}$, $f=0.786$), and ($\alpha =6.91\times 10^{-6}$, $f=0.993$), respectively. In these plots as before we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$

In Fig. 5 we show the evolution of the ratio $\Gamma /3H$ (left panel) and T / H (right panel) on the scalar spectral index $n_s$ in the strong dissipative regime, in the case in which the dissipative coefficient $\Gamma \propto T^3/\phi ^2$ (or analogously $m=3$). In both panels we have studied three different values of the parameter $C_\phi$. In order to write down the ratio $\Gamma /3H$ versus $n_s$ (left panel), we have obtained numerically, from Eqs. (47) and (51), the relation $\Gamma /3H=\Gamma /3H(n_s)$ for the case $m=3$. Likewise, for this case we have found numerically the evolution of the relation $T/H=T/H(n_s)$ (right panel), considering Eqs. (12), (32), and (38) during the strong dissipative regime. As before, in these plots we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$ [33], and $m_p=1$. Analogously to the case of the weak dissipative regime, we have found numerically from Eqs. (43) and (47), for the special case $m=3$, the pair ($\alpha =1.46\times 10^{-5}$, $f=0.703$), corresponding to the parameter $C_\phi =5\times 10^{9}$, using the values $\mathcal {P}_{\mathcal {R}}= 2.4\times 10^{-9}$, $n_s=0.97$, and the number of e-folds is $N=60$. Similarly, for the value of $C_\phi =10^{9}$ we obtain numerically the pair ($\alpha =6.91\times 10^{-6}$, $f=0.786$) and for the parameter $C_\phi =10^{8}$ we find ($\alpha =6.91\times 10^{-6}$, $f=0.993$). From the left panel we note that the values $C_\phi > 10^8$ satisfy the condition for the strong dissipative regime. In this way, the condition $\Gamma /3H>1$ gives a lower bound for the parameter $C_\phi$. Also, we see that the essential condition for warm inflation, $T>H$, is well corroborated from the figure of the right panel, and in fact this condition does not impose a constraint on the parameter $C_\phi$, in the strong dissipative regime.

Fig. 6

Evolution of the tensor-to-scalar ratio r versus the scalar spectral index $n_s$ in the strong dissipative regime for the special case $\Gamma \propto T^3/\phi ^2$ (or analogously $m=3$). Here, we have considered the two-dimensional marginalized constraints from the latest data of Planck; see Ref. [15]. Besides, we have studied three different values of the parameter $C_\phi$. Also, in this plot the dotted, solid, and dashed lines correspond to the pairs ($\alpha =1.46\times 10^{-5}$, $f=0.703$), ($\alpha =6.91\times 10^{-6}$, $f=0.786$), and ($\alpha =6.91\times 10^{-6}$, $f=0.993$), respectively. As before, in this plot we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$

Table 3 Results for the constraints on the parameters $\alpha$, f, and $C_\phi$ during the strong dissipative regime

In Fig. 6 we show the dependence of the tensor-to-scalar ratio on the scalar spectral index. Considering Ref. [15], we have the two-dimensional marginalized constraints at 68 and 95 $\%$ confidence levels on the parameters r and $n_s$. As before, we have considered Eqs. (47) and (51) for the case $m=3$, and we find numerically the consistency relation $r=r(n_s)$. Here we observe that for the value of $C_\phi <5\times 10^9$, the model in the strong dissipative regime is well corroborated by the observational data. In this way, for the case in which the dissipative coefficient is given by $\Gamma \propto T^3/\phi ^2$ (or equivalently $m=3$), the range obtained for the parameter $C_\phi$ is $10^8<C_\phi <5\times 10^9$.

Now considering the case in which $\Gamma \propto T$ (or equivalently $m=1$) during the strong dissipative regime, here we find from the condition $\Gamma >3H$ that the lower bound for $C_\phi$ becomes $C_\phi >0.02$. In this form, the condition for the strong regime gives a lower bound on the parameter $C_\phi$ (figure not shown). Similarly, considering the consistency relation $r=r(n_s)$ from the two-dimensional marginalized constraints by the Planck data, we observe that these values are well corroborated. Moreover, the tensor-to-scalar ratio becomes $r\sim 0$. Similarly, for values of $C_\phi >0.02$, we observe that the condition of warm inflation, $T>H$, also is satisfied. In this way, we find only a lower bound for the parameter $C_\phi$ from the condition $\Gamma /3H>1$. Then for the special case in which $\Gamma \propto T$ (or equivalently $m=1$) the constraint for the parameter $C_\phi$ as a result is $C_\phi >0.02$.

For the cases in which $\Gamma \propto \phi$ (or equivalently $m=0$) and $\Gamma \propto \phi ^2/T$ (or equivalently $m=-1$), we obtain that these models do not work in the strong dissipative regime, since the scalar spectral index $n_s>1$, and then these models are disproved from the observational data.

Table 3 indicates the constraints on the parameters $\alpha$, f and $C_\phi$, for different values of the parameter m, considering a general form for the dissipative coefficient $\Gamma =\Gamma (T,\phi )$, in the strong dissipative regime. We observe that for the special case $m=3$, the constraints on our parameters result as consequence of the condition $\Gamma >3H$ (lower bound), and from the consistency relation $r=r(n_s)$ (upper bound). For the case $m=1$, we find only a lower bound from the condition $\Gamma >3H$. Here we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $A=0.775$, $\beta =0.00126$, and $m_p=1$.

Analogously to the case of the weak dissipative regime, we can also numerically obtain results for the parameters A and $\beta$, from the observational constraints for the power spectrum and the scalar spectral index at $N=60$. In this way, we can fix the values $\alpha$, f, and $C_\phi$. In Fig. 7 we show the plot of the ratio $\Gamma /3H$ (upper panel) and the tensor-to-scalar ratio r (lower panel) as functions of the primordial tilt $n_s$ for the specific case $m=3$, in the strong dissipative regime. As before, for both panels we have considered three values for $C_\phi$. In the upper plot we show the decay of the ratio $R=\Gamma /3H$ during inflation, however, always satisfying the condition $\Gamma >3H$, in agreement with the strong dissipative regime. In the lower panel we show the two-dimensional constraints on the parameters r and $n_s$ from the Planck 2015 data.

Fig. 7

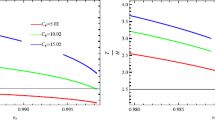
Upper panel Ratio $\Gamma /3H$ versus the scalar spectral index $n_s$. Lower panel Ratio r versus the scalar spectral index $n_s$. For both panels we have used different values of the parameter $C_\phi$, for the special case $m=3$ or equivalently $\Gamma \propto T^3/\phi ^2$ during the strong dissipative regime. In both panels, the dotted, solid, and dashed lines correspond to the pairs ($A=0.22$, $\beta =-0.96$), ($A=0.06$, $\beta =-0.97$), and ($A=0.04$, $\beta =-0.98$), respectively. In these plots we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $\alpha =10^{-3}$, $f=0.6$, and $m_p=1$

Table 4 Results for the constraints on the parameters A, $\beta$ and $C_\phi$ during the strong dissipative regime

As before, we numerically find the ratio $\Gamma /3H$, and the tensor-to-scalar ratio as functions of the scalar spectral index $n_s$, considering Eqs. (36), (51), and (47). Now, we use the values $C_\gamma =70$, $\rho _{Ch0}=1$, $\alpha =10^{-3}$, and $f=0.6$. For the special case $m=3$, we see numerically that the values $A=0.22$ and $\beta =-0.98$ correspond to the parameter $C_\phi =2\times 10^{8}$. As usual, we have considered the values ${\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}$, $n_s=0.97$, and the number of e-folds $N=60$. Similarly, for the value of $C_\phi =5\times 10^{8}$, we obtain the values $A=0.062$ and $\beta =-0.97$. Finally, for the parameter $C_\phi =2 \times 10^{8}$, we obtain the values $A=0.04$ and $\beta =-0.98$. From the upper plot, we may obtain an upper limit for the parameter $C_\phi$, given by $C_\phi <2\times 10^8$, which satisfies $\Gamma >3H$. Analogously, from the upper plot we obtain a lower limit, given by $C_\phi >2\times 10^7$, from the consistency relation $r=r(n_s)$. On the other hand, from the essential condition for warm inflation to occur, i.e., $T>H$, we note that this condition does not impose any constraint on the parameter $C_\phi$, since the condition $T>H$ is always satisfied (plot not shown). Therefore, for the value $m=3$, the allowed range for $C_{\phi }$ is given by $2\times 10^7<C_\phi <2\times 10^8$.

For the case $m=1$, and considering the condition for the strong dissipative regime $\Gamma >3H$, we obtain a lower bound for the parameter $C_\phi$. Analogously as the case $m=3$, we fixed the values $\alpha =10^{-3}$ and $f=0.6$. In this way, we numerically see that the values $A=0.45$ and $\beta =-4.2$ correspond to $C_\phi =2\times 10^{-2}$, for which $\Gamma /3H\gtrsim 1$ (not shown). For the specific case $m=1$, we observe that this value for $C_\phi$ is allowed by the Planck 2015 data. For this value, the tensor-to-scalar ratio becomes $r< 0.05$ and, on the other hand, the essential condition for warm inflation, $T>H$, is always satisfied (not shown). In this way, for $m=1$ we only obtain a lower bound for the parameter $C_\phi$, from the condition $\Gamma /3H>1$. Then for the special case in which $\Gamma \propto T$ (or equivalently $m=1$) the constraints on the parameters are given by $C_\phi >2\times 10^{-2}$, $\beta >-4.2$, and $0<A<0.45$.

For the cases $\Gamma \propto \phi$ ($m=0$) and $\Gamma \propto \phi ^2/T$ ($m=-1$), we find that these models do not work in the strong dissipative regime, because the scalar spectral index $n_s>1$.

Table 4 shows the constraints on the parameters A, $\beta$, and $C_\phi$, for different values of the parameter m in the strong dissipative regime. We observe that for the special case $m=3$, the constraints on these parameters result as consequence of the condition $\Gamma >3H$ (lower bound), and from the consistency relation $r=r(n_s)$ (upper bound). For the case $m=1$, we only find a lower bound from the condition $\Gamma >3H$, and for the cases $m=0$ and $m=-1$ these models do not work. Here we have used the values $C_\gamma =70$, $\rho _{Ch0}=1$, $\alpha =10^{-3}$, $f=0.6$, and $m_p=1$.

5 Conclusions

In this paper we have studied the warm intermediate inflationary model in the context of generalized Chaplygin gas as a variant of gravity. For the weak and strong dissipative regimes, we have found solutions to the background equations under the slow-roll approximation. Here, we have considered a general form of the dissipative coefficient $\Gamma \propto \,T^{m}/\phi ^{m-1}$, and we have analyzed the cases $m=3$, $m=1$, $m=0$, and $m=-1$. On the other hand, we have obtained expressions for the scalar and tensor power spectrum, the scalar spectral index, and the tensor-to-scalar ratio. For both regimes, we have found the constraints on several parameters, considering the Planck 2015 data, together with the condition for warm inflation, $T>H$, and the condition for the weak $\Gamma <3H$ (or strong $\Gamma >3H$) dissipative regime.

In our analysis for both regimes, in the first place we have fixed the parameters A and $\beta$, and then we have found different constraints on the parameters $\alpha$, f, and $C_\phi$. Second, we have fixed the parameters A and f, and then we have obtained constraints over the parameters A, $\beta$, and $C_\phi$. In the latter case, we have found that negative values for $\beta$ are allowed, and also the results weakly depend on the parameter $\beta$ in both regimes.

For the weak dissipative regime we have obtained the constraints on the parameters of our model, only from the conditions $\Gamma <3H$, which gives an upper bound, and $T>H$, which gives a lower bound. This is due that fact that the consistency relation $r=r(n_s)$ does not impose constraints on the parameters. For the strong dissipative regime, we have found the constraints on the parameters from the Planck 2015 data, through the consistency relation $r=r(n_s)$, and the condition $\Gamma >3H$. Here, the condition for warm inflation, $T>H$, does not give constraints on the parameters. On the other hand, for the strong dissipative regime we have seen that for the cases $\Gamma \propto \phi$ (or equivalently $m=0$) and $\Gamma \propto \phi ^2/T$ (or equivalently $m=-1$) these models do not work, since the scalar spectral index becomes $n_s>1$, thus predicting a blue tilted spectrum, and then these models are disproved by the observational data.

On the other hand, we have observed that when the value of the parameter m decreases, the values belonging to the allowed range for $C_{\phi }$ also decrease.

Summarizing, only the cases $m=3$ ($\Gamma \propto T^3/\phi ^2$) and $m=1$ ($\Gamma \propto T$) of the generalized dissipative coefficient, given by Eq. (7), successfully describe a warm intermediate inflationary model in the context of GCG. These models are well supported by the Planck 2015 data, through the consistency relation $r=r(n_s)$, and they satisfy the essential condition for warm inflation, $T>H$, and the requirement to evolve according to the weak ($\Gamma <3H$), or strong ($\Gamma >3H$) dissipative regime. Our results are summarized in Tables 1, 2, 3 and 4, respectively.