D meson spectroscopy and their decay properties using Martin potential in a relativistic Dirac formalism

Abstract

For the present study, we have used the Martin-like potential for the quark confinement. Our predicted states in the S-wave, $2\ ^3S_1$ (2605.86 MeV) and $2\ ^1S_0$ (2521.72 MeV), are in very good agreement with experimental results of $2608\pm 2.4 \pm 2.5$ MeV and $2539.4\pm 4.5\pm 6.8$ MeV, respectively, reported by the BABAR Collaboration. The calculated P-wave D meson states, $1^3P_2$ (2462.50 MeV), $1^3P_1$ (2407.56 MeV), $1^3P_0$ (2373.82 MeV) and $1^1P_1$ (2423.28 MeV), are in close agreement with experimental average (Particle Data Group) values of $2462.6 \pm 0.7$ MeV, $2427 \pm 26 \pm 25$ MeV, $2318 \pm 29$ MeV and $2421.3 \pm 0.6$ MeV, respectively. The pseudoscalar decay constant ($f_P$= 202.57 MeV) of the D meson is in very good agreement with the experiment as well as with the lattice predictions. The Cabibbo favoured nonleptonic decay branching ratios, BR$(D^0\rightarrow K^- \pi ^+)$ of $4.071\,\%$ and BR $(D^0\rightarrow K^+ \pi ^-)$ of $1.135 \times 10^{-4}$, are also in very good agreement with the respective experimental values of $3.91 \pm 0.08\,\%$ and $(1.48\pm 0.07) \times 10^{-4}$ reported by CLEO Collaboration. The mixing parameters of the $D^0$–$\bar{D}^0$ oscillation, $x_q$ (5.14 $\times 10^{-3}$), $y_q$ (6.02 $\times 10^{-3}$) and $R_M$ (3.13 $\times 10^{-5}$), are in very good agreement with BaBar and Belle Collaboration results.

1 Introduction

Very recently, experiments at LHCb [1] have reported a large number of $D_J$ resonances in the mass range of $2.0\,\mathrm{GeV}/c^2$ to $4.0\,\mathrm{GeV}/c^2$, of which many belong to natural excited states of the D meson, while quite a number of them belong to unnatural states [1]. It is important and necessary to exhaust the possible conventional descriptions of $q\bar{Q}$ excitations [2, 3] before resorting to more exotic interpretations [4–6]. Further theoretical efforts are still required in order to explain satisfactorily the recent experimental data concerning these open-charm states.

Apart from the challenges posed by the exotics, there are also many states which are admixtures of their nearby natural states. For example, the discoveries of new resonances of D states such as D(2550) [7], D(2610) [7], D(2640) [8], D(2760) [7] etc. have further generated considerable interest towards the spectroscopy of these open-charm mesons. The study of the D meson is of special interest as it is a hadron with two open flavours ($c, {\bar{u}}$ or ${\bar{d}}$) which restricts its decay via strong interactions. The ground state ($D, D^*$) mesons provide us with a clean laboratory to study weak decay and are useful to study the electromagnetic transitions. The masses of low-lying 1S and $1P_J$ states of the D mesons are recorded both experimentally [2, 3] and theoretically [9–14]. Though lattice QCD and QCD sum rules are quite successful, their predictions for the excited states of the open flavour mesons in the heavy sector are very few. However, recent experimental data on excited D-states are partially inconclusive and require a more detailed analysis involving their decay properties. The understanding of the weak transition form factors of heavy mesons is important for a proper extraction of the quark mixing parameters, for the analysis of nonleptonic decays and CP-violating effects. The QCD sum rule (QSR) [15–19] is a non-perturbative approach to evaluate the hadron properties by using the correlator of the quark currents over the physical vacuum and it is implemented with the operator product expansion (OPE). Lattice QCD (LQCD) [20–22] is also a non-perturbative approach to use a discrete set of spacetime points (lattice) to reduce the analytically intractable path integrals of the continuum theory to a very difficult numerical computation. QCD sum rules are suitable for describing the low $q^2$ region of the form factors; lattice QCD gives good predictions for high $q^2$. As a result these methods do not provide a full picture of the form factors and, more significant, for the relations between the various decay channels. Potential models provide such relations and give the form factors in the full $q^2$-range. However, the potential models are not derived from the basic principles of QCD. In particular, the Martin potential is not really inspired from QCD unlike the case of the Cornell potential. Yet it gives spectacular phenomenological predictions of the hadron spectra. In the case of heavy-light flavour systems ($q\bar{Q} / \bar{q}Q$), its connection with heavy quark effective theory (HQET) remains unclear. Thus it is important to check its consistency for the successful predictions of the properties of other well recorded open flavour hadronic systems. With this perspective we employ the Martin-like potential for the study of open-charm mesonic properties.

Thus any attempts towards the understanding of these newly observed states become very important for our understanding of the light quark/antiquark dynamics within $q\bar{Q}$/$Q\bar{q}$ bound states. So, a successful theoretical model aims to provide important information as regards the quark–antiquark interactions and the behaviour of QCD within the doubly open flavour hadronic system. Though there exist many theoretical models [9–11] in the study of the hadron properties based on its quark structure, the predictions for low-lying states are off by 60–90 MeV with respect to the respective experimental values. Moreover, the issues related to the hyperfine and fine structure splitting of the mesonic states, their intricate dependence with the constituent quark masses and the running strong coupling constant are still unresolved. Though the validity of nonrelativistic models is very well established and had significant success in the description of heavy quarkonia, disparities exist in the description of meson containing light flavour quarks or antiquarks.

For any successful attempt to understand these states we should not only be able to satisfactorily predict the mass spectra but also be able to predict their decay properties. For better predictions of the decay widths, many models have incorporated additional contributions such as radiative and higher order QCD corrections [13, 23–27]. Thus, in this paper we make an attempt to study properties like the mass spectrum, decay constants and other decay properties of the D meson based on a relativistic Dirac formalism. We investigate the heavy-light mass spectra of the D meson in this framework with a Martin-like confinement potential as in the case of $D_s$ mesons studied recently [28].

Along with the mass spectra, the pseudoscalar decay constants of the heavy-light mesons have also been estimated in the context of many QCD-motivated approximations. The predictions of such methods spread over a wide range of values [29, 30]. It is important thus to have reliable estimate of the decay constant as it is an important parameter in many weak processes such as quark mixing, CP violation etc. The leptonic decay of charged meson is another important annihilation channel through the exchange of virtual W boson. Though this annihilation process is rare, we find clear experimental signatures due to the presence of a highly energetic leptons in the final state. The leptonic decays of mesons entails an appropriate representation of the initial state of the decaying vector mesons in terms of the constituent quark and antiquark with their respective momenta and spin. The bound constituent quark and antiquark inside the meson are in definite energy states having no definite momenta. However, one can find the momentum distribution amplitude for the constituent quark and antiquark inside the meson just before their annihilation to a lepton pair. Thus, it is appropriate to compute the leptonic branching ratio and compare our result with the experimental values as well as with the predictions based on other models.

2 Theoretical framework

From the first principles of QCD, the non-perturbative multigluon mechanism is unfeasible to estimate theoretically, but this mechanism is produced in the framework of the quark confining interaction of the meson. On the other hand there exists ample experimental support for the quark structure of the hadrons. This is the origin of phenomenological models which are proposed to understand the properties of hadrons and quark dynamics at the hadronic scale. To a first approximation, the confining part of the interaction is believed to provide the zeroth-order quark dynamics inside the meson through the quark Lagrangian density,

$$\begin{aligned} \mathcal{L}^0_q (x)= \bar{\psi }_q(x) \left[ \frac{i}{2} \gamma ^{\mu } \overrightarrow{\partial _\mu } - V(r) - m_q \right] \psi _q(x). \end{aligned}$$

(1)

In the present study, we assume that the constituent quark–antiquark inside a meson is independently confined by an average potential of the form [28, 31]

$$\begin{aligned} V(r)= \frac{1}{2} (1+\gamma _0) (\lambda r^{\nu }+V_0) \end{aligned}$$

(2)

where $\lambda$ is the potential strength. Here we use the index $\nu = 0.1$, the form of the potential is Martin-like. In the stationary case, the spatial part of the quark wave functions $\psi (\mathbf {r})$ satisfies the Dirac equation given by

$$\begin{aligned}{}[\gamma ^0 E_q - \mathbf {\gamma }. \mathbf {P} - m_q - V (r)]\psi _q (\mathbf {r}) = 0. \end{aligned}$$

(3)

The two component (positive and negative energies in the zeroth order) form represents the solution of the Dirac equation as

$$\begin{aligned} \psi _{nlj}(r) = \left( \begin{array}{c} \psi _{nlj}^{(+)} \\ \psi _{nlj}^{(-)} \end{array} \right) \end{aligned}$$

(4)

where

$$\begin{aligned} \psi _{nlj}^{(+)}(\mathbf {r}) = N_{nlj} \left( \begin{array}{c} i g(r)/r \\ (\sigma .\hat{r}) f(r)/r \end{array} \right) \mathcal{{Y}}_{ljm}(\hat{r}), \end{aligned}$$

(5)

$$\begin{aligned} \psi _{nlj}^{(-)}(\mathbf {r}) = N_{nlj} \left( \begin{array}{c} i (\sigma .\hat{r}) f(r)/r \\ g(r)/r \end{array} \right) (-1)^{j+m_j-l} \mathcal{{Y}}_{ljm}(\hat{r}) \end{aligned}$$

(6)

and $N_{nlj}$ is the overall normalisation constant. The normalised spin angular part is expressed as

$$\begin{aligned} \mathcal{{Y}}_{ljm}(\hat{r}) = \sum _{m_l, m_s}\left\langle l, m_l, \frac{1}{2}, m_s| j, m_j\right\rangle Y^{m_l}_l \chi ^{m_s}_{\frac{1}{2}}. \end{aligned}$$

(7)

Here the spinors $\chi _{\frac{1}{2}{m_s}}$ are eigenfunctions of the spin operators,

$$\begin{aligned} \chi _{\frac{1}{2} \frac{1}{2}} = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) , \quad \chi _{\frac{1}{2} -\frac{1}{2}} = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) . \end{aligned}$$

(8)

The reduced radial part g(r) of the upper component and f(r) of the lower component of Dirac spinor $\psi _{nlj}(r)$ are the solutions of the equations given by

$$\begin{aligned} \frac{\mathrm{d}^2 g(r)}{\mathrm{d}r^2}+ & {} \bigg [(E^{D}+ m_q) [E^{D} - m_q - V(r)] \nonumber \\&- \frac{\kappa (\kappa + 1)}{r^2}\bigg ] g(r) = 0 \end{aligned}$$

(9)

and

$$\begin{aligned} \frac{\mathrm{d}^2 f(r)}{\mathrm{d}r^2}+ & {} \bigg [(E^{D}+ m_q) [E^{D} - m_q - V(r)] \nonumber \\&- \frac{\kappa (\kappa - 1)}{r^2}\bigg ] f(r) = 0. \end{aligned}$$

(10)

It can be transformed into a convenient dimensionless form given by [32]

$$\begin{aligned} \frac{\mathrm{d}^2 g(\rho )}{\mathrm{d}\rho ^2}+\left[ \epsilon - \rho ^{\nu } - \frac{\kappa (\kappa +1)}{\rho ^2}\right] g(\rho ) = 0 \end{aligned}$$

(11)

and

$$\begin{aligned} \frac{\mathrm{d}^2 f(\rho )}{\mathrm{d}\rho ^2}+\left[ \epsilon - \rho ^{\nu } - \frac{\kappa (\kappa -1)}{\rho ^2}\right] f(\rho ) = 0 \end{aligned}$$

(12)

where $\rho = (r / r_0)$ is a dimensionless variable with the arbitrary scale factor chosen conveniently as

$$\begin{aligned} r_0 = \left[ (m_q + E^{D})\frac{\lambda }{2}\right] ^{-\frac{10}{21}}, \end{aligned}$$

(13)

and $\epsilon$ is a corresponding dimensionless energy eigenvalue defined as

$$\begin{aligned} \epsilon = (E^{D} - m_q - V_0) (m_q + E^{D})^{\frac{1}{21}} \left( \frac{2}{\lambda }\right) ^{\frac{20}{21}}. \end{aligned}$$

(14)

Here, it is suitable to define a quantum number $\kappa$ by

$$\begin{aligned}&\kappa = -(\ell + 1) = - \left( j+\frac{1}{2}\right) \ \ for \ \ j= \ell +\frac{1}{2},\end{aligned}$$

(15)

$$\begin{aligned}&\kappa = \ell = + \left( j+\frac{1}{2}\right) \ \ for \ \ j= \ell -\frac{1}{2}. \end{aligned}$$

(16)

Equations (11) and (12) now can be solved numerically [33] for each choice of $\kappa$.

The solutions $g (\rho )$ and $f (\rho )$ are normalised to get

$$\begin{aligned} \int _0^\infty (f_q^2(\rho ) + g_q^2(\rho )) \ \mathrm{d} \rho = 1. \end{aligned}$$

(17)

Using Eqs. (5) and (6), the wavefunction for a $D (c{\bar{q}})$ meson now can be constructed and the corresponding mass of the quark–antiquark system can be written as

$$\begin{aligned} M_{Q {\bar{q}}} \ (n_1l_1j_1, n_2l_2j_2) = E^{D}_Q + E^{D}_{\bar{q}} \end{aligned}$$

(18)

where $E^D_{Q/\bar{q}} = E_{Q/\bar{q}}$ are obtained using Eqs. (14), (15), and (16). The expression for $E_{Q/\bar{q}}$ thus contains the centrifugal repulsion term which includes the centre-of-mass correction also. For the spin triplet (vector) and spin singlet (pseudoscalar) state, the choices of ($j_1$, $j_2$) are $\left( \left( l_1 + \frac{1}{2}\right) , \left( l_2 + \frac{1}{2}\right) \right)$ and $\left( \left( l_{1, 2} + \frac{1}{2}\right) , \left( l_{2, 1} - \frac{1}{2}\right) \right)$, respectively. The previous work of the independent quark model within the Dirac formalism by [28, 31] has been extended here by incorporating the spin–orbit and tensor interactions of the confined one-gluon exchange potential (COGEP) [34, 35], in addition to the j–j coupling of the quark–antiquark. Finally, the mass of the specific $^{2 S+1}L_J$ states of the $Q {\bar{q}}$ system is expressed as

$$\begin{aligned} M_{^{2 S+1}L_J}= & {} M_{Q {\bar{q}}} (n_1l_1j_1, n_2l_2j_2) +\left\langle V_{Q {\bar{q}}}^{j_1j_2}\right\rangle \nonumber \\&+ \left\langle V_{Q {\bar{q}}}^{LS}\right\rangle + \left\langle V_{Q {\bar{q}}}^{T}\right\rangle \end{aligned}$$

(19)

The spin–spin part is defined here as

$$\begin{aligned} \left\langle V^{j_1 j_2}_{Q {\bar{q}}} (r)\right\rangle = \frac{\sigma \ \left\langle j_1 j_2 J M |\hat{j_1}.\hat{j_2}| j_1 j_2 J M \right\rangle }{(E_Q + m_{Q})(E_{\bar{q}} + m_{\bar{q}})} \end{aligned}$$

(20)

where $\sigma$ is the j–j coupling constant. The expectation value of $\langle j_1 j_2 J M |\hat{j_1}.\hat{j_2}| j_1 j_2 J M \rangle$ contains the ($j_1.j_2$) coupling and the square of the Clebsch–Gordan coefficients. The tensor and spin–orbit parts of the confined one-gluon exchange potential (COGEP) [34, 35] are given as

$$\begin{aligned} V^{T}_{Q {\bar{q}}} (r)= & {} - \frac{\alpha _s}{4} \frac{N_Q^2 N_{{\bar{q}}}^2}{(E_Q + m_{Q})(E_{\bar{q}} + m_{\bar{q}})} \nonumber \\&\otimes \ \lambda _Q . \lambda _{{\bar{q}}} \left( \left( \frac{D''_1 (r)}{3}- \frac{D'_1 (r)}{3 \ r} \right) S_{Q {\bar{q}}}\right) \end{aligned}$$

(21)

where $S_{Q {\bar{q}}} = \left[ 3 (\sigma _Q. {\hat{r}})(\sigma _{{\bar{q}}}. {\hat{r}})- \sigma _Q . \sigma _{{\bar{q}}}\right]$ and ${\hat{r}} = {\hat{r}}_Q - {\hat{r}}_{{\bar{q}}}$ is the unit vector in the direction of $\mathbf {r}$ and

Table 1 The fitted model parameters for the D systems

Table 2 S-wave D ($c\bar{u}$ or $c\bar{d}$) spectrum (in MeV)

$$\begin{aligned} V^{LS}_{Q {\bar{q}}} (r)= & {} \frac{\alpha _s}{4} \frac{N_Q^2 N_{{\bar{q}}}^2}{(E_Q + m_{Q})(E_{\bar{q}} + m_{\bar{q}})} \frac{\lambda _Q . \lambda _{{\bar{q}}}}{2 \ r} \\&\otimes \bigg [ \left[ \mathbf {r} \times (\hat{p_Q}-\hat{p_q}). (\sigma _Q + \sigma _q)\right] \left( {D'_0 (r)}+ 2 {D'_1 (r)} \right) \nonumber \\&+ \left[ \mathbf {r} \times (\hat{p_Q}+\hat{p_q}). (\sigma _Q - \sigma _q)\right] \left( {D'_0 (r)}- {D'_1 (r)} \right) \bigg ] \nonumber \end{aligned}$$

(22)

where $\alpha _s$ is the strong coupling constant; it is computed as

$$\begin{aligned} \alpha _s = \frac{4 \pi }{(11-\frac{2}{3}\ n_f )\log \left( \frac{E^2_Q}{\Lambda ^2_\mathrm{QCD}}\right) } \end{aligned}$$

(23)

with $n_f$ = 3 and $\Lambda _\mathrm{QCD}$ = 0.250 GeV obtained by fixing the strong running coupling strength $\alpha _s (M_z^2)$ at the Z-boson mass ($M_Z = 91$ GeV) scale to be equal to 0.11838. In Eq. (22) the spin–orbit term has been split into symmetric $(\sigma _Q + \sigma _q)$ and antisymmetric $(\sigma _Q - \sigma _q)$ terms. It is to be noted that in the relativistic Dirac formalism, the relativistic mass of the quark/antiquark contains contribution from its rest mass ($m_{Q/\bar{q}}$) as well as from the kinetic and interaction part of the Hamiltonian. Hence ($E^{Q/\bar{q}}$ + $m_{Q/\bar{q}}$) appears here for its inertial mass. Though m represents the current quark mass in the MS scheme, ($E^{Q/\bar{q}}$ + $m_{Q/\bar{q}}$) corresponds to the constituent quark mass in its nonrelativistic reduction. For the present calculations, we have taken the quark mass parameters as quoted in the particle data group (PDG) (2014).

We have adopted the same parametric form of the confined gluon propagators as are given by [34, 35]

$$\begin{aligned} D_0 (r) = \left( \frac{\alpha _1}{r}+\alpha _2 \right) \exp (-r^2 c_0^2/2) \end{aligned}$$

(24)

and

$$\begin{aligned} D_1 (r) = \frac{\gamma }{r} \exp (-r^2 c_1^2/2) \end{aligned}$$

(25)

with $\alpha _1 = 0.011$, $\alpha _2 = 0.036$, $c_0 = 0.1017$ GeV, $c_1 = 0.1522$ GeV, $\gamma = 0.0109$ as in our earlier study [28]. Other optimised model parameters employed in the present study are listed in Table 1. The current charm quark mass of 1.27 GeV is taken from the particle data group (PDG) [2, 3]. In the case of $l \ne 0$ orbitally excited states, we find small variations in the choice of $\lambda$ for the $l = 0$ states due to the centrifugal repulsion from the centre of mass of the bound system, which is proportional to ($n+l$). This centrifugal repulsion thus incorporates the centre-of-mass correction.

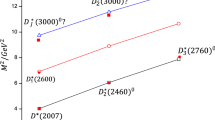
The computed S-wave masses and other P-wave and D-wave masses of D meson states are listed in Tables 2 and 3, respectively. We have also calculated the mixed state of $^3P_1$ and $^1P_1$ and compared with the experimental results and other theoretical results in Table 4. A statistical analysis of the sensitivity of the model parameters (i.e. potential strength ($\lambda$) and j–j coupling strength $\sigma$ in the present case) shows about $0.76 \,\%$ variations in the binding energy with $5\,\%$ changes in the parameters $\lambda$ and $\sigma$. Figure 1 shows the energy level diagram of the D meson spectra along with available experimental results.

Table 3 P-wave and D-wave D ($c\bar{u}$ or $c\bar{d}$) spectrum (in MeV)

Table 4 The comparison of the mixed state of $^3P_1$ and $^1P_1$ for D ($c\bar{u}$ or $c\bar{d}$) meson (in MeV)

Table 5 Magnetic (M1) transition of open-charm meson

3 Magnetic (M1) transitions of open-charm meson

The decay widths of energetically allowed radiative transitions ($A \rightarrow B + \gamma$) of vector and pseudoscalar states of D meson are computed from the spectroscopic studies. The magnetic transition correspond to spin flip and hence the vector meson decay to pseudoscalar $V\rightarrow P\gamma$ represents a typical M1 transition. Such transitions are experimentally important for the identification of newly observed states. Assuming that such transitions are single vertex processes governed mainly by photon emission from independently confined quark and antiquark inside the meson, the S-matrix elements in the rest frame of the initial meson is written in the form

$$\begin{aligned} S_{BA} {=}\left\langle B\gamma \left| -ie\int \mathrm{d}^4 x \ T \left[ \sum _q e_q \bar{\psi _q} (x) \gamma ^\mu \psi _q (x) A_\mu (x) \right] \right| A \right\rangle .\nonumber \\ \end{aligned}$$

(26)

The common choice of the photon field $A_\mu (x)$ is made here in Coulomb-gauge with $\epsilon (k, \lambda )$ as the polarisation vector of the emitted photon having an energy momentum $(k_0 = |\mathbf k |,\mathbf k )$ in the rest frame of A. The quark field operators find possible expansions in terms of the complete set of positive and negative energy solutions given by Eqs. (5) and (6) in the form

$$\begin{aligned} \Psi _q (x)= & {} \sum _\zeta \left[ b_{q\zeta } \ \psi _{q\zeta }^{(+)}(r) \ \exp (-iE_{q\zeta }t) \right. \nonumber \\&\left. +\ b_{q\zeta }^{\dag } \ \psi _{q\zeta }^{(-)}(r) \ \exp (iE_{q\zeta }t)\right] \end{aligned}$$

(27)

where the subscript q stands for the quark flavour and $\zeta$ represents the set of Dirac quantum numbers. Here $b_{q\zeta }$ and $b_{q\zeta }^{\dag }$ are the quark annihilation and the antiquark creation operators corresponding to the eigenmodes $\zeta$. After some standard calculations (the details of the calculations can be found in Refs. [40–42]), the S-matrix elements can be expressed as

$$\begin{aligned} S_{BA}= & {} i \sqrt{\left( \frac{\alpha }{k}\right) }\ \delta (E_B +k-E_A) \sum _{q,m,m'}\bigg \langle B \bigg | \\&\times \left. \left[ J^q_{m' m} (k, \lambda ) b_{qm'}^\dagger b_{qm} - \ \tilde{J}^{\tilde{q}}_{m m'} (k, \lambda ) \tilde{b}_{qm'}^\dagger \tilde{b}_{qm} \right] \right| A \bigg \rangle .\nonumber \end{aligned}$$

(28)

Here $E_A$ = $M_A$, $E_B$ = $\sqrt{k^2 + M^2_B}$ and ($m, m'$) are the possible spin quantum numbers of the confined quarks corresponding to the ground state of the mesons. We have

$$\begin{aligned} J^q_{m' m} (k, \lambda )= & {} e_q \int \mathrm{d}^3 r \exp (-i {\mathbf {k}} \cdot {\mathbf {r}}) \nonumber \\&\times \left[ \bar{\psi }_{q m'}^{\ (+)} (r) {\mathbf {\gamma }} \cdot {\mathbf {\epsilon }} (k, \lambda ) \psi _{qm}^{(+)} (r)\right] , \end{aligned}$$

(29)

Fig. 1

D meson spectra

$$\begin{aligned} \tilde{J}^{\tilde{q}}_{m m'} (k, \lambda )= & {} e_q \int \mathrm{d}^3 r \exp (-i {\mathbf {k}} \cdot {\mathbf {r}}) \nonumber \\&\times \left[ \bar{\psi }_{q m}^{(-)} (r) {\mathbf {\gamma }} \cdot {\mathbf {\epsilon }} (k, \lambda ) \psi _{qm'}^{(-)}(r)\right] . \end{aligned}$$

(30)

One can reduce the above equations to the simple forms of

$$\begin{aligned} J^q_{m' m} (k, \lambda ) = - i\ \mu _q(k)\ [\chi _m^\dagger ({\mathbf {\sigma }} \cdot {\mathbf {K}}) \chi _m ] \end{aligned}$$

(31)

and

$$\begin{aligned} \tilde{J}^{\tilde{q}}_{m m'} (k, \lambda ) = i \ \mu _q(k)\ [\tilde{\chi }_m^\dagger ({\mathbf {\sigma }} \cdot {\mathbf {K}}) \tilde{\chi }_m ] \end{aligned}$$

(32)

where ${\mathbf {K}} = {\mathbf {k}} \times {\mathbf {\epsilon }} (k, \lambda )$. Equation (28) further can be simplified to

$$\begin{aligned} S_{BA}= & {} i \sqrt{\left( \frac{\alpha }{k}\right) }\ \delta (E_B +k-E_A) \nonumber \\&\times \sum _{q,m,m'} \bigg \langle B \bigg | \mu _q (k) \left[ \chi _{m'}^\dagger {\mathbf {\sigma }} \cdot {\mathbf {K}} \chi _m b_{qm'}^\dagger b_{qm} \right. \nonumber \\&\left. \left. + \ \tilde{\chi }_m^\dagger {\mathbf {\sigma }} \cdot {\mathbf {K}} \tilde{\chi }_{m'} \tilde{b}_{qm'}^\dagger \tilde{b}_{qm} \right] \right| A \bigg \rangle \end{aligned}$$

(33)

where $\mu _q(k)$ is expressed as

$$\begin{aligned} \mu _q(k)= \frac{2 e_q}{k} \int _0^\infty j_1(kr)\ f_q (r)\ g_q (r)\ dr \end{aligned}$$

(34)

where $j_1(kr)$ is the spherical Bessel function and the energy of the outgoing photon in the case of a vector meson undergoing a radiative transition to its pseudoscalar state, for instance, $D^* \rightarrow D \gamma$ is given by

$$\begin{aligned} k = \frac{M_{D^*}^2 - M_{D}^2}{2 M_{D^*}}. \end{aligned}$$

(35)

The relevant transition magnetic moment is expressed as

$$\begin{aligned} \mu _{D^+ D^{*+}}(k) = \frac{1}{3}[2 \mu _c (k) - \mu _d (k)], \end{aligned}$$

(36)

$$\begin{aligned} \mu _{D^0 D^{*0}}(k) = \frac{2}{3}[2 \mu _c (k) + \mu _u (k)]. \end{aligned}$$

(37)

Now, the magnetic (M1) transition width of $D^* \rightarrow D \gamma$ can be obtained:

$$\begin{aligned}&\Gamma _{D^{*+} \rightarrow D^+ \gamma } = \frac{4 \alpha }{3} k^3 |\mu _{D^+ D^{*+}} (k)|^2,\end{aligned}$$

(38)

$$\begin{aligned}&\Gamma _{D^{*0} \rightarrow D^0 \gamma } = \frac{4 \alpha }{3} k^3 |\mu _{D^0 D^{*0}} (k)|^2. \end{aligned}$$

(39)

The computed transition widths of the low-lying S-wave states are tabulated in Table 5 and are compared with other model predictions.

4 Decay constant of the D meson

In the study of leptonic or nonleptonic weak decay processes, the decay constant of a meson is an important parameter. The decay constant ($f_p$) of the pseudoscalar state is obtained by parameterizing the matrix elements of weak current between the corresponding meson and the vacuum as [43]

$$\begin{aligned} \langle 0|\bar{q}\gamma ^{\mu } \gamma _5 c| P_\mu \rangle = i f_p \ P^\mu . \end{aligned}$$

(40)

It is possible to express the quark–antiquark eigenmodes in the ground state of the meson in terms of the corresponding momentum distribution amplitudes. Accordingly, the eigenmodes, $\psi _A^{(+)}$ in the state of definite momentum p and spin projection $s'_p$, can be expressed as

$$\begin{aligned} \psi _A^{(+)} = \sum _{s'_p} \int d^3 p \ G_q(p,s'_p) \sqrt{\frac{m}{E_p}}\ U_q (p, s'_p) \exp (i\mathbf {p}\ .\ \mathbf {r})\nonumber \\ \end{aligned}$$

(41)

where $U_q (p, s'_p)$ is for the usual free Dirac spinors.

In the relativistic quark model, the decay constant can be expressed through the meson wave function $G_q (p)$ in the momentum space [41, 44]

$$\begin{aligned} f_P = \left( {\frac{3 | I_p |^2}{2 \pi ^2 M_p\ J_p} }\right) ^{\frac{1}{2}}. \end{aligned}$$

(42)

Here $M_p$ is mass of the pseudoscalar meson and $I_p$ and $J_p$ are defined as

$$\begin{aligned} I_p = \int _0^\infty dp \ p^2 A (p) [G_{q1} (p) G^*_{q2} (-p)]^{\frac{1}{2}}, \end{aligned}$$

(43)

$$\begin{aligned} J_p = \int _0^\infty dp \ p^2 [G_{q1} (p) G^*_{q2} (-p)], \end{aligned}$$

(44)

respectively. Here,

$$\begin{aligned} A (p) = \frac{(E_{p1}+m_{q1})(E_{p2}+m_{q2})-p^2}{[E_{p1}\ E_{p2} (E_{p1}+m_{q1})(E_{p2}+m_{q2})]^{\frac{1}{2}}} \end{aligned}$$

(45)

and $E_{p_i} = \sqrt{{k_i}^2 + m_{q_i}^2}$.

The computed decay constants of the D meson from 1S to 4S states are tabulated in Table 6. The present result for 1S state is compared with experimental as well as other model predictions. There are no model predictions available for a comparison of the decay constants of the 2S to 4S states.

Table 6 Pseudoscalar decay constant ($f_{P}$) of D systems (in MeV)

5 Leptonic decay of the D meson

The leptonic decays of open flavour mesons belong to rare decay [46, 47], they have clear experimental signatures due to the presence of a highly energetic lepton in the final state. Such decays are very clean due to the absence of hadrons in the final state [51]. Charged mesons produced from a quark and antiquark can decay to a charged lepton pair when these objects annihilate via a virtual $W^\pm$ boson as given in Fig. 2. The leptonic width of the D meson is computed using the relation given by [2, 3]

$$\begin{aligned} \Gamma (D \rightarrow l^+\nu _l)=\frac{G_F^2}{8\pi } f^2_{D} |V_{cd}|^2 m_l^2 \left( 1-\frac{m_l^2}{M^2_{D}}\right) ^2 M_{D}\ \ \ \ \ \end{aligned}$$

(46)

Fig. 2

Feynman diagram for leptonic decay $(M \rightarrow l \bar{\nu _l})$

in complete analogy to $\pi ^+ \rightarrow l^+ \nu$. These transitions are helicity suppressed; i.e., the amplitude is proportional to $m_l$, the mass of the lepton l. The leptonic widths of the D ($1^1S_0$) meson are obtained from Eq. (46) where the predicted values of the pseudoscalar decay constant $f_{D}$ along with the masses of $M_{D}$ and the PDG value for $V_{cd}$ = 0.230 are used. The leptonic widths for the separate lepton channel are computed for the choices of $m_{l=\tau , \mu , e}$. The branching ratio of these leptonic widths are then obtained:

$$\begin{aligned} BR = \Gamma (D \rightarrow l^+ \nu _l)\times \tau \end{aligned}$$

(47)

where $\tau$ is the experimental lifetime of the respective D meson state. The computed leptonic widths are tabulated in Table 7 along with other model predictions as well as with the available experimental values. Our results are found to be in accordance with the reported experimental values.

Table 7 The leptonic decay width and leptonic branching ratio (BR) of the D meson

6 Nonleptonic decays of the D meson

The study of flavour changing decays of heavy flavour quarks is useful for determining the parameters of the Standard Model and for testing phenomenological models which include strong effects. The interpretation of the nonleptonic decays of the c-meson within a hadronic state is complicated by the effects of the strong interaction and by its interplay with the weak interaction. The nonleptonic decays of heavy mesons can be understood in this model and we assume that Cabibbo favoured nonleptonic decays proceed via the basic process ($c\rightarrow q+ u +\bar{d}; q \in s,d$), and the decay widths are given by [43]

$$\begin{aligned} \Gamma (D^0\rightarrow K^- \pi ^+)= & {} C_f \frac{G_F^2 \ |V_{cs}|^2 |V_{ud}|^2 f_\pi ^2 }{32 \ \pi \ M^3_{D_s}} \nonumber \\&\times [\lambda (M^2_{D},M^2_{K^-},M^2_{\pi })]^{\frac{3}{2}} |f^2_+(q^2)| \end{aligned}$$

(48)

for $q=s$ and

$$\begin{aligned} \Gamma (D^0\rightarrow K^+ \pi ^-)= & {} C_f \frac{G_F^2 \ |V_{cd}|^2 |V_{us}|^2 f_\pi ^2 }{32 \ \pi \ M^3_{D_s}} \nonumber \\&\times [\lambda (M^2_{D},M^2_{K^+},M^2_{\pi })]^{\frac{3}{2}} |f^2_+(q^2)| \end{aligned}$$

(49)

for $q=d$. Here, $C_f$ is the colour factor and $(|V_{cs}|,|V_{cd}|$, $|V_{us}|)$ are the CKM matrices. $f_\pi$ is the decay constant of $\pi$ meson and its value is taken as 0.130 GeV. Here, $f_+(q^2)$ is the form factor and the factor $\lambda (M^2_{D},M^2_{K^+},M^2_{\pi })$ can be computed as

$$\begin{aligned} \lambda (x, y, z) = x^2 + y^2 + z^2 - xy - yz-zx. \end{aligned}$$

(50)

The renormalised colour factor without the interference effect due to QCD is given by $( C_A^2 + C_B^2)$. The coefficients $C_A$ and $C_B$ are further expressed as [43]

$$\begin{aligned} C_A = \frac{1}{2}(C_+ + C_-), \end{aligned}$$

(51)

$$\begin{aligned} C_B = \frac{1}{2}(C_+ - C_-) \end{aligned}$$

(52)

where

$$\begin{aligned} C_{+} = 1 - \frac{\alpha _s}{\pi } \log \left( \frac{M_W}{m_c}\right) \end{aligned}$$

(53)

and

$$\begin{aligned} C_{-} = 1 + 2 \frac{\alpha _s}{\pi } \log \left( \frac{M_W}{m_c}\right) \end{aligned}$$

(54)

where $M_W$ is the mass of W meson.

Consequently, the form factors $f_{\pm }(q^2)$ correspond to the D final state are related to the Isgur–Wise function as [43]

$$\begin{aligned} f_{\pm }(q^2) = \xi (\omega ) \frac{M_{D}\pm M_{\phi }}{2 \sqrt{M_{D}M_{\phi }}}. \end{aligned}$$

(55)

The Isgur–Wise function, $\xi (\omega )$ can be evaluated according to the relation given by [65]

$$\begin{aligned} \xi (\omega ) = \frac{2}{\omega -1}\left\langle j_0 \left( 2\ E_q \sqrt{\frac{\omega -1}{\omega +1}} \ r\right) \right\rangle \end{aligned}$$

(56)

where $E_q$ is the binding energy of decaying meson and $\omega$ is given by

$$\begin{aligned} \omega = \frac{M^2_{D}+ M^2_{(K^+, K^-)}-q^2}{2 M_{D}\ M_{(K^+, K^-)}}. \end{aligned}$$

(57)

In a good approximation the form factor $f_-(q^2)$ does not contribute to the decay rate, so we have neglected it here. The heavy flavour symmetry provides a model-independent normalisation of the weak form factors $f_{\pm }(q^2)$ either at $q=0$ or $q=q_\mathrm{max}$, and we have applied $q=q_\mathrm{max}$ in Eqs. (48) and (49) for nonleptonic decay. From the computed exclusive semileptonic and hadronic decay widths, the branching ratios are obtained:

$$\begin{aligned} BR = \Gamma \times \tau ; \end{aligned}$$

(58)

here the lifetime ($\tau$) of D $(\tau _{D^+} = 1.040 \ \mathrm{ps}^{-1}$ and $\tau _{D^0} = 0.410 \ \mathrm{ps}^{-1})$ is taken as the world average value reported by Particle Data Group [2, 3]. The decay widths and their branching ratios are listed in Table 8 along with the known experimental and other theoretical predictions for comparison.

Table 8 The nonleptonic decay width and branching ratio (BR) of the D meson

7 Mixing parameters of the $D^0$–$\bar{D}^0$ oscillation

A different $D^0$ decay channel [66–70] has been reported by three experimental groups as evidence of the $D^0$–$\bar{D}^0$ oscillation. We discuss here the mass oscillation of the neutral open-charm meson and the integrated oscillation rate using our spectroscopic parameters deduced from the present study. In the standard model, the transitions $D^{0}$–$\bar{D}^{0}$ and $\bar{D}^{0}$–${D}^{0}$ occur through the weak interaction. The neutral D meson mixes with the antiparticle leading to oscillations between the mass eigenstates [2, 3]. In the following, we adopt the notation introduced in [2, 3], and assume CPT conservation in our calculations. If CP symmetry is violated, the oscillation rates for meson produced as $D^0$ and $\bar{D}^0$ can differ, further enriching the phenomenology. The study of CP violation in $D^0$ oscillation may lead to an improved understanding of possible dynamics beyond the standard model [71–73].

The time evolution of the neutral $D-$meson doublet is described by a Schr$\ddot{o}$dinger equation with an effective $2\times 2$ Hamiltonian given by [43, 74]

$$\begin{aligned} i\frac{d}{dt}\left( \begin{array}{c} D^{0}(t) \\ \bar{D}^{0}(t) \\ \end{array} \right) =\left( \begin{array}{cc} M- \frac{i}{2}\Gamma \end{array} \right) \left( \begin{array}{c} D^{0}(t) \\ \bar{D}^{0}(t) \\ \end{array} \right) \end{aligned}$$

(59)

where the M and $\Gamma$ matrices are Hermitian, and they are defined as

$$\begin{aligned} \left( \begin{array}{cc} M- \frac{i}{2}\Gamma \end{array} \right) =\left[ \left( \begin{array}{cc} M^{q}_{11} &{} M^{q*}_{12} \\ M^{q}_{12} &{} M^{q}_{11}\\ \end{array} \right) - \frac{i}{2}\left( \begin{array}{cc} \Gamma ^{q}_{11} &{} \Gamma ^{q*}_{12} \\ \Gamma ^{q}_{12} &{} \Gamma ^{q}_{11}\\ \end{array} \right) \right] . \end{aligned}$$

(60)

CPT invariance imposes

$$\begin{aligned} M_{11} = M_{22} \equiv M , \Gamma _{11} = \Gamma _{22} \equiv \Gamma . \end{aligned}$$

(61)

The off-diagonal elements of these matrices describe the dispersive and absorptive parts of the $D^0$–$\bar{D}^0$ mixing [77]. The two eigenstates $D_1$ and $D_2$ of the effective Hamiltonian matrix $(M- \frac{i}{2}\Gamma )$ are given by

$$\begin{aligned} |D_1\rangle = \frac{1}{\sqrt{|p|^2+|q|^2}} (p|D^0\rangle + q|\bar{D}^0\rangle ), \end{aligned}$$

(62)

$$\begin{aligned} |D_2\rangle = \frac{1}{\sqrt{|p|^2+|q|^2}} (p|D^0\rangle - q|\bar{D}^0\rangle ). \end{aligned}$$

(63)

The corresponding eigenvalues are

$$\begin{aligned} \lambda _{D_1} \equiv m_1 - \frac{i}{2}\Gamma _1 = \left( M- \frac{i}{2}\Gamma \right) + \frac{q}{p} \left( M_{12} - \frac{i}{2}\Gamma _{12} \right) ,\nonumber \\ \end{aligned}$$

(64)

$$\begin{aligned} \lambda _{D_2} \equiv m_2 - \frac{i}{2}\Gamma _2 = \left( M- \frac{i}{2}\Gamma \right) - \frac{q}{p} \left( M_{12} - \frac{i}{2}\Gamma _{12} \right) ,\nonumber \\ \end{aligned}$$

(65)

where $m_1(m_2)$ and $\Gamma _1(\Gamma _2)$ are the mass and width of $D_1 (D_2)$, respectively, and

$$\begin{aligned} \frac{q}{p} = \left( \frac{M_{12}^* - \frac{i}{2}\Gamma _{12}^*}{{M_{12} - \frac{i}{2}\Gamma _{12}}} \right) ^{1/2}. \end{aligned}$$

(66)

From Eqs. (64) and (65), one can get the differences in mass and width, which are given as

$$\begin{aligned} \Delta m \equiv m_2 - m_1 = - 2 Re \left[ \frac{q}{p} \left( M_{12} - \frac{i}{2}\Gamma _{12}\right) \right] , \end{aligned}$$

(67)

$$\begin{aligned} \Delta \Gamma \equiv \Gamma _2 - \Gamma _1 = - 2 Im \left[ \frac{q}{p} \left( M_{12} - \frac{i}{2}\Gamma _{12}\right) \right] . \end{aligned}$$

(68)

Table 9 Mixing parameters $x_q$, $y_q$, $\chi _q$ and $R_M$ of the D mesons

The calculation of the dispersive and absorptive parts of the box diagrams yields the following expressions for the off-diagonal element of the mass and decay matrices; for example, if $s/\bar{s}$ as the intermediate quark state then [78]

$$\begin{aligned} M_{12}= & {} - \frac{G_F^2 m_W^2 \eta _{D^{0}} m_{D^{0}} B_{D^{0}} f_{D^{0}}^2}{12\pi ^2} S_0(m_s^2/m_W^2) (V_{us}^* V_{cs}^{})^2 ,\,\end{aligned}$$

(69)

$$\begin{aligned} \Gamma _{12}= & {} \frac{G_F^2 m_c^2 \eta _{D^{0}}^{'} m_{D^{0}} B_{D^{0}} f_{D^{0}}^2}{8\pi } \left[ (V_{us}^* V_{cs}^{})^2 \right] \,, \end{aligned}$$

(70)

where $G_F$ is the Fermi constant, $m_W$ is the W boson mass, $m_c$ is the mass of c quark, $m_{D^{0}}$, $f_{D^{0}}$ and $B_{D^{0}}$ are the $D^0$ mass, weak decay constant and bag parameter, respectively. The known function $S_0(x_q)$ can be approximated very well by $0.784\,x_q^{0.76}$ [79] and $V_{ij}$ are the elements of the CKM matrix [80]. The parameters $\eta _D^{0}$ and $\eta '_{D^{0}}$ correspond to the gluonic corrections. The only non-negligible contributions to $M_{12}$ are from box diagrams involving the $s (\bar{s}), d (\bar{d}), b(\bar{b})$ intermediate quarks in Fig. 3. The phases of $M_{12}$ and $\Gamma _{12}$ satisfy

$$\begin{aligned} \phi _{M} - \phi _{\Gamma } = \pi + \mathcal{O}\left( \frac{m^2_c}{m^2_b} \right) \,, \end{aligned}$$

(71)

implying that the mass eigenstates have mass and width differences of opposite signs. This means that, like in the $K{^0}\hbox {--}\overline{K}{^0}$ system, the heavy state is expected to have a smaller decay width than that of the light state: $\Gamma _{1} < \Gamma _{2}$. Hence, $\Delta \Gamma = \Gamma _{2} -\Gamma _{1}$ is expected to be positive in the standard model. Further, the quantity

$$\begin{aligned} \left| \frac{\Gamma _{12}}{M_{12}}\right| \simeq \frac{3\pi }{2} \frac{m^2_c}{m^2_W} \frac{1}{S_0(m_q^2/m_W^2)} \sim \mathcal{O}\left( \frac{m^2_q}{m^2_t} \right) \end{aligned}$$

(72)

is small, and a power expansion of $|q/p|^2$ yields

$$\begin{aligned} \left| \frac{q}{p}\right| ^2 = 1 + \left| \frac{\Gamma _{12}}{M_{12}}\right| \sin (\phi _{M}-\phi _{\Gamma }) + \mathcal{O}\left( \left| \frac{\Gamma _{12}}{M_{12}}\right| ^2\right) \,. \end{aligned}$$

(73)

Therefore, considering both Eqs. (71) and (72), the CP-violating parameter given by

$$\begin{aligned} 1 - \left| \frac{q}{p}\right| ^2 \simeq \mathrm{Im}\left( \frac{\Gamma _{12}}{M_{12}}\right) \end{aligned}$$

(74)

is expected to be very small: $\sim \mathcal{O}(10^{-3})$ for the $D^0- {\bar{D}}^0$ system. In the approximation of negligible CP violation in mixing, the ratio $\Delta \Gamma /\Delta m$ is equal to the small quantity $\left| \Gamma _{12}/M_{12}\right|$ of Eq. (72); it is hence independent of the CKM matrix elements, i.e., the same for the $D^0$–${\bar{D}}^0$ system.

Fig. 3

$D^0$–$\bar{D}^0$ mixing

Theoretically, the hadron lifetime ($\tau _{D^{0}}$) is related to $\Gamma _{11} ( \tau _{D^{0}}=1/ \Gamma _{11})$, while the observables $\Delta m$ and $\Delta \Gamma$ are related to $M_{12}$ and $\Gamma _{12}$ as [2, 3]

$$\begin{aligned} \Delta m =2 |M_{12}| \end{aligned}$$

(75)

and

$$\begin{aligned} \Delta \Gamma =2 |\Gamma _{12}|. \end{aligned}$$

(76)

The gluonic correction can be found from a different model, like the Wilson coefficient and the evolution of the Wilson coefficient from the new physics scale [73]. We have used the values of the gluonic correction ($\eta _{D^0}= 0.86$; $\eta _{D^0}^{'} = 0.21$) from [81, 82]. The bag parameter $B_{D^{0}}= 1.34$ is taken from the lattice result of [83], while the pseudoscalar mass ($M_{D^{0}}$) and the pseudoscalar decay constant ($f_{D}$) of the D mesons are the values obtained from our present study using a relativistic independent quark model using a Martin-like potential. The values of $m_{s}$ (0.1 GeV), $M_{W}$ (80.403 GeV) and the CKM matrix elements $V_{cs} (1.006)$ and $V_{us} (0.2252)$ are taken from the Particle Data Group [2, 3]. The resulting mass oscillation parameter $\Delta m$ are tabulated in Table 9 with the latest experimental results.

The integrated oscillation rate ($\chi _q$) is the probability to observe a ${\bar{D}}$ meson in a jet initiated by a ${\bar{c}}$ quark. As the mass difference $\Delta m_{D}$ is a measure of the frequency of the change from a $D^{0}$ into a ${\bar{D}}^{0}$ or vise versa. This change is reflected in either the time-dependent oscillations or in the time-integrated rates corresponding to the di-lepton events having the same sign. The time evolution of the neutral states from the pure $|D{^0}_\mathrm{phys}\rangle$ or $| \bar{D}{^0}_\mathrm{phys}\rangle$ state at $t=0$ is given by

$$\begin{aligned} | D{^0_\mathrm{phys}}(t)\rangle= & {} g_+(t) \,| D{^0}\rangle + \frac{q}{p} \, g_-(t) \,| \bar{D}{^0}\rangle ,\end{aligned}$$

(77)

$$\begin{aligned} | \bar{D}{^0_\mathrm{phys}}(t)\rangle= & {} g_+(t) \,| \bar{D}{^0}\rangle + \frac{p}{q} g_-(t) \,| D{^0}\rangle , \end{aligned}$$

(78)

which means that the flavour states remain unchanged ($g_+$) or oscillate into each other ($g_-$) with time-dependent probabilities proportional to

$$\begin{aligned} g_{+}(t)\ = e^{ \frac{-\Gamma t}{2}} e^{ {-i\ t\ m_{D^0}}} \cos (t \Delta m/ 2) , \end{aligned}$$

(79)

$$\begin{aligned} g_{-}(t)\ = e^{ \frac{-\Gamma t}{2}} e^{ {-i\ t\ m_{D^0}}} \sin (t \Delta m/ 2). \end{aligned}$$

(80)

Starting at $t = 0$ with an initially pure $D^0$, the probability for finding a $D^0 (\bar{D}^0)$ at time $t \ne 0$ is given by $\left| g_+ (t)\right| ^2 (\left| g_- (t)\right| ^2 )$. Taking $|q/p| = 1$, one gets

$$\begin{aligned} \left| g_\pm (t) \right| ^2\ = \frac{1}{2} e^{ \frac{-\Gamma _D t}{2}} [1 \pm \cos (t \Delta m)]. \end{aligned}$$

(81)

Conversely, from an initially pure $\bar{D}^0$ at $t = 0$, the probability for finding a $\bar{D}^0 (D^0)$ at time $t \ne 0$ is also given by $\left| g_+ (t)\right| ^2 (\left| g_- (t)\right| ^2 )$. The oscillation of $D^0$ or $\bar{D}^0$ as shown by Eq. (81) gives $\Delta m$ directly. Integrating $\left| g_\pm (t) \right| ^2$ from $t = 0$ to $t = \infty$, we get

$$\begin{aligned} \int ^\infty _0 \left| g_\pm (t) \right| ^2 \mathrm{d}t \ = \frac{1}{2} \left[ \frac{1}{\Gamma } \pm \frac{\Gamma }{\Gamma ^2+(\Delta m)^2}\right] \end{aligned}$$

(82)

where $\Gamma = \Gamma _D = (\Gamma _{1} +\Gamma _{2})/2$. The ratio

$$\begin{aligned} r_o = \frac{D^0 \leftrightarrow \bar{D}^0}{D^0 \leftrightarrow {D}^0} = \frac{\int ^\infty _0 \left| g_- (t) \right| ^2 \mathrm{d}t}{\int ^\infty _0 \left| g_+ (t) \right| ^2 \mathrm{d}t} = \frac{x^2}{2 + x^2}, \end{aligned}$$

(83)

where $x_q = x = \frac{\Delta m}{\Gamma }= \Delta m\ \tau _{D}, y_q = \frac{\Delta \Gamma }{2\Gamma }=\frac{\Delta \Gamma \ \tau _{D}}{2} ,$

$$\begin{aligned} \chi _q = \frac{x_q^2+y_q^2}{2(x_q^2+1)}, \end{aligned}$$

(84)

reflects the change of a pure $D^0$ into a $\bar{D}^0$, or vice versa.

The time-integrated mixing rate relative to the time-integrated right-sign decay rate for semileptonic decays [2, 3] is

$$\begin{aligned} R_M = \int ^\infty _0 r (t) \mathrm{d}t = \int ^\infty _0 \left| g_- (t) \right| ^2 \left| \frac{q}{p} \right| ^2 \mathrm{d}t, \end{aligned}$$

(85)

$$\begin{aligned} R_M = \int ^\infty _0 \frac{e^{-t}}{4} (x^2 + y^2) t^2 \left| \frac{q}{p} \right| ^2 \simeq \frac{1}{2} (x^2 + y^2). \end{aligned}$$

(86)

In the standard model, CP violation in charm mixing is small and |q / p| $\approx$ 1.

For the present estimation of these mixing parameters, $x_q$, $y_q$ and $\chi _q$, we employ our predicated $\Delta m$ values and the experimental average lifetime of PDG [2, 3] of the D-meson.

8 Results and discussion

We have studied here the mass spectra and decay properties of the D meson in the framework of the relativistic independent quark model. Our computed D meson spectral states are in good agreement with the reported PDG values of the known states. The predicted masses of the S-wave D meson state $2\ ^3S_1$ (2605.86 MeV) and $2\ ^1S_0$ (2521.72 MeV) are in very good agreement with the respective experimental results of $2608\pm 2.4 \pm 2.5$ MeV [39] and $2539.4\pm 4.5 \pm 6.8$ MeV [39] by the BABAR Collaboration. The expected results of other S-wave excited states of the D meson are also in good agreement with other reported values [14, 36–38]. The predicted P-wave D meson states, $1^3P_2$ (2462.50 MeV), $1^3P_1$ (2407.56 MeV), $1^3P_0$ (2373.82 MeV) and $1^1P_1$ (2423.28 MeV), are in good agreement with experimental [2, 3] results of $2462.6 \pm 0.7$ MeV, $2427 \pm 26 \pm 25$ MeV, $2318 \pm 29$ MeV and $2421.3 \pm 0.6$ MeV, respectively. We have also compared lattice QCD and QCD sum rule results with our predicted results where the numerical values in Table 3 for lattice QCD results are extracted from the energy level diagram available in [20]. With reference to the available experimental masses of D-mesonic states, we observe that the LQCD predictions [20] are off by a standard deviation of $\pm$58.52 and those found by the QCD sum rule [15, 18] predictions are off by $\pm$59.22, while the predicted calculations show a standard deviation of $\pm$21.88.

Table 10 Comparison of centre of mass in D meson in MeV

Table 11 Mass splitting in D meson in MeV

In the limit of one heavy quark, the $1^+$ resonance is expected to show a very simple mixing pattern [88, 89]. The angular momentum $j_q = s_q + L$ of a light quark is a good quantum number, which is a conserved quantum number, while the angular momentum $s_Q$ of a heavy quark is not a good quantum number, so the physically observed two $1^+$ states are mixed states of the $^3P_1$ and $^1P1$. Accordingly, the mixed states can be expressed as [88, 89],

$$\begin{aligned} |\alpha \rangle = \sqrt{\frac{2}{3}}\ |^3P_1\rangle + \sqrt{\frac{1}{3}}\ |^1P_1\rangle , \end{aligned}$$

(87)

$$\begin{aligned} |\beta \rangle = - \sqrt{\frac{1}{3}}\ |^3P_1\rangle + \sqrt{\frac{2}{3}}\ |^1P_1\rangle . \end{aligned}$$

(88)

Further, we can write the masses of these states in terms of the predicted masses of $^3P_1$ and $^1P_1$ states as

$$\begin{aligned} M (|\alpha \rangle ) = \frac{2}{3}\ M(^3P_1) + \frac{1}{3}\ M(^1P_1) = 2412.8\,\mathrm{MeV}, \end{aligned}$$

(89)

which falls within the error bars of the experimentally observed state $D(2427 \pm 26 \pm 25)$ and

$$\begin{aligned} M (|\beta \rangle ) = \frac{2}{3}\ M(^1P_1) + \frac{1}{3}\ M(^3P_1) = 2418\,\mathrm{MeV}, \end{aligned}$$

(90)

which is very close to $D_1(2420 \pm 0.6)$. The calculated mixing states of $^3P_1$ and $^1P_1$ are listed in Table 4. We look forward to see more precise measurements of the mass of the $D_1(2430)$ state as it supports the right contributions from the tensor and spin–orbit interactions.

In the relativistic Dirac formalism, the spin degeneracy is primarily broken; therefore to compare the spin average mass, we employ the relation of

$$\begin{aligned} M_{CW} = \frac{\sum _J (2 J +1) M_J}{\sum _J (2 J +1)}. \end{aligned}$$

(91)

The spin average or the centre of weight masses $M_{CW}$ are calculated from the known values of the different meson states and are compared with other model predictions [14, 37] in Table 10. The table also contains the different spin dependent contributions for the observed state. Mass splittings of the D meson states are calculated and compared with lattice QCD predictions [45] and other model predictions [14, 37] in Table 11.

The precise experimental measurements of the masses of the D meson states provided a real test for the choice of the hyperfine and the fine structure interactions adopted in the study of the D meson spectroscopy. A recent study of the D meson mass splitting in lattice QCD [LQCD] [45] using 2 $\pm$ 1 flavour configurations generated with the Clover–Wilson fermion action by the PACS-CS Collaboration [45] has been listed for comparison. The present results as seen in Table 8 are in very good agreement with the respective experimental values over the lattice results [45]. In this table, the present results, on average, are in agreement with the available experimental value within $12 \,\%$ variations, while the lattice QCD predictions [45] show $30 \,\%$ variations.

The magnetic transitions (M1) can probe the internal charge structure of hadrons, and therefore they will likely play an important role in determining the hadronic structures of the D meson. The present M1 transitions widths of the D meson states as listed in Table 5 are in accordance with the model prediction of [49] while the upper bound provided by PDG [2, 3] is very wide. We do not find any theoretical predictions for M1 transition width of excited states for comparison. Thus we only look forward to see future experimental support to our predictions.

The calculated pseudoscalar decay constant ($f_P$) of the D meson is listed in Table 6 along with other model predictions as well as experimental results. The value of $f_{D} (1S)$ = 202.57 MeV obtained in our present study is in very good agreement with other theoretical predictions for 1S state. The predicted $f_{D}$ for higher S-wave states are found to increase with energy. However, there are no experimental or theoretical values available for a comparison. The computed vector decay constant ($f_V$) and P-wave decay constant ($f_i$) of the D meson are listed in Tables 12 and 13 along with other model predictions. Another important property of the D meson studied in the present case is the leptonic decay widths. The present branching ratios for $D \rightarrow \tau \bar{\nu _\tau }$ ($9.73 \times 10^{-4}$) and $D \rightarrow \mu \bar{\nu _\mu }$ ($3.846 \times 10^{-4}$) are in accordance with the experimental results $(<1.2 \times 10^{-2})$ and $(3.82 \times 10^{-4})$, respectively, over other theoretical predictions; vide Table 7. The large experimental uncertainty in the electron channel makes it difficult to reach any reasonable conclusion.

Table 12 Vector decay constant ($f_{V}$) of D systems (in MeV)

Table 13 P-wave decay constant ($f_{i}$) of D systems (in MeV)

The Cabibbo favoured nonleptonic branching ratios BR$(D^0\rightarrow K^- \pi ^+)$ and BR $(D^0\rightarrow K^+ \pi ^-)$ obtained, respectively, as $4.071 \,\%$ and $1.135 \times 10^{-4}$, are in very good agreement with experimental values of $3.91 \pm 0.08\,\%$ and $(1.48\pm 0.07) \times 10^{-4}$, [76].

We obtained the CP-violation parameter in mixing |q / p| (0.9996) in this case, and the $D^0$ and $\bar{D}^0$ decays show no evidence for CP violation and provides the most stringent bounds on the mixing parameters. The mixing parameter $x_q$, $y_q$, and mixing rate $(R_M)$ are in very good agreement with BaBar, Belle and other Collaborations, as shown in Table 9. However, due to a larger uncertainty in the experimental values it is difficult for us to draw a conclusion on this mixing parameter. Thus, the present study of the mixing parameters of the neutral open-charm meson is found to be one of the successful attempts to extract the effective quark–antiquark interaction in the case of heavy-light flavour mesons. Thus the present study is an attempt to indicate the importance of spectroscopic (strong interaction) parameters in the weak decay processes.

Finally we look forward to see future experimental support of many of our predictions on the spectral states and decay properties of the open-charm meson.