Gravitational Rutherford scattering and Keplerian orbits for electrically charged bodies in heterotic string theory

Abstract

Properties of the motion of electrically charged particles in the background of the Gibbons–Maeda–Garfinkle–Horowitz–Strominger black hole is presented in this paper. Radial and angular motions are studied analytically for different values of the fundamental parameter. Therefore, gravitational Rutherford scattering and Keplerian orbits are analyzed in detail. Finally, this paper complements previous work by Fernando for null geodesics (Phys Rev D 85:024033, 2012), Olivares and Villanueva (Eur Phys J C 73:2659, 2013) and Blaga (Automat Comp Appl Math 22:41–48, 2013; Serb Astron 190:41, 2015) for time-like geodesics.

1 Introduction

The study of the motion of test particles around compact objects is one interesting way to probe some phenomena related to classic tests of the general relativity. In the context of Einstein gravity, orbital precession experienced by the solar planets, particularly Mercury, and the deflection of light were studied earlier by Einstein himself [1, 2] and other renowned scientists [3, 4]. Nearly a century after all that, a lot of research has been conducted on these tests together with other studies (time delay, strong gravity, gravitational waves, etc.). Fundamentals and current advances can be found, for example, in [5, 6].

In other spacetimes containing black hole solutions, the motion of particles has also received a great deal of attention from the physics community. For instance, a review of neutral massive and massless particles moving in the background of the Schwarzschild (S), Reissner–Nordström (RN) and Kerr (K) black holes can be found in [7]. Furthermore, the inclusion of a cosmological constant $\Lambda$ leads to the Kottler solution [8], which spacetime is known as Schwarzschild–de Sitter (SdS) if $\Lambda > 0$, or the Schwarzschild–anti-de Sitter (SAdS) if $\Lambda < 0$. So, trajectories for neutral particles in a purely SdS spacetime can be found in [9–12], while different aspects of the motion of neutral particles in the background of the purely SAdS spacetime have been presented in [13–18]. Uncharged particles in an RN black hole with $\Lambda \ne 0$ were studied by Stuchlík and Hledík [19], whereas circular orbits were presented by Pugliese et al. [20]. Furthermore, Hackmann et al. [21] presented analytical solutions of the geodesic equation of massive test particles in higher dimensional Schwarzschild, Schwarzschild–anti-de Sitter, Reissner–Nordström, and Reissner–Nordström–anti-de Sitter (RNAdS) spacetimes and they obtained complete solutions and a classification of the possible orbits in these geometries in terms of Weierstraß functions. Also, bounded time-like geodesics in a Kerr (K) spacetime are found in [22], whereas a study of equatorial circular motion in Kerr–de Sitter (KdS) and Kerr–Newman (KN) spacetimes was performed by Stuchlík and Slany [23] and by Pugliese et al. [24], respectively.

There is just as much literature dealing with alternatives theories of gravitation. In fact, here we mention only a few studies dealing with the motion of neutral particles. For example, in conformal Weyl gravity, there are many articles studying the motion of particles in addition to some observational tests [25–29], similar to those for asymptotically Lifshitz spacetimes [30–34]. The complete causal structure of the Bardeen spacetime was presented in [35], the Rindler modified Schwarzschild geodesics in [36], while the Shwarzschild version in gravity’s rainbow was performed by Leiva et al. [37]. Not least are the contributions from string theories. Here we can mention the works of Maki and Shiraishi [38], Hackmann et al. [39], Hartmann and Sirimachan [40], and Bhadra [41], among other authors.

The motion of electrically charged particles represents another current line of investigation, which posits interesting features due to the extra interaction between the particle and the electromagnetic field of the background. In this sense, trajectories in a dipole magnetic field and in a toroidal magnetic field on the Schwarzschild background were performed by Prasanna and Varma and Prasanna and Sengupta [42, 43], respectively, whereas Dadhich et al. [44] made calculations for trajectories on the same background when the black hole is immersed in an axially symmetric magnetic field (Ernst spacetime). The general features of radial motion, motion along the axis of symmetry and motion on the equatorial plane in the field of rotating charged black holes was performed in two parts by Balek et al. [45, 46]. Relativistic radial motion of electrically charged particles in the field of a charged spherically symmetric distribution of mass can be found in [47], whereas studies of classical electrically and magnetically charged test particles in the same spacetime were made by Grunau and Kagramanova [48]. Trajectories on the RN black hole were studied by Cohen and Gautreau and Pugliese et al. when $\Lambda =0$ [49, 50], and by Olivares et al. when $\Lambda <0$ (RNAdS) [51]. The motion on a rotating Kerr black hole immersed in a magnetic field has been studied by Aliev and Özdemir [52] and by Takahashi and Koyama [54], the non-Kerr rotating version by Abdujabbarov [53], finally the Kerr–Newmann background has been covered by Hackmann and Xu [55].

The main goal of this paper is to work out the motion of electrically charged particles on the spacetime of a black hole coming from the heterotic string theory, the so-called Gibbons–Maeda–Garfinkle–Horowitz–Strominger (GMGHS) black hole, the causal structure of which has been determined by Fernando for null geodesics [56], and by Olivares and Villanueva [57] and Blaga [58, 59] for time-like geodesics. In this article we use natural units with $c=1$ and $G=1$, together with the value of the heterotic parameter found earlier in [57], $\alpha =0.359$ km. Therefore, in Sect. 2 the charged black hole in heterotic string theory is presented, and in Sect. 3 the fundamental equations of motion for electrically charged particles are obtained using the Hamilton–Jacobi method. In Sect. 4 we perform a full analysis of the radial motion of test particles, and in Sect. 5 we solve angular trajectories analytically and we study the gravitational scattering of Rutherford in detail. Finally, in Sect. 6 we conclude with general comments and final remarks.

2 Charged black holes in heterotic string theory

The simplest 4-dimensional black hole solutions in heterotic sting theory, which contain mass and electric charge, are obtained from the effective action [60]

$$\begin{aligned} \mathcal {I}_\mathrm{hst}=\frac{1}{16\pi }\int \mathrm{d}^4x\sqrt{-g} \left[ R-2(\nabla \Phi )^2-\mathrm{e}^{-2\Phi }F_{\mu \nu }F^{\mu \nu }\right] , \end{aligned}$$

(1)

where $\Phi$ is the dilaton field, R is the scalar curvature, and $F_{\mu \nu }=\partial _{\mu } A_{\nu }-\partial _{\nu } A_{\mu }$ is the Maxwell’s field strength associated with a U(1) subgroup of $E_8\times E_8$ or Spin(32) [60, 61]. The field equations associated with this action read

$$\begin{aligned} \nabla _{\mu }(\mathrm{e}^{-2\Phi }F^{\mu \nu })= & {} 0,\end{aligned}$$

(2)

$$\begin{aligned} \nabla ^2\Phi +\frac{1}{2}\mathrm{e}^{-2\Phi }F^2= & {} 0, \end{aligned}$$

(3)

and

$$\begin{aligned} R_{\mu \nu }=-2\nabla _{\mu }\Phi \,\nabla _{\nu }\Phi -2\mathrm{e}^{-2\Phi }F_{\mu \lambda }F_{\nu }^{\lambda } +\frac{1}{2}g_{\mu \nu }\mathrm{e}^{-2\Phi }F^2,\nonumber \\ \end{aligned}$$

(4)

and they were solved by Gibbons and Maeda [62], and independently by Garfinkle et al. [63], and thus this is known as the Gibbons–Maeda–Garfinkle–Horowitz–Strominger (GMGHS) black hole, whose metric in the Einstein frame is given by [56, 57]

$$\begin{aligned} \mathrm{d}s^2=- \mathcal {F}(r) \mathrm{d}t^2+\frac{\mathrm{d}r^2}{ \mathcal {F}(r)}+\mathcal {R}^2(r)\, (\mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2). \end{aligned}$$

(5)

Here the coordinates are defined in the ranges $0<r<\infty$, $-\infty <t<\infty$, $0\le \theta <\pi$, $0\le \phi <2\pi$, and the radial function $\mathcal {R}(r)$ is given by

$$\begin{aligned} \mathcal {R}(r)= \sqrt{r(r-\alpha )}, \qquad \alpha \equiv \frac{Q^2}{M}, \end{aligned}$$

(6)

where M is the ADM mass, Q is the electric charge, and $\mathcal {F}(r)$ is the well-known lapse function of the Schwarzschild black hole,

$$\begin{aligned} \mathcal {F}(r)=1-\frac{2M}{r}= 1-\frac{r_+}{r}, \qquad r_+=2M. \end{aligned}$$

(7)

Since the coordinates ($t, \phi$) are cyclic in the metric (5), there are two conserved quantities related to two Killing vectors fields:

• the time-like Killing vector $\xi _t= (1, 0, 0, 0)$ is related to the stationarity of the metric: $g_{\alpha \beta }\,\xi _{t}^{\alpha }\,u^{\beta } =-\mathcal {F}(r)\,\dot{t}=-\sqrt{E}$ is a constant of motion which can be associated with the total energy of the test particles, because this spacetime is asymptotically flat, and

• the space-like Killing vector $\xi _\phi = (0, 0, 0, 1)$ is related to the axial symmetry of the metric: $g_{\alpha \beta }\,\xi _{\phi }^{\alpha }\,u^{\beta } =\mathcal {R}^{2}(r)\,\sin ^2 \theta \,\dot{\phi }=L$ is a constant of motion corresponding to the angular momentum of the particles moving in this geometry.

With all this, in the next section the basic equations governing the motion of charged particles in the spacetime generated by the GMGHS black hole are obtained by using the Hamilton–Jacobi formalism.

3 Motion of charged particles

Let us consider the motion of test particles which possess mass m and electric charge $\tilde{q}$. The Hamilton–Jacobi equation for the geometry described by the metric $g_{\mu \nu }$ is given by

$$\begin{aligned} {1\over 2}g^{\mu \nu }\left( \frac{\partial S}{\partial x^{\mu }}+\tilde{q}\, A_{\mu }\right) \left( \frac{\partial S}{\partial x^{\nu }}+\tilde{q}\, A_{\nu }\right) +\frac{\partial S}{\partial \tau }=0, \end{aligned}$$

(8)

where S corresponds to the characteristic Hamilton function and $A_{\mu }$ represents the vector potential components associated with the electrodynamic properties of the black hole. Since we are considering charged static black holes, the only non-vanishing component of the vector potential is the temporal component, $A_{t}=Q/r$. Also, the conservation of the angular motion implies that the motion is developed on an invariant plane, which we choose to be $\theta =\pi /2$, so Eq. (8) reads

$$\begin{aligned} -\frac{1}{\mathcal {F}}\left( \frac{\partial S}{\partial t}+\frac{\tilde{q} }{r}\sqrt{{\alpha r_+ \over 2}}\right) ^{2}+\mathcal {F}\left( \frac{\partial S}{\partial r}\right) ^{2}+\frac{1}{\mathcal {R}^{2}}\left( \frac{\partial S}{\partial \phi }\right) ^{2}+2\frac{\partial S}{\partial \tau }=0. \end{aligned}$$

(9)

Aiming to solve this last equation, we introduce the ansatz [51, 64]

$$\begin{aligned} S=-E t+S_{0}(r)+L \phi +{1\over 2}m^{2}\tau , \end{aligned}$$

(10)

together with the re-definition of the test charge $q=\tilde{q}\sqrt{\frac{\alpha \, r_+}{2}}$, resulting in

$$\begin{aligned} -\frac{1}{\mathcal {F}}\left( -E+\frac{q}{r}\right) ^{2}+ \mathcal {F}\left( \frac{\mathrm{d} S_0(r)}{\mathrm{d} r}\right) ^{2}+ \frac{L^2}{\mathcal {R}^{2}}+m^2=0. \end{aligned}$$

(11)

Therefore, we find that

$$\begin{aligned} S_{0}(r)= \pm \int \frac{\mathrm{d}r}{\mathcal {F}} \sqrt{(E-V_-)\,(E-V_+)}, \end{aligned}$$

(12)

where the radial functions are given by

$$\begin{aligned} V_{\pm }(r)=V_q(r)\pm \sqrt{\mathcal {F} \left( m^{2}+ \frac{L^{2}}{\mathcal {R}^{2}}\right) }, \qquad V_q(r)\equiv \frac{q}{r}. \end{aligned}$$

(13)

Notice that each branch converges to the value $E_+=q/r_+$ at $r=r_+$, which can be either positive or negative, depending on the sign of the electric charge. In Fig. 1 we show the $q>0$ case in which the $V_-$ branch always is negative (except in the region $r_+<r<r_q$, where $r_q$ is solution to the equation $V_-(r_q)=0$). From now on we will call the positive branch $V_\mathrm{eff}=V_{+}\equiv V$ the effective potential.

Employing the Hamilton–Jacobi method, it is possible to obtain three velocities taking into account the motion of test particles. So, taking ${\partial S \over \partial m^2}=0$, ${\partial S \over \partial E}=0$, and ${\partial S \over \partial L}=0$, we obtain

$$\begin{aligned} u(r)\equiv \frac{\mathrm{d}r}{\mathrm{d}\tau }=\pm \sqrt{(E-V_-)\,(E-V)}, \end{aligned}$$

(14)

$$\begin{aligned} v_{t}(r)\equiv \frac{\mathrm{d}r}{\mathrm{d}t}=\pm \frac{\mathcal {F}(r)\,u(r)}{E-V_{q}\left( r\right) }, \end{aligned}$$

(15)

and

$$\begin{aligned} v_{\phi }(r)=\frac{\mathrm{d}r}{\mathrm{d}\phi }=\pm \frac{\mathcal {R}^{2}(r)\, u(r)}{L}, \end{aligned}$$

(16)

respectively. Notice that the zeros in Eq. (14), and therefore of Eqs. (15) and (16), correspond to the so-called turning point, $r_t$. Furthermore, these equations lead to the quadratures that determine the evolution of the electrically charged test particles, so the next sections are devoted to obtaining their analytical solutions.

Fig. 1

Plot of the effective potential V(r) for positive charged particles ($q>0$) in radial motion together with the negative branch $V_-(r)$, which is positive in the range $r_+<r<r_q$. Also, at the event horizon $r_+$, each branch converges to $E_+=q/r_+$

4 Radial trajectories

The radial motion of charged particles is characterized by the condition $L=0$, in which case the effective potential becomes

$$\begin{aligned} V(r)=V_{q}(r)+m\sqrt{\mathcal {F}(r)}. \end{aligned}$$

(17)

In Fig. 2 the effective potential (17) for three different values of the electric charge is shown. A first observation of this graph is that effective potential presents two well-defined behaviors in the region $r_+<r<\infty$:

Fig. 2

Typical graphs of the effective potential as a function of the radial coordinate. Here, we show the curves in terms of the electric ratio $q_{*}=q_c/q$, where $q_c=mr_+/2$. Notice that if $|q_{*}|<1$ and $m<E<E_u$ a frontal scattering is permitted. For $|q_{*}|\ge 1$, the motion is essentially the same as in the Schwarzschild case

The classic domain is characterized by the absence of a maximum, so that particles with $E<m$ inexorably fall to the event horizon, whereas if $E>m$, particles can escape (fall) into the spatial infinity (event horizon). Essentially, the neutral particles exhibit this same behavior in this spacetime, which, as has been pointed out in [57], corresponds to the typical motion in the background of a Schwarzschild black hole. In Fig. 2, the two lower curves correspond to this domain.

The electric domain allows a maximum equal to $E_u=E_{+}\,(1+q_{*}^{2})$, where $q_{*}=q_c/q$ is the electric ratio and $q_{c}=m\,r_+/ 2$. Therefore, particles with $m<E<E_u$ feel a radial repulsion and cannot fall into the event horizon. Furthermore, as in the previous case, if $E>E_u$, particles can escape (fall) into the spatial infinity (event horizon). This domain is represented by the upper curve in Fig. 2.

The extreme of the effective potential is located at

$$\begin{aligned} \rho _{u}={r_+\over 1-q_{*}^{2}}, \end{aligned}$$

(18)

so we can conclude that if $| q_{*} |<1$, then the position of the maximum is in the region $[r_+, \infty ]$, while if $|q_{*} |>1$, then the location of the maximum is in the region $[-\infty , 0]$; finally, if $q_{*}=1$, then the potential has no maximum.

Ultimately, in order to simplify the calculations, it is instructive to rewrite the square of the proper velocity (14) in the generic form

$$\begin{aligned} u^2(r)= & {} (E-V)(E-V_-)\nonumber \\= & {} \left( \frac{m^2-E^2}{r^2}\right) \left[ \frac{q^2}{m^2-E^2} +\frac{2 q (m\,q_{*}-E)}{m^2-E^2}r-r^2\right] \nonumber \\\equiv & {} \left( \frac{m^2-E^2}{r^2}\right) \,p_2(r), \end{aligned}$$

(19)

and, thus, an exhaustive study of the radial motion can be carried out taking into account the values of the fundamental parameters.

4.1 The classic domain

As we have said, basically this domain is analogous to the Schwarzschild counterpart [7]. It is important to note that the electric interaction is weak with respect to gravitational effects, so charged particles behave like neutral particles as we have seen pointed out in Ref. [57].

4.1.1 Bounded trajectories: $|q_{*}|> 1$ and $E_{+}<E<m$

In this case, as shown in Fig. 3, we write the polynomial as $p_2(r)=(r_0-r)(r-\mathrm{d}_0)$, where

$$\begin{aligned} r_0= {1\over 2}\left( b+\sqrt{b^2+4a}\right) ,\quad d_0= {1 \over 2}\left( b-\sqrt{b^2+4a}\right) , \end{aligned}$$

(20)

and

$$\begin{aligned} a= \frac{q^2}{m^2-E^2},\quad b=2 q\left( \frac{m\,q_{*}-E}{m^2-E^2}\right) . \end{aligned}$$

(21)

Inserting this polynomial into Eq. (19), and then integrating Eqs. (14) and (15), we see that the proper time is given by

$$\begin{aligned} \tau (r)={ \sqrt{ p_2(r)}+ g(0)\,\left[ \arctan \left( {g(r)\over \sqrt{p_2(r)}} \right) - \frac{\pi }{2}\right] \over \sqrt{m^2-E^2}}, \end{aligned}$$

(22)

while the coordinate time becomes

$$\begin{aligned} t(r)=\left[ E+\frac{q}{g(0)}\left( \frac{E}{E_+}-1\right) \right] \,\tau (r)+\mathcal {T}(r), \end{aligned}$$

(23)

where

$$\begin{aligned} \mathcal {T}(r)= & {} a \left( \frac{E}{E_+}-1\right) \Bigg [\frac{r_+}{\sqrt{p_2(r_+)}}\log \left( \frac{ (r-r_+)\,g(r_0)}{r_+\,r +r_0\,\mathrm{d}_0-(r+r_+)\,g(0)}\right) \nonumber \\&.-\frac{\sqrt{p_2(r)}}{g(0)} \Bigg ], \end{aligned}$$

(24)

where $g(r)=\frac{1}{2}[ (r_0-r)-(r-\mathrm{d}_0)]$, and we must choose $\tau (r_0)=t(r_0)=0$. In the top panel of Fig. 4 the functions (22) and (23) are plotted together, demonstrating that radial charged particles present the same behavior as radial neutral particles in this spacetime [57].

Fig. 3

Plot of the effective potential for radial charged particles in the classic domain. Bounded trajectories: particles with electric ratio $|q_{*}|> 1$ and energy $E_+<E< m$ cannot escape to spatial infinity, so the distance $r_0$ corresponds to a turning point. Unbounded trajectories: particles with electric ratio $|q_{*}|= 1$ and energy $m<E< E_{\infty }$ arrive at spatial infinity with non-vanished kinetic energy $K\ge 0$. For simplicity, because the motion is essentially the same for all $E \in \{m, E_{\infty }\}$, here we solve the case $E=m$ and the starting point $r_0$ has been chosen in such way that $t(r_0)=\tau (r_0)=0$

Fig. 4

Temporal graphic for the fall of radial charged particles in the classic domain. Basically, the behavior is the same as in the standard spacetimes of general relativity [7]. Top panel bounded trajectory with $E_+<E<m$. Bottom panel unbounded trajectory with $E=m$. For convenience, in both graphics we have used the same starting point, $r_0$

4.1.2 Unbounded trajectories: $q_{*}=1$ and $E\ge m$

This case is characterized by the possibility that particles can arrive at spatial infinity with non-null kinetic energy, $K\ge 0$, where the equality is satisfied when $E=m$; see Fig. 3. Thus, for simplicity, we solve the latter case so the proper and coordinate velocities become

$$\begin{aligned} u(r)\equiv u_c(r)=\pm \frac{q_c}{r} \end{aligned}$$

(25)

and

$$\begin{aligned} v_t(r)=\pm \frac{(1-\frac{2}{m}u_c)\,u_c}{m-u_c}. \end{aligned}$$

(26)

For simplicity, let us choose $r_0$ as the starting distance, where $\tau (r_0)=t(r_0)=0$; therefore, Eqs. (25) and (26) become

$$\begin{aligned} \tau (r)=\pm {r^2-r_{0}^{2}\over 2 \,q_c} \end{aligned}$$

(27)

and

$$\begin{aligned} t(r)=m\tau (r)\pm (r-r_{0})\pm r_+\ln \left( {r-r_{+}\over r_{0}-r_{+}}\right) , \end{aligned}$$

(28)

respectively. Therefore, as we have mentioned before, the motion of charged particles is the same as the motion in Einstein’s spacetimes; see the bottom panel of Fig. 4.

4.2 The electric domain

4.2.1 Frontal Rutherford scattering: $|q_{*}|< 1$ and $m<E<E_u$

As we have said, the GMGHS spacetime allows Rutherford-like scattering of radial charged particles. Thus, if the energy of the particle E is such that $m<E<E_u$, then there are two turning points, one on each side of $\rho _u$. Thus, the turning point $\rho _d>\rho _u$ corresponds to a radial distance of closest approach at the trajectory, whereas $\rho _a<\rho _u$ is the farthest distance for this interval; see Fig. 2. Explicitly, these distances are given by

$$\begin{aligned} \rho _d= \frac{q\left( E-m\,q_{*}\right) }{E^{2}-m^2} \left( 1+\sqrt{1-\frac{E^{2}-m^2 }{\left( E-m\,q_{*}\right) ^2}}\right) \end{aligned}$$

(29)

and

$$\begin{aligned} \rho _a= \frac{q\left( E-m\,q_{*}\right) }{E^{2}-m^2} \left( 1-\sqrt{1-\frac{E^{2}-m^2 }{\left( E-m\,q_{*}\right) ^2}}\right) . \end{aligned}$$

(30)

Therefore, Eq. (19) can be rewritten as

$$\begin{aligned} u^2(r)=\frac{E^2-m^2}{r^2}\,h_2(r), \end{aligned}$$

(31)

where the polynomial is given by $h_2(r)=|r-\rho _d|\,|r-\rho _a|$. Assuming that $t=\tau =0$ at the turning point, and defining the radial function $f(r)=\frac{1}{2}\left[ (r-\rho _d)+(r-\rho _a) \right]$, we found that in the proper system

$$\begin{aligned} \tau (r)=\frac{\sqrt{h_2(r)} +f(0) \,\log \left( \frac{\sqrt{h_2(r)} +f(r)}{\frac{1}{2}(\rho _d-\rho _a)}\right) }{ \sqrt{E^{2}-m^2}}, \end{aligned}$$

(32)

while an external observer will measure

$$\begin{aligned} t(r)=\left[ E+\left( \frac{E}{E_+}-1\right) \right] \,\tau (r)+\bar{\mathcal {T}}(r), \end{aligned}$$

(33)

where

$$\begin{aligned} \bar{\mathcal {T}}(r)= & {} a \left( \frac{E}{E_+}-1\right) \bigg [\frac{r_+}{\sqrt{h_2(r_+)}}\log \left( \frac{ (r-r_+)\,f(\rho _d)}{r_+\,r +\rho _d\,\rho _a-(r+r_+)\,f(0)}\right) \nonumber \\&-\frac{\sqrt{h_2(r)}}{f(0)}\bigg ], \end{aligned}$$

(34)

for $\rho _d<r<\infty$. In Fig. 5 the proper and external temporal behaviors are represented.

Fig. 5

Temporal behavior for charged particles in the frontal Rutherford scattering. Here $\rho _d$ represents the distance of closest approach

4.2.2 Critical radial motion: $|q_{*}|<1$ and $E=E_u$

Particles with energy $E_u$ satisfying the condition $E_u=V(\rho _u)$, where $\rho _u$ is the location of the maximum of the effective potential, see Fig. 6, can arrive at $\rho _u$ either from a distance $\rho _i^{I}<\rho _u$ (region I) or $\rho _i^{II}>\rho _u$ (region II), depending on its initial velocity. Eventually, if the initial conditions are reversed, charged particles can also arrive at the spatial infinity or the event horizon. Under these assumptions, and then integrating the equations of motion, we obtain for the proper time

$$\begin{aligned} \tau _I (r)=\pm {1\over \sqrt{E^{2}_{u}-m^2}} \left[ \rho _u \ln \,A_I(r)-(r-\rho _i^I)\right] \end{aligned}$$

(35)

and

$$\begin{aligned} \tau _{II} (r)=\pm {1\over \sqrt{E^{2}_{u}-m^2}} \left[ (r-\rho _i^{II})- \rho _u \ln \,A_{II}(r)\right] , \end{aligned}$$

(36)

while the coordinate time result to be

$$\begin{aligned} t_I(r)=E_u\, \tau _I\pm \frac{q}{ \sqrt{E^{2}_{u}-m^2}} \left( \frac{E_u}{E_+}-1\right) \,\ln \frac{A_I^{1+\beta }(r)}{B_I^{\beta }(r)} \end{aligned}$$

(37)

and

$$\begin{aligned} t_{II}(r)=E_u\tau _{II}(r)\mp \frac{q}{ \sqrt{E^{2}_{u}-m^2}} \left( \frac{E_u}{E_+}-1\right) \,\ln \frac{A_{II}^{1+\beta }(r)}{B_{II}^{\beta }(r)} \end{aligned}$$

(38)

where we have made $\beta =r_+/(\rho _u-r_+)$, and

$$\begin{aligned} A_I(r)= & {} \frac{\rho _u-\rho _i^I }{\rho _u-r},\quad B_I(r)=\frac{\rho _i^I-r_+}{r-r_+},\end{aligned}$$

(39)

$$\begin{aligned} A_{II}(r)= & {} \frac{\rho _i^{II}-\rho _u }{r-\rho _u},\quad B_{II}(r)=\frac{\rho _i^{II}-r_+}{r-r_+}. \end{aligned}$$

(40)

In Fig. 7 the analytical solutions (35), (36), (37), and (38) are depicted. Clearly, an external observer will see the particles going to $\rho _u$ and spatial infinity faster than in the proper system, while the motion on the horizon possesses the same nature as Einstein’s spacetimes, i.e., with respect to an observer stationed at infinity, the trajectory will take an infinite time to reach the horizon even though by its own proper time it will cross the horizon in a finite time [7].

Fig. 6

Plot of the effective potential for radial charged particles in the electric domain. Frontal Rutherford scattering is allowed when $E_+<E<E_u$ and $r>\rho _d$, while critical radial motion occurs when $E=E_u$

Fig. 7

Temporal behavior for charged particles in critical radial motion, where its energy is $E_u=V(\rho _u)$ and the starting point can be placed at left, $\rho _i^I$ or right of the unstable equilibrium point. Note that in both frames (proper and coordinate) particles arrive asymptotically to $\rho _u$

5 Motion with angular momentum

Particles with angular motion are characterized by $L > 0$. Explicitly, the effective potential (13) can be written as

$$\begin{aligned} V(r)={q\over r}+ \sqrt{\left( 1-{r_+\over r}\right) \left( m^2+{L^2\over r(r-\alpha )}\right) }, \end{aligned}$$

(41)

which is shown in Fig. 8 for two pairs of values of the electric charge q and angular momentum L of the test particle.

Fig. 8

Effective potential for charged particles with non-vanished angular momentum. This plot contains curves for two pairs of values of the electric charge q and angular momentum L of the test particle. The upper curve corresponds to the typical case of dispersion in which the trajectory approaches from infinity, reaches the turning point $r_d$, and then recedes to infinity again

5.1 Gravitational Rutherford scattering

Since the particle interacts with the background via the presence of the term $\alpha$, the straight path is modified in such way that a new trajectory is formed. As Fig. 8 illustrates, particles with $E>m$ are deflected by reaching the distance of closest approach, denoted by $r_d$. Obviously, without the $\alpha$ term the geometry becomes the Schwarzschild one, and its counterpart does not exist (we put the interaction “off”). Moreover, a similar effect can occur when the ratio L / M increases, i.e., tending to the Newtonian regime (see pp. 102 of Chandrasekhar’s book [7]).

In order to obtain the mentioned trajectory, let us rewrite Eq. (16) as

$$\begin{aligned} \phi = {L\over \sqrt{E^2-m^2}} \int _{r_d}^{r} { \,\mathrm{d}r\over \sqrt{(r-\alpha )P(r)}}. \end{aligned}$$

(42)

Here the characteristic polynomial P(r) is given by

$$\begin{aligned} P(r)=r^3- \left( r_{\sigma }+\alpha \right) r^2 -\left( r_L^2 -\alpha \,r_{\sigma } \right) r +R_L\,r_L^2, \end{aligned}$$

(43)

where

$$\begin{aligned} r_{\sigma }={ 2qE-m^2r_+\over E^2-m^2}, R_L=\left( { L^2r_+-\alpha q^2\over L^2-q^2} \right) , r_L=\sqrt{{L^2-q^2\over E^2-m^2}}. \end{aligned}$$

(44)

The condition $P(r)=0$ allows for three real roots, which can be written as

$$\begin{aligned} r_{d}(E)= & {} r_{\alpha }+R \cos \zeta ,\end{aligned}$$

(45)

$$\begin{aligned} r_{A}(E)= & {} r_{\alpha }-\frac{R}{2}(\cos \zeta -\sqrt{3}\sin \zeta ),\end{aligned}$$

(46)

$$\begin{aligned} r_{3}(E)= & {} r_{\alpha }-\frac{R}{2}(\cos \zeta +\sqrt{3}\sin \zeta ), \end{aligned}$$

(47)

where

$$\begin{aligned} r_{\alpha }=\frac{r_{\sigma }+\alpha }{3},\quad R=\sqrt{\frac{\eta _2}{3}},\quad \zeta =\frac{1}{3}\arccos \frac{\eta _3}{R^3}, \end{aligned}$$

(48)

and

$$\begin{aligned} \eta _2= & {} 4\left[ {\left( r_{\sigma }+\alpha \right) ^2 \over 3}+ \left( r_L^2 -\alpha \,r_{\sigma }\right) \right] ,\end{aligned}$$

(49)

$$\begin{aligned} \eta _3= & {} 4\left[ {2 \left( r_{\sigma }+\alpha \right) ^3 \over 27}+ {\left( r_{\sigma }+\alpha \right) \left( r_L^2 -\alpha \,r_{\sigma }\right) \over 3} -R_L\,r_L^2\right] .\nonumber \\ \end{aligned}$$

(50)

Therefore, we can identify the closest approach distance $r_{d}$, and the farthest distance $r_A$ (the third solution $r_3$ is without importance here). Replacing $P(r)=(r-r_d)(r-r_A)(r-r_3)$ in Eq. (42) and performing an integration it is possible to find that

$$\begin{aligned} \kappa \,\phi =\wp ^{-1}\left[ \frac{1}{4}\left( \frac{1}{r-r_d}+\frac{a_1}{3}\right) ; g_2, g_3\right] , \end{aligned}$$

(51)

where $\kappa =2\sqrt{E^2-m^2}/L$ and $\wp ^{-1}(x; g_2, g_3)$ is the inverse $\wp$-Weierstraß elliptic function with the Weierstraß invariant given by

$$\begin{aligned} g_2= & {} \frac{1}{4}\left( \frac{1}{3}a_1^2-a_2\right) , \end{aligned}$$

(52)

$$\begin{aligned} g_3= & {} \frac{1}{16}\left( \frac{1}{3} a_1\,a_2- \frac{2}{27}a_1^3-a_3\right) , \end{aligned}$$

(53)

where $a_1=u_1+u_2+u_3$, $a_2=u_1 u_2+u_1 u_3+u_2 u_3$, $a_3=u_1 u_2 u_3$, with $u_1=(r_d-\alpha )^{-1}$, $u_2=(r_d-r_A)^{-1}$, and $u_3=(r_d-r_3)^{-1}$. Therefore, the inversion of Eq. (51) and a brief manipulation leads to the following expression for the polar trajectory:

$$\begin{aligned} r(\phi )= r_d+\frac{1}{4\wp (\kappa \,\phi ; g_{2},g_{3})-a_1 /3}, \end{aligned}$$

(54)

where $\wp (x; g_2, g_3)$ is the $\wp$-Weierstraß elliptic function. In Fig. 9 we plot the polar trajectory (54), in which we note that, depending on the set of parameters (E, L, q, $\alpha$) across Eqs. (44–50), the trajectory will be deflected as classic Rutherford scattering [65–71] or more specifically a repulsive or attractive scattering between a massive target (composed of a positive charged nuclei) and light projectiles ($\alpha$-particles or $\beta$-particles). Moreover, because our test particles have been chosen as positive, the attractive behavior is driven by the gravitational field over the electric repulsion. From the equation of the orbit (51) it is possible to obtain the angle of deflection $\Theta = 2\phi _{\infty }-\pi$ experienced by the test particles, which turns out to be

$$\begin{aligned} \Theta ={2\over \kappa }\wp ^{-1}\left( { a_1 \over 12}\right) -\pi . \end{aligned}$$

(55)

Therefore, particles with $E=E_1$ do not experience deflection in their trajectory, where $E_1$ is the solution to the transcendental equation $a_1=12\,\wp (\kappa \pi /2)$.

Fig. 9

Top panel gravitational Rutherford scattering. This plot contains curves for various value of the electric charge, q, and impact parameter, b, of the test particle. Clearly, depending on the value of b, the scattering can be either repulsive or attractive. Each circle corresponds to the closest approach distance for a given value of the impact parameter. Bottom panel angle of scattering against energy of the test particles. At $E=E_1$ the deflection angle is equal to zero, so the initial and final direction are the same

Also, a repulsive scattering is performed if $m<E<E_1$, whereas an attractive scattering is carried out if $E_1<E<E_U$. For the scattering problem, the dependence of the differential cross-section on $\Theta \ne 0$ is given by

$$\begin{aligned} {\mathrm{d}\,\sigma \over \mathrm{d}\Omega }\equiv \sigma [\Theta ]={b\over \sin \Theta }\left| {\mathrm{d}\,b\over \mathrm{d}\,\Theta }\right| , \end{aligned}$$

(56)

where b is the impact parameter. Now, we can substitute the constants E and L by the value at spatial infinity [38]:

$$\begin{aligned} E={m \over \sqrt{1-v^2}},\qquad L={m\,v\,b \over \sqrt{1-v^2}}=b\,\sqrt{E^2-m^2} \end{aligned}$$

(57)

where v is the velocity of the test particle at spatial infinity. Because $b=b(E)$, we have $a_1=a_1(b)$ and Eq. (56) is written as

$$\begin{aligned} \sigma [\Theta ]={b\over \sin \Theta }\left| {\mathrm{d}\,a_1\over \mathrm{d}\,\Theta }\right| \left| {\mathrm{d}\,b\over \mathrm{d}\,a_1}\right| . \end{aligned}$$

(58)

Finally, the differential cross-section for the scattering of charged particles by the background of a charged black hole in heterotic string theory is given by

$$\begin{aligned} \sigma [\Theta ]=12\, \csc \Theta \left| \wp ^{\,\prime }\left( {\pi +\Theta \over b}\right) \right| \left| {\mathrm{d}\,b\over \mathrm{d}\,a_1}\right| , \end{aligned}$$

(59)

where $\wp ^{\,\prime }(x)\equiv \wp ^{\,\prime }(x, g_2, g_3)$ represents a derivative of the $\wp$-Weierstraß function with respect to $\Theta$. Note that this last expression represents the exact formula for the scattering problem. Nevertheless, due to the complexity of the relation between the impact parameter b and the quantity $a_1$, the term $\left| {\mathrm{d}\,b\over \mathrm{d}\,a_1}\right|$ is calculated numerically.

5.2 Keplerian orbits

As we have established, the effective potential (41) allows motion between an apastron distance $r_a$ and periastron distance $r_p$, as we show in Fig. 9. Therefore, considering that $E<m$, it is possible to rewrite Eq. (16) as

$$\begin{aligned} \phi = {L\over \sqrt{m^2-E^2}} \int _{r_a}^{r} { \,\mathrm{d}r\over \sqrt{(r-\alpha )\bar{P}(r)}}, \end{aligned}$$

(60)

where the characteristic polynomial $\bar{P}(r)$ is now given by

$$\begin{aligned} \bar{P}(r)=-r^3+ \left( -\bar{r}_{\sigma }+\alpha \right) r^2 -\left( \bar{r}_L^2 -\alpha \,\bar{r}_{\sigma } \right) r +R_L\,\bar{r}_L^2 \end{aligned}$$

(61)

and

$$\begin{aligned} \bar{r}_{\sigma }={ 2qE-m^2r_+\over m^2-E^2}, R_L=\left( { L^2r_+-\alpha q^2\over L^2-q^2} \right) , \bar{r}_L=\sqrt{{L^2-q^2\over m^2-E^2}}. \end{aligned}$$

(62)

The condition $\bar{P}=0$ allows us to get the three roots which are given by

$$\begin{aligned} r_{p}(E)= & {} -\bar{r}_{\alpha }+\bar{R}\sin \bar{\zeta },\end{aligned}$$

(63)

$$\begin{aligned} r_{a}(E)= & {} -\bar{r}_{\alpha }+\frac{\bar{R}}{2}\left( \sqrt{3}\cos \bar{\zeta }- \sin \bar{\zeta }\right) ,\end{aligned}$$

(64)

$$\begin{aligned} r_{f}(E)= & {} -\bar{r}_{\alpha }-\frac{\bar{R}}{2}\left( \sqrt{3}\cos \bar{\zeta }+ \sin \bar{\zeta }\right) \end{aligned}$$

(65)

where

$$\begin{aligned} \bar{r}_{\alpha }=\frac{\bar{r}_{\sigma }-\alpha }{3},\quad \bar{R}=\sqrt{\frac{\bar{\eta }_2}{3}},\quad \bar{\zeta }=\frac{1}{3}\arcsin \frac{\bar{\eta }_3}{ \bar{R}^3}, \end{aligned}$$

(66)

and

$$\begin{aligned} \bar{\eta }_2= & {} 4\left[ {\left( \bar{r}_{\sigma }-\alpha \right) ^2 \over 3}- \left( \bar{r}_L^2 -\alpha \,\bar{r}_{\sigma }\right) \right] , \end{aligned}$$

(67)

$$\begin{aligned} \bar{\eta }_3= & {} 4\left[ {2 \left( \bar{r}_{\sigma }-\alpha \right) ^3 \over 27}- {\left( \bar{r}_{\sigma }-\alpha \right) \left( \bar{r}_L^2 -\alpha \,\bar{r}_{\sigma }\right) \over 3} -R_L\,\bar{r}_L^2\right] .\nonumber \\ \end{aligned}$$

(68)

Defining $\kappa _\mathrm{kep} =2\sqrt{m^2-E^2}/L$ and then integrating Eq. (60) we get

$$\begin{aligned} \kappa _\mathrm{kep}\phi =\wp ^{-1}\left[ \frac{1}{4}\left( \frac{1}{r_a-r}-\frac{\bar{a}_1}{3}\right) ; \bar{g}_2, \bar{g}_3 \right] , \end{aligned}$$

(69)

where the Weierstraß invariants are given by

$$\begin{aligned} \bar{g}_2= & {} \frac{1}{4}\left( \frac{1}{3}\bar{a}_1^2-\bar{a}_2\right) ,\end{aligned}$$

(70)

$$\begin{aligned} \bar{g}_3= & {} \frac{1}{16}\left( \frac{1}{3} \bar{a}_1\,\bar{a}_2- \frac{2}{27}\bar{a}_1^3-\bar{a}_3\right) , \end{aligned}$$

(71)

where $\bar{a}_1=\bar{u}_1+\bar{u}_2+\bar{u}_3$, $\bar{a}_2=\bar{u}_1 \bar{u}_2+\bar{u}_1 \bar{u}_3+\bar{u}_2 \bar{u}_3$, $\bar{a}_3=\bar{u}_1 \bar{u}_2 \bar{u}_3$, and $\bar{u}_1=(r_a-\alpha )^{-1}$, $\bar{u}_2=(r_a-r_p)^{-1}$, $\bar{u}_3=(r_a-r_f)^{-1}$. Therefore, the polar trajectory can be found inverting Eq. (69), which as a result turns out to be

$$\begin{aligned} r(\phi )= r_a-\frac{1}{4\wp (\kappa _\mathrm{kep} \,\phi ; \bar{g}_{2}, \bar{g}_{3})+\bar{a}_1 /3}. \end{aligned}$$

(72)

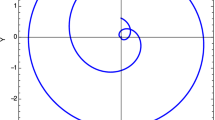
In Fig. 10 we depict the Keplerian orbit in which the precession angle, $\Xi =2\phi _p-2\pi$, is given by

$$\begin{aligned} \Xi =\frac{2}{\kappa _\mathrm{kep}}\,\wp ^{-1}\left[ \frac{1}{4}\left( \frac{1}{r_a-r_p}-\frac{\bar{a}_1}{3}\right) , \bar{g}_2, \bar{g}_3\right] -2\pi . \end{aligned}$$

(73)

Fig. 10

Polar plot for Keplerian orbit performed by charged particles in which the precession angle is given by Eq. (73)

6 Final remarks

In this paper, we have examined the motion of charged particles in the background metric and the fields of a GMGHS black hole. The equations of motion were established and solved exactly following the usual Hamilton–Jacobi method. Thus, the radial motion of the test bodies was studied in terms of its energy E and the specific charge $q_{*}$, allowing two regimens: the classic domain is similar to the radial motion studied in the Schwarzschild spacetimes, thereby allowing bounded trajectories ($|q_{*}|>1$ and $E_+<E<m$) and unbounded trajectories ($|q_{*}|\le 1$ and $E\ge m$); and the electric domain, in which case frontal repulsive Rutherford scattering is permitted ($|q_{*}|<1$ and $m<E<E_u$) together with a critical motion in which a particle falls asymptotically into $\rho _u$ ($|q_{*}|<1$ and $E=E_u$). On the other hand, the motion with non-vanishing angular momentum was studied in detail in two general schemes: the dispersive case $E>m$ and the Keplerian case $E<m$. In the first case, we employed the classic tools to describe the Rutherford scattering between two electric charges (with the same sign of the charge), showing that null dispersion and attractive scattering are possible because the electric dispersion is compensated for by the gravitational effects. Finally, for the second case, we have calculated the apastron and periastron distance of the Keplerian orbit, which is expressed in terms of the elliptic $\wp$-Weierstraß function, whose periastron advance with a precession angle $\Xi$ is given by Eq. (73).