1 Introduction

The spherically symmetric Reissner–Nordström metric [1] is given by

$$\begin{aligned} \mathrm{d}s^2=g_{\mu \nu } \otimes \mathrm{d}x^{\mu } \otimes \mathrm{d}x^{\nu },\quad (\mu ,\nu =0,1,2,3), \end{aligned}$$
(1)

with \(g_{\mu \nu }= \text {diag} (-f(r),f(r)^{-1},r^2,r^2\sin ^2 \theta )\) and

$$\begin{aligned} f(r)=1-\frac{2m}{r}+\frac{q^2}{r^2}, \end{aligned}$$

where m and q, respectively, denote the mass and charge. The solution represents a black hole shielding a singularity, the black hole is being formed as an end state of the collapse of a star. That the gravitational collapse of a sufficiently massive star (\(\sim \)3.5\(M_{\odot }\)) inevitably leads to a spacetime singularity is a fact established by an elegant theorem due to Hawking and Penrose [2] (see also Hawking and Ellis [3]).

However, it is widely believed that these singularities do not exist in Nature, but that they are the creation or an artifact of classical general relativity. The existence of a singularity, by its very definition, means spacetime fails to exist, signaling a breakdown of the laws of physics. Thus, in order for these laws to exist, singularities must be substituted by some other objects in a more suitable theory. The extreme condition, in any form, that may exist at the singularity implies that one should rely on quantum gravity, expanded to resolve this singularity [4]. While we do not yet have any definite quantum gravity allowing us to understand the inside of the black hole and resolve it separately, we must turn our attention to regular models, which are motivated by quantum arguments. The earliest idea, in mid-1960s, due to Sakharov [5] and Gliner [6], suggests that singularities could be avoided by matter, i.e., with a de Sitter core, with the equation of state \(p=-\rho \). This equation of state is obeyed by the cosmological vacuum and hence, \(T_{\mu \nu }\) takes on a false vacuum of the form \(T_{\mu \nu }=\Lambda g_{\mu \nu }\); \(\Lambda \) is the cosmological constant.

Thus spacetime filled with a vacuum could provide a proper discrimination at the final stage of gravitational collapse, replacing the future singularity [6]. The first regular black hole solution, based on this idea, was proposed by Bardeen [7], according to whom there are horizons but there is no singularity. The matter field is a kind of magnetic field. The solution yields a modification of the Reisnner–Nordström black hole solution, with the metric function f(r) being

$$\begin{aligned} f(r)= & {} 1-\frac{2mr^2}{(r^2+g^2)^{3/2}}\\= & {} 1-\left( \frac{m}{g}\right) \frac{2(r/g)^2}{(1+(r/g)^2)^{3/2}},\quad \text {and}\quad r\ge 0. \end{aligned}$$

Numerical analysis of \(f(r)=0\) reveals a critical value \(\chi ^{*}\) such that f(r) has a double root if \(\chi =\chi ^{*}\), two roots if \(\chi <\chi ^{*}\) and no root if \(\chi >\chi ^{*}\), with \(\chi =m/g\). These cases illustrate, respectively, an extreme black hole with degenerate horizons, a black hole with Cauchy and event horizons, and no black hole.

The Bardeen solution is regular everywhere, which can be realized from the scalar invariants

$$\begin{aligned} R_{ab}R^{ab}= & {} \frac{6mg^2(4g^2-r^2)}{(r^2+g^2)^{7/2}},\nonumber \\ R_{abcd}R^{abcd}= & {} \frac{12m^2}{(r^2+g^2)^7}[8g^8-4g^6r^2+47g^4r^4\nonumber \\&-12g^2r^6+48r^8], \end{aligned}$$
(2)

which are well behaved everywhere including at \(r=0\). However, for the Reissner–Nordström case (\(g=0\)), they diverge at \(r=0\) indicating a scalar polynomial singularity [3]. The Bardeen black hole is asymptotically flat, and near the origin it behaves as de Sitter, since

$$\begin{aligned} f(r)\approx 1 - \frac{2m}{g}r^2,\quad r\approx 0^{+}, \end{aligned}$$

whereas for large r, it is according to Schwarzschild.

Thus the black hole interior does not result in a singularity but develops a de Sitter like region, eventually settling with a regular center, thus its maximal extension is the one of the Reissner–Nordström spacetime but with a regular center [8, 9]. There has been an enormous advance in the analysis and application of regular black holes [10–14], however, all subsequent regular black holes were based on the Bardeen idea. The detailed study of circular geodesics of photons of a non-rotating regular black hole can be found in [15]. The deflection of light rays and gravitational lensing in regular Bardeen spacetime was also studied [16]. The ghost images of Keplerian discs, generated by photons with low impact parameters for a regular Bardeen black hole was also discussed [16].

The no-hair theorem suggests that astrophysical black hole candidates are Kerr black holes, but there still lacks direct evidence and its actual nature has not yet been verified. This opens the arena for investigating the properties for black holes that differ from Kerr black holes. Lately, the rotating (spinning) counterpart of Bardeen’s black hole has been proposed, which can be written in Kerr-like form in Boyer–Lindquist coordinates [17]. The rotating Bardeen regular metric has been tested with a black hole candidate in Cygnus X-1 [18], and thereafter more rotating regular black holes were proposed [19–22]. Interestingly the 3\(\sigma \)-bound \(a_{*}>0.95\) [23] and \(a_{*}>0.983\) [24] for the Kerr black hole changes, respectively, to \(a_{*}>0.78\) and \(\mid \chi \mid <0.41\), and \(a_{*}>0.89\) and \(\mid \chi \mid <0.28\) for the rotating Bardeen regular black hole. Further, the measurement of the Kerr spin parameter of rotating Bardeen regular black holes from the shape of the shadow of a black holes was also explored [25]. The rotating Bardeen black holes accommodate the Kerr black holes in the special case when the deviation parameter, \(g =0\), may be regarded as a well-suited framework for exploring astrophysical black holes.

In this paper, we investigate the horizon structure and ergosphere of the rotating Bardeen regular black hole and explicitly show the effect of the Bardeen charge g. The paper is organized as follows. In Sect. 2, we review the rotating Bardeen regular black hole and analyze the horizon structure and ergosphere, with respect to the charge g. We analyze the equatorial equations of motion of the particles and the effective potential in Sect. 3. Section 4 is devoted to the collision of two equal masses particles against the background of a rotating Bardeen regular black hole, and numerically we calculate \(E_\mathrm{CM}\) in a near horizon particle collision, and finally we summarize our results and evoke some perspectives to end the paper in Sect. 5.

Fig. 1
figure 1

Plot showing the behavior of \(\Delta \) vs. r for fixed values of \(\zeta =2\), \(\lambda =3\), \(\theta =\pi /4\), and \(M=1\) by varying a. The case \(a=a_E\) corresponds to an extremal black hole

Full size image
Fig. 2
figure 2

Plot showing the behavior of \(\Delta \) vs. r for fixed values of \(\theta =\pi /2\) and \(M=1\). The case \(a=a_E\) corresponds to an extremal black hole

Full size image

2 Rotating Bardeen regular black hole

We do not have a definite quantum theory of gravity, hence an important direction of research is to consider regular rotating models to solve the singularity problem of the standard Kerr black hole. These are called non-Kerr black holes with different spin. Bambi [17], starting from a regular Bardeen metric, via the Newman–Janis algorithm [26] constructed a Kerr-like regular black hole solution, which in Boyer–Lindquist coordinates reads

$$\begin{aligned} \mathrm{d}{s}^2= & {} -\left( 1-\frac{2mr}{\Sigma }\right) \mathrm{d}t^2 -\frac{4amr \sin ^2 \theta }{\Sigma }\mathrm{d}t\mathrm{d}\phi +\frac{\Sigma }{\Delta }\mathrm{d}r^2 \nonumber \\&+ \Sigma \mathrm{d}\theta ^2 +\left( r^2+a^2+\frac{2a^2mr \sin ^2 \theta }{\Sigma }\right) \sin ^2 \theta \mathrm{d}\phi ^2,\nonumber \\ \end{aligned}$$
(3)

where

$$\begin{aligned} \Sigma =r^2 + a^2\cos ^2\theta ,\quad \Delta = r^2-2mr+a^2, \end{aligned}$$
(4)

and

$$\begin{aligned} m\rightarrow m_{\zeta , \lambda }(r,\theta ) = M\left( \frac{r^{2+\zeta } \Sigma ^{-\zeta /2}}{r^{2+\zeta } \Sigma ^{-\zeta /2}+g^2r^{\lambda } \Sigma ^{-\lambda /2}}\right) ^{3/2},\nonumber \\ \end{aligned}$$
(5)

where \(m=m_{\zeta , \lambda }(r,\theta )\) is a function of both r and \(\theta \); \(\zeta \), \(\lambda \) are two real numbers, and a is the rotation parameter. The parameter g is the magnetic charge of non-linear electrodynamics, which measures the deviation from the Kerr black hole, and when we switch off non-electrodynamics (\(g=0\)), one recovers the Kerr metric. It turns out that the curvature invariants are regular everywhere, when \(g\ne 0\), including at the origin [17]. For definiteness, throughout this paper we shall call the metric (3) a rotating Bardeen regular black hole metric.

Fig. 3
figure 3

Plot showing the behavior of the spin parameter (a) and the magnetic charge parameter (g) plane of the rotating Bardeen regular metric (contour plot of \(\Delta =0\)). The blue dashed line is the boundary which separates the black hole region from the no black hole region

Full size image
Table 1 The values of the horizons of a rotating Bardeen regular black hole with the parameters \(M=1\) and \(\theta =\pi /2\) (\(\delta _{h}^{g}=r^{+}_{H}-r^{-}_{H}\))
Full size table
Fig. 4
figure 4

Plot showing the variation of the infinite redshift surface with the parameters a, g, and \(\theta \)

Full size image
Fig. 5
figure 5

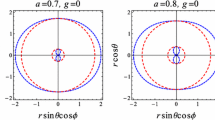
Plot showing the variation of the shape of ergosphere in xz-plane with parameter g, for different values of a, of the rotating Bardeen regular black hole. The blue and the red lines correspond, respectively, to static limit surfaces and horizons. The outer blue line corresponds to the static limit surface, whereas the two red lines correspond to the two horizons

Full size image
Fig. 6
figure 6

Plot showing the variation of the shape of ergosphere for \(a \approx a_E\) (extremal black hole) in xz-plane with parameter g, for different values of a, of the rotating Bardeen regular black hole

Full size image

The Boyer–Lindquist coordinates are most widely used by astrophysicists, as in these coordinates the rotating black hole has just one off-diagonal term. The rotating Bardeen metric, like the Kerr metric, in Boyer–Lindquist coordinates does not depend on \(t, \phi \), which means the Killing symmetries and the Killing vectors are given by \(\eta ^{\mu } = \delta _t^{\mu }\) and \(\xi ^{\mu } = \delta _{\phi }^{\mu }\), with \(\delta _{a}^{\mu }\) the Kronecker delta. The existence of the two Killing vectors \(\eta ^{\mu }\) and \(\xi ^{\mu }\) implies that the corresponding momenta of a test particle, \(p_t\) and \(p_{\phi }\), are constants of the motion.

2.1 Horizons and ergosphere

The metric (3) is singular at \(\Delta =0\), which corresponds to an event horizon of a black hole. The horizons of the rotating Bardeen regular black hole are solutions of

$$\begin{aligned} \left( \eta ^{\nu }\xi _{\mu }\right) ^2 - (\eta ^{\nu }\eta _{\nu }) (\xi ^{\mu }\xi _{\mu }) =0, \end{aligned}$$
(6)

which leads to

$$\begin{aligned}&(r^2+a^2)^2 (r^{2+\zeta } \Sigma ^{-\zeta /2}+g^2r^{\lambda }\Sigma ^{-\lambda /2})^3 \nonumber \\&\quad -4M^2r^{8+3\zeta } \Sigma ^{-3\zeta /2}=0. \end{aligned}$$
(7)

This depends on a, g, and \(\theta \), and it is different from the Kerr black hole where it is \(\theta \) independent. The numerical analysis of (7) suggests the possibility of two roots for a set of values of parameters which corresponds to two horizons of a rotating Bardeen regular black hole. The behavior of the event horizon is shown in Figs. 1, 2, and 3 for different values of a and g. Figure 3 implies that, for \(a<a_{E}\), there exists a set of values of the parameters for which one gets two horizons, and when \(a=a_{E}\) the two horizons coincide, i.e., we have an extremal black hole with degenerate horizons (cf. Table 1). An extremal black holes occurs when \(\Delta =0\) has a double root, i.e., when the two horizons coincide. When \(\Delta =0\) has no root, i.e., no horizon exists, which means there is no black hole (cf. Figs. 1 and 2). There exists an upper bound on the spin parameter, \(a^E{*} \le 0.998\), for astrophysical black holes, which is called Thorne’s bound [27]. In the equatorial plane (\(\theta =\pi /2\)), the mass function \( m_{\zeta , \lambda }(r,\theta ) \) does not depend on the parameters \(\zeta \) and \(\lambda \), and so we have the same for Eq. (7). This is also the case when both \(\zeta = \lambda =0.\) Thus, the two cases \(\theta =\pi /2\), and \(\zeta = \lambda =0\) (for any \(\theta \)) will have the same horizon structure. The non-trivial effect of the parameters \(\zeta \) and \(\lambda \) (\(\theta \ne \pi /2\)) on the horizon structure is shown in Fig. 1. Note that the horizon is called extremal when \(r= r^{E}_{H}\) is a double root of \(\Delta =0\) when \(a=a_{E}\). It is seen that, for \(\zeta =2\), \(\lambda =3\), \(\theta =\pi /4\), and \(g=0.2\), we have \(a_{E}=0.95145807\) and \(r^{E}_{H}=1.02899\), and for \(g=0.4\) one gets \(a_{E}=0.80802796\) and \(r^{E}_{H}=1.08549\). Thus, the extremal value of the rotation parameter \(a_{E}\) decreases due to the presence of the magnetic charge g when compared with the Kerr black hole. Thus, for each g, there exists an extremal rotating Bardeen black hole.

The static limit surface or infinite redshift surface of a black hole is a surface where the time-translation Killing vector becomes null, \(\eta ^{\mu }\;\eta _{\mu }=0\). An infinite redshift surface is referred to as a null Killing surface to distinguish it from the null surface corresponding to the horizons. To find the null Killing surfaces, one sets the \(g_{tt}\) component of the metric tensor in Eq. (3) equal to zero. For the rotating Bardeen regular black hole, we find that \(g_{tt}=0\) gives

$$\begin{aligned}&\Sigma ^2 (r^{2+\zeta } \Sigma ^{-\zeta /2}+g^2r^{\lambda }\Sigma ^{-\lambda /2})^3 \nonumber \\&\quad -4M^2r^{8+3\zeta } \Sigma ^{-3\zeta /2}=0. \end{aligned}$$
(8)
Table 2 The values of the outer static limit surface and event horizon of a rotating Bardeen regular black hole with parameters \(\zeta =2\), \(\lambda =3\), \(M=1\), and \(\theta =\pi /4\) (\(\delta _{e}^{g}=r^{+}_{sls}-r^{+}_{H}\))
Full size table

In Fig. 4, we depict the possible roots of the equation \(g_{tt}=0\) with different combinations of the parameters a and g and different values of \(\theta \). The event horizon of the rotating Bardeen regular metric (3) is located at \(r=r_{H}^{+}\), the larger root of \(\Delta =0\), and the static limit surface is located at \(r=r_{sls}^{+}\), which is zero of \(g_{tt}=0\). Observing the outer event horizon and the stationary limit surface of the rotating Bardeen regular black hole, it is verified that the stationary limit surface always lies outside the event horizon for all values of g. Hence, as in the Kerr black hole, we call the region between two surfaces the ergosphere, which lies outside of the black hole. The ergosphere is given by \(r_{H}^{+}<r<r_{sls}^{+}\), and an important feature of the ergosphere is that the time-like Killing vector becomes space-like after crossing the static limit surface, i.e., in the ergosphere \(\eta ^{\mu }\;\eta _{\mu }=g_{tt}>0\). The existence of the ergosphere allows various kinds of energy extraction mechanisms for a rotating black hole. It has been suggested that the ergosphere can be used to extract energy from rotating black holes through the Penrose process [28]. Further, an observer moving along the time-like geodesics is always stationary in the ergosphere due to the frame-dragging effect [29]. Its shape is that of an oblate spheroid—bulging at the equator, and flattened at the poles of the rotating black hole. We have studied how the parameters a, g affect the shape of the ergosphere, and the behavior of ergosphere for \(a<a_E\) is depicted in Fig. 5 and for \(a \approx a_E\) in Fig. 6. It can be seen that the ergosphere is sensitive to the parameter g, the ergosphere area enlarges with an increase in the parameter g, as well as with a (cf. Table 2). In the extremal case \(a \approx a_E\) (Fig. 6), the inner and outer horizons coincide, and the thickness of the ergosphere still increases with the increase in the parameter g.

Fig. 7
figure 7

The behavior of \(\dot{r}\) vs. r for an extremal black hole. a The magnetic charge \(g=0.2\) and \(a=0.942439535325\). b The magnetic charge \(g=0.4\) and \(a=0.7851573623591\)

Full size image
Fig. 8
figure 8

Plot showing the behavior of \(V_\mathrm{eff}\) vs. r for different angular momenta L

Full size image

3 Equations of motion and the effective potential

In this section, we would like to study the equations of motion of a particle with rest mass \(m_{0}\) falling in the background of the rotating Bardeen regular black hole. Henceforth, we shall restrict our discussion to the case of the equatorial plane (\(\theta =\pi /2 \)), which simplifies the mass function (5) to

$$\begin{aligned} m= M\left( \frac{r^2}{r^2+g^2}\right) ^{3/2}. \end{aligned}$$
(9)

It is easy to see that the mass function (9) can also be obtained from (5) for \(\zeta =\lambda =0\). There are two Killing vectors, time-like (\( \eta _{t}^{\mu } \)) and axial (\( \xi _{\phi }^{\mu } \)) Killing vectors. So there must be two conserved quantities corresponding to these Killing vectors. The conserved quantities corresponding to these time-like and axial Killing vectors are the energy (E) and angular momentum (L), respectively. The conserved quantities at the equatorial plane are defined by the following equations:

$$\begin{aligned} -E = g_{\mu \nu } \eta _{t}^{\mu }u^{\nu } = g_{tt}u^{t} + g_{t \phi }u^{\phi }, \end{aligned}$$
(10)
$$\begin{aligned} L = g_{\mu \nu } \xi _{\phi }^{\mu }u^{\nu } = g_{\phi t}u^{t} + g_{\phi \phi }u^{\phi }, \end{aligned}$$
(11)

where \(u^{\nu }\) is the four-velocity of the particle. To calculate \(E_\mathrm{CM}\) for the colliding particles, first of all we need to calculate the four-velocities of the particles. The four-velocities are calculated by solving Eqs. (10) and (11) simultaneously and using the condition \(u_{\nu }u^{\nu }=-m_{0}^2\). Hence the four-velocities of the falling particles have the following form:

$$\begin{aligned} u^{t} = \frac{1}{r^2} \left[ -a (aE - L) + (r^2 + a^2) \frac{T}{\Delta }\right] , \end{aligned}$$
(12)
$$\begin{aligned} u^{ \phi } = \frac{1}{r^2} \left[ -(aE - L ) + \frac{a T}{\Delta }\right] , \end{aligned}$$
(13)
$$\begin{aligned} u^{r} = \pm \frac{1}{r^2} \sqrt{T^2 -\Delta \left[ m_0^2 r^2 + (L-a E)^2\right] }, \end{aligned}$$
(14)

where \( T = E (r^2 + a^2) -La \). In Eq. (14) the \(+\) sign corresponds to the outgoing geodesic and the \(-\) sign corresponds to the incoming geodesics. The effective potential is calculated as

$$\begin{aligned} \frac{1}{2} (u^{r})^2+ V_\mathrm{eff}=0. \end{aligned}$$
(15)

Hence, the form of the effective potential is like

$$\begin{aligned} V_\mathrm{eff} = -\frac{[E(r^2+a^2)-La]^2 -\Delta [m_0^2 r^2 + (L-a E)^2]}{2r^4}. \end{aligned}$$
(16)

The range of the angular momentum for the falling particles is calculated by the following equations:

$$\begin{aligned} V_\mathrm{eff}=0 \quad \text {and}\quad \frac{\mathrm{d}V_\mathrm{eff}}{\mathrm{d}r}=0. \end{aligned}$$
(17)

The plots of \(\dot{r}\) vs. r can be seen from Fig. 7 for different values of L, a, and g. We can see from this figure that if the angular momentum of the particle \(L>L_{c}\), then the geodesics never fall into the black hole. On the other hand if the angular momentum \(L<L_{c}\), then the geodesics always fall into the black hole and if \(L=L_{c}\), then the geodesics fall into the black hole exactly at the event horizon. The behavior of the effective potential (\(V_\mathrm{eff}\)) with radius (r) can be seen from Fig. 8.

For the time-like particles, \(u^{t} \ge 0\), from Eq. (12) the condition

$$\begin{aligned} E [r^3+2ma^2+a^2r] \quad \ge 2mLa, \end{aligned}$$
(18)

must be satisfied; as \(r \rightarrow r_{H}^{E}\), this condition reduces to

$$\begin{aligned} E \ge \frac{a}{2mr^{E}_{H}}L = \frac{a}{a^2+(r^{E}_{H})^2}L=\Omega _{H}L, \end{aligned}$$
(19)

where \( \Omega _{H} \) is the angular velocity at the event horizon.

Table 3 The limiting values of the angular momentum for different extremal cases of a rotating Bardeen regular black hole
Full size table
Fig. 9
figure 9

Plot showing the behavior of \(E_\mathrm{CM}\) vs. r for an extremal black hole. Top For the magnetic charge \(g=0\), spin \(a_{E}=1\), angular momentum \(L_{1}=2.0\) (blue), 1.8 (green), 1.5 (red), and \(L_{2}=-4.82843\) (left). For \(g=0.2\), \(a_{E}=0.942439535325\), \(L_{1}=2.10714\) (blue), 2.02 (green), 1.90 (red), and \(L_{2}=-4.77988\) (right). Bottom For \(g=0.3\), \(a_{E}=0.875075019710\), \(L_{1}=2.22294\) (blue), 2.12 (green), 1.95 (red), and \(L_{2}=-4.72090\) (left). For \(g=0.4\), \(a_{E}=0.7851573623591\), \(L_{1}=2.37934\) (blue), 2.27 (green), 2.10 (red), and \(L_{2}=-4.63854\) (right)

Full size image

4 Near horizon collision in the rotating Bardeen regular black hole

Recently, Bandos, Silk, and West (BSW) [30] analyzed the possibility that a Kerr black hole can act as a particle accelerator by studying the collision of two particles near the event horizon of the Kerr black hole and found that the center-of-mass energy (\(E_\mathrm{CM}\)) of the colliding particles in the equatorial plane can be arbitrarily high in the limiting case of an extremal black hole. Thus the extremal Kerr black hole can act as a Planck energy scale particle accelerator. This gave an opening to explore ultrahigh energy collisions and astrophysical phenomena, such as gamma ray bursts and active galactic nuclei. Hence, the BSW mechanism received significant attention in the study of the collision of two particles near a rotating black hole [20, 27, 31–37] (see also [38] for a review). In this section, we want to study the properties of \(E_\mathrm{CM}\) as r tends to the event horizon \(r^{+}_{H}\) in the case of a rotating Bardeen regular black hole. Let us find \(E_\mathrm{CM}\) for two colliding particles with the same rest mass, \(m_{1}= m_{2}=m_{0}\), coming from rest at infinity. The collision energy in the center-of-mass frame is defined as

$$\begin{aligned} E_\mathrm{CM} = m_{0} \sqrt{2} \sqrt{1-g_{\mu \nu } u^{\mu }_{(1)} u^{\nu }_{(2)}}, \end{aligned}$$
(20)
Table 4 The limiting values of the angular momentum for different non-extremal cases of a rotating Bardeen regular black hole
Full size table
Fig. 10
figure 10

Plot showing the behavior of \(E_\mathrm{CM}\) vs. r. Left For \(a_{E}=0.942439535325\), \(L_{1}=2.10714\), \(L_{2}=-4.77988\), and \(g=0.2\) (blue), 0.24 (green), 0.28 (red). Right For \(a=0.7851573623591\), \(L_{1}=2.37934\), \(L_{2}=-4.63854\), and \(g=0.4\) (blue), 0.44 (green), 0.48 (red)

Full size image
Fig. 11
figure 11

Plot showing the behavior of \(E_\mathrm{CM}\) vs. r for non-extremal black hole. Top For \(a=0.95\), \(g=0\) (left). For \(a=0.9\), \(g=0.2\) (right). Bottom For \(a=0.8\), \(g=0.3\) (left). For \(a=0.7\), \(g=0.4\) (right)

Full size image

where \(u^{\mu }_{(1)}\) and \(u^{\nu }_{(2)}\) are the four-velocities of the colliding particles. By using Eq. (20) and substituting the values of four-velocities we can get \(E_\mathrm{CM}\) for the black hole (3):

$$\begin{aligned} \frac{E_\mathrm{CM}^2}{2 m_{0}^2 }= & {} \frac{1}{r(r^2-2mr+a^2)} \Big [2a^2 (m+r) \nonumber \\&- 2am(L_{1}+L_{2}) \nonumber \\&-L_{1} L_{2}(-2m+r) +2(-m+r)r^2 \nonumber \\&-\sqrt{2m(a-L_{1})^2 - L_{1}^2r + 2mr^2} \nonumber \\&\times \sqrt{2m(a-L_{2})^2 - L_{2}^2r + 2mr^2}\Big ]. \end{aligned}$$
(21)

Here \(m=(M r^3)/(r^2+g^2)^{3/2}\). Thus the above equation is g dependent, and when \(g=0\), it will look exactly the same with m replaced by M, which is also exactly the same as obtained for the Kerr black hole [30]. Obviously as \(r \rightarrow r_{H}^{E}\), Eq. (21) has an indeterminate form when we choose numerical values of \(r_{H}^{E}\), a, M, and g. We apply l’Hospital’s rule twice, then the value of the \(E_\mathrm{CM}\), as \(r\rightarrow r_{H}^{E}\), becomes

$$\begin{aligned} \frac{E_\mathrm{CM}^2}{2 m_{0}^2 } (r\rightarrow r_{H}^{E})= & {} 8.08-0.51L_{1}L_{2}+0.48(L_{1}+L_{2}) \nonumber \\&- \frac{A_{1}(L_{2}-L_{c})}{2(L_{1}-L_{c})} -\frac{A_{2}(L_{1}-L_{c})}{2(L_{2}-L_{c})} \nonumber \\&-\frac{B_{1}B_{2}}{3(L_{1}-L_{c})(L_{2}-L_{c})}+\frac{B_{1}^2(L_{2}-L_{c})}{6(L_{1}-L_{c})^3} \nonumber \\&+\frac{B_{2}^2(L_{1}-L_{c})}{6(L_{2}-L_{c})^3}, \end{aligned}$$
(22)

with fixed \(a=a_{E}=0.942439535325\), \(r=r_{H}^{E}=1.04769\), \(M=1\), and \(g=0.2\). The constants \(A_{i}\) and \(B_{i}\) correspond to \(A_{i}=3.56+0.91L_{i}-0.51L_{i}^2\) and \(B_{i}=4.35-0.35L_{i}-0.81L_{i}^2\) (\(i=1,2\)). Equation (22) suggests that an unlimited \(E_\mathrm{CM}\) is possible if one of the particles has the critical angular momentum \(L_c\). Therefore, \(E_\mathrm{CM}\) is divergent at the horizon \(r=r_{E}\), if one of the particles satisfies the critical condition \(E - \Omega _{H} L_{c} = 0\). The restriction on the \(L_c\) is shown in Table 3. The numerical value of the critical angular momentum is \(L_{c}= E/\Omega _{H}=2.10714\), which is exactly the same as \(L_{1}\). Hence, we can say that \(E_\mathrm{CM}\) is infinite for the extremal rotating Bardeen regular black hole. We plot in Fig. 9 \(E_\mathrm{CM}\) vs. r for various values of the angular momentum.

4.1 Near horizon collision in non-extremal rotating Bardeen regular black hole

Finally, we study the properties of \(E_\mathrm{CM}\) in the limit \(r \rightarrow r_{H}^{+}\) of a non-extremal rotating Bardeen regular black hole. Again as \(r \rightarrow r_{H}^{+}\), both numerator and denominator of Eq. (21) vanish. Hence, by application of l’Hospital’s rule, we find that \(E_\mathrm{CM}\), for the near horizon case for a non-extremal rotating Bardeen black hole, reads

$$\begin{aligned} \frac{E_\mathrm{CM}^2}{2 m_{0}^2 } (r \rightarrow r_{H}^{+})= & {} \frac{1}{(L_{3}-L'_{c})(L_{4}-L'_{c})}\left[ 12.14 \right. \nonumber \\&\left. +1.19(L_{3}^2+L_{4}^2) \right. \nonumber \\&\left. -4.28(L_{3}+L_{4})- 0.86L_{3}L_{4}\right] . \end{aligned}$$
(23)

In the above calculation we have fixed \(a=0.9\), \(r=r_{H}^{+}=1.31866\), and \(g=0.2\). Equation (23) is the formula for \(E_\mathrm{CM}\) of two colliding particles for a non-extremal rotating Bardeen black hole. \(E_\mathrm{CM}\) will be infinite if either \(L_{3}\) or \(L_{4}\) is equal to \(L'_{c} = E/\Omega _{H}\), where \(L_4 < L < L_3\) is the range for the angular momentum with which a particle can reach the horizon. The critical value of the angular momentum is calculated as \(L'_{c}=2.83213\). Hence, \(L'_{c}\) is not in the acceptable range (cf. Table 4). Therefore, we can say that \(E_\mathrm{CM}\) is finite in the case of a non-extremal black hole (cf. Figs. 10 and 11).

5 Conclusion

There have been made many efforts to push Einstein gravity as much as possible to its limit, trying to avoid the central singularity. Following some very early ideas of Sakharov [5], Gliner [6], and Bardeen [7], solutions possessing a global structure like the one of black hole spacetimes, but in which the central singularity is absent, have been found. The first regular black hole solution having an event horizon was obtained by Bardeen [7], which is a solution of Einstein equations in the presence of an electromagnetic field. Recently, the rotating Bardeen regular black hole was also found [17]. Further, astrophysical black hole candidates are thought to be the Kerr black holes of general relativity, however, the actual nature of these objects is still to be verified. In this paper, we have investigated in detail the horizons and ergosphere for the rotating Bardeen regular black hole and also analyzed the possibility that it can act as a particle accelerator by studying the collision of two particles falling freely from rest at infinity. The horizon structure of the rotating Bardeen regular black hole is complicated as compared to the Kerr black hole. It has been observed that, for each g and suitable choice of the parameters, we can find the critical value \(a=a_{E}\), which corresponds to an extremal black hole with degenerate horizons; i.e., when \(a=a_{E}\), the two horizons coincide (cf. Figs. 1 and 2). Interestingly, the value \(a_{E}\) is sensitive to the parameter g: \(a_{E}\) decreases with the increase in g. However, when \(a<a_{E}\), we have a regular black hole with Cauchy and event horizon, and for \(a>a_{E}\), no horizon exists. Furthermore, the ergosphere area increases with the increase in a. On the other hand, when the value of g increases, the ergosphere area enlarges. It has been suggested that the ergosphere can be used to extract energy from rotating black holes through the Penrose process [28]. However, Penrose himself said that the method is inefficient [39], although later [29] showed that the theoretical efficiency could reach 20 % extra energy up to 60 %. In the case of a rotating black hole the efficiency of the collisional process is not high, if a magnetic field effect is not involved, rather it is efficient in the case of a Kerr naked singularity [40, 41]. Hence, the parameter g may play a significant role in the energy extraction process from rotating Bardeen regular black holes, which is being investigated separately.

It has been shown by BSW [30] that \(E_\mathrm{CM}\) of two colliding particles may occur at an arbitrarily high energy for the case of extremal Kerr black holes. The BSW analysis when extended to the rotating Bardeen regular black hole, with some restriction on the parameters, shows an arbitrary high \(E_\mathrm{CM}\) can be achieved when the collision takes place near the horizon of an extremal rotating Bardeen regular black hole; one of the colliding particles must have a critical angular momentum. We have also calculated the range of the angular momentum for which a particle may reach the horizon; i.e., if the angular momentum lies in the range, the collision is possible near the horizon of the rotating Bardeen regular black holes. The calculation of \(E_\mathrm{CM}\) was performed in the case of a rotating Bardeen regular black hole for various values of g, and we found that they are infinite if one of the colliding particles has the critical angular momentum in the required range. On the other hand, \(E_\mathrm{CM}\) has always a finite upper limit for the non-extremal rotating Bardeen regular black hole. Thus, the BSW mechanism, for the rotating Bardeen regular black hole, depends both on the rotation parameter a as well as on the deviation parameter g. For the non-extremal black hole, we have also seen the effect of g on \(E_\mathrm{CM}\), demonstrating an increase in the value of the \(E_\mathrm{CM}\) with an increase in the value of g.

According to the no-hair theorem, all astrophysical black holes are expected to be like Kerr black holes, but the actual nature of this has still to be verified [18]. The impact of the parameter g on the horizon structure, ergoregion, and particle acceleration presents a good theoretical opportunity to distinguish the rotating Bardeen regular black hole from the Kerr black and to test whether astrophysical black hole candidates are the black holes as predicted by Einsteins general relativity.