1 Introduction

The 4D Universe can be regarded as a brane embedded in a higher-dimensional bulk, in which extra dimensions can be large [1, 2] and either compact or non-compact [3–7]. Brane-world models have been providing new tools to understand various questions, as for instance a solution of the gauge hierarchy problem [1, 5, 6].

Recently, increasingly one has focussed on the study of thick brane scenarios based on gravity coupled to one or more scalars in higher-dimensional space-times [8–22]. Moreover, domain walls have been used in high-energy physics to generate thick branes in models wherein scalar fields can couple with gravity in warped spacetime. Besides, thick branes are well known to avoid some inconsistencies inherent to thin brane-worlds, as for instance the proton decay [23]. For some prominent reviews on domain walls and thick branes, see, e.g., Ref. [24]. In particular, a model described by a single scalar field with internal structure was proposed in Refs. [25, 26]. Analytical solutions of the Einstein equations were obtained with a sine-Gordon potential [27], where a kink, as the scalar field configuration in the system, provides the thick brane-world as a domain wall in the bulk. Similarly, this type of configuration has also been further explored [28, 29]. In addition, an analytic solution of the sine-Gordon domain wall in a 4D global supersymmetric model was obtained [30], and the stability of a more general setup was studied likewise [31]. The localisation of fermions on the brane has been accomplished in the presence of kink-fermion couplings in the background of the sine-Gordon kink [21].

Our aim here is mainly to study the entropic information on thick brane-worlds models, by means of the brane-world configurational entropy, and to further explore its subsequent ramifications. In order to accomplish it, the sine-Gordon kink shall be used, playing a prominent role in the thick brane scenario. The sine-Gordon model is taken into account here to suitably illustrate the framework that we shall use. In fact, its parameters are related to the domain wall thickness and the AdS bulk curvature, providing an interesting physical approach.

This paper is organised as follows: in the next section the thick brane generated by a single scalar field coupled to gravity shall be revisited, with particular attention to the sine-Gordon model. In Sect. III the brane-world configurational entropy is going to be introduced, and we shall calculate the entropic information for the sine-Gordon model, using the Fourier transform of the thick brane (warped) energy density. The entropic information measure shall be shown to be a successful tool for constraining the most suitable range for the AdS curvature. In addition, the configurational entropy is employed to evince a high organisational degree in the configuration of the system, for large values of a parameter of the sine-Gordon model. Furthermore, the Gleiser and Stamatopoulos procedure is going to be applied to obtain a correlation between the brane-world configurational entropy and the energy of the system. In the last section we present our concluding remarks.

2 A brief overview of gravity coupled to a scalar field

In this section the work presented by Gremm is briefly revisited [9], where 4-dimensional gravity arises on a thick domain wall in AdS space. We start with the action in 5-dimensional gravity coupled to one real scalar field, which is given by

$$\begin{aligned} \mathcal {S}=\int \mathrm{d}^{5}x\sqrt{\left| g\right| }\left[ -\frac{R}{4}+ \frac{1}{2}g^{ab}\nabla _a \phi \nabla _b \phi -V(\phi )\right] , \end{aligned}$$
(1)

where \(4\pi G=1\), with the field and the space-time variables being dimensionless, R denotes the scalar curvature, and the scalar field \( \phi \) depends only on the extra dimension. Furthermore, \(V(\phi )\) is the potential describing the model, \(g=\det (g_{ab})\), and the metric is represented by

$$\begin{aligned} \mathrm{d}s^{2}=g_{ab}\mathrm{d}x^{a}\mathrm{d}x^{b}=e^{2A(r)}\eta _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }-\mathrm{d}r^{2}, \end{aligned}$$
(2)

for \(a,b=0,1,2,3,5\), where r is the extra dimension, \(\eta _{\mu \nu }\) denotes the usual Minkowski metric components, and \(e^{2A(r)}\) is the warp factor.

By denoting \(B^{\prime }(r)=\mathrm{d}B(r)/\mathrm{d}r\), for any quantity B depending just upon the variable r, and using the Einstein equations \(\mathcal {G}_{ab}= \mathcal {T}_{ab}\) and the Euler–Lagrange equation \(\nabla _a \phi \nabla ^a\phi +V^{\prime }(\phi ) =0\) as well, the equations of motion read

$$\begin{aligned}&A^{\prime \prime }(r)+\frac{2}{3}\phi ^{\prime 2}(r) =0, \end{aligned}$$
(3)
$$\begin{aligned}&A^{\prime 2}(r)-\frac{1}{6}\phi ^{\prime 2}(r)+\frac{1}{3}V(\phi ) =0, \end{aligned}$$
(4)
$$\begin{aligned}&\phi ^{\prime \prime }(r)+4\phi ^{\prime }(r)A^{\prime }(r)-V^{\prime }(\phi ) =0. \end{aligned}$$
(5)

Moreover, the above equations are equivalently written as

$$\begin{aligned} \phi ^{\prime }(r) = \frac{1}{2}\frac{\mathrm{d}W(\phi )}{\mathrm{d}\phi }, \qquad A^{\prime }(r)=-\frac{1}{3}W(\phi ), \end{aligned}$$
(6)

whenever the potential \(V(\phi )\) is provided by the superpotential \( W(\phi )\) as [8].

$$\begin{aligned} V(\phi )=\frac{1}{8}\left( \frac{\mathrm{d}W(\phi )}{\mathrm{d}\phi }\right) ^{2}-\frac{1}{3} W^2(\phi ). \end{aligned}$$
(7)

Thus, it is straightforward to verify that the first-order equations

$$\begin{aligned} A^{\prime }(r)= & {} -\frac{1}{3}W(\phi ), \end{aligned}$$
(8)
$$\begin{aligned} \phi ^{\prime }(r)= & {} \frac{1}{2}\frac{\mathrm{d}W(\phi )}{\mathrm{d}\phi }, \end{aligned}$$
(9)

also solve Eqs. (3), (4) and (5). In order to find analytical solutions, the sine-Gordon model is employed [32, 33], being defined by the following superpotential:

$$\begin{aligned} W(\phi )=3\alpha \beta \sin \left( \sqrt{\frac{2}{3\alpha }}\phi \right) . \end{aligned}$$
(10)

By using the above equation in Eq. (7), the potential yields

$$\begin{aligned} \!\!\!V(\phi )=\frac{3\alpha \beta ^{2}}{8}\left[ (1-4\alpha )\!-\!(1+4\alpha )\cos \left( \sqrt{\frac{8}{3\alpha }}\phi \right) \right] . \end{aligned}$$
(11)

Now the solutions of Eqs. (8) and (9) are straightforwardly verified to be given by

$$\begin{aligned} A(r)= & {} -\alpha \ln \left[ 2\cosh (\beta r)\right] , \end{aligned}$$
(12)
$$\begin{aligned} \phi (r)= & {} \sqrt{6\alpha }\arctan \left[ \tanh \left( \frac{\beta r}{2} \right) \right] . \end{aligned}$$
(13)

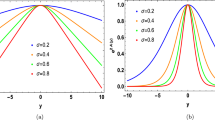
The field \(\phi (r)\) and the warp factor \(e^{2A(r)}\) are shown, respectively, in Figs. 1 and 2. The field configuration in Fig. 1 is evinced to be the so-called kink. Moreover, \(e^{2A(r)}\) is centred on \(r=0\). It is important to remark that in the solutions (12) and (13) the AdS curvature is related to the product \(\alpha \beta \), whereas the thickness of the domain wall is given by the parameter \(\beta \). In addition, the brane core is localised at \(r = 0\), which is consonant to the point of maximum variation of the scalar field, which composes the well-known domain wall. The thick brane presents a thickness \(\Delta \) where deviations from the 4D Newton law occur in these scales. Current precision torsion-balance experiments require that the extra dimension must satisfy the constraint \(\Delta \lesssim 44\,\upmu \)m [34], whereas theoretical reasons thus imply that \(\Delta \gtrsim \ell _{(5)} \approx 2.0 \times 10^{-19}\,\)m. Indeed, since in the 5D scenario with \( M_{(5)}\simeq M_{\mathrm {ew}}\simeq 1\,\)TeV, as is to be considered, the electroweak scale corresponds to the length \( \ell _{(5)}\simeq 2.0\times 10^{-19}\)m. Besides, it was shown in Ref. [23] that the above experimental and theoretical arguments, together with the avoidance of unobserved monopoles with mass scale of order TeV on thick branes, impose physical constraints for the parameter space \(\alpha \beta \) [23]:

$$\begin{aligned} 1.0\times 10^{-19} \beta \lesssim \arccos {\mathrm {h}}\left( \frac{ 10^{13/\alpha }}{2}\right) \lesssim 2.2 \times 10^{-5}\beta . \end{aligned}$$
(14)
Fig. 1
figure 1

Kink-like solution for \(\alpha =\beta =1\)

Full size image
Fig. 2
figure 2

Warp factor with \(\alpha =\beta =1\)

Full size image

In the next section we shall postulate the configurational entropy in brane-world scenarios. As an example, the sine-Gordon model described here shall be explored.

3 Brane-world configurational entropy (BCE)

As argued in the Introduction, Gleiser and Stamatopoulos (GS) [35] have recently proposed a detailed picture of the so-called configurational entropy (CE) for the structure of localised solutions in classical field theories. In this section, analogously to that work, we formulate a configurational entropy measure in the functional space, from the field configurations where brane-world scenarios can be studied. First, the framework shall be formally introduced and thereafter its consequences are going to be explored. Hence, we discuss a prominent feature of this theory.

There is an intimate link between information and dynamics, where the entropic measure plays a prominent role. The entropic measure is well known to quantify the informational content of physical solutions to the equations of motion and their approximations, namely, the configurational entropy in functional space [35]. GS proposed that nature optimises not solely by extremising energy through the plethora of a priori available paths, but also from an informational perspective [35].

To start, let us write the following Fourier transform:

$$\begin{aligned} \mathcal {F}[\omega ]=-\frac{1}{\sqrt{2\pi }}\int \mathrm{d}r\;e^{2A(r)+i\omega r} \mathcal {L}, \end{aligned}$$
(15)

where \(\mathcal {L}\) is the standard Lagrangian density and \(e^{2A(r)}\) denotes the warp factor, as usual. For the sake of simplicity, define \( \varepsilon (r):=-\mathcal {L}e^{2A(r)}\), named the warp density (WD). Thus, using the Plancherel theorem, it follows that

$$\begin{aligned} \int \mathrm{d}\omega \left| \mathcal {F}[\omega ]\right| ^{2}=\int \mathrm{d}r\left| \varepsilon (r)\right| ^{2}. \end{aligned}$$
(16)

Now the modal fraction is defined by the following expression [35–39]:

$$\begin{aligned} f(\omega )=\frac{\left| \mathcal {F}[\omega ]\right| ^{2}}{\int d\omega \left| \mathcal {F}[\omega ]\right| ^{2}}. \end{aligned}$$
(17)

The modal fraction \(f(\omega )\) measures the relative weight of each mode \( \omega \).

Now, the CE was motivated by Shannon’s information theory [35]. Indeed, the configurational entropy was originally defined by the expression \(S_C[f] = -\sum f_n\,\ln (f_n)\), which represents an absolute limit on the best lossless compression of any communication [40, 41]. The CE thus originally provided the informational content of configurations that are compatible with constraints of an arbitrary physical system. When N modes k carry the same weight, then \(f_n = 1/N\), and hence the discrete configurational entropy has a maximum at \(S_C = \ln N\). Instead, if just one mode constitutes the system, then \(S_C = 0\) [35].

Analogously, for arbitrary non-periodic functions in an open interval the continuous CE can be described by the expression

$$\begin{aligned} S_{c}[f]=-\int \mathrm{d}\omega \tilde{f}(\omega )\ln [\tilde{f}(\omega )], \end{aligned}$$
(18)

where \(\tilde{f}(\omega ):=\) \(f(\omega )/f_{\max }(\omega )\) is defined as the normalised modal fraction, whereas the term \(f_{\max }(\omega )\) denotes the maximum fraction. Thus, Eq. (15) can be used to generate the modal fraction, in order to obtain the entropic profile of thick brane solutions. It is important to remark that Eq. (15) differs from that one given by GS. In this framework we are including the warp effect in the function \(\mathcal {F}[\omega ]\), and consequently the framework carries information as regards the warped geometry.

Here, as a straightforward example, we shall calculate the entropic information for the sine-Gordon model. By substituting Eqs. (7) and (9) as well into the WD, and after straightforward manipulations,

$$\begin{aligned} \varepsilon (r)=e^{2A}\left( \frac{1}{4}W_{\phi }^{2}-\frac{1}{3} W^{2}\right) . \end{aligned}$$
(19)

With the sine-Gordon model provided by Eq. (10) and its respective solutions, the above WD can be written in the following form:

$$\begin{aligned} \varepsilon (r)\!=\!\frac{6\alpha \beta ^{2}\!\cosh ^{\!-2}(\beta r) }{\left[ 1+\tanh ^{2}(\beta r)\right] ^{2}}\left[ {{\mathrm{sech}}}^{4}(\beta r)\!-\!6\alpha \tanh ^{2}(\beta r)\right] . \end{aligned}$$
(20)

Now, the Fourier transform of the WD is calculated, which gives the modal fraction in Eq. (17). In fact, we must determine

$$\begin{aligned} \mathcal {F}[\omega ]=\frac{1}{\sqrt{2\pi }}\int \mathrm{d}r\;e^{i\omega r}\varepsilon (r), \end{aligned}$$
(21)

with \(\varepsilon (r)\) given by Eq. (20). After exhaustive calculations, one finds

$$\begin{aligned} \mathcal {F}[\omega ]=\frac{2^{1-2\alpha }\alpha \beta ^{2}}{\sqrt{2\pi }} \sum _{j=1}^{2}\left[ \frac{2(2+9\alpha )}{3}I_{1}^{(j)}-\frac{3\alpha }{4} I_{2}^{(j)}\right] , \end{aligned}$$
(22)

where \(I_{1}^{(j)}\) and \(I_{2}^{(j)}\) are functions given by

$$\begin{aligned} I_{1}^{(j)}= & {} \frac{1}{2\beta }\frac{\Gamma (\lambda _{j}+1)}{\Gamma (\lambda _{j}+2)}{}_{2}G _{1}[\gamma _{j},\lambda _{j}+1;\lambda _{j}+2;-1], \end{aligned}$$
(23)
$$\begin{aligned} \!\!\!I_{2}^{(1)}= & {} 4\left( \bar{I}_{2}^{(1)}+\tilde{I}_{2}^{(1)}\right) ,\qquad I_{2}^{(2)}=4\left( \bar{I}_{2}^{(2)}+\tilde{I}_{2}^{(2)}\right) . \end{aligned}$$
(24)

The above functions are defined as

$$\begin{aligned} \bar{I}_{2}^{(j)}= & {} \frac{1}{2\beta }\frac{\Gamma (\bar{\lambda } _{1}+1)}{\Gamma (\bar{\lambda }_{1}+2)}{}_{2}G _{1}[\bar{\gamma }_{1}, \bar{\lambda }_{1}+1;\bar{\lambda }_{1}+2;-1], \end{aligned}$$
(25)
$$\begin{aligned} \tilde{I}_{2}^{(j)}= & {} \frac{1}{2\beta }\frac{\Gamma (\tilde{ \lambda }_{1}+1)}{\Gamma (\tilde{\lambda }_{1}+2)}{}_{2}G _{1}[\tilde{ \gamma }_{1},\tilde{\lambda }_{1}+1;\tilde{\lambda }_{1}+2;-1]\,, \end{aligned}$$
(26)

where the above expressions \(_{2}G _{1}[\;\cdot \;,\;\cdot \;;\;\cdot \;; \;\cdot \;]\) stand for the well-known hypergeometric functions with

$$\begin{aligned} \gamma _{1}= & {} \gamma _{2}=\bar{\gamma }_{m}=\tilde{\gamma }_{m}=2(\alpha +1), \\ \lambda _{1}= & {} \alpha +i\omega /2\beta ,\qquad \lambda _{2}=\lambda _{1}^{*}, \qquad \bar{\lambda }_{1} =\lambda _{1}+1, \\ \bar{\lambda }_{2}= & {} \bar{\lambda }_{1}^{*},\qquad \tilde{\lambda } _{1}=\lambda _{1}^{*}-1,\qquad \tilde{\lambda }_{2}=\lambda _{1}-1\,, \end{aligned}$$

where the \(\lambda ^*\) denotes the complex conjugate of \(\lambda \). Now, in order to lead the modal fraction to a more compact form, Eq. (22) can be rewritten as

$$\begin{aligned} \mathcal {F}[\omega ]=A_{0}\sum _{j,k=1}^{2}c_{k}I_{k}^{(j)}, \end{aligned}$$
(27)

where the following notation is used:

$$\begin{aligned} A_{0}=\frac{2^{1-2\alpha }\alpha \beta ^{2}}{\sqrt{2\pi }},\quad c_{1}= \frac{2(2+9\alpha )}{3},\quad c_{2}=-\frac{3\alpha }{4}. \end{aligned}$$
(28)

Thus, the modal fraction Eq. (15) becomes

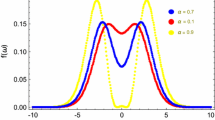
$$\begin{aligned} f(\omega )=\frac{\displaystyle \sum \nolimits _{j,k,m,n=1}^{2}c_{k}c_{n}^{*}I_{k}^{(j)}I_{n}^{(m)*}}{\displaystyle \sum \nolimits _{j,k,m,n=1}^{2}\int \mathrm{d}\omega c_{k}c_{n}^{*}I_{k}^{(j)}I_{n}^{(m)*}}. \end{aligned}$$
(29)

In Figs. 3 and 4 the modal fraction is depicted, for different values of the parameter \(\alpha \). Note that the maximum of the distributions is localised around the zero mode \(\omega =0\). Indeed, the maximum fraction is given by \( f_{\max }=f_{\max }(0)\). By taking into account the modal fraction in Eq. (29) and its maximum contribution, Eq. (18) can now be solved in order to obtain the brane CE. In this case, due to the high complexity of integration, Eq. (18) must be integrated numerically. The results are shown in Fig. 5, where the BCE is plotted as a function of the parameter \(\alpha \). In this case, the rescaled parameter \(\delta =\alpha \beta \) has been defined, which is responsible for the AdS curvature. Moreover, the thickness of the wall is fixed by taking \(\beta =1,2,3\). As a consequence, several remarkable results can be presented here. First, we have found that the entropic information measure provides an accurate way to fix the best values of the AdS curvature. In fact, we demonstrate that the best ordering is given by that ones with lower values of the domain wall thickness. Second, at large values of \(\alpha \), the brane-world CE yields the configurational entropy \(S_{c}=0\), showing a great organisational degree in the structure of configuration of the system.

Fig. 3
figure 3

Modal fractions for \(\alpha =\beta =1\). The maximum is at \(\omega =0\)

Full size image
Fig. 4
figure 4

Modal fractions for \(\alpha =2\) and \(\beta =1\). Note that the maximum is also at \(\omega =0\)

Full size image

Finally, by using a recent approach, presented by GS [35], we have checked that the BCE is correlated to the energy of the system. The higher [lower] the brane configurational entropy, the higher [lower] the energy of the solutions. Moreover, it is straightforward to realise from Fig. 5 that the higher the brane thickness \(\beta \), the higher the respective value for the brane configurational entropy as well.

Fig. 5
figure 5

The brane configurational entropy as a function of the parameter \(\alpha \)

Full size image

We are interested in sine-Gordon models, as the associated parameters \(\alpha \) and \(\beta \), which define the model by Eq. (10), are constrained from experimental and theoretical arguments. As the AdS curvature can be provided by the product \(\alpha \beta \), whereas the thickness of the domain wall is given by the parameter \(\beta \), we can find the best range for the AdS curvature via the analysis above depicted in Fig. 5. This figure evinces that system configurations with less entropy occur for the range \(\alpha \gtrsim 3.0\), irrespectively of the value of the parameter \(\beta \), which provides the brane thickness. Since the AdS curvature is provided by the product \(\alpha \beta \), according to what has been discussed, both current precision torsion-balance experiments and the 5D electroweak scale impose the constraint \( 2.0 \times 10^{-19}\,\mathrm{m}\lesssim \beta \lesssim 44\,\upmu \mathrm{m}\) to the brane thickness. Together with the constraint \(3.0 \lesssim \alpha \), it implies that the AdS curvature is thus limited in the range provided by the product \(6.0 \times 10^{-19}\,\mathrm{m}\lesssim \alpha \beta \).

It is worth to mention that the superpotential \(W_{\alpha ,\beta }(\phi )=3\alpha \beta \sin \left( \sqrt{\frac{2}{3\alpha }}\phi \right) \) in (10) has parameters \(\alpha \) and \(\beta \), which generate a 2-parameter family of superpotentials. We showed that the configurational entropy is able to provide a better selection of the superpotentials in such a family parametrised by \(\alpha \) and \(\beta \) than the ones existent in the literature.

Moreover, BCE also provides an independent criterion to regulate the stability of spatially bound configurations based solely on the informational content of their spatial profiles [36]. In fact, the BCE maximum represents the boundary between stability and instability, as in the case analysed in [36] for Q-balls.

In the next section we shall provide the consequences of the model studied above and point out future perspectives.

4 Concluding remarks and outlook

The entropic information has been studied here in brane-world models, with emphasis on the sine-Gordon model, which has been chosen by its very physical content and usefulness. Indeed, the sine-Gordon model parameters provide the AdS bulk curvature and the domain wall thickness as well. Hence the brane-world entropic information for the sine-Gordon model has been achieved, providing the most suitable values for the AdS curvature. In fact, we proved that the higher the brane thickness \(\beta \), the higher the respective value for the brane configurational entropy. The brane-world configurational entropy is, moreover, used to evince a higher organisational degree in the structure of system configuration likewise, for large values of one of the sine-Gordon model parameters. The Gleiser and Stamatopoulos procedure was also used to acquire the correlation between the brane-world configurational entropy and the energy of the system, withal. Moreover, our analysis is further based on the configurational entropy given by \( S=S(\alpha )\), depicted in Fig. 5. Such configurations for \(\alpha \gtrsim 3.0\) are most probably found by the system, since for such a range of \(\alpha \) the configurational entropy \(S(\alpha )\) approaches zero.

We want to stress that for a fixed set of parameters \((\alpha ,\beta )\) there is a corresponding brane-world model. Hence, each point of the graphics in Fig. 5 corresponds to a distinct brane-world model, which clearly depends on such two parameters. Although different choices of parameters have different associated Hilbert spaces and comparing their CEs is not useful, we proved that for \(\alpha \rightarrow 0\) and for \(\alpha \gtrsim 3.0\) (indeed asymptotically for bigger values of \(\alpha \)) the CEs of all models tend to the same value (asymptotically tend to zero). Hence we may assert that the corresponding brane-world models are in such a sense similar, asymptotically. Moreover, the energy density in Eq. (20) goes to zero for all values of \(\beta \), when \(\alpha \sim 0.5\). It coincides, by Fig. 5, to the highest values of the configurational entropy, for any value of \(\beta \). Hence our results show that for values of the highest entropy (namely, for any \(\beta \) and \(\alpha \sim 0.5\)), the brane energy density has a minimum value. It implies that such models are not allowed, for configurational entropic reasons. When \(\alpha \sim 0.5\) is chosen, by varying \(\beta \) the CE proportionally varies and the CE increases as \(\beta \) also increases, as illustrated by Fig. 5. On the other hand, for fixed \(\beta \) and \(\alpha \) varying, we have bounded the values of the parameters corresponding to a better ordering of the system, according to the CE, for asymptotic values of \(\alpha \rightarrow 0\) and \(\alpha \rightarrow +\infty \).

Furthermore, better ordered models from the informational point of view are related to the ones with less energy. It is based upon the BPS states, which makes it possible in conformal coordinates for the field equations that rule the brane-world model to lead to a 1-dimensional Schrödinger equation. Hence regarding the extra dimension, the problem is reduced to the analysis of a potential in standard quantum mechanics, wherein it is well known that the system tends to the ground state.

It also worth to mention that, although the extra dimension has an infinite extent, the energy density is localised and finite, as well as the sine-Gordon brane itself. The CE framework holds for any physical system whose energy density is localised, as is the case in our current procedure. In fact, the non-singular warp factor makes the brane localised and the extra-dimensional infinite extent is effectively finite.

Once the formalism of the brane-world configurational entropy and the entropic information as well, has been developed, we can further apply a similar procedure to the previous sections to other thick brane-world models. Indeed, an entire new family of models of the sine-Gordon type, starting from the sine-Gordon model, including the double sine-Gordon, the triple one, and so on, have been obtained in [42]. Such models appear as deformations of the starting sine-Gordon model, and as they present different topological sectors, it would be important to probe them from the point of view of the brane-world configurational entropy. Since the solutions of these deformed models can be constructed explicitly from the topological defects of the sine-Gordon model itself, we plan to study in particular the double sine-Gordon model in a brane-world scenario with a single extra dimension of infinite extent, as in this framework a stable gravity scenario has been shown to be allowable [42]. Other interesting brane-world models that are beyond the scope of our article, as for instance the Bloch branes [14], the cyclically deformed topological defects that generate domain walls [43] and the asymmetric sine-Gordon model [44, 45], can be investigated from the point of view of the entropic information and the brane-world configurational entropy.