1 Introduction

Multiparticle production in high-energy collisions often involves many contributing intermediate sub-sources. The cleanest such example is \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4\), or its equivalent with a \((\gamma ^*/{\mathrm Z}^0)(\gamma ^*/{\mathrm Z}^0)\) intermediate state. A more tricky one is multiparton interactions (MPIs) in hadronic collisions, wherein a variable set of (semi)perturbative partonic collisions together with the beam remnants are at the origin of the subsequent hadronization.

In neither case can a first-principles QCD calculation be carried out to describe the particle production process. Instead string or cluster models are used [1]. Both are based on an \(N_C \rightarrow \infty \) limit [2], wherein each color–anticolor pair is unique. Thus, in the string model, each quark is at the end of a string, whereas a gluon is attached to two string pieces and thus forms a kink on a longer string usually stretched between an endpoint quark and ditto antiquark [3]. In simple systems like \({\mathrm e}^+{\mathrm e}^- \rightarrow \gamma ^*/{\mathrm Z}^0 \rightarrow {\mathrm q}\overline{\mathrm q}{\mathrm g}\) such principles give unique topologies, but for more complicated situations ambiguities arise. When these can be associated with the presence of unexpected color topologies we speak of color reconnection (CR). The historical example in this spirit is the decay \({\mathrm B}^+ = {\mathrm u}\overline{\mathrm b}\rightarrow {\mathrm u}\overline{\mathrm c}{\mathrm W}^+ \rightarrow ({\mathrm u}\overline{\mathrm c}) ({\mathrm c}\overline{\mathrm s}) \rightarrow ({\mathrm u}\overline{\mathrm s})({\mathrm c}\overline{\mathrm c}) \rightarrow {\mathrm K}^+ \, {\mathrm J}/\psi \rightarrow {\mathrm K}^+\upmu ^+\upmu ^-\) [4], where we have used brackets in intermediate states to delineate separate color singlet identities.

Similarly, for \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^-\), with \({\mathrm W}^+ \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2\) and \({\mathrm W}^- \rightarrow {\mathrm q}_3 \overline{\mathrm q}_4\), to first approximation the \({\mathrm q}_1 \overline{\mathrm q}_2\) and \({\mathrm q}_3 \overline{\mathrm q}_4\) systems hadronize separately from each other. Deviations from such a production picture could be parametrized as an admixture of alternative color-reconnected \({\mathrm q}_1 \overline{\mathrm q}_4\) and \({\mathrm q}_3 \overline{\mathrm q}_2\) systems. Such CR was highly relevant in the context of the \({\mathrm W}\) mass measurement at LEP2 [5, 6], where a potentially non-negligible uncertainty was predicted. This led to the development of dedicated studies aimed directly at measuring CR in hadronic \({\mathrm W}^+{\mathrm W}^-\) events [7–10]. The most extreme CR models could be ruled out, but not enough statistics was collected to definitely distinguish between the more moderate CR models and no CR [11]. Nevertheless such a moderate-model reconnection in about half of all events provided the best overall description.

Modeling and testing of CR in hadronic collisions is rather more complicated [12, 13]. Yet the case for it playing an important role is compelling, e.g. from the rise of the average transverse momentum with increasing charged multiplicity. Thus, given the predominance of hadronic colliders in recent years, first with the Tevatron and now with the LHC, recent CR studies have rather aimed to address the more complicated issues arising there, and has led to the introduction of several new models [14, 15]. These rely only on the distribution of final state partons just prior to the hadronization, making them directly applicable also to \({\mathrm e}^+{\mathrm e}^-\) colliders. Even if the CR effects are expected to be significantly smaller in \({\mathrm e}^+{\mathrm e}^-\) than in \({\mathrm p}{\mathrm p}\), this is compensated by a cleaner environment allowing for higher precision. On the one hand, it is therefore highly relevant to go back and check whether the newly developed models are consistent with the LEP2 data. Unfortunately, the statistics is then limited, with only about \(10^4\) \({\mathrm W}^+{\mathrm W}^-\) events per LEP experiment, giving non-negligible statistical uncertainties, of the order of 40 MeV for the \({\mathrm W}\) mass [11]. On the other hand, it is useful to consider what further tests may come in the future. As an example, the recently suggested 100 km \({\mathrm e}^+{\mathrm e}^-\) collider [16] would produce \(\mathcal {O} (10^8)\) \({\mathrm W}^+{\mathrm W}^-\) pairs, resulting in a statistical uncertainty on the \({\mathrm W}\) mass below 1 MeV, e.g. from semileptonic decays \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 \ell \nu _{\ell }\). With the calculated mass shifts in the original CR paper of the order 10–20 MeV [5] as a reference, such a precision should make it possible to rule out many CR models, and also (hopefully) definitely confirm the presence of CR effects.

With the discovery of the Higgs boson [17, 18], a new arena for CR studies opens up. The Higgs state is very narrow—the expected width is of the order of 4 MeV—meaning that it is very long-lived. Therefore hadronization of the rest of the event already happened and the produced hadrons already spread out by the time the Higgs decays. That is, the Higgs itself decays essentially in a vacuum, and has no interactions with the rest of the event, be that in \({\mathrm e}^+{\mathrm e}^-\) or \({\mathrm p}{\mathrm p}\) collisions. Among its key decay channels we find \({\mathrm W}^+{\mathrm W}^-\) and \({\mathrm Z}^0{\mathrm Z}^0\), however, and here history repeats itself: fully hadronic decays would be sensitive to CR between the two gauge-boson systems. The variables of interest here are not only masses but even more the angles between the four hadronic jets. Such angles can be modified by CR, a phenomenon which was noted e.g. in the context of top mass studies [14]. CR uncertainties thereby affect precision measurements of the Higgs properties, one of the primary purposes of future e\(^+\)e\(^-\) colliders. To be specific, the SM predicts the Higgs to be a CP-even state, which is also observed to be strongly favored compared with the CP-odd alternative [19, 20]. Extensions of the SM Higgs sector, however, allows for the observed Higgs to be a mixture of both possibilities. One place to search for deviations from the predicted SM Higgs behavior is precisely the angular correlations in hadronic \({\mathrm W}^+{\mathrm W}^-\) (or \({\mathrm Z}^0{\mathrm Z}^0\)) decays [21]. Hence CR could introduce a systematic uncertainty, and in this article we do a first study on the size of such uncertainties in various CR scenarios.

This paper is organized as follows. The different CR models we will compare are briefly summarized in Sect. 2. The three next sections contain studies on three different sets of observables, namely, the \({\mathrm W}\) mass measurement, Sect. 3, the search for CR effects in \({\mathrm W}^+{\mathrm W}^-\) events, Sect. 4, and the Higgs CP measurements, Sect. 5. The article ends with a few conclusions, Sect. 6.

2 The CR models

Our current understanding of QCD does not provide a unique recipe for CR. Therefore the best we can do is contrast different plausible scenarios, and let data judge what works and what does not. In this article we will compare four different CR models, which provide a reasonable spread of properties and predictions. Before briefly presenting each of these models it is useful to outline some of the basic issues that are involved.

One key aspect is what role is given to color algebra. To illustrate this, again consider \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4\). From the onset, \({\mathrm q}_1 \overline{\mathrm q}_2\) form one singlet and \({\mathrm q}_3 \overline{\mathrm q}_4\) another. In addition, there is a 1 / 9 probability that \({\mathrm q}_1 \overline{\mathrm q}_4\) and \({\mathrm q}_3 \overline{\mathrm q}_2\) “accidentally” form singlets. In some models such accidental matches are a prerequisite to allow a CR. In this sense, these models are not really about reconnections but about a choice between already existing singlets. The alternative is to view CR as a dynamical process, wherein (infinitely) soft gluons can mediate any color exchange required to form new singlets. The original non-accidental singlets define an initial state that actively needs to be perturbed to create alternative color topologies. As so often, these two pictures may be viewed as extremes, and the “true” behavior may well be in between, with a bit of each.

Here another aspect enters, namely the role of geometry/causality. With a \(c\tau \approx 0.1\) fm, the \({\mathrm W}^{\pm }\) decays tend to be separated on a scale an order of magnitude below the typical hadronic size, the latter also being the size of the color fields stretched between color-connected partons. It would thereby seem that the \({\mathrm W}^+\) and \({\mathrm W}^-\) color fields fully overlap, at least in the threshold region where the \({\mathrm W}\)’s are not too strongly boosted apart. Introducing causality, however, the color fields take some time to grow to full size (e.g. in the SK-I model described later). Meanwhile they drift apart, thereby only partly overlapping, and with an overlap that depends on the motion of all the string pieces from each \({\mathrm W}\) decay. In models where geometry is allowed to play a role there is also a natural decoupling of the two \({\mathrm W}\) decays at energies well above the threshold region, or if the \({\mathrm W}\) width could be sent to zero, and this should not be spoiled by the “accidental” singlets.

Finally there is also a selection principle: if there are many potential reconnections in an event, which are the one(s) that actually occur? This could be at random or involve some bias. The most common bias is to make use of the \(\lambda \) measure, which characterizes the total string length [22]. That is, the smaller the \(\lambda \), the better ordered are the partons along the strings. The full \(\lambda \) expression is rather messy, so a commonly used approximation is

$$\begin{aligned} \lambda = \sum _{ij} \, \ln \left( 1 + \frac{m_{ij}^2}{m_0^2} \right) , \end{aligned}$$
(1)

where the ij sum runs over all parton pairs connected by a string piece and \(m_0\) is of the order of a typical hadronic mass. The average hadronic multiplicity of a string piece grows roughly logarithmically with its mass, so a reduction of \(\lambda \) corresponds to a reduction of the “free energy” available for particle production.

Among the four different CR models considered in this study, SK-I and SK-II were developed for \({\mathrm W}\) mass uncertainty studies at LEP2 [5]. The gluon-move model, GM, was introduced as a simple model, among a few others, to study the effect of CR in top decays [14]. Finally, the QCD-based model, CS, was introduced to look for effects in soft QCD, especially baryon production [15]. The first two models are only applicable for the hadronic decays in diboson production, whereas the latter two could be used for any process. All of the models are available in (recent versions of) Pythia 8 [23], the first two having been (re)implemented expressly for this study. That program also contains another CR model [13], used by default, that relies on the MPI structure of hadron collisions and therefore cannot be used in \({\mathrm e}^+{\mathrm e}^-\). All of the algorithms are applied after the hard primary process and the subsequent parton-shower evolution, but before the hadronization step. Typically this means that each \({\mathrm W}\) contains a handful of gluons, in addition to the primary \({\mathrm q}\overline{\mathrm q}\) pair, when CR is to be considered.

Both the SK-I and the SK-II models utilize the space–time picture of strings being stretched between the different decay products of the two bosons. A reconnection between two string pieces from different bosons is allowed only when these overlap in their space–time motion. Since such an overlap is assumed associated with the possibility for dynamical soft-gluon exchange between the two overlapping color fields, there is no color-factor suppression for reconnection. The two approaches differ in their definition of what an overlap means, taking two extreme limits by analogy with Type I and Type II superconductors, which explains their names. In SK-I the strings are imagined as elongated bags, and the probability for a reconnection is proportional to the integrated space–time overlap between two string pieces. (Up to saturation effects to ensure that probabilities stay below unity.) This model contains one parameter that directly controls the overall strength of the CR, which made it convenient for experimental LEP2 studies. For SK-II the string is considered to contain a thin core, a vortex line, where all the topological information is stored, even if the full energy still is spread over a larger volume. A reconnection can only occur when the space–time motion makes two such cores cross each other. This model introduces no special parameters, and therefore gives unique predictions. (In both models one parameter is used to describe how the strings decay exponentially in proper time, and in SK-I additionally the string width is a parameter, but these parameters are almost completely fixed within the string model itself.) Normally only one reconnection is made, namely the one that happens first in proper time. By default this reconnection may either increase or decrease the total \(\lambda \) measure, but in the primed variants SK-I\('\) and SK-II\('\) only reconnections that reduce \(\lambda \) are considered. The SK models were tested at LEP2, where only the most extreme versions of SK-I were ruled out. For the SK-I model best agreement with data was obtained with parameter such that approximately 50 % of all events contain a reconnection, as already mentioned.

Fig. 1
figure 1

Example of the gluon-move (a) and the gluon-flip (b) reconnections in the gluon-move model. The dashed lines represent the color configuration of the partons

Full size image

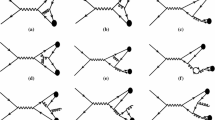
The gluon-move (GM) model was introduced to probe uncertainties in the top mass measurement, while still providing an overall good description of data. It is a very simple framework, in which the reduction of the \(\lambda \) measure is at center, whereas neither color algebra nor space–time geometry are considered at all. It contains two different types of CR, the gluon-move one, which gives the model its name, and a flip mechanism. In the former, the change in \(\lambda \) measure is calculated if any of the gluons is moved from its current location between two color-connected partners to instead be located on the string piece of any other color-connected pair, Fig. 1a. The move that lowers the total \(\lambda \) measure the most is carried out, repeatedly until the minimum \(\lambda \) measure is reached. The move step is quite restrictive, in that a string stretched between a \({\mathrm q}\) and a \(\overline{\mathrm q}\) endpoint will remain so; it is only the gluons in between that may change. Therefore an additional flip step is carried out after no more moves are possible. The flip mechanism flips the color lines between two strings when this can reduce \(\lambda \), Fig. 1b, thereby mixing up also the string endpoints with each other. (This is similar in character to what in another context is called color swing [24].) A string is only allowed to do a single flip, to avoid the formation of gluon loops. The strength of the CR can be controlled by excluding a fraction of the gluons in the above scheme, or by requiring the \(\lambda \) reduction in a potential move/flip to be above some minimal value. The parameters used in this study were tuned to describe the LHC minimum bias data (although not quite as well as the default model). To allow more control, three alternative versions are considered in this article: only including the move mechanism, GM-I, only the flip mechanism, GM-II, and the combination of both methods, GM-III.

The SU(3)-based model, CS, is similar to the GM model, in that it also minimizes the \(\lambda \) measure by doing flips between strings. But it differs in two major aspects. Firstly, it relies on the SU(3) color rules from QCD, together with a space–time causality requirement, to determine whether two strings are allowed to reconnect or not. Secondly, it introduces a junction type of reconnection that is unique to this model. The use of SU(3) color rules is a choice of philosophy, as already discussed. It limits which string pieces may flip with each other by requiring matching color labels, i.e. that the color flow is ambiguous already by the color assignments of the partons. It is possible to change the QCD-based default value, however, in the extreme case such that all string pieces may flip with each other. For a flip between any two string pieces it is further required that they are in causal contact with each other, i.e. that each has had time to form before the other has had time to hadronize. The detailed formulation of this requirement is ambiguous, however, so a few options are available, with a tuneable parameter. The appearance of junction structures offers a clear extension relative to the other models. An (anti)junction is a point where strings stretched from three (anti)colored quarks meet. In \({\mathrm e}^+{\mathrm e}^-\) events they must be created in pairs, one junction and one antijunction. When events hadronize, one (anti)baryon is created around each (anti)junction, thereby introducing a new mechanism for baryon production. It is more important for high-energy hadronic collisions than it is for the studies in this article, however. A possibility not considered is that of color ropes [24–26], where several parallel strings combine into one of a higher color representation. If existing at all, ropes are more likely to play a non-negligible role in hadron or heavy-ion colliders, where the beam axis offers a natural alignment of many strings.

While the overwhelming majority of CR models have been developed for Lund string fragmentation, there have also been a few for cluster models [27, 28]. In the current Herwig++ model CR is based on a minimization of the sum of squared cluster masses (similarly to the generalized area law model for strings [29]) rather than on the logarithmic \(\lambda \) measure used here. While the Herwig++ model can be used for \({\mathrm W}^+{\mathrm W}^-\), no studies in the spirit presented here have been performed so far.

3 W mass measurements

One of the key tasks of LEP2 was to determine the \({\mathrm W}\) mass, on its own right and as a test of the Standard Model consistency. Measurements were done both in the fully hadronic and in the semileptonic channels [10, 30]. Both of them provide similar statistical errors, but the fully hadronic channel has a larger systematic uncertainty, due to the CR contribution. The uncertainty estimate depends on the analysis method as well as on the choice of CR models considered (and on their parameters), but was found to be of the same magnitude as the statistical error. The large expected decrease in the statistical error at future \({\mathrm e}^+{\mathrm e}^-\) colliders would make the fully hadronic channel irrelevant for \({\mathrm W}\) mass measurements, unless the CR uncertainty could be constrained by other means. This was already considered at LEP2 [10], where \({\mathrm W}\) mass measurements for different jet cuts were used to constrain the SK-I strength parameter.

Table 1 Systematic mass shifts for the \({\mathrm W}\) mass at a center-of-mass energy of 170 GeV. The \(\langle \Delta \overline{m}_{\mathrm {W}} \rangle \) value is the average reconstructed minus produced \({\mathrm W}\) mass for the no-CR baseline. The \(\langle \delta \overline{m}_{\mathrm {W}} \rangle \) is the additional shift for each CR model relative to this baseline. The Monte Carlo statistical uncertainty on the latter quantity is 4 MeV
Full size table

In this section we want to turn the table, and study how a precision measurement of the \({\mathrm W}\) mass difference between the fully hadronic and the semileptonic channels would constrain CR models and parameter values. The semileptonic channel is free of CR effects that could affect the \({\mathrm W}\) mass, and thus provides the “true” \({\mathrm W}\) mass baseline as far as CR effects are concerned. For this relative comparison a full optimization of both cuts and analysis methods is not required. Instead we will follow the method outlined in [5] to provide a simple estimate of CR effects.

To this end, one million \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4\) events were simulated for each CR model, a number big enough to clearly discern the effects we are interested in, and also well within the reach of future \({\mathrm e}^+{\mathrm e}^-\) colliders. The events are required to have exactly four jets using the Durham jet algorithm [31], with a \(k_\perp \) cut of 8 GeV. In addition the jets are also required to have an energy of at least 20 GeV each and be separated by an angle of 0.5 radians. The four jets can be combined into two \({\mathrm W}\) bosons in three different ways. A few options for picking the “right” combination are considered:

  1. 1.

    With the access to Monte Carlo truth information, one can try to match each jet with an outgoing parton of the \({\mathrm W}\) decays. This is done by picking the match that minimizes the product of the invariant masses between each jet and its associated parton.

  2. 2.

    One can use that the \({\mathrm W}\) mass is known to be close to 80 GeV, and so minimize \(|\overline{m}_{\mathrm {W}} - 80|\) to find the desired match, where \(\overline{m}_{\mathrm {W}}\) is the average reconstructed \({\mathrm W}\) mass.

  3. 3.

    Instead of requiring the average to be close to the known \({\mathrm W}\) mass, both masses individually could be optimized to be close to 80 GeV, i.e. minimize \(|\overline{m}^{(1)}_{\mathrm {W}} - 80| + |\overline{m}^{(2)}_{\mathrm {W}} - 80|\).

  4. 4.

    At threshold the jets from the same \({\mathrm W}\) are almost back-to-back. A match can therefore be found by maximizing the sum of opening angles.

To a large extent these methods pick the same combinations, and thus they give similar results. Most of the problems arise in events with hard QCD radiation, where none of the methods are expected to work well. As a separate topic it would be interesting to study the effect of perturbative QCD radiation on the hadronic \({\mathrm W}\) mass measurement. The Pythia shower already handles the first emission correctly [32, 33], but to go beyond that one should compare different shower algorithms with and without merging and matching to yet higher orders.

The \({\mathrm W}\) mass is calculated as the average of the two chosen \({\mathrm W}\) combinations. Since the target of this study is CR effects, the Breit–Wigner broadening of the mass spectrum is removed by subtracting the average of the produced \({\mathrm W}\) bosons. The results for all the methods are listed in Table 1. The results for SK-I and SK-II differ slightly from the result in the original paper [5], which is due to the \(p_\perp \)-ordered shower in the newer versions of Pythia not being identical with the older mass-ordered ones of the time.

The GM model shows an interesting behavior; the move mechanism lowers the \({\mathrm W}\) mass, while the flip mechanism increases it, and the two effects accidentally cancel each other in the combined result. This may be understood as follows. If a gluon from \(W_1\) is radiated at a large angle, such that it will move closer to the decay products from \(W_2\), the move mechanism will connect the gluon to \(W_2\), Fig. 1a. This will increase the mass of \(W_2\) and decrease the mass \(W_1\), but the decrease is larger than the increase, leading to the observed lower average mass. The flip mechanism instead will connect jets between the two Ws, and thereby increase hadronization production of particles outside the \({\mathrm W}\) “cones”. This leads to larger opening angles, and thereby larger \({\mathrm W}\) masses. These two explanation will be revisited when studying the dedicated CR measurements. The complete cancellation is accidental, however, which becomes clear when the energy is varied. The SK-I and SK-II models also show opposite-sign effects, thereby further stressing the message that the mass-shift direction of CR effects cannot be taken for granted. Finally, the CS model shows no significant shifts, which will be a general trend throughout all the analyses. In this model the limitation from the color rules and the requirement of a lower \(\lambda \) make the majority of the e\(^+\)e\(^-\) collider events have no CR. By removing the color constraints (CS max), the model starts to show an effect. This extreme case is already excluded at hadron colliders, however.

A new collider should have the capacity to increase the energy beyond the \({\mathrm W}^+{\mathrm W}^-\) threshold. As was already observed for the SK-I model [5], the CR effects depend on the CM energy. There are two competing effects: firstly, the effect of a single reconnection becomes larger with increased energy, and secondly, the probability to have two overlapping strings decreases with energy. The CR mass shifts for different CM energies can be studied in Table 2. Method 4 is here not included, since the maximum-angle method is only reliable close to the threshold. The differences between the methods become smaller at higher energies, since the boost makes it easier to find the right combinations. The actual shifts increase at the intermediate energy, but drop when the energy is increased further. The only model that does not show this trend is the CS model, for which almost no effect is seen at any energy. The large shifts at the two higher energies for the other models provide a compelling argument to repeat the measurements at these energies. It should be recalled, however, that less statistics is expected at the higher energies.

Table 2 Systematic \({\mathrm W}\) mass shifts at center-of-mass energies of 240 and 350 GeV, respectively. The \(\langle \delta \overline{m}_{\mathrm {W}} \rangle \) is the mass shift in the CR models relative to the no-CR result. The Monte Carlo statistical uncertainty is 5 MeV
Full size table

4 Four-jet angular distributions

The direct searches for CR in \({\mathrm W}^+{\mathrm W}^-\) events at LEP ruled out extreme parameter values for SK-I and potentially could also rule out some of the new CR models. Especially the GM-I and GM-II models have that potential, since they were already observed to have a larger effect on the \({\mathrm W}\) mass measurement than the other models.

The analysis relies on the particle multiplicities in the angular regions between two jets from the same \({\mathrm W}\) decay and from different \({\mathrm W}\) decays, respectively, to provide a ratio that is sensitive to CR. The idea is that a reconnection will form a string between jets from different \({\mathrm W}\) decays, thereby increasing the multiplicity between those jets. In general, we will therefore expect the same-to-different ratio to become lower when CR is switched on. Several LEP experiments [7–9] performed this measurement. The results presented in the studies are after detector simulation, however, and as such are not directly comparable with the results obtained in this study. Instead we will rely on the ratio between the CR and the no-CR results (r; see below for the exact definition), since detector effects are reduced for this observable. A preliminary combination of the different experiments gave \(r = 0.969 \pm 0.011 (\mathrm {stat.}) \pm 0.009 (\mathrm {syst.\,corr.}) \pm 0.006 (\mathrm {syst.\,uncorr.})\) [34] corresponding to a 2.2 standard deviation disagreement with the no-CR scenario. A later combined study [11] has increased this to disfavor the no-CR model at a 2.8 standard deviation level, by combining with the mass-shift results and performing a \(\Delta \chi ^2\) fit. No separate r results were shown, however, and therefore we will have to rely on the preliminary combination.

The event selection and analysis procedure varied slightly between the different LEP experiments. Two of the experiments relied purely on the angles to pair the jets [8, 9], while one experiment also used the invariant masses [7]. We decided to mimic the analysis from the L3 collaboration [8]. A short recap of the event selection and analysis is presented, but for more details we refer to the experimental studies.

The event selection requires each event to have exactly four jets with the Durham jet algorithm, with \(y_\mathrm {cut} = 0.005\). The two smallest of the six interjet angles are required to be below \(100^{\circ }\) and be non-adjacent. These are assumed to be the two regions between the different \({\mathrm W}\) decays, and are normally referred to as regions B and D (Fig. 2). In addition two more angles are required to be between \(100^{\circ }\) and \(140^{\circ }\) and be non-adjacent. These are assumed to be the regions inside the \({\mathrm W}\) decays, and are normally referred to as region A and C (Fig. 2). If several combinations are allowed, the one with the largest total opening angle is chosen. For each region the particles are projected onto the plane spanned by the two jets, and all particles are assigned a rescaled angle \(\varphi _r = \varphi /\varphi _{\mathrm {jj}}\), where \(\varphi \) is the angle from the particle to one of the jets and \(\varphi _{\mathrm {jj}}\) is the angle between the two jets. This distribution is shown in Fig. 3, where the different regions are separated by adding an integer to each. The final observable is defined as

Fig. 2
figure 2

Illustration of the four interjet regions used in the analysis

Full size image
Fig. 3
figure 3

The \(\varphi _r\) distribution at a center-of-mass energy of 183 GeV

Full size image
Table 3 Results for \(R_N\) and r for different intervals in \(\varphi _r\) at a center-of-mass energy of 183 GeV. Two maximal CR models are included for SK-I and for the QCD based method, respectively. The Monte Carlo statistical uncertainty on r is around 0.0025
Full size table
$$\begin{aligned} R_N = \frac{\int _{0.2}^{0.8}\frac{\hbox {d}n}{\hbox {d}\varphi _r}(A+C)\hbox {d}\varphi _r}{\int _{0.2}^{0.8}\frac{\hbox {d}n}{\hbox {d}\varphi _r}(B+D)\hbox {d}\varphi _r}. \end{aligned}$$
(2)

The regions closest to the jets are excluded since they are mainly sensitive to the internal jet evolution. Finally the ratio between the different CR models and the no-CR baseline is defined as \(r = R_N^{\mathrm {CR}} / R_N^{\mathrm {no CR}}\). Thus a deviation from unity would disfavor the no-CR scenario. The results for the various CR schemes are shown in Table 3. As expected, all CR models, except for GM-I, predicts an r below unity. The GM-I model only allows the gluon-move reconnections, and therefore it does not reconnect the quarks at the string endpoints. Instead, it can take gluons emitted at large angles and move them to the other \({\mathrm W}\) string, thereby actually lowering the amount of radiation in region B and D, Fig. 1a. This is the same explanation as for the lower \({\mathrm W}\) mass observed in Sect. 3. The GM-II model only does flips, which is exactly what this observable is optimized to measure. This is in fair agreement with observations, since this model shows relative large deviations from unity. The SK-I model with default strength is quite well in agreement with the actual measurement. For comparison a SK-I max model, where a reconnection is always done, is also included. It gives too large shifts and so can be excluded. The SK-II models and the CS model do not produce any large shifts. The maximal CS model, where the SU(3) rules are ignored and CR is only limited by the \(\lambda \) measure, shows a larger effect and it can potentially be ruled out by experiments. It is, however, still relatively small compared to the other maximal CR models. In this study we consider several intervals, and not only the 0.2–0.8 considered in the original study. A clear trend shows that the smaller the interval, the more sensitive the observable becomes, i.e. varies more from unity. This is not surprising since the region closest to the jets are dominated by their perturbative behavior. It should be noted that the statistics becomes worse for smaller intervals, but with the larger expected statistics at a new collider, a smaller interval than at LEP2 would most likely be preferable.

To check if the new models are already excluded by the LEP measurements, the number of standard deviations from the measured result is calculated, see Table 4. The experimental uncertainties are assumed Gaussian and added in quadrature. The only model excluded at the three \(\sigma \) level is the GM-I model, which is the only model predicting a larger than unity r. The uncertainty is still too large to invalidate the other models, and a new collider with higher precision is needed to constrain these.

Table 4 Deviations from the measured result shown in number of standard deviations (\(n_\sigma =(r_\mathrm {exp}-r_\mathrm {th})/(\delta r)_\mathrm {exp}\)), where the \(r_\mathrm {th}\) are those in the 0.2–0.8 region of Table 3
Full size table

The \({\mathrm W}\) mass measurement was seen to be more sensitive to CR at higher energies, and hence a similar effect is expected here. The method described above cannot directly be applied at higher energies, however, since the increased boost of the \({\mathrm W}\) bosons changes the angular distributions between the jets. Instead we apply a method similar to method 3 in the \({\mathrm W}\) mass section to define the two angles within the \({\mathrm W}\) decays. The two other angles are defined to minimize the total sum of their angles. The results for the different energies are shown in Table 5. The new method performs slightly worse at 183 GeV, i.e. the ratios lie closer to unity. This is especially evident when considering the maximal CR models. At higher energies, however, the deviation from unity becomes larger for some of the more extreme models, indicating a better sensitivity, but this observable shows no sensitivity for the CS model. The moderate models do not show any significant variation with energy, and as such it is difficult to tell whether the potential limits on CR can be stronger at higher energies. In general we expect a falling fraction of events with CR for higher energies, but more spectacular effects for the events where CR occurs, so in the future we will need to search for more selective tests.

Table 5 Results for \(R_N\) and r for different center-of-mass energies for a fixed interval (0.2–0.8). The Monte Carlo statistical uncertainty on r is around 0.0015
Full size table

As a slightly simpler observable, to test CR, it is possible to study the overall multiplicity. In most models CR minimizes the \(\lambda \) measure and therefore also lowers the total multiplicity. This is normally compensated by a retuning of the hadronization parameters or the perturbative regime. But by comparing the multiplicity in fully hadronic and semileptonic \({\mathrm W}^+{\mathrm W}^-\) events, it is possible to directly probe CR. If no CR is switched on, the ratio \(N_{\mathrm {ch}}^{{\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4} / (N_{\mathrm {ch}}^{{\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 \ell \nu _{\ell }} -1) \) is expected to be exactly equal to 2 (with \(\ell = {\mathrm e}\) or \(\mu \), but excluding \(\tau \)). A simple study at a center-of-mass of 170 GeV shows that indeed it is interesting to use this observable. Both the individual GM models show an effect, 1.96 and 1.97 for GM-I and GM-II, respectively. Contrary to the earlier observables, the two effects add coherently and the combined result is 1.93. With 1.97 the CS model also shows more sensitivity in this observable as compared to the more complicated four-angle measurement. Similar results are also obtained for the SK models, so this would be an intriguing measurement for a future \({\mathrm e}^+{\mathrm e}^-\) collider.

5 Higgs parity measurements

As discussed in the introduction, hadronic \({\mathrm W}^+{\mathrm W}^-\) and \({\mathrm Z}^0{\mathrm Z}^0\) decays of the 125 GeV Higgs offers a novel system for CR effects. Like in the \({\mathrm W}^+{\mathrm W}^-\) studies above we should not expect big effects, so it is unlikely to be discernible in the busy LHC environment. In a process like \({\mathrm e}^+{\mathrm e}^- \rightarrow \gamma ^*/{\mathrm Z}^{0*} \rightarrow {\mathrm H}^0{\mathrm Z}^0 \rightarrow {\mathrm H}^0\ell ^+\ell ^-\), or \(\upmu ^+\upmu ^- \rightarrow {\mathrm H}^0\) for that matter, detailed studies should become possible, however, assuming sufficient luminosity. As before, reconstructed masses and angles may become affected. Rather than simply repeating discussions along the lines of the previous two sections, we choose to illustrate possible effects for another set of observables, related to setting limits for CP violation in Higgs decays. We are aware that such tests can be performed in purely leptonic decays, say \({\mathrm H}\rightarrow {\mathrm Z}^0{\mathrm Z}^0 \rightarrow \upmu ^+ \upmu ^- {\mathrm e}^+ {\mathrm e}^-\), although with a much lower branching ratio. It can also be probed by the decay angles of the \({\mathrm Z}^0\) produced in the association with the \({\mathrm H}^0\) [35]. The purpose of this brief study is not to compare the relative merits of CP-violation tests in these different channels, but to stay with \({\mathrm H}\rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4\) and check what CR could mean there. To this end we will use a simplistic \(\chi ^2\) test on what could be the most sensitive variable.

Fig. 4
figure 4

The three angles sensitive to the parity of the Higgs boson. Three different parity scenarios are shown together with a small selection of different CR models

Full size image

To simulate a mixed CP-even and CP-odd Higgs boson, we will use the Higgs doublet model already implemented in Pythia, with the option to allow CP-violation based on the expressions in [21]. We will assume that the 125 GeV Higgs is almost completely CP-even, with a small admixture of CP-odd. Allowing for an interference term between the two, the Higgs cross section can be written as

$$\begin{aligned} \sigma \propto k_{\mathrm {even}}^2 A + k_{\mathrm {odd}}^2 B + k_{\mathrm {even}}k_{\mathrm {odd}} C, \end{aligned}$$
(3)

where A, B, C depend on the kinematics of the event and the k determine the contributions to the different types. Since A, B, and C are not of the same order of magnitude, a characterization in terms of a mixing angle is not convenient. Instead we use a definition based on the fraction, later referred to as parity fraction, of the events coming from either of the odd and the interference parts of the cross section:

$$\begin{aligned} f = \frac{|k_{\mathrm {odd}}^2 B| + |k_{\mathrm {even}}k_{\mathrm {odd}} C|}{|k_{\mathrm {even}}^2 A| + |k_{\mathrm {odd}}^2 B| + |k_{\mathrm {even}}k_{\mathrm {odd}} C| } \, . \end{aligned}$$
(4)

For an almost CP-even Higgs, \(f \approx 0\), this quantity provides a reasonable estimate of the amount of CP-violating interference introduced for the Higgs boson.

The parity of the Higgs can be measured by studying the angles between the fermions from the boson decays. In the standard analyses of the spin/parity of the Higgs boson (see e.g. [36, 37]), five such angles are defined, out of which three are sensitive to the parity of the Higgs. These three angles are: \(\theta _1\), the polar angle of a fermion in the rest frame of its \({\mathrm W}\) mother, with respect to the direction of motion of the \({\mathrm W}\) in the \({\mathrm H}\) rest frame, \(\theta _2\), similarly but for the other \({\mathrm W}\), and \(\varPhi \), the angle between the two planes spanned by the decay products of the respective \({\mathrm W}\) bosons. The rest of this section will therefore be a study of the effect of CR on these three angles.

To only have to consider the Higgs decay itself we have studied the process \(\upmu ^+\upmu ^- \rightarrow {\mathrm H}^0\), but this should only be viewed as a technical trick. All models are set up to easily handle this, whereas \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm H}^0 {\mathrm Z}^0\) would require a bit more bookkeeping for the SK models. Otherwise the models remain unchanged relative to previous studies. The fact that at least one of the \({\mathrm W}\)’s have to be strongly off-shell implies that its lifetime is considerably reduced, and this is taken into account in the SK models. To estimate the effect of CR on the angles, 100 million \(\upmu ^+\upmu ^- \rightarrow {\mathrm H}^0 \rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1\overline{\mathrm q}_2{\mathrm q}_3\overline{\mathrm q}_4\) events are simulated for each CR model and for each parity fraction, respectively.

The events are required to have exactly four jets using the Durham jet algorithm with a \(k_\perp \) cut of 8 GeV, followed by an additional energy cut of at least 10 GeV per jet and a angular separation of 0.5. Two different methods to pair the jets were considered, either to maximize the opening angles, or to minimize \(|M_{{\mathrm W}} - 80|\) for a single \({\mathrm W}\). The second method was found to be significantly more sensitive, and we will therefore restrict ourselves to this method. The distribution for the three angles are shown in Fig. 4. Deviations between the SM Higgs and the different parity fractions are visible by eye for all the three angles. Both of the curves with nonvanishing CP-oddness show almost identical behaviors, indicating that the sign of the interference term is unimportant for these observables (at least for small deviations). Comparing the pattern of variation for the CP-violating models and the CR models, respectively, shows an interesting picture. For \(\theta _1\) and \(\theta _2\) the deviations go in the same direction, whereas for \(\varPhi \) the deviations are in opposite directions. Thus a simultaneous study in principle would allow one to disentangle the two potential effects.

To quantify the deviation from the no-CP-odd no-CR baseline, a simple \(\chi ^2\) test is applied to the distributions. The most sensitive angle is \(\theta _1\), and we therefore restrict our studies to this observable. A complete experimental analysis most likely would combine all the angles in a multivariate analysis. For each parity fraction the \(\chi ^2\) is calculated, Fig. 5. As expected the \(\chi ^2\) increases smoothly with this fraction. Similarly, the \(\chi ^2\) is also included for the different CR models. The crossover point is a simple indicator for when CR becomes an issue for Higgs parity measurements. This point occurs around 2–5 %, with the higher values for somewhat more extreme CR models. Thus any limits significantly above this estimate can safely ignore CR effects. It should be stressed that also limits below 2 % should be reachable, once CR is carefully taken into account. This can involve (anti)correlations between the three angles, as already noted, but also studies of particle production patterns between the jets, like the one in Sect. 4.

Fig. 5
figure 5

Deviations between a CP-even Higgs without CR and models with either increased CP-oddness or a CR model. The deviation is quantified as the \(\chi ^2/\mathrm {NDF}\) deviation for the \(\theta _1\) angle

Full size image

6 Conclusions

In this article we have studied the effects of CR at \({\mathrm e}^+{\mathrm e}^-\) colliders, with emphasis on fully hadronic \({\mathrm W}^+{\mathrm W}^-\) events. We find that some newer models, implemented to study CR effects at hadron colliders, show different behaviors for \({\mathrm e}^+{\mathrm e}^-\). The CS model gives rise to very limited variations, whereas for the GM models one specific scenario even shows large enough deviations to be excluded by the LEP data.

Even if the concept of CR is quite straightforward, it allows for several different mechanisms to be at play. These potentially act in opposite directions, making interpretations difficult. This is clearly illustrated by the GM models, where GM-I predicts a smaller reconstructed \({\mathrm W}\) mass and GM-II a larger one. This highlights the need for studying multiple models using several observables, to disentangle what is going on. It is clear that further studies will be needed to extend the range of interesting models, to understand the pattern of potentially balancing effects within each model, to clarify which factors lead to an energy dependence of effects, and so on. There are also separate but related topics, on the one hand to improve the precision of the perturbative description, specifically that of parton showers, on the other hand to improve the modeling of the nonperturbative hadronization even in the absence of CR. Nevertheless, the outcome of the current simple study is fairly optimistic: given enough luminosity, at a few different energies, \({\mathrm e}^+{\mathrm e}^-\) should offer insights into CR mechanisms that complement those obtainable at hadron colliders. This complementarity between the “clean” \({\mathrm e}^+{\mathrm e}^-\) environment and the “dirty” \({\mathrm p}{\mathrm p}\) one may hold the key to a deeper understanding of CR.

The \({\mathrm e}^+{\mathrm e}^- \rightarrow {\mathrm W}^+{\mathrm W}^-\) channel is not the only \({\mathrm e}^+{\mathrm e}^-\) process where CR effects may be relevant. As an example we studied a Higgs parity measurement in the \({\mathrm H}\rightarrow {\mathrm W}^+{\mathrm W}^- \rightarrow {\mathrm q}_1 \overline{\mathrm q}_2 {\mathrm q}_3 \overline{\mathrm q}_4\) channel. The variations from CR were of the same size as the introduction of 2–5 % CP-oddness into the CP-even Higgs, depending on the choice of CR model. The main lesson is not the precise number for this particular observable, but to highlight the need to be aware of potential CR uncertainties for any nontrivial hadronic final state.

Plans for future \({\mathrm e}^+{\mathrm e}^-\) collider usually include the possibility to reach the \({\mathrm t}\overline{\mathrm t}\) threshold. Then hadronic final states will start out with three color singlets: one \({\mathrm W}\) from each top decay, plus one encompassing the \({\mathrm b}\) and \(\overline{\mathrm b}\) from the two decays. Like for the \({\mathrm W}^+{\mathrm W}^-(\gamma ^*/{\mathrm Z}^0)\) background this increases the possibilities for CR effects. Some early studies are found in [38], but updated and extended studies should be performed, including the new models. At the very least, it will be needed in order to estimate the expected CR uncertainty in the measurements of the top properties for possible future colliders. Many of the necessary tools are already in place in Pythia 8, although e.g. the administrative machinery in the SK models needs to be extended appropriately.