Axion production and CMB spectral distortion in cosmological tangled magnetic field

Abstract

Axion production due to photon–axion mixing in tangled magnetic fields prior to the recombination epoch and magnetic field damping can generate cosmic microwave background (CMB) spectral distortions. In particular, the contribution of both processes to the CMB $\mu$ distortion in the case of resonant photon–axion mixing is studied. Assuming that the magnetic field power spectrum is approximated by a power law, $P_B(k)\propto k^n$ with spectral index n, it is shown that for magnetic field cut-off scales 172.5 pc $\le \lambda _B\le 4\times 10^3$ pc, the axion contribution to the CMB $\mu$ distortion is subdominant in comparison with magnetic field damping in the cosmological plasma. Using the COBE upper limit on $\mu$ and for the magnetic field scale $\lambda _B\simeq 415$ pc, a weaker limit in comparison with other studies on the magnetic field strength ($B_0\le 8.5\times 10^{-8}$ G) up to a factor 10 for the DFSZ axion model and axion mass $m_a\ge 2.6\times 10^{-6}$ eV is found. A forecast for the expected sensitivity of PIXIE/PRISM on $\mu$ is also presented.

1 Introduction

During the last decades intensive studies have been done regarding the existence and nature of a primordial magnetic field at both small and large scales. Its existence could have a strong impact in different cosmological scenarios, such as big bang nucleosynthesis (BBN), structure formation, CMB temperature anisotropy etc. In general, in all those scenarios, it is possible to probe its existence only indirectly, namely through the coupling of the magnetic field with the cosmological plasma. Consequently, based on information that we have on BBN, CMB temperature anisotropy etc., it is possible to speculate about the magnetic field structure and estimate its strength at a given scale. In particular, the CMB temperature anisotropy has been one of the most important benchmarks to test the existence of primordial magnetic fields. Indeed, an ubiquitous, anisotropic, and homogeneous magnetic field with strength at present time $B_0\lesssim 3\times 10^{-9}$ G would create the observed CMB temperature anisotropy due to anisotropic expansion of the Universe [1–3]. For a general review on cosmological magnetic field, see Refs. [4–9].

In the presence of a large scale magnetic field, CMB photons can in principle convert into axions or other similar particles due to their coupling with the magnetic field. In Refs. [10, 11] we have studied such a mechanism in the presence of a large scale uniform (spatially homogeneous) magnetic field and applied it to CMB spectral distortions and temperature anisotropy. However, several interesting questions arise as to what happens in the case when the background magnetic field is not homogeneous (tangled magnetic field). Does the magnetic field have an impact on the spectral distortions? Is the impact of the magnetic field on the spectral distortions dominant or subdominant with respect to photon–axion oscillations?

As in the case of density perturbations in the primordial baryonic plasma suffering from Silk damping, we can expect that a spatially varying magnetic field can couple to the baryon plasma and dissipate energy. This would eventually lead to the damping of the primordial magnetic field spectrum on different scales [12, 13]. In general, a distinguishing feature of a non-homogeneous magnetic field in comparison with an uniform field is that the former can have an impact on the CMB by distorting its spectrum. Indeed, it has been shown in Ref. [14] that a spatially varying stochastic magnetic field may significantly dissipate in the cosmological plasma prior to the recombination epoch. By dissipation, the magnetic field energy would transform into kinetic energy of the cosmological plasma and in turn the plasma’s kinetic energy would be efficiently transformed into heat due to high shear viscosity of the plasma. In the limit when the photon mean free path $l_\gamma$ is smaller than the magnetic field mode $\lambda$, $l_\gamma \ll \lambda$, Alfvén, slow, and fast magnetosonic waves with $\lambda <d_\gamma$ are effectively dissipated, where $d_\gamma =(l_\gamma \,t)^{1/2}$ is the photon diffusion length and t is the cosmological time.

In the case when there is an energy injection into the cosmological plasma such as conversion of magnetic field energy into heat, electrons gain energy and the electron temperature $T_e$ becomes higher than the photon temperature T, $T_e>T$. Depending on the redshift at which the magnetic field energy is converted into heat, this effect would eventually lead to CMB spectral distortions if energy is injected for redshift $z\lesssim 2\times 10^6.$ For an early treatment of CMB spectral distortion see Refs. [15, 16]; for further developments see Refs. [17–26], and for production mechanisms of spectral distortions see Refs. [27–30].

2 Dissipation of tangled magnetic field

During the evolution of the universe, it is usually assumed that the conductivity of the cosmological plasma is infinite. In this case the field amplitude scales as $B\sim B_0 a^{-2}(t)$ where a is the cosmological scale factor. Even though this is a good approximation, it does not reflect the more general case, namely the case of tangled magnetic fields when the magnetic field dissipates energy. In order to make contact with the results that follow, we assume that the magnetic field is generated by random processes (stochastic) in the early universe during the inflation or radiation epoch and it evolves according to the following law:

$$\begin{aligned} \mathbf {B}(\mathbf {x}, t)=\mathbf {b}_0(\mathbf {x}, t)\left( \frac{a_0}{a}\right) ^2, \end{aligned}$$

(1)

where $a_0$ is the cosmological scale factor at the present epoch and $\mathbf b_0(\mathbf x, t)$ is the tangled magnetic field of which the amplitude evolves as $b=b_0\exp (i\int _{t_0}^t dt^\prime \omega )$, where $\omega$ is the magnetic field mode frequency; see Refs. [12–14]. Moreover, we assume that the magnetic field is statistically homogeneous and isotropic with ensemble average

$$\begin{aligned} \langle b_i(\mathbf k)b_j^*(\mathbf q)\rangle =\delta ^3(\mathbf k-\mathbf q)P_{ij}(\mathbf k)P_B(k), \end{aligned}$$

(2)

where $P_{ij}$ is a projection tensor and $P_B$ is the power spectrum of the primordial magnetic field, which in general is assumed to be a power law, $P_B=C k^{n}$ with C a constant and n the spectral index of the magnetic field. The constant C is fixed by taking the spatial average (or ensemble average) of the energy density of the magnetic field over a volume V,

$$\begin{aligned} \rho _B(t_0)=\frac{\langle \mathbf B_0(\mathbf x)\mathbf B_0(\mathbf x)\rangle }{2}=\frac{B_0^2}{2}, \end{aligned}$$

(3)

with co-moving cut-off wavelength $\lambda _B=2\pi /k_\lambda$ where $k_\lambda$ is a cut-off co-moving wave-vector. The cut-off wavelength (or wave-vector) is in general a free parameter, connected with the Fourier decomposition of $\mathbf B(\mathbf x)$, and in principle can assume values from zero to infinity. However, for physical reasons it depends essentially on the generation mechanism of the primordial magnetic field. In the case of a magnetic field generated by a causal mechanism, the value of $\lambda _B$ should be smaller than or equal to the Hubble horizon while in the case of a magnetic field generated by a non-causal mechanism (in general negative spectral indices) the value of $\lambda _B$ can be greater than the Hubble horizon. As we see below, in the case of causal mechanisms, we consider $\lambda _B$ to be smaller than or equal to the Hubble horizon during the $\mu$ epoch; see Figs. 1, 2, and 3. In the case of magnetic fields generated by non-causal mechanisms we set for simplicity $\lambda _B$ to be of the order of Mpc, even though it can be larger than this value; see Figs. 4b and 5.

With this kind of normalization the magnetic field power spectrum is given by

$$\begin{aligned} P_B=\frac{B_0^2}{4\pi }(n+3)\left( \frac{k}{k_\lambda }\right) ^n. \end{aligned}$$

(4)

Another possibility of fixing the constant C, which is also used in the literature, is to use a Gaussian filter $e^{-(k/k_\lambda )^2}$ in the definition of $\rho _B(t_0)$; see Refs. [31, 32]. In this case the form of $P_B$ is different from Eq. (4) but the spatial average of $\rho _B(t_0)$ remains invariant as it should be. In this work we shall not adopt this definition.

Fig. 1

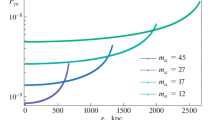
Exclusion plot in the parameter space $B_0$–$\lambda _B$ in the resonant case due to $\mu$-distortion. In a the exclusion plot for COBE [34] upper limit on $\mu$ and DFSZ axion model for $n=2$ is shown and in b the exclusion plot for COBE upper limit on $\mu$ and DFSZ axion model for $n=3$ is shown. In both a and b the region above the solid line represents the excluded region without photon–axion mixing, while the region above the dashed, dot dashed, and dotted lines represents the excluded region including photon–axion mixing for $\bar{m}_a=4.88\times 10^{-5}$ eV, $\bar{m}_a=1\times 10^{-5}$, and $\bar{m}_a=3\times 10^{-6}$ respectively

Fig. 2

Sensitivity plot in the parameter space $B_0$–$\lambda _B$ for PIXIE/PRISM [37, 38] expected value on $\mu \simeq 5\times 10^{-8}$ and for the DFSZ axion model. Values of the magnetic field spectral index n and axion mass $\bar{m}_a$ are the same as in Fig. 1

Fig. 3

In a the exclusion plot in the parameter space $B_0$–$\lambda _B$ for COBE limit on $\mu < 9\times 10^{-5}$ for the KSVZ axion model and $n=2$ is shown and in b the sensitivity plot in the parameter space B–$\lambda _B$ for the PIXIE/PRISM expected value on $\mu \simeq 5\times 10^{-8}$ for the KSVZ axion model and $n=2$ is shown. Values of the axion mass are the same as in Fig. 1

Fig. 4

Exclusion plot in the parameter space $B_0$–$\lambda _B$ for COBE limit on $\mu < 9\times 10^{-5}$. In a the region above the solid line is excluded with no photon–axion mixing included, while the regions above dashed and dot dashed are, respectively, excluded by the KSVZ and DFSZ axion models only. In b the exclusion plot for the magnetic field spectral index $n=-2.9$ and the DFSZ axion model is shown. The values of the axion mass are the same as in Fig. 1

Fig. 5

Sensitivity plot in the parameter space $B_0$–$\lambda _B$ for the PIXIE/PRISM expected limit on $\mu \simeq 5\times 10^{-8}$. In a the sensitivity plot for the KSVZ axion model and $n=-2$ is shown, while in b the sensitivity plot for the KSVZ axion model and $n=-1$ is shown

Let $\dot{Q}_B$ indicate the energy loss per unit time of the magnetic field that would convert into heat in the plasma. If energy injection (or heat) occurs in the redshift interval $2.88\times 10^5\le z\le 2\times 10^6$, Compton scattering would eventually create a Bose–Einstein distribution for the photon spectrum with chemical potential $\mu$.¹ The evolution of the chemical potential with respect to time is governed by the Sunyaev–Zel’dovich equation [15, 16],

$$\begin{aligned} \frac{\hbox {d}\mu }{\hbox {d}t}=-\frac{\mu }{t_{dC}}+1.4\,\frac{\dot{Q}_B}{\rho _R}, \end{aligned}$$

(5)

where $t_{dC}=2.09\times 10^{33}(1-Y_p/2)^{-1}(h^2\Omega _B)^{-1}(1+z)^{-9/2}$ s is the characteristic time for double Compton scattering. Here $Y_p\simeq 0.24$ is the helium primordial weight by mass and $h^2\Omega _B\simeq 0.022$ is the density parameter of the baryons [33].

To solve Eq. (5) we need to know the rate of heat flow into the plasma due to magnetic field dissipation. It can be shown that in the photon diffusion limit, i.e. $\Gamma _\gamma ^{-1}\ll \lambda _B$ [12, 13] (where $\Gamma _\gamma =\sigma _T n_e$ with $\sigma _T$ being the Thomson cross section and $n_e$ the number density of free electrons)

$$\begin{aligned} \frac{\dot{Q}_B}{\rho _R}= & {} \frac{B_0^2}{2\rho _R(t_0)}\frac{(n+3)}{k_\lambda ^{n+3}}\int _0^{k_\lambda }\,\hbox {d}k\frac{k^{n+4}}{5(1+z)\Gamma _\gamma (t_0)}\nonumber \\&\times \exp {\left( -\frac{2k^2}{k_D^2(t_0)}\frac{1}{(1+z)^3}\right) }, \end{aligned}$$

(6)

where $\rho _R$ is the energy density of relativistic particles, $t_0$ denotes the present time, and $k_D^2(t_0)=15\,\Gamma _\gamma (t_0)/t_*\simeq 6.27\times 10^{-19}\Gamma _\gamma (t_0)$ s$^{-1}$. The term $t_*$ is connected to the thermalization redshift,² $z_\mu$, through the relation $t_*=5t_{dC}/(4(1+z_\mu )^{5/2})$. Substituting Eq. (6) into Eq. (5), the general solution of Eq. (5) in terms of the redshift is given by

$$\begin{aligned} \mu (z)= & {} \frac{1.4\, B_0^2}{10\, \rho _R(t_0)}\frac{(n+3)}{\Gamma _\gamma (t_0)\,k_\lambda ^{n+3}}\int _{0}^{k_\lambda }\int _z^{z_i}\hbox {d}z^\prime \hbox {d}k\,\frac{k^{n+4}}{(1+z^\prime )^4}\nonumber \\&\times \exp {\left( -\frac{1+z^\prime }{1+z_\mu }\right) ^{5/2}}\exp {\left( -\frac{2k^2}{k_D^2(t_0)(1+z^{\prime })^3}\right) },\nonumber \\ \end{aligned}$$

(7)

where $z_i$ is an initial redshift, $z_i\gg z_\mu$, and the term proportional to $\mu (z_i)$ is absent, since for $z_i$ we have $\mu (z_i)=0.$ In obtaining Eq. (7) we have used the fact that in the radiation dominated universe $\hbox {d}t=-\hbox {d}z\,2 t_*/(1+z)^3$ and z is the redshift in the radiation dominated universe $z\ll z_\mu .$

In general it is not possible to find an analytic solution of Eq. (7) due to the non-trivial form of the integrands. Indeed, one can recognize that the double integral of Eq. (7) can be expressed in terms of the incomplete gamma functions, $\gamma (s, 2k_\lambda ^2/k_D^2)$ where s is an integer that in our case is either $s=(n+5)/2$ or $s=(3n+9)/5$. However, it is possible to consider some limiting cases, which allows to find analytic expressions in terms of the Euler gamma function $\Gamma$. Let us consider the limit $k_\lambda ^2\gg k_D^2(t_0)(1+z_\mu )^3$ and then evaluate the residual chemical potential at redshift $z=0$ (today). In this limit we get the following relation between the magnetic field strength $B_\text {0}$ and $\mu$:

$$\begin{aligned} B_0=3.19\times 10^{-6}\sqrt{\frac{\mu }{C_n}}\left( \frac{k_D}{k_\lambda }\right) ^{-(n+3)/2}\,\text {G}, \end{aligned}$$

(8)

where $C_n$ is a constant

$$\begin{aligned} C_n= & {} 1.4\,\Gamma (n/2+5/2)\,\Gamma (3n/5+9/5)\nonumber \\&\times \,2^{-(n+5)/2}\,(6/5)\,(n+3). \end{aligned}$$

(9)

Here the term $k_D=k_D(t_0)z_\mu ^{3/2}$ in Eq. (8) is the scale damped by one e-fold at redshift $z_\mu .$ Its corresponding co-moving wavelength is $\lambda _D=2\pi /k_D=415.5$ pc. In the opposite case, in the limit $k_\lambda ^2\ll k_D^2(t_0)(1+z_\mu )^3$, we get

$$\begin{aligned} B_0=3.19\times 10^{-6} \sqrt{\frac{\mu }{D_n}}\left( \frac{k_D}{k_\lambda }\right) \,\text {G}, \end{aligned}$$

(10)

where $D_n$ is a numerical constant that is given by

$$\begin{aligned} D_n=1.4\,\Gamma (-6/5)\left( \frac{n+3}{n+5}\right) (6/5). \end{aligned}$$

(11)

3 Axion contribution to spectral distortion

We have seen that tangled magnetic fields can dissipate energy and create $\mu$ distortion in the early universe. However, their presence would make possible the transition of CMB photons into axions.³ In Refs. [10, 11] we have derived the equations of motions for the photon–axion system in the steady state approximation in the case of a uniform magnetic field. Here we calculate the transition probability in the resonance case in the presence of a tangled magnetic field. The resonant regime is the axion mass range that makes a resonant transition in the redshift interval $2.88\times 10^5\lesssim 1+z\lesssim 2\times 10^6$; see Refs. [10, 11] for details. The difference in this case is that the magnetic field depends on the position, $\mathbf B(\mathbf x, t)$. However, one does not need to calculate the equation of motion for the density operator $\hat{\rho }$ again. It is sufficient to only replace in the equations of motions for $\hat{\rho }$: $\mathbf B(t)\rightarrow \mathbf B(\mathbf x, t)$; then we should take the spatial average of the transition probability, $P_a\rightarrow \langle P_a\rangle$. Since the transition probability depends on $\mathbf B_0^2$ [10, 11] and using the fact that $\langle \mathbf B_0(\mathbf x)\mathbf B_0(\mathbf x)\rangle =B_0^2$, in the resonant case we get

$$\begin{aligned} \langle P_a(\bar{T})\rangle =5.75\times 10^{-27}\,x\,C_{a\gamma }^2\,B_\text {nG}^2 \left( \frac{\bar{T}}{T_0}\right) ^3, \end{aligned}$$

(12)

where $B_\text {nG}=(B_0/\text {nG})$, and $C_{a\gamma }$ is defined as

$$\begin{aligned} C_{a\gamma }\equiv \left( \frac{E}{N}-\frac{2}{3}\frac{4+w}{1+w}\right) \frac{1+w}{w^{1/2}}, \end{aligned}$$

(13)

where for $w=0.56$, $|C_{a\gamma }|\simeq 4$ for $E/N=0$ (KSVZ axion model) and $|C_{a\gamma }|\simeq 1.49$ for $E/N=8/3$ (DFSZ axion model). Here w is defined in terms of the mass ratio of up and down quarks, $w=m_u/m_d$. For a small chemical potential $\mu$ we can write $\langle P_a\rangle =\mu e^x/(e^x-1)$ where $x=\omega /T$ with $\omega$ being the photon energy and T the CMB temperature. In this case we can easily find

$$\begin{aligned} B_\text {0}=6.76\times 10^{-11}\,\frac{\sqrt{\mu }}{\bar{m}_a\,C_{a\gamma }}\, \text {G}, \end{aligned}$$

(14)

where $\bar{T}$ and $\bar{m}_a=m_a/\hbox {eV}$ are, respectively, the resonance temperature and axion mass. Since we are looking for a spectral distortion in the redshift interval $2.88\times 10^5\lesssim 1+z\lesssim 2\times 10^6$, the corresponding resonant axion mass is within the interval $2.66\times 10^{-6}\, \text {eV}\,\lesssim \bar{m}_a\lesssim 4.88\times 10^{-5}\, \text {eV}$ [10, 11].

Equation (8) gives only the contribution to the $\mu$ distortion from the magnetic field itself. Now we must add to it also the contribution from axion creation from the CMB. Indeed, adding to Eqs. (8) and (14) we get the following relation between the magnetic field strength, the $\mu$-parameter, and $\lambda _B$:

$$\begin{aligned} B_0= & {} \sqrt{\mu }\left( 1.6\times 10^{-6}\,C_n^{-1/2}(\lambda _B/\lambda _D)^{-\left( \frac{n+3}{2}\right) }\right. \nonumber \\&\left. +\,3.38\times 10^{-11}\frac{1}{\bar{m}_a\,C_{a\gamma }}\right) \, \text {G},\quad (\lambda _B\ll \lambda _D). \end{aligned}$$

(15)

On the other hand, in the limiting case $\lambda _D\ll \lambda _B$ and adding to Eqs. (10) and (14) we get

$$\begin{aligned} B_0= & {} \sqrt{\mu }\left( 1.6\times 10^{-6}\,D_n^{-1/2}(\lambda _B/\lambda _D)\right. \nonumber \\&\left. +\,3.38\times 10^{-11}\frac{1}{\bar{m}_a\,C_{a\gamma }}\right) \,\text {G},\quad (\lambda _D\ll \lambda _B). \end{aligned}$$

(16)

We notice from Eq. (16) that the magnetic field strength depends on the spectral index n only through $D_n$. It is interesting to know at what scales the axion contribution to the $\mu$ distortion is smaller than the magnetic field contribution. In the case $\lambda _B\ll \lambda _D$ we get

$$\begin{aligned} \lambda _B\ge \left( 4.73\times 10^4\, \frac{\bar{m}_a C_{a\gamma }}{C_n^{1/2}}\right) ^{2/(n+3)}\,\lambda _D,\quad (\lambda _B\ll \lambda _D),\nonumber \\ \end{aligned}$$

(17)

while in the case $\lambda _D\ll \lambda _B$ we get

$$\begin{aligned} \lambda _B\le 2.11\times 10^{-5}\,\frac{D_n^{1/2}}{\bar{m}_a C_{a\gamma }}\,\lambda _D,\quad (\lambda _D\ll \lambda _B). \end{aligned}$$

(18)

We can see from Eqs. (17) and (18) that $\lambda _B$ does not depend on the average strength of the magnetic field $B_0$ but only on $n, C_{a\gamma }$, and $\bar{m}_a$. For example for $n=-2.9, -2, -1, 0, 1, 2, 3$ we have, respectively, $C_n=1.27, 0.78, 0.77, 1.1, 2.08, 4.93, 14.05$ and $D_n=0.38, 2.71, 4.07, 4.88, 5.43, 5.82, 6.11$. If we consider for example the DFSZ axion model, $n=2$ and axions with mass $\bar{m}_a=3.5\times 10^{-6}$ eV, we see that for $\lambda _B\ll 415.5$ pc, the axion contribution to the $\mu$ distortion is subdominant to magnetic field damping for $\lambda _B\ge 172. 5$ pc. In the opposite limit, $\lambda _B\gg 415.5$ pc, we get $\lambda _B\le 4.03\times 10^{3}$ pc. On the other hand, if we have $\mu$ given by the experiment and ask at what scales the axion contribution in the $B_0$–$\lambda _B$ plane is subdominant to magnetic field damping, we must simply reverse the inequality signs in both Eqs. (17) and (18); see Fig. 4a.

In Fig. 1 the exclusion plot for the scale averaged magnetic field, $B_0$ vs. $\lambda _B$, is shown. In both (a) and (b) the plots for the upper limit on $\mu$ found by COBE [34] are shown. Here we have chosen magnetic fields with $n\ge 2$, which are generated in the early universe by causal mechanisms [35]. For such magnetic fields, the field wavelength $\lambda$ or $\lambda _B$ must be smaller than the Hubble distance at redshift z, namely $\lambda _B\le H^{-1}(z)$. Indeed, in Fig. 1 we have chosen $H^{-1}(z_{\mathrm{QCD}})\le \lambda _B\le H^{-1}(z_\mu )$ where $H^{-1}(z_{\mathrm{QCD}})\sim 1$ pc is the QCD co-moving horizon and $z_\mu =2.88\times 10^5$ (lower redshift of $\mu$ epoch). Our exclusion and sensitivity plots in Figs. 1, 2, and 3 have been obtained for $\mu$ distortion and $n=2, 3$. The region above the solid line is excluded with no photon–axion mixing taken into account, while regions above the dashed, dot dashed, and dotted lines are excluded by taking it into account. The exclusion plot with no photon–axion mixing has been obtained by using Eqs. (8) and (10) and extrapolating them until $\lambda _B\rightarrow \lambda _D$.

We can see from Figs. 1, 2, and 3 that when we take into account photon–axion mixing, there are significant deviations for 200 pc $\le \lambda _B\le$ $10^3$ pc, in comparison with the case of no photon–axion mixing. Depending on the axion mass and axion model, deviations range from a factor 2 up to a factor 11. In our plots we have chosen three representative axion masses, $\bar{m}_a=4.88\times 10^{-5}$ eV, $\bar{m}_a=1\times 10^{-5}$ eV, and $\bar{m}_a=3.5\times 10^{-6}$ eV. Axions with mass $\bar{m}_a=4.88\times 10^{-5}$ eV are resonantly produced at the beginning of the $\mu$-epoch, while axions with mass $\bar{m}_a\ge 3.5\times 10^{-6}$ eV are experimentally allowed by the ADMX collaboration⁴ [36]. Axions with mass $\bar{m}_a\simeq 3.5\times 10^{-6}$ eV give weaker limits on $B_0$ in comparison with axions with bigger masses. This can be seen from Eq. (14) where the axion mass is in the denominator.

In the case of the expected limits on $\mu$ by future missions such as PIXIE/PRISM [37, 38], our plots are shown as sensitivity plots; see Figs. 2, 3 and 5. For example we can see in Fig. 2 that PIXIE/PRISM have a much better sensitivity with respect to COBE in the $B_0$–$\lambda _B$ plane. Depending on the axion mass and axion model the improvement is in general one or two orders of magnitude. In Fig. 4a plots of Eqs. (14)–(16) are shown. In this figure we can see the regions where the axion contribution in the $B_0$–$\lambda _B$ plane is dominant or subdominant. In Figs. 4b and 5 plots for negative spectral indices, for example $n=-2.9$ and $n=-2$, are shown. In general, magnetic fields with negative spectral indices are generated by non-causal processes, for example during the inflationary epoch [4–9].

4 Summary

In this work we have considered the impact of spatially varying stochastic magnetic fields and resonant photon–axion mixing on the CMB $\mu$ distortion. The contribution of magnetic field to the $\mu$ distortion depends on the cut-off scale $\lambda _B$ and on the damping scale $\lambda _D$. On the other hand, the axion contribution is scale independent as can be seen from Eq. (14). Taking into account the axion contribution to the $\mu$ distortion, in general, one finds weaker limits on the scale averaged magnetic field $B_0$ in comparison with the case of no photon–axion mixing included. Our main results have been shown as exclusion and sensitivity plots in the $B_0$–$\lambda _B$ plane, where the value of the chemical potential has been chosen either equal to the upper limit found by COBE or equal to the expected limit of PIXIE/PRISM.

In this work we have considered only resonant photon–axion mixing on generating a non-zero chemical potential. In the resonant case, the axion mass is not arbitrary but is connected with the $\mu$ epoch redshift, $z_\mu$. This constrains the resonant axion mass in the range $2.66\times 10^{-6}\, \text {eV}\,\lesssim \bar{m}_a\lesssim 4.88\times 10^{-5}\, \text {eV}$ [10, 11]. Axions with masses outside this interval make a non-resonant transition into photons.

The inferiority of the axion contribution to $\mu$ distortions in comparison with magnetic field damping is scale dependent as given by Eqs. (17) and (18). Obviously this is parameter dependent and a certain number of approximations are in order. If we consider a magnetic field generated by a causal mechanism, $n\ge 2$ [35], and axions with a mass $\bar{m}_a\ge 3.5\times 10^{-6}$ eV allowed by the ADMX [36] and the DFSZ axion model, we find that a bigger contribution to the $\mu$ distortion with respect to magnetic field damping occurs for cut-off scales, $\lambda _B\le$ 172.5 pc and $\lambda _B\ge 4\times 10^3$ pc. In the $B_0$–$\lambda _B$ plane the axion contribution dominates over magnetic field damping for a scale of 172.5 pc $\le \lambda _B\le 4\times 10^3$ pc. For scales $\lambda _B\simeq \lambda _D$, $B_0$ weakly depends on the spectral index n. For example by using Eq. (15) we see that, for $\mu < 9\times 10^{-5}$, $\bar{m}_a=2.66\times 10^{-6}$ eV (lower limit of resonant axion mass) and DFSZ axion, the upper limit on the scale averaged magnetic field is $B_0\le 8.77\times 10^{-8}$ G for $n=2$, $B_0\le 8.49\times 10^{-8}$ G for $n=3$, and $B_0\le 9.81\times 10^{-8}$ G for $n=-1$. If we had neglected the contribution of a resonant photon–axion contribution to $\mu$ distortion, we would get $B_0\le 1.36\times 10^{-8}$ G for $n=2$, $B_0\le 8\times 10^{-9}$ G for $n=3$, and $B_0\le 3.45\times 10^{-8}$ G for $n=-1$. Therefore we can conclude that for values of the parameters as assumed above, resonant photon–axion production gives weaker limits on $B_0$ up to a factor in 10 in comparison with the case of no photon–axion mixing included.

Limits on $B_0$ in the case of the KSVZ axion model are in general stronger than those from the DFSZ axion model (for a given axion mass). For example, if we consider axions with mass $\bar{m}_a=4.88\times 10^{-5}$ eV (allowed upper limit) and $\mu$ fixed, the contribution of resonant photon–axion production to Eqs. (15) and (16) is almost marginal. In the $B_0$–$\lambda _B$ plane the curve corresponding to the KSVZ axion model and $\bar{m}_a=4.88\times 10^{-5}$ eV is almost indistinguishable from the curve corresponding to the case with no photon–axion mixing included. In general, the two curves differ from each other up to a factor 1.5 for 172.5 pc $\le \lambda _B\le 4\times 10^3$ pc.

A forecast for the future PIXIE/PRISM space missions has been presented. In Fig. 2 we can see the level of sensitivity in the case where photon–axion mixing is not included and in the case when it is. In the former case we find that, for scales $\lambda _B\simeq 415.5$ pc, PIXIE/PRISM will probe magnetic fields $B_0\ge 10^{-10}$ G, while in the latter case it is parameter dependent. For axions with masses $\bar{m}_a\ge 2.66\times 10^{-6}$ eV, we find $B_0\ge 2$ nG for the DFSZ axion and $B_0\ge 8.8 \times 10^{-10}$ G for the KSVZ axion. In the case of axions with masses $\bar{m}_a=4.88\times 10^{-5}$ eV the contribution of photon–axion mixing is marginal, as can be seen from Fig. 2.

It is important to stress two things. First in this work we did not consider any limit from the CMB y distortion, since at the moment we are currently working on an effective approach of y distortion in the case of photon–axion mixing. Second, the contribution of magnetic field damping to the $\mu$ distortion has been derived by using linearized magnetohydrodynamic equations in the photon diffusion limit [14]. Moreover, we have extrapolated both Eqs. (15) and (16) for $\lambda _B\rightarrow \lambda _D$. A detailed behavior of $B_0$ around $\lambda _D$ requires a numerical integration that is beyond the scope of this paper, but we expect that extrapolated results are very accurate for $\lambda _B\rightarrow \lambda _D$.