Abstract
We compute the decays \({B\rightarrow D^*_0}\) and \({B\rightarrow D^*_2}\) with finite masses for the b and c quarks. We first discuss the spectral properties of both the B meson as a function of its momentum and the \(D^*_0\) and \(D^*_2\) at rest. We compute the theoretical formulae leading to the decay amplitudes from the three-point and two-point correlators. We then compute the amplitudes at zero recoil of \({B\rightarrow D^*_0}\), which turns out not to be vanishing contrary to what happens in the heavy quark limit. This opens the possibility to get better agreement with experiment. To improve the continuum limit we have added a set of data with smaller lattice spacing. The \({B\rightarrow D^*_2}\) vanishes at zero recoil and we show a convincing signal but only slightly more than 1 sigma from 0. In order to reach quantitatively significant results we plan to exploit fully smaller lattice spacings as well as another lattice regularisation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding the composition of the final state in B meson semileptonic decay into charm meson is of key importance to control the theoretical error on the CKM matrix element \(V_{cb}\). The discrepancy between the inclusive determination and the exclusive one, based on \(B \rightarrow D^{(*)} l \nu \), is still of the order of 3\(\sigma \) [1]. A significant part of the total width \(\Gamma (B \rightarrow X_{c} l \nu )\) comes from excited states: it was recently argued that the radial excitation \(D'\) might be particularly favoured, implying a suppression of the \(B \rightarrow D^{*}\) form factors as suggested by a study performed using the operator product expansion formalism [2]. Another group of states that contribute to the width, about one quarter of it, is orbital excitations, in other words, positive parity charmed mesons, that we will note \(D^{**}\) hereafter. They are not well understood: indeed there seems to be a persistent discrepancy between claims from theory and from experiment [3], while a comparison between semileptonic decay and non-leptonic decay \(B \rightarrow D^{**} \pi \), involving the same form factors (at least in the case of the so-called Class I process), is quite confusing on the experimental side [4]. Two types of \(D^{**}\) are observed: two “narrow resonances” \(D_{3/2}\) and a couple of “broad resonances” \(D_{1/2}\), in the same mass region [5]. While experiments point towards a dominance of the broad resonances in semileptonic decays, theory points rather towards the dominance of the narrow resonances: not only a series of sum rules [6, 7] derived from QCD obtains that hierarchy, but also calculations with quark models [8–10] and lattice computations performed in the quenched approximation [11] and with \({N_{f}}=2\) dynamical quarks [12]. However, the main limitation of these results is that they are derived in the heavy quark limit. \(1/m_{c}\) corrections might be pretty large and, before getting any definitive conclusion on the disagreement between theory and experiment in that sector of flavour physics, it is mandatory to reduce the sources of systematic errors on the theory side.
2 Theoretical framework
In this paragraph, all the main formulae up to the differential decay rates will be given for the semileptonic decays of a B heavy meson into the first orbitally excited \(D^{**}\) mesons.
We will focus our study on the production of the  (scalar \(D^{*}_0\)) and the
(scalar \(D^{*}_0\)) and the  (tensor \(D^{*}_2\)) states.Footnote 1
(tensor \(D^{*}_2\)) states.Footnote 1
Finally, we will also give relations in the case where the mass of the lepton cannot be neglected.
2.1 Form factors
In order to derive the decay rates, we need the transition amplitudes. They can be described using six form factors [15]:




where \(V_\mu \) denotes the vector current \(\bar{c}\gamma _\mu b\) and \(A_\mu \) the axial current \(\bar{c}\gamma _\mu \gamma _5 b\).
\(\varepsilon (p_{_{\!D^{*}_2}},\,\lambda )\) is the polarisation tensor of the  state (\(\lambda \) being the projection of the \(J=2\) total angular momentum along some quantification axis).
state (\(\lambda \) being the projection of the \(J=2\) total angular momentum along some quantification axis).
Moreover, the chosen normalisation of the mesonic states is
Finally, because of parity and time-reversal invariance of the strong interactions, those form factors are real numbers.
2.2 Differential decay rates
The goal is to compute the differential decay width \(\text {d}\Gamma (\bar{B}\rightarrow D^{**}\,\ell \,\bar{\nu })\) whose general expression is
In the last equality, \(W_{\mu \nu }\) denotes the hadronic tensor

where the transition amplitudes have been given in the preceding paragraph (let us note that there are no summation nor average over the initial spins since the \(\bar{B}\) meson has a spin equal to 0) and \(\ell ^{\mu \nu }\) represents the leptonic tensor
In that last formula, \(u_\ell (p_{_{\!\ell }},s)\) is the lepton \(\ell \) spinor (s denotes the usual projection of its spin), while \(v_\nu ({p}_{_{\!\nu }})\) represents the antineutrino \(\bar{\nu }\) spinor.
All that remains is to compute the leptonic tensor, and then the hadronic tensor and the measure \(\text {d}\Phi \) of the phase space in order to obtain the expressions of the differential decay widths.
2.2.1 Leptonic tensor \(\varvec{\ell ^{\mu \nu }}\)
The calculation is classical and straightforward, leading to
We notice that the mass of the lepton has vanished, which renders the expression valid in the situations where \(m_{_{\!\ell }}= 0\) as well as \(m_{_{\!\ell }}\ne 0\).
2.2.2 Hadronic tensor \(\varvec{W_{\mu \nu }}\)
By looking at the expressions of the transition amplitudes given above, the general structure of the hadronic tensor can be inferred and put into the form [15]
The coefficients \({\alpha }\), \({\beta _{_{++}}}\), \({\beta _{_{+-}}}\), \({\beta _{_{-+}}}\), \({\beta _{_{--}}}\) and \({\gamma }\) are given in the “Appendix” for the  and the
and the  states.
states.
2.2.3 Kinematics and notations
For reasons of simplicity, we now choose to compute the decay rates in the rest frame of the \(\bar{B}\) meson.
We then define two dimensionless parameters x and y according to
where \(E_{_{\!\ell }}\) is the energy of the lepton in the \(\bar{B}\) rest frame.
We introduce also the mass ratio \(r_{_{\!X}}\)
Many kinematical terms can be expressed with these three parameters, such as
2.2.4 Measure \(\varvec{\text {d}\Phi }\) of the phase space
The goal is to get the differential widths \(\text {d}\Gamma \) with respect to the lepton energy \(E_{_{\!\ell }}\) and the momentum transfer \((p_{_{\!B}}-p_{_{\!D^{**}}})^2\), in other words with respect to the variables x and y: \( {\text {d}^2\Gamma }/{\text {d}x\,\text {d}y}\).
So we must integrate over the antineutrino momentum \(\vec {p}_{_{\!\nu }}\), then over all possible orientations of \(\vec {p}_{_{\!\ell }}\), so that only the dependence on \(E_{_{\!\ell }}\) (i.e. on x) remains, and finally over all possible directions of the three-vector \(\vec {p}_{_{\!D^{**}}}\), since we want to keep the dependence on \(E_{_{\!D^{**}}}\) (i.e. on y). We finally get:
where \(\theta (z)\) is the usual Heaviside function.
2.2.5 Constraints on \(\varvec{x}\) and \(\varvec{y}\)
The parameters x and y, that is, the lepton energy (\(E_{_{\!\ell }}\)) and the \(D^{**}\) meson energy (\(E_{_{\!D^{**}}}\)), cannot be arbitrary. They are constrained by two conditions: one which is obvious in the expression of \(\text {d}\Phi \) above (the Heaviside function) and another one which appeared during the integration over the direction of \(\vec {p}_{_{\!\ell }}\). In other words, we have access to the variation domains of both parameters x and y whether we consider \(x=x(y)\) or \(y=y(x)\): they are given in the “Appendix”.
2.2.6 Differential decay widths in the \(\varvec{\bar{B}}\) rest frame
Using the definition of \(\text {d}\Gamma \) as well as all the preceding results, the construction of the differential decay widths proceeds in the following way:
where \(|\bar{\mathscr {M}}|^2 = W_{\mu \nu }\ell ^{\mu \nu }\) becomes in this particular frame
We notice that, for a zero mass lepton, only the coefficients \({\alpha }\), \({\beta _{_{++}}}\) and \({\gamma }\) survive.
The expressions for each \(D^{**}\) are also written in the “Appendix”. However, their use requires the knowledge of the momentum dependence of the form factors. In the following, we will focus on a method to obtain such a dependence.
2.3 Extracting the form factors from the transition amplitudes
On the lattice, we compute the transition amplitudes for different momenta of the mesons. But we need the momentum dependence of the form factors in order to calculate the decay rates of the semileptonic decays of the B to a \(D^{**}\). So we must devise a way to extract the form factors from the lattice transition amplitudes.
2.3.1 Kinematics
We will work in the rest frame of the \(D^{**}\) mesonFootnote 2 so the B meson will carry the momentum. Moreover, we will consider the B’s whose spatial momentum is symmetrical.
We will also choose the Minkowski metric: \(g_{\mu \nu } = \text {Diag}(+,-,-,-)\).
The other piece we need is the expression of the polarisation tensor for the  state in the \(D^{**}\) rest frame, that is, \(\varepsilon (\vec {0},\,\lambda )\). We can construct it from the combination of two spin-1 states,
state in the \(D^{**}\) rest frame, that is, \(\varepsilon (\vec {0},\,\lambda )\). We can construct it from the combination of two spin-1 states,
where the Clebsch–Gordan coefficients for \(1 + 1 \rightarrow 2\) appear as well as the polarisation vector \(\varepsilon ^{\mu }(\vec {0},\,s)\) of a spin-1 state. The final expressions are gathered in the “Appendix”.
2.3.2 \({^3}{P}_0\) form factors
Using the notation

we explicitely get from Eq. (2.2):
So it is straightforward to express \(\tilde{u}_+\) and \(\tilde{u}_-\) with the \({\mathscr {T}}_{\mu }^A\)’s. The results are presented in the “Appendix”.
2.3.3 \({^3}{P}_2\) form factors
In the following, we will adopt the notation

In order to extract one particular form factor, we can choose in Eq. (2.1) either some spatial direction where each coefficient of the other form factors vanishes, or we can construct a linear combination of the \({\mathscr {T}}_{i(\lambda )}^A\) and/or the \({\mathscr {T}}_{i(\lambda )}^V\).
This procedure can be carried out by using the expressions for the polarisation tensor and the four-momenta at our disposal and calculating the contribution of the corresponding terms appearing in the matrix elements (2.1) which define the form factors (those contributions are gathered in Table 1).
 transition amplitude
transition amplitudeA few possibilities are collected in the “Appendix”.
2.4 Summary
We have constructed all the theoretical formulae which allow us to calculate the decay widths of the semileptonic \(B \rightarrow D^{**}\) channels. The strategy to use them is the following:
-
1.
Compute, on the lattice, the transition amplitudes for the \(B \rightarrow D^{**}\) processes.
-
2.
Extract the form factors from them.
-
3.
Use the formulae in the “Appendix” to obtain the decay widths.
Since we expect the lattice  computation to be somewhat tricky, we are first going to estimate the contribution of the \(\tilde{k}\), \(\tilde{b}_+\), \(\tilde{b}_-\) and \(\tilde{h}\) form factors to the \(\bar{B} \rightarrow D^*_2\,\ell \,\bar{\nu }\) decay width.
computation to be somewhat tricky, we are first going to estimate the contribution of the \(\tilde{k}\), \(\tilde{b}_+\), \(\tilde{b}_-\) and \(\tilde{h}\) form factors to the \(\bar{B} \rightarrow D^*_2\,\ell \,\bar{\nu }\) decay width.
2.5 Estimation of the contribution of the form factors to the \({^3}P_{2}\) decay width
There are four form factors needed to describe the transition amplitudes from a B to a  state which increases the difficulty in the lattice computations. So it could be useful to have an idea of each of their contribution to the decay widths.
state which increases the difficulty in the lattice computations. So it could be useful to have an idea of each of their contribution to the decay widths.
In order to get a quantitative hint, we will relate these form factors to their infinite mass limit \(\tau _{_{\!3/2}}\)and use this \(\tau _{_{\!3/2}}\)to produce a numerical estimation.
2.5.1 Infinite mass limit
In the limit where the heavy quark of the meson has an infinite mass, new symmetries (and thus additionnal conserved quantities) appear. These new symmetries provide additional relations between the transition amplitudes so that the form factors become dependent. It can be proven [13] that this reduction of the form factors leads to the following relations for the  state:
state:

where the parameter w is defined by
and \(\tau _{_{\!3/2}}\)is one of the so-called Isgur–Wise functions.
2.5.2 Fit of \(\varvec{\tau }_{_{\mathbf{\!3/2}}}\)
Using a covariant construction of the transition amplitudes in the infinite mass limit (quark models à la Bakamjian-Thomas), it has been shown [8, 14] that the Isgur–Wise function \(\tau _{_{\!3/2}}\)can be well fitted by
where the accessible phase space domain is given by
We will also take (GI model [15] in [8]):
2.5.3 Quantitative prediction of each contribution to the total width
We are now in a position to estimate the contribution of each form factor to the total width of the \(\bar{B}\rightarrow D^{*}_2\,\ell \,\bar{\nu }\) decay channel. Let us take the case of a zero mass lepton to simplify the calculations. Starting from the expression of \(\dfrac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y}\) and with the notations given in the “Appendix”, we can perform both the integrations over x and over y and we get:
\({C_i}\) | \(C_1\times {\tilde{k}}^2\) | \(C_2\times {\tilde{h}}^2\) | \(C_3\times {\tilde{b}}_+^2\) | \(C_5\times 2\,{\tilde{k}}\,{\tilde{b}}_+\) | \(C_8\) |
|---|---|---|---|---|---|
\({{\iint C_i}}\times {{\mathbf{FF}}}^{{\mathbf{2}}}\) | \(-\)61.3 | \(-\)0.86 | \(-\)4.43 | 29.0 | 0 |
We notice that the biggest contributions come from the terms where the \({\tilde{k}}\) form factor appears; that is why we will focus on its determination in the actual lattice computation.
3 Simulation set up
In our analysis we use gauge ensembles produced by European Twisted Mass Collaboration [16–18] with \(N_f=2\) twisted-mass fermions tuned at maximal twist. Parameters of the simulations are collected in Table 2.
The gauge action is tree-level Symanzik improved [21] and reads
where \(b_0 = 1 - 8 b_1\) and \(b_1 = -1/12\). The fermionic action with two degenerate flavours is Wilson-like with a twisted-mass term and reads [22–24]:
where \(D_\mathrm{W}\) is the massless Wilson–Dirac operator. In the valence sector we add two doublets of charm quarks and “bottom” quarks. Moreover, as we are interested in computing form factors at different momenta we implement \(\theta \)-boundary conditions [25], using \(\vec {\theta }\equiv (\theta ,\theta ,\theta )\), for the b doublet:
This is equivalent to defining the auxiliary field
and the Dirac operator
The whole fermionic action finally reads
We use all to all propagators with stochastic sources \(\eta [i]\) diluted in time [26] and improve the variance-to-signal ratio with the one-end trick [27, 28]. When it is generalised to \(\theta \)-boundary conditions, it consists in solving the Dirac equations,
where \(\tau ^3 \chi = r \chi \), f represents the fermion flavour and
The stochastic source
is diluted in spinor and is non-zero in a single time slice \(\tilde{t}\). It is normalized by
In order to improve the overlap of the interpolating fields for the ground states or to create an operator of higher spin (for instance the tensor meson \(D^*_2\)), one has to use interpolating fields, generically written as \(\bar{\chi }_1 S \times \Gamma \chi _2\), where S is a path of links and \(\Gamma \) is any Dirac matrix. We use interpolating fields of the so-called Gaussian smeared form [29]
where \(\kappa _G=0.15\) is a hopping parameter, \(R=30\) is the number of applications of the operator \((1 + \kappa _G a^2 \Delta )/(1+6\kappa _G)\) and \(\Delta \) the gauge-covariant 3D Laplacian constructed from three-times APE-blocked links [30]. If necessary, we also incorporate in S a covariant derivative:
This is relevant to create a tensor meson.
The Dirac equations, which we then have to solve, read
We compute the “charged” B and D two-point correlators \(C^{(2)\,hl}_{\vec {\theta };S_1\,\Gamma _1;S_2\,\Gamma _2}(t)\), which read [32]
where \(\left\langle \ldots \right\rangle \) stands for the gauge ensemble average and \(h\equiv c\) or b.
We recall that, in twisted-mass QCD, quark propagators have the hermiticity property:
We also compute the “neutral” \(B \rightarrow D\) three-point correlators \(C^{(3)\,b\Gamma c}_{\vec {\theta };S_1\,\Gamma _1;\Gamma ;S_2\,\Gamma _2}(t,t_s)\), which read
Those two types of correlators are depicted in Fig. 1. On each of the two ensembles, we estimate the statistical error from a jackknife procedure.
4 Masses and energies
We decide to concentrate our effort on the analysis of smeared–smeared two-point correlators because the benefit of such a technique has been already clearly observed in a previous work by ETMC [31]. Masses and energies of pseudoscalar B and D mesons are first extracted from a fit of the form
in a time range where the contribution from the first excitation is small compared to the statistical error. The stability of the fit is checked by enlarging the time interval and adding a second exponential in the formula, i.e.,
The last step in the analysis is to measure the effective energy \(E_P \equiv E^{(1)}_P\) of the ground state from the ratio
We show in Fig. 2 examples of plateaus for ”B”-mesons energies at three different momenta.
We study the dispersion relation to get an idea of the magnitude of cut-off effects. We display in Fig. 3 the B meson energies and compare them to the theoretical formula
The agreement is good at the two lightest heavy masses but really bad at the heaviest one: cut-off effects are pretty large.
Interpolating fields of the \(2^+\) state are given by the formula \(O^{(\lambda )}=\epsilon ^{*(\lambda )}_{\mu \nu } \bar{\chi }_c \gamma _\mu \nabla _\nu \chi _l\), \(\lambda =\pm 2,\, \pm 1,\, 0\). Actually we choose to use linear combinations of the interpolating fields that read
The two first interpolating fields live in the E representation of the \(O_h\) cubic group symmetry of rotations and inversion in a 3D spatial lattice, while the last three live in the \(T_2\) representation of that group [33]. We finally consider the r-symmetrized smeared–smeared two-point correlators
and
The masses we extract by studying the ratios \(\frac{C^{(2)}_{2^+,E}(t)}{C^{(2)}_{2^+,E}(t+1)}\) and \(\frac{C^{(2)}_{2^+,T_2}(t)}{C^{(2)}_{2^+,T_2}(t+1)}\) are in principle equal: any discrepancy comes from cut-off effects. We show in Fig. 4 that, indeed, lattice artefacts are present.
As parity is broken by the twisted-mass action at finite lattice spacing [23] and the states we consider are not made with quarks of the same flavour doublet, contrary to what is discussed in Sect. 5.2 of [24], the scalar D meson can in principle mix with the pseudoscalar D meson. We have to build a matrix of correlators \(\{C_{ij}(t)\}\) and solve a generalised eigenvalue problem (GEVP) [34–36]. We study a \(2\times 2\) system whose entries correspond to the interpolating fields with Dirac structures \(\bar{\chi }_c \gamma ^5 \chi _l\) and \(\bar{\chi }_c \chi _l\):
We solve the system
We set \(t_0=3\) \((\beta =3.9)\) and 5 \((\beta =4.05)\). \(\lambda ^{(n)}(t,t_0)\) and \(v^{(n)}(t,t_0)\) are the eigenvalues and eigenvectors of the matrix \(C^{-1}(t_0)C(t)\). The effective mass \(m_{D^*_0}\) of the scalar meson is given by
We show in Fig. 5 \(m_{D^*_0}\) for the ensemble (\(\beta =3.9, \mu _\mathrm{sea}=0.0085\)). The signal is unfortunately quite short, but still acceptable for our qualitative study.
We collect in the “Appendix” all the masses and energies that we extracted in our analysis. The total error includes the statistical one and the discrepancy of results when we change the time range \([t_\mathrm{min}, t_\mathrm{max}]\) of the fits by \(t_\mathrm{min}\pm 1\) and \(t_\mathrm{max}\pm 1\), when we take different \(t_0\) in the range [3, 6] and, in the case of pseudoscalar B mesons, when we perform a two-state exponential fit.
4.1 \({M_{D^*_2}-M_D}\) and \({M_{D^*_0}-M_D}\) in the continuum limit and experiment
In Table 7 in the “Appendix” are given the masses of the \({D^*_2}, {D^*_0}\) and D mesons. It is interesting to perform an extrapolation to the continuum and compare with the experimental data. For the latter we will take the \(c \bar{s}\) mesons. It does not change anything for the tensor meson as compared to the non-strange charmed mesons (\(M_{D^*_2}(2460) -M_D \simeq M_{D^*_{2s}}(2573) -M_{D_s}\)) but for the scalar mesons it does, since the \(D^*_{0s}(2317)\) has a narrow and clear signal which is not the case of the \(D^*_{0}(2400)\) whose signal is very broad due to its S-wave decay into \(D \pi \).
We perform the extrapolation to the continuum limit and compute the error using jackknife. We show our results in Table 3. We see that the agreement with experiment is not so good but the errors are large. For the moment we cannot say much, except that the future will tell whether this issue comes mainly from statistical fluctuations or whether the lattice regularisation is in cause. A similar conclusion was drawn recently in a lattice study with \({N_f}=2+1+1\) dynamical quarks regularised by TmQCD [39]. Also, we have not considered yet the possible effect of the opening of the decay channel \(D^*_0 \rightarrow D\pi \) S-wave state as proposed in [40].
5 B decay to the scalar \({D^*_0}\) charmed meson
In this section we will restrict our treatment to the zero recoil kinematics, in other words, the initial B meson is taken at rest. We restrict ourselves to this simpler case because the momentum dependence of the \(B \rightarrow D^*_0\) decay is very difficult to study on the lattice (three-point correlators are very noisy) and we cannot yet say anything significant about it, but also because the non-vanishing of the zero recoil amplitude is of utmost phenomenological relevance: in the infinite mass limit, the \(B \rightarrow D^*_0\) amplitude vanishes at zero recoil [13]. This forbids the decay into an S-wave between the lepton pair and the \(D^*_0\), since an S-wave clearly does not vanish at zero recoil. The S-wave is a major contribution to these decays, since their available phase space is rather small, and higher waves are suppressed by the so-called centrifugal barrier effect. With finite heavy quark masses we will show that the zero recoil amplitude does not vanish, there is a non-vanishing S-wave and this may change drastically the ratio between \(\Gamma (B \rightarrow D^*_2)\) and \(\Gamma (B \rightarrow D^*_0)\), since the \(B \rightarrow D^*_2\) decay amplitude does vanish at zero recoil whether the mass of the c and b is taken infinite or finite, thus implying only D-wave decay. The possible importance of a non-vanishing zero recoil amplitude was stressed in [37], where the authors estimated subleading corrections to the infinite mass limit: although subleading in the \(\Lambda /m_{c,b}\) expansion, the S-wave may not be negligible. Our computation confirms this conclusion as shall be seen.
5.1 Computation of the amplitude ratio \({(B \rightarrow D^*_0})\) over \({(B \rightarrow D)}\) at zero recoil
We will compute the ratio of the amplitudes \(A(B \rightarrow D^*_0)/A(B \rightarrow D)\). We take \(A(B \rightarrow D)\) as a benchmark, since it is experimentally fairly well known, and D being a \(J=0\) state as \(D^*_0\), it is expected that the momentum dependence of these decays will be rather similar. We recall some formulae neglecting for the moment the D–\(D^*_0\) mixing due to the parity violation at finite lattice spacing when using twisted-mass quarks. The matrix elements \(\langle B|V_{0}|D\rangle \) and \(\langle B|A_0|D^*_0\rangle \) are given by the following ratio:
where \(t_s< t < t_p\) are, respectively, the source, current and sink times (cf. Fig. 1).
\(Z_0 = Z_V (Z_A)\) when \(H_c = D (D^*_0)\). \(Z_{H_c}\) and \(Z_B\) are defined from the fit of the two-point correlators of the \(H_{c}\) and B mesons, assuming we are far enough from the centre of the lattice to be allowed to neglect the backward exponential in time while the contribution of excited states is small:
Then we compute
5.2 Taking into account the scalar–pseudoscalar mixing
In Sect. 4 we have detailed the generalised eigenvalue method. As explained there and in Sect. 3, we restrict ourselves to a \(2 \times 2\) matrix of smeared and stochastic two-point correlators. The largest (smallest) eigenvalue \(\lambda ^{(1)}\) (\(\lambda ^{(2)}\)) will be related to the mass of the D (\(D^*_0\)) state. The corresponding eigenvectors give the linear combination of \(\bar{\chi }_{c} \gamma _5 \chi _{l}\) and \(\bar{\chi }_{c}\chi _{l}\) interpolating fields that have the largest coupling to the \(D(D^{*}_{0})\) state. The eigenvectors turn out to be not far from orthogonal
as seen for example in Table 4. One might say that 0.07 is not so small but this is not surprising, since there are other states in which the B might decay than only the ground state scalar and pseudoscalar that we consider in our analysis. We can thus to a fair approximation orthonormalise the eigenvectors so that
without changing the eigenvalues, since in Eq. (4.4) the same factor multiplies both sides of the equation. Thus, we define the two-point correlator of the \(D^{*}_{0}\) meson by
where we fit with
since \(\lambda ^{(i)}(t_0,t_0) = 1\) from Eq. (5.6). We define \(Z_2^{(1)}\) and \(Z_2^{(2)}\) from
In Eq. (5.1) we see that the factors \(Z_i\) appear only via their square root.
5.2.1 Symmetry properties of the matrix elements
In the continuum it is obvious by parity conservation that
However, parity is not conserved by the twisted-mass quark action at finite lattice spacing. But this action has an exact symmetry [23], the flavour-parity
where \(\mathscr {P}\) is the spatial parity, and \(\mu _l, \mu _c, \mu _b\) are the twisted-mass terms for the light, charm and beauty quarks. We assume we are at maximal twist (vanishing of \(m_\mathrm{PCAC}\)). Therefore if we use
we get the validity of Eq. (5.9) also for finite lattice spacing. This symmetrisation will be assumed in the following.
5.2.2 GEVP on the three-point correlators
In this section we assume \(t_s< t < t_p\) and \(t_0 \le t-t_s\). Starting from the three-point correlators \(C^{(3)}_{B A_0(V_0) O_i} (t_{p},t,t_s)=\langle \bar{\chi }_b \gamma _5 \chi _l(t_p) A_0(V_0) (t) O_i(\bar{\chi }_c,\chi _l,t_s)\rangle \), \(O_i(\bar{\chi }_c,\chi _l)\!\equiv \! \{\bar{\chi }_c \gamma _5 \chi _l, \bar{\chi }_c \chi _l\}\) and following the authors [38] as regards their way of extracting the decay constant \(f_B\), we consider the projected three-point correlators
We recall that the normalisation factor \(Z^{(2)}_2\) cancels between \(\langle \bar{\chi }_b \gamma _5 \chi _l(t_p) A_0(V_0) (t) \bar{\chi }_c (\gamma _5) \chi _l(t_s)\rangle \) and \(\sqrt{v^{\dag (2(1))}_{i}(t-t_s,t_0) C^{(2)}_{ij}(t-t_s)v^{(2(1))}_j(t-t_s,t_0)}\) while the factor \(\left( \frac{\lambda ^{(2(1))}(t_0+a,t_0)}{\lambda ^{(2(1))}(t_0+2a,t_0)}\right) ^{(t-t_s)/2a}\sim e^{-E_{D^*_0(D)}(t-t_s)/2a}\) compensates the residual time exponential dependence. We do not take into account the contributions \( \propto \, v_{\bar{\chi }_c \gamma _5 \chi _l}^{(2)}(t-t_s,t_0)\) and \(v_{\bar{\chi }_c \chi _l}^{(1)}(t-t_s,t_0)\) to the projected correlators \(\sum _i \langle \bar{\chi }_b \gamma _5 \chi _l(t_p) A_0(V_0) (t) O_i(\bar{\chi }_c, \chi _l,t_s)v^{(2(1))}_i(t-t_s,t_0)\rangle \) because the B meson goes through operator \(A_0\) (\(V_0\)) only to a pure scalar (pseudoscalar) state.
The ratio in Eq. (5.3) becomes
using Eq. (5.7)
Of course the ratio of branching fractions has to take into account the difference in phase space. However, we ignore totally the dependence of the amplitude on the recoil, having only estimated the zero recoil contribution. Therefore, we will for the moment neglect the phase space dependence. We collect the results of Eq. (5.13) in Table 5 and show plateaus in Fig. 6.
The ratio in Eq. (5.13) once symmetrised according to Eq. (5.11) extrapoleted from the three b quark masses to the physical B mass: 5.2 GeV, linearly in \(1/M_B\). We have used data from \(\beta = 3.9, 4.05, 4.2\). The time unit is the lattice spacing for \(\beta = 4.2\): \(a \simeq 0.054 \; \mathrm{fm}\). The ratios for \(\beta = 3.9, 4.05\) have been interpolated to points in \(a_{\beta = 4.2}\) lattice units using the formula which is detailed in the caption of Table 5. The plot starts at \(t = 6\), the time \(t_0\) of the GEVP procedure. We see acceptable plateaus up to \(t = 10\) and we compute the averages to be between 6 and 10, as reported in Table 5. For larger times the signal falls down, presumably because of the parity violation when using twisted masses which induces the scalar \(D^\star _0\) to “decay” into the pseudoscalar D meson. The error bars are only statistical errors
The values of the plateaus are reported in Table 5. The dependence in \(m_B\) agrees with the formula \(c/m_B+b\). We show both the extrapolation to the physical B meson and the vanishing lattice spacing. When both extrapolations are combined we get a ratio of 0.17(6)(6). This is a non-vanishing signal, thanks to the data at \(\beta =4.2\), which, lying closer to the continuum, constrain more efficiently the continuum limit.
As a gross estimate the ratio of branching fractions is the square of the ratio of amplitudes reported in Table 5. The experimental value of the ratios of branching fractions can be very grossly estimated to be around 0.1–0.2, which would correspond to a ratio of amplitudes \(\sim \)0.3–0.45. Our estimate lies below this value, but at this stage we must remain very careful: the experimental status of the \(D^*_0\) is unclear, the resonance being very broad, and our theoretical estimate is affected by very large uncertainties. Also the experimental situation is far from clear for the moment [4].
6 B decay to the tensor (\({J=2^+}\)) charmed meson
In this section we want to estimate the amplitudes for \(B \rightarrow D^*_2 \ell \nu \) decay. In [1] the spin-2 charmed mesons are named \(D^*_2(2460)\) (\(D^*_{s2}(2573)\)). For the initial B meson, we use three “\(B_i,\ i=1,\,2,\,3\)” with increasing masses valued 2.55, 3.18 and 3.97 GeV. As was mentioned before, the “\(B_i,\ i=1,\,2,\,3\)” are moving while the final charmed meson is at rest. We concentrate on the calculation of the form factor \(\tilde{k}\), since it was shown in Sect. 2.5 that it is, by large, dominant in the decay width.
6.1 Three-point correlators computed for \({B \rightarrow D(2^+)}\)
We start from the formulae recalled in Sect. 2.5. We use a symbolic notation to represent the hadronic matrix elements
The various combinations to extract \(\tilde{k}\) are collected in Table 6. We consider all of these combinations and average the resulting value for \(\tilde{k}\). To eliminate artefacts we must also apply the symmetrized result according to Eq. (5.11)
6.2 Subtracting zero momentum three-point correlators
The three-point correlation functions involving a tensor D meson are unfortunately very noisy: hence it is extremely difficult to get a large enough signal-to-noise ratio. We will use a trickFootnote 3 which consists in subtracting to every three-point correlator the correlator with the same gauge configuration and the same operators at zero momentum. Indeed we know that the decay \(B \rightarrow D^*_2\) vanishes at zero recoil. This is obvious in the continuum limit, since we start with a B meson of vanishing angular momentum J. The weak interaction operator (axial current \(A_\mu \)), having \(J=0\) for \(A_0\) and \(J=1\) for \(A_i\, (i=1,2,3)\), cannot generate a \(J=2\) state: at zero recoil there is no momentum to generate a higher angular momentum.
However, this vanishing is also exact on a lattice. The proof goes as follows: the three-point correlators which contribute to the \( D^*_2 \rightarrow B\) are linear combinations of correlators of the type
where \(i,j,k\in \{1,2,3\}\) may be different or equal. All operators are at rest (zero recoil). We have assumed the \(D^*_2\) meson (B meson) interpolating field to be at the source time \(t_s\) (sink time \(t_p\)), and the current at time t with \(t_p \ge t \ge t_s \).
Let us choose one of the three spatial directions \(\hat{l}\) and consider the rotation \({\mathscr {R}}_l(\pi )\) of angle \( \pi \) around it: the spatial coordinates perpendicular to \(\hat{l}\) change sign. All vector operators, \(D_i, V_i\ \text {and}\ A_i\), change sign if i is perpendicular to \(\hat{l}\), whereas they remain unchanged if \(i=l\).
\({\mathscr {R}}_l(\pi )\) belongs to the 3D cubic symmetry group. The lattice actions are invariant under \({\mathscr {R}}_l(\pi )\), even the twisted-mass action since \({\mathscr {R}}_l(\pi )\) is parity even. In Eq. (6.1), there are three operators at three different times. Being at rest, we may assume that their spatial nesting is invariant under \({\mathscr {R}}_l(\pi )\): it can be a stochastic source, a local operator at the origin of three-space, a smeared operator symmetric around the origin of three-space or a local operator integrated over three-space (for the current). If an odd number among the indices i, j, k are perpendicular to \(\hat{l}\), then the correlator in Eq. (6.1) changes sign under \({\mathscr {R}}_l(\pi )\) and the amplitude must vanish. This happens if \(i=j=k\), \(\hat{l}\) being any other direction, or if \(i= j \ne k\), \(l=i\).
However, if i, j, k are all different it does not work: any \({\mathscr {R}}_l(\pi )\) will keep the \(C^{(3)}\) of Eq. (6.1) unchanged and thus cannot be proven to vanish on the lattice although it should in the continuum limit. This type of term does generate lattice artefacts. A parity operation would change its sign (changing the sign of all three operators) but parity is not an invariant of the twisted-mass action. We must then use correlators symmetrised according to the exact symmetry of the twisted-mass action [23], i.e. we apply Eq. (5.11): the lattice artefact should then disappear and \(C^{(3)\,\text {sym}}_{i,j,k}(t_s,t_c,t_p) = 0\) on the lattice, at zero recoil.
Since it must vanish at zero recoil on the lattice, we may subtract from the three-point correlator at non-vanishing recoil the same configuration at zero recoil. This reduces some correlated noise, and indeed it turns out that the signal, although still very noisy, is significantly improved. We have computed the three-point functions with both all \(\mu \) positive (set \(sp_0\)) and all opposite in sign (set \(sp_1\)). It turns out that the real parts of the three-point functions are very similar for both \(sp_0\) and \(sp_1\) sets, while the imaginary parts are approximatively opposite in signs, from which we can guess that the contributions with i, j, k not all different are dominantly real, while the ones with i, j, k different are dominantly imaginary. This is related to the fact that the terms odd in the \(\mu \) have an i with respect to the ones which are even, but for the sake of brevity we will skip an exact proof (Fig. 7).
The ratio of the matrix element for \(B \rightarrow D^*_2\) over the value derived from the infinite mass limit, Eq. (6.6), for \(w=1.3\), once the three-point function has been symmetrised according to Eq. (5.11) and once the three-point function at zero recoil has been subtracted. We show the three b quark masses. The plots on the left correspond to \(\beta =3.9\) and \(t_p-t_s = 14\), those to the right to \(\beta =4.05\) and \(t_p-t_s = 18\). The upper line corresponds to the B meson of continuum mass 2.55 GeV, the second to 3.18 GeV and the third to 3.97 GeV. We use for the three-point functions the average of the combinations expanded in Table 6
6.3 Extracting the matrix element
An estimate of \(p \,\tilde{k}\) is thus given by
where the three-point correlators are the combinations of correlators listed in Table 6, symmetrised according to Eq. (5.11) and with the corresponding zero recoil three-point correlators subtracted. Let us recall that \(\vec p = \vec {\theta }\pi /L\) where L is the spatial length of the lattice. We have used systematically \(\vec {\theta }_x = \vec {\theta }_y = \vec {\theta }_z = \theta \) whence \(|\vec p|= \sqrt{3}\, \theta \,\pi /L\). In fact we prefer to present another ratio. Since the estimate of \(B \rightarrow D^*_2\) in the infinite mass limit is rather successful, in good agreement with experiment, we will compute the ratio of the three-point correlators divided by the one which is derived from the infinite mass limit formula [8]:
Here the fit gives \(\sigma ^2_{3/2} \simeq 1.5\) and \( \tau _{3/2}(1) \simeq 0.54 \) and the formula in Sect. 2.5.1
with \(r_{D^*_2} = M_{D^*_2}/M_B\). This \(\tilde{k}_\mathrm{inf}\) will be used as a benchmark for \(\tilde{k}\) extracted from our present calculations. From our benchmark \(\tilde{k}_\mathrm{inf}\) we compute the benchmark three-point correlator, the \(D^*_2\) meson being created at time \(t_s\) the current inserted at time t and the B annihilated at time \(t_p\):
We thus consider the ratio
To increase the signal we take the average of the 11 expressions for \(\tilde{k}\) in Table 6, for all three masses of the B meson, for \(\beta =3.9\) and \(\beta =4.05\). For the two-point functions in Eq. (6.5) we have used the numerical values. As can be seen all these plots show similar shapes. There is a positive noisy signal, of the order 1 for \(\beta =4.05\). For \(\beta =3.9\) the ratio is about one order of magnitude smaller. We do not understand this feature.
To conclude we may claim that there is a hint of a signal for \(B \rightarrow D^*_2 \ell \nu \) with finite \(m_{c,b}\). But the size of the statistical and systematic errors do not allow us to provide any quantitative result. It is clear that improving the signal is a major goal. This can be performed using larger statistics, using the points at \(\beta =4.2\), using different times for the sink, using other lattice actions and trying to find better interpolating fields.
7 Conclusions and prospects
The major goal of this paper concerned the orbitally excited states of the charmed mesons and the semileptonic decay of the B meson into the latter. We have concentrated on \(D^*_2\) and \(D^*_0\) (see [39] for a study of the mass spectrum including the spin-1 particles). We have considered three “B mesons” with, respectively, masses of 2.55, 3.18 and 3.97 GeV. We have used only two lattice spacings, 0.085 and 0.069 fm, with the addition of data with 0.054 fm for \(D^*_0\).
Concerning the spectroscopy, we have noted a discrepancy between the masses of the \(D^*_2\) states which are in the E (\(D_i\,V_i\)) discrete group and the ones in the \(T_2\) (\(D_i\,V_j; j \ne i\)). This is, of course, a lattice artefact. We have also studied the B meson energy as a function of the momentum. There is a clear departure from the theoretical formula for the heaviest meson. This is presumably also an artefact. The \(D^*_0\) state can decay into a D meson due to the parity violation when using twisted quarks. It was necessary to use the GEVP method to overcome this difficulty. The mass differences between the \(D^*_2\) (\(D^*_0\)) with the D meson mass, extrapolated to the continuum, do not agree well with experiment. There are indications that reducing the cut-off effects improves this result.
To compute the form factors and branching fractions we have derived all the needed theoretical formulae necessary to estimate any form factor from lattice calculation.
Concerning \(B \rightarrow D^*_0\) we have, up to now, only considered the zero recoil quantity. Our result is that, contrary to the case of infinite b and c masses, the zero recoil amplitude does not vanish. This should increase drastically the ratio of \(B \rightarrow D^*_0\) branching fraction over the \(B \rightarrow D^*_2\) one, as compared to the infinite mass case. We estimate the ratio of zero recoil amplitudes \((B \rightarrow D^{*}_{0} l \nu )/(B \rightarrow D l \nu ) = 0.17(6)(6)\). The corresponding ratio of branching fractions should be around 0.02, with very large errors. Some experimental semileptonic branching ratios seem to indicate fort this ratio a figure of the order of 0.1, but the experimental situation is far from clear and our theoretical estimate still needs much work.
The \(B \rightarrow D^*_2\) is treated by a subtraction of the zero recoil contribution which we prove to be theoretically vanishing. There is a signal, although still very noisy. We take the infinite mass result as a benchmark. The ratio to the infinite mass prediction is around 1 for \(\beta = 4.05\) but around 0.1 for \(\beta = 3.9\), which indicates that beyond the very large statistical errors the systematic effects are not yet well understood.
Altogether, this paper has to be taken as a preliminary study. To our knowledge it is the first study of semileptonic decays to orbitally excited charmed mesons with finite masses for the b and c. The considered process is very noisy and it is already rewarding that we got signals which seem to make sense, although the uncertainty is still much too large.
To improve the situation it seems that the path to follow is to further analyse the data set of ETMC at \(\beta =4.2\) (\(a \simeq 0.055\) fm) and check against another lattice regularisation. The extrapolation to the continuum will thus be on a much safer ground. An increase of the statistics might also help.
We also stress that \(B_s\) and \(D_s\) sectors are presumably interesting to examine. Indeed, the \(D^*_{s0}(2317)\) and \(D^*_{s1}(2460)\) states stand below the DK and \(D^* K\) thresholds: hence they are narrow. At LHCb, according to a phenomenological study [44], about 100 events in the channel \(B_s \rightarrow D^{*-}_{s0} \pi ^+\) are expected with 1 \(\mathrm{fb}^{-1}\) of integrated luminosity. It is an encouragement to extend our effort of measuring the form factors of \(B \rightarrow D^{**}\) semileptonic decays in the heavy-strange sector.
Notes
We use the
 notation of the states, where S is the spin angular momentum, \(L=1\) the orbital angular momentum and \(J=L+S\) the total angular momentum of the \(D^{**}\) state.
notation of the states, where S is the spin angular momentum, \(L=1\) the orbital angular momentum and \(J=L+S\) the total angular momentum of the \(D^{**}\) state.This will greatly simplify the calculations on the lattice.
We are indebted to Philippe Boucaud who suggested this trick.
References
K.A. Olive et al. [Particle Data Group Collaboration], Chin. Phys. C 38, 090001 (2014)
P. Gambino, T. Mannel, N. Uraltsev, \(B\rightarrow D^*\) zero-recoil formfactor and the heavy quark expansion in QCD: a systematic study. JHEP 1210, 169 (2012). arXiv:1206.2296 [hep-ph]
I.I. Bigi, B. Blossier, A. Le Yaouanc, L. Oliver, O. Pene, J.-C. Raynal, A. Oyanguren, P. Roudeau, Memorino on the ‘1/2 vs. 3/2 puzzle’ in \(\bar{B} \rightarrow \ell \,\bar{\nu }\, X(c)\): a year later and a bit wiser. Eur. Phys. J. C 52, 975 (2007). arXiv:0708.1621 [hep-ph]
A. Le Yaouanc, O. Pene. arXiv:1408.5104 [hep-ph]
P. del Amo Sanchez et al. [BaBar Collaboration], Observation of new resonances decaying to \(D\pi \)10.58 GeV. Phys. Rev. D 82, 111101 (2010). arXiv:1009.2076 [hep-ex]
A. Le Yaouanc, L. Oliver, O. Pene, J.C. Raynal, New heavy quark limit sum rules involving Isgur–Wise functions and decay constants. Phys. Lett. B 387, 582 (1996). arXiv:hep-ph/9607300
N. Uraltsev, New exact heavy quark sum rules. Phys. Lett. B 501, 86 (2001). arXiv:hep-ph/0011124
V. Morenas, A. Le Yaouanc, L. Oliver, O. Pene, J.C. Raynal, Quantitative predictions for \(B\) in quark models a la Bakamjian–Thomas. Phys. Rev. D 56, 5668 (1997). arXiv:hep-ph/9706265
D. Ebert, R.N. Faustov, V.O. Galkin, Exclusive semileptonic decays of \(B\) mesons in the relativistic quark model. Phys. Lett. B 434, 365 (1998). arXiv:hep-ph/9805423
D. Ebert, R.N. Faustov, V.O. Galkin, Heavy quark \(1/m_Q\) mesons. Phys. Rev. D 61, 014016 (2000). arXiv:hep-ph/9906415
D. Becirevic, B. Blossier, P. Boucaud, G. Herdoiza, J.P. Leroy, A. Le Yaouanc, V. Morenas, O. Pene, Lattice measurement of the Isgur–Wise functions \(\tau _{1/2}\). Phys. Lett. B 609, 298 (2005). arXiv:hep-lat/0406031
B. Blossier et al. [European Twisted Mass Collaboration], Lattice calculation of the Isgur–Wise functions \(\tau _{1/2}\) with dynamical quarks. JHEP 0906, 022 (2009). arXiv:0903.2298 [hep-lat]
N. Isgur, M.B. Wise, Excited charm mesons in semileptonic \(\bar{B}\) decay and their contributions to a Bjorken sum rule. Phys. Rev. D 43, 819 (1991)
B. Bakamjian, L.H. Thomas, Phys. Rev. 92, 1300 (1953)
N. Isgur, D. Scora, B. Grinstein, M.B. Wise, Semileptonic \(B\) and \(D\) decays in the quark model. Phys. Rev. D 39, 799 (1989)
P. Boucaud et al. [ETM Collaboration], Dynamical twisted mass fermions with light quarks. Phys. Lett. B 650, 304 (2007). arXiv:hep-lat/0701012
C. Urbach [European Twisted Mass Collaboration], Lattice QCD with two light Wilson quarks and maximally twisted mass. PoS LAT 022 (2007). arXiv:0710.1517 [hep-lat]
P. Boucaud et al. [ETM Collaboration], Dynamical twisted mass fermions with light quarks: simulation and analysis details. Comput. Phys. Commun. 179, 695 (2008). arXiv:0803.0224 [hep-lat]
B. Blossier et al. [ETM Collaboration], Average up/down, strange and charm quark masses with \(N_f=2\) twisted mass lattice QCD. Phys. Rev. D 82, 114513 (2010). arXiv:1010.3659 [hep-lat]
B. Blossier et al. [ETM Collaboration], Ghost-gluon coupling, power corrections and \(\Lambda _{\overline{{\rm MS}}}\). Phys. Rev. D 82, 034510 (2010). arXiv:1005.5290 [hep-lat]
P. Weisz, Continuum limit improved lattice action for pure Yang–Mills theory. 1. Nucl. Phys. B 212, 1 (1983)
R. Frezzotti et al. [Alpha Collaboration], Lattice QCD with a chirally twisted mass term. JHEP 0108, 058 (2001). arXiv:hep-lat/0101001
R. Frezzotti, G.C. Rossi, Chirally improving Wilson fermions. 1. \(O(a)\) improvement. JHEP 0408, 007 (2004). arXiv:hep-lat/0306014
A. Shindler, Twisted mass lattice QCD. Phys. Rep. 461, 37 (2008). arXiv:0707.4093 [hep-lat]
K. Jansen, C. Liu, M. Luscher, H. Simma, S. Sint, R. Sommer, P. Weisz, U. Wolff, Nonperturbative renormalization of lattice QCD at all scales. Phys. Lett. B 372, 275 (1996). arXiv:hep-lat/9512009
J. Foley, K.J. Juge, A. O’Cais, M. Peardon, S.M. Ryan, J.-I. Skullerud, Practical all-to-all propagators for lattice QCD. Comput. Phys. Commun. 172, 145 (2005). arXiv:hep-lat/0505023
M. Foster et al. [UKQCD Collaboration], Hadrons with a heavy color adjoint particle. Phys. Rev. D 59, 094509 (1999). arXiv:hep-lat/9811010
C. McNeile et al. [UKQCD Collaboration], Decay width of light quark hybrid meson from the lattice. Phys. Rev. D 73, 074506 (2006). arXiv:hep-lat/0603007
S. Gusken, U. Low, K.H. Mutter, R. Sommer, A. Patel, K. Schilling, Nonsinglet axial vector couplings of the baryon octet in lattice QCD. Phys. Lett. B 227, 266 (1989)
M. Albanese et al. [APE Collaboration], Glueball masses and string tension in lattice QCD. Phys. Lett. B 192, 163 (1987)
N. Carrasco et al. [ETM Collaboration], PoS LATTICE 2012, 105 (2012). arXiv:1211.0565 [hep-lat]
R. Frezzotti et al. [ETM Collaboration], Electromagnetic form factor of the pion from twisted-mass lattice QCD at \(N_f = 2\). Phys. Rev. D 79, 074506 (2009). arXiv:0812.4042 [hep-lat]
P. Lacock et al. [UKQCD Collaboration], Orbitally excited and hybrid mesons from the lattice. Phys. Rev. D 54, 6997 (1996). arXiv:hep-lat/9605025
C. Michael, Adjoint sources in lattice gauge theory. Nucl. Phys. B 259, 58 (1985)
M. Luscher, U. Wolff, How to calculate the elastic scattering matrix in two-dimensional quantum field theories by numerical simulation. Nucl. Phys. B 339, 222 (1990)
B. Blossier, M. Della Morte, G. von Hippel, T. Mendes, R. Sommer, On the generalized eigenvalue method for energies and matrix elements in lattice field theory. JHEP 0904, 094 (2009). arXiv:0902.1265 [hep-lat]
A.K. Leibovich, Z. Ligeti, I.W. Stewart, M.B. Wise, Semileptonic \(B\) decays to excited charmed mesons. Phys. Rev. D 57, 308 (1998). arXiv:hep-ph/9705467
B. Blossier et al. [ALPHA Collaboration], JHEP 1012, 039 (2010). arXiv:1006.5816 [hep-lat]
M. Wagner, M. Kalinowski, Twisted mass lattice computation of charmed mesons with focus on \(D^{\ast \ast }\). arXiv:1310.5513 [hep-lat]
D. Mohler, S. Prelovsek, R.M. Woloshyn, Phys. Rev. D 87(3), 034501 (2013). arXiv:1208.4059 [hep-lat]
D. Spehler, S.F. Novaes, Helicity wave functions for massless and massive spin-2 particles. Phys. Rev. D 44, 3990 (1991)
S.Y. Choi, J. Lee, J.S. Shim, H.S. Song, Spin-2 particle polarization. J. Korean Phys. Soc. 25, 576 (1992)
S. Weinberg, The Quantum Theory of Fields. Vol. 1: Foundations (Univ. Pr., Cambridge, 1995), p. 609
D. Becirevic, A. Le Yaouanc, L. Oliver, J.C. Raynal, P. Roudeau, J. Serrano, Phys. Rev. D 87(5), 054007 (2013). arXiv:1206.5869 [hep-ph]
Acknowledgments
We acknowledge many enlightening discussions with Philippe Boucaud, Francesco Sanfilippo and Marc Wagner. We have intensively used NISAN, the software created by F. Sanfilippo. This work was granted access to the HPC resources of IDRIS under the allocation 2013-052271 made by GENCI. Many calculations were performed on the computing centre or IN2P3 in Lyon. Mariam Atoui acknowledges the “Conseil National de la Recherche Scientifique au Liban (CNRS), Liban” for her thesis grant.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Coefficients of the hadronic tensor \({W_{\mu \nu }}\)
In order to compute explicitly the coefficients \({\alpha }\), \({\beta _{_{++}}}\), \({\beta _{_{+-}}}\), \({\beta _{_{-+}}}\), \({\beta _{_{--}}}\) and \({\gamma }\) given in (2.3), we will have to evaluate the possible summation over the \(D^{**}\) spins. Scalar meson We have no summation and we get
Tensor meson We have \(J=2\); the polarisation tensor \( \varepsilon _{\mu \nu }^{(p)}\) satisfies [41, 42]:
After calculation, we obtain
1.2 Variation domains of x and y
1.2.1 First type of constraints: \({x = x(y)}\)
-
Non-zero mass lepton
We have
$$\begin{aligned}&(m_{_{\!\ell }}\ne 0)\quad \left\{ { \begin{array}{l} x_\text {max} = \dfrac{1}{2}\left\{ { 1 + y - r_{_{\!D^{**}}}^2 + r_{_{\!\ell }}^2\left[ { 1 + \dfrac{1}{y}\left( {1 - r_{_{\!D^{**}}}^2}\right) }\right] + \left( {1 - \dfrac{r_{_{\!\ell }}^2}{y}}\right) \sqrt{[{y - (1-r_{_{\!D^{**}}})^2}][{y-(1+r_{_{\!D^{**}}})^2}]} }\right\} , \\ x_\text {min} = \dfrac{1}{2}\left\{ { 1 + y - r_{_{\!D^{**}}}^2 + r_{_{\!\ell }}^2\left[ { 1 + \dfrac{1}{y}\left( {1 - r_{_{\!D^{**}}}^2}\right) }\right] - \left( {1 - \dfrac{r_{_{\!\ell }}^2}{y}}\right) \sqrt{[{y - (1-r_{_{\!D^{**}}})^2}][{y-(1+r_{_{\!D^{**}}})^2}]} }\right\} , \end{array} }\right. \end{aligned}$$$$\begin{aligned} \text {with}\quad r_{_{\!\ell }}^2\leqslant y\leqslant (1 - r_{_{\!D^{**}}})^2. \end{aligned}$$ -
Zero mass lepton We have
$$\begin{aligned}&(m_{_{\!\ell }}= 0)\quad \left\{ { \begin{array}{l} x_\text {max} = \dfrac{1}{2}[{ 1 + y - r_{_{\!D^{**}}}^2 + \sqrt{[{y - (1-r_{_{\!D^{**}}})^2}][{y-(1+r_{_{\!D^{**}}})^2}]} }], \\ x_\text {min} = \dfrac{1}{2}[{ 1 + y - r_{_{\!D^{**}}}^2 - \sqrt{[{y - (1-r_{_{\!D^{**}}})^2}][{y-(1+r_{_{\!D^{**}}})^2}]} }], \end{array} }\right. \end{aligned}$$$$\begin{aligned} \text {with}\quad 0\leqslant y\leqslant \left( 1 - r_{_{\!D^{**}}}\right) ^2. \end{aligned}$$
1.2.2 Second type of constraints: \({y = y(x)}\)
-
Non-zero mass lepton We have
$$\begin{aligned} (m_{_{\!\ell }}\ne 0)\quad \left\{ { \begin{array}{l} y_\text {max} = \dfrac{1}{2}\left[ { x - \dfrac{r_{_{\!D^{**}}}^2(x - 2r_{_{\!\ell }}^2)}{1 - x + r_{_{\!\ell }}^2} + \left( {1 - \dfrac{r_{_{\!D^{**}}}^2}{1-x+r_{_{\!\ell }}^2}}\right) \sqrt{x^2 - 4r_{_{\!\ell }}^2} }\right] , \\ y_\text {min} = \dfrac{1}{2}\left[ { x - \dfrac{r_{_{\!D^{**}}}^2(x - 2r_{_{\!\ell }}^2)}{1 - x + r_{_{\!\ell }}^2} - \left( {1 - \dfrac{r_{_{\!D^{**}}}^2}{1-x+r_{_{\!\ell }}^2}}\right) \sqrt{x^2 - 4r_{_{\!\ell }}^2} }\right] , \end{array} }\right. \end{aligned}$$$$\begin{aligned} \text {with}\quad 2\,r_{_{\!\ell }}\leqslant x\leqslant 1 - r_{_{\!D^{**}}}^2 + r_{_{\!\ell }}^2. \end{aligned}$$ -
Zero mass lepton We have
$$\begin{aligned} (m_{_{\!\ell }}= 0)\quad \left\{ { \begin{array}{l} y_\text {max} = x\left( {1 - \dfrac{r_{_{\!D^{**}}}^2}{1-x}}\right) , \\ y_\text {min} = 0, \end{array} }\right. \end{aligned}$$$$\begin{aligned} \text {with}\quad 0\leqslant x\leqslant 1 - r_{_{\!D^{**}}}^2. \end{aligned}$$
1.3 Expressions for the various decay widths
1.3.1
 differential decay width
differential decay width
\(\blacktriangleright \) 
-
Non-zero mass lepton:
We have
$$\begin{aligned} \boxed { \begin{aligned} \dfrac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y}&= -\,\dfrac{G_F^2\,|V_{cb}|^2}{128\pi ^3}\, \,m_{_{\!B}}^5\,\Biggl \{{}\Biggr . - {\tilde{u}_+}^2\,\Big [{4\,\Big [{x\,r_{_{\!D^{*}_0}}^2 + (1-x)(y-x)}\Big ]+r_{_{\!\ell }}^2\Big [{3\,y -4(x+r_{_{\!D^{*}_0}}^2)+r_{_{\!\ell }}^2}\Big ]}\Big ]\\&\quad + 2\,{\,{\tilde{u}_+}{\tilde{u}_-}\,}\,r_{_{\!\ell }}^2\Big [{2(1-x-r_{_{\!D^{*}_0}}^2) + y + r_{_{\!\ell }}^2}\Big ]\\&\quad + {\tilde{u}_-}^2\,r_{_{\!\ell }}^2\,(y - r_{_{\!\ell }}^2) \Biggl .{}\Biggr \}. \end{aligned} } \end{aligned}$$ -
Zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y} = \dfrac{G_F^2\,|V_{cb}|^2}{32\pi ^3}\, \,m_{_{\!B}}^5\, {\tilde{u}_+}^2\,\Big [{x\,r_{_{\!D^{*}_0}}^2 + (1-x)(y-x)}\Big ]. } \end{aligned}$$
\(\blacktriangleright \) 
-
Non-zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y} = -\,\dfrac{m_{_{\!B}}}{256\pi ^3}\,\dfrac{G_F^2\,|V_{cb}|^2}{2}\, \,\{ C_1\,{\tilde{k}}^2 + C_2\,{\tilde{h}}^2 + C_3\,{\tilde{b}_+}^2 + C_4\,{\tilde{b}_-}^2 + 2\,C_5\,{\tilde{k}}\,{\tilde{b}_+} + 2\,C_6\,{\tilde{k}}\,{\tilde{b}}_- + 2\,C_7\,{\tilde{b}}_+\,{\tilde{b}}_- + 2\,C_8\,{\tilde{h}}\,{\tilde{k}} \} } \end{aligned}$$where the \(C_i\) coefficients are given by
$$\begin{aligned}&\boxed {\begin{array}{ll}C_1 &{}= \dfrac{m_{_{\!B}}^4}{3\,r_{_{\!D^{*}_2}}^4}\Biggl \{{}\Biggr . \left[ {y^2-\left( 2+r_{_{\!D^{*}_2}}^2\right) \,y+\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] \left[ {2(1-x)(x-y) +r_{_{\!D^{*}_2}}^2(3\,y-2\,x)}\right] - 3\,y^2\,r_{_{\!D^{*}_2}}^4\\ &{}\quad - r_{_{\!\ell }}^2\Big [{ (1-2\,x+y)\left[ {2(1-y)^2-3\,r_{_{\!D^{*}_2}}^2(1+y)}\right] - r_{_{\!D^{*}_2}}^4\left( 2\,x-r_{_{\!D^{*}_2}}^2\right) }\Big ] \\ &{}\quad -2\,r_{_{\!\ell }}^4\Big [{y^2-2\left( 1+r_{_{\!D^{*}_2}}^2\right) \,y +1 - r_{_{\!D^{*}_2}}^2 + r_{_{\!D^{*}_2}}^4}\Big ] \Biggl .{}\Biggr \}, \end{array} }\\&\boxed {\begin{array}{ll}C_2 &{}= \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^2}\left[ y-(1-r_{_{\!D^{*}_2}})^2\right] \left[ y-(1+r_{_{\!D^{*}_2}})^2\right] \\ &{}\quad \times \Big [y\left[ { 2(1-x+r_{_{\!D^{*}_2}})(1-x-r_{_{\!D^{*}_2}}) -(1-y+r_{_{\!D^{*}_2}}^2)(1+y-2\,x-r_{_{\!D^{*}_2}}^2) }\right] \\ &{}\quad + r_{_{\!\ell }}^2\left[ { (1+y-r_{_{\!D^{*}_2}}^2)(1+y-2\,x-r_{_{\!D^{*}_2}}^2) + 2\,r_{_{\!\ell }}^2 }\right] \Big ], \end{array} }\\&\boxed {C_3 = \dfrac{m_{_{\!B}}^8}{6\,r_{_{\!D^{*}_2}}^4}\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] ^2\left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] ^2 \Big [{ 4\,x\left( 1-x-r_{_{\!D^{*}_2}}^2\right) -4\,y(1-x) + r_{_{\!\ell }}^2\left[ {4\left( x+r_{_{\!D^{*}_2}}^2\right) - 3\,y -r_{_{\!\ell }}^2}\right] }\Big ] ,}\\&\boxed {C_4 = \dfrac{m_{_{\!B}}^8}{6\,r_{_{\!D^{*}_2}}^4}\,r_{_{\!\ell }}^2\,(y - r_{_{\!\ell }}^2)\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] ^2\left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] ^2,}\\&\boxed {\begin{array}{ll}C_5 &{}= \dfrac{m_{_{\!B}}^6}{3\,r_{_{\!D^{*}_2}}^4}\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] \\ &{}\quad \times \left[ { 2\left( 1-y-r_{_{\!D^{*}_2}}^2\right) \left[ {(1-x)(x-y)-x\,r_{_{\!D^{*}_2}}^2}\right] -r_{_{\!\ell }}^2\left[ {\left( 1-y+r_{_{\!D^{*}_2}}^2\right) \left( 1-3\,x+2\,y-r_{_{\!D^{*}_2}}^2+r_{_{\!\ell }}^2\right) + 2\,x\,r_{_{\!D^{*}_2}}^2} \right] }\right] , \end{array} }\\&\boxed {\begin{array}{ll}C_6 &{}= \dfrac{m_{_{\!B}}^6}{3\,r_{_{\!D^{*}_2}}^4}\,r_{_{\!\ell }}^2\,\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] \\ &{}\quad \times \left[ { \left( 1-y+r_{_{\!D^{*}_2}}^2\right) \left( 1-x+r_{_{\!D^{*}_2}}^2\right) +2r_{_{\!D^{*}_2}}^2(x-2) + r_{_{\!\ell }}^2\left( 1-y+r_{_{\!D^{*}_2}}^2\right) }\right] , \end{array} }\\&\boxed {C_7 = \dfrac{m_{_{\!B}}^8}{6\,r_{_{\!D^{*}_2}}^4}\,r_{_{\!\ell }}^2\,\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] ^2\left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] ^2 \left[ 2\left( 1 - x - r_{_{\!D^{*}_2}}^2\right) + y + r_{_{\!\ell }}^2\right] },\\&\boxed {C_8 = -\,\dfrac{m_{_{\!B}}^6}{r_{_{\!D^{*}_2}}^2}\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] \left[ {y\left( 1+y-2\,x-r_{_{\!D^{*}_2}}^2\right) + r_{_{\!\ell }}^2\left( 1+y-r_{_{\!D^{*}_2}}^2\right) }\right] .} \end{aligned}$$ -
Zero mass lepton: We notice that the coefficients of \(C_4\), \(C_6\) and \(C_7\) cancel in this limit, leading to
$$\begin{aligned} \boxed { \dfrac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y} = -\,\dfrac{m_{_{\!B}}}{256\pi ^3}\,\dfrac{G_F^2\,|V_{cb}|^2}{2}\, \,[C_1\,{\tilde{k}}^2 + C_2\,{\tilde{h}}^2 + C_3\,{\tilde{b}_+}^2 + 2\,C_5\,{\tilde{k}}\,{\tilde{b}}_+ + 2\,C_8\,{\tilde{h}}\,{\tilde{k}}] } \end{aligned}$$where the \(C_i\) coefficients are given by
$$\begin{aligned}&\boxed {C_1 = \dfrac{m_{_{\!B}}^4}{3\,r_{_{\!D^{*}_2}}^4}\left[ \left[ {y^2-\left( 2+r_{_{\!D^{*}_2}}^2\right) \,y+\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] \left[ {2(1-x)(x-y) +r_{_{\!D^{*}_2}}^2(3\,y-2\,x)}\right] - 3\,y^2\,r_{_{\!D^{*}_2}}^4\right] ,}\\&\boxed {\begin{array}{ll}C_2 &{}= \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^2}\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] \\ &{}\quad \times y\left[ { 2\left( 1-x+r_{_{\!D^{*}_2}}\right) \left( 1-x-r_{_{\!D^{*}_2}}\right) -\left( 1-y+r_{_{\!D^{*}_2}}^2\right) \left( 1+y-2\,x-r_{_{\!D^{*}_2}}^2\right) }\right] , \end{array} }\\&\boxed {C_3 = \dfrac{m_{_{\!B}}^8}{6\,r_{_{\!D^{*}_2}}^4}\left[ y-\Big (1-r_{_{\!D^{*}_2}}\Big )^2\right] ^2\left[ y-\Big (1+r_{_{\!D^{*}_2}}\Big )^2\right] ^2 \left[ { 4\,x\Big (1-x-r_{_{\!D^{*}_2}}^2\Big )-4\,y(1-x) }\right] , }\\&\boxed {C_5 = \dfrac{m_{_{\!B}}^6}{3\,r_{_{\!D^{*}_2}}^4}\Big [y-\Big (1-r_{_{\!D^{*}_2}}\Big )^2\Big ]\Big [y-\Big (1+r_{_{\!D^{*}_2}}\Big )^2\Big ] \left[ { 2\Big (1-y-r_{_{\!D^{*}_2}}^2\Big )\left[ {(1-x)(x-y)-x\,r_{_{\!D^{*}_2}}^2}\right] }\right] , }\\&\boxed {C_8 = -\,\dfrac{m_{_{\!B}}^6}{r_{_{\!D^{*}_2}}^2}\Big [y-\Big (1-r_{_{\!D^{*}_2}}\Big )^2\Big ]\Big [y-\Big (1+r_{_{\!D^{*}_2}}\Big )^2\Big ] {y\,\Big (1+y-2\,x-r_{_{\!D^{*}_2}}^2\Big ) }.} \end{aligned}$$
1.4
 differential decay width
differential decay width
The form factors depend only on the y parameter, but in an unknown way. So, the integration over the x variable can be done through the use the expressions of the type \(x = x(y)\).
\(\blacktriangleright \) 
-
Non-zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}\Gamma }{\text {d}y} = -\,\dfrac{G_F^2\,|V_{cb}|^2}{128\pi ^3}\,m_{_{\!B}}^5\, \,\Big [ D_1\,{\tilde{u}_+}^2 + 2\,D_2\,{\tilde{u}}_+\,{\tilde{u}}_- + D_3\,{\tilde{u}_-}^2 \Biggr ] } \end{aligned}$$where the \(D_i\) coefficients are functions of y and are given by
$$\begin{aligned}&\boxed {\begin{array}{ll}D_1 &{}= \dfrac{1}{3\,y^3}\,\left( y-r_{_{\!\ell }}^2\right) ^2\,\Big [{\left[ y-(1-r_{_{\!D^{*}_0}})^2\right] \left[ y-(1+r_{_{\!D^{*}_0}})^2\right] }\Big ]^{1/2}\\ &{}\quad \times \Biggl \{{ 2\,y\,{\left[ y-\left( 1-r_{_{\!D^{*}_0}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_0}}\right) ^2\right] } + r_{_{\!\ell }}^2\,\Big [{y^2-2\,y\,\left( 1+r_{_{\!D^{*}_0}}^2\right) +4\,\left( 1-r_{_{\!D^{*}_0}}^2\right) ^2}\Big ] }\Biggr \}, \end{array} }\\&\boxed {D_2 = \dfrac{1}{y^2}\,r_{_{\!\ell }}^2\,(y-r_{_{\!\ell }}^2)^2\,\left( 1-r_{_{\!D^{*}_0}}^2\right) \,\left[ {\left[ y-(1-r_{_{\!D^{*}_0}})^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_0}}\right) ^2\right] }\right] ^{1/2} ,}\\&\boxed {D_3 = \dfrac{1}{y}\,r_{_{\!\ell }}^2\,(y-r_{_{\!\ell }}^2)^2\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_0}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_0}}\right) ^2\right] }\right] ^{1/2} .} \end{aligned}$$Let us recall that, in that expression of \(\text {d}\Gamma /\text {d}y\), the y parameter belongs in the interval: \(\ r_{_{\!\ell }}^2\leqslant y\leqslant (1-r_{_{\!D^{*}_0}})^2\)
-
Zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}\Gamma }{\text {d}y} = -\,\dfrac{G_F^2\,|V_{cb}|^2}{128\pi ^3}\,m_{_{\!B}}^5\, \,{\tilde{u}_+}^2\,D_1 }\quad \text {where } \boxed {D_1 = \dfrac{2}{3}\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_0}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_0}}\right) ^2\right] }\right] ^{3/2},} \end{aligned}$$since the other coefficients, \(D_2\) and \(D_3\), give zero in this case.
\(\blacktriangleright \) 
-
Non-zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}\Gamma }{\text {d}y} = -\,\dfrac{m_{_{\!B}}}{256\pi ^3}\,\dfrac{G_F^2\,|V_{cb}|^2}{2}\, \,\{ D_1\,{\tilde{k}}^2 + D_2\,{\tilde{h}}^2 + D_3\,{\tilde{b}_+}^2 + D_4\,{\tilde{b}_-}^2 + 2\,D_5\,{\tilde{k}}\,{\tilde{b}}_+ + 2\,D_6\,{\tilde{k}}\,{\tilde{b}}_- + 2\,D_7\,{\tilde{b}}_+\,{\tilde{b}}_- + 2\,D_8\,{\tilde{h}}\,{\tilde{k}}\} } \end{aligned}$$where the \(D_i\) coefficients are given by
$$\begin{aligned}&\boxed {\begin{array}{ll}D_1 &{}= \dfrac{m_{_{\!B}}^4}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{9\,y^3}\,(y-r_{_{\!\ell }}^2)^2\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{3/2}\\ &{}\quad \times \left\{ { y\,\left[ {y^2-2\,y\,\left( 1-4\,r_{_{\!D^{*}_2}}^2\right) +\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] + r_{_{\!\ell }}^2\,\left[ {2\,y^2-y\,\left( 4-r_{_{\!D^{*}_2}}^2\right) +2\,\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] }\right\} , \end{array} }\\&\boxed {D_2 = \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^2}\,\dfrac{1}{3\,y^2}\,(y-r_{_{\!\ell }}^2)^2\,(2\,y+r_{_{\!\ell }}^2)\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,}\\&\boxed {\begin{array}{ll}D_3 &{}= \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{18\,y^3}\,(y-r_{_{\!\ell }}^2)^2\,\Big [{\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\Big ]^{5/2}\\ &{}\quad \times \left\{ { 2\,y\,{\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] } + r_{_{\!\ell }}^2\,\left[ {y^2-2\,y\,\left( 1+r_{_{\!D^{*}_2}}^2\right) +4\,\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] }\right\} , \end{array} } \end{aligned}$$$$\begin{aligned}&\boxed {D_4 = \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{6\,y}\,r_{_{\!\ell }}^2\,(y-r_{_{\!\ell }}^2)^2\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,}\\&\boxed {D_5 = \dfrac{m_{_{\!B}}^6}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{18\,y^3}\,(y-r_{_{\!\ell }}^2)^2\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} \Big [{ 2\,y\,{\left( 1 - y - r_{_{\!D^{*}_2}}^2\right) } + r_{_{\!\ell }}^2\,\left( {4 - y - 4\,r_{_{\!D^{*}_2}}^2}\right) }\Big ], }\\&\boxed {D_6 = \dfrac{m_{_{\!B}}^6}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{6\,y^2}\,r_{_{\!\ell }}^2\,(y-r_{_{\!\ell }}^2)^2\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,}\\&\boxed {D_7 = \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{6\,y^2}\,r_{_{\!\ell }}^2\,(y-r_{_{\!\ell }}^2)^2\,\left( 1-r_{_{\!D^{*}_2}}^2\right) \,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,}\\&\boxed {D_8 = 0. } \end{aligned}$$We recall that, in those formulae, the y parameter varies inside the domain \(\ r_{_{\!\ell }}^2\leqslant y\leqslant (1-r_{_{\!D^{*}_2}})^2\)
-
Zero mass lepton: We have
$$\begin{aligned} \boxed { \dfrac{\text {d}\Gamma }{\text {d}y} = -\,\dfrac{m_{_{\!B}}}{256\pi ^3}\,\dfrac{G_F^2\,|V_{cb}|^2}{2}\, \,[ D_1\,{\tilde{k}}^2 + D_2\,{\tilde{h}}^2 + D_3\,{\tilde{b}_+}^2 + 2\,D_5\,{\tilde{k}}\,{\tilde{b}}_+ + 2\,D_8\,{\tilde{h}}\,{\tilde{k}}] } \end{aligned}$$where the \(D_i\) coefficients are given by
$$\begin{aligned}&\boxed {D_1 = \dfrac{m_{_{\!B}}^4}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{9}\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{3/2} \left[ {y^2-2\,y\,\left( 1-4\,r_{_{\!D^{*}_2}}^2\right) +\left( 1-r_{_{\!D^{*}_2}}^2\right) ^2}\right] ,}\\&\boxed {D_2 = \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^2}\,\dfrac{2}{3}\,y\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,} \end{aligned}$$$$\begin{aligned}&\boxed {D_3 = \dfrac{m_{_{\!B}}^8}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{9}\,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{7/2} ,}\\&\boxed {D_5 = \dfrac{m_{_{\!B}}^6}{r_{_{\!D^{*}_2}}^4}\,\dfrac{1}{9}\,\left( 1-y-r_{_{\!D^{*}_2}}^2\right) \,\left[ {\left[ y-\left( 1-r_{_{\!D^{*}_2}}\right) ^2\right] \left[ y-\left( 1+r_{_{\!D^{*}_2}}\right) ^2\right] }\right] ^{5/2} ,}\\&\boxed {D_8 = 0. } \end{aligned}$$Here, the y parameter lies in the domain \(0\leqslant y\leqslant (1-r_{_{\!D^{*}_2}})^2\).
1.4.1
 differential decay width
differential decay width
It is impossible to give general expressions for the leptonic spectra \(\dfrac{\text {d}\Gamma }{\text {d}x}\), since the integration over y cannot be performed because we do not know the dependence of the form factors on y.
Nevertheless, the procedure to do those calculations is the following:
-
1.
We start from the expressions of the \(\frac{\text {d}^2\Gamma }{\text {d}x\,\text {d}y}\) decay widths given above.
-
2.
We use the constraints of the type \(y = y(x)\) in order to perform the integration over y from \(y_\text {min}\) to \(y_\text {max}\) (expressions given also above). Incidentally, we must not forget that the maximum of \(E_{_{\!D^{**}}}\) corresponds to the minimum of y and vice versa. So, to integrate over \(E_{_{\!D^{**}}}\) from \(E_{_{\!D^{**}}}^\text { min}\) to \(E_{_{\!D^{**}}}^\text { max}\), we have to integrate equivalently over y from \(y_\text {max}\) to \(y_\text {min}\):

with
$$\begin{aligned} \left\{ { \begin{array}{l} y_\text {max} = \dfrac{1}{2}\left[ { x - \dfrac{r_{_{\!D^{**}}}^2(x - 2r_{_{\!\ell }}^2)}{1 - x + r_{_{\!\ell }}^2} + \left( {1 - \dfrac{r_{_{\!D^{**}}}^2}{1-x+r_{_{\!\ell }}^2}}\right) \sqrt{x^2 - 4r_{_{\!\ell }}^2} }\right] , \\ y_\text {min} = \dfrac{1}{2}\left[ { x - \dfrac{r_{_{\!D^{**}}}^2(x - 2r_{_{\!\ell }}^2)}{1 - x + r_{_{\!\ell }}^2} - \left( {1 - \dfrac{r_{_{\!D^{**}}}^2}{1-x+r_{_{\!\ell }}^2}}\right) \sqrt{x^2 - 4r_{_{\!\ell }}^2} }\right] . \end{array} }\right. \end{aligned}$$\(r_{_{\!\ell }}= 0\) gives the relations in the case of a zero mass lepton.
-
3.
The last free parameter x lies in the domain
$$\begin{aligned} 2\,r_{_{\!\ell }}\leqslant x\leqslant 1 - r_{_{\!D^{**}}}^2 + r_{_{\!\ell }}^2. \end{aligned}$$Once again, \(r_{_{\!\ell }}= 0\) gives the variation domain in the case of a zero mass lepton.
1.5 Total decay width \({\Gamma }\)
The problem, mentioned for the leptonic spectra, pops up here again because, in order to get \(\Gamma \), we will have to integrate over y at some point. So we will have to follow the same procedure.
1.6 Polarisation tensor for the \(^{3}P_{2}\) state
Using expressions for the spin-1 polarisation vector found in [43] for instance and the values of the Clebsch–Gordan coefficient from the Particle Physics Booklet, we get
We dropped the \(\vec {0}\) in the notation.
1.7 Extraction of the form factors
The following expressions are not exhaustive.
Note that it is possible to recover the momentum transfer \(y\,m_{_{\!B}}^2 = (p_{_{\!B}}- p_{_{\!D^{**}}})^2\) using
leading to

With  :
:
-
\({\text {form factor}\,\, \tilde{u}_+}\)
$$\begin{aligned} \boxed {\tilde{u}_+}= & {} -\,\dfrac{1}{2\,m_{_{\!D^{**}}}}\left[ {\dfrac{E_{_{\!B}}- m_{_{\!D^{**}}}}{p}{\mathscr {T}}_{i}^A - {\mathscr {T}}_{0}^A}\right] \\= & {} -\,\dfrac{1}{2\,m_{_{\!D^{**}}}}\left[ {\dfrac{E_{_{\!B}}- m_{_{\!D^{**}}}}{3\,p}({\mathscr {T}}_{1}^A+{\mathscr {T}}_{2}^A+{\mathscr {T}}_{3}^A) - {\mathscr {T}}_{0}^A}\right] , \end{aligned}$$ -
\({\text {form factor} \,\,\tilde{u}_-}\)
$$\begin{aligned} \boxed {\tilde{u}_-}= & {} \dfrac{1}{2\,m_{_{\!D^{**}}}}\left[ {\dfrac{E_{_{\!B}}+ m_{_{\!D^{**}}}}{p}{\mathscr {T}}_{i}^A - {\mathscr {T}}_{0}^A}\right] \\= & {} \dfrac{1}{2\,m_{_{\!D^{**}}}}\left[ {\dfrac{E_{_{\!B}}+ m_{_{\!D^{**}}}}{3\,p}({\mathscr {T}}_{1}^A+{\mathscr {T}}_{2}^A+{\mathscr {T}}_{3}^A) - {\mathscr {T}}_{0}^A}\right] . \end{aligned}$$
With  :
:
-
\({\text {form factor }\tilde{k}}\)
$$\begin{aligned} \boxed {\tilde{k}}= & {} -\,\dfrac{\sqrt{6}}{p}\,{\mathscr {T}}_{1(0)}^A = -\,\dfrac{\sqrt{6}}{p}\,{\mathscr {T}}_{2(0)}^A = \dfrac{\sqrt{6}}{2\,p}\,{\mathscr {T}}_{3(0)}^A \\= & {} \dfrac{1}{p}\,\left[ {{\mathscr {T}}_{1(+2)}^A + {\mathscr {T}}_{1(-2)}^A}\right] = -\,\dfrac{1}{p}\,\left[ {{\mathscr {T}}_{2(+2)}^A + {\mathscr {T}}_{2(-2)}^A}\right] , \end{aligned}$$ -
\({\text {form factors } \tilde{b}_+ \text { and }\tilde{b}_-}\)
$$\begin{aligned}&\left\{ \begin{array}{l} \boxed {\tilde{b}_{+}} = -\,\dfrac{1+i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}- m_{_{\!D^{**}}})(i\,{\mathscr {T}}_{1(+2)}^A + {\mathscr {T}}_{2(+2)}^A)\\ \qquad \qquad \,\, - p(1+i){\mathscr {T}}_{0(+2)}^A],\\ \boxed {\tilde{b}_{-}} = \dfrac{1+i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}+ m_{_{\!D^{**}}})(i\,{\mathscr {T}}_{1(+2)}^A + {\mathscr {T}}_{2(+2)}^A)\\ \qquad \qquad \,\, - p(1+i){\mathscr {T}}_{0(+2)}^A], \end{array} \right. \\&\left\{ \begin{array}{l} \boxed {\tilde{b}_{+}} = \dfrac{1-i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}- m_{_{\!D^{**}}})(i\,{\mathscr {T}}_{1(-2)}^A - {\mathscr {T}}_{2(-2)}^A)\\ \qquad \qquad \,\, + p(1-i){\mathscr {T}}_{0(-2)}^A],\\ \boxed {\tilde{b}_{-}} = -\,\dfrac{1-i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}+ m_{_{\!D^{**}}})(i\,{\mathscr {T}}_{1(-2)}^A - {\mathscr {T}}_{2(-2)}^A)\\ \qquad \qquad \,\, + p(1-i){\mathscr {T}}_{0(-2)}^A], \end{array} \right. \\&\left\{ \begin{array}{l} \boxed {\tilde{b}_{+}} = \dfrac{1+i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}- m_{_{\!D^{**}}})({\mathscr {T}}_{1(+1)}^A +{\mathscr {T}}_{2(+1)}^A\\ \qquad \qquad \,\, -{\mathscr {T}}_{3(+1)}^A)- p\,{\mathscr {T}}_{0(+1)}^A],\\ \boxed {\tilde{b}_{-}} = -\,\dfrac{1+i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}+ m_{_{\!D^{**}}})({\mathscr {T}}_{1(+1)}^A +{\mathscr {T}}_{2(+1)}^A\\ \qquad \qquad \,\, -{\mathscr {T}}_{3(+1)}^A)- p\,{\mathscr {T}}_{0(+1)}^A], \end{array} \right. \\&\left\{ \begin{array}{l} \boxed {\tilde{b}_{+}} = -\,\dfrac{1-i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}- m_{_{\!D^{**}}})({\mathscr {T}}_{1(-1)}^A +{\mathscr {T}}_{2(-1)}^A\\ \qquad \qquad \,\,-{\mathscr {T}}_{3(-1)}^A) - p\,{\mathscr {T}}_{0(-1)}^A],\\ \boxed {\tilde{b}_{-}} = \dfrac{1-i}{4}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[(E_{_{\!B}}+ m_{_{\!D^{**}}})({\mathscr {T}}_{1(-1)}^A +{\mathscr {T}}_{2(-1)}^A\\ \qquad \qquad \,\,-{\mathscr {T}}_{3(-1)}^A) - p\,{\mathscr {T}}_{0(-1)}^A], \end{array} \right. \\&\left\{ \begin{array}{l} \boxed {\tilde{b}_{+}} = \dfrac{1}{2\,i}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[{(E_{_{\!B}}- m_{_{\!D^{**}}}){\mathscr {T}}_{3(+2)}^A - p\,{\mathscr {T}}_{0(+2)}^A}] ,\\ \boxed {\tilde{b}_{-}} = \dfrac{1}{2\,i}\,\dfrac{1}{p^3\,m_{_{\!D^{**}}}}[{-\,(E_{_{\!B}}+ m_{_{\!D^{**}}}){\mathscr {T}}_{3(+2)}^A + p\,{\mathscr {T}}_{0(+2)}^A}], \end{array} \right. \end{aligned}$$ -
\({\text {form factor }\tilde{h}}\)
$$\begin{aligned} \boxed {\tilde{h}}= & {} \dfrac{1}{2\,i}\,\dfrac{1}{p\,m_{_{\!D^{**}}}}\dfrac{{\mathscr {T}}_{1(\lambda )}^V}{\varepsilon ^{*3\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*2\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }}\\= & {} \dfrac{1}{2\,i}\,\dfrac{1}{p\,m_{_{\!D^{**}}}}\dfrac{{\mathscr {T}}_{2(\lambda )}^V}{\varepsilon ^{*1\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*3\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }}\\= & {} -\dfrac{1}{2\,i}\,\dfrac{1}{p\,m_{_{\!D^{**}}}}\dfrac{{\mathscr {T}}_{3(\lambda )}^V}{\varepsilon ^{*2\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*1\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }} \end{aligned}$$where
\({\lambda }\)
\({\varepsilon ^{*3\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*2\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }}\)
\({\varepsilon ^{*1\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*3\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }}\)
\({\varepsilon ^{*2\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }-\varepsilon ^{*1\alpha }_{(\lambda )}\,{p_{_{\!B}}}_{\!\alpha }}\)
+2
\(-\,\dfrac{p}{2}(1+i)\)
\(-\,\dfrac{p}{2}(1-i)\)
p
+1
\(\dfrac{p}{2}\)
\(i\,\dfrac{p}{2}\)
\(-\,\dfrac{p}{2}(1+i)\)
0
\(-\,p\,\sqrt{\dfrac{3}{2}}\)
\(p\,\sqrt{\dfrac{3}{2}}\)
0
\(-\)1
\(-\,\dfrac{p}{2}\)
\(i\,\dfrac{p}{2}\)
\(\dfrac{p}{2}(1-i)\)
\(-\)2
\(-\,\dfrac{p}{2}(1-i)\)
\(-\,\dfrac{p}{2}(1+i)\)
p
1.8 Masses and energies
We collect in Table 7 the masses and energies that we extract in our analysis.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Atoui, M., Blossier, B., Morénas, V. et al. Semileptonic \(\varvec{B\rightarrow D^{**}}\) decays in lattice QCD: a feasability study and first results. Eur. Phys. J. C 75, 376 (2015). https://doi.org/10.1140/epjc/s10052-015-3585-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-015-3585-4










 notation of the states, where S is the spin angular momentum,
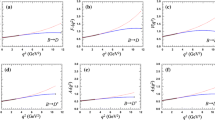
notation of the states, where S is the spin angular momentum,  differential decay width
differential decay width differential decay width
differential decay width differential decay width
differential decay width