Radiative leptonic $B_c\rightarrow \gamma \ell {\bar{\nu }}$ decay in effective field theory beyond leading order

Abstract

We study the radiative leptonic $B_c\rightarrow \gamma \ell {\bar{\nu }}$ decays in nonrelativistic QCD effective field theory, and we explore the contribution from a fast-moving photon. As a result, interactions between the photon and the heavy quarks can be integrated out, resulting in the factorization formula for the decay amplitude. We calculate not only the relevant short-distance coefficients at leading order and next-to-leading order in $\alpha _s$, but also the nonrelativistic corrections at the order $|\mathrm {v}|^2$ in our analysis. We find that the QCD corrections can significantly decrease the branching ratio, and this is of great importance in extracting the long-distance operator matrix elements of $B_c$. For phenomenological application, we present our results for the photon energy, lepton energy and lepton-neutrino invariant mass distribution.

1 Introduction

The search for new degrees of freedom may proceed in two distinctive directions. At the high energy frontier, new particles have different signatures from the standard model (SM) particles, and measurements of their production may provide definitive evidence of their existence. On the other hand, it is likely that low energy processes will be influenced through loop effects. Rare decays of heavy mesons, with tiny decay rates in the SM, are sensitive to the new degrees of freedom and thus can be exploited as indirect searches of these unknown effects; for a recent review see Ref. [1].

The $B_c$ meson is the unique pseudo-scalar meson that is long lived and composed of two different heavy flavors. Since this hadron is stable against strong interactions, its weak decays provide rich phenomena for the study of CKM matrix elements and also a platform to study the effects of weak interactions in a heavy quarkonium system [2, 3]. In the past decades it has received growing attention since the first observation by the CDF Collaboration [4]. This is particularly shown by the recent LHCb measurements of the $B_c$ lifetime [5, 6], the decay widths of $B_c\rightarrow J{/}\psi \pi$ and $B_c\rightarrow J{/}\psi \ell {\bar{\nu }}$ [7, 8], and various other decay modes [9–12]. One may expect that more decay channels of $B_c$ can be measured by the LHCb, ATLAS, and CMS experiments [13–15].

On the theoretical side, various approaches have been applied to calculation of the decay width of $B_c$ decays [16–52], but most of them are phenomenological. Since both constituents of the $B_c$ are heavy and can only be treated nonrelativistically, an effective field theory can be established [53]. Taking the $B_c\rightarrow J{/}\psi \ell {\bar{\nu }}$ as an example, one has the conjectured factorization formula in nonrelativistic QCD (NRQCD) for its decay amplitude [39, 46, 47]

$$\begin{aligned} \mathcal{A}(B_c\rightarrow J{/}\psi )\propto & {} C_{ij} \langle 0|\mathcal{O}_{i}^{{\bar{c}}b}|\overline{B}_c\rangle \times \langle J{/}\psi |\mathcal{O}_{j}^{\bar{c}c}|0\rangle , \end{aligned}$$

(1)

where the $\mathcal{O}_{i,j}^{ff'}$ are constructed by low energy operators. The short-distance, or hard, contributions at the length scale $1/m_{b,c}$ are encapsulated by the coefficients $C_{ij}$, which can be computed in perturbation theory. It is necessary to stress that a proof of the above factorization in Eq. (1) is not available.

The long-distance, or soft, part of the matrix elements have to be extracted in a non-perturbative approach, for instance the lattice QCD simulation, or these have to be constrained by much simpler processes, for instance the annihilation modes $B_c\rightarrow \ell {\bar{\nu }}$ and $B_c\rightarrow \gamma \ell {\bar{\nu }}$. However, the usefulness of the $B_c\rightarrow \ell {\bar{\nu }}$ is challenged in two respects. First, its decay rate is given by

$$\begin{aligned} \Gamma (B_c\rightarrow \ell {\bar{\nu }}_\ell )=\frac{G_F^2}{8\pi } |V_{cb}|^2 f_{B_c}^2 m_{B_c}^3 \frac{m_\ell ^2}{m_{B_c}^2} \left( 1-\frac{m_\ell ^2}{m_{B_c}^2}\right) ^2, \end{aligned}$$

(2)

in which the suppression factor ${m_\ell ^2}/{m_{B_c}^2}$ arises from the helicity flip. As a result, $B_c\rightarrow \mu {\bar{\nu }}_\mu$ and $B_c\rightarrow e{\bar{\nu }}_e$ have tiny branching fractions, which may be beyond the detector capability at the current experimental facilities. Second, there is only one physical observable, namely the decay rate, and thus $B_c\rightarrow \ell {\bar{\nu }}$ is not capable to uniquely determine all long-distance matrix elements (LDMEs), there being typically more than one when relativistic corrections are taken into account.

On the contrary, $B_c\rightarrow \gamma \ell {\bar{\nu }}$ can provide a wealth of information [54–58] in terms of a number of observables ranging from the decay probabilities and polarizations, to an angular analysis. It is interesting to notice that the counterpart in B sector, $B\rightarrow \gamma \ell {\bar{\nu }}$, has been widely discussed as regards the understanding of the B meson light-cone distribution amplitudes [59–63]. The small branching fraction of $B_c\rightarrow \gamma \ell {\bar{\nu }}$ can be compensated by the high luminosity at the ongoing hadron colliders and the experimental facilities under design. The main purpose of this paper is to explore $B_c\rightarrow \gamma \ell {\bar{\nu }}$ at next-to-leading order (NLO) in $\alpha _s$ and in $|\mathrm v|^2$, which shall catch up with the progress in $B_c\rightarrow \ell {\bar{\nu }}$ [55, 64]. For the leptonic decay constant, the two-loop calculation is also available in Refs. [65, 66].

The rest of this paper is organized as follows. In Sect. 2, we will derive the formulas for the various partial decay widths of $B_c\rightarrow \gamma \ell {\bar{\nu }}$. Section 3 is devoted to an extensive next-to-leading order calculation. We will discuss the phenomenological results in Sect. 4. We summarize our findings and conclude in Sect. 5. We relegate the details of the calculation to the appendix.

2 $B_c\rightarrow \gamma \ell {\bar{\nu }}$

In the SM, leading-order (LO) Feynman diagrams for the $B_c\rightarrow \gamma \ell {\bar{\nu }}$ decay are shown in Fig. 1. The photon emission from a virtual W-boson is suppressed by $1/m_W^2$ compared to other contributions, and thus the second diagram in Fig. 1 can be neglected. Integrating out the off-shell W-boson, we arrive at the effective electro-weak Hamiltonian

$$\begin{aligned} H_{\mathrm{eff}} = \frac{G_F}{\sqrt{2}} V_{cb} {\bar{c}} \gamma _\mu (1-\gamma _5) b \bar{\ell }\gamma ^\mu (1-\gamma _5)\nu +\hbox {h.c.}, \end{aligned}$$

(3)

where $V_{cb}$ is the CKM matrix element. The decay amplitude, the matrix element of the above Hamiltonian between the $B_c$ and the $\gamma \ell {\bar{\nu }}$ state,

$$\begin{aligned} \mathcal{A}=\langle \gamma l^- {\bar{\nu }}| H_\mathrm{eff}|\overline{B}_c\rangle \end{aligned}$$

(4)

is responsible for the process $B_c\rightarrow \gamma \ell {\bar{\nu }}$.

Fig. 1

Leading-order Feynman diagrams for the radiative leptonic $B_c\rightarrow \gamma \mu {\bar{\nu }}_\mu$ decay in the SM. The lepton $\mu$ can also be e or $\tau$. The photon emission from a virtual W-boson, shown in the second panel, is suppressed by $1/m_W^2$ compared to the other contributions

2.1 Differential decay widths

Since there is no strong interaction connection between the leptonic and the hadronic part, the decay amplitude can be decomposed into two individual sectors:

$$\begin{aligned} \mathcal{A}= & {} \frac{G_F}{\sqrt{2}} V_{cb} \{\langle 0 |{\bar{c}}\gamma _\mu (1-\gamma _5) b |\overline{B}_c\rangle \times \langle \gamma l^-{\bar{\nu }}| \bar{l} \gamma ^\mu (1-\gamma _5)\nu |0\rangle \nonumber \\&+\,\langle \gamma |{\bar{c}}\gamma _\mu (1-\gamma _5) b |\overline{B}_c\rangle \times \bar{u}_l \gamma ^\mu (1-\gamma _5)v_{\nu }\}, \end{aligned}$$

(5)

with the matrix elements encoding the hadronic effects:

$$\begin{aligned} \langle 0 |{\bar{c}}\gamma _\mu (1-\gamma _5) b |\overline{B}_c\rangle ,\quad \langle \gamma |{\bar{c}}\gamma _\mu (1-\gamma _5) b |\overline{B}_c\rangle . \end{aligned}$$

(6)

The first one defines the $B_c$ decay constant

$$\begin{aligned} \langle 0| {\bar{c}}\gamma _\mu \gamma _5 b|\overline{B}_c (p_{B_c})\rangle = i f_{B_c} p_{B_c,\mu }, \end{aligned}$$

(7)

while the $B_c\rightarrow \gamma$ transition is parametrized by two form factors:

$$\begin{aligned}&\langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu b |\overline{B}_c (p_{B_c})\rangle = - e\frac{V(L^2)}{p_{B_c}\cdot k} \epsilon _{\mu \nu \rho \sigma } \epsilon ^{*\nu } p_{B_c}^\rho k^\sigma , \end{aligned}$$

(8)

$$\begin{aligned}&\langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu \gamma _5 b |\overline{B}_c (p_{B_c})\rangle = i eA(L^2) \left( \epsilon _{\mu }^* -k_\mu \frac{p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k} \right) \nonumber \\&\quad -\,\frac{i e}{p_{B_c}\cdot k}f_{B_c} p_{B_c\mu } p_{B_c}\cdot \epsilon ^*, \end{aligned}$$

(9)

with the momentum transfer $L= p_{B_c}- k$. Here and throughout this work we adopt the convention $\epsilon ^{0123}=+1$. The above equations are similar to the parameterization of the $B\rightarrow \gamma$ form factors as given in Ref. [67]. The last term in Eq. (9), which is proportional to the $B_c$ decay constant, has been added in order to maintain the gauge invariance of the full amplitude [68, 69]; see Appendix A for a derivation.

Substituting Eqs. (7)–(9) into Eq. (5), we obtain

$$\begin{aligned} \mathcal{A}= & {} -i\frac{G_F}{\sqrt{2}} V_{cb} e f_{B_c} \bar{u}_\ell \gamma ^\mu (1-\gamma _5)v_{\nu } \bigg \{[1+a(s_l)]\nonumber \\&\times \,\left( \epsilon _{\mu }^* -k_\mu \frac{p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k} \right) - \frac{iv(s_l)}{p_{B_c}\cdot k} \epsilon _{\mu \nu \rho \sigma } \epsilon ^{*\nu } p_{B_c}^\rho k^\sigma \bigg \},\nonumber \\ \end{aligned}$$

(10)

where $s_l=L^2$ and terms due to lepton mass corrections have been neglected. Apparently, this expression is gauge invariant. For the sake of simplicity, we have defined two abbreviations in the above¹

$$\begin{aligned} a(s_l) \equiv \frac{A(s_l)}{ f_{B_c}},\quad v(s_l) \equiv \frac{V(s_l)}{f_{B_c}}. \end{aligned}$$

(11)

In terms of the decay constant and form factors, the differential decay width for the $B_c\rightarrow \gamma \ell ^-{\bar{\nu }}$ is given as

$$\begin{aligned}&\frac{\mathrm{d}^2\Gamma }{\mathrm{d}E_k \mathrm{d}E_l} = \frac{1}{64 m_{B_c}\pi ^3} |\mathcal{A}|^2 \nonumber \\&\quad =\frac{\alpha _\mathrm{em}f_{B_c}^2 | V_{cb} |^2G_F^2m_{B_c}}{4\pi ^2x_k^2}(1-x_k) \nonumber \\&\qquad \times \, [a^2 (x_k^2+2 x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\qquad +\,2 a ((v+1) x_k^2+2 (v+1) x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\qquad +\,2 v x_k (x_k+2 x_l-2) \nonumber \\&\qquad +\,v^2 (x_k^2+2 x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\qquad +\,x_k^2+2 x_k x_l-2 x_k+2 x_l^2-4 x_l+2], \end{aligned}$$

(12)

where $x_k=2E_k/m_{B_c}$ and $y=2E_l/m_{B_c}$, and $E_k$ and $E_l$ are the energy of the photon and of the charged lepton in the $B_c$ rest frame, respectively. One can integrate out $E_l$ and obtain

$$\begin{aligned} \frac{\mathrm{d}\Gamma }{\mathrm{d}E_k} =\frac{\alpha _\mathrm{em}f_{B_c}^2| V_{cb}|^2G_F^2m_{B_c}^2x_k(1-x_k)((1+a)^2+v^2)}{12\pi ^2}.\nonumber \\ \end{aligned}$$

(13)

The differential distributions can also be converted to

$$\begin{aligned}&\frac{\mathrm{d}^2\Gamma }{\mathrm{d}s_l \mathrm{d}\cos \theta _l} =\frac{m_{B_c}^2-s_l}{ 32 m_{B_c} \pi ^2} | V_{cb} |^2 \alpha _\mathrm{em} f_{B_c}^2 G_F^2 (1-x_k)\nonumber \\&\quad \times \,\frac{1}{x_k^2}[a^2(x_k^2+2 x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\quad +\,2 a ((v+1) x_k^2+2 (v+1) x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\quad +\,2 v x_k (x_k+2 x_l-2) +v^2(x_k^2+2 x_k (x_l-1)+2 (x_l-1)^2)\nonumber \\&\quad +\,x_k^2+2 x_k x_l-2 x_k+2 x_l^2-4 x_l+2], \end{aligned}$$

(14)

using the relation

$$\begin{aligned} E_k= & {} \frac{m_{B_c}^2 -s_l}{2m_{B_c}},\end{aligned}$$

(15)

$$\begin{aligned} E_l= & {} \frac{1}{4m_{B_c}} \left[ (m_{B_c}^2+s_l)- (m_{B_c}^2-s_l)\cos \theta _l\right] . \end{aligned}$$

(16)

The $\theta _l$ is the polar angle between the lepton $\ell$ flight direction and the opposite direction of the $B_c$ meson in the rest frame of the $\ell {\bar{\nu }}_{\ell }$ pair. Likewise one can integrate out $\theta _l$,

$$\begin{aligned} \frac{\mathrm{d}\Gamma }{\mathrm{d}s_l}=\frac{\alpha _\mathrm{em}f_{B_c}^2 | V_{cb} |^2G_F^2(m_{B_c}^2-s_l)s_l((1+a)^2+v^2)}{24\pi ^2m_{B_c}^3}. \end{aligned}$$

(17)

2.2 NRQCD factorization

The factorization properties for $B_c\rightarrow \gamma \ell {\bar{\nu }}$ depend on the kinematics of the photon. In particular, the contribution from a soft photon, $E_k\sim {\Lambda }_\mathrm{QCD}$ with ${\Lambda }_\mathrm{QCD}$ being the hadronic scale, will introduce complexities as discussed for B decays in [70], and we will leave such a contribution for future work. Fortunately in the region where the photon is hadron, namely $E_k\gg {\Lambda }_\mathrm{QCD}$, its interaction with heavy quarks is highly virtual and thus should be encoded in the short-distance coefficients. In the NRQCD scheme, we only need retain those color-singlet operator matrix elements that connect the $B_c$ state to the vacuum. To the desired order, one expects the following factorization formula:

$$\begin{aligned} f_{B_c}= & {} \sqrt{\frac{2}{m_{B_c}}}\left[ c_{0}^f \langle 0|\chi ^\dagger _c \psi _b |\overline{B}_c(\mathbf p )\rangle \right. \nonumber \\&\left. +\, \frac{c_{2}^f}{m_{B_c}^2} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| \overline{B}_c(\mathbf p )\right\rangle +\mathcal{O}({\mathrm v}^4)\right] ,\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} V= & {} \sqrt{\frac{2}{m_{B_c}}}\left[ \frac{c_{0}^V}{m_{B_c}} \langle 0|\chi ^\dagger _c \psi _b |\overline{B}_c(\mathbf p )\rangle \right. \nonumber \\&\left. +\, \frac{c_{2}^V}{m_{B_c}^3} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| \overline{B}_c(\mathbf p )\right\rangle +\mathcal{O}({\mathrm v}^4)\right] ,\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} A= & {} \sqrt{\frac{2}{m_{B_c}}}\left[ \frac{ c_{0}^A}{m_{B_c}} \langle 0|\chi ^\dagger _c \psi _b |\overline{B}_c(\mathbf p )\rangle \right. \nonumber \\&\left. +\, \frac{c_{2}^A}{m_{B_c}^3} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b\right| \overline{B}_c(\mathbf p )\right\rangle +\mathcal{O}({\mathrm v}^4)\right] ,\nonumber \\ \end{aligned}$$

(20)

where ${\mathrm v}$ denotes half the relative velocity between the charm and bottom quarks in the meson, $c_0^{f,V,A}$ and $c_2^{f,V,A}$ are the dimensionless short-distance coefficients, which can be expanded in terms of the strong coupling constant.² We shall calculate the one-loop corrections to the $c_{0}^ {f,V,A}$, but we give only the LO results for $c_2^{f,V,A}$ since the latter ones are already power-suppressed. $\psi _Q$ and $\chi ^\dagger _Q$ represent Pauli spinor fields that annihilate the heavy quark Q and anti-quark $\bar{Q}$, respectively. Besides, one needs to note that the state $|H(p)\rangle$ in QCD has the standard normalization: $\langle H(p^\prime )|H(p)\rangle =2E_p(2\pi )^3\delta ^3 (\mathbf p -\mathbf p ^\prime )$, while an additional factor $2E_p$ is abandoned in the nonrelativistic normalization where $\langle H(\mathbf p ^\prime )|H(\mathbf p )\rangle =(2\pi )^3\delta ^3 (\mathbf p -\mathbf p ^\prime )$.

3 Next-to-leading order calculation

3.1 Kinematics

Let $p_1$ and $p_2$ represent the momenta for the heavy quark Q and anti-quark $\bar{Q^\prime }$. Without loss of generality, one may adopt the decomposition:

$$\begin{aligned} p_1= & {} \alpha \,P_{B_c}-q,\end{aligned}$$

(21)

$$\begin{aligned} p_2= & {} \beta \, P_{B_c}+q, \end{aligned}$$

(22)

where $P_{B_c}$ is the total momentum of the quark pair. q is half of the relative momentum between the quark pair with $P_{B_c}\cdot q=0$. $\alpha$ and $\beta$ are the energy fractions for Q and $\bar{Q^\prime }$ in the meson, respectively. The explicit expressions for all the momentum in the rest frame of the $B_c$ meson are given by

$$\begin{aligned} P_{B_c}^\mu= & {} (E_1+E_2,0),\end{aligned}$$

(23)

$$\begin{aligned} q^\mu= & {} (0,\mathrm {q}\,),\end{aligned}$$

(24)

$$\begin{aligned} p_1^\mu= & {} (E_1,-\mathrm {q}\,),\end{aligned}$$

(25)

$$\begin{aligned} p_2^\mu= & {} (E_2,\mathrm {q}\,). \end{aligned}$$

(26)

In the rest frame, the meson momentum becomes purely timelike while the relative momentum is spacelike. One obtains the relations $\alpha ={\sqrt{m_b^2-q^2}}/({\sqrt{m_b^2-q^2}+\sqrt{m_c^2-q^2}})$ and $\beta =1-\alpha$ with the on-shell conditions $E_1=\sqrt{m_b^2-q^2}$, $E_2=\sqrt{m_c^2-q^2}$, and $q^2=-\mathrm {q}^2$.

3.2 Covariant projection method

In the following calculation, we will adopt the covariant spin-projector method, which can be applied to all orders in $\mathrm {v}$.

The Dirac spinors for the $B_c$ system may be written as

$$\begin{aligned} u_b(p_1,\lambda )= & {} \sqrt{\frac{E_1+m_b}{2E_1}}\left( \begin{array}{ll} \xi _\lambda \\ \frac{\vec {\sigma }\cdot \overrightarrow{p_1}}{E_1+m_b}\xi _\lambda \end{array} \right) ,\end{aligned}$$

(27)

$$\begin{aligned} v_c(p_2,\lambda )= & {} \sqrt{\frac{E_2+m_c}{2E_2}}\left( \begin{array}{ll} \frac{\vec {\sigma }\cdot \overrightarrow{p_2}}{E_2+m_c}\xi _\lambda \\ \xi _\lambda \end{array} \right) , \end{aligned}$$

(28)

where $\xi _\lambda$ is the two-component Pauli spinors and $\lambda$ is the polarization parameters. It is straightforward to derive the covariant form of the spin-singlet combinations of the spinor bilinears:

(29)

with the auxiliary parameter $\omega =\sqrt{E_1+m_b}\sqrt{E_2+m_c}$. Here $\mathrm {1}_c$ is the unit matrix in the fundamental representation of the color SU(3) group.

3.3 Perturbative matching

Due to the simplicity of the final state, one can directly match the QCD currents onto the NRQCD ones. To determine the values of $c_0$ and $c_2$, we work in the spirit of taking those short-distance coefficients to be insensitive to the long-distance hadronic dynamics. As a convenient choice, one can replace the physical $B_c^-$ meson by a free ${\bar{c}}b$ pair of the quantum number ${}^1S_0^{[1]}$, so that both the full amplitude, ${\mathcal A}[{\bar{c}}b ({}^1S_0^{[1]})\rightarrow \gamma \ell {\bar{\nu }}]$, and the NRQCD operator matrix elements can be directly accessed in perturbation theory. The short-distance coefficients $c_i$ can then be solved by equating the QCD amplitude ${\mathcal A}$ and the corresponding NRQCD amplitude, order by order in $\alpha _s$. For this purpose, we introduce a decay constant and two form factors at the free quark level:

(30)

$$\begin{aligned}&\langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu b |{\bar{c}}b ({}^1S_0^{[1]})\rangle = - e\frac{1}{k\cdot p_{B_c}} {\mathbb {V}} \epsilon _{\mu \nu \rho \sigma } \epsilon ^{*\nu }p_{B_c}^\rho k^\sigma ,\nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned}&\langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu \gamma _5 b |{\bar{c}}b ({}^1S_0^{[1]})\rangle = ie{\mathbb {A}}\left( \epsilon _{\mu }^* -k_\mu \frac{p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k} \right) \nonumber \\&-\,i e\frac{1}{p_{B_c}\cdot k}{\mathbb {f}} p_{B_c\mu } p_{B_c}\cdot \epsilon ^*.\nonumber \\ \end{aligned}$$

(32)

Analogous to (18–20), one can write down the matching formula:

$$\begin{aligned} \mho= & {} c_{0}^f \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle + \frac{c_{2}^f}{(m_b+m_c)^2} \nonumber \\&\times \,\left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| {\bar{c}}b ({}^1S_0^{[1]})\right\rangle ,\end{aligned}$$

(33)

$$\begin{aligned} {\mathbb {V}}= & {} \frac{1}{ {m_b+m_c}}\left[ c_{0}^V \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle + \frac{c_{2}^V}{(m_b+m_c)^2}\right. \nonumber \\&\times \,\left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| {\bar{c}}b ({}^1S_0^{[1]})\rangle \right] , \end{aligned}$$

(34)

$$\begin{aligned} {\mathbb {A}}= & {} \frac{1}{{m_b+m_c}}\left[ c_{0}^A \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle + \frac{c_{2}^A}{(m_b+m_c)^2} \right. \nonumber \\&\times \,\left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| {\bar{c}}b ({}^1S_0^{[1]})\rangle \right] , \end{aligned}$$

(35)

where we have adopted the nonrelativistic normalization.

One can organize the full amplitudes defined in Eqs. (30)–(32) in powers of the relative momentum between ${\bar{c}}$ and b, denoted by $\mathbf{q}$. To the desired accuracy, one can truncate the series at $\mathcal{O}(\mathbf{q}^2)$, with the first two Taylor coefficients. We will compute both amplitudes at LO in $\alpha _s$ in Sect. 3.4, and the calculation at NLO in $\alpha _s$ will be conducted in Sect. 3.5.

The NRQCD matrix elements encountered in the above equations are particularly simple at LO in $\alpha _s$:

$$\begin{aligned}&\langle 0\vert \chi ^\dagger \psi \vert {\bar{c}}b({}^1S_0^{[1]})\rangle ^{(0)} = \sqrt{2N_c},\nonumber \\&\left\langle 0\left| \chi ^\dagger \left( -\frac{i}{2} {\overleftrightarrow { {\mathrm D}}}\right) ^2\psi \right| {\bar{c}}b({}^1S_0^{[1]})\right\rangle ^{(0)}=\sqrt{2 N_c}\,\mathbf{q}^2, \end{aligned}$$

(36)

where the factor $\sqrt{2N_c}$ is due to the spin and color factors of the normalized ${\bar{c}}b({}^1S_0^{[1]})$ state. The computation of these matrix elements to $\mathcal{O}(\alpha _s)$ will be addressed in Sect. 3.6.

3.4 Tree-level amplitude

Adopting the above notation, one can easily obtain the tree-level amplitude for the decay constant,

$$\begin{aligned}&\langle 0| {\bar{c}}\gamma _\mu \gamma _5 b|{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)} = \mathrm{Tr}\left[ \Pi _0(q)\gamma _\mu \gamma _5\right] \nonumber \\&\quad = ip_{B_c}^\mu \sqrt{2N_c}\frac{ (E_1+m_b)(E_2+m_c) + q^2}{ 2\sqrt{ E_1E_2(E_1+m_b)(E_2+m_c)} (E_1+E_2)} \nonumber \\&\quad = i g_{\mu 0} \sqrt{2N_c} \left( 1- \frac{\mathrm {q}^2}{8m_{\mathrm{red}}^2}\right) , \end{aligned}$$

(37)

where the $q^\mu$ terms have been omitted and

$$\begin{aligned} m_{\mathrm{red}}=\frac{m_bm_c}{m_b+m_c} \end{aligned}$$

(38)

is defined as the reduced mass of the ${\bar{c}}b$ system.

The vector current is similarly evaluated as

$$\begin{aligned}&\langle \gamma |{\bar{c}}\gamma _\mu b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}\nonumber \\&\quad = \mathrm{Tr}\left[ \Pi _0(q) i ee_c \epsilon \!\!\!\slash ^*\frac{i(k\!\!\!\slash -p\!\!\!\slash _2+m_c)}{(k-p_2)^2-m_c^2}\gamma _\mu \right] \nonumber \\&\qquad \ +\, \mathrm{Tr}\left[ \Pi _0(q) \gamma _\mu \frac{i(p\!\!\!\slash _1-k\!\!\!\slash +m_b)}{(p_1-k)^2-m_b^2}i ee_b \epsilon \!\!\!\slash ^*\right] \nonumber \\&\quad =-\frac{ e \sqrt{2N_c} }{4w\sqrt{E_1E_2 } } \left( \frac{ e_c }{ E_2k\cdot p_{B_c} + Ek\cdot q}\right. \nonumber \\&\qquad \left. +\,\frac{e_b}{E_1k\cdot p_{B_c}-Ek\cdot q}\right) \nonumber \\&\qquad \times \, \{ E_{bc}\epsilon _{\mu \nu \rho \sigma } \epsilon ^{*\nu } k^\rho p_{B_c}^\sigma + E(E_1+E_2+m_b-m_c)\nonumber \\&\qquad \times \,\epsilon _{\mu \nu \rho \sigma } \epsilon ^{*\nu } k^\rho q^\sigma \}. \end{aligned}$$

(39)

We have introduced the abbreviations $E=E_1+E_2$ and $E_{bc}=(E_1+m_b)(E_2+m_c) +q^2$. Here $e_c= 2/3$ and $e_b=-1/3$ are the electric charges of the c and b quark, respectively.

One can perform the Taylor expansion of the amplitudes in powers of $q^\mu$:

$$\begin{aligned} \mathcal{A}(q)= & {} \mathcal{A}(0)+\frac{\partial \mathcal{A}(0)}{\partial q^\mu }\Bigg |_{q=0}q^\mu +\frac{1}{2!}\frac{\partial ^2 \mathcal{A}(0)}{\partial q^\mu \partial q^\nu }\Bigg |_{q=0}q^\mu q^\nu +\cdots .\nonumber \\ \end{aligned}$$

(40)

Those terms linear in q should be dropped, since they do not contribute to the short-distance coefficient. In this paper, the $\mathcal{O}(|\mathrm {q}|^2)$ contributions will be retained. In order to simplify the calculation in the covariant derivation, one should use the following replacement:

$$\begin{aligned} q^\mu q^\nu \rightarrow \frac{|\mathrm {q}|^2}{D-1} \left( -g^{\mu \nu }+\frac{P_{B_c}^\mu P_{B_c}^\nu }{P_{B_c}^2}\right) . \end{aligned}$$

(41)

The result for the axial-vector current is a bit lengthy:

$$\begin{aligned}&\langle \gamma |{\bar{c}}\gamma _\mu \gamma _5 b |{\bar{c}}b({}^1S_0^{[1]})\rangle ^{(0)}\nonumber \\&\quad = -i e \sqrt{2N_c}\frac{ 1}{4\sqrt{E_1E_2(E_1+m_b)(E_2+m_c)}} \nonumber \\&\qquad \times \,\left\{ \epsilon _{\mu }^* e_c\frac{ k\cdot p_{B_c} E_{bc}+k\cdot q E(E_1-E_2+m_b-m_c)}{ E_2 k\cdot p_{B_c}+E k\cdot q} \right. \nonumber \\&\qquad -\, \epsilon _{\mu }^* e_b\frac{ k\cdot p_{B_c} E_{bc} +k\cdot q E(E_1-E_2+m_b-m_c)}{ E_1 k\cdot p_{B_c}-E k\cdot q} \nonumber \\&\qquad +\, q_\mu e_c \frac{2 (E_1-E_2+m_b-m_c)(E_2\epsilon ^*\cdot p_{B_c}+E\epsilon ^*\cdot q)}{E_2 k\cdot p_{B_c}+Ek\cdot q}\ \nonumber \\&\qquad -\, q_\mu e_b \frac{2 (E_1-E_2+m_b-m_c)(E_1\epsilon ^*\cdot p_{B_c}-E\epsilon ^*\cdot q)}{E_1 k\cdot p_{B_c}-Ek\cdot q} \nonumber \\&\qquad +\, p_{B_c \mu } e_c\frac{2E_{bc}(E_2\epsilon ^*\cdot p_{B_c} +E\epsilon ^*\cdot q)}{E(E_2 k\cdot p_{B_c}+E k\cdot q)} \nonumber \\&\qquad -\,p_{B_c \mu } e_b\frac{2(E_1E_{bc}\epsilon ^*\cdot p_{B_c} +E\epsilon ^*\cdot q(E_{bc}+q^2)}{E(E_1 k\cdot p_{B_c}-E k\cdot q)} \nonumber \\&\qquad -\,k_{\mu } e_c\frac{E_{bc}\epsilon ^*\cdot p_{B_c} +E\epsilon ^*\cdot q(E_1-E_2+m_b-m_c)}{ E_2 k\cdot p_{B_c}+E k\cdot q} \nonumber \\&\qquad \left. +\,k_{\mu } e_b\frac{E_{bc}\epsilon ^*\cdot p_{B_c} +E\epsilon ^*\cdot q(E_1-E_2+m_b-m_c)}{ E_1 k\cdot p_{B_c}-E k\cdot q}\right\} .\nonumber \\ \end{aligned}$$

(42)

In order to extract the $\mathcal{A}$ form factor, we only need to keep the $\epsilon _\mu$ term which corresponds to Feynman gauge $\epsilon \cdot p_{B_c}=0$, but we have explicitly checked the gauge invariance up to $\mathrm {v}^2$ order.

The tree-level NRQCD matrix elements for ${\bar{c}}b$ are given in Eq. (36), and thus the above results in Eqs. (37), (39), and (42) lead to the tree-level Wilson coefficients,

$$\begin{aligned} c_{0}^{f,0}= & {} 1, \end{aligned}$$

(43)

$$\begin{aligned} c_{2}^{f,0}= & {} -\frac{\tilde{z}^4}{8z^2},\end{aligned}$$

(44)

$$\begin{aligned} c_{0}^{V,0}= & {} -\frac{e_c}{2z}- \frac{e_b}{2},\end{aligned}$$

(45)

$$\begin{aligned} c_{2}^{V,0}= & {} -\tilde{z}^2 \left( \frac{e_c(3z^2+2z+11)}{48 z^3} + \frac{e_b(11z^2+2z+3)}{48 z^2}\right) ,\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} c_{0}^{A,0}= & {} \frac{e_b}{2} - \frac{e_c}{2z},\end{aligned}$$

(47)

$$\begin{aligned} c_{2}^{A,0}= & {} -\tilde{z}^2 \bigg ( \frac{e_c[(3z^2+2z+11)+ 8 z(1-z) m_b/E_k]}{48 z^3} \nonumber \\&-\frac{e_b[(11z^2+2z+3)- 8 z(1-z) m_b/E_k]}{48 z^2}\bigg ). \end{aligned}$$

(48)

In the above results, we have defined $z= m_c/m_b$ and $\tilde{z}=1+z$. $c_{i}^{f,0}$ means the LO of the Wilson coefficient $c_{i}^f$. It is interesting to notice that the Wilson coefficient $c_{2}^{A,0}$ depends on the energy of the emitted photon, which will induce a nontrivial behavior, as will be demonstrated later.

3.5 NLO amplitudes in QCD

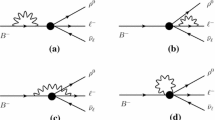
Typical one-loop diagrams for the QCD corrections to the $B_c\rightarrow \gamma \ell \bar{\nu }_\ell$ decay are shown in Fig. 2. In calculating the one-loop amplitudes, we use the dimensional regularization to regulate the ultraviolet (UV) and infrared (IR) divergence.

The diagram (a) in Fig. 2 contributes to the NLO decay constant:

$$\begin{aligned} \mho ^{1}_{0,a}= & {} \sqrt{2N_c} \frac{C_F \alpha _s}{4\pi }\bigg [\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{2}{\hat{\epsilon }_{\mathrm{IR}}}+3\ln \frac{\mu ^2}{m_b^2} -2\nonumber \\&+\,2t_1-\frac{6\ln z}{ z+1}\bigg ], \end{aligned}$$

(49)

with

$$\begin{aligned} t_1= & {} \frac{1}{ {2|\mathrm {v}|}} \left( \pi ^2 - i\pi \left[ \frac{1}{\hat{\epsilon }_{\mathrm{IR}}} -\ln \frac{16m_{\mathrm{red}}^2|\mathrm {v}|^2}{\mu ^2}\right] \right) ,\nonumber \\ \mathrm v= & {} \frac{\mathrm q}{2m_{\mathrm{red}}}. \end{aligned}$$

(50)

We have introduced the abbreviation

$$\begin{aligned} \frac{1}{\hat{\epsilon }_{\mathrm{UV},\mathrm{IR}}}=\frac{1}{\epsilon _{\mathrm{UV},\mathrm{IR}}}-\gamma _E+\ln 4\pi . \end{aligned}$$

(51)

Fig. 2

Typical NLO Feynman diagrams for the radiative leptonic $B_c\rightarrow \gamma \mu {\bar{\nu }}_\mu$ decay in the SM. The other four diagrams can easily be obtained by interchanging the bottom and anti-charm quarks lines

The heavy quark field renormalization and mass term are given as

$$\begin{aligned} Z^{OS}_{q}= & {} 1-\frac{C_F \alpha _s}{4\pi }\left[ \frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{2}{\hat{\epsilon }_{\mathrm{IR}}}+3\ln \frac{\mu ^2}{m^2}+4\right] ,\nonumber \\ \delta _{m}= & {} -\frac{3mC_F\alpha _s }{4\pi } \bigg [\frac{1}{\hat{\epsilon }_{\mathrm{UV}}} +\ln \frac{\mu ^2}{m^2} +\frac{4}{3}\bigg ]. \end{aligned}$$

(52)

For the vector current form factor, the sub-diagram in Fig. 2 gives out the corresponding contribution

$$\begin{aligned} {\mathbb {V}}_{b}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ -\frac{1}{\hat{\epsilon }_{\mathrm{IR}}}+\frac{4 \tilde{z}}{y^2-\tilde{z}^2}+\frac{\tilde{z}^2+y^2}{y^2 \tilde{z}-\tilde{z}^3}b_1\right. \nonumber \\&-\,\frac{1}{\tilde{z}}b_2+\frac{2 \left( y^2-z (z+1)\right) }{z \left( y^2-\tilde{z}^2\right) }b_3-\frac{2 y^2}{z \left( y^2-\tilde{z}^2\right) }b_4\nonumber \\&\left. -\,\frac{y^2}{ \tilde{z}}c_4 -(1-z)c_3-(\tilde{z}^2-y^2)d_1\right] ,\nonumber \\ {\mathbb {V}}_{c}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ -\frac{1}{2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{y^2+z^2+4 z+3}{\tilde{z}^2-y^2}\right. \nonumber \\&+\,\frac{\tilde{z}+y^2}{\tilde{z}^2-y^2}b_1-\frac{\tilde{z} \left( 3 y^2-z^2+1\right) }{2 z \left( \tilde{z}^2-y^2\right) }b_4\nonumber \\&+\,\frac{\left( 2 z^2+3 z-1\right) \tilde{z}-y^2 (2 z+3)}{2 z \left( y^2-\tilde{z}^2\right) }b_3\nonumber \\&\quad \left. +\,({\tilde{z}+y^2-z^2}) c_4\right] ,\nonumber \\ {\mathbb {V}}_{d}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ -\frac{1}{2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{y^2-z^2+4 z+5}{\tilde{z}^2-y^2}\right. \nonumber \\&+\,\frac{y^2-z^2+z+2}{\tilde{z}^2-y^2}b_2 \left. +\frac{y^2-z^2+4 z+5}{2(y^2-\tilde{z}^2)}b_3+c_1\right] ,\nonumber \\ {\mathbb {V}}_{e}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ \frac{-y^2+z^2+8 z+7}{2(\tilde{z}^2-y^2)}+\frac{\tilde{z}^2-y^2}{2 \left( y^2-z \tilde{z}\right) }\right. \nonumber \\&-\,\frac{\tilde{z}\left( y^2-z^2+1\right) }{2 \left( y^2-z \tilde{z}\right) \left( y^2-\tilde{z}^2\right) }b_2 \nonumber \\&\left. +\,\frac{\left( z^2+6z+1\right) \tilde{z}^2+y^4-2 y^2 \left( z^2+4 z+3\right) }{2(y^2-\tilde{z}^2)\left( y^2-z \tilde{z}\right) }b_3\right] ,\nonumber \\ \end{aligned}$$

(53)

where the auxiliary functions $b_i$, $c_i$, and $d_i$ are defined in Appendix B.

The mass counter-terms and wave function renormalization corrections give

$$\begin{aligned} {\mathbb {V}}_{\mathrm{CT}-m}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ \frac{3 \tilde{z}}{y^2-\tilde{z}^2}\left( \frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\ln \frac{\mu ^2}{m_b^2}+\frac{4}{3}\right) \right] , \nonumber \\ {\mathbb {V}}_{\mathrm{CT}-F}= & {} \frac{\sqrt{2N_c}e_b C_F \alpha _s}{4\pi m_b}\left[ \frac{1}{\hat{\epsilon }_{\mathrm{IR}}}+\frac{1}{2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+ \frac{3}{2}\ln \frac{\mu ^2}{zm_b^2}+2\right] .\nonumber \\ \end{aligned}$$

(54)

For the axial-vector current form factor, the sub-diagram has gauge-dependent contributions; however, the summed result is gauge invariant. We will show the details in Appendix C.

3.6 NLO amplitudes in NRQCD

The NRQCD Lagrangian can be derived by integrating out the degrees of freedom of order heavy quark mass [53]:

$$\begin{aligned} {\mathcal L}_{\mathrm{NRQCD}}= & {} \psi ^{\dagger }\left( iD_t+{\mathbf{D}^2 \over 2m}\right) \psi +\psi ^{\dagger } {\mathbf{D}^4 \over 8m^3}\psi \nonumber \\&+\, \frac{c_F}{2 m} \psi ^\dagger {\varvec{\sigma }} \cdot g_s \mathbf{B} \psi +\frac{c_D}{8 m^2} \psi ^\dagger \nonumber \\&\times \, (\mathbf{D}\cdot g_s \mathbf{E}- g_s\mathbf{E}\cdot \mathbf{D})\psi \nonumber \\&+\,\frac{i c_S}{8 m^2} \psi ^\dagger {\varvec{\sigma }} \cdot (\mathbf{D}\times g_s \mathbf{E}- g_s \mathbf{E}\times \mathbf{D})\psi \nonumber \\&+\,\left( \psi \rightarrow i\sigma ^2 \chi ^*, A_\mu \rightarrow - A_{\mu }^T\right) +{\mathcal L}_{\mathrm{light}}. \end{aligned}$$

(55)

The replacement in the last line implies that the corresponding heavy anti-quark bilinear sector can be obtained through the charge conjugation transformation. ${\mathcal L}_\mathrm{light}$ represents the Lagrangian for the light quarks and gluons. The coefficients $c_D$, $c_F$, and $c_S$ have perturbative expansions in powers of $\alpha _s$, which can be written as $c_i=1+\mathcal{O}(\alpha _s)$.

The matrix element of the ${\bar{c}}b$ to vacuum at NLO can be written as

$$\begin{aligned}&\langle 0\vert \chi ^\dagger \psi \vert {\bar{c}}b({}^1S_0^{[1]})\rangle ^{(1)}\nonumber \\&\quad =\sqrt{2N_c}\frac{\alpha _sC_F}{2\pi \, {2|\mathrm {v}|}} \left( \pi ^2 - i\pi \left[ \frac{1}{\epsilon _{\mathrm{IR}}} -\ln \frac{16m_{\mathrm{red}}^2|\mathrm {v}|^2}{\mu ^2}\right] \right) .\nonumber \\ \end{aligned}$$

(56)

This is in agreement with the results in Ref. [71].

3.7 Determination of $c_i$: matching QCD to NRQCD

Up to ${ \alpha }_s$ and $\mathrm {v}^2$, one can expand the decay constant and form factors as

$$\begin{aligned} \mho= & {} c_{0}^{f,0} \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}+c_{0}^{f,1} \langle 0|\chi ^{\dagger }_c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}\nonumber \\&+\, c_{0}^{f,0} \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(1)}\nonumber \\&+\, \frac{c_{2}^{f,0}}{(m_b+m_c)^2} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow D\right) ^2 \psi _b \right| {\bar{c}}b({}^1S_0^{[1]})\right\rangle ^{(0)},\nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} {\mathbb {V}}= & {} \frac{1}{ {m_b+m_c}}\left[ c_{0}^{V,0} \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}\right. \nonumber \\&+\,c_{0}^{V,1} \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)} +\,c_{0}^{V,0} \langle 0|\chi ^\dagger _c \psi _b |{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(1)}\nonumber \\&\left. +\,\frac{c_{2}^{V,0}}{(m_b+m_c)^2} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow D\right) ^2 \psi _b\right| {\bar{c}}b ({}^1S_0^{[1]})\right\rangle ^{(0)}\right] ,\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned} {\mathbb {A}}= & {} \frac{1}{{m_b+m_c}}\left[ c_{0}^{A,0} \langle 0|\chi ^\dagger _c \psi _b ^{(0)}|{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}\right. \nonumber \\&+\,c_{0}^{A,1} \langle 0|\chi ^\dagger _c\psi _b^{(0)}|{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(0)}\nonumber \\&+\,c_{0}^{A,0} \langle 0|\chi ^\dagger _c \psi _b ^{(0)}|{\bar{c}}b ({}^1S_0^{[1]})\rangle ^{(1)}\nonumber \\&\left. +\,\frac{c_{2}^{A,0}}{(m_b+m_c)^2} \left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow D\right) ^2 \psi _b\right| {\bar{c}}b ({}^1S_0^{[1]})\right\rangle ^{(0)}\right] .\nonumber \\ \end{aligned}$$

(59)

Matching the QCD results onto the NRQCD, one can obtain the UV and IR finite short-distance coefficient,

$$\begin{aligned} c_{0}^{f,1}= & {} -\frac{3C_F \alpha _s }{4 \pi } \left( 2 + \frac{1-z}{1+z}\ln z\right) ,\end{aligned}$$

(60)

$$\begin{aligned} c_{0}^{V,1}= & {} \frac{C_F\alpha _s}{4\pi }\left\{ e_b\left[ \ln \frac{\mu ^2}{z m_b^2}-\frac{\tilde{z}^2 \left( -3 z \tilde{z}+\tilde{z}+2 y^2\right) +y^4}{2 \left( y^2-z \tilde{z}\right) \left( y^2-\tilde{z}^2\right) }\right. \right. \nonumber \\&+\,\frac{\tilde{z}^3+y^2 (3 z-1)}{4 \left( \tilde{z}^3-y^2 \tilde{z}\right) }b_1+\frac{y^2-2 z \tilde{z}}{2 z \left( y^2-z \tilde{z}\right) }b_3\nonumber \\&+\,\frac{1}{4}\left( \frac{2 \tilde{z}}{y^2-z \tilde{z}}+\frac{2}{\tilde{z}-y}+\frac{2}{\tilde{z}+y}- \frac{4}{\tilde{z}}-3\right) b_2\nonumber \\&+\,\frac{-z \tilde{z}^2+\tilde{z}^2+3 y^2 z-y^2}{2 z \left( y^2-\tilde{z}^2\right) }b_4\nonumber \\&+\,\frac{-\tilde{z}-y^2 z+z^3+z^2}{z \tilde{z}}c_1+\frac{y^2 z-z^3+2 z+1}{z}c_2\nonumber \\&\left. +\,(z-1)c_3+(y^2-\tilde{z}^2)d_1\right] \nonumber \\&\left. +\,\left( e_b\rightarrow \frac{e_c}{z}, z\rightarrow \frac{1}{z},y\rightarrow \frac{y}{z}\right) \right\} ,\end{aligned}$$

(61)

$$\begin{aligned} c_{0}^{A,1}= & {} \frac{ C_F \alpha _s }{4\pi }\left\{ e_b\left[ -\ln \frac{\mu ^2}{z m_b^2}+\frac{1}{2 \left( y^2-z \tilde{z}\right) \left( y^2-\tilde{z}^2\right) ^2}\right. \right. \nonumber \\&\times \,(y^4 (z+11) \tilde{z}-y^2 (z (5 z+34)+5) \tilde{z}^2\nonumber \\&+\,(z (z (3 z+23)+5)+1) \tilde{z}^3+y^6) +\frac{b_1}{4 \tilde{z}(y^2-\tilde{z}^2)^2}\nonumber \\&\times \,(-2 y^2(z-3) \tilde{z}^2-(z^2+14 z-3) \tilde{z}^3+y^4 (3 z-1))\nonumber \\&+\,\frac{b_2}{4 \tilde{z} \left( y^2-z \tilde{z}\right) \left( y^2-\tilde{z}^2\right) }(y^2 (y^2 (3 z+7)\nonumber \\&-\,(2 z+3) (3 z-1)\tilde{z})+(3 (z-1) z-2) \tilde{z}^3)\nonumber \\&-\,\frac{b_3}{2 z (z\tilde{z}-y^2) (y^2-\tilde{z}^2)^2}(y^2(13 z^2-2 z+1)\tilde{z}^2\nonumber \\&-\,2 (3 z^3+z) \tilde{z}^3+y^4 (y^2-8 z^2-6 z+2))\nonumber \\&-\,\frac{(z-1)^2 \tilde{z}^3+y^4 (3 z+1)-2 y^2 \left( 2 z^3+5 z^2+2 z-1\right) }{2 z \left( y^2-\tilde{z}^2\right) ^2}b_4\nonumber \\&+\,\frac{y^2 \left( y^2 (-z)+z^2 (2 z+5)-3\right) -(z-1) (z (z+4)-1) \tilde{z}^2}{z \tilde{z} \left( \tilde{z}^2-y^2\right) }c_1\nonumber \\&-\,\frac{((z-2) z (z+4)+1) \tilde{z}^2+y^2 \left( z \left( y^2-2 z (z+2)+3\right) +3\right) }{z \left( y-\tilde{z}\right) \left( \tilde{z}+y\right) }c_2\nonumber \\&\left. +\,\frac{(z-1) \left( -y^2+z^2-1\right) }{y^2-\tilde{z}^2}c_3+(-y^2+z^2+4 z-1)d_1\right] \nonumber \\&\left. -\,\left( e_b\rightarrow \frac{e_c}{z}, z\rightarrow \frac{1}{z},y\rightarrow \frac{y}{z}\right) \right\} . \end{aligned}$$

(62)

Note that the scale-dependent terms in the braces of Eqs. (61) and (62) will cancel each other; the residual dependence only lies in the strong coupling constant. The result for the short-distance coefficient $c_{0}^{f,1}$ is in agreement with the previous calculation in Ref. [72].

4 Phenomenological results

The input parameters are adopted as [73]: $m_{B_c}=6.2756$ GeV; $G_F=1.16637\times 10^{-5}\mathrm{GeV^{-2}}$; $\alpha =1/128$; for the CKM parameters, we adopt $|V_{cb}|=0.041$. For the heavy quark mass, we adopt $m_b=4.8$ GeV and $m_c=1.5$ GeV [46]. The $B_c$-meson lifetime is taken using the latest measurement by the LHCb Collaboration, i.e. $\tau _{B_c}=0.50~\mathrm{ps}$ [5, 6].

We first present the numerical results for the decay constant $f_{B_c}$:

$$\begin{aligned} \begin{aligned}&1.07c_2^{f,0} = - \frac{\tilde{z}^4}{8z^2} = -3.8,\\&c_{0}^{f,1} = -\frac{3C_F\alpha _s}{4 \pi } \left( 2 + \frac{1-z}{1+z}\ln z\right) =-0.44\times \alpha _s.\\ \end{aligned} \end{aligned}$$

(63)

The strong coupling constant at the Z-boson peak is [73]

$$\begin{aligned} \alpha _s(m_Z)= 0.1185\pm 0.0006, \end{aligned}$$

(64)

which corresponds to

$$\begin{aligned} \alpha _s(m_b)= 0.218,\quad \alpha _s(m_c)=0.368. \end{aligned}$$

(65)

With these values, one can see that the $\alpha _s$ corrections can reduce the decay constant by approximately 9.5–16.2 %.

To estimate the size of $\mathcal{O}(|\mathrm v|^2)$ effects, one requires the size of non-perturbative LDMEs, for which we use a Buchmüller–Tye (B-T) potential model [74]:

$$\begin{aligned}&\langle 0|\chi ^\dagger _c \psi _b |\overline{B}_c(\mathbf {p})\rangle =x\sqrt{\frac{N_{c}}{2\pi }}|R_{S}^{\mathrm{B-T}}(0)| \simeq 0.884~\hbox {GeV}^{3/2},\nonumber \\ \end{aligned}$$

(66)

$$\begin{aligned}&\left\langle 0\left| \chi ^\dagger _c \left( -\frac{i}{2} \overleftrightarrow {\mathrm D}\right) ^2 \psi _b \right| \overline{B}_c(\mathbf {p})\right\rangle \simeq {\mathbf {q}}^{2} \langle 0|\chi ^\dagger _c \psi _b|\overline{B}_c(\mathbf {p})\rangle . \end{aligned}$$

(67)

For an estimate of ${\mathbf {q}}^{2}$, one may make use of the relative velocity. Using the heavy quarks kinetic and potential energy approximation [53], we have

$$\begin{aligned} |{{\mathbf {v}}}|\simeq \alpha _s(2m_{\mathrm{red}}|{{\mathbf {v}}}|). \end{aligned}$$

(68)

Choosing $m_b=4.8$ GeV and $m_c=1.5$ GeV, and using the two-loop strong coupling constant, we get

$$\begin{aligned} |{{\mathbf {v}}}|^2_{J{/}\psi }\approx 0.267,\quad |{{\mathbf {v}}}|^2_{\Upsilon }\approx 0.108,\quad |{{\mathbf {v}}}|^2_{B_c}\approx 0.186. \end{aligned}$$

(69)

For a value $\langle {\mathbf {v}}^2\rangle _{B_c}\simeq 0.186$, we have

$$\begin{aligned} {\mathbf {q}}^{2}\simeq 0.9718~\mathrm{GeV}^{2}. \end{aligned}$$

(70)

As a result, the decay constant will be further reduced by about $9~\%$.

For the short-distance coefficients for the $B_c\rightarrow \gamma$ transition form factors V and A, our results are shown in Fig. 3. The solid line denotes the leading-order coefficient $c_0^{V(A),0}$, the dotted line correspond to the coefficient $c_2^{V(A),0}$ from relativistic corrections, and the thick curve is the coefficient $c_0^{V(A),2}$ from $\alpha _s$ corrections. From these figures, one can see that the relativistic corrections give constructive contributions, but the $\mathcal{O}( \alpha _s)$ QCD corrections are destructive and thus have important consequences.

Fig. 3

Dependence of short-distance coefficients $c^{V(A)}$ on the $s_l$. The solid line denotes the coefficient $c_0^{V(A),0}$, the dotted line is the coefficient $c_2^{V(A),0}$ from relativistic corrections, and the thick curve is the coefficient $c_0^{V(A),2}$ from $\alpha _s$ corrections. The results are not valid for a soft photon, which corresponds to $s_l\sim m_{B_c}^2$

With the estimated long-distance matrix elements, the results for differential distributions are given in Figs. 4 and 5, where the QCD and relativistic corrections are shown, respectively. The integrated branching ratios of $B_c\rightarrow \gamma \ell {\bar{\nu }}$ and $B_c\rightarrow \ell {\bar{\nu }}$ are presented in Tables 1, 2, and 3. Note that the factorization in Eqs. (18)–(20) is valid only for a hard photon, while the soft-photon contribution requires special treatment [70]. Thus a cut-off on the photon energy should be introduced, and we adopt three cases for the estimate of errors, i.e. $E_k\ge 0.25$ GeV for Cut-I, $E_k\ge 0.5$ GeV for Cut-II, and $E_k\ge 1$ GeV for Cut-III, where the corresponding results are given in Table 2. Ignoring the lepton mass, the branching ratio of $B_c\rightarrow \gamma e {\bar{\nu }}_e$ is identical to that of $B_c\rightarrow \gamma \mu {\bar{\nu }}_\mu$. The LO results are in agreement with Refs. [54–58] with the same input parameters. From the calculation, one can see that both the QCD and the relativistic corrections give destructive contributions to the process $B_c\rightarrow \ell \nu$. However, relativistic corrections produce a constructive contribution to the $B_c\rightarrow \gamma \ell {\bar{\nu }}$. Our results demonstrate that the QCD and relativistic corrections are mandatory toward a more accurate extraction of the value of LDMEs for $B_c$ system.

Fig. 4

The dependence of the branching ratio $\mathcal{B}(B_c\rightarrow \gamma \mu {\bar{\nu }}_{\mu })$ on the photon and lepton energy. The dotted line denotes the leading-order result, the dashed line is the result with relativistic corrections, the blue line is the result with QCD corrections, and the thick curve denotes the total results with both the QCD and the relativistic corrections. The results are not valid for a soft photon, namely when $E_k$ becomes small, and $E_l$ becomes large

Fig. 5

Similar to Fig. 4 but for the $s_l$ dependence. The results are not valid for a soft photon, which corresponds to the region where $s_l\sim m_{B_c}^2$

5 Summary

In this work, we have analyzed the radiative leptonic $B_c\rightarrow \gamma \ell {\bar{\nu }}$ decays in the NRQCD effective field theory. NRQCD factorization ensures the separation of short-distance and long-distance effects of $B_c\rightarrow \gamma \ell {\bar{\nu }}$ to all orders of $\alpha _s$. Treating the photon as a hard object whose interactions with the heavy quarks can be integrated out, we arrive at a factorization formula for the decay amplitude.

Table 1 Branching ratios of $B_c\rightarrow \ell \nu$. Here and in the following table $\tau _{B_c}=0.50$ ps, and we vary the heavy quark masses with $m_b=4.8\pm 0.1$ GeV and $m_c=1.5\mp 0.1$ GeV. For the relativistic corrections, we adopt $\langle {\mathbf {v}}^2 \rangle _{B_c}\simeq 0.186$

Table 2 Branching ratios of $B_c\rightarrow \gamma \ell {\bar{\nu }}$. Here we adopt three cut conditions for photon energy, i.e. $E_k\ge 0.25$ GeV in Cut-I, $E_k\ge 0.5$ GeV in Cut-II, and $E_k\ge 1$ GeV in Cut-III

Table 3 Branching ratios of $B_c\rightarrow \gamma \ell {\bar{\nu }}$ and $B_c\rightarrow \ell \nu$ compared with other theories or models, including Lattice QCD (LQCD), Light front model (LFM), Constituent quark model (CQM). Here $\tau _{B_c}=0.50$ ps is adopted and we use the cut-I result for comparison

We have calculated not only the short-distance coefficients at leading order and next-to-leading order in $\alpha _s$, but also the nonrelativistic corrections at the order $|\mathrm {v}|^2$ in our analysis. We found that the QCD corrections can significantly decrease the branching ratio, which has a very important impact on extracting the long-distance operator matrix elements of $B_c$. For phenomenological applications, we have estimated the long-distance matrix elements, which are further used to explore the photon energy, lepton energy, and lepton-neutrino invariant mass distribution. These results can be examined at the LHCb experiment.

Appendices

Appendix A: Ward identities for matrix elements

In this section, following Ref. [69] we will explicitly derive the constraints on the $B_c\rightarrow \gamma$ form factors arising from a Ward identity for the conservation of the electromagnetic current. To be more specific, let us consider the following matrix element:

$$\begin{aligned}&\langle \gamma (k,\epsilon ) |({\bar{c}}\gamma _\nu \gamma _5 b)(0)|\overline{B}_c\rangle \nonumber \\&\quad =ie\epsilon ^{*\mu }\int \text{ d }^4x \mathrm{e}^{ik\cdot x}\langle 0|\text{ T } j^\mathrm{e.m.}_\mu (x)\,({\bar{c}}\gamma _\nu \gamma _5 b)(0)|\overline{B}_c\rangle . \end{aligned}$$

(A1)

In this case, the electromagnetic current includes contributions from heavy quarks $j^{\mathrm{e.m.}}_\mu = e_c {\bar{c}}\gamma _\mu c + e_b\bar{b}\gamma _\mu b$.

The conservation of the electromagnetic current implies a Ward identity for the matrix element of the time-ordered product in (A1),

$$\begin{aligned}&ik^\mu \int \text{ d }^4x \mathrm{e}^{ik\cdot x}\langle 0|\text{ T } j^\mathrm{e.m.}_\mu (x)\, |({\bar{c}}\gamma _\nu \gamma _5 b)(0)|\overline{B}_c\rangle \nonumber \\&\quad = \int \text{ d }^3x \mathrm{e}^{ik\cdot x}(\langle 0|j^\mathrm{e.m.}_0(x)\,({\bar{c}}\gamma _\nu \gamma _5 b)(0)|\overline{B}_c\rangle \theta (x^0)\nonumber \\&\qquad +\,\langle 0|({\bar{c}}\gamma _\nu \gamma _5 b)(0)\,j^\mathrm{e.m.}_0(x)|\overline{B}_c\rangle \theta (-x^0))\big |^{x^0\rightarrow \infty }_{x^0\rightarrow -\infty } \nonumber \\&\quad = \int \text{ d }^3x \mathrm{e}^{-i\vec {k}\cdot \vec {x}}(\langle 0|j^\mathrm{e.m.}_0(\vec {x})\,({\bar{c}}\gamma _\nu \gamma _5 b)(0)|\overline{B}_c\rangle \nonumber \\&\qquad -\,\langle 0|({\bar{c}}\gamma _\nu \gamma _5 b)(0)\,j^\mathrm{e.m.}_0(\vec {x})|\overline{B}_c\rangle ) \nonumber \\&\quad = \int \text{ d }^3x \mathrm{e}^{-i{\vec {k}}\cdot {\vec {x}}} \langle f|[j^\mathrm{e.m.}_0({\vec {x}}), ({\bar{c}}\gamma _\nu \gamma _5 b)( {\vec {0}})]|\overline{B}_c\rangle . \end{aligned}$$

(A2)

The commutator on the right-hand side is non-vanishing, since the operator ${\bar{c}}\gamma _\nu \gamma _5 b$ carries an electric charge. It can be evaluated as

$$\begin{aligned}&\int \text{ d }^3x \mathrm{e}^{-i{\vec {k}}\cdot {\vec {x}}}\langle 0|[j^\mathrm{e.m.}_0({\vec {x}}), ({\bar{c}}\gamma _\nu \gamma _5 b)({\vec {0}})] |\overline{B}(p_{B_c})\rangle \nonumber \\&\quad =\int \text{ d }^3x \mathrm{e}^{-i{\vec {k}}\cdot {\vec {x}}}\langle 0|[e_c c_m^\dag (\vec {x}) c_m(\vec {x})\nonumber \\&\qquad +\, e_b b_m^\dag (\vec {x}) b_m(\vec {x}),c_n^\dag (0) (\gamma ^0\gamma _\nu \gamma _5)_{ns} b_s(0)]|\overline{B}(p_{B_c})\rangle \nonumber \\&\quad = (e_c - e_b)\langle 0|({\bar{c}}\gamma _\nu \gamma _5 b)({\vec {0}})|\overline{B}_c(p_{B_c}) \rangle \nonumber \\&\quad = i(e_c - e_b) f_{B_c} p_{B_c,\nu }. \end{aligned}$$

(A3)

The most general parametrization of the matrix element on the left-hand side without $k^\mu$ can be written in terms of five form factors $f_i(k^2,p_{B_c}\cdot k)$,

$$\begin{aligned}&i\int \text{ d }^4x \mathrm{e}^{ik\cdot x} \langle 0|\text{ T } j^\mathrm{e.m.}_\mu (x)\, ({\bar{c}}\gamma _\nu \gamma _5 b)(0)| \overline{B}_c\rangle \nonumber \\&\quad = i[f_1 g_{\mu \nu } + f_2 p_{B_c,\mu } p_{B_c,\nu } + f_3 k_\mu k_\nu \nonumber \\&\qquad +\, f_4 k_\mu p_{B_c,\nu }+ f_5 p_{B_c,\mu } k_\nu ]. \end{aligned}$$

(A4)

The Ward identity (A3) implies two constraints on these form factors,

$$\begin{aligned}&(p_{B_c}\cdot k) f_2 + k^2 f_4 = (e_c-e_b) f_{B_c},\nonumber \\&\quad f_1 + k^2 f_3 + (p_{B_c}\cdot k) f_5 = 0. \end{aligned}$$

(A5)

For a real photon, $k^2=0$, these constraints fix uniquely the form factor $f_2(0,p_{B_c}\cdot k)$, and relate $f_1(0,p_{B_c}\cdot k)$ and $f_5(0,p_{B_c}\cdot k)$, which leads to

$$\begin{aligned} \langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu \gamma _5 b |\overline{B}_c (p_{B_c})\rangle= & {} i e p_{B_c}\cdot k f_5\left( \epsilon _{\mu }^* -k_\mu \frac{p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k} \right) \nonumber \\&-\,\frac{i e}{p_{B_c}\cdot k}f_{B_c} p_{B_c\mu } p_{B_c}\cdot \epsilon ^*.\nonumber \\ \end{aligned}$$

(A6)

This is the same as the result in Eq. (9) as presented in the text, with the identification $p_{B_c}\cdot k f_5 = A$.

Appendix B: Passarino–Veltman integrals

The coefficients $b_i$, $c_i$, and $d_i$ are related to the scalar Passarino–Veltman integrals defined in Refs. [76, 77], and we have split the finite pieces $b_i=B_i^{\mathrm{{finite}}}$, $c_i=C_i^{\mathrm{{finite}}}/m_b^2$, and $d_i=D_i^{\mathrm{{finite}}}/m_b^4$:

$$\begin{aligned} B_1= & {} B_0(0,z^2m_b^2,z^2 m_b^2),\nonumber \\ B_2= & {} B_0(0,m_b^2, m_b^2),\nonumber \\ B_3= & {} B_0(m_b^2(y^2-z\tilde{z})/\tilde{z},0,m_b^2),\nonumber \\ B_4= & {} B_0(y^2 m_b^2,m_b^2,z^2 m_b^2),\nonumber \\ C_1= & {} \text {C}_0(m_b^2,0,m_b^2(y^2-z\tilde{z})/ \tilde{z},0,m_b^2,m_b^2),\nonumber \\ C_2= & {} \text {C}_0(\tilde{z}^2 m_b^2,y^2 m_b^2,0,m_b^2, z^2 m_b^2,m_b^2),\nonumber \\ C_3= & {} \text {C}_0(m_b^2,z^2 m_b^2,\tilde{z}^2 m_b^2,m_b^2, 0,z^2 m_b^2),\nonumber \\ C_4= & {} \text {C}_0(m_b^2(y^2-z\tilde{z})/\tilde{z},m_b^2y^2, m_b^2z^2, 0, m_b^2, m_b^2z^2),\nonumber \\ D_1= & {} \text {D}_0(m_b^2,z^2 m_b^2,y^2 m_b^2,0, \tilde{z}^2 m_b^2,m_b^2(y^2-z\tilde{z})/\nonumber \\&\tilde{z},m_b^2,0,z^2 m_b^2,m_b^2). \end{aligned}$$

(B1)

Here we give the results of the divergence integrals:

$$\begin{aligned} B_1= & {} \frac{1}{\epsilon _{\mathrm{UV}}}+\ln \frac{\mu ^2}{z^2m_b^2},\nonumber \\ B_2= & {} \frac{1}{\epsilon _{\mathrm{UV}}}+\ln \frac{\mu ^2}{m_b^2},\nonumber \\ B_3= & {} \frac{1}{\epsilon _{\mathrm{UV}}}+\ln \frac{\mu ^2}{m_b^2} -\frac{ (y^2-\tilde{z}^2 ) \ln (\tilde{z}-\frac{y^2}{\tilde{z}} )}{y^2-z \tilde{z}}+2,\nonumber \\ B_4= & {} \frac{1}{\epsilon _{\mathrm{UV}}}+\ln \frac{\mu ^2}{y^2m_b^2} +2+\sum _{i=1}^2(\gamma _i(y)\ln \left( \frac{\gamma _i(y)-1}{\gamma _i(y)}\right) \nonumber \\&-\ln (\gamma _i(y)-1)),\nonumber \\ C_3= & {} -\frac{1}{2zm_b^2}\left( \frac{1}{\epsilon _{\mathrm{IR}}}+t_1+\ln \frac{\mu ^2}{m_b^2}-2-\frac{2\ln z}{1+z}\right) ,\nonumber \\ D_1= & {} \frac{\tilde{z}}{2 m_b^4 z \left( \tilde{z}^2-y^2\right) }\left( \frac{1}{\epsilon _{\mathrm{IR}}}+t_1+\ln \frac{\mu ^2}{m_b^2}-2\ln \frac{\tilde{z}^2-y^2}{\tilde{z}}\right. \nonumber \\&+\,\frac{1}{(y-\tilde{z}) (y+\tilde{z})}(2 (\tilde{z}^2 -2 y^2 \ln y- (y^2+z^2-1 ) \ln z\nonumber \\&-\,y^2 (1+2\ln 2))+(-g_5+y^2+z^2-1)g_1\nonumber \\&+\,(g_5+y^2-z^2+1)g_2+(-g_5+y^2-z^2+1)g_3\nonumber \\&\left. +\,(g_5+y^2+z^2-1)g_4)\right) , \end{aligned}$$

(B2)

where

$$\begin{aligned}&\gamma _{1,2}(x)=\frac{\pm \sqrt{\left( x^2-z^2+1\right) ^2-4 x^2}+x^2-z^2+1}{2 x^2},\nonumber \\&g_1=\ln \left( \sqrt{\left( y^2-z^2+1\right) ^2-4 y^2}-y^2-z^2+1\right) ,\nonumber \\&g_2= \ln \left( \sqrt{\left( y^2-z^2+1\right) ^2-4 y^2}+y^2-z^2+1\right) ,\nonumber \\&g_3= \ln \left( -\sqrt{\left( y^2-z^2+1\right) ^2-4 y^2}+y^2-z^2+1\right) ,\nonumber \\&g_4=\ln \left( -\sqrt{\left( y^2-z^2+1\right) ^2-4y^2}-y^2-z^2+1\right) ,\nonumber \\&g_5=\sqrt{y^4-2 y^2 \left( z^2+1\right) +\left( z^2-1\right) ^2}. \end{aligned}$$

(B3)

Appendix C: One-loop corrections to the axial-vector form factor A

The most general structure of the matrix element of the axial-vector current is parametrized by

$$\begin{aligned} \langle \gamma (\epsilon , k)|{\bar{c}}\gamma _\mu \gamma _5 b |[{\bar{c}}b ({}^1S_0^{[1]})]\rangle= & {} i e\left( \epsilon _{\mu }^* {\mathbb {A}}^\epsilon -k_\mu \frac{p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k} {\mathbb {A}}^k\right) \nonumber \\&-\,i e\frac{ p_{B_c}\cdot \epsilon ^*}{p_{B_c}\cdot k}{\mathbb {f}}^A p_{B_c\mu }. \end{aligned}$$

(C1)

This section will be devoted to a demonstration of the gauge invariance at the one-loop level in $\alpha _s$, namely

$$\begin{aligned} {\mathbb {A}}^\epsilon= & {} {\mathbb {A}}^k\equiv {\mathbb {A}},\end{aligned}$$

(C2)

$$\begin{aligned} \mho ^A= & {} \mho . \end{aligned}$$

(C3)

The contributions from individual diagrams to ${\mathbb {A}}^\epsilon$ are given by

$$\begin{aligned} {\mathbb {A}}^\epsilon _{b}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\left[ \frac{1}{\hat{\epsilon }_{\mathrm{IR}}}-\frac{4 (z-1)\tilde{z}^2}{(y^2-\tilde{z}^2)^2}\right. \nonumber \\&+\,\frac{y^2 \tilde{z}^2-2(z-1) \tilde{z}^3-y^4}{(y^2-\tilde{z}^2)^2\tilde{z}}b_1 +\frac{y^2}{(y^2-\tilde{z}^2)\tilde{z}}b_2\nonumber \\&+\,\frac{2 y^2 \tilde{z}-y^4+(z^2-1)^2 }{z (y^2-\tilde{z}^2)^2}b_3+\frac{-2 y^2 \tilde{z}+(z-1) \tilde{z}^3+y^4 }{z(y^2-\tilde{z}^2)^2}b_4\nonumber \\&-\,\frac{2 (3 z-1) \tilde{z}^2+y^4-y^2(z^2+4 z+3)}{ (\tilde{z}^2-y^2)\tilde{z}}c_4\nonumber \\&\left. -\,\frac{(z^2-1)(y^2-z^2+1)}{(y^2-\tilde{z}^2)\tilde{z}}c_3 +(-y^2+z^2+4 z-1)d_1\right] , \nonumber \\ \end{aligned}$$

(C4)

$$\begin{aligned} {\mathbb {A}}^\epsilon _{c}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b} \left[ \frac{1}{2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{ \tilde{z}+y^2 }{y^2-\tilde{z}^2}b_1\right. \nonumber \\&+\,\frac{ -y^2 (2 z+3)+2 z^3+5 z^2+2 z-1 }{2z(\tilde{z}^2-y^2)}b_3\nonumber \\&+\,\frac{y^2+z^2+4z+3}{y^2-\tilde{z}^2}+\frac{\tilde{z}(-3 y^2+z^2-1)}{2z(y^2-\tilde{z}^2)}b_4\nonumber \\&+\,({-y^2+z^2+z-1})c_4\bigg ],\end{aligned}$$

(C5)

$$\begin{aligned} {\mathbb {A}}^\epsilon _{d}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b} \left[ \frac{1}{2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{ y^2-z^2+1}{y^2-\tilde{z}^2}+\frac{y^2-z \tilde{z}}{y^2-\tilde{z}^2}b_2\right. \nonumber \\&\left. +\,-\frac{ y^2-z^2+1}{2 \left( y^2-\tilde{z}^2\right) }b_3-\tilde{z}c_1\right] , \end{aligned}$$

(C6)

$$\begin{aligned} {\mathbb {A}}^\epsilon _{e}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b} \left[ -\frac{1}{2\hat{\epsilon }_{\mathrm{UV}}}+\frac{ y^2-z^2+1 }{2 \left( y^2-z \tilde{z}\right) }+\frac{\tilde{z}}{2 y^2-2 z \tilde{z}}b_2\right. \nonumber \\&\left. -\,\frac{ y^2-z^2+1}{2 \left( y^2-z \tilde{z}\right) }b_3\right] . \end{aligned}$$

(C7)

The mass counter-term and wave function renormalization give the contributions:

$$\begin{aligned} {\mathbb {A}}^\epsilon _{\mathrm{CT}-m}= & {} 0,\nonumber \\ {\mathbb {A}}^\epsilon _{\mathrm{CT}-F}= & {} -\mathbb {V}_{\mathrm{CT}-F}. \end{aligned}$$

(C8)

The contributions from individual diagrams to ${\mathbb {A}}^k$ are given as

$$\begin{aligned}&{\mathbb {A}}^k_{b}=\frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\nonumber \\&\quad \times \,\bigg [-\frac{\tilde{z} \left( y^2 \left( -7 z^2+10 z+1\right) \tilde{z}^2+(z-1) \tilde{z}^5+y^4 \left( 3 y^2+3 z^2-8 z-11\right) \right) }{\left( y^2-z \tilde{z}\right) \left( y^3-y \tilde{z}^2\right) ^2}\nonumber \\&\quad +\,\frac{2 y^2 (3-2 z) \tilde{z}^2+z \tilde{z}^4+y^4 (-(z+2))}{\left( y^3-y \tilde{z}^2\right) ^2}b_1\nonumber \\&\quad +\,\frac{\tilde{z}+y^2}{y^4-y^2 z \tilde{z}}b_2 -\frac{2 \tilde{z} \left( -y^2+z^2+3\right) }{ \left( y^2-\tilde{z}^2\right) }c_4\nonumber \\&\quad +\,\frac{-y^2 \tilde{z}^2 \left( y^2+z^2-4 z+5\right) +\left( z^3-3 z^2+5 z+1\right) \tilde{z}^3+y^6}{z \left( -y^2+z^2+z\right) \left( y^2-\tilde{z}^2\right) ^2}b_3\nonumber \\&\quad +\,\frac{y^2 (3 z-5) \tilde{z}^3-(z-1) \tilde{z}^5+y^4 \left( y^2+z^2-1\right) }{z \left( y^3-y \tilde{z}^2\right) ^2}b_4\bigg ]+{\mathbb {A}}^\epsilon _{b}, \end{aligned}$$

(C9)

$$\begin{aligned}&\quad {\mathbb {A}}^k_{c} = \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\nonumber \\&\quad \times \,\left[ \frac{\tilde{z} \left( y^2 \left( -7 z^2+10 z+1\right) \tilde{z}^2+(z-1) \tilde{z}^5+y^4 \left( 3 y^2+3 z^2-8 z-11\right) \right) }{\left( y^2-z \tilde{z}\right) \left( y^3-y \tilde{z}^2\right) ^2}\right. \nonumber \\&\quad +\,\frac{ 2 y^2 (2 z-3) \tilde{z}^2-z \tilde{z}^4+y^4 (z+2)}{\left( y^3-y\tilde{z}^2\right) ^2}b_1\nonumber \\&\quad +\,\frac{ \tilde{z}+y^2}{y^4-y^2 z \tilde{z}}b_2-\frac{2 \tilde{z} \left( -y^2+z^2+3\right) }{ \left( y^2-\tilde{z}^2\right) }c_4\nonumber \\&\quad -\,\frac{-y^2 \tilde{z}^2 \left( y^2+z^2-4 z+5\right) +\left( z^3-3 z^2+5 z+1\right) \tilde{z}^3+y^6}{z \left( z \tilde{z}-y^2\right) \left( y^2-\tilde{z}^2\right) ^2}b_3\nonumber \\&\quad \left. -\,\frac{y^2 (3 z-5) \tilde{z}^3-(z-1) \tilde{z}^5+y^4 \left( y^2+z^2-1\right) }{z \left( y^3-y \tilde{z}^2\right) ^2}b_4\right] +{\mathbb {A}}^\epsilon _{c},\end{aligned}$$

(C10)

$$\begin{aligned}&\quad {\mathbb {A}}^k_{d} = {\mathbb {A}}^\epsilon _{d}+\ \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\left[ \frac{\tilde{z} \left( 5 y^2-5 z^2-6 z-1\right) }{ \left( y^2-\tilde{z}^2\right) \left( y^2-z \tilde{z}\right) }\right. \nonumber \\&\quad +\,\frac{\tilde{z} \left( 3 y^2-3 z^2-4 z-1\right) }{ \left( y^2-\tilde{z}^2\right) \left( y^2-z \tilde{z}\right) }b_2\nonumber \\&\left. +\,\frac{\tilde{z} \left( -3 y^2+3 z^2+4 z+1\right) }{ \left( y^2-\tilde{z}^2\right) \left( y^2-z \tilde{z}\right) }b_3\right] , \end{aligned}$$

(C11)

$$\begin{aligned}&\quad {\mathbb {A}}^k_{e} = {\mathbb {A}}^\epsilon _{e}+ \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\left[ \frac{3 \tilde{z}}{y^2-\tilde{z}^2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{\tilde{z}}{-y^2+z^2+z}\right. \nonumber \\&\quad \left. +\,\frac{\tilde{z}^2}{\left( y^2-\tilde{z}^2\right) \left( y^2-z \tilde{z}\right) }b_2+\frac{\tilde{z} \left( 3 y^2-3 z^2-4 z-1\right) }{ \left( y^2-\tilde{z}^2\right) \left( y^2-z\tilde{z}\right) }b_3\right] . \end{aligned}$$

(C12)

Similar, the mass counter-terms and wave function renormalization corrections give

$$\begin{aligned} {\mathbb {A}}^k_{\mathrm{CT}-m}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi m_b}\left[ \frac{3\tilde{z} }{\tilde{z}^2-y^2}\left( \frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\ln \frac{\mu ^2}{m_b^2}+\frac{4}{3}\right) \right] , \nonumber \\ {\mathbb {A}}^k_{\mathrm{CT}-F}= & {} {\mathbb {A}}^\epsilon _{\mathrm{CT}-F}. \end{aligned}$$

(C13)

Adding the above contributions, one may derive the relation ${\mathbb {A}}^\epsilon = {\mathbb {A}}^k$, which is guaranteed by gauge invariance. One can obtain the one-loop results for ${\mathbb {A}}$ by adding up the anti-symmetrical part with $e_b\rightarrow e_c$ and $m_b\leftrightarrow m_c$.

The contributions from individual diagrams to ${\mathbb {f}}^A$ are given as

$$\begin{aligned} \mho ^{A}_{b}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi }\left[ -\frac{2}{\hat{\epsilon }_{\mathrm{IR}}}\right. \nonumber \\&+\,\frac{y^2(3z^2-6 z-1)\tilde{z}^2-(z-1) \tilde{z}^5+y^4(-3 y^2+z^2+8 z+7)}{y^2 (y^2-\tilde{z}^2)(y^2-z\tilde{z})}\nonumber \\&+\,\frac{-3 y^2 (z-1) \tilde{z}^2+z \tilde{z}^4-y^4}{y^2 \tilde{z} (y^2-\tilde{z}^2)}b_1\nonumber \\&+\,\frac{-(y^4+3)z+(y^2-1)z^3+(y^2-3)z^2-1}{y^2 \tilde{z} (y^2-z\tilde{z})}b_2\nonumber \\&+\,\frac{4 y^2 \tilde{z}+(z^2-4 z-1)\tilde{z}^2-y^4}{z (y^2-\tilde{z}^2)(y^2-z\tilde{z})}b_3\nonumber \\&+\,\frac{\tilde{z}(-(z-1)\tilde{z}^3+y^4+2 y^2 (z^2-z-2))}{y^2 z(y^2-\tilde{z}^2)}b_4\nonumber \\&\left. -\,2\tilde{z} c_4+4zc_3\right] , \end{aligned}$$

(C14)

$$\begin{aligned} \mho ^{A}_{c}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi }\left[ -\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}\right. \nonumber \\&+\,\frac{y^2(-5 z^2+4z+1)\tilde{z}^2+(z-1) \tilde{z}^5+y^4(y^2+3 z^2-2 z-5)}{y^2 (y^2-\tilde{z}^2)(y^2-z \tilde{z})} \nonumber \\&-\,\frac{\tilde{z}(z\tilde{z}^2+y^2 (2-3 z))}{y^4-y^2 \tilde{z}^2}b_1 +\frac{\tilde{z}^2}{y^4-y^2 z \tilde{z}}b_2\nonumber \\&+\,\frac{-4 y^2 \tilde{z}+(-z^2+4 z+1) \tilde{z}^2+y^4}{z (y^2-\tilde{z}^2)(y^2-z\tilde{z})}b_3\nonumber \\&\left. +\,\frac{\tilde{z} ((z-1)\tilde{z}^3-y^2 (y^2+2 z^2-2 z-4))}{y^2 z(y^2-\tilde{z}^2)}b_4+2 \tilde{z} c_4\right] , \end{aligned}$$

(C15)

$$\begin{aligned} \mho ^{A}_{d}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi }\left[ -\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}\right. \nonumber \\&+\,\frac{(z^2+10 z+1) \tilde{z}^2+y^4-2 y^2 (z^2+6 z+5)}{(y^2-\tilde{z}^2)(y^2-z \tilde{z})} \nonumber \\&+\,\frac{\tilde{z}(-5 y^2+5 z^2+6 z+1)}{(y^2-\tilde{z}^2)(y^2-z \tilde{z})}b_2\nonumber \\&\left. -\,\frac{(z^2+6 z+1)\tilde{z}^2+y^4-2 y^2 (z^2+4 z+3)}{(y^2-\tilde{z}^2)(y^2-z \tilde{z})}b_3\right] , \end{aligned}$$

(C16)

$$\begin{aligned} \mho ^{A}_{e}= & {} \frac{e_b C_F \alpha _s\sqrt{2N_c}}{4\pi }\left[ \frac{y^2-z^2-8z-7}{y^2-\tilde{z}^2}\frac{1}{\hat{\epsilon }_{\mathrm{UV}}}+\frac{\tilde{z}^2-y^2}{y^2-z \tilde{z}}\right. \nonumber \\&+\,\frac{\tilde{z} (-y^2+z^2-1)}{ (y^2-\tilde{z}^2)(y^2-z\tilde{z})}b_2\nonumber \\&\left. \frac{(z^2+6 z+1) \tilde{z}^2+y^4-2 y^2(z^2+4 z+3)}{(y^2-\tilde{z}^2)(y^2-z\tilde{z})}b_3\right] , \end{aligned}$$

(C17)

$$\begin{aligned} \mho ^A_{\mathrm{CT}-m}= & {} -\frac{2}{\tilde{z}}{\mathbb {A}}^\epsilon _{\mathrm{CT}-m}, \nonumber \\ \mho ^A_{\mathrm{CT}-F}= & {} -\frac{2}{\tilde{z}}{\mathbb {A}}^\epsilon _{\mathrm{CT}-F}. \end{aligned}$$

(C18)

The sum of them is

$$\begin{aligned} \mho ^A_{b-e+\mathrm{CT}}= & {} -\frac{3 e_b C_F \alpha _s\sqrt{2N_c} ((z-1)\ln (z)-2 \tilde{z}+2/3t_1)}{4 \pi \tilde{z}}.\nonumber \\ \end{aligned}$$

(C19)

We can get the one-loop result in Eq. 60 after adding up the symmetrical part with $e_b\rightarrow e_c$ and $m_b\leftrightarrow m_c$.