1 Introduction

Black holes are highly localized simplest objects in our cosmos that may carry charges (i.e. hairs) of various kinds. No-hair conjecture [1] refers simply to the degrees of freedom other than the well-accepted ones such as mass, electric/magnetic charge and the angular momentum. Internal degrees of freedom such as the non-abelian gauge charges can naturally be added to the abelian electromagnetic charges to extend the list of hairs for the black holes.

With the advent of surface-layer formalism and thin-shells in general relativity [2–8], the question naturally arises whether the hairs of the black hole can be screened against external observer at infinity. Thin-shell and its stability in Schwarzschild black hole spacetime was studied by Brady, Louko and Poisson in [9] where they have shown that a thin-shell with positive energy density which satisfies the dominant energy conditions may be stable against a radial perturbation. Nonradial linear oscillations of shells was studied by Schmidt in [10, 11] and inclusion of a cosmological constant was done by Ishak and Lake in [12]. A generalized study on thin-shells in vacuum was investigated by Goncalves [13] and following [9], Lobo and Crawford [14], by considering a spacetime satisfying the transparency condition, have studied generic dynamic spherically symmetric thin-shells. Accelerated shells and the relation between stress-energy and motion for such layers has been considered by Krisch and Glass in [15] while the stability of charged thin-shells has been studied by Eiroa and Simeone [16] and the same authors worked on thin-shells in \(2+1\)-dimensions including Born–Infeld matter sources in the bulk [17]. Very recently stability of thin-shell interfaces inside compact stars has been worked out by Pereira, Coelho, and Rueda in [18]. Application of thin-shell formalism in making dark energy stars has been considered by Bhara and Rahaman in [19] while the gravitational vacuum star or gravastar, based on the same formalism, has been proposed by Mazur and Mottola in [20] which was developed further by Visser and Wiltshire in [21] and the references therein.

Our aim in this study is to apply such a formalism to the standard Reissner–Nordström (RN) black hole which carries a static electric or magnetic charge. The thin-shell is assumed concentric with the RN black hole and with a radius greater than the event horizon of the latter. A toy-model version of our formalism in \(2+1\)-dimensional case was considered before in connection with the regular Bardeen black hole [22]. The source of the Bardeen black hole therein was assumed to be of non-linear electrodynamic origin. In the present problem the inside spacetime is taken to be RN while the external spacetime is Schwarzschild geometry. Application of the boundary conditions at the thin-shell in between serves to screen the charge of the internal RN geometry against outside. That is, beyond the thin-shell no trace of electric charge Q of the RN black hole is left. In this sense the thin-shell acts as a perfect absorber of the electric charge of the RN black hole. Such a screening process, however, is not without consequences. The imposed boundary conditions fix the mass/energy and charge of the shell to play its absorbent role. The energy density \(\sigma \) of the thin-shell at equilibrium radius turns out to be negative, \(\sigma <0.\) This situation is known to be notorious enough in the topic of wormholes and thin-shell wormholes [23–28], although it may be considered natural in the realm of quantum field theory. Once this situation is taken for granted we proceed with the stability analysis of the thin-shell against linear radial perturbations. With perturbation, besides the energy density at the equilibrium state we have emerging pressure tensions satisfying an equation of state of the form \(\frac{\mathrm{d}P}{\mathrm{d}\sigma }=\omega \), where P \(=\) pressure, \(\sigma \) \(=\) energy density and \(\omega \) is a constant proportional to the speed of sound. It turns out that the thin-shell around a RN black hole which screens its electric/magnetic charge from outside is stable against radial perturbations. The stability configuration is plotted numerically. We may anticipate that a similar analysis can naturally be carried out for a black hole carrying a Yang–Mills charge. Since these non-abelian gauge charges are trapped/confined inside nuclei it may lead effectively to a geometrical theory of confinement for fractionally charged fermions. For this purpose, however, the relevant proper boundary conditions should be those of Einstein–Maxwell–Dirac–Yang–Mills theory, which lies beyond our scope in this paper. Let us add that the range of applications for our method seems limitless and for all these, thanks to the Einstein’s junction equations with tuned sources satisfied on layers/surfaces.

2 The formalism

Let’s assume that a RN black hole with mass m and total charge Q sits at the origin of a spherically symmetric spacetime whose event horizon is located at \(r=r_{\mathrm{e}}.\) A timelike thin-shell of dust is located at \(r=a>r_{\mathrm{e}}\) with energy momentum tensor \(S^{ij}=\mathrm{diag}[ \sigma ,0,0] \) with respect to an observer on the shell of line element

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}\tau ^{2}+a^{2}( \tau ) \mathrm{d}\Omega ^{2} \end{aligned}$$
(1)

in which \(\tau \) is the proper time on the shell and \(\mathrm{d}\Omega ^{2}\) is the line element on \(S^{2}\). Next, we are interested to see the possibility of having charge of the black hole unseen by a distant observer. In other words, is it possible to have the spacetime outside the shell a Schwarzschild black hole with mass M,  different from m,  but related to m and Q?

Using the well-known Darmois–Israel formalism [2, 3] one may consider two pseudo Riemannian manifolds \(\mathcal {M}_{1}\) and \(\mathcal {M}_{2}\) with identical timelike boundaries located at \(r=a\) with spherically symmetric line elements

$$\begin{aligned}&\mathrm{d}s_{1}^{2}=-f_{1}( r) \mathrm{d}t^{2}+\frac{1}{f_{1}( r) } \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}, \nonumber \\&\quad \text {for }r\le a\text { and }f_{1}( r) =1-\frac{2m}{r}+\frac{ Q^{2}}{r^{2}} \end{aligned}$$
(2)

and

$$\begin{aligned}&\mathrm{d}s_{2}^{2}=-f_{2}( r) \mathrm{d}t^{2}+\frac{1}{f_{2}( r) } \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}, \nonumber \\&\quad \text { for }r\ge a\text { and }f_{2}( r) =1-\frac{2M}{r} \end{aligned}$$
(3)

in which m and Q are the mass and charge of the inner black hole while M is a constant to be identified. By gluing these manifolds from their boundaries we construct a complete manifold \(\mathcal {M}\). The hypersurface boundaries used for gluing is given by (1) and the Israel junction conditions imposes (\(c=G=1\))

$$\begin{aligned} k_{i}^{j}-k\delta _{i}^{j}=-8\pi S_{i}^{j}. \end{aligned}$$
(4)

Here \(k_{i}^{j}=K_{i}^{j( 2) }-K_{i}^{j( 1) }\) is the effective extrinsic curvature tensor of the shell with \(K_{i}^{j( 2) }\) and \(K_{i}^{j( 1) }\) on each side of the shell and \( k=k_{i}^{i}\) is the extrinsic curvature scalar of the shell. In brief

$$\begin{aligned} K_{ij}^{( 1,2) }=-n_{\gamma }^{( 1,2) }\left( \frac{ \partial ^{2}x^{\gamma }}{\partial y^{i}\partial y^{j}}+\Gamma _{\alpha \beta }^{\gamma }\frac{\partial x^{\alpha }}{\partial y^{i}}\frac{\partial x^{\beta }}{\partial y^{j}}\right) \end{aligned}$$
(5)

with

$$\begin{aligned} n_{\gamma }^{( 1,2) }=\frac{\partial _{\gamma }F}{\sqrt{g^{\alpha \beta ( 1,2) }\partial _{\alpha }F\partial _{\beta }F}} \end{aligned}$$
(6)

the normal 4-vector on the sides of the shell given by the surface \(F=r-a=0\). We note that \(x^{\alpha }\in \{ t,r,\theta ,\varphi \} \) while \(y^{i}\in \{ \tau ,\theta ,\varphi \} \) and \(\partial _{\alpha }=\frac{\partial }{\partial x^{\alpha }}.\) For the static thin-shell, the explicit calculation admits

$$\begin{aligned} \frac{1}{4\pi a}\left( \sqrt{f_{1}}-\sqrt{f_{2}}\right) =\sigma \end{aligned}$$
(7)

and

$$\begin{aligned} \frac{2f_{2}+af_{2}^{\prime }}{16\pi a\sqrt{f_{2}}}-\frac{ 2f_{1}+af_{1}^{\prime }}{16\pi a\sqrt{f_{1}}}=0 \end{aligned}$$
(8)

in which a prime stands for the derivative with respect to r and all functions are calculated at \(r=a.\) In order to have the second condition satisfied we must have

$$\begin{aligned} M=\frac{a( r_{\mathrm{e}}-m) }{( a-m) +( r_{\mathrm{e}}-m) } \end{aligned}$$
(9)

in which \(r_{\mathrm{e}}\) is the event horizon of the RN black hole given by

$$\begin{aligned} r_{\mathrm{e}}=m+\sqrt{m^{2}-Q^{2}}. \end{aligned}$$
(10)

Having M,  one can find \(\sigma \) of the thin-shell which is given by

$$\begin{aligned} \sigma= & {} -\frac{1}{4\pi a}\left( \frac{\sqrt{a-r_{\mathrm{e}}}}{\sqrt{( a-m) +( r_{\mathrm{e}}-m) }}\right. \nonumber \\&\left. - \frac{\sqrt{a( a-2m) -r_{\mathrm{e}}( r_{\mathrm{e}}-2m) }}{a} \right) . \end{aligned}$$
(11)

Herein, due to the fact that \(a>r_{\mathrm{e}}\) and \(m\le r_{\mathrm{e}}\le 2m\), \(\sigma \) remains real but negative. Therefore the shell is like a bubble of exotic matter. The amount of total exotic matter can be found as

$$\begin{aligned} \Omega= & {} \int \nolimits _{0}^{2\pi }\int \nolimits _{0}^{\pi }\int \nolimits _{0}^{\infty }\sigma \delta ( r-a) \sqrt{-g} \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi =4\pi a^{2}\sigma \nonumber \\= & {} -\left( \frac{a\sqrt{a-r_{\mathrm{e}}}}{\sqrt{( a-m) +( r_{\mathrm{e}}-m) }}-\sqrt{a( a-2m) -r_{\mathrm{e}}( r_{\mathrm{e}}-2m) } \right) .\nonumber \\ \end{aligned}$$
(12)

In terms of m,  M and Q we find

$$\begin{aligned} \Omega =-\sqrt{( m-\Delta ) ( m+\Delta -2M) }, \end{aligned}$$
(13)

in which \(\Delta =\sqrt{m^{2}-Q^{2}}.\) Let’s remark that at the extremal limits one finds

$$\begin{aligned} \lim _{Q\rightarrow 0}M=m,\quad \lim _{Q\rightarrow 0}\Omega =0, \end{aligned}$$
(14)

which implies the absence of the thin-shell and

$$\begin{aligned} \lim _{Q\rightarrow m}M=0,\quad \lim _{Q\rightarrow m}\Omega =-m=-Q. \end{aligned}$$
(15)

Here \(\sigma =-\frac{m}{4\pi a^{2}}=-\frac{Q}{4\pi a^{2}}\) which is nothing but the mass density over the surface area of the thin-shell with the same mass and charge of the black hole. It should be added that the charge of the spherical thin-shell must be the negative (\(-Q\)) of the black hole charge. This can be verified as follows.

The electric potential of the Reissner–Nordström black hole, up to a gauge transformation can be expressed appropriately by

$$\begin{aligned} \mathbf {A}=Q\left( \frac{1}{r}-\frac{1}{a}\right) \Theta ( a-r) \mathrm{d}t. \end{aligned}$$
(16)

Note that \(\Theta ( a-r) \) is the unit step function defined by

$$\begin{aligned} \Theta ( a-r) =\left\{ \begin{array}{cc} 1, &{}\quad r<a \\ 0, &{}\quad r>a \end{array} \right. . \end{aligned}$$
(17)

Accordingly, the Maxwell 2-form is

$$\begin{aligned} \mathbf {F}=\frac{Q}{r^{2}}\Theta ( a-r) \mathrm{d}t\wedge \mathrm{d}r \end{aligned}$$
(18)

with its dual 2-form

$$\begin{aligned} ^{\star }\mathbf {F}=Q\sin \theta \Theta ( a-r) \mathrm{d}\theta \wedge \mathrm{d}\varphi . \end{aligned}$$
(19)

The sourceful Maxwell equation takes the form

$$\begin{aligned} d( ^{\star }\mathbf {F}) =^{\star }\mathbf {j} \end{aligned}$$
(20)

with the current density 3-form

$$\begin{aligned} ^{\star }\mathbf {j}=-Q\sin \theta \delta ( a-r) \mathrm{d}r\wedge \mathrm{d}\theta \wedge \mathrm{d}\varphi \end{aligned}$$
(21)

in which \(\delta ( a-r) \) stands for the Dirac delta function on the shell.

The integral of \(^{\star }\mathbf {j}\) yields the charge on the shell as

$$\begin{aligned} -Q=\frac{1}{4\pi }\int {}^{\star }\mathbf {j}. \end{aligned}$$
(22)

This verifies that beyond the spherical thin-shell charge does not exist, justifying the Schwarzschild metric.

To conclude this section we would like to express our variables and quantities in terms of m. By introducing \(\frac{a}{m}=\alpha \), and \(\frac{ Q^{2}}{m^{2}}=\epsilon \) we find

$$\begin{aligned} \frac{M}{m}= & {} \frac{\alpha \sqrt{1-\epsilon }}{\alpha -1+\sqrt{1-\epsilon }},\end{aligned}$$
(23)
$$\begin{aligned} \frac{\Omega }{m}= & {} -\frac{\left( 1-\sqrt{1-\epsilon }\right) \sqrt{\alpha ^{2}-2\alpha +\epsilon }}{\alpha -1+\sqrt{1-\epsilon }} \end{aligned}$$
(24)

and

$$\begin{aligned} \sigma m=-\frac{\sqrt{\alpha ^{2}-2\alpha +\epsilon }}{4\pi \alpha ^{2}} \frac{1-\sqrt{1-\epsilon }}{\alpha -1+\sqrt{1-\epsilon }}, \end{aligned}$$
(25)

with \(0\le \epsilon \le 1\) and \(1+\sqrt{1-\epsilon }<\alpha .\) These allow us to set the quantity m to unity without losing the generality of the problem. In the same line we remark that the location of horizon (i.e., the horizon observed by a distant frame) is given by

$$\begin{aligned} \bar{r}_{\mathrm{e}}=2M=m\frac{2\alpha \sqrt{1-\epsilon }}{\alpha -1+\sqrt{1-\epsilon }}. \end{aligned}$$
(26)

The latter clearly shows that \(\frac{\bar{r}_{\mathrm{e}}}{m}=\frac{2\alpha \sqrt{ 1-\epsilon }}{\alpha -1+\sqrt{1-\epsilon }}<\alpha \) which implies that the event horizon is located inside the shell with respect to a distant observer.

3 Stability analysis

As we have shown in the previous section, one can consider a thin-shell of exotic dust surrounding a RN black hole which screens the electric charge of the black hole. The resulting solution from a distant observer will be a Schwarzschild black hole with a new effective mass. In this section we shall investigate the stability of such a thin-shell. To do so let’s consider the radius of the shell to be a function of \(\tau \) the proper time on the shell. By using the Israel formalism we find

$$\begin{aligned} \sigma =\frac{1}{4\pi a}\left( \sqrt{f_{1}+\dot{a}^{2}}-\sqrt{f_{2}+\dot{a} ^{2}}\right) \end{aligned}$$
(27)

and

$$\begin{aligned} P=-\frac{\sigma }{2}+\frac{1}{16\pi }\left( \frac{2\ddot{a}+f_{2}^{\prime }}{ \sqrt{f_{2}+\dot{a}^{2}}}-\frac{2\ddot{a}+f_{1}^{\prime }}{\sqrt{f_{1}+\dot{a }^{2}}}\right) . \end{aligned}$$
(28)

We note that although for the static equilibrium we assumed \(P=0\) in the dynamic regime, P may not be zero as the matter is not at rest any more. Therefore while we consider the relation between M and other parameters given by (9) i.e., dictated by static equilibrium, in the dynamic case we adopt \(\frac{\mathrm{d}P}{\mathrm{d}\sigma }=\omega \) in which \(\omega \) is a real constant. The energy conservation, on the other hand, imposes

$$\begin{aligned} S_{;j}^{ij}=0 \end{aligned}$$
(29)

in which for \(i=\tau \) one finds

$$\begin{aligned} \sigma ^{\prime }=-\frac{2}{a}( \sigma +P) \end{aligned}$$
(30)

with \(^{^{\prime }}\equiv \frac{\mathrm{d}}{\mathrm{d}a}.\)

As a result from Eq. (27) we find a one dimensional equation of motion for the dynamical shell given by [16]

$$\begin{aligned} \dot{a}^{2}+V( a) =0 \end{aligned}$$
(31)

in which

$$\begin{aligned} V( a) =-4\pi ^{2}a^{2}\sigma ^{2}+\frac{f_{1}+f_{2}}{2}-\frac{ ( f_{1}-f_{2}) ^{2}}{64\pi ^{2}a^{2}\sigma ^{2}}. \end{aligned}$$
(32)

We must add that in (31), \(\sigma =\sigma ( a) \) is a function of a – the radius of the shell after perturbation – which is no longer the same as its equilibrium value, say \(\sigma _{0}=\sigma ( a=a_{0}) \) which is given by

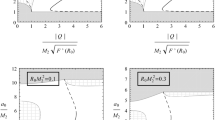
$$\begin{aligned} \sigma _{0}=\frac{1}{4\pi a_{0}}\left. \left( \sqrt{f_{1}}-\sqrt{f_{2}} \right) \right| _{a=a_{0}}. \end{aligned}$$
(33)

In order to have the thin-shell stable against a radial perturbation, Eq. (32) must admit an oscillatory motion which means that at the equilibrium point (say at \(a=a_{0}\)) where \(V( a_{0}) =\) \(V^{\prime }( a_{0}) =0\) and \(V^{\prime \prime }( a_{0}) >0.\) In Fig. 1 we plot \(V^{\prime \prime }( a_{0}) \) for the specific value of \( m=1.0\) and \(Q=0.2.\) As one observes in the region with \(\omega >0\) the thin-shell is stable while otherwise it occurs for \(\omega <0.\) Let’s add also that, \(\omega =\mathrm{cons.}\) yields

$$\begin{aligned} P=\omega ( \sigma -\sigma _{0}) \end{aligned}$$
(34)

which in turn implies that with \(\sigma >\sigma _{0}\)/\(\sigma <\sigma _{0}\) and \(\omega >0,\) to have the shell stable, the pressure must be negative/positive after the perturbation. We add that this behavior is not only for the specific value of m and Q.

Fig. 1
figure 1

A plot of \(V^{\prime \prime }=0\) at \(a=a_{0}\) in terms of \( a(=a_{0}) \) and \(\omega \) for \(m=1.0\) and \(Q=0.1,0.3,0.5,0.9.\) The region with \(V^{\prime \prime }>0\) which is the stability zone is also indicated by S. The effect of charge on stability/instability is clearly seen

Full size image

As a final remark we comment that our formalism allows to interchange the roles of inner and outer spacetimes. That means this time the inner spacetime is Schwarzschild while the outer one is the RN. We have

$$\begin{aligned}&\mathrm{d}s_{1}^{2}=-f_{1}( r) \mathrm{d}t^{2}+\frac{1}{f_{1}( r) } \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}, \nonumber \\&\quad \text {for }r\le a\text { and }f_{1}( r) =1-\frac{2M}{r} \end{aligned}$$
(35)

and

$$\begin{aligned}&\mathrm{d}s_{2}^{2}=-f_{2}( r) \mathrm{d}t^{2}+\frac{1}{f_{2}( r) } \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}, \nonumber \\&\quad \text {for }r\ge a\text { and }f_{2}( r) =1-\frac{2m}{r}+\frac{ Q^{2}}{r^{2}}. \end{aligned}$$
(36)

Obviously the thin-shell of radius \(r=a\) carries the charge Q to make the charge of the external RN geometry. Following the foregoing analysis we conclude that M, m and Q are related as given in Eq. (22) while the energy density is positive now given by

$$\begin{aligned} \sigma =\frac{\sqrt{\alpha ^{2}-2\alpha +\epsilon }}{4\pi m\alpha ^{2}}\frac{ 1-\sqrt{1-\epsilon }}{\alpha -1+\sqrt{1-\epsilon }} \end{aligned}$$
(37)

in which \(\epsilon \) and \(\alpha \) are as before and consequently \(\Omega >0. \) In this case the charge distribution lies on the spherical shell at \( r=a\). The new thin-shell is also stable against a radial perturbation with an equation of state \(\frac{\mathrm{d}P}{\mathrm{d}\sigma }=\omega >0\) as in the other case.

4 Conclusion

Although in the present study we investigated the erasure of a RN black hole charge to the external world through junction conditions imposed on a contrived outer thin-shell the method seems more generic, apt for more general central objects. We have shown, for instance, that the roles of inner RN and outer Schwarzschild geometries is reversible with a positive mass on the shell. Not to mention, a counter-rotating cylindrical shell may absorb the rotational hair of a black hole to turn it into a static one. The question may be raised: can naturally formed absorber shells, thin or thick in cosmology hide/screen the reality from our telescopes? If yes, then the effect of screening becomes as important as the lensing of light while passing near massive heavenly objects. No doubt this may revise our ideas of black holes and their no-hair theorem. More interestingly this may pave the way toward a geometrical description of quark confinement provided the boundary conditions are modified to cover the Dirac and Yang–Mills fields. Naturally this takes us away from classical physics into the realm of gravity coupled QCD. Let us add that hiding of charge by geometrical structures has been considered before for example in [29]. Therein with cited references, it has been shown that non-linear contributions (see for instance [30, 31]) in an effective theory beyond standard Einstein–Maxwell plays crucial roles. Finally we must admit that the negative mass of the thin, stable layer encountered in the formalism remains to be our concern.

It should also be supplemented that the extremal RN case with \(m=Q( \epsilon =1) \) with the flat space (\(M=0\)) inside constitutes a particular case. The energy density of the thin-shell which becomes a bubble now takes the form

$$\begin{aligned} \sigma =\frac{1}{4\pi m\alpha ^{2}},\quad \text { (}\alpha >1\text {).} \end{aligned}$$
(38)

From a different approach the similar problem was considered also in [32]. It follows that such a bubble in an extremal RN spacetime becomes stable against perturbations described above. As a final remark let us add that our results have holographycal implications which may be investigated further.