Electroweak bounds on Higgs pseudo-observables and $h\rightarrow 4\ell$ decays

Abstract

We analyze the bounds on the Higgs pseudo-observables following from electroweak constraints, under the assumption that the Higgs particle is the massive excitation of an $\text {SU}(2)_L$ doublet. Using such bounds, detailed predictions for $h\rightarrow 4\ell$ decay rates, dilepton spectra, and lepton-universality ratios are presented.

1 Introduction

The decays of the Higgs particle, h(125), can be characterized by a set of pseudo-observables (PO) that describe, in great generality, possible deviations from the Standard Model (SM) in the limit of heavy New Physics (NP) [1]. These PO should be considered as independent variables in the absence of specific symmetry or dynamical assumptions; however, relations among themselves and also between Higgs and non-Higgs PO arise in specific NP frameworks. Testing if such relations are verified by data provides a systematic way to investigate the nature of the Higgs particle and, more generally, to test the underlying symmetries of physics beyond the SM.

The constraints on the Higgs PO following from the hypotheses of CP invariance, flavor universality and custodial symmetry have been discussed in Ref. [1]. These symmetries lead to a series of relations among PO that can be tested using Higgs data only. In this paper we analyze the constraints following from the hypothesis that the Higgs particle is the massive excitation of a pure $\text {SU}(2)_L$ doublet, i.e. constraints and relations among the PO that hold in the so-called linear effective field theory (EFT) regime.

Under this assumption, the h field appears in the effective SM+NP Lagrangian through the combination $(v + h)^n$, where $v \approx 246 \text { GeV}$ is the $\text {SU}(2)_L$-breaking vacuum expectation value. This implies that processes involving the Higgs particle can be related to electroweak (EW) precision observables that do not involve the physical Higgs boson. As pointed out in Ref. [2], testing if such relations are satisfied represents a very powerful tool to discriminate linear and non-linear EFT approaches to Higgs physics. In particular, sizable deviations from the SM in the $h\rightarrow 4\ell$ spectra are allowed, in general, in the non-linear EFT (i.e. if v and h are decoupled) [3], while they are significantly constrained by EW precision observables in the linear EFT [4–6]. Observing sizable deviations from the SM in the $h\rightarrow 4\ell$ spectra could therefore allow to exclude that h is the massive excitation of a pure $\text {SU}(2)_L$ doublet [2] (for additional tests about the $\text {SU}(2)_L$ properties of the h boson see Ref. [7]).

In order to precisely quantify the above statement, in this paper we present a systematic evaluation of the bounds on the Higgs PO following the EW constraints in the linear EFT regime, with particular attention to the PO entering both $h\rightarrow 4\ell$ and $h\rightarrow 2\ell 2\nu$ decays. Using such bounds, we derive predictions for $h\rightarrow 4\ell$ decay rates, dilepton invariant-mass spectra, and lepton-universality ratios.

2 Relating Higgs pseudo-observables to EW observables

Given the present and near-future level of precision in Higgs physics, and the absence of any significant deviation from the SM, it is a good approximation to work at the tree level in the linear EFT, as far as NP effects are concerned. In this limit, the Higgs PO ($\kappa _i$ and $\epsilon _i$) can be expressed as linear combinations of the Wilson coefficients of the EFT Lagrangian. Analogously, the EW PO, such as the Z- and W-pole effective couplings, the W mass, and the effective triple gauge boson couplings (TGC), can be expressed as linear combinations of the same Wilson coefficients. By inverting these relations it is possible to get rid of some of the (basis-dependent) Wilson coefficients and derive basis-independent relations between Higgs and EW PO.

In doing so, one realizes that the Higgs contact terms $\epsilon _{Zf}$ and $\epsilon _{Wf}$ [1] can be expressed in a closed form in terms of quantities already strongly constrained by LEP and Tevatron data [6, 8, 9], such as the Z and W effective on-shell couplings to fermions, and the effective anomalous TGC:

$$\begin{aligned} \epsilon _{Z f}= & {} \frac{2m_Z}{v} ( \delta g^{Zf} - (c_\theta ^2 T^3_f + s_\theta ^2 Y_f) \mathbf{1}_3 \delta g_{1,z} + t_\theta ^2 Y_f \mathbf{1}_3 \delta \kappa _\gamma ), \nonumber \\ \epsilon _{W f}= & {} \frac{\sqrt{2} m_W}{v} ( \delta g^{Wf} - c_\theta ^2 \mathbf{1}_3 \delta g_{1,z} ). \end{aligned}$$

(1)

Here, generalising the notation of Ref. [1], we treat $\epsilon _{Z f}$ and $\epsilon _{W f}$ as $3\times 3$ matrices in flavor space (with implicit flavor indices). On the right-hand side, $\delta g^{Zf}$ and $\delta g^{Wf}$ denote the anomalous effective on-shell Z and W couplings to the fermion f, again in an implicit $3\times 3$ notation, $\mathbf{1}_3$ is the identity matrix, and $\delta g_{1,z}$ and $\delta \kappa _\gamma$ are the effective anomalous TGC extracted from $e^+ e^- \rightarrow W^+ W^-$ and single W production [10] (see “Appendix” for the definition of the various terms).¹ The parameters $\{c_\theta , s_\theta , t_\theta \}$ denote the cosine, sine and tangent of the Weinberg angle, defined as in Ref. [11].

The parameters $\delta g^{Zf}$ relevant to this work are the leptonic Z couplings, which are tightly constrained by LEP-I data [6, 10, 12]. In particular, lepton flavor non-universal effects in the Z couplings are strongly suppressed, leading to per-mil constraints on the $\delta g^{Z\ell }$ even in the most generic flavor scenario [13]. This is why we set these couplings to their SM values in the following. It must be stressed that the analyses of Refs. [6, 10, 13] neglect the impact of off-shell Z effects [14] and that of NLO terms in the EFT expansion, implicitly assuming a high EFT cutoff scale. A consistent inclusion of the latter effects may lead to a significant (relative) enlargement of the error on the $\delta g^{Zf}$ couplings, especially in the case of a low cut-off scale for the EFT (see e.g. Ref. [15]). As we will comment in the following, we have explicitly checked that relaxing the bounds on $\delta g^{Zf}$ to $\mathcal {O}(1\,\%)$ does not lead to appreciable differences in our numerical analysis. The leptonic W couplings $\delta g^{W\ell }$ are instead constrained only at the few percent level. In the following we consider the bounds from the non-universal fit of Ref. [13], reported also in “Appendix”.

In general, the parameters describing anomalous TGC in the effective Lagrangian are not PO [16]. Here we follow the approach of Ref. [10] where the $e^+ e^- \rightarrow W^+ W^-$ cross-section is parameterized in terms of the effective on-shell Z and W couplings to fermions plus the three parameters $\{\delta g_{1,z}, \delta \kappa _\gamma , \lambda _Z\}$, which therefore represent a consistent TGC PO set. The constraints on this set obtained in Ref. [10] are collected in “Appendix”. It should be stressed that a flat direction is present when all three TGC PO are included at the linear level [17] (see also [18]), which reflects into a very loose bound on $\delta g_{1,z}$ when $\lambda _Z$ is marginalized. In the following we will present results both for this case and for the case where $\lambda _Z$ is fixed to zero, which is a common condition in many interesting explicit UV models.²

As anticipated, given the strong bounds on $\delta g^{Z \ell }$, and the expected experimental sensitivity on the Higgs contact terms, we can fix the former parameters to their SM values in Eq. (1) and study the allowed range of $\epsilon _{Z f}$ and $\epsilon _{W \ell }$ as determined by the TGC (whose constraints are obtained in the same limit) and W couplings only.

EW data also allows to bound the following custodial-symmetry-violating combination of PO [1, 9],

$$\begin{aligned}&\kappa _{WW} - \kappa _{ZZ} + \frac{2}{g}\left( \sqrt{2} \epsilon _{W e} + 2 c_\theta \epsilon _{Z e_L} \right) \nonumber \\&\quad = 2 \delta g^{We} + 4 \delta g^{Z e_L} + 4 \delta m, \end{aligned}$$

(2)

where $\delta m \equiv \delta m_W / m_W$ is also constrained to be below the per-mil level [10, 13]. Substituting the contact terms from Eq. (1) one gets [9]: $\kappa _{WW} - \kappa _{ZZ} = -2 s_\theta ^2 \delta g_{1,z} + 2 t_\theta ^2 \delta \kappa _\gamma + 4 \delta m$.

The remaining nine Higgs pseudo-observables $\epsilon ^{(\mathrm{CP})}_{ZZ,WW,Z\gamma ,\gamma \gamma }$ and $\kappa _{ZZ}$ are not constrained by EW data alone. However, only five of them are independent in the linear EFT due to the following relations:

$$\begin{aligned}&\delta \epsilon _{ZZ} = \delta \epsilon _{\gamma \gamma } +\frac{2}{t_{2\theta }} \delta \epsilon _{Z\gamma } - \frac{1}{c_\theta ^2} \delta \kappa _{\gamma },\end{aligned}$$

(3)

$$\begin{aligned}&\delta \epsilon _{WW} = c_\theta ^2 \delta \epsilon _{ZZ} + s_{2\theta } \delta \epsilon _{Z\gamma } + s_\theta ^2 \delta \epsilon _{\gamma \gamma }, \end{aligned}$$

(4)

and likewise for their CP counterparts (see also Refs. [4, 9, 11]). Here and in the following we denote by $\delta \epsilon _X$ the NP contribution to the pseudo-observable $\epsilon _X$ once the one-loop SM contribution is removed: $\delta \epsilon _X = \epsilon _X - \epsilon _X^\mathrm{SM-1L}$.

Since no LEP bound is available on the CP-violating TGC coupling $\delta \tilde{\kappa }_\gamma$, at present $\epsilon ^\mathrm{CP}_{ZZ}$ is an independent variable. However, in the future significant constraints on $\delta \tilde{\kappa }_\gamma$ could be obtained from LHC data [19]. All in all, we are left with 3 CP-conserving couplings, $\kappa _{ZZ}$ and $\epsilon _{\gamma \gamma ,Z\gamma }$, and 3 CP-violating ones, $\epsilon ^\mathrm{CP}_{\gamma \gamma ,Z\gamma ,{ZZ}}$.

In principle, the measurements of the partial decay widths $\Gamma (h \rightarrow \gamma \gamma , Z\gamma )$ allow to set strong bounds on $\epsilon ^{(\mathrm{CP})}_{\gamma \gamma ,Z\gamma }$ that, when combined with the TGC bounds, imply strong limits on $\epsilon _{ZZ,WW}$ through Eqs. (3) and (4). In practice, the extraction of such bounds is not straightforward since, at present, only the measurements of the so-called signal strengths (or $\sigma \times \mathrm{BR}$ normalized to SM) are available. The latter include also possible non-standard effects in the Higgs production and in the total decay width (e.g. via $\kappa _{ZZ}\ne 1$). We benefit from various global fits available in the literature [6, 20–22], which imply per-mil level limits on $\epsilon ^{(\mathrm{CP})}_{\gamma \gamma }$ and per-cent level limits on $\epsilon ^{(\mathrm{CP})}_{Z\gamma }$. In particular, in the following we use the values [20]

$$\begin{aligned} \kappa _{\gamma \gamma } = 0.90 \pm 0.15, \quad |\kappa _{Z\gamma }| < 3.18 \, (95\,\%\,\mathrm{CL}), \end{aligned}$$

(5)

where $\kappa _{\gamma \gamma ,Z\gamma } \equiv \epsilon _{\gamma \gamma ,Z\gamma } / \epsilon _{\gamma \gamma ,Z\gamma }^\mathrm{SM-1L}$, with $\epsilon _{\gamma \gamma }^\mathrm{SM-1L} \approx 3.8 \times 10^{-3}$, and $\epsilon _{Z\gamma }^\mathrm{SM-1L} \approx 6.7 \times 10^{-3}$. As discussed above, the constraints on $\epsilon _{\gamma \gamma ,Z\gamma }^\mathrm{CP}$ are equivalent to those shown above for their CP-conserving counterparts $\epsilon _{\gamma \gamma ,Z\gamma }$, whereas no bound is available for $\kappa _{ZZ}$ and $\epsilon _{ZZ}^\mathrm{CP}$ (before analyzing $h\rightarrow 4\ell$  data).

Combining the bounds on the TGC with those on the W couplings to leptons, we find the following constraints on the Higgs contact terms

$$\begin{aligned}&\left( \begin{array}{c} \epsilon _{Z e_L} \\ \epsilon _{Z e_R} \\ \epsilon _{W e} \\ \epsilon _{W \mu } \end{array} \right) = \left( \begin{array}{c} -0.32(13) \\ -0.17(6) \\ 0.29(12) \\ 0.29(12) \end{array} \right) _{\lambda _Z\ne 0} = \left( \begin{array}{c} -0.029(14) \\ -0.023(12) \\ 0.017(11) \\ 0.015(11) \end{array} \right) _{\lambda _Z=0} , \end{aligned}$$

(6)

with the following correlation matrix

$$\begin{aligned} \rho= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0.9961 &{} -0.9993 &{} -0.9993 \\ \cdot &{} 1 &{} -0.9929 &{} -0.9929 \\ \cdot &{} \cdot &{} 1 &{} 0.9994 \\ \cdot &{} \cdot &{} \cdot &{} 1 \end{array} \right) _{\lambda _Z\ne 0} \nonumber \\= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0.92 &{} -0.93 &{} -0.93 \\ \cdot &{} 1 &{} -0.75 &{} -0.76 \\ \cdot &{} \cdot &{} 1 &{} 0.93 \\ \cdot &{} \cdot &{} \cdot &{} 1 \end{array} \right) _{\lambda _Z=0} . \end{aligned}$$

(7)

Up to per-mil corrections due to deviations in the Z couplings to leptons and in $\delta m$, the following relations among Higgs PO are satisfied:

$$\begin{aligned}&\delta \epsilon _{ZZ} = \delta \epsilon _{\gamma \gamma } + \frac{2}{t_{2\theta }} \delta \epsilon _{Z\gamma } - \frac{v}{c_\theta ^2 m_Z} \left( \epsilon _{Z e_L} - \frac{1}{2 s_\theta ^2} \epsilon _{Z e_R} \right) ~ \nonumber \\&\delta \epsilon _{WW} = \delta \epsilon _{\gamma \gamma } + \frac{1}{t_\theta } \delta \epsilon _{Z\gamma } - \frac{v}{m_Z} \left( \epsilon _{Z e_L} - \frac{1}{2 s_\theta ^2} \epsilon _{Z e_R} \right) ~\nonumber \\&\kappa _{WW} - \kappa _{ZZ} = -\frac{v}{m_Z} \epsilon _{Z e_R}, \end{aligned}$$

(8)

which can be used to derive constraints on these PO given the bounds in Eqs. (5–7).

In the first row of Fig. 1 we present the bounds on the $\epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ pseudo-observables (relevant for $h \rightarrow 2e2\mu$, 4e, $4\mu$ decays) both in the general case ($\lambda _Z\not =0$, marginalised) and for $\lambda _Z=0$. It is interesting to notice that, even in the general case, only the direction

$$\begin{aligned} \epsilon _{Z e_R} \approx 0.48 \times \epsilon _{Z e_L} \end{aligned}$$

(9)

is loosely bounded, and that sizable positive values of the contact terms are excluded. The particular flat direction in the contact terms can be understood analytically by the fact that $\delta \kappa _\gamma$ is much more constrained than $\delta g_{1,z}$. As a result, we can also set $\delta \kappa _\gamma \approx 0$ in Eq. (1), which implies $\epsilon _{Z e_R} \approx 2 s_\theta ^2 \epsilon _{Z e_L} \approx 0.46 \times \epsilon _{Z e_L}$ (up to a $\sim$ $10\,\%$ accuracy). To check the robustness of our conclusions we relaxed the permil bounds on the $\delta g^{Z \ell }$ couplings and allowed them to vary independently with a benchmark error of $\pm$ $1\,\%$. The constraints in the first row of Fig. 1 are only marginally worsened, even for the $\lambda _Z = 0$  case.

Fig. 1

Bounds on the contact terms $\epsilon _{Z e_L}, \epsilon _{Z e_R}$ (upper row) and $\epsilon _{W e}, \epsilon _{W \mu }$ (lower row) (at 68, 95 and 99.7 % CL) obtained from the W couplings and TGC constraints, where $\lambda _Z$ has been marginalized (left plots) or set to zero (right plots). The dotted contours are $\Gamma /\Gamma _\mathrm{SM}(h\rightarrow 2e2\mu )$ and $\Gamma /\Gamma _\mathrm{SM}(h\rightarrow e\mu \nu _e\nu _\mu )$ iso-lines

In the second row of Fig. 1 we show the constraints on $\epsilon _{W e}$ and $\epsilon _{W \mu }$ (relevant for $h \rightarrow e\mu \nu _e \nu _\mu , 2e2\nu _e, 2\mu 2\nu _\mu$ decays) for both hypotheses on $\lambda _Z$. In particular we notice that in the general $\lambda _Z \ne 0$ case, since the bound on $\delta g_{1,z}$ is much worse than those on $\kappa _\gamma$ and $\delta g^{We}, \delta g^{W \mu }$, all four contact terms in Eq. (6) are highly correlated since – effectively – they all depend on the single variable $\delta g_{1,z}$. This implies to further relations in addition to the one in Eq. (9):

$$\begin{aligned}&\epsilon _{W e} \approx \epsilon _{W \mu }, \end{aligned}$$

(10)

$$\begin{aligned}&\epsilon _{W e} \approx \frac{v^2}{\sqrt{2} m_W m_Z} (\epsilon _{Z e_R} - \epsilon _{Z e_L}). \end{aligned}$$

(11)

In the rest of this work we study the implications of these constraints for $h\rightarrow 4\ell ~ (\ell =e,\mu )$ decay rates and dilepton invariant-mass distributions. More specifically, we will propagate the errors shown above and analyze the allowed room for non-standard effects. We include quadratic terms in all following calculations, which in general should represent subleading corrections in the EFT expansion. However, this is not always the case in the general scenario $\lambda _Z \ne 0$, since values as large as 0.4 are allowed for some of the pseudo-observables. The subsequent predictions for $h\rightarrow 4\ell$ observables should be taken with care in this case, and interpreted as the room for New Physics taking into account that very little is known on certain pseudo-observables.

$$\begin{aligned}&X = \left( \begin{array}{ccccccccc} 1.0 &{} 3.0 &{} -2.4 &{} 3.0 &{} -2.4 &{} 0.55 &{} -1.1 &{} 0.021 &{} 0 \\ 0 &{} 6.2 &{} 0 &{} 1.7 &{} -1.4 &{} 0.80 &{} -13 &{} 0.36 &{} 0 \\ 0 &{} 0 &{} 6.2 &{} -1.4 &{} 1.1 &{} -0.64 &{} -13 &{} 0.36 &{} 0 \\ 0 &{} 0 &{} 0 &{} 6.2 &{} 0 &{} 0.80 &{} -13 &{} 0.36 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 6.2 &{} -0.64 &{} -13 &{} 0.36 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.099 &{} -0.39 &{} 0.0094 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 52 &{} -1.9 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 31 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} X_{3\times 3}^\mathrm{CP} \\ \end{array} \right) _{2e2\mu }~ \!\!\!\!\!\!\!\!\!= \left( \begin{array}{ccccccccc} 1.0 &{} 6.3 &{} -5.0 &{} 0 &{} 0 &{} 0.52 &{} -0.89 &{} 0.50 &{} 0.0 \\ 0 &{} 16 &{} -2.8 &{} 0 &{} 0 &{} 1.6 &{} -25 &{} 2.9 &{} 0.0 \\ 0 &{} 0 &{} 15 &{} 0 &{} 0 &{} -1.3 &{} -25 &{} -1.1 &{} 0.0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.085 &{} -0.27 &{} -0.07 &{} 0.0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 44 &{} -1.6 &{} 0.0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 26 &{} 0.0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} X_{3\times 3}^\mathrm{CP} \\ \end{array} \right) _{4e} \end{aligned}$$

(12)

$$\begin{aligned}&X_{3\times 3}^\mathrm{CP} = \left( \begin{array}{ccc} 0.04 &{} -0.20 &{} 0.007 \\ 0 &{} 34 &{} -1.6 \\ 0 &{} 0 &{} 29 \\ \end{array} \right) _{2e2\mu }~ = \left( \begin{array}{ccc} 0.033 &{} -0.14 &{} -0.18 \\ 0 &{} 27 &{} -1.1 \\ 0 &{} 0 &{} 23 \\ \end{array} \right) _{4e} \end{aligned}$$

(13)

3 $h\rightarrow 4\ell$ phenomenology under EW constraints

3.1 Partial decay rates

We compute the modification of the $h\rightarrow 4\ell$ integrated decay rates due to non-standard contributions to the pseudo-observables. In order to regulate the photon pole and simultaneously resemble the realistic present analysis [20, 21], we employ a minimum invariant-mass cut on the opposite sign same flavor lepton pairs of $m_{\ell \ell }^\mathrm{min}=\mathrm{12~GeV}$. This way we determine

$$\begin{aligned} \frac{\Gamma _{4\ell }}{\Gamma _{4\ell }^\mathrm{SM}} = \sum _{i,j} X^{4\ell }_{ij} \kappa _i \kappa _j, \end{aligned}$$

(14)

where

$$\begin{aligned} \kappa\equiv & {} \{ \kappa _{ZZ},\epsilon _{Z e_{L}},\epsilon _{Z e_{R}},\epsilon _{Z \mu _{L}},\epsilon _{Z \mu _{R}},\epsilon _{ZZ},\epsilon _{Z \gamma },\\&\epsilon _{\gamma \gamma },\epsilon ^\mathrm{CP}_{ZZ},\epsilon ^\mathrm{CP}_{Z\gamma },\epsilon ^\mathrm{CP}_{\gamma \gamma } \} \end{aligned}$$

and $X^{2e2\mu }, X^{4e}$ are given in Eqs. (12) and (13) ($X^{4\mu }$ is trivially obtained from $X^{4e}$). The measurements of the integrated decay rates constrain only these particular PO combinations.

Some comments on these expressions are in order. First, it is easy to see that the contributions from the CP-violating terms $\epsilon _{ZZ,Z\gamma ,\gamma \gamma }^\mathrm{CP}$ are negligible once the constraints from $\Gamma (h \rightarrow \gamma \gamma , Z\gamma )$ are taken into account. We stress that this conclusion holds even for $m_{\ell \ell }^\mathrm{min}$ as low as $\mathrm{1~GeV}$. Indeed, despite the lack of bounds on $\epsilon _{ZZ}^\mathrm{CP}$, its contribution to the total rate is below 4 % even for O(1) values. Thus, $\Gamma (h\rightarrow 4\ell )$ can be expressed in terms of $\kappa _{ZZ}$ and the five pseudo-observables $\epsilon _{Ze_R,Ze_L,{ZZ},Z\gamma ,\gamma \gamma }$ bounded by Eqs. (5), (6) and (8).

The global fit of Ref. [20], that allows approximately for 30 % non-standard contributions in $\Gamma (h\rightarrow 4\ell )$, can in principle be used to obtain a bound on $\kappa _{ZZ}$ via Eq. (14). However, the error in the contact terms gets significantly enhanced when propagated to the total rate, which makes difficult to set a meaningful bound on $\kappa _{ZZ}$ at this point. Moreover, the fit of Ref. [20] assumes SM-like differential spectra in $h\rightarrow 4\ell$, that is not necessarily a safe assumption in the presence of sizable contact terms. We will come back to the combined bounds on $\kappa _{ZZ}$ and the contact terms from the partial rates at the end of this section, after addressing the possible non-standard effects on the dilepton invariant-mass spectra.

The dependence of the partial widths, $\Gamma (h\rightarrow 4\ell )$, from all the PO but for $\kappa _{ZZ}$ is illustrated in Fig. 2. In the left plot we consider the general TGC case (no assumptions on $\lambda _Z$). As can be seen, $\mathcal {O}(1)$ variations on the rates are allowed because of the weak bounds on the contact terms (see Fig. 1 left). However, a tight correlation between $h\rightarrow 2e2\mu$ and $h\rightarrow 4e (4\mu )$ rates holds because of the flavor universality implied by LEP data under the hypothesis that h(125) belongs to a pure $\text {SU}(2)_L$ doublet. In the right plot we consider the $\lambda _Z=0$ case: in this limit the overall modifications are much reduced but still visible, while the correlation between $h\rightarrow 2e2\mu$ and $h\rightarrow 4e (4\mu )$ remains very strong, with possible deviations below any future realistic resolution.

Fig. 2

Predictions for $h\rightarrow 4e$ versus $h\rightarrow 2e2\mu$ decay rates implied by TGC constraints. Left $\lambda _Z\not =0$ case. Right $\lambda _Z=0$ case. The results obtained varying $\epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ only (via $\delta g_{1,z}$ and $\delta \kappa _\gamma$), according to Eq. (1) are shown in green ($68\,\%$ CL) and yellow ($95\,\%$ CL). The additional impact of varying $\epsilon _{Z\gamma }$ within its current limits is shown in dark ($68\,\%$ CL) and light gray ($95\,\%$ CL) in the right plot. In both plots we have set $\kappa _{ZZ}=1$

The different effect of the photon pole in the two channels, discussed in Ref. [23], manifests itself in Eq. (12) as a $\sim$ $25$ times larger interference term of $\epsilon _{\gamma \gamma }$ with $\kappa _{ZZ}$ in $h \rightarrow 4e(4\mu )$ vs. $h \rightarrow 2e2\mu$. However, we stress that this is a tiny effect on the partial rates (below $1\,\%$ with present cuts) once the LHC bound on $\epsilon _{\gamma \gamma }$ is taken into account. This is why this effect is not visible in Fig. 2. The smallness of this effect also implies that improving the bounds on $\epsilon _{\gamma \gamma }$ from $h\rightarrow 4e (4\mu )$ is extremely challenging, especially in the general case where the SM deviations from all the PO are considered at the same time.

The strict correlation between $h\rightarrow 2e2\mu$ and $h\rightarrow 4e (4\mu )$ rates represents a firm prediction of the linear EFT frameworks that is worth to test with future data: any violation of the correlation would not only imply the existence of NP, but would also imply that (i) NP does not respect lepton universality, (ii) the Higgs particle has a non-$\text {SU}(2)_L$ component.³

3.2 Single dilepton invariant-mass spectra

In addition to the partial widths, the rich kinematics of the $h\rightarrow 4\ell$ processes offers additional handles to probe the relevant pseudo-observables. Since the contact terms $\epsilon _{Ze_L,Ze_R}$ have the same Lorentz structure as the SM term, angular distributions are not modified and the only effect is on the differential distributions in the dilepton invariant masses. On the other hand, the other pseudo-observables, $\epsilon _{ZZ,Z\gamma ,\gamma \gamma }^{(\mathrm{CP})}$, modify also angular distributions and thus a complete study of the full kinematics of the events is necessary in order to extract them as efficiently as possible (see in particular Refs. [23–27] for a recent discussion). In this work we focus only on the invariant-mass distributions, both because the effect of the contact terms in $h\rightarrow 4\ell$ is the one less studied in the previous literature and because, as shown above, these PO are the less constrained at the moment (at least in the general TGC case).

Since the effects on the partial widths have already been discussed, here we focus on the shapes, i.e. the normalized differential distributions. To this purpose, we have sampled sets of PO inside the 68 and $95\,\%$ CL bounds, keeping into account their correlations. For each set we have determined the normalized dilepton invariant-mass spectrum and its ratio to the one obtained in the SM at tree level, and we have finally built the envelopes of such spectra.

In Fig. 3 we present the distributions for $h\rightarrow 2e2\mu$ and $h\rightarrow 4e (4\mu )$, setting $k_{ZZ} = 1$, $\epsilon _{ZZ,Z\gamma ,\gamma \gamma } = 0$ and letting vary $\epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ within their allowed bounds. As can be seen, although the effect of the contact terms on the total rate is very large, of $\mathcal {O}(100\,\%)$ in the $\lambda _Z \ne 0$ case, the difference in the shape with respect to the SM is much smaller, namely $\lesssim$ $15\,\%$ for $\lambda _Z \ne 0$. A similar cancellation is present also in the $\lambda _Z = 0$ case, although the relative effect is less pronounced. The cancellation of the non-standard effects in the normalized spectrum is, at least in part, a consequence of the strong positive correlation between $\epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ shown in Fig. 1. The same quantitative conclusion remains valid also after relaxing the bounds on the $\delta g^{Z\ell }$ couplings as discussed previously.

Fig. 3

Electron pair invariant mass spectrum with a 4 GeV binning for $h\rightarrow 2e2\mu$ (top row) and $h \rightarrow 4e$ (bottom row) decay obtained by varying $\epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ within the $68\,\%$ (green) and $95\,\%$ (yellow) CLs bound from TGC (Fig. 1) with $\lambda _Z$ generic in a, c, and $\lambda _Z=0$ in b, d. In the $h\rightarrow 4e$ channel we pair randomly two opposite-sign leptons

In Fig. 4 we study the effect of $\epsilon _{ZZ,Z\gamma ,\gamma \gamma }$ on the invariant-mass distribution. Here it is important to notice that the sensitivity to $\epsilon _{Z\gamma ,\gamma \gamma }$ depends strongly on the infrared cutoff imposed on the dilepton invariant masses, as expected due to the associated photon pole(s). As shown in Ref. [23], decreasing the cut on $m_{\ell \ell }$ from 12 to $4\text { GeV}$ substantially improves the sensitivity to these couplings, even excluding the $m_{\ell \ell }$ region around the $\Upsilon$ resonances. Moreover, as demonstrated in Ref. [28], the irreducible contribution of quarkonium resonances to the $h\rightarrow 4\ell$ spectrum is small and under good theoretical control.

Fig. 4

Single differential distributions in the electron pair invariant mass for $h\rightarrow 2e2\mu$ decay obtained by varying $\epsilon _{\gamma \gamma }$, $\epsilon _{Z\gamma }$ and $\epsilon _{ZZ}$ inside the $95\,\%$ CL bounds obtained from Eqs. (5) and (3) and setting $\epsilon _{Z\ell }=0$, $\kappa _{ZZ} = 1$. A lower cut on both lepton pair’s invariant masses of 4 GeV is applied. In the upper plot the differential rate is normalized to the total rate while in the lower one we take the ratio of this quantity to the one obtained in the SM at the tree level

For these reasons, we show the differential decay rate in Fig. 4 with a $m_{\ell \ell }^\mathrm{min}=\mathrm{4~GeV}$ cut. One observes that also in this case the effect of the pseudo-observables $\epsilon _{ZZ,Z\gamma ,\gamma \gamma }$ on the shape is at most of $\mathcal {O}(10\,\%)$, except for the low $m_{\ell \ell }$ region, where the sensitivity is significantly enhanced. We further stress that lowering the infrared cut on both dilepton invariant masses also leads to an enhancement of the rate in the 30–80$\text { GeV}$ region, since then the other lepton pair is allowed to be near the photon pole.

Finally, in Fig. 5 we show the same plots letting vary all five Higgs PO in Eq. (6) within their allowed range. We also impose the total rate to be within $30\,\%$ of the SM value, as obtained in the global fit of Ref. [20], analyzing the impact of a 50 % variation in the remaining pseudo-observable $\kappa _{ZZ}$ from its SM value. By construction, this figure summarise the room for non-standard effects in the $h\rightarrow 4\ell$ shape within the linear EFT scenario.

Fig. 5

Single differential distributions in the electron pair invariant mass for the $h\rightarrow 2e2\mu$ decay obtained by varying $\epsilon _{\gamma \gamma ,Z\gamma ,{ZZ}}, \epsilon _{Z e_L}$ and $\epsilon _{Z e_R}$ within the $95\,\%$ CL limits from Eqs. (5–7) in the $\lambda _Z \ne 0$ (left) and $\lambda _Z = 0$ (right) case. The blue shaded regions are obtained for $k_{ZZ} = 1$ while the red ones are obtained using $k_{ZZ} \in [0.5, 1.5]$. In both cases we impose that the total rate, computed with a $12\text { GeV}$ infrared cut on $m_{\ell \ell }$, as in Eq. (14), is within $30\,\%$ of the SM one

The difference between Fig. 5 (left) and (right) could be used, in the future, to indirectly improve the current bounds on $\lambda _Z$. Notice that $\kappa _{ZZ}$ has a negligible impact on the normalized shape in Fig. 5 (right). This is because varying $\kappa _{ZZ}$ corresponds to an overall rescaling of the amplitude assuming a SM-like kinematical dependence, and thus this effect cancels at linear order (in $\delta$PO$_i$). In the $\lambda _Z \not =0$ case a residual effect survives because of quadratic corrections; in the $\lambda _Z = 0$ case all the PO are constrained to be close to their SM values and the effect vanishes, as expected by a consistent EFT expansion.

3.3 The $\kappa _{ZZ}$ vs. $\epsilon _{Z\ell }$ bound from $\Gamma (h\rightarrow 4 \ell )$

From the above discussion we conclude that, even when sizable modifications in the rates occurs, namely in the $\lambda _Z \ne 0$ case, the $h\rightarrow 4\ell$ spectrum remains SM like compared to the present level of experimental precision. As a result, the only useful bound on the PO that can be set at present from $h\rightarrow 4\ell$ data, within the linear EFT framework, is the one following from the partial decay rates. We also learned that, given the existing constraints on the PO, the structure of Eq. (14), and the present level of precision on $\Gamma (h\rightarrow 4\ell )$, this bound is an effective constraint on $\kappa _{ZZ}$ vs. $\epsilon _{Z e_L}$, fixing $\epsilon _{Z e_R} = 0.48 \times \epsilon _{Z e_L}$, as implied by Fig. 1.

A detailed extraction of such bound would require a re-analysis of $h \rightarrow 4 \ell$ data. However, a good approximation can be obtained as follows: we assume the combined result on $\Gamma (h\rightarrow 4\ell )/\Gamma _\mathrm{SM}$ by ATLAS [20] and CMS [22] to be $\mu _{ZZ} = 1.2 \pm 0.2$. Using this constraint and setting $\epsilon _{Z e_R}=0.48\times \epsilon _{Z e_L}$ leads to the result in Fig. 6 (left). Assuming the same constraint on $\Gamma (h\rightarrow 4\ell )/\Gamma _\mathrm{SM}$, setting $\lambda _Z=0$, and allowing all the PO to vary according to Eqs. (5–7), leads to the result shown in Fig. 6 (right). We note that this procedure neglects non-standard effects in $\mu _{ZZ}$ from production and Higgs width, which can be taken into account in a combined re-analysis of Higgs data. In fact, the number chosen here is compatible with a global fit extraction of $\kappa _Z^2 \sim \Gamma (h\rightarrow 4\ell )/\Gamma _\mathrm{SM}$, see for instance Ref. [20].

Fig. 6

Bounds on $\kappa _{ZZ}$ vs. $\epsilon _{Ze_L}$ from the combined ATLAS [20] and CMS [22] $h\rightarrow 4\ell$ signal strength measurements ($\mu _{ZZ}=1.2\pm 0.2$). Left $68\,\%$ (dark gray) and $95\, \%$ (light gray) CL bounds valid in the $\lambda _Z\not =0$ case, setting $\epsilon _{Ze_R} = 0.48 \times \epsilon _{Ze_L}$; the $68\,\%$ (yellow) and $95 \,\%$ (green) CL TGC bounds on $\epsilon _{Ze_L}$ are also shown. Right the combined fit of TGC and Higgs data assuming $\lambda _Z=0$, and marginalising over $\epsilon _{Ze_R}$, $\epsilon _{ZZ}$ and $\epsilon _{Z\gamma }$, is shown in red ($68\,\%$ CL) and orange ($95 \,\%$ CL). As an illustration, we show in grey the constraint from $\mu _{ZZ}$ measurement only setting $\epsilon _{Ze_R}$, $\epsilon _{ZZ}$ and $\epsilon _{Z\gamma }$ to 0

4 Conclusions

In this paper we have presented a systematic evaluation of the bounds on the Higgs PO that follow from the EW constraints in the linear EFT regime, with particular attention to the PO appearing in $h\rightarrow 4\ell$ and $h\rightarrow 2\ell 2\nu$ decays. Using such bounds we have derived a series of predictions for $h\rightarrow 4\ell$ decay rates and differential distributions. A dedicated analysis of the $h\rightarrow 2\ell 2\nu$ modes will be presented in a separate publication.

The results of the EW bounds are summarized in Fig. 1 and Eqs. (6) and (7). We find that, because of the flat direction in TGC bounds ($\lambda _Z \simeq - \delta g_{1,z}$ unconstrained), EW plus Higgs data leave open the room for sizable $h\rightarrow 4\ell$ contact terms ($\epsilon _{Z\ell }$), provided they are flavor universal and with the specific L–R alignment shown in Fig. 1 (left). In principle, $h\rightarrow 4\ell$ data can be used to remove the degeneracy in the EFT parameter space implied by the TGC flat direction; however, the present level of precision is not good enough. As a result, the uncertainty on the contact terms reflects into a poor knowledge of $\kappa _{ZZ}$, as shown in Fig. 6 (left). If the TGC direction is closed (by model-dependent dynamical considerations suggesting $\lambda _Z=0$), the contact terms are bounded at the few percent level, as shown in Fig. 1 (right), and have a minor impact in the determination of $\kappa _{ZZ}$, as shown in Fig. 6 (right).

The phenomenological implications for $h\rightarrow 4\ell$ decays of the EW bounds on the Higgs PO are summarized in Figs. 2, 3 and 4. On the one hand, the uncertainty of the predictions thus obtained determine the level of precision necessary, in future $h\rightarrow 4\ell$ analyses, to improve our constraints on the Higgs linear EFT. In this respect, we confirm the conclusion of Refs. [6, 27] that shape-modifications in $h\rightarrow 4\ell$ are significantly constrained in the linear EFT regime, although we find that deviations from the SM as large as $10\,\%$ ($20\,\%$) are still possible for $\lambda _Z=0$ ($\lambda _Z\not =0$). These predictions are robust under relaxation of LEP-I bounds to the $\sim 1\%$ level.

On the other hand, these predictions can be interpreted as a series of tests that, if falsified by future $h\rightarrow 4\ell$ data, would allow us not only to establish the existence of NP but also to exclude that h is the massive excitation of a pure $\text {SU}(2)_L$ doublet. In this respect, we stress the firm prediction on the lepton-flavor universality ratios in Fig. 2, and the bounds on the normalized dilepton invariant-mass spectrum in Fig. 5.

Appendix: Higgs PO, TGC, and the Higgs basis

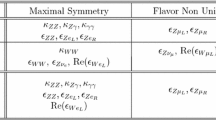
A dimension-6 operator basis particularly useful to implement experimental constraints on the EFT, at tree-level accuracy, is the so-called Higgs basis, developed by the Higgs cross section LHC Working Group [11]. This basis has been developed following a similar logic to the so-called ”BSM primaries” approach of Refs. [8, 9] (see also Ref. [13]): the coefficients are specifically built to be directly related to the observables which provide the best constraints on the EFT. This basis is defined from an effective Lagrangian describing interactions between mass eigenstates fields with canonical kinetic terms, in the unitary gauge. For the list of the independent couplings and their definition we refer to Ref. [11]. The Z and W couplings are defined from the Lagrangian

$$\begin{aligned}&\mathcal L^{d=6}_{Zff} = \sum _{f} \sqrt{g^2 + g^{\prime 2}} Z^\mu \bar{f} \delta g^{Zf} \gamma _\mu f , \\&\mathcal L^{d=6}_{Wff'} = \frac{g}{\sqrt{2}} W^+_\mu \bar{\nu }_L \gamma ^\mu \delta g^{W\ell } e_L \nonumber \\&\quad + \frac{g}{\sqrt{2}} ( W^+_\mu \bar{u}_L \gamma ^\mu \delta g^{W q_L} V_\mathrm{CKM} d_L + W^+_\mu \bar{u}_R \gamma ^\mu \delta g^{W q_R} d_R ), \nonumber \end{aligned}$$

(A.1)

where $f = e_{L,R},\nu ,u_{L,R},d_{L,R}$ and fermion fields all have an implicit flavor index. For our purposes it is worth stressing that the fermion couplings to Z and W bosons are chosen as independent couplings in this basis. Only the Z couplings to neutrinos and the W couplings to left-handed quarks are dependent of the others:

$$\begin{aligned} \delta g^{Z \nu } = \delta g^{Z e_L} + \delta g^{W \ell }, \quad \delta g^{W q_L} = \delta g^{Z u_L} - \delta g^{Z d_L}. \end{aligned}$$

(A.2)

This implies that, at tree-level, SLD and LEP-I pseudo-observables from the Z-pole and from W decays can be directly related to these couplings. In particular deviations in the Z couplings can be constrained at the per-mil level while deviations in the W couplings only at the percent level [13].

The tree-level matching between the Higgs pseudo-observables of Ref. [1] and the EFT coefficients in the Higgs basis is

$$\begin{aligned}&\kappa _{ZZ} = 1 + \delta c_z + g^2 c_{z \Box },\nonumber \\&\kappa _{WW}= 1 + \delta c_w + g^2 c_{w \Box },\nonumber \\&\epsilon _{Zf} =\frac{2 m_Z}{v} \left( \delta g^{Zf} + \frac{g^2}{2} (T_3^f - Q_f s_\theta ^2) c_{z \Box } + \frac{e^2 Q_f}{2} c_{\gamma \Box } \right) ,\nonumber \\&\epsilon _{Wf} = \frac{\sqrt{2} m_W}{v} \left( \delta g^{Wf} + \frac{g^2}{2} c_{w \Box } \right) ,\nonumber \\&\epsilon _{ZZ} = \epsilon _{ZZ}^\mathrm{SM-1L} - \frac{g^2 + g^{\prime 2}}{2} c_{ZZ}, \\&\epsilon _{Z\gamma } = \epsilon _{Z\gamma }^\mathrm{SM-1L} - \frac{g g^{\prime }}{2} c_{z\gamma } ,\nonumber \\&\epsilon _{\gamma \gamma } = \epsilon _{\gamma \gamma }^\mathrm{SM-1L} - \frac{e^2}{2} c_{\gamma \gamma } ,\nonumber \\&\epsilon _{WW} = \epsilon _{WW}^\mathrm{SM-1L} - \frac{g^2}{2} c_{ww} , \nonumber \end{aligned}$$

(A.3)

where the dependent couplings $\delta c_w, c_{ww}, c_{w\Box }, c_{\gamma \Box }$ are given, in terms of the independent ones, by [11]

$$\begin{aligned}&\delta c_w = \delta c_z + 4 \delta m, \nonumber \\&c_{ww} = c_{ZZ} + 2 s_\theta ^2 c_{z\gamma } + s_\theta ^4 c_{\gamma \gamma }, \\&c_{w \Box }= \frac{1}{g^2 - g^{\prime 2}}\nonumber \\&\quad \times \left[ g^2 c_{z\Box } + g^{\prime 2} c_{ZZ} - e^2 s_\theta ^2 c_{\gamma \gamma } - (g^2 - g^{\prime 2} ) s_\theta ^2 c_{z\gamma } \right] ,\nonumber \\&c_{\gamma \Box } = \frac{1}{g^2 - g^{\prime 2}} \nonumber \\&\quad \times \left[ 2 g^2 c_{z\Box } + (g^2 + g^{\prime 2}) c_{ZZ} - e^2 c_{\gamma \gamma } - (g^2 - g^{\prime 2} ) c_{z\gamma } \right] . \nonumber \end{aligned}$$

(A.4)

We stress here that the choice of keeping $c_{z\Box }$ as an independent coupling instead of $\delta c_w$ implies that the pseudo-observables $\kappa _{ZZ}$ and $\kappa _{WW}$ are not in one-to-one correspondence with the $\delta c_z$ and $\delta c_w$ couplings, and also the contact terms $\epsilon _{Vf}$ are not in one-to-one correspondence with the $c^{Vf}$ coefficients defined in Ref. [11]. Even though this choice is not optimal for our purposes, the relations between observables presented in Sect. 2 are of course independent on this basis choice.

The CP-conserving anomalous TGC are defined by the Lagrangian

$$\begin{aligned} \mathcal L^\mathrm{TGC}= & {} i e \delta \kappa _\gamma A_{\mu \nu } W^{+\mu } W^{- \nu } + i g c_\theta \delta \kappa _z Z^{\mu \nu } W^+_\mu W^-_\nu \nonumber \\&+ i g c_\theta \delta g_{1,z} (W^+_{\mu \nu } W^{-\mu } - W^-_{\mu \nu } W^{+\mu })Z^\nu \nonumber \\&+ i \frac{g c_\theta }{m_W^2} \lambda _{Z} W^+_{\mu \nu } W^{-\nu \rho } Z_\rho ^\mu + i \frac{e}{m_W^2} \lambda _{\gamma } W^+_{\mu \nu } W^{-\nu \rho } A_\rho ^\mu . \nonumber \\ \end{aligned}$$

(A.5)

In general, at dimension-6 in the linear EFT, $\delta \kappa _z = \delta g_{1,z} - t_\theta ^2 \delta \kappa _\gamma$ and $\lambda _\gamma = \lambda _Z$. Moreover, in this basis also $\delta g_{1,z}$ and $\delta \kappa _\gamma$ are dependent couplings:

$$\begin{aligned} \delta g_{1,z}= & {} \frac{1}{2(g^2 - g^{\prime 2})} \left[ - g^2 (g^2 + g^{\prime 2}) c_{z\Box } - g^{\prime 2} (g^2 \right. \nonumber \\&+ g^{\prime 2}) c_{ZZ} + \left. e^2 g^{\prime 2} c_{\gamma \gamma } +g^{\prime 2} (g^2 - g^{\prime 2} ) c_{z\gamma } \right] , \\ \delta \kappa _\gamma= & {} - \frac{g^2}{2} \left( c_{\gamma \gamma } \frac{e^2}{g^2 + g^{\prime 2}} + c_{z\gamma } \frac{g^2 - g^{\prime 2}}{g^2 + g^{\prime 2}} - c_{ZZ} \right) , \nonumber \end{aligned}$$

(A.6)

while only $\lambda _Z$ is an independent coupling. Since we are interested in studying the constraints from TGC on Higgs observables it is convenient for us to exchange the two independent Higgs couplings $c_{z\Box }$ and $c_{ZZ}$ in favour of these TGC using Eq. (A.6). By doing so and substituting the result in Eq. (A.3) we obtain the relations of Sect. 2. We also checked independently those relations by employing a basis of manifestly $\text {SU}(2)_L\times {U}(1)_Y$ invariant operators.

Once the per-mil constraints from LEP-1 measurements have been imposed, the TGC can be constrained from a fit to LEP-2 data on $\sigma (e^+e^-\rightarrow WW)$ and single W production. We use the results of the fit performed in Ref. [10]:

$$\begin{aligned} \left( \begin{array}{c} \delta g_{1Z} \\ \delta \kappa _{\gamma } \\ \lambda _Z \end{array}\right)= & {} \left( \begin{array}{c} -0.83 \pm 0.34 \\ 0.14 \pm 0.05 \\ 0.86 \pm 0.38 \end{array}\right) , \nonumber \\&\rho = \left( \begin{array}{ccc} 1 &{} - 0.71 &{} -0.997 \\ . &{} 1 &{} 0.69 \\ . &{} . &{} 1 \end{array}\right) . \end{aligned}$$

(A.7)

The large allowed range for $\delta g_{1,z}$ and $\lambda _Z$ is due to an approximately blind direction in LEP-2 WW data corresponding to $\lambda _Z \approx - \delta g_{1,z}$ [17]. This implies a very loose bound on $\delta g_{1,z}$ upon marginalizing on $\lambda _Z$. Since in a wide class of explicit ultraviolet completions of the linear EFT $\lambda _Z$ is expected to be loop suppressed compared to $\delta g_{1,z}$ and $\delta \kappa _\gamma$, it is worth considering explicitly the case $\lambda _Z = 0$. In this limit the bound on $\delta g_{1,z}$ is much stronger:

$$\begin{aligned} \left( \begin{array}{c} \delta g_{1Z} \\ \delta \kappa _{\gamma } \\ \end{array}\right) = \left( \begin{array}{c} -0.06 \pm 0.03 \\ 0.06 \pm 0.04 \end{array}\right) , \quad \rho = \left( \begin{array}{cc} 1 &{} - 0.5 \\ . &{} 1 \end{array}\right) . \end{aligned}$$

(A.8)

The W couplings to electron and muon are constrained at the percent level. We use the results from the non-universal fit of Ref. [13]:

$$\begin{aligned} \left( \begin{array}{c} \delta g^{We} \\ \delta g^{W\mu } \\ \delta g^{W\tau } \end{array}\right)&= \left( \begin{array}{c} -1.00 \pm 0.64 \\ -1.36 \pm 0.59 \\ 1.95 \pm 0.79 \end{array}\right) \times 10^{-2}, \nonumber \\ \rho&= \left( \begin{array}{ccc} 1 &{} - 0.12 &{} -0.63 \\ . &{} 1 &{} -0.56 \\ . &{} . &{} 1 \end{array}\right) . \end{aligned}$$

(A.9)

These bounds can be used to constrain at the percent level the Z couplings to neutrinos, using Eq. (A.2).